CAPÍTULO 4 - PREVENDO RESULTADOS USANDO REGRESSÃO LINEAR
Alice Gallindo, Aristides Olivieri, Débora Myrlan, Gabriela Ivo, Guilherme Gusmão, Sylas Freitas
March 07, 2022
CAPÍTULO 4 - PREVENDO RESULTADOS USANDO REGRESSÃO LINEAR
Neste capítulo aprenderemos um processo conhecido como regressão linear. Esse processo consiste em como resumir com uma linha a relação entre a variável de resultado de interesse e outra variável chamada preditor. Como ilustração, analisamos dados de 170 países para prever o crescimento do PIB com base nas mudanças na emissão de luz noturna.
4.1 - PIB e emissões de luz noturna
PIB é um índice que mede a atividade econômica de um país;
Refere-se ao valor monetário produzido de bens e serviços em um determinado período de tempo específico;
Cientistas sociais notaram que mudanças nas emissões de luz à noite altamente correlacionadas com a atividade econômica.
4.2 - Preditores, observados contra resultados previstos, e erros de previsão
Algumas vezes nas ciências sociais não conseguimos observar o valor de uma determinada variável de interesse, Y, ou porque não ocorreu ou porque é difícil de medir.
Nessas situações observamos os valores de outras variáveis que, se correlacionadas com Y, podem ser usadas para predizer Y.
Por exemplo, se estamos interessados em prever o PIB usando o PIB anterior, então o PIB é a variável de resultado e o PIB anterior é o preditor.
4.2 - Preditores, observados contra resultados previstos, e erros de previsão
Para fazer boas previsões, escolhemos preditores altamente correlacionados com a variável de resultado de interesse.
A correlação não implica necessariamente em causação.
Fazer previsões é um processo de duas etapas: (i) Ajuste de modelo; (i) Usamos o modelo ajustado para prever valores médios específicos da variável
4.3 - Resumindo a relação entre duas variáveis com uma linha
Sempre resumimos a relação entre X e Y com uma linha e, em particular, a linha de melhor ajuste.
Cada ponto representa uma observação específica de X e Y.
4.3 - Resumindo a relação entre duas variáveis com uma linha
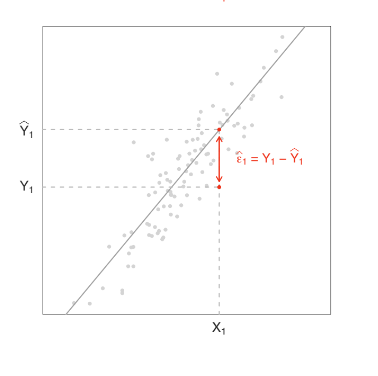
4.3.1 - O modelo linear
O modelo linear, também conhecido por regressão linear, pode ser representado através da fórmula:

- Yi é o resultado da observação,
- alpha é a interceptação do coeficiente,
- beta é a inclinação,
- Xi é o valor de projeção de Yi,
- “sub i” é o erro de i.
4.3.2 - O coeficiente de intercepção
De um modo geral, a intercepção de uma linha especifica a localização vertical da linha. Veja, por exemplo, as linhas que têm diferentes interceptações, mas a mesma inclinação, aumentar e diminuir a interceptação move a linha para cima e para baixo, respectivamente.
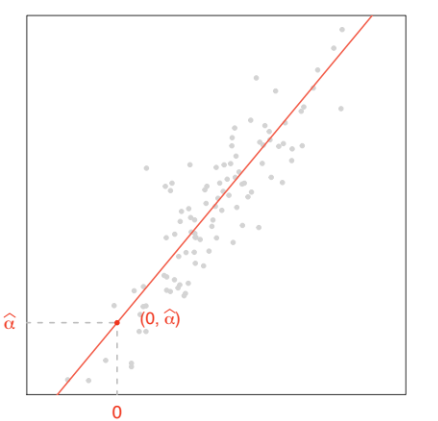
4.3.3 - O coeficiente de inclinação
Podemos Interpretar o valor da inclinação como a diferença da elevação relacionado à uma unidade da declinação, isto é, a cada aumento na linha elevação, diferencia-se 1 unidade da linha de declínio, sendo o valor da inclinação, igual à variação da elevação (quando ΔX = 1)

4.3.3 - O coeficiente de inclinação
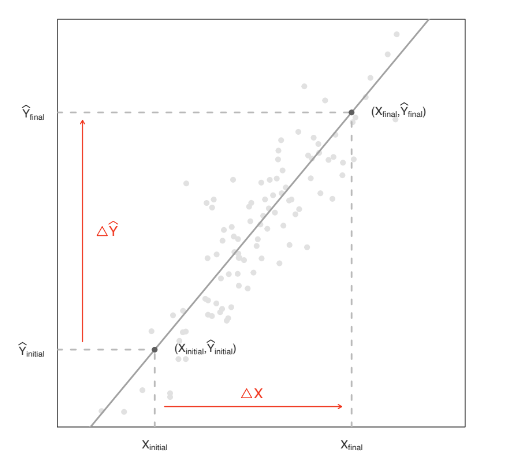
Pontos importantes para interpretação do gráfico: Considera-se um elevado quando se mostra positiva; Considera-se um declínio quando se mostra negativo; Quando é zero (0), não há alteração.
4.4. Prevendo o PIB utilizando o PIB anterior (predicting GDP using prior GDP)
- Lendo o banco de dados (data), Observações da tabela e numero total de observações
## country gdp prior_gdp light prior_light
## 1 USA 11.106793 7.3734457 4.227017 4.4821710
## 2 Japan 543.016934 464.1676591 11.925918 11.8079539
## 3 Germany 2.152312 1.7925027 10.573267 9.6994249
## 4 China 16.558167 4.9006940 1.451034 0.7350175
## 5 UK 1.098384 0.7537479 11.855543 13.3919541
## 6 France 1.582367 1.2079045 8.512996 6.9090375## [1] 170 5Com base na tabela, vemos:
- “country” é uma variável de caracteres que identifica o país.
- “gdp e prior_gdp” é o PIB de cada país em dois diferentes pontos no tempo, com 13 anos de intervalo, de 2005 a 2006 e de 1992 a 1993, respectivamente.
- “light e prior_light” são as médias noturnas de cada país emissões de luz a dois diff diferentes pontos no tempo, com 13 anos de diferença, de 2005 a 2006 e de 1992 a 1993, respectivamente.
- Conclusão: No EUA o PIB foi de US$ 11 trilhões de 2005 á 2006 e U$ 7 trilhões de 1992 à 1993, e as emissões médias de luz noturna foram de 4,2 unidades de 2005 a 2006 e 4,5 unidades de 1992 a 1993.
4.5 Prevendo o crescimento do PIB usando emissão de luzes noturnas
- A análise começa criando duas variáveis que serão relacionadas. Nesse modelo, a primeira informação relevante é a porcentagem de mudança no PIB entre dois pontos diferentes, que é definido por:

No R
A mudança de porcentagem da emissão de luz noturna no mesmo período de tempo, sendo definida por:

- A partir desse gráfico é possível interpretar essas duas variáveis e entender como elas se relacionam. Como esperado, percebe-se que em países com maior crescimento nos valores de emissão de luz noturna tendem a apresentar um maior crescimento do PIB.
## [1] 0.4577672- Agora, para prever o crescimento do PIB utilizando a mudança na emissão de luzes noturnas, temos:
Mudanca_PIB i = α + β mudanca_luz i (i = país)
- Estima-se que coeficientes sejam α = 49.82 e β = 0.25
##
## Call:
## lm(formula = gdp_change ~ light_change, data = co)
##
## Coefficients:
## (Intercept) light_change
## 49.8202 0.2546-A partir disso podemos usar esse modelo para fazer previsões. Para saber saber o crescimento do PIB de um país durante o período de 13 anos e observamos que a emissão de luz cresceu em 20%.
mudanca_PIB = 49.82 + 0.25xmudanca_luz = 49.82 + 0.25 × 20 = 54.82
Conclui-se, portanto, que o crescimento médio do PIB de tal país foi cerca de 55% durante o período de 13 anos.
4.6 - Medindo o quanto o modelo é compatível com a informação (data) e com o coeficiente de determinação ou R²
- Quando usamos um modelo para fazer previsões, nós queremos saber o quão bem um modelo é compatível e “se encaixa” com as informações, pois uma relação fraca pode gerar resultados imprecisos. Para isso, utilizamos um conceito estatístico chamado coeficiente de determinação ou R². O valor de R² varia de 0 a 1 e representa a proporção da variação de Y em um dado modelo.
4.6 - Medindo o quanto o modelo é compatível com a informação (data) e com o coeficiente de determinação ou R²
- Por exemplo, nós interpretamos um R² de 0.8 indicando que aquele modelo demonstra 80% de variação de Y (0.8×100 = 80%). Portanto, quanto maior for o R², mais compatível é o modelo com as informações (data).
- Dada a definição de R², fica claro que quanto maior for a correlação entre X e Y (em termos absolutos), mais compatível é o modelo com as informações.
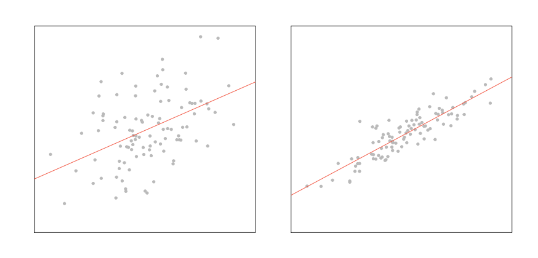
Na situação extrema, quando a relação entre X e Y é perfeitamente linear (a correlação entre X e Y é igual ou a 1 ou -1), o modelo demonstra 100% da variação de Y (R² =1).
4.7 - Resumo
Esse capítulo nos introduz ao modelo de regressão linear para fazer previsões. Aprendemos como criar uma linha para definir a relação entre uma variável preditora e uma variável resultante (predictor and outcome variable). Depois, aprendemos como usar a linha para prever a média de uma variável resultante dado o valor do preditor e também prever a variação média da resultante associada à mudança de valor do preditor. Também aprendemos sobre previsão de erros, a diferença entre resultados observados e previstos e como interpretar dois coeficientes de uma linha: a interseção e a inclinação. Concluiu-se o capítulo com a exposição de como calcular e interpretar o R².