4 Probability
4.1 Probability axioms
The mathematical principles of probability as a function assigning numerical values to events can be expressed through a few axioms. A formal description can be found, for example, here.
In simplified terms, the axioms can be formulated as follows:
1. The probability of any event A is non-negative.
\[\begin{equation} \mathbb{P}(A) \ge 0 \tag{4.1} \end{equation}\]
2. If events A and B are mutually exclusive (disjoint), then the probability of their union equals the sum of the probabilities:
\[\begin{equation} \mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) \tag{4.2} \end{equation}\]
3. The probability of the sample space (the event that is certain) \(\Omega\) is 1.
\[\begin{equation} \mathbb{P}(\Omega) = 1 \tag{4.3} \end{equation}\]
4.2 Probability interpretations:
1. Classical probability
If we have a finite number of equally probable elementary events, then the probability of event A is the share of elementary events favorable to event A in the total number of elementary events.
2. Frequentist interpretation of probability
The probability of an event is "the relative frequency of its occurrence found after repeating the process a great number of times under similar conditions" (von Mises).
Visualization for tossing a perfect coin: https://seeing-theory.brown.edu/basic-probability/index.html
3. Subjective interpretation of probability
According to this interpretation, probability is a measure of the certainty that can be attributed to individual events.
4.3 Events – basic concepts
4.3.2 Compound event
A compound event is a set consisting of (not necessarily all) elementary events. Elementary events that make up a compound event are elementary events favorable to the compound event.
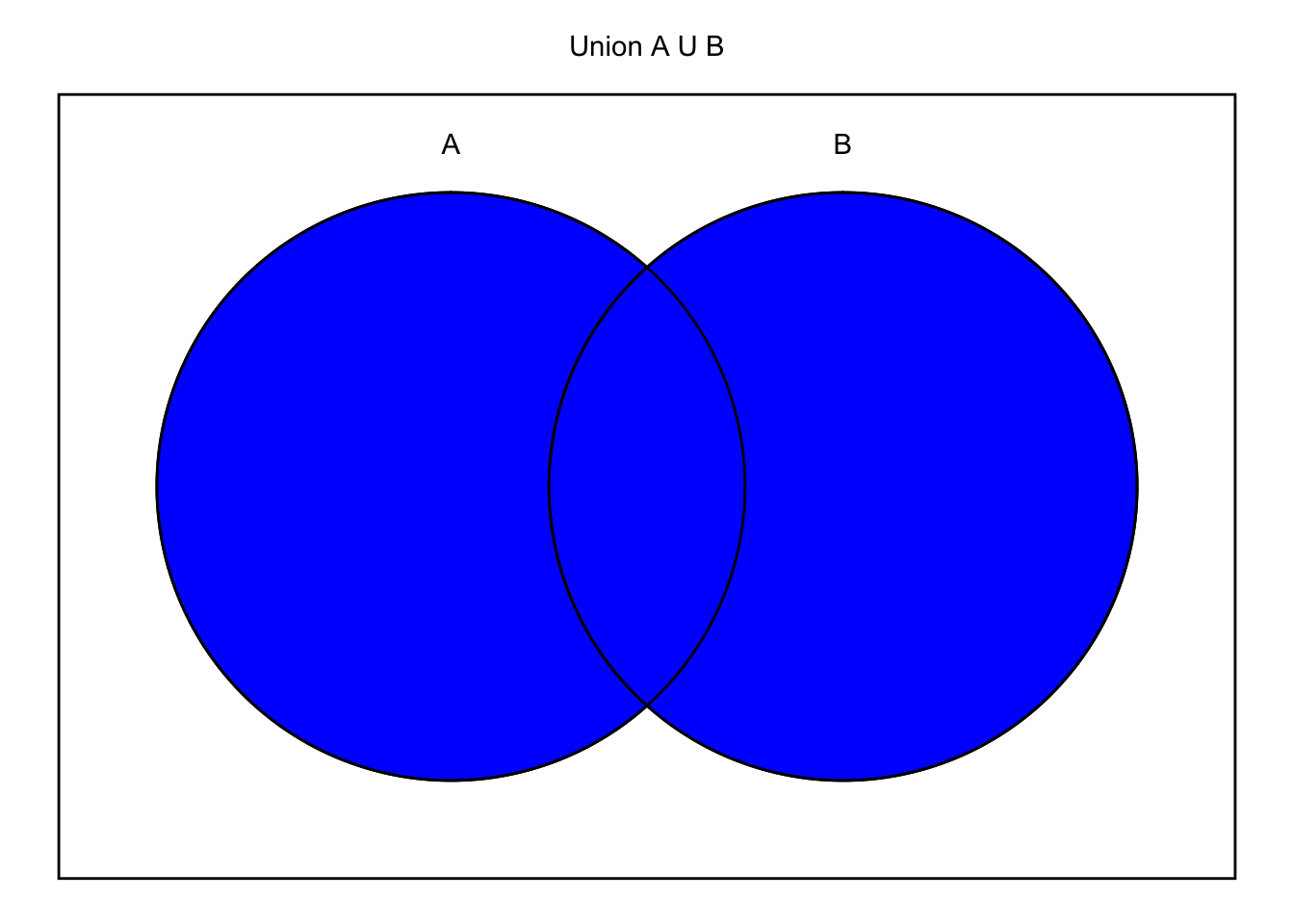
4.3.4 Union of events
The union of events “A or B” represents the occurrence of either event A, event B, or both. To avoid misunderstandings, it is important to note that the union also includes the intersection (the "overlap") between the two events.
The union of events A and B can be written as \(A \cup B\) and read “A or B”, “A union B”. In some textbooks, the union of events is written as \(A + B\).
4.3.5 Intersection of events
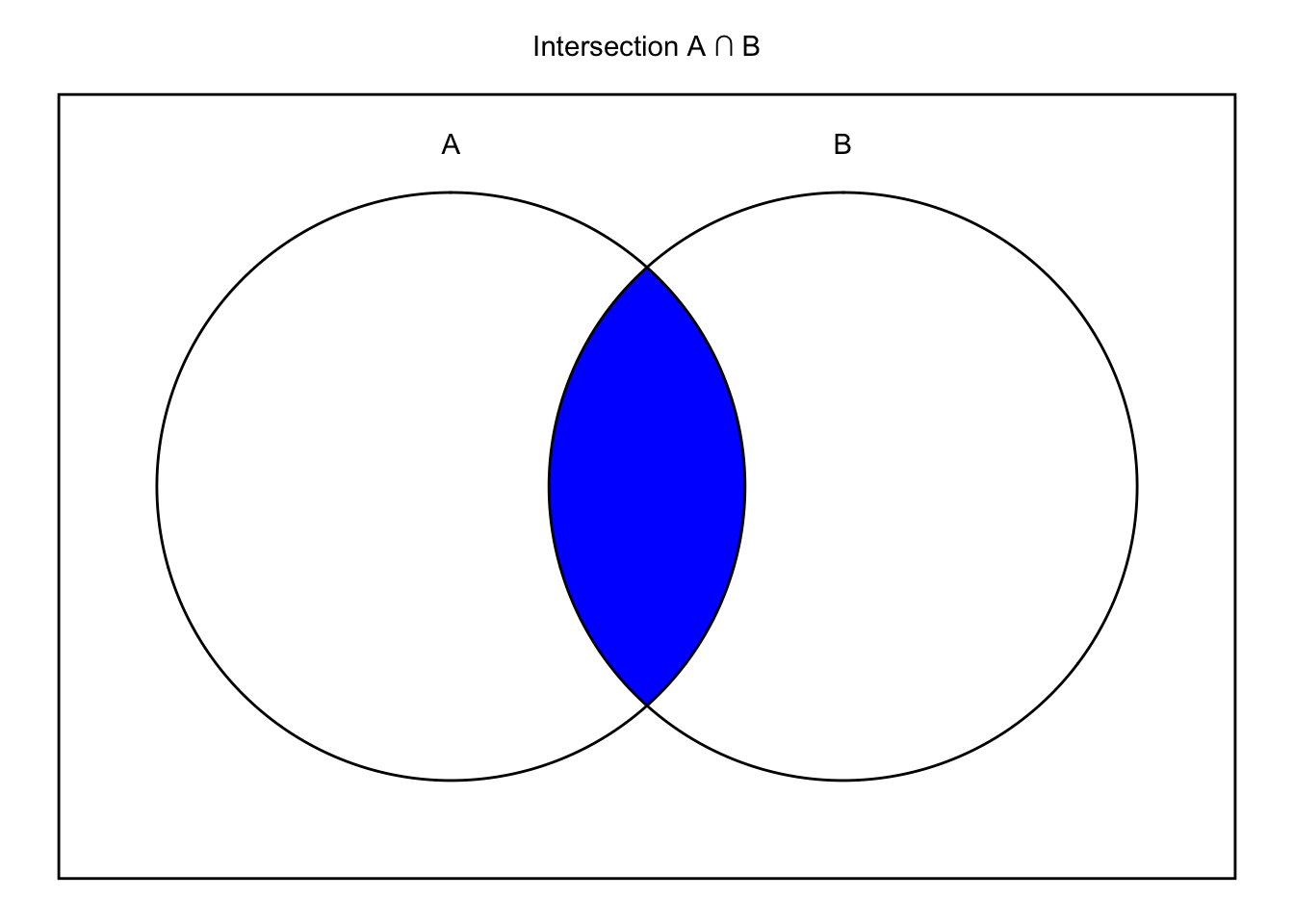
Intersection refers to the occurrence of both event A and event B.
The intersection of events A and B is denoted as \(A \cap B\) and read as “A and B”, “A intersect B”, , “A intersection B”. In some textbooks, the intersection is written as \(AB\) by analogy with the product notation.
4.3.6 Complementary event
The complementary event of event \(A\) is “not \(A\)”. We denote the complement using the symbol “\({}^C\)”. Other common notations used in textbooks include \(A'\), \(\bar{A}\), or \(\neg A\).

4.3.7 Conditional probability
Conditional probability is the probability of an event occurring given or assuming that another event occurs.
The formula (asuming non-zero \(\mathbb{P}(B)\)) is the following:
\[\begin{equation} \mathbb{P}(A|B) = \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)} \tag{4.4} \end{equation}\]
Conditional probability – visualisation
4.3.8 Mutually exclusive (disjoint) events
Events A and B are mutually exclusive if they have no common outcomes (i.e., no elementary event favors both A and B simulataneously). In other words, the intersection of A and B is an impossible event (an empty set).
\[\begin{equation} \mathbb{P}(A\cap B) = \mathbb{P}(\emptyset) = 0 \tag{4.5} \end{equation}\]
4.3.9 Independent events
Events A and B are independent if the probability of their intersection equals the product of their individual probabilities:
\[\begin{equation} \mathbb{P}(A\cap B) = \mathbb{P}(A)\mathbb{P}(B) \tag{4.6} \end{equation}\]
If A and B are independent, then knowing or assuming that event A has occurred does not affect the probability of B, and vice versa:
\[\begin{equation} \mathbb{P}(B|A) = \mathbb{P}(B) \tag{4.7} \end{equation}\]
\[\begin{equation} \mathbb{P}(A|B) = \mathbb{P}(A) \tag{4.8} \end{equation}\]
Events that are not independent are called dependent events.
4.4 Probability – basic rules
It is worth exploring visualization 1 and visualization 2, which allow verification of some of the rules below.
4.4.1 Complement rule
The sum of the probabilities of complementary events (event \(A\) and its complement \(A^C\)) is always 1.
\[\begin{equation} \mathbb{P}(A) + \mathbb{P}(A^C) = 1 \tag{4.9} \end{equation}\]
4.4.2 Addition Rule
The probability of the union of two events equals the sum of their probabilities minus the probability of their intersection.
\[\begin{equation} \mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) - \mathbb{P}(A \cap B) \tag{4.10} \end{equation}\]
Of course, if events A and B are mutually exclusive, this formula simplifies. In such a case, the probability of the union of events is simply the sum of their probabilities:
\[\begin{equation} \mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) \tag{4.11} \end{equation}\]
Equations (4.10) and (4.11) refer to two events. The formulas for three events can be found in section A.
4.4.3 Multiplication rule
The probability of the intersection of events A and B is equal to the product of the probability of event A and the conditional probability of event B given A.
\[\begin{equation} \mathbb{P}(A \cap B) = \mathbb{P}(A) \mathbb{P}(B|A) \tag{4.12} \end{equation}\]
or
\[\begin{equation} \mathbb{P}(A \cap B) = \mathbb{P}(B) \mathbb{P}(A|B) \tag{4.13} \end{equation}\]
These formulas simplify for independent events (see formula (4.6)).
Analogous formulas for three events can be found in section A.
4.5 Exercises
Exercise 4.1 Suppose we toss two coins and observe the outcomes (heads/tails).
List all elementary events of this experiment.
Assign probabilities to each elementary event. (Are all elementary events equally probable?)
Let A be the event that exactly one head appears, and let B be the event that at least one head appears. List all elementary events for A and B.
Based on your answer to (c), find \(\mathbb{P}(A)\), \(\mathbb{P}(B)\), \(\mathbb{P}(A \cap B)\), \(\mathbb{P}(A \cup B)\), \(\mathbb{P}(A^C \cup B)\).
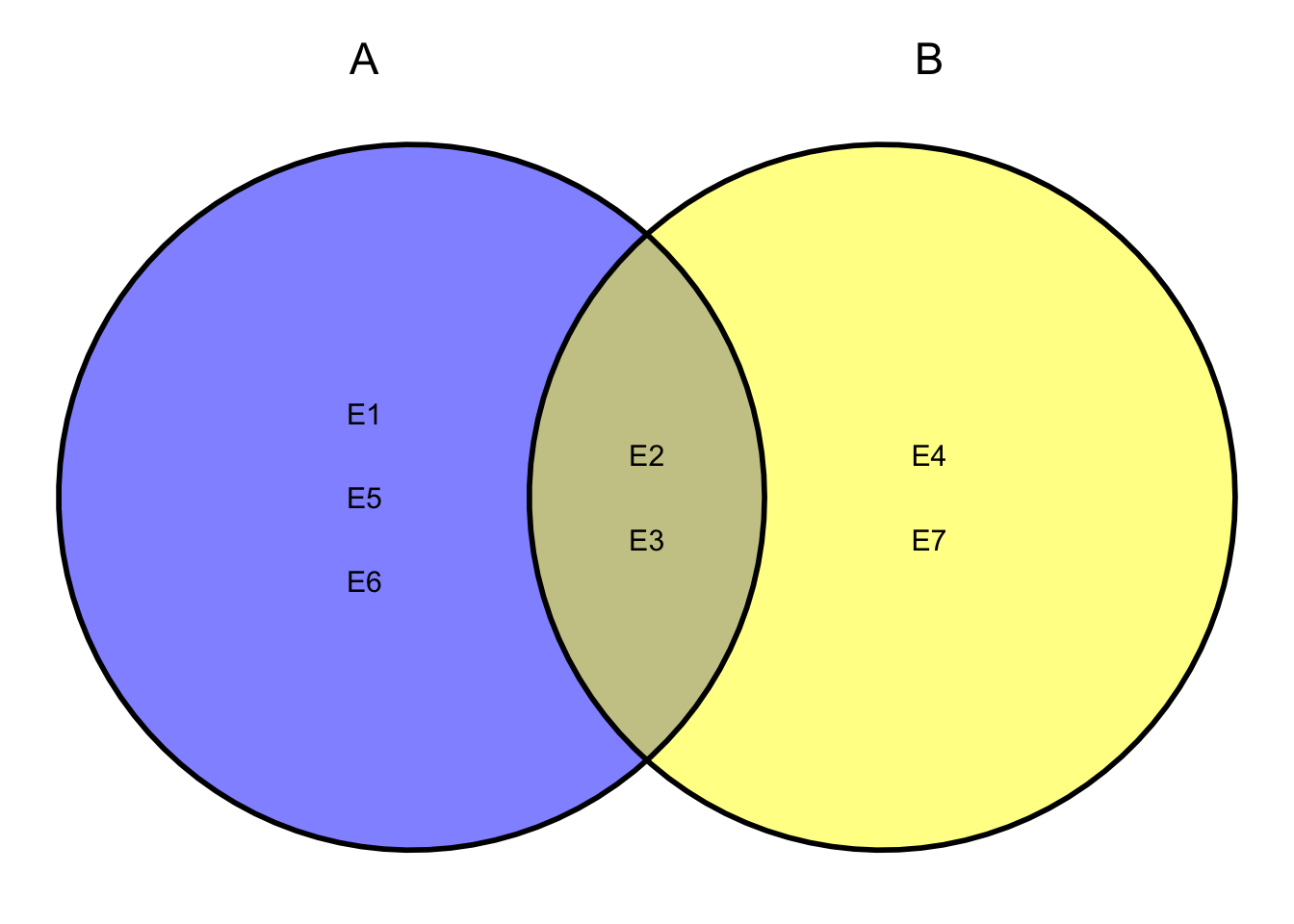
Exercise 4.2 The elementary events shown in the Venn diagram below (there are seven of them) have the following probabilities:
\(\mathbb{P}(E_2)=\mathbb{P}(E_3)=\frac{1}{5}\), \(\mathbb{P}(E_4)=\mathbb{P}(E_5)=\frac{1}{20}\), \(\mathbb{P}(E_6)=\frac{1}{10}\), \(\mathbb{P}(E_7)=\frac{1}{5}\).
Find the probabilities of the following events:
- \(\mathbb{P}(A)\)
- \(\mathbb{P}(B)\)
- \(\mathbb{P}(A\cup B)\)
- \(\mathbb{P}(A\cap B)\)
- \(\mathbb{P}(A^C)\)
- \(\mathbb{P}(B^C)\)
- \(\mathbb{P}(A^C \cup A)\)
- \(\mathbb{P}(A^C \cap B)\)
- \(\mathbb{P}(A)\)
- \(\mathbb{P}(B)\)
- \(\mathbb{P}(A\cup B)\)
- \(\mathbb{P}(A\cap B)\)
- \(\mathbb{P}(A^C)\)
- \(\mathbb{P}(B^C)\)
- \(\mathbb{P}(A^C \cup A)\)
- \(\mathbb{P}(A^C \cap B)\)
Exercise 4.3 We randomly draw two cards from a deck. What is the probability that both will be aces if:
we draw with replacement,
we draw without replacement?
Exercise 4.4 (Miller and Miller 2012) Two mobile phones are randomly selected from a shipment of 240 phones, of which 15 are defective. What is the probability that both selected phones are defective?
Exercise 4.5 (Miller and Miller 2012) At a certain highway exit, the probability that a stopped truck has faulty brakes or excessively worn tires is 0.23 and 0.24, respectively. The probability that a stopped truck has at least one of these defects is 0.38. What is the probability that the truck has both faulty brakes and excessively worn tires?
Exercise 4.6 (Aczel and Sounderpandian 2018) An electronic device consists of two components, A and B, and functions as long as at least one of them works. The probability of failure in one month is 0.02 for component A and 0.1 for component B. The components function independently. What is the probability that the device will work for the entire month?
Exercise 4.7 Three coin tosses result in eight equally likely outcomes: HHH, HHT, HTH, THH, HTT, THT, TTH, and TTT. Let A be the event that the first two tosses result in heads, B be the event that the third toss results in tails, and C be the event that exactly two tails appear in three tosses. Show that:
Events A and B are independent.
Events B and C are dependent.
Exercise 4.8 (DeFusco et al. 2015) A company uses three criteria to pre-select potential acquisition targets from a list of 500 firms:
Criterion 1. Compatible product lines – proportion of firms meeting the criterion: 0.20.
Criterion 2. The merged companies will have a higher revenue growth rate – proportion of firms meeting the criterion: 0.45.
Criterion 3. The acquisition is feasible in terms of asset and liability management – proportion of firms meeting the criterion: 0.78.
How many firms are expected to remain after filtering the list, assuming the three criteria operate independently?
Exercise 4.9 Consider the outcomes of a double dice roll. Draw a Venn diagram for this sample space and indicate the event “the second roll is higher than the first roll.” Calculate the probability of this event.
Exercise 4.10 A brokerage firm deals in stocks and bonds. An analyst wants to estimate the probability that a person seeking advice will want to buy stocks (event S) or bonds (event B). Define the union and intersection of these two events.
Exercise 4.11 Events A, B, and C are (mutually) independent. \(\mathbb{P}(A)=0.6\); \(\mathbb{P}(B)=0.7\); \(\mathbb{P}(C)=0.8\). What is the probability of the union of events A, B, and C?
Exercise 4.12 (Miller and Miller 2012) Among married couples in a certain city, the probability that the husband votes in a school board election is 0.21, the probability that the wife votes is 0.28, and the probability that both vote is 0.15. What is the probability that at least one of them votes?
Exercise 4.13 (Miller and Miller 2012) Among 200 university students, 138 enrolled in psychology, 115 enrolled in sociology, and 91 enrolled in both. How many students enrolled in neither of these two subjects? (Hint: You can use a Venn diagram and enter the numbers in the corresponding areas).
Exercise 4.14 (Maddala 2006) Four equally qualified individuals, two women and two men, are applying for a job at Compact S.A. The company will select two people at random, ignoring gender. What is the probability that both selected individuals will be of the same gender?
A student answered as follows: there are three possible outcomes – 2 women, 2 men, and 1 woman & 1 man. The number of favorable outcomes is 2, so the probability is 2/3. Was the student correct?
Exercise 4.15 (Maddala 2006) A company drills four independent wells in search of oil. The probability of finding oil in each well is the same and equal to \(p\). Consider the following events:
event \(A\): Oil is found in exactly two wells.
event \(B\): Oil is found in at least three wells.
event \(C\): Oil is found in the third well.
event \(D\): Oil is found in fewer than three wells.
Derive the following probabilities:
\(\mathbb{P}(A)\)
\(\mathbb{P}(B)\)
\(\mathbb{P}(C)\)
\(\mathbb{P}(D)\)
\(\mathbb{P}(A\cap B)\)
\(\mathbb{P}(A \cup B)\)
\(\mathbb{P}(B\cap C)\)
\(\mathbb{P}(B \cup C)\)
\(\mathbb{P}(B\cap D)\)
\(\mathbb{P}(A|B)\)
\(\mathbb{P}(B|C)\)
\(\mathbb{P}(C|D)\)
\(\mathbb{P}(D|C)\)
Exercise 4.16 We know the following about events A and B: \(\mathbb{P}(A) = 1/3\) and \(\mathbb{P}(A\cap B) = 1/5\). Calculate, if possible:
\(\mathbb{P}(B|A)\)
\(\mathbb{P}(A^C \cup B^C)\)