ANOVA de una vía

Bioestadística básica/Posgrados CUCS

Pérez-Guerrero Edsaúl Emilio

Instituto de Investigación en Ciencias Biomédicas

2024-11-08

Introducción

La distribución t de Student es muy útil al hacer inferencias comparando dos muestras simultáneamente, pero no es adecuada cuando tenemos más de dos.
En estos casos, podemos utilizar el análisis de varianza, que es un procedimiento que toma la variabilidad total de una serie de datos y la divide en dos o más fuentes de variación.
Este procedimiento estadístico evalúa la hipótesis nula de que no existe diferencia entre dos o más medias poblacionales

ANOVA de una vía

## ANOVA de una vía

El análisis de varianza de una vía es un procedimiento estadístico que se utiliza para comparar dos o más medias.
La \(H_0\) es que no hay diferencias entre las medias de los grupos.
La \(H_1\) es que al menos una de las medias es diferente.

ANOVA de una vía

Una técnica en la que la varianza total de un conjunto de datos se divide en dos o más componentes, y cada uno de ellos se asocia con una fuente especifica de variación, de manera que durante el análisis es posible encontrar la magnitud con la que contribuye cada una de esas fuentes en la variación total

Tipos de ANOVA

ANOVA de una vía: Analiza las diferencias entre las medias de tres o más grupos independientes en función de una sola variable independiente (factor) categórica.
ANOVA de dos vías: Analiza las diferencias en las medias considerando dos factores independientes, permitiendo estudiar no solo los efectos individuales de cada factor, sino también su posible interacción.
ANOVA de medidas repetidas: Utilizado cuando se mide a los mismos sujetos en múltiples condiciones o tiempos. Evalúa las diferencias en las medias de diferentes mediciones repetidas en el mismo grupo de sujetos.

Tipos de ANOVA

ANOVA de dos vías con medidas repetidas: Combinación de ANOVA de dos vías y de medidas repetidas, considerando dos factores, uno de los cuales puede estar basado en medidas repetidas.
MANOVA (ANOVA Multivariante): Extensión del ANOVA que permite analizar múltiples variables dependientes al mismo tiempo, lo cual es útil cuando las variables están correlacionadas.
ANCOVA (Análisis de Covarianza): Combina ANOVA con regresión al ajustar los efectos de una o más covariables, controlando su efecto para obtener una comparación más precisa entre grupos.

ANOVA de una vía

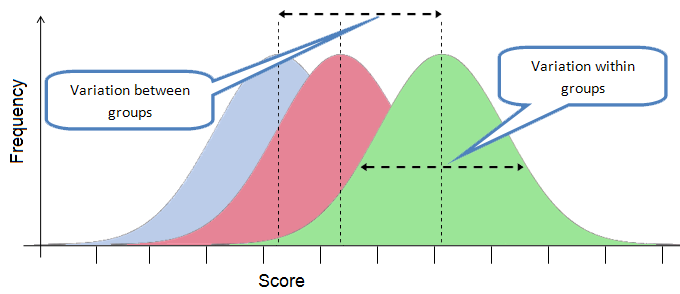
El análisis de varianza de una vía se basa en la comparación de dos tipos de variabilidad:
- Variabilidad entre grupos: se refiere a la variabilidad entre los grupos que estamos comparando.
- Variabilidad dentro de los grupos: se refiere a la variabilidad dentro de cada grupo.

Cuando la variación dentro los grupos es mayor que la variación entre los grupos se dice que hay diferencias entre los grupos

ANOVA de una vía

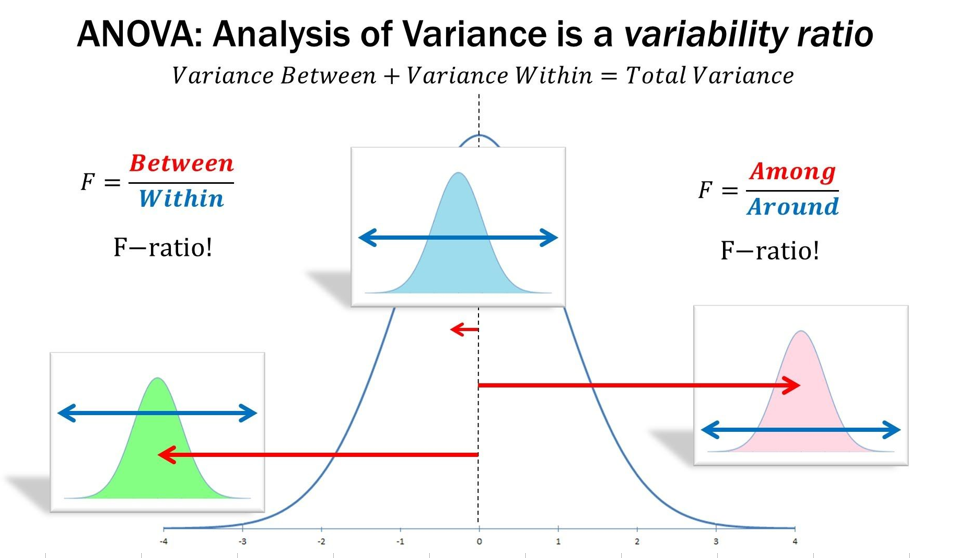
Fuentes de variación

ANOVA de una vía

ANOVA de una vía. Conceptos básicos

Es una técnica que divide la variabilidad total en componentes separados, por una parte, la variabilidad entre tratamientos y por otra, la variabilidad de los tratamientos

Factor: Variable independiente. Grupos a comparar.
Tratamiento: Niveles del factor.
Respuesta: Variable dependiente. Variable numérica que se mide en cada grupo.

Tabla ANOVA

Table 1: N = Total de datos a = Número de tratamientos : Tabla de ANOVA

Fuente de variación	Suma de cuadrados	Grados de libertad	Cuadrados medios	Fo (F calculada)
Tratamientos	SC trat.	a-1	SC trat./(a-1)	CM trat./CM error
Error	SC error	N-a	SC error/(N-a)	-
Total	SC total	N-1	-	-

Tabla ANOVA. Valor de F pequeño

Table 2: Tabla de ANOVA. Valores de F grandes

Fuente de variación	Suma de cuadrados	Grados de libertad	Cuadrados medios	Fo (F calculada)
Tratamientos	20	2	\(\frac{20}{2}=10\)	\(\frac{10}{0.6}=16.67\)
Error	10	15	\(\frac{10}{15}=0.6\)	-
Total	30	N-1	-	-

Tabla ANOVA. Valor de F grande

Table 3: Tabla de ANOVA. Valores de F pequeños

Fuente de variación	Suma de cuadrados	Grados de libertad	Cuadrados medios	Fo (F calculada)
Tratamientos	0.5	2	\(\frac{0.5}{2}=0.25\)	\(\frac{0.25}{0.6}=0.41\)
Error	10	15	\(\frac{10}{15}=0.6\)	-
Total	10.5	N-1	-	-

Supuestos para la realización de un ANOVA

Independencia de las Observaciones: Cada grupo o muestra debe ser independiente de los demás. Esto significa que la selección de un individuo en un grupo no debe influir en la selección de individuos en otro grupo.
Normalidad: Los datos en cada grupo deben distribuirse normalmente. Esto es más relevante en muestras pequeñas, ya que las pruebas ANOVA son “robustas” a este supuesto en muestras grandes.

Supuestos para la realización de un ANOVA

Homogeneidad de Varianzas: Las varianzas de los grupos deben ser aproximadamente iguales. Este supuesto, conocido como homocedasticidad, es importante porque la ANOVA compara las varianzas entre los grupos. Si las varianzas son muy diferentes, las conclusiones de la ANOVA podrían no ser válidas.
Nivel de Medición: Las variables dependientes deben ser medidas al menos a nivel de intervalo o de razón. Esto significa que los datos deben ser numéricos y permitir comparaciones significativas de tamaño.

Distribución F

La distribución F es una distribución de probabilidad continua que se utiliza en el análisis de varianza.
Presenta las siguientes características:
- Es asimétrica y no simétrica.
- Tiene un rango de valores de 0 a infinito.
- Tiene dos grados de libertad: uno para el numerador y otro para el denominador.
- Se utiliza para comparar varianzas de dos o más poblaciones.
- Es una familia de distribuciones, cada una de las cuales se define por dos grados de libertad.

Distribución F

Grafica de una distrubición F

Cálculo del valor F de tablas

En R se utiliza la familia de funciones pf, qf

pf: se utiliza para obtener la probabilidad dado un valor de F
- pf(q, df1, df2, ncp, lower.tail = TRUE, log.p = FALSE)
qf: dada una probabilidad y grados de libertad devuelve el valor de F
- qf(p, df1, df2, ncp, lower.tail = TRUE, log.p = FALSE)

Cálculo del valor F de tablas

Por ejemplo:

[1] 3.354131

Con un alfa de 0.05 (generalmente se emplea una hipótesis unilateral ya que el valor de F siempre es positivo)
Con 2 grados de libertad para los tratamientos
Con 27 grados de libertad para el error

Ejemplo 1. ANOVA de una vía

En la elaboración de un nuevo producto se quiere comparar el efecto de diferentes antibióticos sobre la vida de anaquel de un suero fetal bovino. Para ello se tomaron 3 tipos de envase, con los cuales se realizaron 10 réplicas en cada uno y se midieron los días de duración. Los resultados fueron los siguientes:

Antibiótico A: 23, 28, 21, 27, 35, 41, 37, 30, 32, 36
Antibiótico B: 35, 36, 29, 40, 43, 49, 51, 28, 50, 52
Antibiótico C: 50, 43, 36, 34, 45, 52, 52, 43, 49, 34

¿Existe evidencia significativa para demostrar que el de Antibiótico influye en la vida de anaquel en el producto? Utilice \(\alpha\)=0.05. Suponga que los datos siguen una distribución normal y que las varianzas son iguales entre los grupos.

Crear base de datos

Copie y pegue el siguiente código:

AntiA <- c(23
           , 28, 21, 27, 35, 41, 37, 30, 32, 36)
AntiB <- c(35, 36, 29, 40, 43, 49, 51, 28, 50, 52)
AntiC <- c(50, 43, 36, 34, 45, 52, 52, 43, 49, 34)
Dias <- c(AntiA, AntiB, AntiC)
Antibiotico <- rep(c("Antibiótico A", "Antibiótico B", 
                     "Antibiótico C"), each = 10)
Datos <- data.frame(Dias, Antibiotico)

Gráficos

library(ggplot2)
Datos|>
  ggplot(aes(x = Antibiotico, y = Dias, fill = Antibiotico)) +
  geom_boxplot(alpha=0.5) +
  labs(title = "Comparación de la vida de anaquel por Antibiótico",
       x = "Antibiótico",
       y = "Días de vida de anaquel") +
  theme_linedraw()

Gráficos

Replique esta gráfica

03:00

Otros gráficos

library(ggrain)
Datos|>
  ggplot(aes(y = Dias,x=1)) +
  geom_rain(alpha=0.5, fill="cyan4") +
  labs(title = "Comparación de la vida de anaquel por Antibiótico",
       x = "Días de anaquel",
       y = "") +
  theme_linedraw()+
  facet_grid(~Antibiotico)

Otros gráficos

Prueba de ANOVA en R

ANOVA Para varianzas homogeneas

            Df Sum Sq Mean Sq F value  Pr(>F)   
Antibiotico  2  920.6   460.3   7.928 0.00196 **
Residuals   27 1567.7    58.1                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ANOVA Para varianzas diferentes

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  2   1.247 0.3034
      27


    One-way analysis of means (not assuming equal variances)

data:  Dias and Antibiotico
F = 9.5867, num df = 2.000, denom df = 17.674, p-value = 0.001515

ANOVA con otras librerías

ANOVA Table (type II tests)

       Effect DFn DFd     F     p p<.05  ges
1 Antibiotico   2  27 7.928 0.002     * 0.37

ANOVA con ggstsastplot

Prueba post-hoc

Una prueba post-hoc es una prueba estadística que se realiza después de un ANOVA para determinar qué grupos son significativamente diferentes entre sí. La elección de la prueba post-hoc depende de la cantidad de grupos y de si las varianzas son iguales o no. De momento solo evaluaremos las diferencias de los ANOVAS con la prueba de Tukey

Prueba post-hoc

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = Dias ~ Antibiotico, data = Datos)

$Antibiotico
                            diff       lwr      upr     p adj
Antibiótico B-Antibiótico A 10.3  1.850825 18.74917 0.0145503
Antibiótico C-Antibiótico A 12.8  4.350825 21.24917 0.0023469
Antibiótico C-Antibiótico B  2.5 -5.949175 10.94917 0.7458942

Prueba post-hoc

Ejercicios de tarea

Ejercicio 1

Se sabe por antecedentes previos que los grupos de edad de menores de 30, de 31 a 45 y más de 45 presentan niveles de glucosa diferentes en la mujeres de Pima. Pruebe esta afirmación utilizando una prueba de hipótesis. Utilice Pima.tr2 y un α=0.05. Realice y grafique la prueba de Tukey. Evalué la homogenidad de las varianzas.

Ejercicio 2

Un investigador desea conocer la efectividad de varios suplementos alimenticios (feed) sobre la tasa de crecimiento (weight) de los pollos. Cargue la base de datos chickwts que se encuentra en R. Use ANOVA para examinar la efectividad de los suplementos alimenticios. La linea de comando para cargar la base chickwts es data("chickwts"). Realice y grafique la prueba de Tukey. Evalue la homogenidad de las varianzas. Ejercicio adaptado de: Biostatistics with R. Shahbaba (2012). Springer

Ejercicio 3

Usando la libreria MASS llame a la base de datos “genotype”. Esta base de datos contiende los resultados de una investigación realizad por Bailey y cols. en 1953 enla que investigaron la herencia del y su asociación con el crecimiento de varios grupo de ratas. En este estudio, las camadas de ratas se separaron de sus madres naturales, y fueron criadas por madres adoptivas. Las madres y las camadas pueden tener cuatro genotipos diferentes: A, B, I y J. Supongamos que queremos investigar si el aumento de peso (Wt) de la camada (en gramos) a los 28 días está relacionado con el genotipo de la madre adoptiva Madre (A, B, I y J). Utilice la prueba de ANOVA de una vía y realice gráficos de caja y bigotes en ggplot. Realice y grafique la prueba de Tukey. Evalue la homogenidad de las varianzas. Ejercicio adaptado de: Biostatistics with R. Shahbaba (2012). Springer

Ejercicio 4

Cargue el conjunto de datos de anorexia del paquete MASS. Este conjunto de datos se recopiló para investigar la efectividad de diferentes tratamientos (Treat) en el aumento de peso para pacientes jóvenes con anorexia. Cree una nueva variable llamada Diferencia restando el peso del paciente antes del período de estudio (Prewt) de su peso después del período de estudio (Postwt): Diferencia = Postwt - Prewt. Use una gráfica de medios para visualizar cómo cambia esta variable según el tipo de tratamiento. Use ANOVA para investigar si el tipo de tratamiento hace una diferencia en la cantidad de aumento de peso. Realice y grafique la prueba de Tukey. Evalue la homogenidad de las varianzas. Realice gráficos de densidad en ggplot y otro de raincloud utilizando facetas. Ejercicio tomado de: Biostatistics with R. Shahbaba (2012). Springer

Ejercicio 5

El conjunto de datos de Cushings, que está disponible en el paquete MASS. El síndrome de Cushing es un trastorno hormonal asociado con un alto nivel de cortisol secretado por la glándula suprarrenal. El conjunto de datos de Cushings incluye 27 observaciones (n = 27). Para cada individuo de la muestra, se registran las tasas de excreción urinaria de dos metabolitos de esteroides. Estos son la tasa de excreción urinaria (mg/24 h) de tetrahidrocortisona y la tasa de excreción urinaria (mg/24 h) de pregnanetriol. La variable Tipo en el conjunto de datos muestra el tipo de síndrome subyacente, que puede ser una de cuatro categorías: adenoma (a), hiperplasia bilateral (b), carcinoma (c) y desconocido (u)

Use ANOVA para investigar si la tasa de excreción urinaria de tetrahidrocortisona y pregnanetriol difiere entre los cuatro tipos de síndrome. Realice y grafique la prueba de Tukey. Evalue la homogenidad de las varianzas. Realice gráficos de densidad en ggplot y otro de raincloud utilizando facetas.