| Density | Fat |
|---|---|
| 1.0708 | 12.3 |
| 1.0853 | 6.1 |
| 1.0414 | 25.3 |
| 1.0751 | 10.4 |
| 1.0340 | 28.7 |
| 1.0502 | 20.9 |
| 1.0549 | 19.2 |
| 1.0704 | 12.4 |
| 1.0900 | 4.1 |
| 1.0722 | 11.7 |
| 1.0830 | 7.1 |
| 1.0812 | 7.8 |
| 1.0513 | 20.8 |
| 1.0505 | 21.2 |
| 1.0484 | 22.1 |
Correlación y regresión lineal simple.
- Autor: Edsaúl Emilio Pérez Guerrero
- Afiliación: Universidad de Guadalajara
- mail: edsaul.perezg@academicos.udg.mx
- Última actualización: 2024-06-03
En este capítulo se abordará la pruebas de correlación y la regresión lineal simple.
Introducción
La correlación lineal y la regresión lineal simple son métodos estadísticos que estudian la relación lineal existente entre dos variables. Partiremos de un ejemplo
Un grupo de investigadores desean conocer a relación existe entre la densidad mineral y el porcentaje de grasa corporal. Una vista de 15 de los 265 datos del data frameÇ original se muestra en la tabla @ref(tab:tab14-1)
Note como ambas variables son de tipo cuantitativo. Para conocer la relación de las variables anteriores, es estadística podemos emplear dos opciones:
Transformar una de las variables cuantitativas a un factor y poder hacer la comparación de la segunda variable cuantitativa entre este factor. Sin embargo, este proceso muchas de las ocasiones, fomenta la pérdida de información.
La segunda opción es emplear técnicas de regresión o de correlación.
Diferencias entre correlación y regresión
Por definición la la correlación mide la asociación de dos variables numéricas y en cierta medida mide que tanto cambia una variable con respecto al cambio de la otra. Aunque este relación nunca será cuasal.
Mientras que la La regresión se usa para explicar o modelar la relación entre una variable continua Y, llamada variable respuesta o variable dependiente.
Otras diferencias importantes entre la correlación y la regresión son:
La correlación se usa para medir el grado de asociación entre dos variables sin implicar causalidad, mientras que la regresión lineal se utiliza para generar un modelo matemático que permita predecir el valor de una variable a partir de la otra.
A diferencia de la regresión lineal, la correlación no tiene en cuenta la asignación de las variables a X e Y, únicamente mide la relación entre dos variables y no es necesario que una de ellas sea dependiente o independiente. De hecho en la correlación no hay una variable dependiente ni independiente (Y y X, respectivamente). En cambio, la regresión lineal si hay una variable dependiente (Y) que dependerá de los cambios que suceden en un variable independiente (X).
A nivel experimental, la correlación se suele emplear cuando ninguna de las variables se ha controlado, simplemente se han medido ambas y se desea saber si están relacionadas. En el caso de estudios de regresión lineal, es más común que una de las variables se controle (tiempo, concentración de reactivo, temperatura…) y se mida la otra.
Es común que los estudios de correlación precedan a los de regresión lineal para analizar la relación entre las variables y, si se comprueba que están correlacionadas, se procede a generar el modelo de regresión lineal. Es importante tener en cuenta que la regresión lineal no implica causalidad, sino que proporciona una manera de predecir la relación entre las variables.
La correlación es una medida estadística que indica el grado de asociación entre dos variables, pero no implica causalidad. En cambio, la regresión lineal es un modelo matemático que puede utilizarse para predecir la relación entre dos variables y puede proporcionar información sobre la causalidad. En resumen, la correlación se utiliza para medir la fuerza de la relación entre dos variables, mientras que la regresión lineal se utiliza para modelar y predecir la relación entre ellas.
Pruebas de correlación
La correlación es la medida que se emplea en estadística para conocer que tan asociadas están dos variables, algunas de sus características son:
- Su finalidad es examinar la dirección y la magnitud de la asociación entre dos variables cuantitativas.
- La correlación es una medida que va de -1 a 1, donde -1 indica una correlación negativa perfecta, 0 indica que no hay correlación y 1 indica una correlación positiva perfecta.
- La correlación no implica causalidad. Aunque dos variables puedan estar correlacionadas, no significa que una variable cause la otra.
- La correlación se puede calcular utilizando diferentes métodos, siendo el coeficiente de correlación de Pearson el más común, sobre todo cuando los datos tienen una relación lineal.
- La correlación es simétrica, es decir, que la correlación entre A y B es igual a la correlación entre B y A.
- Permite conocer si al aumentar una variable, aumenta la otra o disminuye.
- Si la relación entre dos variables es perfecta e inversa, r=–1, mientras que si es lineal y directa, r=1.
- Cuando las dos variables no están correlacionadas, r=0
Por favor nunca olvide que la correlación no impla causalidad:

Existen varios criterios para establecer si la relación es buena o no, algunos autores sugieren:
- 0: asociación nula.
- 0.1: asociación pequeña.
- 0.3: asociación mediana.
- 0.5: asociación moderada.
- 0.7: asociación alta.
- 0.9: asociación muy alta.
Aunque nosotros emplearemos la propuesta por la universidad de Emory que se relaciona con el tamaño del efecto de Cohen:
- 0.1: Efecto pequeño (relación pequeña)
- 0.3: Efecto moderado (Relación moderada)
- 0.5: Efecto fuerte (Relación fuerte)
Pruebas de hipótesis en correlación y coeficientes de correlación
Existen tres formas de estimar la correlación mediante los coeficientes de correlación de pearson, spearman y kendall. Se describen a continuación las principales características de los primeros dos.
Coeficiente de correlación pearson
La formula para estimar el coeficiente de correlación de pearson es:
\[\begin{equation} r_{xy} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}} \end{equation}\]
En esta fórmula, \(r_{xy}\) representa el coeficiente de correlación entre las variables \(x\) e \(y\). \(x_i\) e \(y_i\) son los valores de las variables \(x\) e \(y\) en la i-ésima observación, mientras que \(\bar{x}\) y \(\bar{y}\) son las medias de x e y, respectivamente.
Existe una relación muy importante entre el coeficiente de correlación de pearson y la covarianza. Para fines prácticos la covarianza mide cuanto variación hay entre una variable y una segunda, es decir, la covarianza se refiere a cuanto varía y si una segunda variable lo hace de la misma forma. Por ejemplo, si dos variables tienen la misma variación una con respecto de la otra, la covariación sería de uno. Un ejemplo de esto, aunque quizá cerece se sentido, imagine que mide el peso de un paciente en kg y en libras. Estas mediciones tendrían una covarición de 1.
Por lo tanto la formula para estimación del coeficiente de correlación de pearson se puede simplificar como:
\[\begin{equation} r_{xy} = \frac{cov(x, y)}{s_x s_y} \end{equation}\]
Donde: \(r_{xy}\) representa el coeficiente de correlación entre las variables \(x\) e \(y\). \(cov(x, y)\) es la covarianza entre \(x\) e \(y\), mientras que \(s_x\) y \(s_y\) son las desviaciones estándar de \(x\) e \(y\), respectivamente.
Prueba de hipótesis en el coeficiente de correlación pearson
Nuestra intención es tratar de demostrar que el coeficiente de correlación es distinto de cero. Por lo tanto:
- \(H_0: r = 0\)
- \(H_A: r \neq 0\)
Para poder concluir si rechazamos o aceptamos nuestra hipótesis, utilizamos la distribución \(t\) y la siguiente formula que :
\[\begin{equation} t = \frac{r_{xy} \sqrt{n-2}}{\sqrt{1-r_{xy}^2}} \end{equation}\]
Donde: \(t\) es el valor calculado para la prueba de significancia del coeficiente de correlación de Pearson. \(r_{xy}\) es el coeficiente de correlación de Pearson, y \(n\) es el tamaño de la muestra
Los supuestos que se deben cumplir para utilizar el coeficiente de correlación de Pearson:
- Las variables se observan sobre una muestra aleatoria de individuos (cada individuo debe tener un par de valores).
- Existe una asociación lineal entre las dos variables.
- Para una prueba de hipótesis válida y cálculo de intervalos de confianza, ambas variables deben tener una distribución aproximadamente normal.
- Ausencia de valores atípicos en el conjunto de datos.
Coeficiete de correlación Spearman
Mientras que el coeficiente de correlación de Pearson asume linealidad, el coeficiente de correlación de Spearman asume una relación monotónica (las variables tienden a moverse en la misma dirección relativa, pero no necesariamente a un ritmo constante) entre dos variables. El coeficiente de correlación de Spearman se utiliza como una alternativa no paramétrica al coeficiente de correlación de Pearson. Se aplica en casos en los que los valores son ordinales o en aquellos casos en los que los valores son continuos, pero no cumplen con la condición de normalidad. La ventaja de utilizar el coeficiente de Spearman es que trabaja con rangos, lo que lo hace menos sensible a valores extremos que el coeficiente de Pearson.
La estimación del coeficiente de correlación de Spearman \(\rho\) o \(r_s\) se basa en la siguiente ecuación:
\[\begin{equation} \rho = 1 - \frac{6\sum d_i^2}{n(n^2 - 1)} \end{equation}\]
En esta fórmula, \(\rho\) es el coeficiente de correlación de Spearman, \(n\) es el tamaño de la muestra y \(d_i\) es la diferencia en los rangos de los valores i en cada variable.
La hipótesis nula para este coeficiente es: \(H_0: \rho = 0\) que se puede comprobar mediante el estadístico \(t\) con la siguiente formula:
\[\begin{equation} t = \frac{r_s}{\sqrt{\frac{1-r_s^2}{n-2}}} \end{equation}\]
Donde: \(t\) es el valor calculado para la prueba de significancia del coeficiente de correlación de Spearman. \(r_s\) es el coeficiente de correlación de Spearman, y \(n\) es el tamaño de la muestra.
Para utilizar el coeficiente de correlación de Spearman, es necesario que:
- las variables se observen en una muestra aleatoria de individuos y que haya una asociación monótona entre ellas.
- Que la varible utiliazada sea al menos de tipo ordinal.
No olvide que: La asociación monótona indica que las variables tienden a moverse en la misma dirección relativa, pero no necesariamente a un ritmo constante. Es importante destacar que todas las correlaciones lineales son monótonas, pero no todas las asociaciones monótonas son lineales, ya que también puede haber asociaciones monótonas no lineales. Simplemente un número de \(\rho\) positivo indica que ambas variables incrementan o disminuyen en el mismo sentido, mientras que un coeficiente negativo indica que una aumenta y la otra disminuye.
La siguiente taba muestra una comparación entre el coeficiente de correlación de Spearman y Pearson:
| Coeficiente de correlación de Pearson | Coeficiente de correlación de Spearman | |
|---|---|---|
| Tipo de variable | Variables continuas que tengan una relación lineal y una distribución normal | Variables continuas que no cumplen con e supuesto de normalidad o variables ordinales |
| Supuestos | 1. Las variables se observan sobre una muestra aleatoria de individuos (cada individuo debe tener un par de valores). 2. Existe una asociación lineal entre las dos variables. 3. Para una prueba de hipótesis válida y cálculo de intervalos de confianza, ambas variables deben tener una distribución aproximadamente normal. 4. Ausencia de valores atípicos en el conjunto de datos. |
No tiene supuestos específicos sobre la distribución o la forma funcional de las variables. Los datos son obtenidos de una muestra aleatoria |
| Fórmula | \(r_{xy} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}}\) o \(r_{xy} = \frac{cov(x, y)}{s_x s_y}\) | \(\rho = 1 - \frac{6\sum d_i^2}{n(n^2 - 1)}\) |
| Interpretación | El coeficiente de correlación de Pearson mide la fuerza y la dirección de la relación lineal entre dos variables continuas. Los valores oscilan entre -1 y 1. Una correlación cercana a 1 indica una fuerte correlación positiva, mientras que una correlación cercana a -1 indica una fuerte correlación negativa. Una correlación cercana a 0 indica que no hay correlación lineal. |
El coeficiente de correlación de Spearman mide la fuerza y la dirección de la relación monotónica entre dos variables. Los valores oscilan entre -1 y 1. Una correlación cercana a 1 indica una fuerte correlación positiva, mientras que una correlación cercana a -1 indica una fuerte correlación negativa. Una correlación cercana a 0 indica que no hay correlación monotónica. |
| Ventajas | Funciona bien cuando las variables tienen una relación lineal. Permite la prueba de hipótesis y el cálculo de intervalos de confianza. |
No requiere una distribución normal. Menos sensible a valores atípicos que el coeficiente de Pearson debido a que se basa en los rangos de los valores. |
| Desventajas | Requiere que las variables sean continuas y lineales. Sensible a valores atípicos. |
No proporciona información sobre la fuerza de la relación monotónica, solo su dirección. No se pueden calcular intervalos de confianza. |
La correlación y el problema visual
Establecer la fuerza de correlación es muy difícil de visualizar mediante gráficas.
Loading required package: ggplot2
Pruebas de correlación en R
Existen varios métodos para medir la correlación entre dos variables, los más utilizados son:
Pearson: Para realizarlo en
Rse puede utilizar la función:cor.test(x,y,method = "spearman"). Donde x y y son dos vectores numéricos.Spearman: Para realizarlo en
Rse puede utilizar la función:cor.test(x,y,method = "Spearman"). Donde x y y son dos vectores numéricos. Es la alternativa no paramétrica para las pruebas de correlación.Kendall: Prueba útil para correlacionar variables ordinales. Para realizarlo en
Rse puede utilizar la función:cor.test(x,y,method = "kendall"). Donde x y y son dos vectores numéricos.
Ejercicios para pruebas de correlación
Para realizar los siguientes ejemplos utilice la base de datos “bodyfat” la cual contiene mediciones antopométricas de un grupo de pacientes. Puede descargar la base aquí. Utilice el menú de RStudio para la importanción de la base de datos, tome en cuenta que es un archivo .txt. En la sección @ref(Importar-Texto) se puede consultar más detalle para la importación.
Se muestran los primero 6 datos de la base bodyfat
head(bodyfat) Density Fat Age Weight Height Neck Chest Abdomen Hip Thigh Knee Ankle
1 1.0708 12.3 23 154.25 67.75 36.2 93.1 85.2 94.5 59.0 37.3 21.9
2 1.0853 6.1 22 173.25 72.25 38.5 93.6 83.0 98.7 58.7 37.3 23.4
3 1.0414 25.3 22 154.00 66.25 34.0 95.8 87.9 99.2 59.6 38.9 24.0
4 1.0751 10.4 26 184.75 72.25 37.4 101.8 86.4 101.2 60.1 37.3 22.8
5 1.0340 28.7 24 184.25 71.25 34.4 97.3 100.0 101.9 63.2 42.2 24.0
6 1.0502 20.9 24 210.25 74.75 39.0 104.5 94.4 107.8 66.0 42.0 25.6
Biceps Forearm Wrist
1 32.0 27.4 17.1
2 30.5 28.9 18.2
3 28.8 25.2 16.6
4 32.4 29.4 18.2
5 32.2 27.7 17.7
6 35.7 30.6 18.8Para fines de estos ejercicios adjunte la base datos utilizando la función attach()
attach(bodyfat)- Supongamos que queremos conocer la correlación de las variables
WeightyHeight. Determine los coeficientes de correlación: pearson, spearman y kendall.
Para Pearson
cor(Weight, Height)[1] 0.3082785cor.test(Weight, Height)
Pearson's product-moment correlation
data: Weight and Height
t = 5.1239, df = 250, p-value = 5.99e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.1920207 0.4160038
sample estimates:
cor
0.3082785 Para Spearman
cor(Weight, Height, method = "spearman")[1] 0.5153362cor.test(Weight, Height, method = "spearman")Warning in cor.test.default(Weight, Height, method = "spearman"): Cannot
compute exact p-value with ties
Spearman's rank correlation rho
data: Weight and Height
S = 1292660, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.5153362 Para Kendall
cor(Weight, Height, method = "kendall")[1] 0.3657961cor.test(Weight, Height, method = "kendall")
Kendall's rank correlation tau
data: Weight and Height
z = 8.5352, p-value < 2.2e-16
alternative hypothesis: true tau is not equal to 0
sample estimates:
tau
0.3657961 Ahora determine la correlación que existe entre el peso
Weighty la densidad mineral óseaDensity.Cree gráficos de dispersión y agregue a las gráficas anteriores los valores de p de la prueba de pearson
Matrices de correlación y gráficos de dispersió
Pairs panels
En R existen muchas funciones que permiten la creación de gráficos y matrices de correlación. En este compendio revisaremos la función: airs.panels de la librería (psych).
Primero instale la librería
install.packages("psych")Una vez instalada, llame a la librería
library(psych)
Attaching package: 'psych'The following objects are masked from 'package:ggplot2':
%+%, alphaAhora podemos utilizar la función pairs.panels, que se aplica a todo el data frame, por lo que es importante que su selección solo tenga variables numéricas
pairs.panels(bodyfat)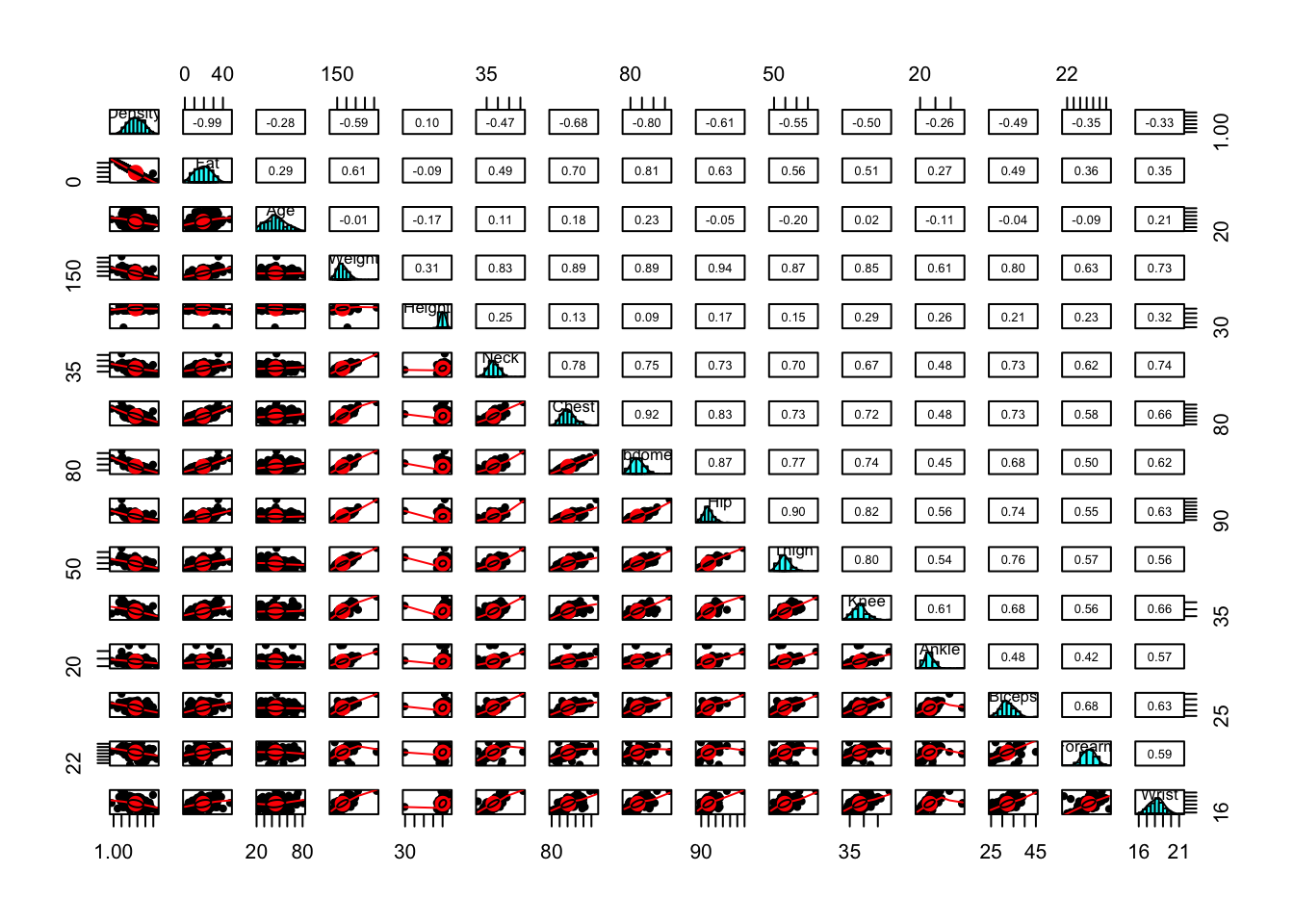
Es imposible visualizar correctamente este gráfico, por lo que podemos hacer pedir que se haga primero de algunas variables y luego de otras. Para este ejemplo se harán las primeras 7 y luego las últimas 8
pairs.panels(bodyfat[, 1:7], main="Matriz de correlación de las primeras 7 variables")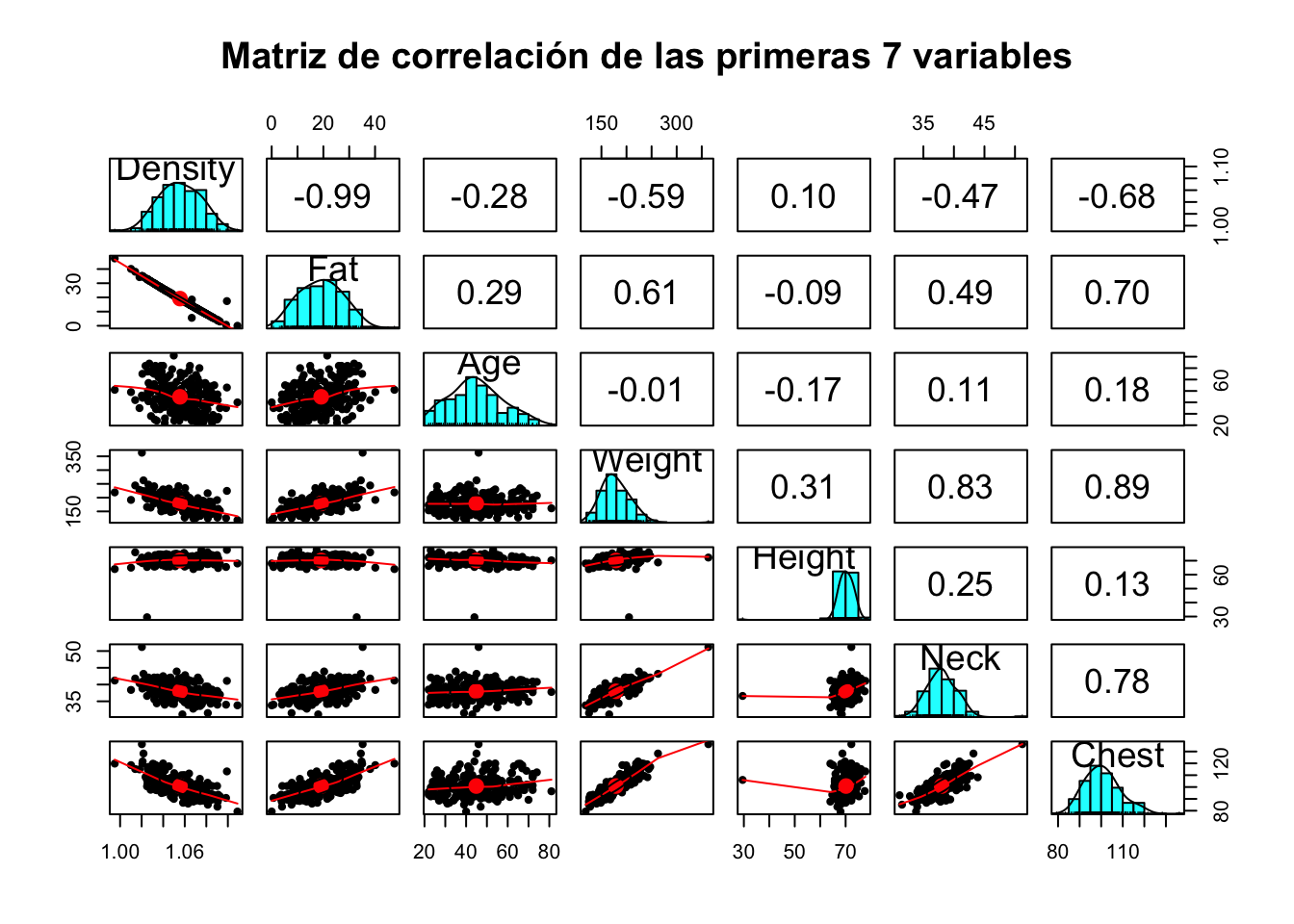
pairs.panels(bodyfat[, 8:14], main= "Matriz de correlación de las últimas 8 variables")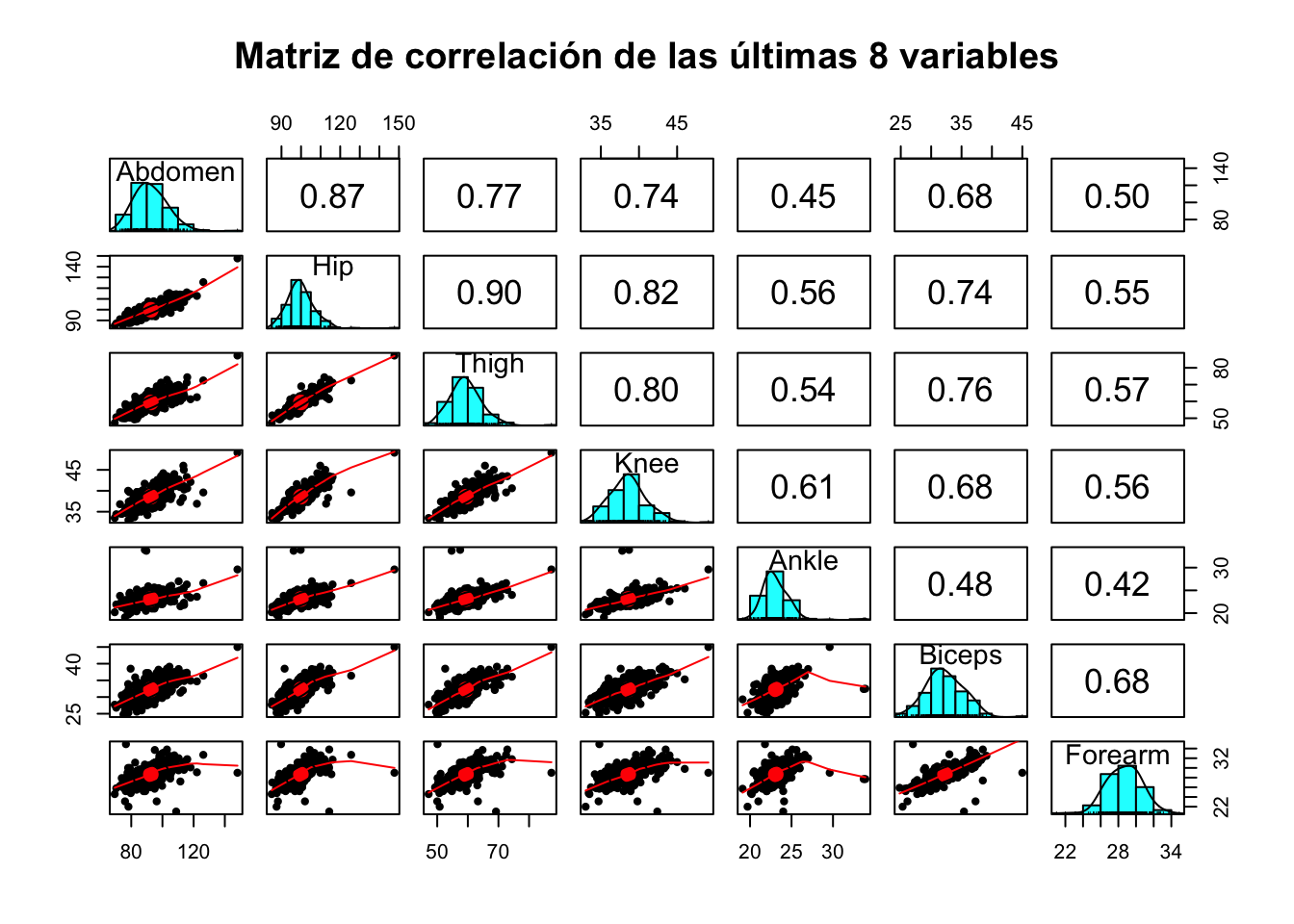
corPlot(bodyfat[, 8:14], main= "Matriz de correlación de las últimas 8 variables")
También puede marcar los coeficientes de correlación que son significativos con el argumento stars = T
corPlot(bodyfat[, 8:14], main= "Matriz de correlación de las últimas 8 variables", stars = T)
Corrr
Otra librería muy intersante es la librería corrr la cual es una herramienta para explorar correlaciones y hacer matrices de correlación.
install.packages("corrr") # Si es necesarioLlame la librería
library(corrr)corrr::correlate(df)Correlation computed with
• Method: 'pearson'
• Missing treated using: 'pairwise.complete.obs'# A tibble: 15 × 16
term Density Fat Age Weight Height Neck Chest Abdomen Hip
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Density NA -0.988 -0.278 -0.594 0.0979 -0.473 -0.683 -0.799 -0.609
2 Fat -0.988 NA 0.291 0.612 -0.0895 0.491 0.703 0.813 0.625
3 Age -0.278 0.291 NA -0.0127 -0.172 0.114 0.176 0.230 -0.0503
4 Weight -0.594 0.612 -0.0127 NA 0.308 0.831 0.894 0.888 0.941
5 Height 0.0979 -0.0895 -0.172 0.308 NA 0.254 0.135 0.0878 0.170
6 Neck -0.473 0.491 0.114 0.831 0.254 NA 0.785 0.754 0.735
7 Chest -0.683 0.703 0.176 0.894 0.135 0.785 NA 0.916 0.829
8 Abdomen -0.799 0.813 0.230 0.888 0.0878 0.754 0.916 NA 0.874
9 Hip -0.609 0.625 -0.0503 0.941 0.170 0.735 0.829 0.874 NA
10 Thigh -0.553 0.560 -0.200 0.869 0.148 0.696 0.730 0.767 0.896
11 Knee -0.495 0.509 0.0175 0.853 0.286 0.672 0.719 0.737 0.823
12 Ankle -0.265 0.266 -0.105 0.614 0.265 0.478 0.483 0.453 0.558
13 Biceps -0.487 0.493 -0.0412 0.800 0.208 0.731 0.728 0.685 0.739
14 Forearm -0.352 0.361 -0.0851 0.630 0.229 0.624 0.580 0.503 0.545
15 Wrist -0.326 0.347 0.214 0.730 0.322 0.745 0.660 0.620 0.630
# ℹ 6 more variables: Thigh <dbl>, Knee <dbl>, Ankle <dbl>, Biceps <dbl>,
# Forearm <dbl>, Wrist <dbl>ggstaplot
En ggstaplot también podemos hacer una gráficos de correlación.
library(ggstatsplot)You can cite this package as:
Patil, I. (2021). Visualizations with statistical details: The 'ggstatsplot' approach.
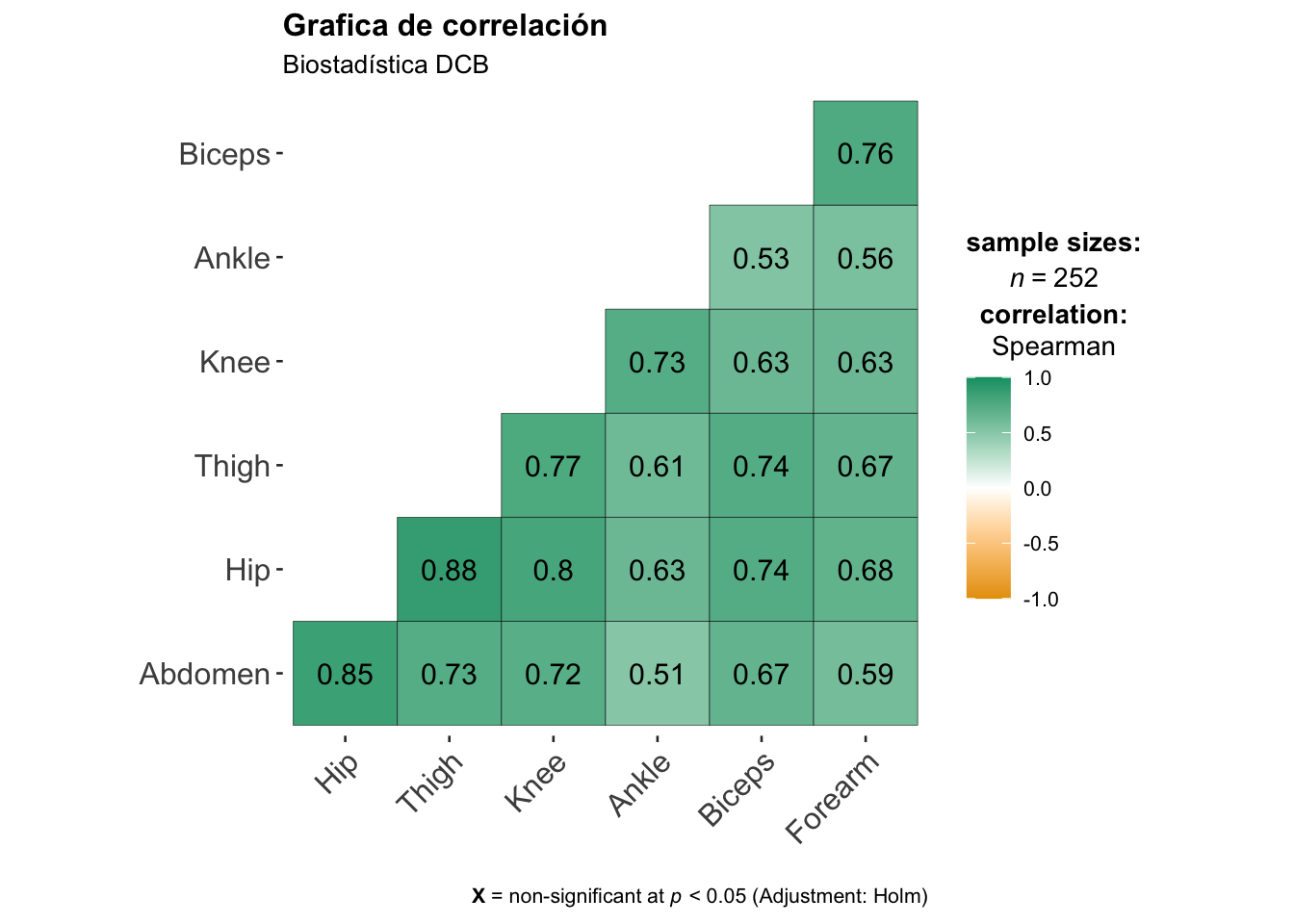
Journal of Open Source Software, 6(61), 3167, doi:10.21105/joss.03167ggcorrmat(
data = df[, 8:14], ## Data Frame
type = "np", ## which correlation coefficient is to be computed
matrix.type = "lower", ## Estructura de la gráfica
title = "Grafica de correlación", ## custom title
subtitle = "Biostadística DCB" ## custom subtitle
)
Gráficos scarterplot
Se pueden realizar gráficos de dispersión y agregar valores p y una línea de tendencia de regresión
El siguiente código muestra la correlación entre la densidad mineral y el porcentaje de grasa
cor.test(Density, Fat)
Pearson's product-moment correlation
data: Density and Fat
t = -100.22, df = 250, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9904570 -0.9843641
sample estimates:
cor
-0.9877824 plot(Density, Fat, main = "Densidad mineral vs Porcentaje de grasa ",xlab="Densidad mineral", ylab="Porcentaje de grasa", col="cyan4", pch=20)
# Segunda capa
text(x=1.06, y=40, label="r=-0.99; p<0.001")
# Tercera capa
abline(lm(Fat~Density))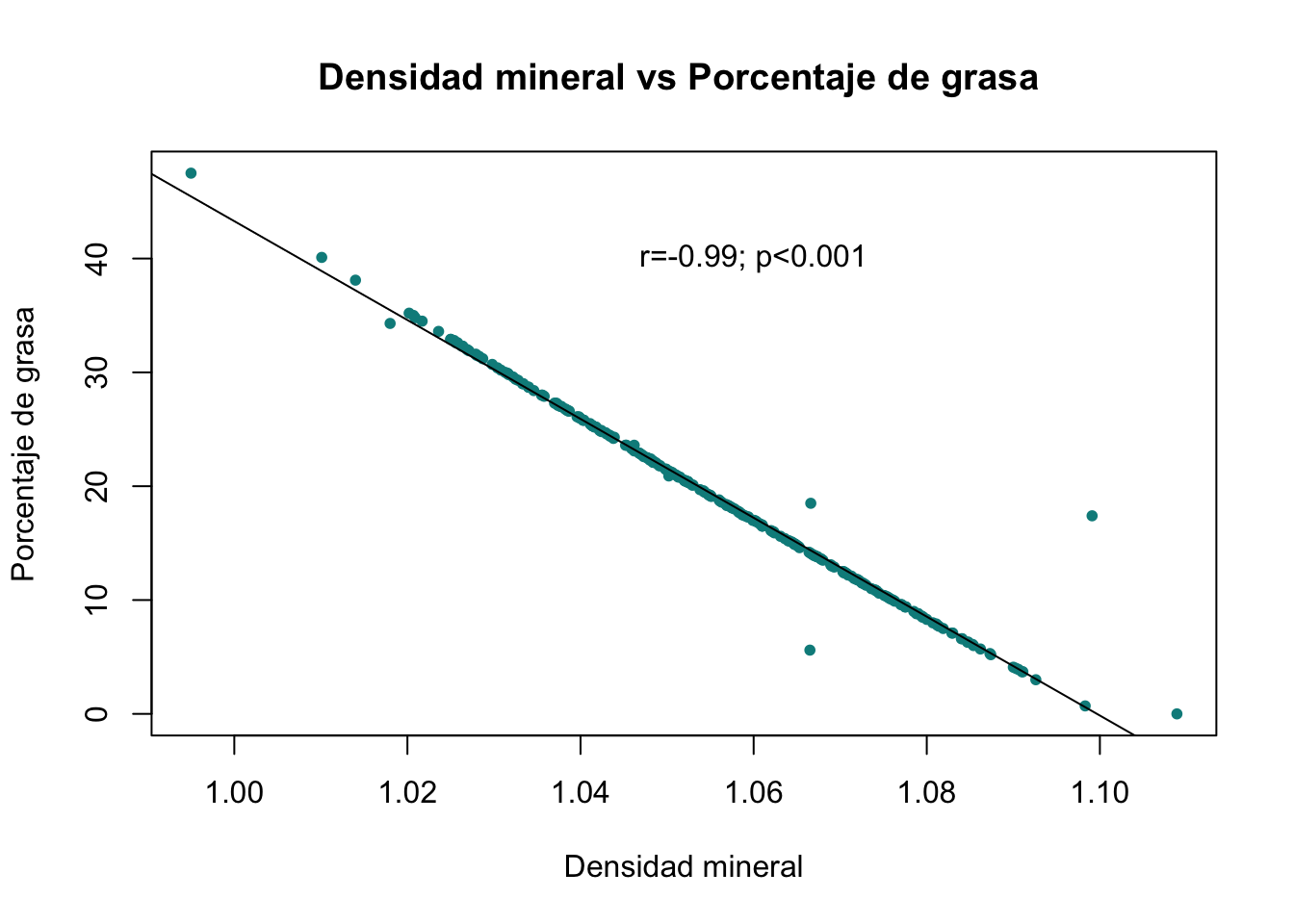
Con ggstatplot los gráficos serían
bodyfat|>
ggstatsplot::ggscatterstats(
x= Density,
y =Fat,
type = "p"
)Registered S3 method overwritten by 'ggside':
method from
+.gg ggplot2`stat_xsidebin()` using `bins = 30`. Pick better value with `binwidth`.
`stat_ysidebin()` using `bins = 30`. Pick better value with `binwidth`.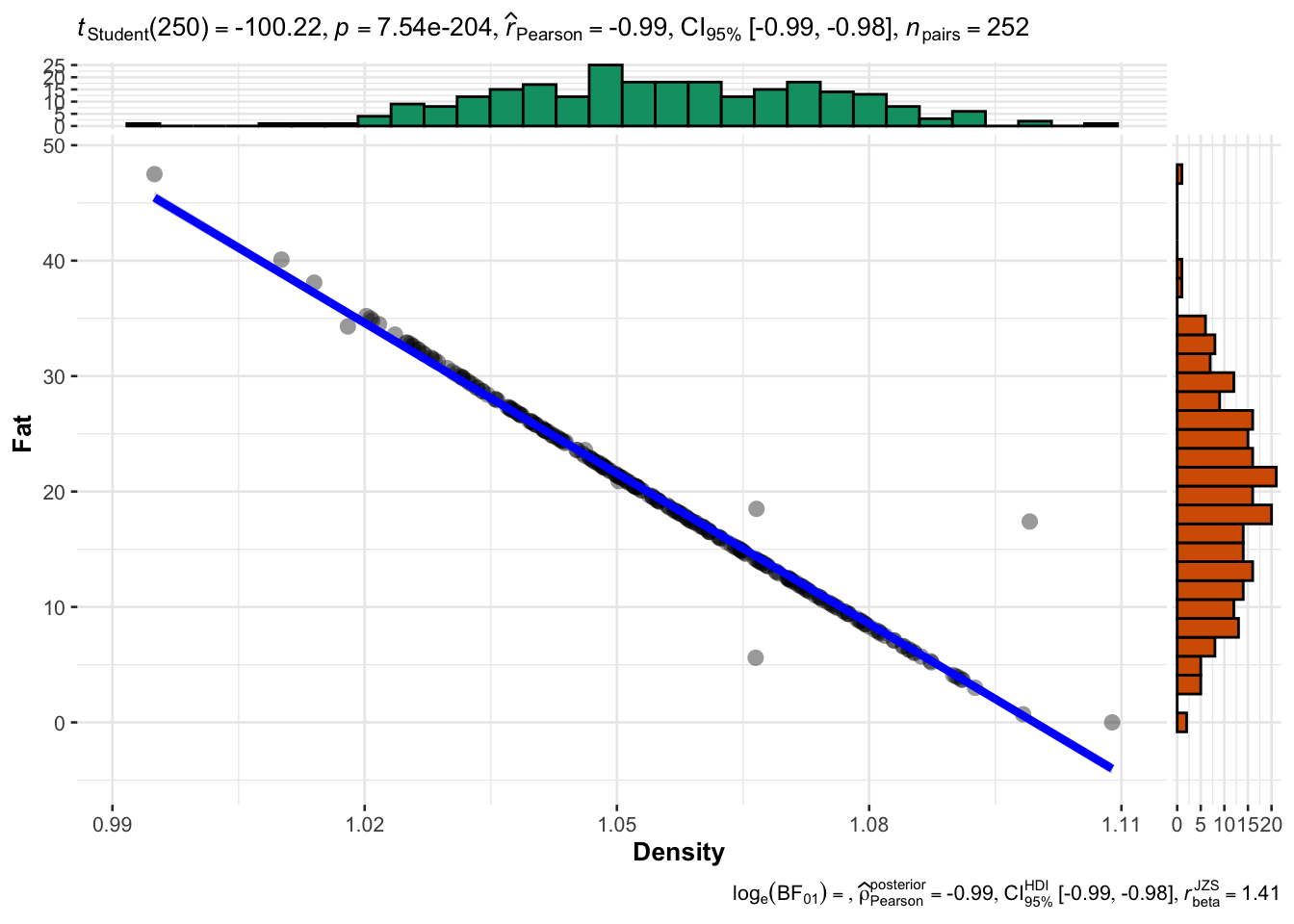
Para pruebas no paramétricas sería:
bodyfat|>
ggstatsplot::ggscatterstats(
x= Density,
y =Fat,
type = "np"
)`stat_xsidebin()` using `bins = 30`. Pick better value with `binwidth`.
`stat_ysidebin()` using `bins = 30`. Pick better value with `binwidth`.
Ejercicios correlación
Ejercicio 14.1
Utilizando la base de datos bodyfat estime: la correlación entre el porcentaje de grasa y e resto de las variabes a) realice gráficas de dispersión b) realice la preuabd e correlación con la función cor.test()
Ejercicio 14.2
La base de datos Health searches by US Metropolitan Area que puede descargar aquí, contiene datos del número de busquedas de problemas de salud por código postal en EUA. Con estos datos se puede estimar la relación mediante correlación entre diferentes problemas de salud en las regiones estudiadas.
Realice al menos tres matrices de correlación distintas para identificar si determinados problemas de salud estar correlacionados. Separe sus resultados por año. En esta versión de la base de datos, solamente se incluyen datos del 2010 al 2017
Si es necesario realice pruebas de normalidad para conocer el tipo de coeficiente de correlación a aplicar.
Ejercicio 14.3
utilice la función ggscatterstats de la librería ggstatplot para realizar al menos 5 gráficos de dispersión, puede utilizar la base de datos bodyfat o la base de datos Health searches by US Metropolitan Area
Regresión
Los aspectos teóricos de la regresión lineal fuero revisados en la presentación. Aquí solo se revisaran los ejercicios prácticas sobre regresión lineal
Ejemplos de regresión linela simple
Utilizando la base de datos saltBP.txt que puede descargar aquí realice un modelo de regresión lineal simple para evaluar la relación entre el consumo de sal (salt) y la presión arterial (BP)
- Correlación y relación lineal
Un buen comienzo es evaluar la correlación que existen entre las variables de interés
El objeto saltBP contiene la base de datos para el ejercicio.
cor.test(saltBP$BP, saltBP$salt)
Pearson's product-moment correlation
data: saltBP$BP and saltBP$salt
t = 7.3888, df = 23, p-value = 1.631e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.6636134 0.9267667
sample estimates:
cor
0.8387992 ggscatterstats(data=saltBP, x="BP", y= "salt", )`stat_xsidebin()` using `bins = 30`. Pick better value with `binwidth`.
`stat_ysidebin()` using `bins = 30`. Pick better value with `binwidth`.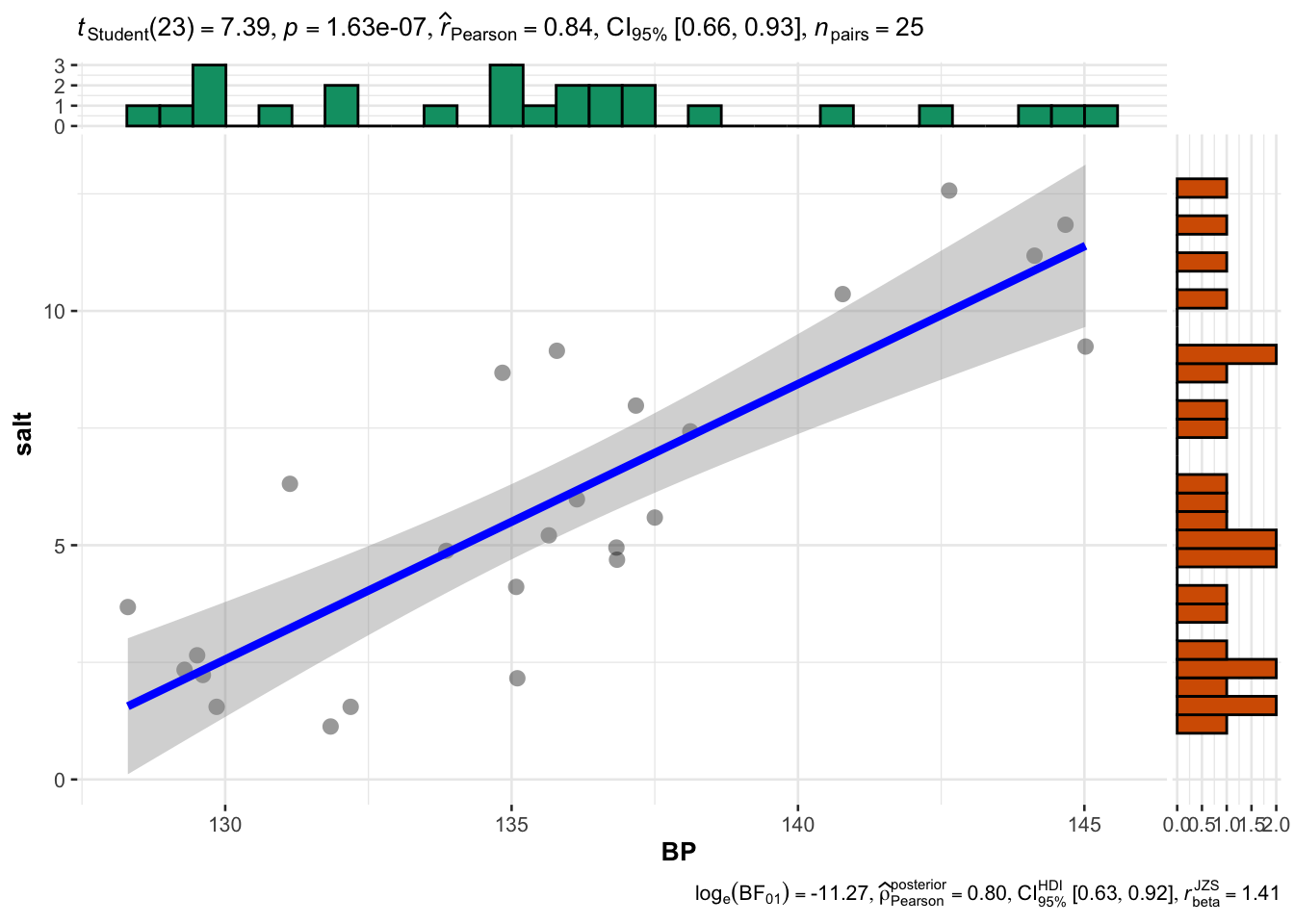
- Crear un objeto que contenga nuestro modelo de regresión lineal
mod1 <- lm(saltBP$BP~saltBP$salt)# Primero variable dependiente- Obtener los parámetros del modelo
summary(mod1)
Call:
lm(formula = saltBP$BP ~ saltBP$salt)
Residuals:
Min 1Q Median 3Q Max
-5.0388 -1.6755 0.3662 1.8824 5.3443
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 128.616 1.102 116.723 < 2e-16 ***
saltBP$salt 1.197 0.162 7.389 1.63e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.745 on 23 degrees of freedom
Multiple R-squared: 0.7036, Adjusted R-squared: 0.6907
F-statistic: 54.59 on 1 and 23 DF, p-value: 1.631e-07- Interpretación
- El modelo es útil ya que se obtuvo un valor de \(p\) en el ANOVA de 1.631e-07. Esto indica que la variación de los residuos no es mayor a la del modelo y por tanto mi regresión es valida. Una variación mayor en los residuos indica que el modelo no explica el comportamiento de los datos
- El coeficiente \(\beta_1\) es significativo (saltBP$BP 0.58784 0.07956 7.389 1.63e-07 ***), por tanto podemos decir que es distinto de cero.
- El valor de \(\beta_1\) es de 1.197, esto indica que en promedio aumento en una unidad del consumo de sal la presión arterial aumenta en 1.197.
- El valor de \(R^2\) es de 0.7036 lo cual indica que el modelo explica un 76% la variación en la BP daba por salt
- Obtener los intervalos de confianza. Se pueden obtener los intervalos de confianza para los coeficientes de la regresión utilizando la función
confint
confint(mod1) 2.5 % 97.5 %
(Intercept) 126.3369606 130.895834
saltBP$salt 0.8617951 1.531993- Validez del modelo. Para probar la validez del modelo se grafican los residuales. Esto lo puede hacer utilizando la función plot
plot(mod1)
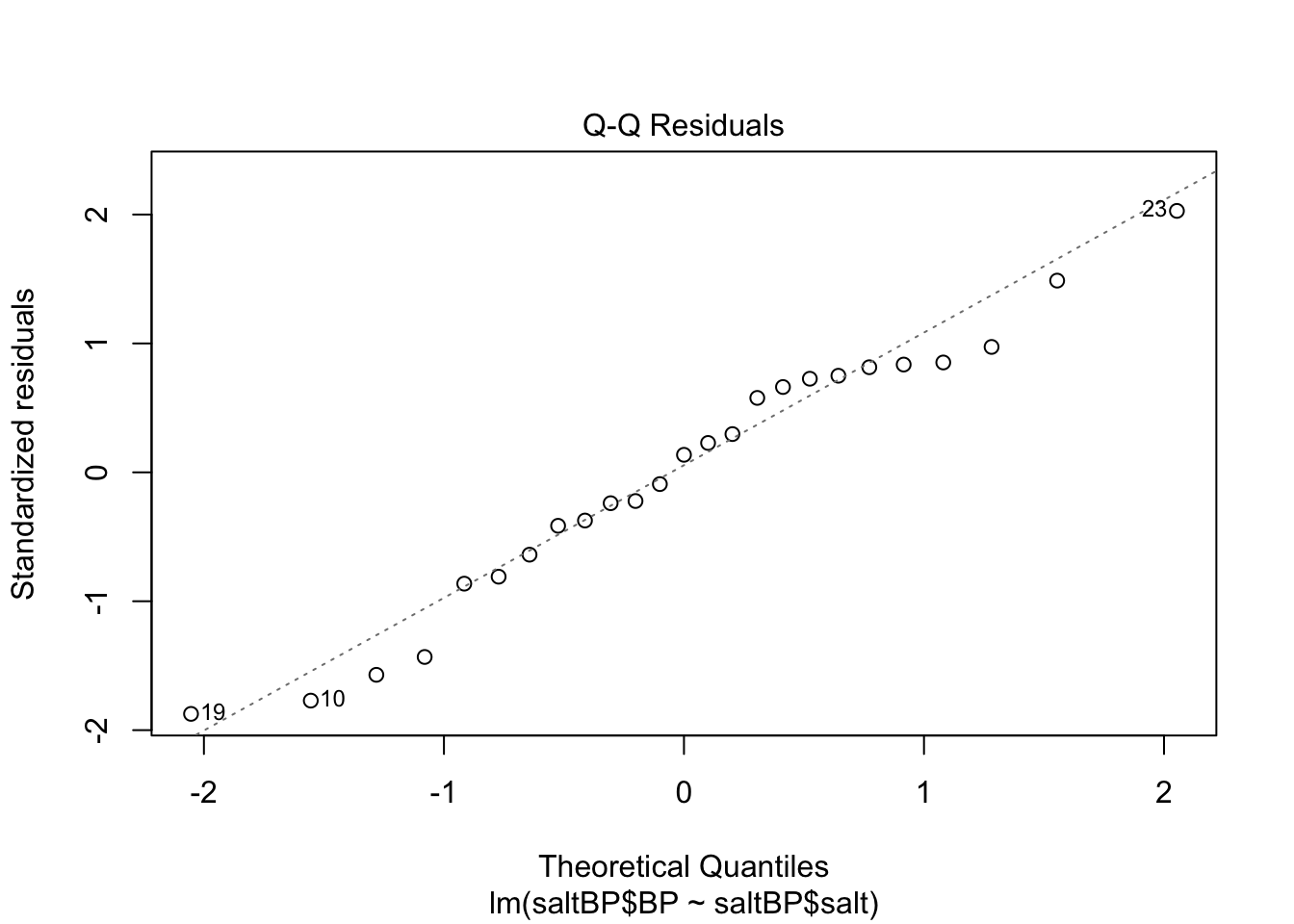
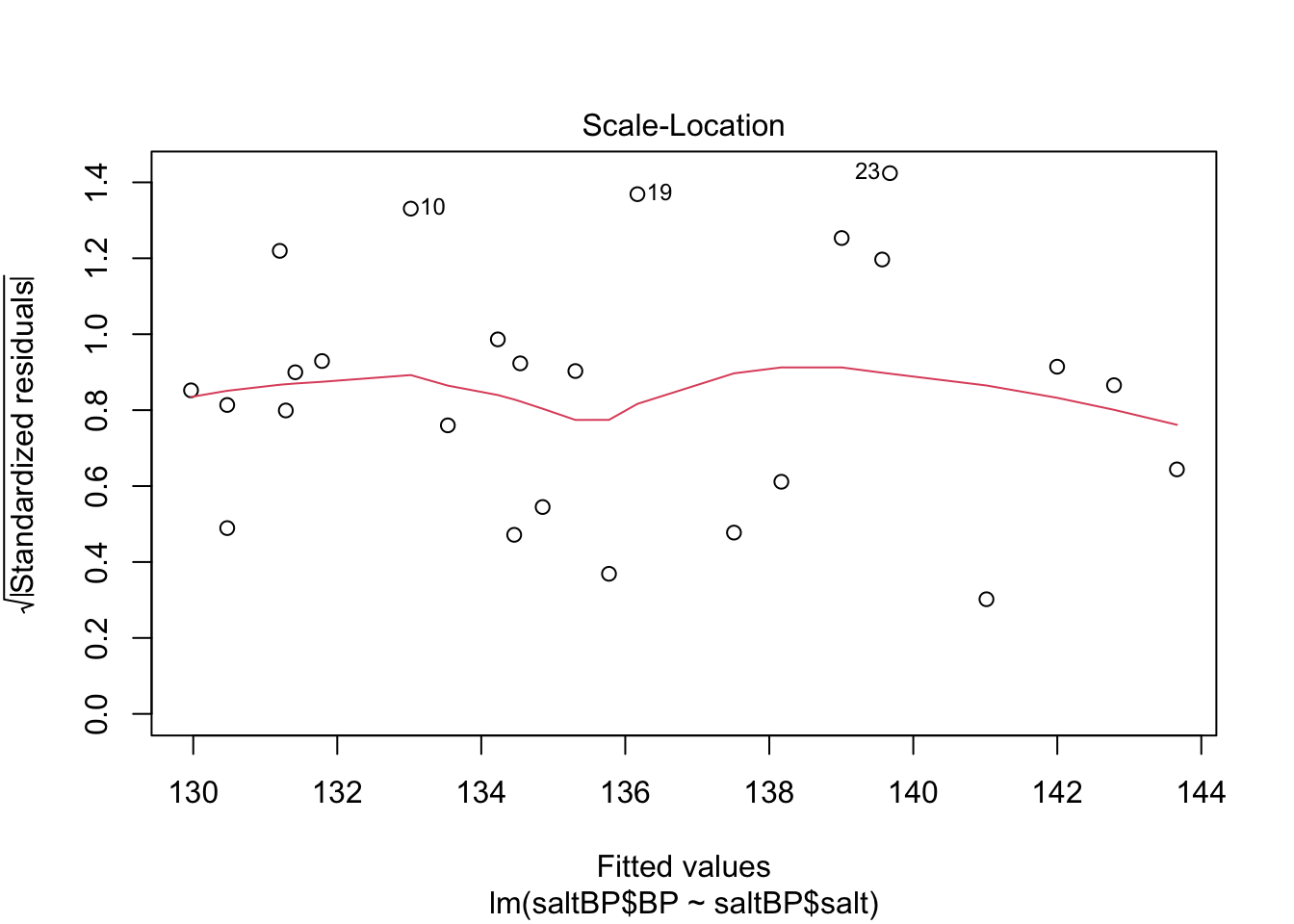

Otro ejemplo
Se desea comprobar la dependencia de la edad sobre la adiponectina. Construya un modelo de regresión lineal utilizando la base de datos SLE Dataset 3
Puede descargar la base de datos aquí
- Correlación
plot(SLE_dataset3$Adiponectin~ SLE_dataset3$Age, main="Concentraciones de adiponectina por edad")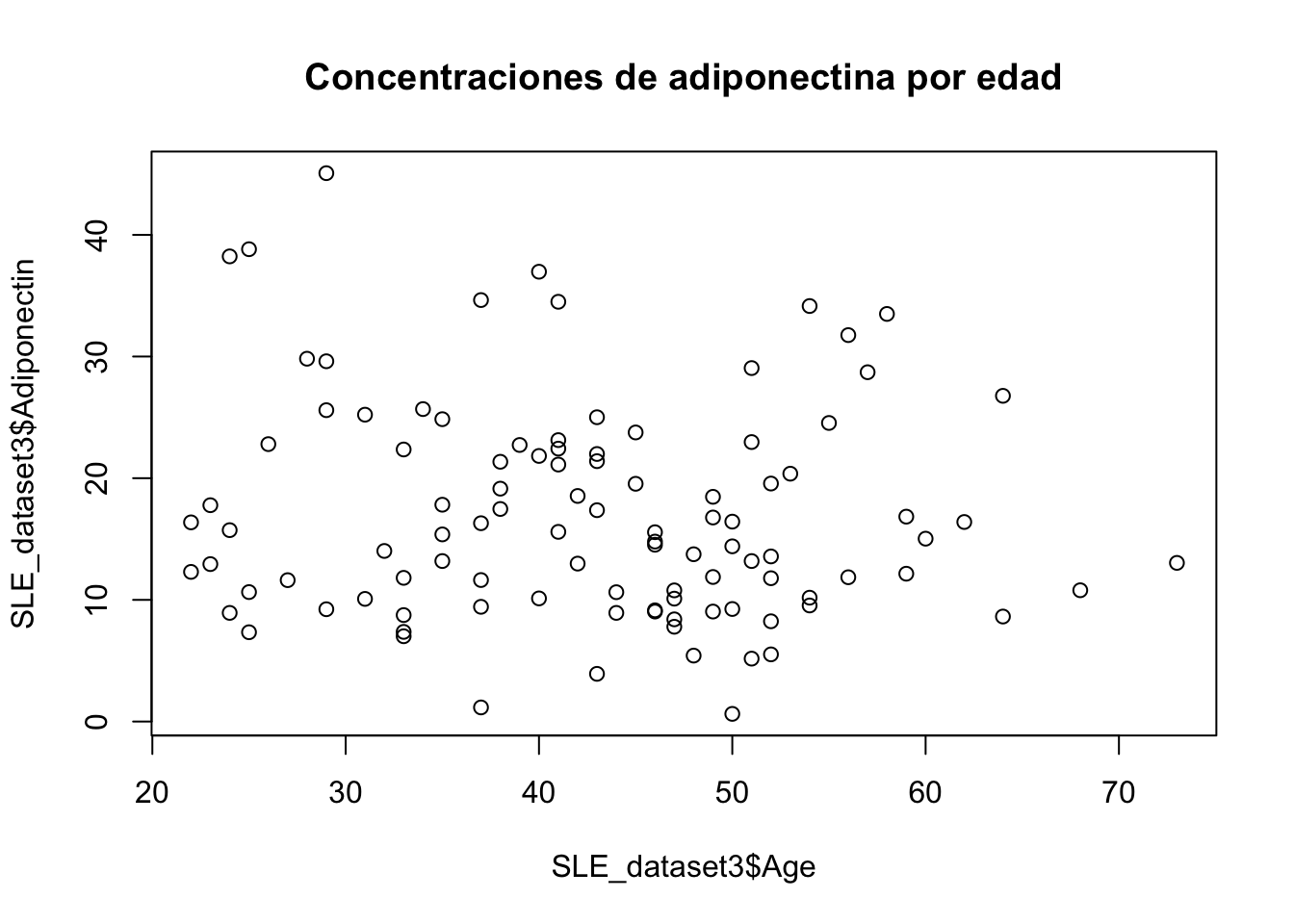
cor.test(SLE_dataset3$Adiponectin,SLE_dataset3$Age)
Pearson's product-moment correlation
data: SLE_dataset3$Adiponectin and SLE_dataset3$Age
t = -1.2614, df = 101, p-value = 0.2101
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.31057423 0.07069386
sample estimates:
cor
-0.1245346 ggscatterstats(data=SLE_dataset3, x="Adiponectin", y="Age")`stat_xsidebin()` using `bins = 30`. Pick better value with `binwidth`.
`stat_ysidebin()` using `bins = 30`. Pick better value with `binwidth`.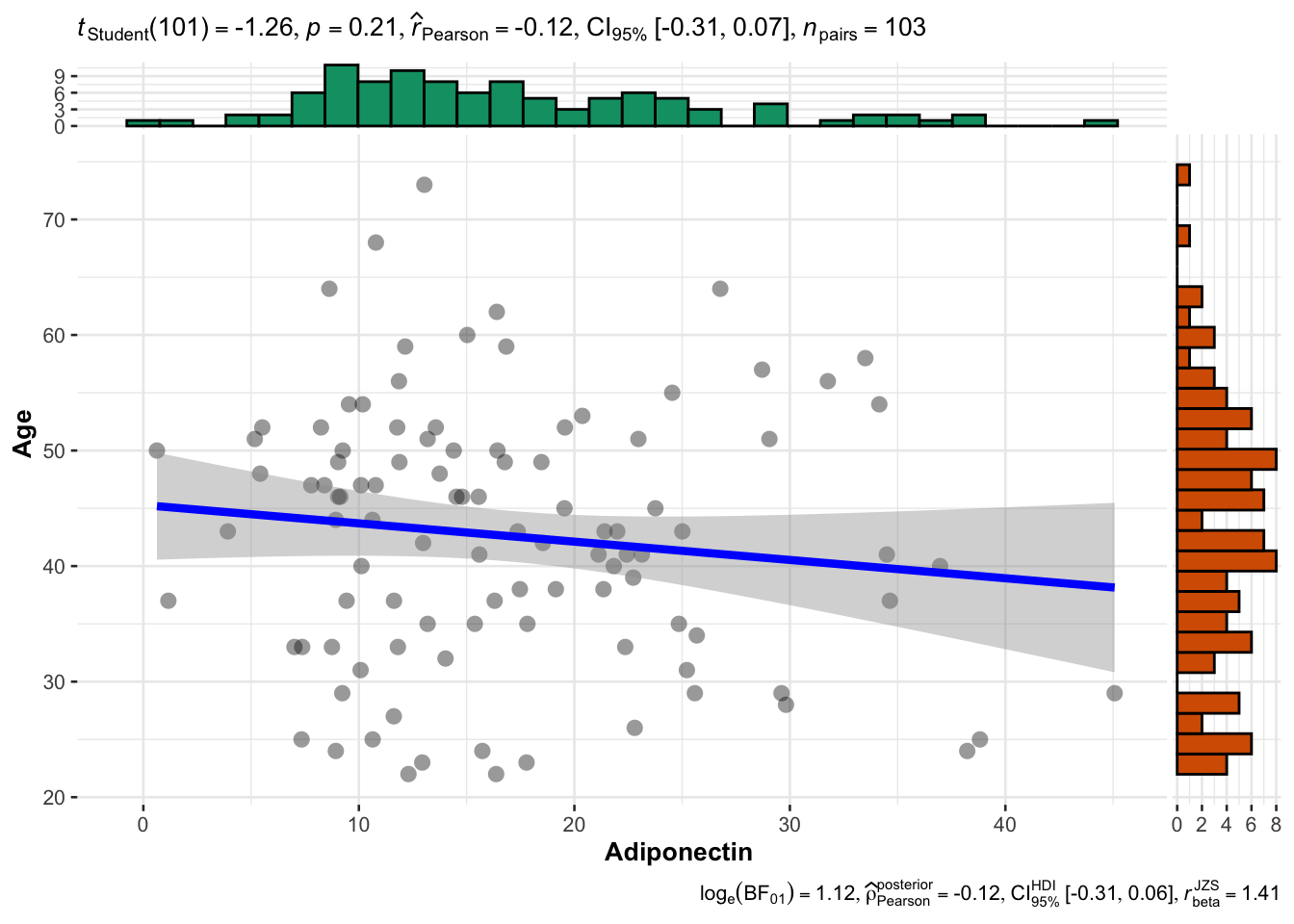
- Construir objeto
mod2 <- lm(SLE_dataset3$Adiponectin~ SLE_dataset3$Age)- Resultados del modelo
summary(mod2)
Call:
lm(formula = SLE_dataset3$Adiponectin ~ SLE_dataset3$Age)
Residuals:
Min 1Q Median 3Q Max
-16.372 -6.577 -1.860 4.818 26.754
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 21.15562 3.41905 6.188 1.32e-08 ***
SLE_dataset3$Age -0.09792 0.07763 -1.261 0.21
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8.832 on 101 degrees of freedom
Multiple R-squared: 0.01551, Adjusted R-squared: 0.005761
F-statistic: 1.591 on 1 and 101 DF, p-value: 0.2101- Interpretación
- La adiponectina es independiente de la edad. El ANOVA nos dice que el modelo no es adecuado ya que la variación de los residuales es muy alta
- El coeficiente \(\beta_1\) no es siginifativo por lo tanto no podemos asegurar que sea distinto de cero
- Validez del modelo
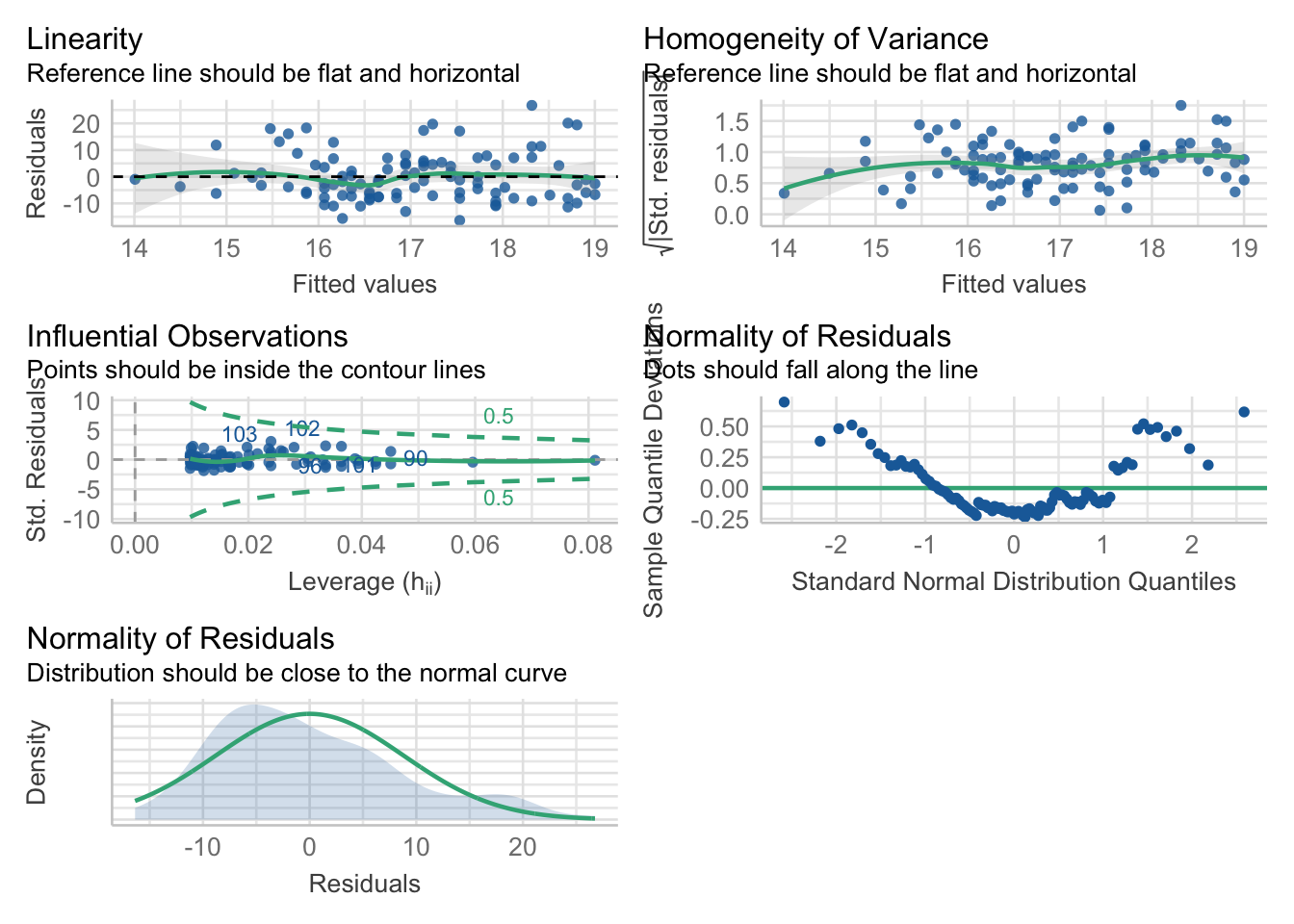
plot(mod2)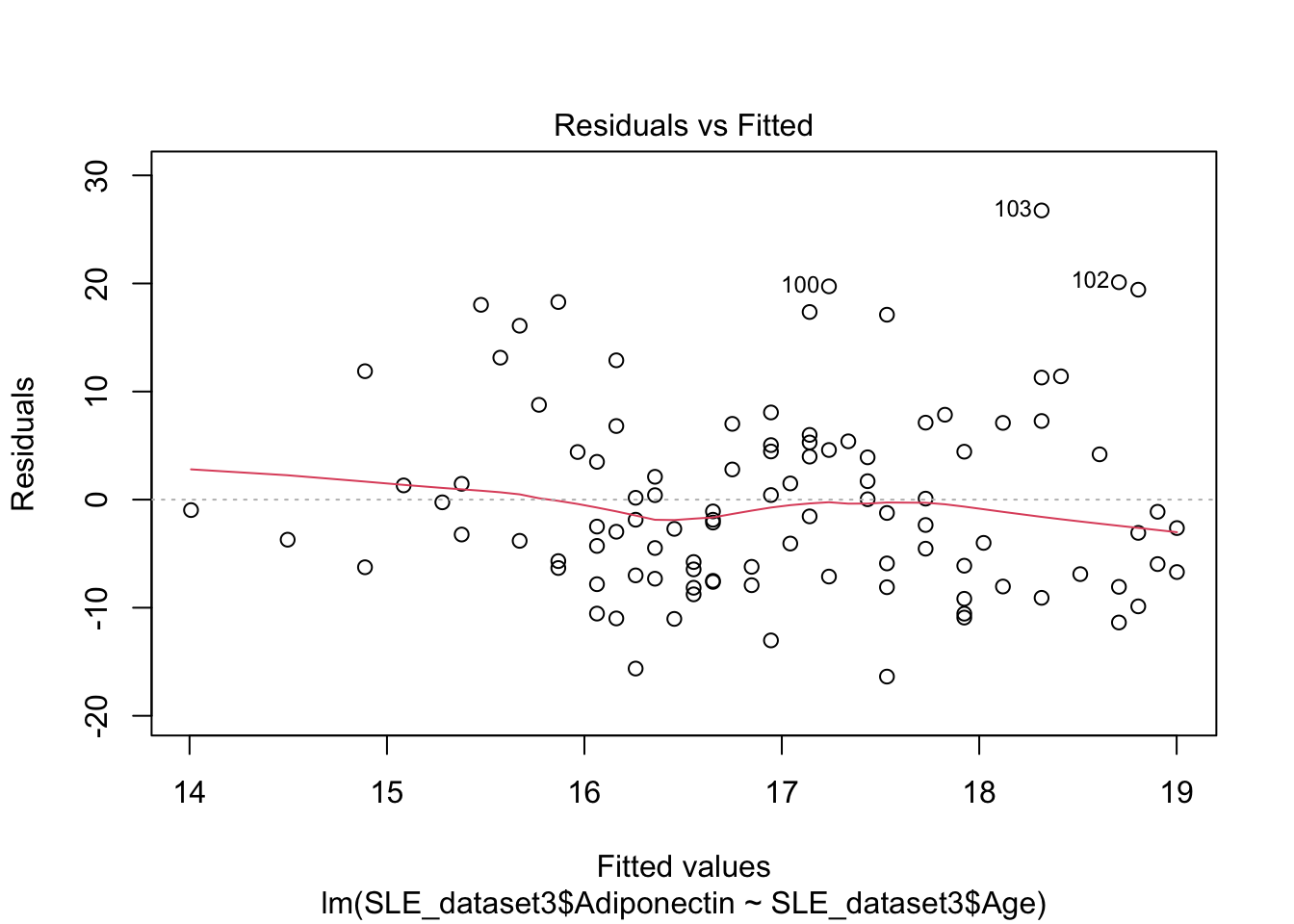
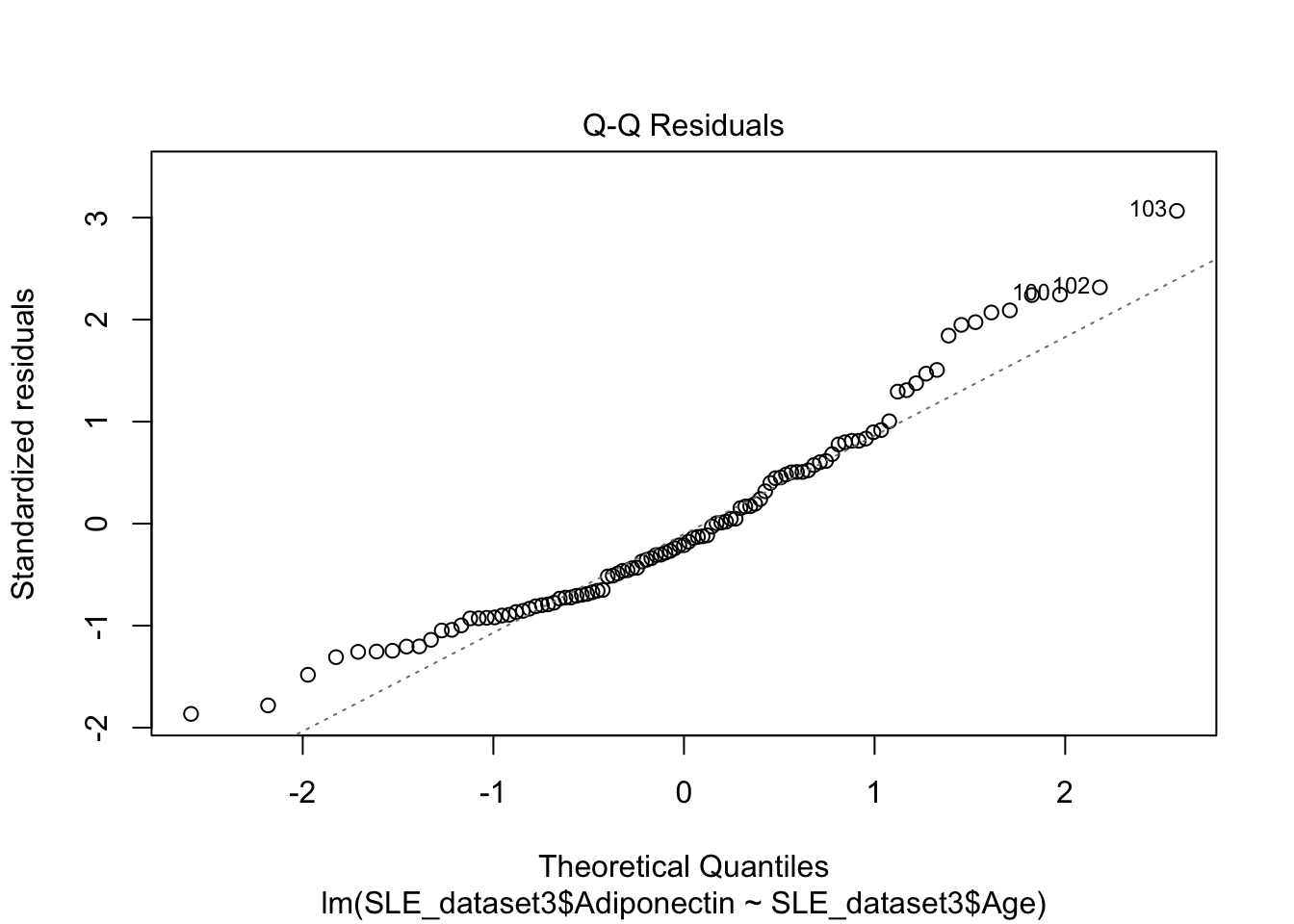

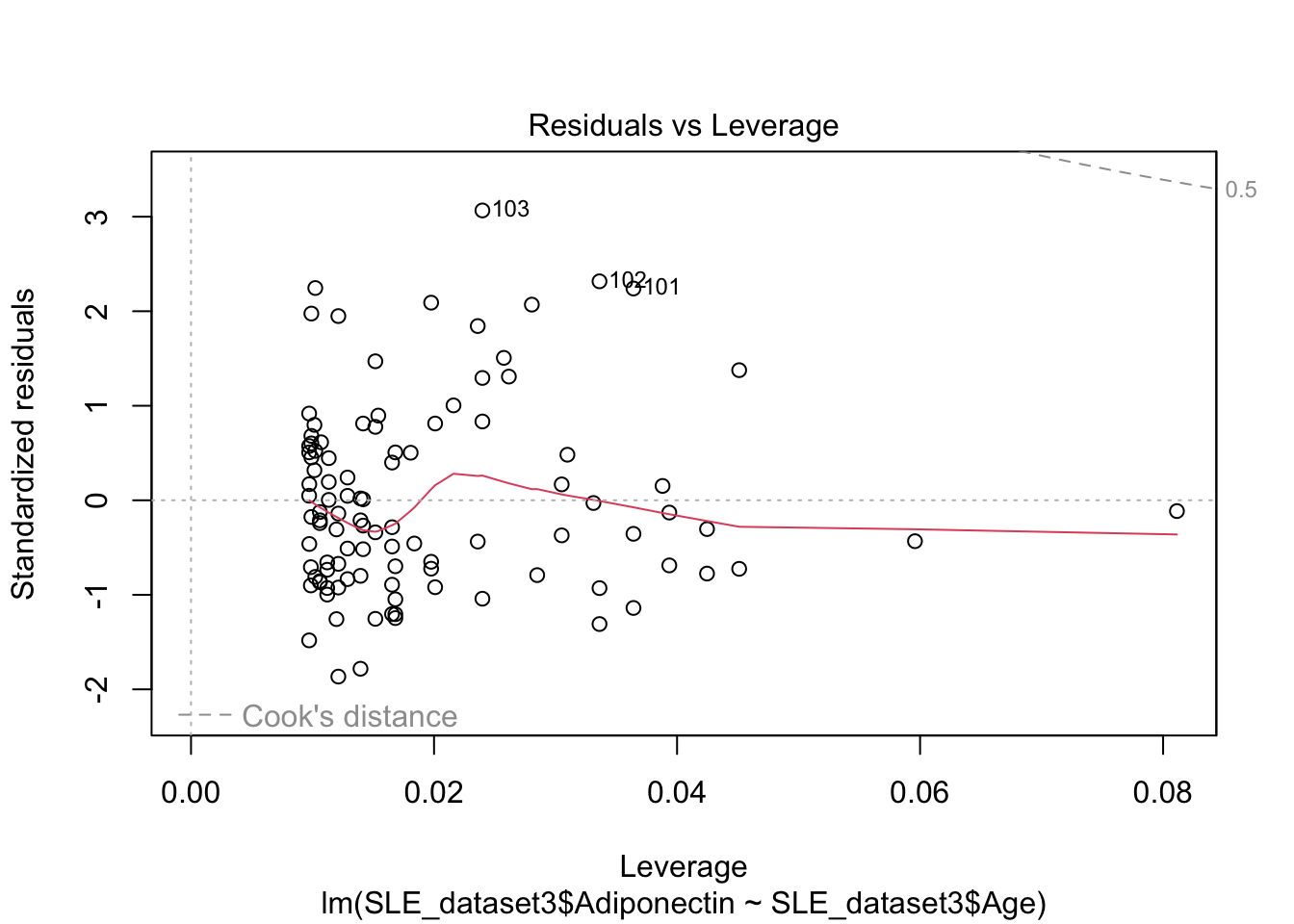
El gráfico Q-Q muestra que los residuos no se apegan a una distribución normal. Por tanto nuestro modelo no es valido.
Ejercicios regresión lineal simple y correlacioón
Ejercicio 14.4
Construya un modelo para evaluar la asociación de la capacidad pulmonar (LungCap) y la edad (Age). Utilice la base de datos LungCapData. Haga una interpretación del modelo y de sus gráficas.
Puede descargar la base de datos aquí
Ejercicio 14.5
Construya un modelo para evaluar la asociación del peso (Weight) y la talla (Height) utilizando la base de datos bodyfat. Haga una interpretación del modelo y de sus gráficas
Ejercicio 14.6
Utilizando la base de datos bodyfat, realice modelos de regresión para identificar la relación de las variables del data frame y el peso de los pacientes. Si lo necesita cree una función
Ejercicio 14.7
Cree una función que le permita crear un gráfico de dispersión y los valores para los tres coeficientes de correlación (pearson, spearman y kenall) con su respectivo valor.
Utilizando la base de datos BodyTemperature.txt y la función creada anteriormente, responda lo siguiente:
- evalué la correlación de estás variables.
- Demuestre que las variables muestran asociación lineal
- construya un modelo de regresión lineal simple para la temperatura corporal usando la frecuencia cardíaca como predictor.
- Interprete la estimación del coeficiente de regresión y examine su significación estadística.
- Encuentre el intervalo de confianza del 95% para el coeficiente de regresión.
- Encuentre el valor de R 2 y demuestre que es igual al coeficiente de correlación muestral.
- Cree gráficas de diagnóstico simples para su modelo e identifique posibles valores atípicos.
- Si la frecuencia cardíaca de alguien es 75, ¿cuál sería su estimación de la temperatura corporal de esta persona?
Puede descargar la base de datos aquí
Ejercicio 14.8
Cree un modelo para evaluar la dependencia del peso al nacer de un bebé (bwt) con el peso de su madre en el último período menstrual (lwt). Utilice la base de datos birthwt.
- Con la función creada en la pregunta anterior evalué la correlación de estás variables.
- Demuestre que las variables muestran asociación lineal
- Interprete su estimación del coeficiente de regresión y examine su significación estadística.
- Encuentre el intervalo de confianza del 95% para el coeficiente de regresión.
- Si el peso de la madre en el último período menstrual es de 170 libras, ¿cuál sería su estimación del peso al nacer de su bebé?
Ejercicio 14.9
Utilizando la base de datos del problema anterior construya un modelo para evaluar la dependencia del peso de la madre en el último período menstrual (lwt) y la edad.
- Con la función creada anteriormente evalué la correlación de estás variables.
- Demuestre que las variables muestran asociación lineal
- Interprete las estimaciones de los coeficientes de regresión y comente su significación estadística.
- Encuentre el intervalo de confianza del 95% para los coeficientes de regresión.