Introduction to Pure Mathematics
Florian Bouyer and John Mackay
16 September 2024
- 1 Introduction
- 2 The building blocks of pure mathematics - sets and logic
- 3 The rationals are not enough
- 4 Proof by induction
- 5 Studying the integers
- 6 Moving from one set to another - Functions
- 7 Cardinality
- 8 Sets with structure - Groups
- 9 Linking groups together
- 10 Modular arithmetic and Lagrange
- 11 Taming infinity
1 Introduction
A mathematical theory is not to be considered complete until you have made it so clear that you can explain it to the first man whom you meet on the street. – David Hilbert –
Proofs are at the heart of mathematics, distinguishing what we know is mathematically true (or untrue) from what we still don’t know. The first aim of this course is to see different types of proofs and mathematical reasoning, and learning how to make your own mathematical arguments. Reading proofs will develop our critical thinking, e.g., how does this sentence follow from the previous one; how have we used all our assumptions; what happen if we tweak our assumptions; etc. Writing proofs will develop our creative and communication skills, e.g., how do we put together various ideas to come up with a new one; how do we explain our argument to someone else; etc.
As we can not see mathematical arguments without mathematical content, the second aim of this course is to give you a strong foundation to pure mathematics - a very broad branch of mathematics.
This notes are based on the notes from a previous Introduction to Proofs and Group Theory course (Steffi Zegowitz; Lynne Walling; Jos Gunns; Jeremy Rickard; John Mackay), and the early chapters from a previous Analysis course (Thomas Jordan; Ivor McGillivray; Oleksiy Klurman); .
1.1 How to use these notes
These notes are colour coded to help you identify the important bits.
Results from the course, which will either be theorems, lemmas, propositions or corollaries, will have this background colour. It is important to know them so to be able to apply them to different situations.
After most results, there will be a proof with this background colour. It is important to understand each proof as similar techniques can be applied in different mathematical situations. Note that many proofs are left as exercises so that one can practice coming up and writing proofs.
□
Interest, History and Etymological (origin of words) notes will not have a background colour, however there is a line to show the start and the end of the note. These notes are there for general interest and is not examinable content.
Most of the Etymology notes comes from the book “The words of Mathematics” by Steven Schwartzman (The Mathematical Association of America, 1994)
Most of the history of the development of Group Theory comes from the article “The Evolution of Group Theory: A Brief Survey” by Israel Kleiner (Mathematics Magazine, Vol 59, No 4, 192-215, 1986).2 The building blocks of pure mathematics - sets and logic
To be able to prove mathematical results, we need two ingredients - the setting in which we are doing maths; and the logical reasoning we use to do maths.
2.1 Sets
Before we can start to do maths, we need to know the setting in which we are doing maths. For this reason, sets can be seen as the building block of all maths.
We use curly brackets { and } to denotes sets.
We use the symbol \(\in\) to say an element is in a set. We drawn a line through it to negate it, i.e. we use \(\notin\) to say an element is not in a set.
We use the symbol \(<\) to mean “(strictly) less than” and \(\leq\) to mean “less than or equal to”. Similarly we use \(>\) to mean “greater than” and \(\geq\) to mean “greater than or equal to”The set of trigonometric functions: \(\{\sin(x),\cos(x),\tan(x)\}=\{\cos(x),\tan(x),\cos(x),\sin(x)\}\).
The set of integers between \(2\) and \(6\): \(\{2,3,4,5,6\}=\{6,4,2,2,3,4,6,5\}\).
Since \(2\leq 6\) and \(6\leq 6\), we have \(6 \in \{2,3,4,5,6\}\), however \(15 \notin \{2,3,4,5,6\}\) as \(15>6\).
If a set does not have any elements, we call it the empty set and use \(\emptyset\) (or \(\{\ \}\)).
\(\mathbb{Z}\) is the set of integers, that is \(\mathbb{Z}=\{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\}\).
The symbol \(\mathbb{Z}\) comes from the German “Zahlen” - which means numbers. It was first used by David Hilbert (German mathematician, 1862 - 1943), and popularised in Europe by Nicolas Bourbaki (a collective of mainly French mathematicians, 1935 - ) in their 1947 book “Algèbre”. Integers come from the Latin in, which means “not”, and tag which means “to touch”. An integer is a number that has been “untouched”, i.e. “intact” or “whole”.
The set of integers is equipped with the operations of additions \(+\) and multiplication \(\cdot\) that satisfy the following 10 arithmetic properties (5 relating to addition; a Distributive Law; and 4 relating to multiplication):
(A1) - Closure under addition For all \(x,y \in \mathbb{Z}\) we have \(x+y \in \mathbb{Z}\).
(A2) - Associativity under addition For all \(x,y,z \in \mathbb{Z}\) we have \(x+(y+z)=(x+y)+z\).
(A3) - Commutativity of addition For all \(x,y\in\mathbb{Z}\) we have \(x+y=y+x\).
(A4) - Additive identity For all \(x \in \mathbb{Z}\) we have \(x+0=x\).
(A5) - Additive inverse For all \(x \in \mathbb{Z}\) we have \(-x\in\mathbb{Z}\) and \(x+(-x)=0\).
(A6) - Distributive Law For all \(x,y,z\in\mathbb{Z}\) we have \(x(y+z)=xy+xz\).
(A7) - Closure under multiplication For all \(x,y \in \mathbb{Z}\) we have \(xy \in \mathbb{Z}\).
(A8) - Associativity under multiplication For all \(x,y,z \in \mathbb{Z}\) we have \(x(yz)=(xy)z\).
(A9) - Commutativity of multiplication For all \(x,y\in\mathbb{Z}\) we have \(xy=yx\).
(A10) - Multiplicative identity For all \(x \in \mathbb{Z}\) we have \(1\cdot x=x\).
Formally speaking, this is saying that \(\mathbb{Z}\) with \(+\) and \(\cdot\) is a ring. The notion of a ring is explored in more details in later units such as the second year unit Algebra 2. Properties (A1) to (A5) tells us that \(\mathbb{Z}\) with \(+\) is an abelian group. We will explore the notion of groups and abelian groups later in this unit.
On top of these 10 arithmetic properties, \(\mathbb{Z}\) is well ordered, i.e., it comes with 4 order properties:
(O1) - trichotomy For all \(x,y\in\mathbb{Z}\) either \(x<y\), \(x=y\) or \(x>y\).
(O2) - transitivity For all \(x,y,z\in\mathbb{Z}\), if \(x<y\) and \(y<z\) then \(x<z\).
(O3) - compatibility with addition For all \(x,y,z in \mathbb{Z}\), if \(x<y\) then \(x+z<y+z\).
(O4) - compatibility with multiplication For all \(x,y,z \in \mathbb{Z}\), if \(x<y\) and \(z>0\) then \(zx<zy\).
There are many words above that seems to have come from nowhere, but can be related back to words used in everyday English.
Associative comes from the Latin ad meaning “to” and socius meaning “partner, companion”. An associate is someone who is a companion to you. The property \(x+(y+z)=(x+y)+z\) shows that it doesn’t matter who \(y\) “keeps company with”, the result is still the same.
Commutative comes from the Latin co meaning “with” and mutare meaning “to move”. To commute is “to change, to exchange, to move”. In everyday situation, a commute is the journey (i.e., moving) from home to work. The property \(x+y=y+x\) shows that we can move/exchange \(x\) and \(y\) and the result is the same.
Identity comes from the Latin idem meaning “same”. The additive identity is the element which keeps other elements the same when added to it. The multiplicative identity is the element which keeps other elements the same when multiplied by it.
Inverse comes from in and vertere which is the verb “to turn”. The additive inverse of \(x\) is the quantity that turns back “adding \(x\)”.
Trichotomy comes from the Greek trikha meaning “in three parts” and temnein meaning “to cut”. If you pick \(x\in \mathbb{Z}\), then you can cut \(\mathbb{Z}\) into three parts, the integers less than \(x\), the integers equal to \(x\) and the integers greater than \(x\).
Transitive comes from the Latin trans meaning “across, beyond” and the verb itus/ire meaning “to go”. Knowing \(x<y\) and \(y<z\) allows us to go across/beyond \(y\) to conclude \(x<z\).
As seen from the properties above, we often need to quantify objects in mathematics, that is we need to distinguish between a criteria always being met (“for all”), or the existence of a case where a criteria is met (“there exists”). Sometimes we also need to distinguish whether there is a unique case where a criteria is met.
We have the following symbolic notation:
The symbol \(\forall\) denotes for all, or equivalently, for every.
The symbol \(\exists\) denotes there exists.
We use \(\exists !\) to denote there exists a unique, or equivalently there exists one and only one.
□
We can use \(\mathbb{Z}\) as a starting point to construct different sets.
Within the curly brackets of a set, we use colon, \(\colon\), to mean “such that”.
Returning to the previous example, the set of integers between \(2\) and \(6\) can be written as \(\{x \in \mathbb{Z}\colon 2\leq x \leq 6\}\);
We use \(+\) to denote the positive numbers in a set. I.e., \(\mathbb{Z}_+= \{x\in \mathbb{Z}: x> 0\} = \{1,2,\dots,\}\) denotes the set of positive integers.
Similarly, \(\mathbb{Z}_- = \{x\in \mathbb{Z}: x<0 \} = \{-1,-2,-3,\dots\}\) denotes the set of negative integers.
We denote the set of non-negative integers by \(\mathbb{Z}_{\geq 0}=\{x\in \mathbb{Z}: x\geq 0\} = \{0,1,2,\dots,\}\).
If \(n \in \mathbb{Z}\), we write \(n\mathbb{Z} = \{nx:x\in \mathbb{Z}\} = \{y \in \mathbb{Z}: \exists x \in \mathbb{Z} \text{ with } y=xn\} = \{\dots,-3n,-2n,-n,0,n,2n,3n,\dots\}\).
You may have also heard of the natural numbers denoted \(\mathbb{N}\). However, some sources consider \(0\) as a natural number (so \(\mathbb{N} = \mathbb{Z}_{\geq 0}\)) and other consider \(0\) not to be a natural number (so \(\mathbb{N} = \mathbb{Z}_+\)). To avoid any confusion (and because we will need \(\mathbb{Z}_{\geq 0}\) sometimes and \(\mathbb{Z}_+\) at other times), we will not be using \(\mathbb{N}\) in this course.
\(\mathbb{Q}\) is the set of rational numbers, that is \(\mathbb{Q}=\left\{\frac{a}{b}:\ a\in\mathbb{Z},\ b\in\mathbb{Z}_+ \right\}\).
We will later see how \(\mathbb{Q}\) can be constructed from \(\mathbb{Z}\) and how this lead to a “natural” way to write each rational numbers
The symbol \(\mathbb{Q}\) stands for the word “quotient”, which is Latin for “how often/how many”, i.e., the quotient \(\frac{a}{b}\) is “how many times does \(b\) fit in \(a\)”. Surprisingly, the word “rational” to describe some numbers came after the use of “irrational” number. Ratio is Latin for “thinking/reasoning”. When the Phythagorean school in Ancient Greece realised some numbers could not be expressed as the quotient of two whole numbers (such as \(\sqrt{2}\), which we will prove later), they called those “irrational”, i.e. numbers that should not be thought about. “Rational” numbers were numbers that were not “irrational”, i.e., one could think about them.
We extend the operations of addition and multiplication as well as the order relation for the integers to the rational numbers. Let \(\frac{a}{b}, \frac{c}{d} \in \mathbb{Q}\), then:
\[\frac{a}{b}+\frac{c}{d} = \frac{ad+bc}{bd} \text{ and } \frac{a}{b}\cdot\frac{c}{d} = \frac{ac}{bd}.\] Similarly to \(\mathbb{Z}\), we have that \(\mathbb{Q}\) with \(+\) and \(\cdot\) satisfies the properties (A1) to (A10) as well as (O1) to (O4). It also satisfy the extra arithmetic property:
(A11) - multiplicative inverse For all \(x\in\mathbb{Q}\) with \(x\neq 0\), we have \(x^{-1} = \frac{1}{x} \in \mathbb{Q}\) and \(x^{-1}x = 1\).
Notice that (A11) is similar to (A5) but for multiplication. As we will see later in the course, another way of saying (A7) to (A11) is that \(\mathbb{Q}\) without \(0\) under \(\cdot\) is an abelian group. As you will see in Linear Algebra, the arithmetic properties of \(\mathbb{Q}\) ((A1) to (A11)) comes from the fact that \(\mathbb{Q}\) is a field.
Similarly with \(\mathbb{Z}\), using \(\mathbb{Q}\) we can construct the sets \(\mathbb{Q}_+\), \(\mathbb{Q}_-\), \(\mathbb{Q}_{\geq 0}\) etc.
2.2 Truth table
Now that we have some objects to work with, we want to know what we can do with them. In a mathematical system, statements are either true or false, but not both at once. We sometimes say a statement \(P\) holds to mean it is true. The label ‘true’ or ‘false’ associated to a given statement is its truth value.
Definitions (i.e., \(\mathbb{Z}\)) and axioms (i.e., (A1)-(A11) ) are statements we take to be true, while propositions, theorems and lemmas are statements that we want to prove are true and often consist of smaller statements linked together. While we often don’t write statements symbolically, looking at truth table and statements help us understand the fundamentals of how a proof works. We first introduce the four building blocks of statements.
We use the symbol \(\neg\) to mean not. The truth table below shows the value \(\neg P\) takes depending on the truth value of \(P\).
| \(P\) | \(\neg P\) |
|---|---|
| T | F |
| F | T |
We will see concrete examples of how to negate statements later in this chapter.
We use the symbol \(\wedge\) to mean and. Let \(P\) and \(Q\) be two statements, we have that \(P\wedge Q\) is true exactly when \(P\) and \(Q\) are true. The corresponding truth table is as follows:
| \(P\) | \(Q\) | \(P\wedge Q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
We use the symbol \(\vee\) to mean or. Let \(P\) and \(Q\) be two statements, we have that \(P\vee Q\) is true exactly when at least one of \(P\) or \(Q\) is true. The corresponding truth table is as follows.
| \(P\) | \(Q\) | \(P\vee Q\) |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
We use the symbol \(\implies\) to mean implies. Let \(P\) and \(Q\) be two statements “\(P \implies Q\)” is the same as “If \(P\), then \(Q\)”, or “for \(P\) we have \(Q\)”. The corresponding truth table is as follows.
| \(P\) | \(Q\) | \(P\implies Q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
The above truth table can seem confusing, but consider the following example.
Recall (A1) - “For all \(x,y \in \mathbb{Z}\) we have \(x+y \in \mathbb{Z}\)”. Let \(P\) be the statement \(x,y \in \mathbb{Z}\) and \(Q\) be the statement \(x+y \in \mathbb{Z}\), then (A1) can be written symbolically as \(\forall x,y, P \implies Q\). This statement is true, regardless of what the value of \(x\) and \(y\) are. But let us look at the truth value of \(P\) and \(Q\) with different \(x\) and \(y\)
| \(x\) | \(y\) | \(P\) | \(Q\) |
|---|---|---|---|
| \(0\) | \(1\) | T | T |
| \(0\) | \(\frac{3}{2}\) | F | F |
| \(\frac{1}{2}\) | \(1\) | F | F |
| \(\frac{1}{2}\) | \(\frac{3}{2}\) | F | T |
Many theorems are of the type “If \(P\) then \(Q\)”. A common method to prove such statement is to start with the assumption \(P\) (i.e., assume \(P\) is true) and use logical steps to arrive at \(Q\).These are often referred to as “direct proofs”.
The above example also shows that you can not start a proof with what you want to prove, as you could start with something false and end up with something true.□
Turning back to sets, we look at examples of direct proofs.
A set \(A\) is a subset of a set \(B\), denoted by \(A\subseteq B\), if every element of \(A\) is also an element of \(B\) (Symbolically: \(\forall x \in A\), we have \(x \in B\)).
We write \(A\not\subseteq B\) when \(A\) is not a subset of \(B\), so there is at least one element of \(A\) which is not an element of \(B\) (Symbolically: \(\exists x \in A\) such that \(x\notin B\)).
A set \(A\) is a proper subset of a set \(B\), denoted by \(A\subsetneq B\), if \(A\) is a subset of \(B\) but \(A\neq B\).Let \(A = 4\mathbb{Z}= \{4n: n\in\mathbb{Z}\}\) and \(B = 2\mathbb{Z}=\{ 2n: n\in \mathbb{Z}\}\). We will prove \(A \subseteq B\) using a direct proof. [If we let \(P\) be the statement \(x \in A\) and \(Q\) be the statement \(x \in B\), note that \(\forall x \in A\) we have \(x\in B\) translate symbolically to \(\forall x, P \implies Q\).]
Let \(x\in A\) [i.e., suppose \(P\) is true]. Then there exists \(n\in\mathbb{Z}\) such that \(x=4n\). Hence, \(x=4n=2(2n)=2m\), for some \(m\in\mathbb{Z}\), i.e. there exists \(m\in \mathbb{Z}\) such that \(x = 2m\). Hence, \(x\in B\) [i.e., \(Q\) is true]. Since this argument is true for any \(x \in A\), we have that for all \(x \in A, x \in B\), hence \(A\subseteq B\).
We will now prove that \(B \not\subseteq A\) by showing there is an element of \(B\) which is not an element of \(A\). Take \(x=10\). Then \(x\in B\) [as \(x=5\cdot 2\)] but \(x\not\in A\) [as \(x = \frac{5}{2} \cdot 4\) but \(4\notin \mathbb{Z}\)].
Combining the two statements above, it follows that \(A\subsetneq B\).To prove something is true for all \(x\in X\), we “let \(x\in X\)” or “suppose \(x\in X\)” with no further conditions. Whatever we conclude about \(x\) is true for all \(x\in X\). This is the technique we used in Part 1. above.
Suppose \(A\) and \(B\) are sets. Showing that \(A=B\) is the same as showing that \(A\subseteq B\) and \(B\subseteq A\).□
We show that \(2\mathbb{Q} = \mathbb{Q}\), by showing \(2\mathbb{Q} \subseteq \mathbb{Q}\) and \(\mathbb{Q} \subseteq 2\mathbb{Q}\).
Let \(x \in 2\mathbb{Q}\). Then there exists \(y \in \mathbb{Q}\) such that \(x = 2y\). By (A6), since \(2,y\in\mathbb{Q}\), we have \(x=2y\in \mathbb{Q}\). As this is true for all \(x\in 2\mathbb{Q}\) we have \(2\mathbb{Q} \subseteq \mathbb{Q}\).
Let \(x \in \mathbb{Q}\). Let \(y = \frac{x}{2}\). Note that \(\frac{1}{2} \in \mathbb{Q}\) so by (A6), since \(\frac{1}{2},x \in \mathbb{Q}\), we have \(y = \frac{x}{2} \in \mathbb{Q}\). Hence, there exists \(y \in \mathbb{Q}\) such that \(x = 2y\), so \(x\in 2\mathbb{Q}\). As this is true for all \(x\in \mathbb{Q}\) we have \(\mathbb{Q} \subseteq 2\mathbb{Q}\).
We can combine the three basic symbols together to make more complicated statements, and use truth tables to find when their truth values based on the truth values of \(P\) and \(Q\).
Let \(P\) and \(Q\) be two statements. The corresponding truth table for \((\neg P) \vee Q\) is as follows.
| \(P\) | \(Q\) | \(\neg P\) | \((\neg P)\vee Q\) |
|---|---|---|---|
| T | T | F | T |
| T | F | F | F |
| F | T | T | T |
| F | F | T | T |
Let \(P\) and \(Q\) be two statements. The corresponding truth table for \((\neg Q) \implies (\neg P)\) is as follows.
| \(P\) | \(Q\) | \(\neg P\) | \(\neg Q\) | \((\neg Q) \implies (\neg P)\) |
|---|---|---|---|---|
| T | T | F | F | T |
| T | F | F | T | F |
| F | T | T | F | T |
| F | F | T | T | T |
2.3 Logical Equivalence
As well as combining statements together to make new statements, we also want to know whether two statements are equivalent, that is they are the same.
We use the symbol \(\iff\) to mean if and only if. For two statements \(P\) and \(Q\), “\(P \iff Q\)” means \(P\implies Q\) and \(Q \implies P\). In this case we say “\(P\) and \(Q\) are equivalent”. The corresponding truth table is as follows.
| \(P\) | \(Q\) | \(P\iff Q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
If we take two statements which are logically equivalent, say \(P\) is equivalent to \(Q\), then proving \(P\) to be true is equivalent to proving \(Q\) to be true. Similarly, proving \(Q\) to be true is equivalent to proving \(P\) to be true. We can use truth tables to prove if two (abstract) statements are equivalent.This will prove to be useful later on when we turn a statement we want to prove is true into another equivalent statement that may be easier to prove.
Let \(P\) and \(Q\) be two statements.
\(P\implies Q\) is equivalent to \((\neg Q)\implies(\neg P)\).
\(P\implies Q\) is equivalent to \((\neg P)\vee Q\).
Using the last two examples and the truth table for \(P\implies Q\), we have the following truth table.
| \(P\) | \(Q\) | \(P\implies Q\) | \((\neg Q)\implies(\neg P)\) | \((\neg P)\vee Q\) |
|---|---|---|---|---|
| T | T | T | T | T |
| T | F | F | F | F |
| F | T | T | T | T |
| F | F | T | T | T |
Hence, for all truth values of \(P\) and \(Q\), we have that \(P\implies Q\) and \((\neg Q)\implies (\neg P)\) have the same truth values. Therefore, \(P\implies Q\) is equivalent to \((\neg Q)\implies(\neg P)\).
Similarly, for all truth values of \(P\) and \(Q\), we have that \(P\implies Q\) and \((\neg P)\vee Q\) have the same truth values. Therefore, \(P\implies Q\) is equivalent to \((\neg P)\vee Q\).□
Notice that the above proof has several sentences to explain to the reader what is going on. It is made up of full sentences with a clear conclusion on what the calculation (in this case the truth table) shows. A proof should communicate clearly to the reader why the statement (be that a theorem, proposition or lemma) is true.
How much detail you put in a proof will be influenced by who your target audience is - this is a skill you will develop over your time as a student.□
Suppose \(P\) and \(Q\) are two statements. Then:
\(P\iff (\neg(\neg P))\).
\((P\vee Q)\iff((\neg P)\implies Q)\)
Exercise.
□
The next proposition shows that \(\wedge\) and \(\vee\) are associative, that is, \(P\wedge Q\wedge R\) and \(P\vee Q\vee R\) are statements that are clear without parentheses (and therefore do not require parentheses).
Suppose \(P,Q,R\) are statements.
\(((P\wedge Q)\wedge R)\iff (P\wedge(Q\wedge R)).\)
\(((P\vee Q)\vee R )\iff (P\vee(Q\vee R)).\)
We prove part a. and leave the proof of part b. as an exercise. We have the following truth table.
| \(P\) | \(Q\) | \(R\) | \(P\wedge Q\) | \((P\wedge Q)\wedge R\) | \(Q\wedge R\) | \(P\wedge (Q\wedge R)\) |
|---|---|---|---|---|---|---|
| T | T | T | T | T | T | T |
| T | T | F | T | F | F | F |
| T | F | T | F | F | F | F |
| T | F | F | F | F | F | F |
| F | T | T | F | F | T | F |
| F | T | F | F | F | F | F |
| F | F | T | F | F | F | F |
| F | F | F | F | F | F | F |
□
Let \(P, Q, R\) be statements. Then \(P \implies (Q \iff R)\) and \((P\implies Q) \iff R\) are not equivalent.
We have the following truth table
| \(P\) | \(Q\) | \(R\) | \(Q \iff R\) | \(P \implies (Q \iff R)\) | \((P\implies Q)\) | \((P\implies Q) \iff R\) |
|---|---|---|---|---|---|---|
| T | T | T | T | T | T | T |
| T | T | F | F | F | T | F |
| T | F | T | F | F | F | F |
| T | F | F | T | T | F | T |
| F | T | T | T | T | T | T |
| F | T | F | F | T | T | F |
| F | F | T | F | T | T | T |
| F | F | F | T | T | T | F |
□
The above proposition shows that the statement \(P \implies Q \iff R\) therefore has no clear meaning without parenthesis. Similarly, there is an exercise to show that \(P \iff (Q \implies R)\) and \((P\iff Q) \implies R\) are not equivalent, so \(P \iff Q \implies R\) is likewise not clear. Hence the meaning of assertions such as \(P\implies Q \iff R \implies S\) is undefined (unless one puts in parenthesis).
As an exercise, one may also prove the following sometimes useful equivalences.
Let \(P,Q,R\) be statements. Then:
\((P\wedge (Q\wedge R))\iff\left((P\wedge Q)\wedge(P\wedge R)\right)\);
\((P\vee (Q\vee R))\iff\left((P\vee Q)\vee(P\vee R)\right).\)
Exercise.
□
Let \(P,Q,R\) be statements. Then
(\(P\wedge(Q\vee R))\iff ((P\wedge Q)\vee(P\wedge R)).\)
(\(P\vee(Q\wedge R))\iff ((P\vee Q)\wedge(P\vee R)).\)
We will prove part a. and leave the proof of part b. as an exercise. We have the following truth table.
| \(P\) | \(Q\) | \(R\) | \(Q\vee R\) | \(P\wedge (Q \vee R)\) | \(P\wedge Q\) | \(P\wedge R\) | \((P\wedge Q) \vee (P\wedge R)\) |
|---|---|---|---|---|---|---|---|
| T | T | T | T | T | T | T | T |
| T | T | F | T | T | T | F | T |
| T | F | T | T | T | F | T | T |
| T | F | F | F | F | F | F | F |
| F | T | T | T | F | T | F | F |
| F | T | F | T | F | F | F | F |
| F | F | T | T | F | F | F | F |
| F | F | F | F | F | F | F | F |
□
Let us return to sets to see how logic may be applied to prove statements.
Suppose that \(A\) and \(B\) are subsets of some set \(X\).
\(A\cup B\) denotes the union of \(A\) and \(B\), that is \[A\cup B=\{x\in X:\ x\in A\text{ or }x\in B\ \}.\]
\(A\cap B\) denotes the intersection of \(A\) and \(B\), that is \[A\cap B=\{x\in X:\ x\in A \text{ and }x\in B\ \}.\]
When \(A\cap B=\emptyset\), we say that \(A\) and \(B\) are disjoint.
We have \(\mathbb{Z}_{\geq 0}\cup \mathbb{Z}_- = \mathbb{Z}\). We also see that \(\mathbb{Z}_{\geq 0} \cap \mathbb{Z}_- =\emptyset\), hence they are disjoint.
The word union comes from the Latin unio meaning “a one-ness”. The union of two sets is a set that lists every element in each set just once (even if the element appears in both sets). While the symbol \(\cup\) looks like a “U” (the first letter of union), this is a coincidence. While the symbol \(\cup\) was first used by Hermann Grassmann (Polish/German mathematician, 1809 - 1877) in 1844, Giuseppe Peano (Italian mathematician, 1858-1932) used it to represent the union of two sets in 1888 in his article Calcolo geometrico secondo Ausdehnungslehre di H. Grassmann. However, at the time the union was referred to as the disjunction of two sets.
The word intersect comes from the Latin inter meaning “within, in between” and sectus meaning “to cut”. The interesection of two curves is the place they cut each other, the intersection of two sets is the “place” where two sets overlaps. While the symbol \(\cap\) was first used by Gottfried Leibniz (German mathematician, 1646 - 1716), he also used it to represent regular multiplication (there are some links between the two ideas). Again, \(\cap\) was used by Giuseppe Peano in 1888 to refer to intersection only.
The word disjoint comes from the Latin dis meaning “away, in two parts” and the word joint. Two sets are disjoint if they are apart from each other without any joints between them. (Compare this to disjunction, which has the same roots but is used to mean joining two things that are apart).Let \(X\) be a set, and for \(x\in X\), let \(P(x)\) be the statement that \(x\) satisfies the criteria \(P\), and let \(Q(x)\) be the statement that \(x\) satisfies the criteria \(Q\). Set \[A=\{x\in X:P(x) \} \qquad\text{and}\qquad B=\{x\in X: Q(x) \}.\] Then \[\begin{align*} A\cap B&=\{x\in X: P(x) \wedge Q(x) \} ,\\ A\cup B&=\{x\in X: P(x) \vee Q(x) \}. \end{align*}\]
For \(x\in X\), we have that \(x\in A\) if and only if the statement \(P(x)\) holds. Similarly, we have that \(x\in B\) if and only if the statement \(Q(x)\) holds. Then \[\begin{align*} A\cap B&=\{x\in X:( x\in A) \wedge (x\in B) \}\\ &=\{x\in X: P(x)\wedge Q(x) \} \end{align*}\] and \[\begin{align*} A\cup B&=\{x\in X:( x\in A) \vee (x\in B) \}\\ &=\{x\in X: P(x)\vee Q(x) \}. \end{align*}\]
□
We can use our work on logical equivalence to show that that \(\cap\) and \(\cup\) are associative.
Suppose \(A,B,C\) are subsets of a set \(X\). Then
\(A\cap(B\cap C)=(A\cap B)\cap C\).
\(A\cup(B\cup C)=(A\cup B)\cup C\).
We will prove part a. and leave part b. as an exercise
Suppose \(x\in X\). Let \(P\) be the statement that \(x\in A\), let \(Q\) be the statement that \(x\in B\), and let \(R\) be the statement that \(x\in C\). Recall Proposition 2.10, \(P\wedge(Q\wedge R)\iff(P\wedge Q)\wedge R\). Then \[\begin{align*} x\in A\cap(B\cap C)&\iff (x\in A)\wedge (x\in B\cap C)\\ &\iff (x\in A)\wedge((x\in B)\wedge (x\in C))\\ &\iff P\wedge(Q\wedge R)\\ &\iff (P\wedge Q)\wedge R\\ &\iff ((x\in A)\wedge (x\in B))\wedge (x\in C)\\ &\iff (x\in A\cap B)\wedge (x\in C)\\ &\iff x\in(A\cap B)\cap C. \end{align*}\] Hence, we have that \(x\in A\cap(B\cap C)\) if and only if \(x\in (A\cap B)\cap C\). It follows that \(A\cap(B\cap C)=(A\cap B)\cap C.\)□
□
Similarly, we have that \(\cup\) and \(\cap\) are distributive.
Let \(A,B,C\) be subsets of a set \(X\). Then
\(A\cap(B\cup C)=(A\cap B)\cup(A\cap C).\)
\(A\cup(B\cap C)=(A\cup B)\cap(A\cup C).\)
We will prove part a. and leave part b. as an exercise
Suppose \(x\in X\). Let \(P\) be the statement that \(x\in A\), let \(Q\) be the statement that \(x\in B\), and let \(R\) be the statement that \(x\in C\). Recall Proposition 2.13 that \(P\wedge(Q\vee R)\iff (P\wedge Q)\vee(P\wedge R).\) Then \[\begin{align*} x\in A\cap(B\cup C) &\iff\ (x\in A)\wedge (x\in B\cup C)\\ &\iff\ (x\in A)\wedge ((x\in B)\vee (x\in C))\\ &\iff\ P\wedge(Q\vee R)\\ &\iff\ (P\wedge Q)\vee(P\wedge R)\\ &\iff\ ((x\in A)\wedge (x\in B))\vee((x\in A)\wedge (x\in C))\\ &\iff\ (x\in A\cap B)\vee(x\in A\cap C)\\ &\iff\ x\in (A\cap B)\cup(A\cap C). \end{align*}\] Hence, we have that \(x \in A\cap(B\cup C)\) if and only if \(x \in (A\cap B)\cup(A\cap C)\). It follows that \(A\cap(B\cup C)=(A\cap B)\cup(A\cap C)\).□
2.4 Negations
Being able to negate statements is important for two reasons:
Instead of proving \(P\) is true, it might be easier to prove that \(\neg P\) is false (proof by contradiction).
Instead of proving \(P \implies Q\) it might be easier (by Theorem 2.8 ) to prove \(\neg Q \implies \neg P\) (proof by contrapositive).
We will expand on these two points later. We already know how to negate most simple statements, for example:
the negation of \(x = 5\) is \(x\neq 5\).
the negation of \(x > 5\) is \(x\leq 5\) (notice the strict inequality became unstrict).
the negation of \(x \in X\) is \(x\notin X\).
To negate simple statements that have been strung together, we use the following theorem.
Suppose \(P,Q\) are two statements. Then
\(\neg(P\wedge Q) \iff ((\neg P) \vee (\neg Q)).\)
\(\neg(P\vee Q) \iff ((\neg P) \wedge (\neg Q)).\)
\(\neg(P\implies Q)\iff (P\wedge (\neg Q)).\)
We will prove part a. and leave part b. and c. as exercises. We have the following truth table.
| \(P\) | \(Q\) | \(\neg P\) | \(\neg Q\) | \(P\wedge Q\) | \(\neg(P\wedge Q)\) | \((\neg P)\vee (\neg Q)\) |
|---|---|---|---|---|---|---|
| T | T | F | F | T | F | F |
| T | F | F | T | F | T | T |
| F | T | T | F | F | T | T |
| F | F | T | T | F | T | T |
□
If \(x\) is not between \(5\) and \(10\), then \(x\) is either less than \(5\) or more than \(10\). Formally speaking \(\neg(5\leq x\leq 10)\) if and only if \(\neg(5\leq x)\) or \(\neg(x\leq 10)\) if and only if \(x<5\) or \(10<x\).
For statements that involves quantifiers (i.e., \(\forall, \exists\)), we use the following theorem.
Let \(X\) be a set, and suppose that \(P(x)\) is a statement involving \(x\in X\). Then
\[\neg(\forall\ x\in X,\ P(x) )\quad \iff\quad \exists \ x\in X \text{ such that } \neg P(x).\]
We also have
\[\neg(\exists\ x\in X \text{ such that } P(x) )\quad \iff \quad \forall\ x\in X,\ \neg P(x).\]
Suppose that \(\forall\ x\in X, P(x)\) is a false statement. Then there must be at least one \(x\in X\) such that \(P(x)\) does not hold. That is, \[\begin{equation} \neg(\forall\ x\in X,\ P(x)) \quad \implies\quad \exists\ x\in X \text{ such that } \neg P(x). \tag{2.1} \end{equation}\]
Conversely, suppose that \(\exists\ x\in X \text{ such that } \neg P(x)\) is a true statement. Then it is not the case that \(P(x)\) holds for all \(x\in X\), that is \[\begin{equation} \exists\ x\in X \text{ such that } \neg P(x) \quad \implies\quad \neg(\forall\ x\in X,\ P(x)). \tag{2.2} \end{equation}\]
By (2.1) and (2.2), it follows that \[\neg(\forall\ x\in X,\ P(x) \quad \iff\quad \exists \ x\in X \text{ such that } \neg P(x).\]
Equivalently, we have \[\begin{align*} \neg(\neg(\forall\ x\in X,\ P(x)))\quad &\iff \quad\neg (\exists\ x\in X \text{ such that } \neg P(x))\\ &\iff \quad\forall\ x\in X,\ P(x). \end{align*}\] Setting \(Q(x)=\neg P(x)\), we have \[ \neg(\exists\ x\in X \text{ such that } Q(x) )\quad \iff \quad \forall\ x\in X,\ \neg Q(x). \]□
Let \(X\) be a set and let us negate the statement “\(\forall x \in X, P(x)\implies Q(x)\)”, by writing equivalent statements using Theorem 2.18 and Theorem 2.19.
\[\begin{align*} \neg(\forall x \in X, P(x)\implies Q(x)) &\ \iff &\ \exists x \in X \text{such that} \neg(P(x) \implies Q(x)) \\ &\ \iff &\ \exists x \in X \text{such that } (P(x) \wedge \neg Q(x)). \end{align*}\]
To make this more concrete, let \(P(x)\) be the statement \(x \in 2\mathbb{Z}\) and \(Q(x)\) the statement \(x \in 4\mathbb{Z}\). We have already shown that \(2\mathbb{Z} \nsubseteq 4\mathbb{Z}\), i.e. \(\forall x \in \mathbb{Z}, P(x) \implies Q(x)\) is false. We did this by showing when \(x=10\), \(P(x)\) is false while \(Q(x)\) is true, i.e., \(\exists x \in \mathbb{Z}\) such that \(P(x)\) is true and \(Q(x)\) is false.Negating statements is also very useful to see when an object does not satisfy a definition. We will see more examples of this later in the course, but for the moment here is an example.
Using (O2) as an example, a set \(X\) satisfies transitivity (with respect to \(<\) ) if for all \(x,y,z\in X\) if \(x<y\) and \(y<z\) then \(x<z\). Let us see what it means for \(X\) not to satisfy (O2). First we turn the definition into symbolic language \(\forall x,y,z \in X, (x<y)\wedge(y<z)\implies (x<z)\). We then negate this
\[\begin{align*} &\neg(\forall x,y,z \in X, (x<y)\wedge(y<z)\implies (x<z)) \\ \iff & \exists x,y,z \in X \text{ such that } \neg((x<y)\wedge(y<z) \implies (x<z)) \\ \iff & \exists x,y,z \in X \text{ such that } ((x<y)\wedge(y<z))\wedge \neg(x<z)) \\ \iff & \exists x,y,z \in X \text{ such that } (x<y)\wedge(y<z)\wedge (x\geq z). \end{align*}\]
□
To negate a statement with the quantifier \(\exists!\), it is useful to first translate this notation to not include “!”.
Suppose \(X\) is a set, and \(P(x)\) is a proposition dependent on \(x\in X\). When we say there is a unique \(x\in X\) so that \(P(x)\) holds we mean first that:
there is some \(x\in X\) so that \(P(x)\) is true, and
if we have \(x_1,x_2\in X\) with \(P(x_1)\) and \(P(x_2)\) are true, then \(x_1=x_2\).
More symbolically, we have \[\left[\exists!x\in X, P(x)\right] \iff \left[(\exists x\in X,\ P(x))\wedge(\forall x_1,x_2\in X,\ (P(x_1)\wedge P(x_2))\implies x_1=x_2)\right].\] So negating, we get: \[\begin{align*} &\neg\left[\exists!x\in X, P(x)\right]\\ &\iff \neg\left[(\exists x\in X,\ P(x))\wedge(\forall x_1,x_2\in X,\ (P(x_1)\wedge P(x_2))\implies x_1=x_2)\right]\\ &\iff \left[\neg(\exists x\in X,\ P(x))\vee\neg[(\forall x_1,x_2\in X,\ (P(x_1)\wedge P(x_2)\implies x_1=x_2)]\right]\\ &\iff \left[(\forall x\in X,\ \neg P(x))\vee[\exists x_1,x_2\in X,\ \neg(P(x_1)\wedge P(x_2)\implies x_1=x_2)]\right]\\ &\iff \left[(\forall x\in X,\ \neg P(x))\vee[\exists x_1,x_2\in X,\ (P(x_1)\wedge P(x_2)\wedge x_1\not=x_2)]\right]. \end{align*}\]
Thus the negation of exactly one \(x\) such that \(P(x)\) holds is “either there exists no \(x\) such that \(P(x)\) holds or there exists more than one \(x\) such that \(P(x)\) holds”2.5 Contradiction and the contrapositive
As mentioned earlier, negating statements are useful when trying to prove statements using different methods. First we look at proof by contradiction.
□
While we will use this method more extensively later, let us see an easy example.
Statement: Let \(x,y \in \mathbb{Q}\). If \(x<y\) then \(-x>-y\).
Proof: For the sake of a contradiction let us assume that \(x<y\) and \(-x\leq-y\). (Recall the negation of \(P \implies Q\) is \(P \vee \neg Q\).) Since \(x<y\) we have \(x-x<y-x\) [by (O3)], i.e. \(0<y-x\). Since \(-x\leq -y\) then \(-x+y\leq -y+y\), i.e. \(y-x\leq 0\). So \(0<y-x\) and \(y-x\leq 0\), i.e. [by (O1)] \(0<0\), which is a contradiction. Hence \(x<y\) and \(-x\leq-y\) is false, so If \(x<y\) then \(-x>-y\). \(\square\)Another technique is a proof by contrapositive.
The contrapositive of (A1), “for all \(x,y\), if \(x,y \in \mathbb{Z}\) then \(x+y \in \mathbb{Z}\)” is “for all \(x,y\), if \(x+y \notin \mathbb{Z}\) then \(x\notin\mathbb{Z}\) or \(y\notin\mathbb{Z}\).”
The contrapositive of (O3), “for all \(x,y,z \in \mathbb{Q}\), if \(x<y\) then \(x+z<y+z\)” is “$for all \(x,y,z\in\mathbb{Q}\) if \(x+z\geq y+z\) then \(x\geq y\)”.By Theorem 2.8, we know that \(P \implies Q\) is equivalent to its contrapositive. Sometimes, proving the contrapositive is easier than proving \(P \implies Q\) (we will see more examples of this later).
Statement: Let \(x,y \in \mathbb{Q}\). If \(x<y\) then \(-x>-y\).
Proof: We prove the contrapositive. The contrapositive is “if \(-x\leq -y\) then \(x\geq y\)”. Suppose \(-x\leq -y\) then \(-x+(x+y) \leq -y+(x+y)\) [since \(x+y \in \mathbb{Q}\) by (A1) and using (O3)*]. In other words \(y\leq x\), i.e. \(x\geq y\). \(\square\)Note that we have proven “\(x<y \implies -x>-y\)” by contradiction and by contrapositive. It is also worth noting that we could have proven it directly. This is meant to show that often there are numerous way to prove the same thing.
Note that the contrapositive doesn’t just change the implication symbol, but it also negates \(P\) and \(Q\). The contrapositive can often be confused with the converse:
Note that \(P \implies Q\) is not equivalent to its converse. Be careful when using a theorem/lemma/proposition that you are not using the converse by accident (which may not be true).
If the converse of \(P\implies Q\) is true, then we can deduce that \(P \iff Q\).
The converse of “If \(x<y\) then \(-x>-y\)” is “\(-x>-y\) then \(x<y\)”. We can show this is true, suppose \(-x>-y\) then \(-x+(x+y)>-y+(x+y)\), i.e. \(y>x\), i.e. \(x<y\).
Therefore we conclude, for all \(x,y \in \mathbb{Q}\), \(x<y\) if and only if \(-x>-y\).
Contradiction comes from the Latin contra which means “against” and dict which is a conjugation of the verb “to say, tell”. A contradiction is a statement that speaks against another statement.
Contrapositive also comes from the Latin contra and the Latin positus which is a conjugation of the verb “to put”. The contrapositive of a statement is a statement “put against” the original statement, we have negated both parts and reversed the order. Furthermore it is “positive” as it has the same truth value as the original statement.
On the other hand, while sounding similar, converse comes from the Latin con which means “together with” and vergere which means “to turn”. The converse turns the order of \(P\) and \(Q\).2.6 Set complement
We finish this section by looking at the complement of sets.
Suppose that \(A\) and \(B\) are subsets of some set \(X\).
\(A\setminus B\) denotes the relative complement of \(A\) with respect to \(B\), that is \[A\setminus B=\{x\in X: \ x\in A \text{ and }x\not\in B\ \}.\]
\(A^c\) denotes the complement of \(A\), that is \[A^c=\{x\in X:\ x\not\in A\ \}.\]
Suppose \(A,B\) are subsets of a set \(X\). Then
- \(A\setminus B=A\cap B^c.\)
- \((A\setminus B)^c=A^c\cup B\).
We will prove part a. and leave part b. as an exercise.
Let \(x\in X\). Then \[\begin{align*} x\in A\setminus B &\iff (x\in A)\wedge (x\not\in B)\\ &\iff (x\in A)\wedge (x\in B^c)\\ &\iff x\in A\cap B^c. \end{align*}\] Hence, we have that \(x\in A\setminus B\) is equivalent to \(x\in A\cap B^c\). It follows that \(A\setminus B=A\cap B^c.\)□
Suppose that \(A,B,C\) are subsets of a set \(X\). Then
\(A\setminus (B\cup C)=(A\setminus B)\cap(A\setminus C).\)
\(A\setminus (B\cap C)=(A\setminus B)\cup(A\setminus C).\)
\((A\cap B)^c=A^c\cup B^c\).
\((A\cup B)^c=A^c\cap B^c\).
We will prove parts a. and d. and leave parts b. and c. as exercises.
Proving a.) Let \(x\in X\). Recall that for statements \(P,Q,R\), we have that \(P\wedge(Q\wedge R)\iff(P\wedge Q)\wedge(P\wedge R).\) Then \[\begin{align*} x\in A\setminus(B\cup C) &\iff (x\in A)\wedge(x\not\in B\cup C)\\ &\iff (x\in A)\wedge (\neg(x\in B\cup C))\\ &\iff (x\in A)\wedge (\neg((x\in B) \vee (x\in C)))\\ &\iff (x\in A)\wedge ((x\not\in B)\wedge (x\not\in C))\\ &\iff ((x\in A)\wedge (x\not\in B))\wedge((x\in A)\wedge (x\not\in C))\\ &\iff (x\in A\setminus B)\wedge(x\in A\setminus C)\\ &\iff x\in (A\setminus B)\cap(A\setminus C). \end{align*}\]
Hence, we have that \(x\in A\setminus(B\cup C)\) if and only if \(x\in(A\setminus B)\cap(A\setminus C)\). It follows that \(A\setminus(B\cup C)=(A\setminus B)\cap(A\setminus C).\)
Proving d.) Let \(x\in X\). Then \[\begin{align*} x\in (A\cup B)^c &\iff \neg(x\in A\cup B)\\ &\iff \neg((x\in A)\vee (x\in B))\\ &\iff \neg((x\in A)\wedge(\neg(x\in B)))\\ &\iff (x\in A^c)\wedge (x\in B^c)\\ &\iff x\in A^c \cap B^c. \end{align*}\]
Hence, we have that \(x\in (A\cup B)^c\) if and only if \(x\in A^c\cap B^c\). It follows that \((A\cup B)^c=A^c\cap B^c\).□
The above theorem is often known as De Morgan’s Laws, or De Morgan’s Theorem. Augustus De Morgan (English Mathematician, 1806 - 1871) was the first to write this theorem using formal logic (the one we are currently seeing). However this result was known and used by mathematicians and logicians since Aristotle (Greek philosopher, 384BC - 322BC), and can be found in the medieval texts by William of Ockham (English philosopher, 1287 - 1347) or Jean Buridan (French philosopher, 1301 - 1362).
It is often convenient to denote the elements of a set using indices. For example, suppose \(A\) is a set with \(5\) elements. Then we can denote these elements as \(a_1,a_2,a_3,a_4,a_5\). So we can write \[A=\{a_i:\ i\in I\ \}, \text{ where } I=\{1,2,3,4,5\}.\] The set \(I\) is called the indexing set.
Let \(\{A_i\}_{i\in I}\) be a collection of subsets of a set \(X\) where \(I\) is an indexing set. Then we write \(\bigcup\limits_{i\in I}A_i\) to denote the union of all the sets \(A_i\), for \(i\in I\). That is, \[\bigcup_{i\in I}A_i=\{x\in X: \exists\ i\in I \text{ such that } x\in A_i \}.\] Furthermore, we write \(\bigcap\limits_{i\in I}A_i\) to denote the intersection of all the sets \(A_i\), for \(i\in I\). That is, \[\bigcap_{i\in I}A_i=\{x\in X: \forall\ i\in I,\ x\in A_i \}.\]
Let \(X\) be a set, let \(A\) be a subset of \(X\), and let \(\{B_i\}_{i\in I}\) be an indexed collection of subsets, where \(I\) is an indexing set. Then we have
\(A\setminus \bigcap\limits_{i\in I}B_i = \bigcup\limits_{i\in I}(A\setminus B_i).\)
\(A\setminus \bigcup\limits_{i\in I}B_i = \bigcap\limits_{i\in I}(A\setminus B_i).\)
We will prove part a. and leave part b. as an exercise.
We know that \(x\in \bigcap\limits_{i\in I}B_i\) if and only if we have that \(x\in B_i\), for all \(i\in I\). Then \(x\not\in \bigcap\limits_{i\in I}B_i\) if and only if there exists an \(i\in I\) such that \(x\not\in B_i\). Now, suppose that \(x\in A\setminus \bigcap\limits_{i\in I}B_i\). Then \(x\in A\), and for some \(i\in I\), we have that \(x\not\in B_i\). Hence, for some \(i\in I\), we have that \(x\in A\setminus B_i\). Then \(x\in\bigcup\limits_{i\in I}(A\setminus B_i)\) which shows that \(A\setminus \bigcap\limits_{i\in I}B_i\,\subseteq\,\bigcup\limits_{i\in I}(A\setminus B_i).\)
Now, suppose that \(x\in \bigcup\limits_{i\in I}(A\setminus B_i).\) Hence, for some \(i\in I\), we have that \(x\in A\setminus B_i\). Then for some \(i\in I\), we have that \(x\in A\) and \(x\not\in B_i\). Since there exists some \(i\in I\) such that \(x\not\in B_i\), we have \(x\not\in \bigcap\limits_{i\in I}B_i\). Then \(x\in A\setminus \bigcap\limits_{i\in I}B_i\) which shows that \(\bigcup\limits_{i\in I}(A\setminus B_i)\,\subseteq\, A\setminus \bigcap\limits_{i\in I}B_i\). Summarising the above, we have that \(A\setminus \bigcap\limits_{i\in I}B_i\,=\,\bigcup\limits_{i\in I}(A\setminus B_i).\)□
We finish this section with a brief side-note. How does one differentiate whether a statement is a definition, a theorem, a proposition, a lemma etc? The team at Chalkdust Magazine made the following flowchart which while is not meant to be serious, does reflect quite well how one can classify different statements. That is: a definition is a statement taken to be true; roughly speaking a proposition is an interesting but non-important result; while a theorem is an interesting, important main result; and a lemma is there to build up to a theorem. The original figure can be found at https://chalkdustmagazine.com/regulars/flowchart/which-type-of-statement-are-you/
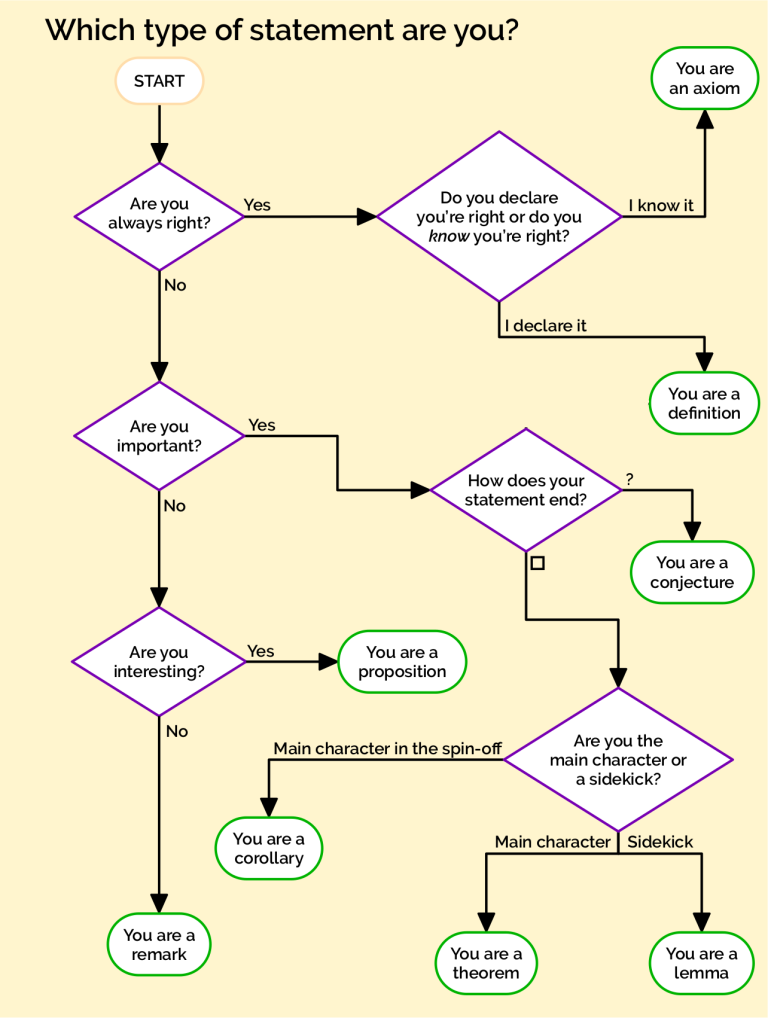
Figure 2.1: What statement are you? Copyright Chalkdust Magazine, Issue 17.
3 The rationals are not enough
Now that we have a solid foundation of logic and abstract set notation, let us explore sets within \(\mathbb{Q}\). That is, let us look at subsets of the rationals. This will lead us to notice that irrational numbers exists, and hence exploring a new set called the reals, \(\mathbb{R}\).
3.1 The absolute value
Before we look at subsets of \(\mathbb{Q}\), we introduce the notion of absolute value.
For \(x\in \mathbb{Q}\), the absolute value or modulus of \(x\), denoted \(|x|\), is defined by \[|x| := \begin{cases}x &\text{ if } x\geq 0;\\ -x &\text{ if } x<0.\end{cases}\]
It is often helpful to think of the absolute value \(|x|\) as the distances between the point \(x\) and the origin \(0\). Likewise, \(|x-y|\) is the distance between the points \(x\) and \(y\).
For any \(x, y \in \mathbb{Q}\)
\(|x|\geq 0\) with \(|x| = 0\) if and only if \(x=0\);
\(|xy| = |x||y|\);
\(|x^2| = |x|^2 = x^2\).
Exercise
□
Statement Show that \(a^2+b^2\geq 2ab\) for any \(a,b \in \mathbb{Q}\).
Solution Let \(a,b\in\mathbb{Q}\). We have that \((a-b)^2\geq 0\), so [expanding the bracket] \(a^2-2ab+b^2\geq 0\). Rearranging, this gives \(a^2+b^2 \geq 2ab\).
For all \(x,y \in \mathbb{Q}\) we have \(|x+y|\leq |x|+|y|\).
We prove this by case by case analysis. First note that for all \(x\in\mathbb{Q}\) we have \(x\leq |x|\) and \(-x\leq |x|\). Let \(x,y \in \mathbb{Q}\).
Case 1: Suppose \(x\geq -y\) then \(x+y\geq 0\) and so \(|x+y| = x+y \leq |x|+|y|\).
Case 2: Suppose \(x< -y\) then \(x+y<0\) and so \(|x+y|=-(x+y)=-x+(-y)\leq |x|+|y|\).□
3.2 Bounds for sets
With this notion of absolute value, we can start asking whether a subset of \(\mathbb{Q}\) contains arbitrarily large or small elements.
Let \(A \subseteq \mathbb{Q}\) be non-empty. We that that \(A\) is:
bounded above (in \(\mathbb{Q}\)) by \(\alpha \in \mathbb{Q}\) if for all \(x\in A\), \(x\leq \alpha\);
bounded below (in \(\mathbb{Q}\)) by \(\alpha \in \mathbb{Q}\) if for all \(x\in A\), \(x\geq \alpha\);
bounded if it is bounded above and below;
If \(A\) is bounded above by \(\alpha\) and below by \(\beta\), then by setting \(\gamma = \max\{|\alpha|,|\beta|\}\) we have \(A\) is bounded by \(\gamma\), i.e., for all \(x\in A\), we have \(|x|\leq \gamma\).
Note that \(\alpha\) is far from unique. For example, take the set \(A = \left\{\frac{1}{n}:n\in \mathbb{Z}_+\right\}\). Then we can see that \(A\) is bounded above by \(1\), but it is also bounded above by \(2\) and by \(100\) etc.
Let \(A \subseteq \mathbb{Q}\) be non-empty. The least (or smallest) upper bound of \(A\) (in \(\mathbb{Q}\)) is \(\alpha \in \mathbb{Q}\) such that:
\(\alpha\) is an upper bound, i.e. for all \(x\in A\), \(x\leq \alpha\);
any rational number \(\beta\) less than \(\alpha\) is not an upper bound, i.e. for all \(\beta \in \mathbb{Q}\) with \(\beta < \alpha\), there exists \(x\in A\) with \(\beta<x\).
The greatest (or largest) lower bound of \(A\) (in \(\mathbb{Q}\)) is \(\alpha \in \mathbb{Q}\) such that:
\(\alpha\) is a lower bound, i.e. for all \(x\in A\), \(x\geq \alpha\);
any rational number \(\beta\) greater than \(\alpha\) is not a lower bound, i.e. for all \(\beta \in \mathbb{Q}\) with \(\beta > \alpha\), there exists \(x\in A\) with \(\beta>x\).
We use our work on negating statements to negate the above definition and say
\(\alpha \in \mathbb{Q}\) is not the least upper bound of \(A\) if:
there exists \(x\in A\) such that \(x>\alpha\) (\(\alpha\) is not an upper bound) or;
there exists \(\beta \in \mathbb{Q}\) with \(\beta < \alpha\) and for all \(x\in A\) we have \(x\leq \beta\) (there is an upper bound lower than \(\alpha\)).
Similarly, \(\alpha \in \mathbb{Q}\) is not the greatest lower bound of \(A\) if:
there exists \(x\in A\) such that \(x<\alpha\) (\(\alpha\) is not a lower bound) or;
there exists \(\beta \in \mathbb{Q}\) with \(\beta > \alpha\) and for all \(x\in A\) we have \(x\geq \beta\) (there is an lower bound greater than \(\alpha\)).
Let \(A = \left\{\frac{1}{n}:n\in \mathbb{Z}_+\right\}\). We show that \(1\) is the least upper bound of \(A\). As remarked before, we have \(1\) is an upper bound since if we take \(x \in A\) then \(x = \frac{1}{n}\) with \(n\in \mathbb{Z}_+\). In particular \(n\geq 1\), so \(x=\frac{1}{n}\leq \frac{1}{1}=1\).
We now show that \(1\) is the least upper bound by showing any number less than \(1\) is not an upper bound. Let \(\beta <1\). By taking \(n=1 \in \mathbb{Z}_+\), we see that \(1=\frac{1}{1} \in A\), hence \(\beta<1\) means \(\beta\) is not an upper bound. Hence \(1\) is the least upper bound.
We show that \(0\) is the greatest lower bound. First we show \(0\) is a lower bound. Let \(x \in A\) then \(x = \frac{1}{n}\) with \(n\in \mathbb{Z}_+\). In particular \(n > 0\), so \(x=\frac{1}{n}> 0\).
We now show that \(0\) is the greatest lower bound by showing any number greater than \(0\) is not a lower bound. Let \(\beta = \frac{a}{b} >0\) [so \(a,b \in \mathbb{Z}_+\)]. Set \(n=b+1 \in \mathbb{Z}\), so \(\frac{1}{n}\in A\). Then \[\frac{1}{n}=\frac{1}{b+1}<\frac{1}{b}\leq a\frac{1}{b} = \frac{a}{b} = \beta.\]
So we have found \(x \in A\) such that \(x<\beta\), so \(\beta\) is not a lower bound.
The argument for \(\beta\) not being a lower bound above seems to come from nowhere. Sometimes it is hard to see where to start a proof, so mathematician first do scratch work. This is the rough working we do as we explore different avenues and arguments, but that is not included in the final proof (so to keep the proof clean and easy to understand). The scratch work for the above proof of might have been along the lines:
We want to find \(n \in \mathbb{Z}_+\) such that \(\beta =\frac{a}{b}>\frac{1}{n}\). Rearranging, this gives \(an>b\) (as both \(n\) and \(b\) are positive), so \(n>\frac{b}{a}\). Since \(a\geq 1\), we have \(\frac{b}{a}\leq b\). Picking \(n=b+1\) would satisfy \(n=b+1>b\geq\frac{b}{a}\).□
Note that in the example above the greatest lower bound of \(A\) is not in \(A\) itself [if \(0\in A\), then there exists \(n\in \mathbb{Z}_+\) such that \(0=\frac{1}{n}\), i.e. \(0=1\), which is a contradiction.]. If a set is a bounded subset of \(\mathbb{Z}\), then we get a different story.
Any non-empty subset of \(\mathbb{Z}_{\geq 0}\) contains a minimal element.
Exercise to be done after we have introduced the completeness axiom.
□
Let \(A \subseteq \mathbb{Z}\) be non-empty. If \(A\) is bounded below, it contains a minimal element (i.e. its greatest lower bound is in \(A\)). If it is bounded above, it contains a maximal element (i.e., its least upper bound is in \(A\)).
As we saw above with the set \(A = \left\{\frac{1}{n}:n\in \mathbb{Z}_+\right\}\), this is not the case for general subsets of \(\mathbb{Q}\). However, it is even worst, because a general subset of \(\mathbb{Q}\) might be bounded and not have a greatest lower bound or least upper bound in \(\mathbb{Q}\), as we will see in the next section.
3.3 The irrationals and the reals
We first show that there exists irrational numbers (i.e., numbers that are not rational) and show that this means that there exists subsets of \(\mathbb{Q}\) whose lower upper bound is not rational (and hence we need a bigger number system).
There does not exists \(x\in \mathbb{Q}\) such that \(x^2=2\).
For the sake of a contradiction, suppose there exists \(x =\frac{a}{b} \in \mathbb{Q}\) such that \(x^2 =2\). Without loss of generality, since \(x^2=(-x)^2\) and \(0^2=0\), we can assume \(x>0\), i.e. \(a,b \in \mathbb{Z}_+\). Furthermore, if \(0<x\leq 1\), then \(x^2\leq 1<2\), and if \(x\geq 2\) then \(x^2\geq 4>2\). So we assume that \(1<x<2\).
Let \(A = \{r \in \mathbb{Z}_+:rx \in \mathbb{Z}\} \subseteq \mathbb{Z}\). Note that \(A\) is non-empty since, \(bx = a \in \mathbb{Z}_+\), so \(b \in A\). We have that \(A\) is bounded below by \(0\), so by the Well Ordering Principle, \(A\) contains a minimal element, call if \(m\). We will prove that \(m\) is not minimal by finding \(0<m_1<m\) with \(m\in A\). This will be a contradiction to the Well Ordering Principle.
Define \(m_1=m(x-1)= mx-m \in \mathbb{Z}\). Since \(1<x\), we have \(x-1>0\) so \(m_1=m(x-1)>0\). Similarly, since \(x<2\) we have \(x-1<1\) so \(m_1=m(x-1)<m\). Hence \(0<m_1<m\). Now \[m_1x=m(x-1)x=mx^2-mx = 2m-mx \in \mathbb{Z}.\] Hence \(m_1 \in A\) and \(0<m_1<m\) which is a contradiction.□
Since irrational numbers exists if we restrict ourselves to only using rational number then there are many unanswerable questions. From simple geometrical problems (what is the length of the diagonal of a square with length side 1), to the fact that there are some bounded set of rationals which do not have a rational least upper bower.
Consider the set \[A = \{x\in \mathbb{Q}:x^2<2\}.\] We have \(A\) is bounded above (for example, by \(2\) or \(10\)), but we show it does not have a least upper bound in the rational.
Let \(\alpha =\frac{a}{b} \in \mathbb{Q}\) be the least upper bound of \(A\) and note we can assume \(\alpha>0\). We either have \(\alpha^2<2\), \(\alpha^2=2\) or \(\alpha^2>2\). We will show that all three of these cases leads to a contradiction.
Case 1: \(\alpha^2<2\). We show that in this case \(\alpha\) is not an upper bound by finding \(x \in A\) such that \(\alpha<x\).
[Scratch work: We look for \(c\in \mathbb{Z}\) such that \(\left(\alpha+\frac{1}{bc}\right)^2=\left(\frac{ac+1}{bc}\right)^2<2\). Rearranging, we get \(a^2c^2+2ac+1<2b^2c^2\), then \(2ac+1<c^2(2b^2-a^2)\). Since \(\alpha^2<2\), we know \(a^2<2b^2\), so \(2b^2-a^2>0\). Since \(2b^2-a^2 \in \mathbb{Z}\), we have \(2b^2-a^2\geq 1\), so \(c^2(2b^2-a^2)\geq c^2\). So to find \(c\) such that \(2ac+1<c^2\), i.e. \(0<c^2-2ac-1\), i.e. by completing the square \(0<(c-a)^2-(a^2+1)\). To simplify our life, let us take \(c\) to be a multiple of \(a\), say \(ka\), then we are looking for \(0<(k-1)^2a^2-a^2-1 = ((k-1)^2-1)a^2-1\), i.e. \((k-1)^2-1)>2\), so \(k=3\) should work, i.e. \(c=3a\).]
Let \(x = \alpha+\frac{1}{3ab}>\alpha\). We prove that \(x\in A\) (and hence \(\alpha\) is not an upper bound) by showing \(x^2<2\). We have \[\begin{align*} x^2 &= \left(\frac{3a^2+1}{3ab}\right)^2 &\\ &= \frac{9a^4+6a^2+1}{9a^2b^2} &\\ &< \frac{9a^4+9a^2}{9b^2a^2} & \text{ (since $6a^2+1<9a^2$ )}\\ &=\frac{a^2+1}{b^2}& \\ &< \frac{a^2+(2b^2-a^2)}{b^2}& \text{ (since $a^2<2b^2$)}\\ &<2.& \end{align*}\]
Case 2: \(\alpha^2=2\). This is a contradiction to Theorem 3.8
Case 3: \(\alpha^2>2\). We leave this as an exercise. [Hint: Find appropriate \(c\) so that \(x = \alpha - \frac{1}{bc} \in \mathbb{Q}\) is such that \(x^2>2\). Argue that \(x\) is an upper bound for \(A\) and \(x<\alpha\) to conclude \(\alpha\) is not the least upper bound. ]
Notice that in the above we made sure to have \(x>\alpha\) by setting \(x = \alpha+\epsilon\) where \(\epsilon>0\). By doing so, we reduced the numbers of properties we needed \(x\) to have.
□
We use this as a motivation to introduce the real numbers.
The set of real numbers, denoted \(\mathbb{R}\), equipped with addition \(+\), multiplication \(\cdot\) and the order relation \(<\) satisfies axioms (A1) to (A11), (O1) to (O4) and the Completeness Axiom
Completeness Axiom: Every non-empty subset \(A\) of \(\mathbb{R}\) which is bounded above has a least upper bound.
It can be shown that there is exactly one quadruple \((\mathbb{R};+;\cdot;<)\) which satisfies these properties - up to isomorphism. We do not discuss the notion of isomorphism in this context here (although we will later look at it in the context of groups) save to remark that any two real number systems are in bijection (we will define this later) and preserves certain properties. This allows us to speak of the real numbers.
There are several ways of constructing the real number system from the rational numbers. One option is to use Dedekind cuts. Another is to define the real numbers as equivalence classes of Cauchy sequences of rational numbers (you will explore Cauchy sequences in Analysis).You may continue to imagine the real numbers as a number line as you did pre-university.
The definition of the absolute value is the same for real numbers as for the rational numbers, as is the notion of bounded sets (and therefore all the results in the previous section still holds for \(\mathbb{R}\)).
We can use the absolute value to define a distance or metric on \(\mathbb{R}\). To do so we define \[d(x,y) = |x-y|\] for any two points \(x,y\in \mathbb{R}\). This distance has the following properties, for any \(x,y,z \in \mathbb{R}\):
\(d(x,y)\geq 0\) and \(d(x,y)=0\) if and only if \(x=y\);
\(d(x,y)=d(y,x)\);
\(d(x,y)\leq d(x,z)+d(z,y)\).
We deduce two important result about \(\mathbb{R}\).
Every non-empty subset \(A\) of \(\mathbb{R}\) bounded below has a greatest lower bound.
Let \(A\subset \mathbb{R}\) be non-empty and bounded below. Let \(c\in \mathbb{R}\) be a lower bound. Define the set \[B=\{-x:x\in A\}.\] Let \(x\in B\), so \(-x\in A\). Since \(c\) is a lower bound, \(-x\geq c\), i.e. \(x\leq -c\). So \(-c\) is an upper bound for \(B\), and \(B\) is non-empty [since \(A\) is non-empty]. By the Completeness Axiom \(B\) has a least upper bound, \(u\in \mathbb{R}\). Let \(\ell = -u\). We prove that \(\ell\) is the greatest lower bound for \(A\).
We first show \(\ell\) is a lower bound. Let \(x\in A\), then \(-x\in B\) so \(-x\leq u\). Hence \(x\geq -u=\ell\).
We now show \(\ell\) is the greatest lower bound by showing any real number bigger than \(\ell\) is not a lower bound. Let \(y\in \mathbb{R}\) be such that \(y>\ell\), so \(-y<-\ell=u\). Now \(-y\) is not an upper bound for \(B\) since \(u\) is the least upper bound of \(B\). So by definition, there exists \(b\in B\) such that \(b>-y\), i.e. \(-b<y\). Since \(b\in B\), we have \(-b\in A\). Hence \(y\) is not a lower bound for \(a\).
So \(\ell\) is the greatest lower bound for \(A\).□
For any \(x\in \mathbb{R}\) there exists \(n\in \mathbb{Z}_+\) such that \(x\leq n\).
We prove this by contradiction.
\(\big[\neg(\forall x \in \mathbb{R}, \exists n\in \mathbb{Z}_+\) such that \(x\leq n\)) \(\iff \exists x \in \mathbb{R}\) such that \(\forall n \in \mathbb{Z}_+, x>n \big]\).
Suppose there exists \(x\in \mathbb{R}\) such that \(n<x\) for all \(n\in \mathbb{Z}_+\). In particular, this means \(\mathbb{Z}_+\subseteq \mathbb{R}\) is bounded above. So by the completeness axiom, \(\mathbb{Z}_+\) has a least upper bound \(\alpha\) [in \(\mathbb{R}\)]. Since \(\alpha\) is the least upper bound, \(\alpha-\frac{1}{2}\) is not an upper bound, i.e. there exists \(b \in \mathbb{Z}_+\) such that \(\alpha-\frac{1}{2}<b<\alpha\). But then, \(b+1\in \mathbb{Z}\) and \(\alpha+\frac{1}{2}<b+1<\alpha+1\) so \(\alpha<b\). This contradicts the fact \(\alpha\) is an upper bound for \(\mathbb{Z}_+\).□
The above property is named after Archimedes of Syracuse (Sicilian/Italian mathematician, 287BC - 212 BC) although when Archimedes wrote down this theorem, he credited Eudoxus of Cnidus (Turkish mathematician and astronomer, 408BC - 355BC). It was Otto Stolz (Austrian mathematician, 1842 - 1905) who coined this property - partly because he studied fields where this property is not true and therefore needed to coin a term to distinguish between what is now know as Archimedean fields and non-Archimedean fields.
We finish this section by introducing notation for some common subsets of \(\mathbb{R}\).
Let \(a,b \in \mathbb{R}\) are such that \(a\leq b\), we denote:
the open interval of \(a,b\) by \((a,b)=\{x\in \mathbb{R}:a<x<b\}\);
the closed interval of \(a,b\) by \([a,b] = \{x \in \mathbb{R}:a\leq x\leq b\}\).
\([a,b) = \{x \in \mathbb{R}: a\leq x<b\}\); \((a,b] = \{x\in \mathbb{R}:a<x \leq b\}\);
\((a,\infty) = \{x \in \mathbb{R}:a<x\}\); \([a,\infty) = \{x\in \mathbb{R}:a\leq x\}\);
\((-\infty,b) = \{x \in \mathbb{R}: x<b\}\); \((-\infty,b] = \{x \in \mathbb{R}: x\leq b\}\).
By convention we have \((a,a)=[a,a)=(a,a]=\emptyset\), while \([a,a]=\{a\}\).
3.4 The supremum and infimum of a set.
Since \(\mathbb{R}\) is complete, i.e., every bounded set has a least upper bound and greatest lower bound, we introduce the notion of supremum and infimum of a set.
Let \(A\subseteq \mathbb{R}\). We define the supremum of \(A\), denoted \(\sup(A)\) as follows:
If \(A=\emptyset\), then \(\sup(A) = -\infty\).
If \(A\) is non-empty and is bounded above [i.e., there exists \(\alpha \in \mathbb{R}\) such that for all \(x\in A\), \(x\leq \alpha\)] then \(\sup(A)\) is the least upper bound of \(A\) (which we know exists by the Completeness Axiom)
If \(A\) is non-empty and is not bounded above [i.e., for all \(\alpha \in \mathbb{R}\), there exists \(x\in A\) such that \(x>\alpha\)] then \(\sup(A)= +\infty\).
Let \(A\subseteq \mathbb{R}\). We define the infimum of \(A\), denoted \(\inf(A)\) as follows:
If \(A=\emptyset\), then \(\inf(A) = +\infty\).
If \(A\) is non-empty and is bounded below [i.e., there exists \(\alpha \in \mathbb{R}\) such that for all \(x\in A\), \(x\geq \alpha\)] then \(\inf(A)\) is the greatest lower bound of \(A\) (which we know exists by the Completeness Axiom)
If \(A\) is non-empty and is not bounded below [i.e., for all \(\alpha \in \mathbb{R}\), there exists \(x\in A\) such that \(x<\alpha\)] then \(\sup(A) = -\infty\).
Supremum comes from the Latin super meaning “over, above” while infimum comes from the Latin inferus meaning “below, underneath, lower” (these words gave rise to words like superior and inferior).
Let \(A = \left\{\frac{1}{n}:n \in \mathbb{Z}_+\right\}\). We have already seen that \(\sup(A) = 1\) (in \(A\)) and \(\inf(A)= 0\) (not in \(A\)).
Let \(a,b \in \mathbb{R}\) with \(a<b\). Then
\(\sup((a,b)) = \sup((a,b]) = \sup([a,b))= \sup([a,b]) = b\);
\(\inf((a,b)) = \inf((a,b]) = \inf([a,b)) = \inf([a,b]) = a\);
\(\sup((a,\infty)) = \sup([a,\infty)) = +\infty\);
\(\inf((-\infty,a)) = \inf((-\infty,a]) = -\infty\);
\(\sup((-\infty,a)) = \sup((-\infty,a]) = \inf([a,\infty)) = \inf((a,\infty)) = a\).
We will only prove \(\sup((a,b)) = b\) and \(\sup((a,\infty)) = +\infty\) and leave the rest as the arguments are very similar.
Let \(a,b \in \mathbb{R}\) with \(a<b\), we will show \(\sup((a,b)) = b\). [Note that \((a,b)\) is non-empty (as \(a\neq b\)) and it is bounded above.]
First we show that \(b\) is an upper bound. Indeed, let \(x\in (a,b)\) then by definition \(a<x<b\) so \(x\leq b\) as required.
Next we show that \(b\) is the least upper bound [by showing any real number less than \(b\) is not an upper bound]. Let \(y\in \mathbb{R}\) with \(y<b\).Suppose \(a<y\) (i.e. \(y\in (a,b)\)) and let \(x=\frac{b+y}{2}=y+\frac{b-y}{2}=b-\frac{b-y}{2}\). Note that \(x<b\) and \(x>y>a\), so \(x\in (a,b)\). Since \(x>y\), we have \(y\) is not an upper bound. Suppose \(y\leq a\) (i.e. \(y\notin(a,b)\)) and let \(x=\frac{a+b}{2}=a+\frac{b-a}{2}=b-\frac{b-a}{2}\). Then \(x<b\) and \(x>a\leq y\), so \(x\in(a,b)\). Since \(x>y\), we have \(y\) is not an upper bound. In either cases, \(y\) is not an upper bound, so \(b\) is the least upper bound.
Let \(a \in \mathbb{R}\), we show that \(\sup((a,\infty))=+\infty\). [Note that \((a,\infty)\) is non-empty, so we want to show it is not bounded above].
Suppose for contradiction that \((a,\infty)\) is bounded above [i.e., \(\sup((a,\infty))\neq +\infty\)]. Let \(u \in \mathbb{R}\) be an upper bound for \((a,\infty)\). Set \(x=|a|+|u|+1 \in \mathbb{R}\). Note that \(x>|a|\geq a\), so \(x\in (a,\infty)\). Hence \(u\) being an upper bound means \(x\leq u\), however \(x>|u|\geq u\). This is a contradiction.□
Problem: Let \[A=\left\{\frac{n^2+1}{|n+1/2|}:n\in\mathbb{Z}\right\}.\] Show that \(\sup(B) = +\infty\) and \(\inf(B)=4/3\).
Solution: Let us first look at the supremum. [The question is asking us to show \(B\) is not bounded above.] Let \(x\in \mathbb{R}\). By the Archimedean Principle, choose \(n\in\mathbb{Z}_+ \subseteq \mathbb{Z}\) such that \(n>2x\) [Scratch work missing to work out why we choose this particular \(n\)]. Define \(a = \frac{n^2+1}{n+1/2} \in A\). Then \[\begin{align*} a &= n\frac{n+\frac{1}{n}}{n+\frac{1}{2}} &\\ &\geq n\frac{n}{n+\frac{1}{2}} &\text{as $x+\frac{1}{n}\geq n$}\\ &\geq n\frac{n}{2n} & \text{as $n+\frac{1}{2}\leq 2n$} \\ &= \frac{n}{2} &\\ &> x&. \end{align*}\] So we have found \(a\in A\) such that \(a>x\), so \(A\) is not bounded above. Hence \(\sup(A) = +\infty\).
We now look at the infimum. We first show that \(4/3\) is a lower bound. Let \(a=\frac{n^2+1}{|n+1/2|}\) for some \(n \in \mathbb{Z}\), so \(a\in A\). Consider \[\begin{align*} n^2+1-(4/3)|n+1/2| &\geq n^2+1-(4/3)(|n|+1/2) &\text{ by the triangle inequality}\\ &=n^2-(4/3)|n|+1/3& \\ &=(|n|-2/3)^2 - 1/9 & \text{ by completing the square } \\ &\geq 0& \text{ since for all $n\in \mathbb{Z}$, $(|n|-2/3)^2\geq 1/9$}. \end{align*}\] Therefore \(n^2+1\geq (4/3)|n+1/2|\), i.e. \(a =\frac{n^2+1}{|n+1/2|}\geq 4/3\) as required.
We next show that \(4/3\) is the greatest lower bound for \(A\) [by showing any number greater than it is not a lower bound]. First note that by setting \(n=1\), we have \[\frac{n^2+1}{|n+\frac{1}{2}|} = \frac{2}{3/2} = \frac{4}{3}.\] So \(4/3\in A\). Thus, no value \(y>4/3\) can be a lower bound for \(B\). This shows that \(4/3\) is the greatest lower bound. Hence \(\inf(B) = 4/3\).
The next example is more theoretical.
Problem: Let \(A\) and \(B\) be bounded non-empty subsets of \(\mathbb{R}\). Define the sum set as \[A+B = \{a+b:a\in A, b\in B\}.\] Show that \(\sup(A+B) = \sup(A)+\sup(B)\).
Solution: Let \(\alpha =\sup(A)\) and \(\beta \sup(B)\). Note that \(\alpha, \beta \in \mathbb{R}\) as both \(A\) and \(B\) are bounded. We show \(\alpha+\beta = \sup(A+B)\).
We first show \(\alpha+\beta\) is an upper bound for \(A+B\). Let \(c\in A+B\), by definition, there exists \(a\in A\) and \(b\in B\) such that \(c=a+b\). Now \(a\leq \alpha\) and \(b\leq \beta\), so \(c=a+b\leq \alpha+\beta.\)
We now show \(\alpha+\beta\) is the least upper bound for \(A+B\). Let \(\epsilon>0\), we show that \(\alpha+\beta-\epsilon\) is not an upper bound. Since \(\alpha\) is the least upper bound of \(A\), then \(\alpha-\epsilon/2\) is not an upper bound, so there exists \(a\in A\) such that \(a>\alpha-\epsilon/2\). Similarly, there exists \(b\in B\) such that \(b>\beta-\epsilon/2\). Define \(c=a+b \in A+B\). Then \[c=a+b>(\alpha-\epsilon/2)+(\beta-\epsilon/2)=\alpha+\beta-\epsilon.\] This shows for any \(\epsilon>0\), \(\alpha+\beta-\epsilon\) is not an upper bound for \(A+B\). So \(\alpha+\beta\) is the least upper bound for \(A+B\), hence the supremum of \(A+B\).
Sometimes, instead of showing something is true for all \(y>x\), it is easier to show it is true for all \(x+\epsilon\) where \(\epsilon>0\). We can do this because if \(y>x\), then setting \(epsilon = y-x>0\), we see that \(y=x+\epsilon\).
□
Let \(A\subseteq \mathbb{R}\). We say that \(A\) has a maximum if \(\sup(A)\in A\). In this case we write \(\max (A)\) to stand for the element \(a\in A\) with \(a = \sup(A)\).
Similarly we say that \(A\) has a minimum if \(\inf(A)\in A\). In this case we write \(\min (A)\) to stand for the element \(a\in A\) with \(a = \inf(A)\).Note that a set may not have a minimum or a maximum.
Let \[A=\left\{\frac{n^2+1}{|n+1/2|}:n\in\mathbb{Z}\right\}.\] We have seen \(\inf(A)=4/3\in A\), so \(\min(A)=4/3\). However \(A\) does not have a maximum as \(\sup(A)=+\infty \not\in A\) (as \(\infty \notin \mathbb{R}\) and \(A\subseteq \mathbb{R}\)).
Let \(A = \left\{\frac{1}{n}: n \in \mathbb{Z}_+\right\}\). Then we have seen that \(\sup(A)=1\) and \(1\in A\), so \(\max(A)=1\). However it does not have a minimum as we have seen \(\inf(A)=0\) and \(0\notin A\).
4 Proof by induction
We have seen several type of proofs so far:
direct proof (sometimes known as deductive proof);
proof by case analysis;
proof by contradiction;
proof using the contrapositive.
In this chapter, we introduce a new type of proof, called proof by induction.
Let \(n_0 \in \mathbb{Z}_+\) and let \(P(n)\) be a statement for \(n\geq n_0\). A proof by induction is where one prove that:
\(P(n_0)\) is true, and
\(P(n) \implies P(n+1)\) for all \(n\geq n_0\).
□
The word induction comes from the Latin in and ductus meaning “to lead”. An inductive proof is one where a starting case leads into the next case and so on.
(In contrast, deduction has the prefix de meaning “down from”. When we do a proof by deduction, we start from certain rules and truths that “lead down” to specific things that must follow as a consequence.)Statement: Show that, for every \(n\in\mathbb{Z}_+\), we have \[1+2+3+\cdots+n=\sum_{i=1}^n=\frac{n(n+1)}{2}.\]
Proof: For \(n\in\mathbb{Z}_+\), let \(P(n)\) be the following statement. \[1+2+3+\cdots+n=\frac{n(n+1)}{2}.\] We will show that \(P(n)\) is a true statement, for all \(n\in\mathbb{Z}_+\) by giving a proof by induction.
First, let us consider \(P(1)\). We have \(1=\frac{1(1+1)}{2}\), hence, \(P(1)\) holds.
Now, suppose that \(P(k)\) is true for some positive integer \(k\), that is
\[1+2+3+\cdots+k=\frac{k(k+1)}{2}.\]
Then
\[\begin{align*}
1+2+3+\cdots+k+(k+1)&=\frac{k(k+1)}{2}+(k+1)\\
&=\frac{k(k+1)}{2}+\frac{2(k+1)}{2}\\
&=\frac{k^2+3k+2}{2}\\
&=\frac{(k+1)(k+2)}{2}.
\end{align*}\]
This shows that if \(P(k)\) is true then \(P(k+1)\) is true. By the Principle of Mathematical Induction, it follows that \(P(n)\) is true for all natural numbers \(n\).
It is not enough to show \(P(n)\implies P(n+1)\), we need to also show \(P(n_0)\) holds. As we saw in the above example, we often have that \(n_0=1\). However, this is not always the case. The following example highlights these two points.
Let \(P(n)\) be the statement \(n^2\leq 2^{n-1}\). To highlight the importance of the base case, let us first show that for \(n\geq 3\) we have \(P(n) \implies P(n+1)\).
Suppose that \(P(k)\) is a true statement for some natural number \(k\geq 3\), that is \(k^2\leq 2^{k-1}\).
ThenIf we set \(n_0=1\), we do have \(P(1)\) holds (since \(1\leq 1\)), but have not proven \(P(1) \implies P(2)\) (since \(1\not\geq 3\)). In fact, we can not prove \(P(1) \implies P(2)\) since \(P(2)\) is false (\(2^2\not\leq 2^1\)).
Since we have shown that for \(n\geq 3\) we have \(P(n) \implies P(n+1)\), we might want to set \(n_0=3\). However, \(P(3)\) is also false since \(3^2\not\leq 2^2\). In fact, we can check that \(P(3), P(4), P(5)\) and \(P(6)\) are all false. However, \(P(7)\) is true since we have that \(7^2=49\leq 64 = 2^6\).
Therefore, we have \(n_0=7\) and by the Principle of mathematical induction, we have shown that \(n^2\leq 2^{n-1}\) for all \(n\in\mathbb{Z}_+\) such that \(n\geq 7\).Sometimes, the principle of induction is not strong enough, either because we need more than one base case, or because to prove \(P(n)\) is true we need to know \(P(m)\) is true for some unknown \(m<n\). This is where we can use the strong principle of mathematical induction.
Let \(n_0 \in \mathbb{Z}_+\) and let \(P(n)\) be a statement for \(n\geq n_0\). A proof by strong induction is where one prove that:
\(P(n_0), P(n_0+1),\dots P(n_0+k)\) is true (for some \(k\geq 0\)), and
for all \(n\geq n_0+k\), show that \(P(i)\) is true for all \(i\leq n \implies P(n+1)\) is true.
□
Statement: Suppose that \(x_1 = 3\) and \(x_2 = 5\) and for \(n \geq 3\), define \(x_n = 3x_{n-1} -2x_{n-2}\). Show that \(x_n = 2^n + 1\), for all \(n\in\mathbb{Z}_+\).
Proof: Let \(P(n)\) be the statement “\(x_n= 2^n+1\)”. We will show that \(P(n)\) is a true statement, for all \(n\in\mathbb{Z}_+\), by giving a proof by induction. First, we consider our base cases \(n_0=1\) and \(n_{0+1}=2\). We have the given initial conditions \(x_1=3\) and \(x_2=5\). Using the formula \(x_n=2^n+1\), we indeed have \(x_1= 2^{1}+1=3\) and \(x_2= 2^2+1= 5\).Therefore, \(P(1)\) and \(P(2)\) hold.
Let \(n\in\mathbb{Z}_+\) and suppose for all \(i\in \mathbb{Z}_+\) such that \(i \leq n\) we have \(P(n)\) holds. Then by our assumption \(x_{n-1}= 2^{n-1}+1\) and \(x_n = 2^n +1\). We have: This shows that if \(P(i)\) is true, for \(1\leq i\leq n\), then \(P(n+1)\) is true. By the Strong Principle of Mathematical Induction, it follows that \(P(n)\) is true for all natural numbers \(n\). \(\square\)Statement: Show that every natural number can be written as the sum of distinct powers of \(2\). That is for all \(n\in\mathbb{Z}_+\), we can write \(n=2^{a_1}+2^{a_2}+\dots+2^{a_r}\) with \(a_i \in \mathbb{Z}\), \(a_i\geq 0\), and \(a_i\neq a_j\) if \(i\neq j\).
Proof: Let \(P(n)\) be the statements “there exists \(a_1,\dots a_r \in \mathbb{Z}\) such that \(a_i\geq0\), \(a_i\neq a_j\) if \(i\neq j\) and \(n=2^{a_1}+2^{a_2}+\dots+2^{a_r}\)”. We check that our base case \(n_0=1\) is true. Indeed \(1=2^0\) so \(P(1)\) holds.
Let \(n\in\mathbb{Z}_+\) and suppose for all \(i\in \mathbb{Z}_+\) such that \(i \leq n\) we have \(P(n)\) holds. Consider \(A = \{n+1-2^\ell: \ell\in\mathbb{Z}_{>0} \wedge n+1-2^\ell\geq 0\}\). We note that \(A \subseteq \mathbb{Z}_{\geq 0}\) by definition. Taking \(\ell = 1\), we see that \(n-1\in A\), so \(A \neq \emptyset\). So, by the Well Ordering Principle, \(A\) has a minimal element, call it \(m\). If \(m=0\) then \(n+1 = 2^\ell\) and \(P(n+1)\) holds. If \(m\neq 0\), then since \(P(m)\) holds, we have there exists \(a_1,\dots a_r \in \mathbb{Z}\) such that \(a_i\geq0\), \(a_i\neq a_j\) if \(i\neq j\) and \(m=2^{a_1}+2^{a_2}+\dots+2^{a_r}\). Then \(n+1 = 2^\ell+2^{a_1}+2^{a_2}+\dots+2^{a_r}\), so we just need to show \(\ell \neq a_i\) for all \(i\). For a contradiction, suppose \(\ell = a_i\) for some \(i\). Then \(n+1 \geq 2^\ell+2^\ell = 2^{\ell+1}\), so \(0\leq n+1-2^{\ell+1}<m\) which contradicts the definition of \(m\). Therefore the powers are distinct and \(P(n+1)\) holds.
Therefore, by the principle of strong induction, we have showed that every natural number can be written as the sum of distinct powers of \(2\).
A proof by induction is a special case of a proof by strong induction (taking \(k=0\))! We present these two ideas separately as it is easier to understand induction before understanding strong induction. However, most mathematician will say “induction” to mean both induction and strong induction and do not distinguish between the two (so feel free to also not distinguish between the two).
5 Studying the integers
The integers, \(\mathbb{Z}\), is an interesting set as unlike \(\mathbb{Q}\) or \(\mathbb{R}\), we can not divide. This restriction bring a lot of interesting properties that we will now study in more details. (The Well Ordering Principle also sets \(\mathbb{Z}\) apart from \(\mathbb{Q}\) and \(\mathbb{R}\) and we’ll also make use of that principle.)
5.1 Greatest common divisor
While we can not do division in general, there are cases when we can divide \(b \in \mathbb{Z}\) by \(a \in \mathbb{Z}\).
Notice that if we tried to extend this definition into \(\mathbb{Q}\), we will find that for all \(a\in\mathbb{Q}\setminus\{0\}\), \(b\in \mathbb{Q}\) we have \(a\mid b\).
Note that if \(b\neq 0\) then \(a\mid b\) implies \(|a|\leq |b|\).
Let \(a,b \in \mathbb{Z}\) with \(a\neq 0\). Then there exists a unique \(q,r\in \mathbb{Z}\) such that \(b=aq+r\) and \(0\le r<|a|\).
We call \(q\) the quotient and \(r\) the remainder
Let \(A = \{b-ak: k \in \mathbb{Z} \wedge b-ak \in \mathbb{Z}_{\geq 0}\}\). By definition \(A\subseteq \mathbb{Z}_{\geq 0}\). If \(b\geq0\), taking \(k=0\) gives \(b\in A\). If \(b<0\), taking \(k=a\cdot b\) gives \(b-a^2b = b(1-a^2) \in A\), since \(b<0\) and \((1-a^2)\leq 0\). So \(A\) is non-empty, and contains a least element. Let this element be \(r\) and the corresponding \(k\) be \(q\). Since \(r\in A\), we know \(r\geq 0\). We show \(r<|a|\) by contradiction. Suppose \(r\geq |a|\) and consider \(r>r-|a|\geq 0\). Note that \(r-|a| = (b-ak)-|a| =b-(k\pm 1)a \in A\), which contradicts the minimality of \(r\). Hence \(r<a\) as required.
It remains to show that \(r\) and \(q\) are unique. For the sake of a contradiction, suppose there exists \(q_1,q_2,r_1,r_2 \in \mathbb{Z}\) with \(0\leq r_1 < r_2 <|a|\) (without loss of generality, we assume \(r_1<r_2\) as they are not equal) and \(b = q_ia+r_i\) for \(i=1,2\). Then \(q_1a+r_1 = q_2a+r_2\) means \(r_2-r_1 = q_1a-q_2a = a(q_1-q_2)\). Since \(q_1,q_2\in \mathbb{Z}\), we have \(q_1-q_2 \in \mathbb{Z}\), so \(a|(r_2-r_1)\), i.e. \((r_2-r_1) \in a\mathbb{Z}\). But \(0<r_2-r_1 < |a|\) and there are no integers between \(0\) and \(|a|\) which is divisible by \(a\). This is a contradiction to our assumption. Hence \(r_1=r_2\), and we deduce that \(q_1=q_2\).□
Note that the division theorem shows that \(a|b\) if and only if the remainder is equal to \(0\).
Because we have a notion of division, the following definition is natural.
Note that \(1\) is always a common divisor of \(a\) and \(b\), and if \(a\not=0\), no integer larger than \(|a|\) can be a common divisor of \(a\) and \(b\).
Let \(a_1,a_2,\dots,a_n \in \mathbb{Z}\) with not all the \(a_i\)’s being equal to \(0\). We define the greatest common divisor of \(a_1\) to \(a_n\), denoted by \(\gcd(a_1,\dots,a_n)\), to be the largest positive divisor that divides \(a_i\) for all \(1\leq i \leq n\).
The following lemma showcases different properties of the gcd.
Suppose \(a,b\in\mathbb{Z}\) with \(a\) and \(b\) not both 0.
We have \(\gcd(a,b)=\gcd(|a|,b)=\gcd(a,|b|)=\gcd(|a|,|b|).\)
Set \(c=\gcd(a,b)\), and take \(x,y\in\mathbb{Z}\) so that \(a=cx\), \(b=cy\); then \(\gcd(x,y)=1\).
For all \(x\in \mathbb{Z}\) we have \(\gcd(a,b)=\gcd(a,ax+b)\).
For all \(a_1,a_2,a_3 \in \mathbb{Z}\) we have \(\gcd(a_1,a_2,a_3) = \gcd(\gcd(a_1,a_2),a_3)\).
Exercise.
□
Let \(a,b\in\mathbb{Z}\) with \(a,b\) not both equal to \(0\), and let \(\gcd(a,b)=c.\) Then there exists \(s,t\in\mathbb{Z}\) such that \(c=as+bt.\)
Let \(A\) be the set \(A=\{as+bt: (s,t\in\mathbb{Z}) \wedge (as+bt>0)\ \}.\)
By taking \(s=a, t=b\) we see that \(a^2+b^2 \in A\), hence \(A\) is a non-empty subset of \(\mathbb{Z}_+\). By the Well Ordering Principle, it has a minimal value. We denote this minimum value by \(d\) and take \(s,t\in\mathbb{Z}\) such that \(d=as+bt.\) Note that since \(c\mid a\) and \(c\mid b\), we have \(c|(as+bt)\), so \(c|d\). Hence, \(c\le d\).
Now, using Theorem 5.2 on \(a\) and \(d\), let \(q,r\in\mathbb{Z}\) be such that \(a=dq+r\) with \(0\le r<d\). Then \[r=a-dq=a-(as+bt)q=a(1-sq)+b(-tq).\] If \(r>0\), then \(r\in A\) with \(r<d\), contrary to how we chose \(d\). Hence, we must have that \(r=0\), which means \(d\mid a\). Similarly, we can show that \(d\mid b\), so \(d\) is a common divisor of \(a\) and \(b\). Since \(c=\gcd(a,b),\) we have that \(d\le c\).
Since \(c\le d\) and \(d\le c\), it follows that \(c=d\). Hence, \(\gcd(a,b)=c=d=as+bt.\)□
□
This theorem has several important corollaries (and one generalisation).
Let \(a,b,c\in\mathbb{Z}\) with \(c\neq 0\).
If \(c\mid ab\) and \(\gcd(b,c)=1\), then \(c\mid a\).
If \(c\mid a\) and \(c \mid b\) then \(c\mid \gcd(a,b)\).
Exercise.
□
Let \(a_1,\dots,a_n\in\mathbb{Z}\), not all \(a_i\)’s equal to \(0\). Then there exists \(s_1,\dots,s_n \in \mathbb{Z}\) such that \(\gcd(a_1,\dots,a_n) = a_1s_1+\dots+a_ns_n\).
Exercise.
□
Note that the proof of Theorem 5.7 only shows the existence of \(s\) and \(t\) but doesn’t give us a way to find/calculate the value of \(s\) and \(t\) (that is the proof is not constructive). To find \(s\) and \(t\) we need to use an algorithm. An algorithm is a logical step-by-step procedure for solving a problem in a finite number of steps. Many algorithms are recursive, meaning that after one or more initial steps, a general method is given for determining each subsequent step on the basis of steps already taken.
The word algorithm comes from Abu Ja’far Muhammad ibn Musa Al-Khwarizmi (Arabic Mathematician, 780-850). Al-Khwarizmi (meaning “from Khwarazm”) wrote a book detailing how to use Hindu-Arabic numerals. When this book was translated for Europeans, it was given the Latin name Liber Algorismi meaning “Book of al-Khowarazmi”. As a consequence, any manipulation of Arabic numerals (which are the ones we use nowadays) was known as an algorism. The current form algorithm is due to a “pseudo-etymological perversion” where algorism was confused with the word arithmetic to give the current spelling of algorithm.
It is interesting to note that Al-Khwarizmi also wrote the book Hisab al-jabr w’al-muqabala. We have al-jabr comes from the Arabic al- meaning “the” and jabara meaning “to reunite”, so his book was on “the reunion of broken part”, i.e. how to solve equations with unknowns. When the book made its way to Europe, Europeans shorten the Arabic title to algeber. Over time, this mutated to the word algebra which is currently used.
Input: Integers \(a\) and \(b\) such that \(a> 0\).
Output: Integers \(s\), \(t\) and \(\gcd(a,b)\) such that \(\gcd(a,b)=as+bt\).
Algorithm:
Step 0: Set \(s_0=0\), \(t_0=1\) and \(r_0 = a\)
Step 1: Set \(s_1=1\) and \(t_1=0\). Find unique \(q_1, r_1 \in \mathbb{Z}\) such that \(b = aq_1+r_1\) and \(0\leq r_1 < a\). If \(r_1 = 0\) then proceed to the final step, else go to Step 2.
Step 2: Set \(s_2=s_0-q_1s_1\) and \(t_2=t_0-q_1t_1\). Find unique \(q_2, r_2 \in \mathbb{Z}\) such that \(a = r_1q_2+r_2\) and \(0\leq r_2<r_1\). If \(r_2=0\) then proceed to the final step, else go to Step 3.
Step \(k\) (for \(k\geq 3\)): Set \(s_k=s_{k-2}-q_{k-1}s_{k-1}\) and \(t_k=t_{k-2}-q_{k-1}t_{k-1}\). Find unique \(q_k, r_k \in \mathbb{Z}\) such that \(r_{k-2} = r_{k-1}q_k + r_k\) and \(0\leq r_k < r_{k-1}\). If \(r_k = 0\) then proceed to the final step, else go to Step \(k+1\).
Final Step: If the last step was Step \(n\) (with \(n\geq 1\)) then output \(r_{n-1}=\gcd(a,b)\), \(s_n = s\) and \(t_n = t\).
The Extended Euclidean algorithm terminates and is correct.
Notice that after \(k\) steps, we have \(a>r_1>r_2>\cdots>r_k\ge 0.\) Hence, the algorithm must terminate after at most \(a\) steps.
If it terminates after Step 1 (i.e. \(r_1=0\)), then \(\gcd(a,b)=a=r_0\). Furthermore \(a = a\cdot 1+ b\cdot 0 = as_1+bt_1.\)
So suppose the algorithm terminates after \(n\) steps, for \(n>1\). We note that \(r_1=b-a\cdot q_1\) and \(r_2=a-r_1\cdot q_2\), and for \(3\le k<n\), we have \(r_k=r_{k-2}-r_{k-1}\cdot q_k\). Then by Lemma 5.6, we have \[\gcd(a,b)=\gcd(a,r_1)=\gcd(r_1,r_2)=\cdots=\gcd(r_{n-1},r_n)=\gcd(r_{n-1},0)=r_{n-1}.\]
Finally, we prove by (strong) induction that \(as_n+bt_n = r_{n-1}\) at every stage of the algorithm. So let \(P(n)\) be the statement that \(as_n+bt_n = r_n\). We have seen above that \(P(1)\) holds. We also have \(s_2=-q_1\) and \(t_2=1\). So \(r_1=b-a\cdot q_1 = a\cdot (-q_1)+b\cdot 1 = as_2+bt_2\). So \(P(2)\) holds. Assume \(P(n)\) holds for all \(n<k\), then we have \[\begin{align*} as_{k}+bt_{k}&=a(s_{k-2}-q_{k-1}s_{k-1})+b(t_{k-2}-q_{k-1}t_{k-1}) \\ &=(as_{k-2}+bt_{k-2})+q_{k-1}(as_{k-1}+bt_{k-1}) \\ &=r_{k-3}-r_{k-2}\cdot q_{k-1} \\ &= r_{k-1}. \end{align*}\] Hence \(P(k)\) holds, so by strong induction \(P(n)\) holds.□
Notice that if \(a<0\), then apply the above algorithm to \(|a|\) and \(b\) then use \(-s\) instead of \(s\).
Theorem 5.7 is often known as Bezout’s identity named after Étienne Bézout (French mathematician 1730–1783), while the Extended Euclidean algorithm is named after Euclid of Alexandria (Greek mathematician, 325BC-265BC). One might wonder at the gap between between those two mathematicians given Bezout’s identity follows immediately from the algorithm.
In his series of books The Elements, Euclid gives an algorithm to find the gcd of two numbers. The algorithm uses the fact that \(\gcd(a,b) = \gcd(a,b-a)\) and Euclid uses repeated subtractions. This was improved to give the above algorithm without \(s_k\) and \(t_k\). Around 1000 years later, Aryabhata (Indian mathematician, 476-550) wrote the book Aryabhatiya which contained a version of the Extended Euclidean Algorithm. It is not clear when the algorithm was known in Europe, but it was used by Claude Gaspar Bachet de Méziriac (French mathematician, 1581-1638), who was alive a full 100 years before Bezout. What Bezout did was to show that a version the Extended Euclidean Algorithm could be used for polynomials and a version of Bezout’s identity existed for polynomials (You can find out how polynomial rings are similar to \(\mathbb{Z}\) in units like Algebra 2).We want to compute \(\gcd(323,1451)\) and find \(s,t\in\mathbb{Z}\) such that \(\gcd(1451,323)=323s+1451t\). We go through the algorithm using the following table
| \(k\) | \(s_k\) | \(t_k\) | Calculation | \(q_k\) | \(r_k\) |
|---|---|---|---|---|---|
| \(0\) | \(0\) | \(1\) | - | - | - |
| \(1\) | \(1\) | \(0\) | \(1451=323\cdot 4+159\) | \(4\) | \(159\) |
| \(2\) | \(0-1\cdot 4 = -4\) | \(1-0\cdot4=1\) | \(323=159\cdot 2+5\) | \(2\) | \(5\) |
| \(3\) | \(1-(-4)\cdot2=9\) | \(0-1\cdot2=-2\) | \(159=5\cdot 31+4\) | \(31\) | \(4\) |
| \(4\) | \(-4-9\cdot31 = -283\) | \(1-(-2)\cdot31=63\) | \(5=4\cdot 1+1\) | \(1\) | \(1\) |
| \(5\) | \(9-(-283)\cdot1=292\) | \(-2-63\cdot1=-65\) | \(4=1\cdot 4+0\) | \(4\) | \(0\) |
Hence \(\gcd(323,1451)= 1 = 323\cdot(292)+1451\cdot(-65)\).
5.2 Primes and the Fundamental Theory of Arithmetic
We now move on to look at a fundamental property of \(\mathbb{Z}\). First we need some more definitions.
We say an integer \(p>1\) is prime if for all \(a,b \in \mathbb{Z}\) if \(p\mid ab\) then \(p\mid a\) or \(p\mid b\).
Equivalently, if \(ab \in p\mathbb{Z}\) then \(a \in p\mathbb{Z}\) or \(b \in p\mathbb{Z}\).An integer \(p>1\) is a prime if and only if the only positive divisors of \(p\) are \(1\) and \(p\).
We prove both directions separately.
\(\Rightarrow).\) For a proof by contradiction, suppose \(p\) is prime but there exists a positive divisor \(a\) which is not \(1\) or \(p\). Then we have \(1<a<p\) and there exists \(b \in \mathbb{Z}\) such that \(ab = p\). Since \(p>1\) and \(a>1\), we have \(1<b<p\). Now \(p=ab\) means \(p|ab\). However, \(p\nmid a\) and \(p\nmid b\) since \(1<a,b<p\). Hence \(p\) is not prime, which is a contradiction. So if \(p\) is prime, then the only positive integers of \(p\) are \(1\) and \(p\).
\(\Leftarrow).\) Suppose \(p>1\) is an integer whose only positive divisors are \(1\) and \(p\). Let \(a,b \in \mathbb{Z}\) be such that \(p \mid ab\). If \(p\mid a\) then we satisfy the definition of \(p\) being prime. So suppose \(p\nmid a\), then \(\gcd(p,a) = 1\) (since \(p\) has no other positive divisors). By Corollary 5.8, we have that \(p\mid b\), hence satisfying the definition of being prime.□
Most student are used to Theorem 5.13 to be the definition of a prime number. In fact, Euclid introduced prime numbers to be ones that satisfied that definition (he used the Greek word protos meaning first, as prime numbers are the first numbers from which every other numbers arise. The word prime comes from Latin “primus” which also means first). Around the 19th century, it was discovered that there are some rings in which elements satisfying Definition 5.12 and elements satisfying Theorem 5.13 are different. Following this, mathematician decided that elements satisfying Theorem 5.13 should be called irreducible (they can not be reduced into smaller elements). You can learn more about irreducible elements in general rings in a unit like Algebra 2.
Let \(n\in\mathbb{Z}_+\) be such that \(n>1\). Then there exist primes \(p_1,\dots,p_r\) such that \(n=p_1p_2\dots p_r\).
Furthermore, this factorisation is unique up to re-arranging, that is if \(n=p_1\dots p_r=q_1\dots q_t\) where \(q_1,\dots,q_t\) are also primes, then \(r=t\) and, if we order \(p_i\) and \(q_i\) such that \(p_i\leq p_{i+1}\) and \(q_i \leq q_{i+1}\) for all \(i\), then \(p_i=q_i\) for all \(i\).
We use a proof by induction to show the existence of the prime divisors of \(n\). Let \(P(n)\) be the statement that “there exists some primes \(p_1,\dots,p_r\) such that \(n=p_1\dots p_r\)”. We note that \(2\) is prime, hence \(P(2)\) holds. Assume \(P(k)\) holds for all \(k\leq n\) and consider \(P(n+1)\).
If \(n+1\) is prime, then \(P(n+1)\) holds. If \(n+1\) is composite, then it has a non-trivial divisor, say \(a\). So \(n+1=ab\). Note as before that \(1<a,b<n+1\). So by the induction hypothesis, both \(a\) and \(b\) can be written as a product of prime. Hence \(n\) can be written as a product of prime and \(P(n)\) holds. So by the principle of (strong) induction, we have all integers \(n\geq 2\) can be written as a product of primes.
We use a proof by contradiction to show the uniqueness (up to re-ordering) of the prime divisors of \(n\). Let \(S\) be the subset of \(\mathbb{Z}_+\) containing the integers whose factorisation is not unique. For a contradiction, we assume \(S\) is non-empty, hence by the Well Ordering Principle, it has a least element, call it \(n\). Suppose \(n=p_1\dots p_r=q_1\dots q_t\) where \(p_i\) and \(q_i\) are primes.
Note that since \(p_1|n\) we have \(p_1\mid q_1\dots q_t = q_1(q_2\dots q_t)\). If \(p_1\nmid q_1\), by definition \(p_1\mid (q_2\dots q_t)\). In this case, if \(p_1 \nmid q_2\) then by definition \(p_1 \mid (q_3\dots q_t)\). Continuing this argument, we see that there exists \(i\) such that \(p_1\mid q_i\). Without loss of generality, re-order the \(q_i\)’s so that \(p_1|q_1\). Since \(q_1\) is prime, it has two positive divisors, \(1\) and \(q_1\). Since \(p_1>1\) (as it is prime), and a divisor of \(q_1\) we deduce \(p_1 = q_1\). Hence \(p_1\dots p_r=q_1\dots q_t\) implies \(p_2\dots p_r=q_2\dots q_t=a\). Since \(p_2\dots p_r=q_2\dots q_t\) is two distinct prime factorisation of \(a\), we have \(a\in S\). However, \(a<n\) contradicting the minimality of \(n\). Hence \(S\) must be empty, so every \(n>1\) has a unique factorisation.□
There are infinitely many prime numbers in \(\mathbb{Z}_+\).
To the contrary, suppose that there are only finitely many primes, say \(p_1,p_2,\ldots,p_m\) for some \(m\in\mathbb{Z}_+\). Set \(n=p_1 p_2\cdots p_m+1\). Clearly \(m \ge 2\), as \(2\) is a prime. Hence \(n>1\). By the Fundamental Theorem of Arithmetic, \(n\) can be factored as a product of primes. So we let \(q\) be some prime dividing \(n\). Then \(n=qk\) for some \(k\in \mathbb{Z}_+\). Since there are only finitely many primes, we must have that \(q=p_j\) for some \(j\in \mathbb{Z}_+\), \(1\le j\le m\). Hence, \[n=p_jk=p_1p_2\cdots p_m+1,\] so \[1=n-p_1p_2\cdots p_m=p_j\left(k-\frac{p_1p_2\cdots p_m}{p_j}\right).\] Hence the prime \(p_j\) divides \(1\), which is a contradiction. The result follows.
□
The above proof is often called Euclid’s proof as it can be found in his books the elements. The proof follows directly his proof that every number can be factorised as a product of primes. Euclid did not prove the uniqueness of such factorisation, instead a proof of the uniqueness of such factorisation can be found in Diophantus of Alexandria (Greek mathematician, 200BC - 284BC) book Arithmetica (the title presumably linked to the Greek word arithmos meaning “number”).
The Fundamental Theorem of Arithmetic can be used to find solutions to equations such as the one below.
Problem: Find all square numbers \(n^2 \in \mathbb{Z}_+\) such that there exists a prime \(p\) with \(n^2 = 5p+9\).
Solution: First, we suppose we have a prime \(p\) such that \(5p+9=n^2\) for some \(n\in\mathbb{Z}_+\). We want to find constraints on \(p\). We have that \(5p=(n+3)(n-3).\) By the Fundamental Theorem of Arithmetic, the only positive factors of \(5p\) are \(1, 5, p\) and \(5p\). That is \(n+3 \in \{1, 5, p, 5p\}\), so let us analyse these four cases.
Suppose \(n+3=1\). Then \(n-3=-5\), that is \(5p=(n+3)(n-3)=-5\). But this implies that \(p=-1\), which is not prime. It follows that \(n+3\neq 1\).
Suppose \(n+3=5\). Then \(n-3=-1\), so \(5p=(n+3)(n-3)=-5\) and hence \(p=-1\), which is a contradiction. Hence, \(n+3\neq 5\).
Suppose \(n+3=p\). Then \(n-3=p-6\), so \(5p=p(p-6)\). Hence \(5=p-6\), so \(p=11\), which is prime.
Suppose \(n+3=5p\). Then \(5p=(n+3)(n-3)=5p(n-3)\). Hence \(n-3=1\), and so \(n=4\). Then \(5p=(n+3)(n-3)=7\). But this is not possible since \(5\nmid 7\). Hence, \(n+3\neq 5p\).
Summarising all of the above cases, we have that if \(p\) is a prime such that \(5p+9=n^2\), for some \(n\in\mathbb{Z}_+\), then \(p=11.\)
On the other hand, let \(p=11\). Then \(5p+9=55+9=64=8^2\). Hence, the only squares \(n \in \mathbb{Z}_+\) such that there exists a prime \(p\) with \(5p+9=n^2\) is \(n=8\) (and \(p=11\)).Two things to note:
One can use Theorem 5.14 to show that for \(x\in\mathbb{Q}_+\), there are \(a,b\in\mathbb{Z}_+\) so that \(\gcd(a,b)=1\) and \(x=\frac{a}{b}.\) Furthermore, one can show that \(a,b\) are unique. We leave this as an exercise.
Every \(n\in \mathbb{Z}\) with \(n>1\) can be expressed uniquely as \[n=\prod_{i=1}^r p_i^{n_i}\] where \(p_i\) are distinct primes and \(n_i\in \mathbb{Z}_{\geq 0}\). We can extend this representation to include \(1\) by saying \(1\) is equal to the empty product.
With the above representation of integers, we can revisit the greatest common divisor.
Let \(a,b \in \mathbb{Z}_+\) and write \(a=\prod_{i=1}^r p_i^{a_i}\) and \(b=\prod_{i=1}^r p_i^{b_i}\) where \(a_i,b_i\in \mathbb{Z}\) and \(p_i\) are the prime divisors of \(a\) or \(b\) (and hence \(a_i,b_i\) can be \(0\)). Then \(a\mid b\) if and only if \(a_i\leq b_i\) for all \(i\).
We prove both directions separately.
\(\Rightarrow).\) For a contradiction, suppose \(a\mid b\) and there exists \(i\) such that \(a_i>b_i\). We can write \(a = p_i^{a_i} \cdot A\) where \(\gcd(p_i,A)=1\), and we can write \(b = p_i^{b_i} \cdot B\) where \(\gcd(p_i,B) = 1\). Since \(a|b\), there exists \(c\in \mathbb{Z}_+\) such that \(ac = b\), that is \(p_i^{a_i} \cdot A \cdot c = p_i^{b_i} \cdot B\). Rearranging, we have \(p_i^{a_i-b_i} \cdot A \cdot c = B\). Now since \(a_i-b_i>0\), we have \(p_i|B\), which is a contradiction since \(\gcd(B,p_i)=1\). Hence, for all \(i\), \(a_i\leq b_i\).
\(\Leftarrow).\) If \(a_i\leq b_i\) for all \(i\) then \[ b = \left(\prod_{i=1}^r p_i^{a_i}\right)\left(\prod_{i=1}^r p_i^{b_i-a_i}\right) = ac.\] Hence \(a\mid b\).□
Let \(a,b \in \mathbb{Z}\) such that neither are \(0\) and write \(|a|=\prod_{i=1}^r p_i^{a_i}\) and \(|b|=\prod_{i=1}^r p_i^{b_i}\) where \(a_i,b_i\in \mathbb{Z}\) and \(p_i\) are the prime divisors of \(|a|\) or \(|b|\) (and hence \(a_i,b_i\) can be \(0\)). Then \[\gcd(a,b) = \gcd(|a|,|b|) = \prod_{i=1}^r p_i^{\min(a_i,b_i)}.\]
The greatest common divisor is a divisor of both and therefore the prime factorization of the gcd can contain only primes that appear in both \(|a|\) and \(|b|\). Each of those primes can only appear with at most the minimum power appearing in both. The greatest common divisor will then be obtained by choosing as many primes as possible with the minimum power appearing.
□
The word co-prime is to demonstrate that there are no prime factors in common between \(a\) and \(b\) (they are prime with respect to each other).
Let \(a,b \in \mathbb{Z}\) such that neither are \(0\) and write \(|a|=\prod_{i=1}^r p_i^{a_i}\) and \(|b|=\prod_{i=1}^r p_i^{b_i}\) where \(a_i,b_i\in \mathbb{Z}\) and \(p_i\) are the prime divisors of \(|a|\) or \(|b|\) (and hence \(a_i,b_i\) can be \(0\)). Then \[\text{lcm}(a,b) = \text{lcm}(|a|,|b|) = \prod_{i=1}^r p_i^{\max(a_i,b_i)}.\]
The lowest common multiple is a multiple of both and therefore the prime factorization of the lcm must contain all the primes that appear in both \(|a|\) and \(|b|\). Those primes must appear with at least the maximum power appearing in each. The lest common multiple will then be obtained by choosing as few primes as possible with the maximum power appearing.
□
Let \(a,b\in\mathbb{Z}\) such that neither are \(0\). Then \(\text{lcm}(a,b)\gcd(a,b)=|ab|.\)
We first note that for any two numbers \(a_i,b_i\) we have \(\min(a_i,b_i)+\max(a_i,b_i) = a_i+b_i\). Write \(|a|=\prod_{i=1}^r p_i^{a_i}\) and \(|b|=\prod_{i=1}^r p_i^{b_i}\). Then: \[\begin{align*} \text{lcm}(a,b)\gcd(a,b) &= \left(\prod_{i=1}^r p_i^{\max(a_i,b_i)}\right)\left(\prod_{i=1}^r p_i^{\min(a_i,b_i)}\right)\\ &= \prod_{i=1}^r p_i^{\min(a_i,b_i)+\max(a_i,b_i)} \\ &= \prod_{i=1}^r p_i^{a_i+b_i} \\ &= \left(\prod_{i=1}^r p_i^{a_i}\right)\left(\prod_{i=1}^r p_i^{b_i}\right) \\ &= |a||b| = |ab|. \end{align*}\]
□
Let \(a,b\in\mathbb{Z}\) such that neither are \(0\). If \(gcd(a,b)=1\), then \(\text{lcm}(a,b)=|ab|.\)
If there’s time, we’ll talk more about polynomial ring or famous open problems in Number Theory or the fundamental theorem of algebra.
6 Moving from one set to another - Functions
In mathematics, we are very often concerned with functions (also called maps). Some functions model the behaviour of complex systems, while other functions allow us to compare two sets. Loosely speaking, a function is a black box which takes an input from one set and gives an output in another. Every input must have an output, and there is no randomness, so the same input always gives the same output. To give a formal definition of functions, we need to go back to sets.
6.1 Definitions
Before we can start working with functions, we need to give a precise mathematical definition.
Let \(X=\{1,2,3\}\) and \(Y=\{4,5,6\}\). Then \[X\times Y=\{(1,4),\,(1,5),\,(1,6),\,(2,4),\,(2,5),\,(2,6),\,(3,4),\,(3,5),\,(3,6)\},\] \[Y\times X=\{(4,1),\,(4,2),\,(4,3),\,(5,1),\,(5,2),\,(5,3),\,(6,1),\,(6,2),\,(6,3)\}.\]
Note that \(X\times Y \neq Y \times X\).Let \(X,Y\) be non-empty sets. A function \(f\) from \(X\) into \(Y\), denoted by \(f:X\to Y\), is a set \(f\subseteq X\times Y\) which satisfies that for each element \(x\in X\) there exists exactly one element \(f(x)\in Y\) such that \((x,f(x))\in f\). That is, \[f=\{(x,f(x)):\ x\in X\ \}\subseteq X\times Y.\]
Symbolically, we have \(f\subseteq X \times Y\) is a function if \(\forall x \in X, \exists! y \in Y\) such that \((x,y)\in f\) (or \(y = f(x)\)).We negate the above statement to say that, symbolically, \(f \subseteq X\times Y\) is not a function if \(\exists x \in X\) such that \(\forall y \in Y, (x,y)\notin f\), or, \(\exists x \in X\) such that \(\exists y_1,y_2 \in Y\) such that \((x,y_1)\in f, (x,y_2) \in f\) and \(y_1\neq y_2\).
In other words, \(f \subseteq X\times Y\) is not a function if there is \(x\in X\) such that either \((x,y)\notin f\) for all \(y\in Y\), or there exists two distinct \(y_1,y_2\in Y\) with \((x,y_1),(x,y_2)\in f\).
Consider \(f:X\to Y\) and let \(A\subseteq X\). Then, the image of \(A\) under \(f\) is denoted by \[f[A] = \{f(x):x \in A\} = \{y \in Y: \exists x \in A \text{ with } y=f(x)\}.\]
We have \(f[\emptyset] = \emptyset\).
The word function comes from the Latin functus which is a form of the verb meaning “to perform”. A function can be thought as a set of operations that are performed on each values that are inputed. Interestingly, the word function (which was first introduced by Gottfried Leibniz (German mathematician, 1646 - 1716) ) was used for maps that returned more than one output for the same input. It was only in the later half of the 20th century that a function was restricted to “exactly one output for each input”.
The word domain comes from the Latin domus which means “house, home”. The domain is the place where all the inputs of \(f\) live in. Another way to look at it is, the word domus gave the word dominus which means “lord, master”, the person that ruled the house (i.e., a domain is the property owned by a Lord). The domain of a function is the set of all the \(x\) that \(f\) has “control over”.Define \(f:\mathbb{Z}\times\mathbb{Z}\to\mathbb{Z}\) by \(f((m,n))=n^2\), for all \(m,n\in\mathbb{Z}\). We have \(\mathbb{Z}\times \mathbb{Z}\) is the domain of \(f\), while \(\mathbb{Z}\) is the codomain. The image of \(f\) is \(\{n^2: n\in\mathbb{Z}\}\) (i.e., the square numbers).
Now, let \(A=\{(m,n):m,n\in\mathbb{Z}, n=2m \}\). Note that \(A=\{(m,2m): m\in\mathbb{Z} \}.\) The image of \(A\) under \(f\) is \[\begin{align*} f[A]&=\{f((m,n)): (m,n)\in A \}\\ &=\{f((m,2m)): m\in\mathbb{Z} \}\\ &=\{(2m)^2: m\in\mathbb{Z} \}\\ &=\{4m^2: m\in\mathbb{Z} \}. \end{align*}\]Consider \(f:X\to Y\) and \(g:X\to Y\). Then \(f=g\) if and only if \(f(x)=g(x)\) for all \(x\in X\).
We prove both implication separately.
\(\Rightarrow\)). First, suppose that \(f=g\). Take (arbitrary) \(x\in X\) and choose (the unique) \(y\in Y\) such that \((x,y)\in f\). Then \((x,y)\in g\) (since \(f=g\)) and by definition \(f(x)=y=g(x)\). This is true for all \(x\in X\), so it follows that \(f(x)=g(x)\) for every \(x\in X\).
\(\Leftarrow\)). Second, suppose that \(f(x)=g(x)\) for all \(x\in X\). Then \[f=\{(x,f(x)): x\in X \}=\{(x,g(x)): x\in X \}=g.\]
It follows that \(f=g\) if and only if \(f(x)=g(x),\) for all \(x\in X\).□
Notice that in this proof (and all others) that the correct punctuation follows each equations, whether they are in-line or own their own (displayed). Maths should be read as part of a grammatically correct sentence. For example “Consider \(f:X\to Y\) and \(g:X\to Y\)” reads “Consider \(f\) a function from \(X\) to \(Y\) and \(g\) a function from \(X\) to \(Y\)”, or “then \(f=\{(x,f(x)): x\in X \}=\{(x,g(x)): x\in X \}=g.\)” reads as “then \(f\) is equal to the set of pairs \((x,f(x))\) where \(x\) is in \(X\) which is equal to….”.
It is for this reason that we should not start a sentence with maths symbol.□
6.2 Injective, surjective and bijective
We now introduce three important properties that a function may or may not have.
We say a function \(f:X\to Y\) is injective (or one-to-one, or an injection) if for all \(x_1,x_2\in X\), we have that if \(x_1\not=x_2\) then \(f(x_1)\not=f(x_2)\).
Using the contrapositive, an alternative definition is that a function \(f:X \to Y\) is injective if for all \(x_1,x_2 \in X\), we have if \(f(x_1)=f(x_2)\) then \(x_1 = x_2\).
Figure 6.1: An injective function from \(X\) to \(Y\), there are at most one arrow going to any point in \(Y\). However the function is not surjective as there are some points in \(Y\) with no arrow going to it. Figure made with Geogebra.
Figure 6.2: A surjective function from \(X\) to \(Y\), every point in \(Y\) has at least one arrow going to it. However the function is not injective as there are some points in \(Y\) with at least two arrows going to it. Figure made with Geogebra
Define \(f:\mathbb{R}\times \mathbb{R}\to \mathbb{R}\times\mathbb{R}\) by \(f((m,n))=(m+n,m-n),\) for all \(m,n\in\mathbb{R}\). We want to show that \(f\) is bijective.
We first show it is injective by using the contrapositive. Let \((m_1,n_1), (m_2,n_2)\in \mathbb{R}\times\mathbb{R}\) (the domain) be such that \(f((m_1,n_1))=f((m_2,n_2))\). That is \((m_1+n_1,m_1-n_1) = (m_2+n_2,m_2-n_2)\), i.e. \(m_1+n_1 = m_2+n_2\) and \(m_1-n_1 = m_2-n_2\). Therefore, \(2m_1 = (m_1+n_1)+(m_1-n_1)=(m_2+n_2)+(m_2-n_2)=2m_2\). Since \(2\neq 0\), we can divide by \(2\) to deduce \(m_1 = m_2\). Hence \(m_1+n_1=m_2+n_2=m_1+n_2\) means \(n_1=n_2\). Therefore \((m_1,n_1)=(m_2,n_2)\) and \(f\) is injective.
We next show that \(f\) is surjective. We begin by choosing \((u,v)\in\mathbb{R}\times\mathbb{R}\) [the co-domain].
[Scratch work: We want to find \((m,n)\in\mathbb{R}\times\mathbb{R}\) such that \(f(m,n)=(u,v)\). So we need to find \((m,n)\in\mathbb{R}\times \mathbb{R}\) such that \(m+n=u\) and \(m-n=v\). Hence, we must have \(m=u-n\) and \(m=v+n\). Then \(u-n=v+n\), or equivalently, \(u-v=2n\), or equivalently, \(\frac{u-v}{2}=n\). If we have \(\frac{u-v}{2}=n\) and \(m=u-n\), then \(m=u-\frac{u-v}{2}=\frac{u+v}{2}.\)]
We set \(m=\frac{u+v}{2}\) and \(n=\frac{u-v}{2}\). Then \((m,n)\in\mathbb{R}\times\mathbb{R}\) [the domain], and \[f(m,n)=(m+n,m-n)=\left(\frac{u+v}{2}+\frac{u-v}{2},\frac{u+v}{2}-\frac{u-v}{2}\right)=(u,v).\] It follows that \(f\) is surjective.
Since \(f\) is injective and surjective, it is bijective.Let \(f_1:\mathbb{Z}_+\to\mathbb{Z}_+\) be defined by \(f_1(n) = n^2\) for all \(n\in \mathbb{Z}_+\). We claim that \(f_1\) is injective but not surjective.
We first show \(f_1\) is injective. Let \(n_1,n_2 \in \mathbb{Z}_+\) be such that \(n_1\neq n_2\). Without loss of generality, we assume \(n_1<n_2\). Note that \(n_1,n_2>0\) by definition, so \(n_1<n_2\) means \(n_1^2<n_2n_1\) and similarly, \(n_1n_2<n_2^2\). Combining these two inequalities together, we get \(n_1^2<n_1n_2<n_2^2\), i.e. \(f_1(n_1)<f_1(n_2)\) so \(f(n_1)\neq f(n_2)\). So \(f_1\) is injective.
We next show \(f_1\) is not surjective. We take \(2 \in \mathbb{Z}_+\) and claim that for all \(n\in \mathbb{Z}_+\) we have \(f_1(n)=n^2 \neq 2\). For a contradiction, suppose such an \(n\) exists, i.e. \(n^2 = 2\). Note that \(n>1\) since \(1^1 = 1<2\). However, if \(n\geq 2\), then \(n^2 \geq 4 >2\) which is not possible. Hence \(1<n<2\), but there are no natural numbers between \(1\) and \(2\). Hence \(n\) does not exists and \(f_1\) is not surjective.Consider \(f:X\to Y\). Then we have that \(f\) is injective if and only if for all\(y\in f[X]\), there exists a unique \(x\in X\) such that \(f(x)=y\).
We show the two implications separately.
\(\Rightarrow\)). Suppose that \(f\) is injective, and take \(y\in f[X]\). Hence, \(\exists x_1\in X\) such that \(f(x_1)=y\). Now, suppose \(\exists x_2\in X\) such that \(x_2\not=x_1\). Since \(f\) is injective, we have that \(f(x_1)\not=f(x_2)=y.\) Hence, \(\forall y\in f[X]\), \(\exists ! x\in X\) such that \(f(x)=y\).
\(\Leftarrow\)). Suppose that \(\forall y\in f[X]\), \(\exists ! x\in X\) such that \(f(x)=y\). Take \(x_1,x_2\in X\) such that \(x_1=x_2\) and let \(y=f(x_1).\) By assumption, \(x\) is the only element of \(X\) that \(f\) maps to \(y\). Then \(y\not=f(x_2),\) so \(f(x_1)\not=f(x_2).\) Hence, we have shown that for \(x_1,x_2\in X\) with \(x_1\not=x_2\), we have that \(f(x_1)\not=f(x_2)\). Therefore, \(f\) is injective.
It follows that \(f\) is injective if and only if \(\forall y\in f[X]\), \(\exists ! x\in X\) such that \(f(x)=y\).□
Caution! Note that the converse of the above definition is, “for all \(x\in X\), there exists a unique \(y\in Y\) such that \(f(x)=y\)”, which is the definition of a function.
So do not confuse the definition of injectivity with the definition of a function. In particular, one definition can be true without the other being true.
For example, consider \(f=\{(y^2,y):\ y\in\mathbb{Z}\ \}\subseteq \mathbb{Z}\times \mathbb{Z}\). We have that for each \(y\in\mathbb{Z}\), there exists a unique \(x\in \mathbb{Z}\) such that \((x,y)\in f\) (namely \(x=y^2\)) so \(f\) satisfies the definition of being injective. However \(f\) is not a function since, for example, \((4,2), (4,-2) \in f\) (so it doesn’t make sense to talk about whether \(f\) is injective or not).Consider \(f:X\to Y\). Then \(f\) is surjective if and only if \(f[X]=Y\).
We show the two implications separately.
\(\Rightarrow\)). Suppose \(f\) is surjective, we will show \(f[X]=Y\) by showing \(f[X]\subseteq Y\) and \(Y\subseteq f[X]\). Note that by definition \(f[X] = \{y\in Y: \exists x\in X \text{ with } f(x)=y\} \subseteq Y\).
Take \(y_0 \in Y\). Since \(f:X\to Y\) is surjective, there exists \(x_0 \in X\) so that \(f(x_0)=y_0\). Thus \(y_0 \in f[X]\). As \(y_0\) was arbitrary, we have \(\forall y_0 \in Y\), \(y_0\in f[x]\). Hence \(Y\subseteq f[X]\).
\(\Leftarrow\)). Suppose \(f[X]=Y\). Choose \(y_0 \in Y = f[X]\). By definition of \(f[X]\), there exists \(x_0 \in X\) such that \(y_0 = f(x_0)\). This argument holds for all \(y_0 \in Y\), hence \(f\) is surjective.□
Consider \(f:X\to Y\). Then we have that \(f\) is bijective if and only if \(\forall y\in Y\), \(\exists !\, x\in X\) such that \(f(x)=y\).
We show the two implications separately.
\(\Rightarrow\)). Suppose \(f\) is bijective, then it is surjective so by Proposition 6.9 \(Y=f[X]\). We also have \(f\) is injective, so by Proposition 6.8 we have \(\forall y\in f[X]=Y\), \(\exists !\, x\in X\) such that \(f(x)=y\) as required.
\(\Leftarrow\)). Suppose that \(\forall y\in Y\), \(\exists ! x\in X\) such that \(f(x)=y\). In particular, \(\forall y\in Y\), \(\exists x\in X\) such that \(f(x)=y\), i.e. by definition \(f\) is surjective. By Proposition 6.9 \(Y=f[X]\), so our assumption becomes \(\forall y\in Y=f[X]\), \(\exists ! x\in X\) such that \(f(x)=y\). Hence by Proposition 6.8, \(f\) is injective. Since we have shown \(f\) is surjective and injective, we deduce \(f\) is bijective.□
The words injective, surjective and bijective all have the same ending “-jective”. This comes from the Latin verb jacere which means “to throw”.
Injective has the prefix in, a Latin word meaning “in, into”. This gave rise to the medical term “injection” where we throw some medecine into the body. An injective function is one that throws the set \(X\) into the set \(Y\) (every elements of \(X\) stay distincts once they are in \(Y\).)
Surjective has the prefix sur a French word meaning “over”, itself coming from the Latin super which means “(from) above”. A surjective function is one that covers the whole of \(Y\) (in the sense \(X\) is thrown from above to cover \(Y\)).
Bijective has the prefix bi, a Latin word meaning “two”. Once we talk about inverse functions, it will become clear that a bijection is a function that works in two directions.
Consider \(f:X\to Y\) and let \(X=U\cup V\). Then
\(f[X]=f[U]\cup f[V]\).
if \(f\) is injective and \(U\cap V=\emptyset\), then \(f[U]\cap f[V]=\emptyset\).
a.) Since \(U,V\subseteq X\), we have that \(f[U], f[V]\subseteq f[X]\), so \(f[U]\cup f[V]\subseteq f[X]\). On the other hand, take \(x\in X\). Then \(x\in U\) or \(x\in V\), so \(f(x)\in f[U]\) or \(f(x)\in f[V]\). Therefore \(f(x)\in f[U]\cup f[V]\). Since this holds for all \(x\in X\), we have \(f[X]\subseteq f[U]\cup f[V]\). Hence, \(f[X]=f[U]\cup f[V]\).
b.) Suppose that \(f\) is injective and \(U\cap V=\emptyset\). To the contrary, suppose that there exists some \(y\in f(U)\cap f(V)\). Hence, there exists some \(u\in U\) such that \(y=f(u)\), and there exists some \(v\in V\) such that \(y=f(v)\). It follows that \(f(u)=y=f(v)\). Since \(f\) is injective, we have that \(u=v\). Hence, \(u\in U\cap V\), which contradicts our initial assumption. It follows that \(f(U)\cap f(V)=\emptyset.\)□
Suppose that \(f:X\to Y\) is bijective, and let \(A\subseteq X\) and \(B=X\setminus A\). Then \(f[A]\cap f[B]=\emptyset\) and \(f[A]\cup f[B] = Y\).
Since \(f\) is bijective it is surjective and \(Y=f[X]\). We also note that \(A\cup B = X\), so we satisfy the hypothesis of the above theorem and deduce \(f[A] \cup f[B] = f[X] =Y\).
Furthermore since \(f\) is bijective, it is injective and we have \(A\cap B = \emptyset\). Hence we satisfy the hypothesis of part b.) of the above theorem and can deduce that \(f[A]\cap f[B]=\emptyset\).□
6.3 Pre-images
As well as looking at the image of various subset of \(X\) under the function \(f:X\to Y\), we are often interested in looking at where certain subsets of \(Y\) come from.
Consider \(f:X\to Y\) and let \(V\subseteq Y\). We define the pre-image (or inverse image) of \(V\) under \(f\) by \[f^{-1}[V]=\{x\in X:\ f(x)\in V \}.\]
We have \(f^{-1}[\emptyset]=\emptyset\).Let \(X=\{1,2,3\}\) and \(Y=\{4,5,6\}\). Define the function \(f=\{(1,5),(2,5),(3,4)\} \subseteq X\times Y\). Then:
\(f^{-1}[\{4,6\}]=\{3\}\),
\(f^{-1}[\{4,5\}]=\{1,2,3\}=X\),
\(f^{-1}[\{6\}]=\emptyset\),
\(f^{-1}[\{5\}]=\{1,2\}\).
Let \(f:\mathbb{R}\times \mathbb{R}\to\mathbb{R}\) be defined by \(f((x,y))=2x-5y\). We will find \(f^{-1}[\{0\}]\) and \(f^{-1}[(0,1)]\) (recall that the open interval \((0,1)=\{x\in\mathbb{R}:0<x<1\}\)).
\[\begin{align*} f^{-1}[\{0\}]&=\{(x,y)\in\mathbb{R}\times\mathbb{R}:\ f((x,y))\in\{0\} \}\\ &=\{(x,y)\in\mathbb{R}\times\mathbb{R}:\ 2x-5y=0 \}\\ &=\{(x,y)\in\mathbb{R}\times\mathbb{R}: \ y=\tfrac{2x}{5} \}\\ &=\left\{\left(x,\tfrac{2x}{5}\right):\ x\in\mathbb{R} \right\}. \end{align*}\]
\[\begin{align*} f^{-1}[(0,1)]&=\{(x,y)\in\mathbb{R}\times\mathbb{R}:\ f((x,y))\in (0,1) \}\\ &=\{(x,y)\in\mathbb{R}\times\mathbb{R}:\ 2x-5y\in(0,1)\}\\ &=\{(x,y)\in\mathbb{R}\times\mathbb{R}:\ 0<2x-5y<1 \}\\ &=\left\{(x,y)\in\mathbb{R}\times\mathbb{R}:\ \tfrac{5}{2}y<x<\tfrac{5}{2}y+\tfrac{1}{2} \right\}. \end{align*}\]
We can also rearrange the last line to say:
\[f^{-1}[(0,1)]=\left\{\left(\tfrac{5}{2}y+\varepsilon,y\right):\ \epsilon,y\in\mathbb{R},\ 0<\varepsilon<\tfrac{1}{2} \right\}.\]Define \(g:\mathbb{R}\to \mathbb{R}\) by \(g(x)=x^2\). Take \(V=[4,\infty)=\{x\in \mathbb{R}: 4\leq x\}\). Then
\[\begin{align*} g^{-1}[V]&=\{x\in\mathbb{R}:\ g(x)\in V \}\\ &=\{x\in\mathbb{R}:\ x^2\in [4,\infty) \}\\ &=\{x\in\mathbb{R}:\ (x\ge 2)\ \vee\ (x\le -2) \}\\ &=(-\infty,-2 ]\cup[2,\infty). \end{align*}\]We have the nice results that union and intersection behave as expected.
Consider \(f:X\to Y\) and let \(U,V\subseteq Y.\) Then
\(f^{-1}[U\cap V]=f^{-1}[U]\cap f^{-1}[V]\);
\(f^{-1}[U\cup V]=f^{-1}[U]\cup f^{-1}[V].\)
We prove a. and leave b. as an exercise.
We have \[\begin{align*} f^{-1}[U\cap V]&=\{x\in X:\ f(x)\in U\cap V\ \}\\ &=\{x\in X:\ f(x)\in U \wedge f(x)\in V\ \}\\ &=\{x\in X:\ f(x)\in U\ \}\cap\{x\in X:\ f(x)\in V\ \}\\ &=f^{-1}[U]\cap f^{-1}[V]. \end{align*}\]
Therefore the two sets are equal, i.e. \(f^{-1}[U\cap V]=f^{-1}[U]\cap f^{-1}[V].\)□
The link between images and pre-images is explored in the following theorem.
Consider \(f:X\to Y\), and let \(U\subseteq X\) and \(V\subseteq Y\). Then
\(f[f^{-1}[V]]\subseteq V\), and for \(f\) surjective, we have \(f[f^{-1}[V]]=V\).
\(U\subseteq f^{-1}[f[U]]\), and for \(f\) injective, we have \(U=f^{-1}[f[U]].\)
We prove a. and leave b. as an exercise.
If \(V=\emptyset\), then \(f^{-1}[V]=\emptyset\) and \(f[f^{-1}[V]]=\emptyset=V\). So we assume \(V\neq\emptyset\). Similarly, as \(\emptyset\subseteq V\), we have that if \(f[f^{-1}[V]]=\emptyset\) then \(f[f^{-1}[V]]\subseteq V\). So we also assume \(f[f^{-1}[V]]\neq\emptyset\).
Suppose that \(y\in f[f^{-1}[V]]\). Then \(y=f(w)\) for some \(w\in f^{-1}[V]\). By the definition of \(f^{-1}[V]\), we have \(f(w)\in V\). Hence, \(y=f(w)\in V\). Since \(y\) is arbitrary, this shows that every element of \(f[f^{-1}[V]]\) lies in \(V\), that is \(f[f^{-1}[V]]\subseteq V\).
Now suppose that \(f\) is surjective. We need to show that \(V\subseteq f[f^{-1}[V]].\) Suppose that \(v\in V\). Since \(f\) is surjective, there exists an \(x\in X\) such that \(f(x)=v\). Then \(f(x)\in V\), and it follows that \(x\in f^{-1}[V].\) Hence, \(v=f(x)\in f[f^{-1}[V]].\) Since \(v\) was arbitrary, this shows that \(V\subseteq f[f^{-1}[V]].\) Summarising, we have that \(f[f^{-1}[V]]=V\) whenever \(f\) is surjective.□
6.4 Composition and inverses of functions
We now turn our attention on how to apply several functions in a row.
Composition has the same roots as components and composite. It comes from co meaning “together with” and ponere meaning “to put”. So something composite is something “put together” from different components. The composition of two functions is the result of putting two functions together.
Since \(f\) assigns to \(x\in X\) exactly one value \(f(x)\in Y\), and \(g\) assigns to \(f(x)\in Y\) exactly one value in \(Z\), we have that \(g\circ f\) is a function from \(X\) to \(Z\), that is \(g\circ f:X\to Z\).
We have that composition of functions is associative. That is:
Consider \(f:X\to Y\), \(g:Y\to Z\) and \(h:Z\to W\). Then \(h\circ(g\circ f)=(h\circ g)\circ f\).
By Theorem 6.4, to show \(h\circ(g\circ f)=(h\circ g)\circ f\), we need to show that \(\forall\,x\in X\), we have \((h\circ(g\circ f))(x)=((h\circ g)\circ f)(x)\). Let \(x\in X\). Then \[(h\circ(g\circ f))(x)=h((g\circ f)(x))=h(g(f(x))), \forall\, x\in X\] and \[((h\circ g)\circ f)(x)=(h\circ g)(f(x))=h(g(f(x))), \forall\, x\in X.\] Thus, \(h\circ(g\circ f)=(h\circ g)\circ f\).
This argument holds for all \(x\in X\), hence \(h\circ(g\circ f)=(h\circ g)\circ f\).□
The above theorem tells us that the notation \(h\circ g\circ f\) is unambiguous.
Let \(a,b,c,d\in\mathbb{R}\) be such that \(a<b\) and \(c<d\). Recall that \([a,b]\) denotes the closed interval from \(a\) to \(b\), that is \[[a,b]=\{x\in\mathbb{R}:\ a\le x\le b\ \}.\]
We define the following three functions:
\(f_1:[a,b]\to[0,b-a]\) defined by \(f_1(x)=x-a\);
\(f_2:[0,b-a]\to[0,d-c]\) defined by \(f_2(x)=x\frac{d-c}{b-a}\);
\(f_3:[0,d-c]\to[c,d]\) defined by \(f_3(x) = x+c\).
We briefly check that \(f_2\) is indeed a function from \([0,b-a]\) to \([0,d-c]\) by checking \(f_2([0,b-a])\subseteq [0,d-c]\) (in theory one should also do the same with \(f_1\) and \(f_3\), but these two cases are clearer). Pick \(x\in[0,b-a]\), so \(0\leq x\leq b-a\) by definition. Then since \(b-a>0\) we have \(0\leq \frac{x}{b-a}\leq 1\), and since \(d-c>0\) we have \(0\leq x\frac{d-c}{b-a}\leq d-c\). So \(f_2(x) \in [0,d-c]\). As this is true for all \(x\in [0,b-a]\), we indeed have \(f_2\) is a function with co-domain \([0,d-c]\).
We can construct \(f:[a,b]\to [c,d]\) by composing \(f_3\) with \(f_2\) with \(f_1\), i.e., \(f = f_3\circ f_2 \circ f_1\) is defined by \(f(x) = c + \frac{(x-a)(d-c)}{b-a}\).Properties of functions carry through composition.
Consider \(f:X\to Y\) and \(g:Y\to Z\). Then:
if \(f\) and \(g\) are injective, we have that \(g\circ f\) is injective.
if \(f\) and \(g\) are surjective, we have that \(g\circ f\) is surjective.
We prove a. and leave b. as an exercise.
Suppose that \(f,g\) are injective, and suppose that \(x_1,x_2\in X\) are such that \(x_1\not=x_2\). Since \(f\) is injective, we have that \(f(x_1)\not=f(x_2)\). Now, set \(y_1=f(x_1)\) and \(y_2=f(x_2)\). Then \(y_1,y_2\in Y\) with \(y_1\not=y_2\). Further, since \(g\) is injective, we have \(g(y_1)\not=g(y_2)\). It follows that \[(g\circ f)(x_1)=g(f(x_1))=g(y_1)\not=g(y_2)=g(f(x_2))=(g\circ f)(x_2).\] To conclude, for any \(x_1,x_2\in X\) with \(x_1\not=x_2\), we have \((g\circ f)(x_1)\not=(g\circ f)(x_2).\) Hence \(g\circ f\) is injective.□
Consider \(f:X\to Y\) and \(g:Y\to Z\) be bijective, then \(g\circ f:X\to Z\) is also bijective.
We say that a function \(f:X\to Y\) is invertible if there exists a function \(g:Y\to X\) such that:
\(g\circ f\) is the identity function on \(X\) (that is, \(\forall\,x\in X\), \((g\circ f)(x)=x\)), and
\(f\circ g\) is the identity function on \(Y\) (that is, \(\forall\,y\in Y\), \((f\circ g)(y)=y\)).
We say \(g\) is an inverse of \(f\).
If \(g\) is an inverse for \(f\), then we also have that \(f\) is an inverse for \(g\).We’ve already seen that inverse comes from in and vertere which is the verb “to turn”. The inverse of an function, is one that turns the original function inside out to give back what was originally put in.
Suppose \(f:X\to Y\), and suppose that \(g:Y\to X\) and \(h:Y\to X\) are inverses of \(f\). Then \(g=h\), that is, if \(f\) has an inverse then its inverse is unique.
Exercise.
□
Since the inverse is unique, the inverse of \(f:X\to Y\) is often denoted by \(f^{-1}:Y\to X\).
Note the difference between \(f^{-1}[ ]\) which is about pre-images (also known as inverse images), and \(f^{-1}( )\) which is about the inverse function. In particular, when using \(f^{-1}[ ]\) (i.e., calculating pre-images), we are not making any claim that \(f\) is invertible or indeed that \(f^{-1}:Y\to X\) is a function that exists. However, when using \(f^{-1}( )\), we are at the same time claiming that \(f\) is invertible and hence \(f^{-1}\) is a function.It is important to note that we have two conditions to prove \(f:X\to Y\) is invertible. As an exercise, one can find examples of \(f:X\to Y\) and \(g:Y\to X\) such that \(f\circ g\) is the identity, but \(g\circ f\) is not. However, if we have some constraints on \(f\) or \(g\) then only one condition needs to be met.
Suppose that \(f:X\to Y\) and \(g:Y\to X\) are such that \(g\circ f\) is the identity function on \(X\).
If \(g\) is injective, then \(f\circ g\) is the identity map on \(Y\) (and hence \(g=f^{-1}\)).
If \(f\) is surjective, then \(f\circ g\) is the identity map on \(Y\) (and hence \(g=f^{-1}\)).
Exercise.
□
This next theorem gives another way to test if a function is invertible or not.
Suppose that \(f:X\to Y\). Then \(f\) is invertible if and only if \(f\) is bijective.
We prove both implications separately.
\(\Rightarrow\)). First, we will show that if \(f\) is invertible, then \(f\) is bijective. So suppose \(f\) is invertible, and let \(g:Y\to X\) denote the inverse of \(f\). Then \(g\circ f\) is the identity function on \(X\), and \(f\circ g\) is the identity function on \(Y\). We first show \(f\) is surjective. Take \(y_1 \in Y\), then \(y_1=f\circ g(y_1)=f(g(y_1))\). So set \(x_1=g(y_1)\). Then \(x_1 \in X\) and \(f(x_1)=f(g(y_1))=y_1\). So for all \(y\in Y\), there exists \(x\in X\) such that \(f(x)=y\).
We prove that \(f\) is also injective using the contrapositive. Suppose we have \(x_1,x_2 \in X\) with \(f(x_1)=f(x_2)=y\). Then since \(g\circ f\) is the identity on \(X\), we have \(x_1 = g(f(x_1))=y=g(f(x_2))=x_2\). Hence \(f\) is injective and surjective, so it is bijective.
\(\Leftarrow\)). Second, we will show that if \(f\) is bijective, then \(f\) is invertible. So suppose that \(f\) is bijective. We set \[g=\{(y,x)\in Y\times X: (x,y)\in f \}\subseteq Y\times X.\] Since \(f\) is bijective, by Corollary 6.10 we have that for all \(y\in Y\), there is a unique \(x\in X\) such that \(f(x)=y\). Hence, \(g\) is a function, that is \(g:Y\to X\).
We will show that \(g\) is the inverse of \(f\). For this, we first take \(x\in X\) and set \(y\in Y\) to be \(y=f(x)\). Then by the definition of \(g\), we have that \(g(y)=x\), so \((g\circ f)(x)=g(y)=x\). Since \(x\) was arbitrary, this shows that \(g\circ f\) is the identity function on \(X\). Now, choose any \(y\in Y\). Since \(f\) is bijective then for all \(y\in Y\), there exists a unique \(x\in X\) such that \(f(x)=y\). Further, since \(g\) is a function, we must have that \(g(y)=x\), and hence \((f\circ g)(y)=f(x)=y\). Since \(y\) was arbitrary, this shows that \(f\circ g\) is the identity function on \(Y\). Hence if \(f\) is bijective, we have that \(f\) is invertible.
It follows that \(f\) is invertible if and only if \(f\) is bijective.□
Suppose that \(f:X\to Y\) is bijective. In the above proof, we found a way of defining \(f^{-1}:Y\to X\). That is, \(\forall\,y\in Y\), we can write \(f^{-1}(y)=x\) where \(x\in X\) such that \(f(x)=y.\)
Let \(a,b,c,d\in\mathbb{R}\) be such that \(a<b\) and \(c<d\). In the previous example, we defined \(f:[a,b]\to[c,d]\) as the composition of three functions and to be \(f(x) = c+\frac{(x-a)(d-c)}{b-a}\). We want to prove \(f\) is bijective. One method would be to show all three functions that made up its composition are bijective (and this is relatively easy to do so). But we will instead show \(f\) is invertible by constructing the inverse.
By symmetry (replacing \(a\) with \(c\), \(b\) with \(d\) etc), let us define \(g:[c,d]\to[a,b]\) via \(g(x)=a+\frac{(x-c)(b-a)}{d-c}\). We have \[\begin{align*} (g\circ f)(x)&=g(f(x))\\ &=a+(f(x)-c)\left(\frac{b-a}{d-c}\right)\\ &=a+\left[c+(x-a)\left(\frac{d-c}{b-a}\right)-c\right]\left(\frac{b-a}{d-c}\right)\\ &=a+(x-a)\\ &=x, \end{align*}\] for all \(x\in[a,b].\) Similarly, \[\begin{align*} (f\circ g)(x)&=f(g(x))\\ &=c+(g(x)-a)\left(\frac{d-c}{b-a}\right)\\ &=c+\left[a+(x-c)\frac{(b-a)}{(d-c)}\right]\left(\frac{d-c}{b-a}\right)\\ &=x, \end{align*}\] for all \(x\in[c,d]\). It follows that \(g:[c,d]\to[a,b]\) is the inverse of \(f\). Therefore, \(f\) is bijective.Suppose \(f:X\to Y\) and \(g:Y\to Z\) are bijective. Then \((g\circ f)^{-1}=f^{-1}\circ g^{-1}\).
Exercise.
□
7 Cardinality
Now that we know about functions, we return to sets, in particular “measuring their size”. One reason sets were introduced was to “tame” and understand infinity. Indeed, as we will see at the end of course, the study of sets leads us to realise that there are different kinds of infinities.
Bijective functions allowed us to construct a “dictionary” from one set to another: every element in one set is in one-to-one correspondence with the elements in another bijective set. This brings the idea that there’s a fundamental property shared by these two sets. This is the motivation of this section, but first some notation.
Let \(A\) be a set, we denoted by \(|A|\) the cardinality of \(A\).
The above notation doesn’t actually define what we mean by the cardinality of a set.
We build our notion of the cardinality of different sets as follows.
We define \(|\emptyset| = 0\).
For \(n\in\mathbb{Z}_+\) we define \(|\{1,2,\dots,n\}| = n\).
If \(A\) and \(B\) are two non-empty sets, we say \(|A| = |B|\) if and only if there exists a bijective \(f:A\to B\).
Again, for an individual infinite set \(A\) this does not define what we mean by \(|A|\), but it does define what we mean by \(|A|=|B|\) for two infinite sets \(A\) and \(B\).
We need to ensure that our last definition makes sense by checking the following:
For any non-empty set \(A\), we expect \(|A|=|A|\). We verify this is true by noting that \(f:A\to A\) defined by \(f(a)=a\) is bijective.
For any non-empty sets \(A\), \(B\), we expect that if \(|A|=|B|\) then \(|B|=|A|\). Let us verify this. Suppose \(|A|=|B|\), then there exists a bijective \(f:A\to B\). Since \(f\) is bijective it is invertible, so there exists \(f^{-1}:B\to A\). Since \(f^{-1}\) is invertible, it is bijective, hence \(|B|=|A|\) by definition.
For any non-empty sets \(A\), \(B\), \(C\), we expect that if \(|A|=|B|\) and \(|B|=|C|\) then \(|A|=|C|\). Let us verify this. Suppose \(|A|=|B|\) and \(|B|=|C|\), then there exists bijective \(f:A\to B\) and \(g:B\to C\). Consider \((g\circ f):A\to C\), which is bijective by Corollary 6.19, hence \(|A|=|C|\) as required.
By combining the last two definitions together, we see that if \(f:\{1,2,\dots, n\}\to A\) is bijective, then \(|A|=n\) and we say \(A\) has \(n\) elements. Note that in this case we can enumerate the elements of \(A\) as \(a_1,\dots,a_n\) (where \(a_i=f(i)\)).
We have two cases
When \(|A| \in \mathbb{Z}_{\geq 0}\) then we say \(A\) is a finite set.
If \(A\) is not a finite set, we say \(A\) is an infinite set.
We take as a fact that \(\mathbb{Z}_+\) is infinite (which makes sense since by the Archimedean Property, \(\mathbb{Z}_+\) is not bounded above).
Finite comes from the Latin finis meaning “end”. A finite set is one that ends. While infinite has the prefix in- meaning “not”, so an infinite set is one that has no end.
Cardinality comes from the Latin cardin meaning “hinges” (which are used to pivot doors). This was used to talk about the “Cardinal virtues”, i.e., the pivotal virtues, the most important one. From there, the word developed to mean “principal”. This was used by mathematician to name the set of whole numbers \(\{0,1,2,3,\dots\}\) to be the Cardinals, as they are the principal numbers (compared to fractions, reals etc.). From there, the cardinality of a set referred to the whole number/the cardinal associated to the set.Suppose \(f:X\to Y\) is injective and \(A\subseteq X\). Then \(|A|=|f[A]|\).
Let \(B=f[A]\). Restrict \(f\) to \(A\) by defining \(g:A\to B\) via \(g(a)=f(a)\), for all \(a\in A\). By the definition of \(B\), we have that \(B=f[A]=g[A]\), so \(g\) is surjective. Now, suppose that \(a_1,a_2\in A\) are such that \(g(a_1)=g(a_2)\). Then \(f(a_1)=f(a_2)\), and since \(f\) is injective, this means that \(a_1=a_2\). Hence, \(g\) is injective. It follows that \(g\) is bijective, so \(|A|=|g[A]|\). We also know that \(g[A]=B=f[A]\), so \(|A|=|g[A]|=|f[A]|\).
□
Let \(A\), \(B\) be two finite sets with \(|A| = n\) and \(|B| = m\). If there exists an injective \(f:A\to B\) then \(n\leq m\).
Let \(C = f[A]\), then by the previous lemma we have \(|C|=|A|=n\) and we know \(C\subseteq B\). Hence \(B\) has at least \(n\) elements, so \(m=|B|\geq n\).
□
The contrapositive of the theorem is “If \(|A|>|B|\) then for any \(f:A\to B\) there exist distinct \(a_1,a_2\in A\) such that \(f(a_1)=f(a_2)\)”. Theorem 7.5 is often known as the Pigeonhole Principle as it can be understood as “if you have more pigeons than pigeonholes, then two pigeons will need to share a pigeonhole”.
We extend the above principle to all (finite or infinite) sets.
Note that in particular, for any two sets \(A\) and \(B\) such that \(B\subseteq A\), since we can define an injective function \(f:B\to A\) via \(f(b)=b\) for all \(b\in \mathbb{B}\), we have \(|B|\leq |A|\).
Let \(A\) and \(B\) be two sets such that \(B\subseteq A\). Then
If \(A\) is finite then \(B\) is finite.
If \(B\) is infinite then \(A\) is infinite.
Assume \(|A|=n\). We have \(|B| \leq |A|=n\), i.e. \(|B| = m\) for some \(0\leq m \leq n\). By definition, \(B\) is finite.
Note that part b.) is the contrapositive of part a.)□
If \(X,Y\) are sets with \(|X|\le |Y|\) and \(|Y|\le |X|\) then \(|X|=|Y|\).
In particular, if there exists injective \(f:X\to Y\) and injective \(g:Y\to X\) then there exists bijective \(h:X\to Y\). (Note: we are not claiming \(f\) or \(g\) are bijective).Non-examinable. It is beyond the scope of this course.
□
Theorem 7.8 has many names: Cantor-Schröder-Bernstein Theorem; Schröder–Bernstein theorem or (as above) the Cantor-Bernstein theorem. Cantor himself suggested that it should be called the equivalence theorem.
The reasons for so many names is that Georg Cantor (Russian mathematician, 1845-1912) first stated the theorem in 1887, but did not prove it. In 1897, Sergei Bernstein (Ukranian mathematician, 1880-1968) and Ernst Schröder (German mathematician, 1841-1902) independently published different proofs. However, five years later, in 1902, Alwin Korselt (German mathematician, 1864-1947) found a flaw in Schröder’s proof (which was confirmed by Schröder just before he died).Let \(X\) be a set and let \(A,B\subseteq X\) be disjoint (\(A\cap B=\emptyset\)) finite sets. Then \(|A\cup B|=|A|+|B|\).
Let \(m,n\in\mathbb{Z}_+\) such that \(|A|=m\) and \(|B|=n\). Then \[ A=\{a_1,a_2,\ldots,a_m\}\] where \(a_i=a_j\) only if \(i=j\), for integers \(1\le i,j\le m\). Similarly, we have \[ B=\{b_1,b_2,\ldots,b_n\} \] where \(b_i=b_j\) only if \(i=j\), for integers \(1\le i,j\le n\). Since \(A\cap B=\emptyset\), we know that for any integers \(i,j\) with \(1\le i\le m\) and \(1\le j\le n\), we have \(a_i\not=b_j\). Now, define \(f:\{1,2,\ldots,m+n\}\to A\cup B\) by \[f(k)=\begin{cases} a_k&\text{if $1\le k\le m$,}\\ b_{k-m}&\text{if $m<k\le m+n$.}\end{cases}\] We leave it as an exercise that \(f\) is bijective.
□
Let \(X\) be a set and let \(A,B\subseteq X\) be finite sets. Then \(|A\cup B|=|A|+|B|-|A\cap B|\)
Exercise.
□
We will return to the idea of cardinality in Chapter 11, where we see there are different infinite cardinalities.
8 Sets with structure - Groups
Having looked at sets and functions between sets, we now turn our attention to “groups”. Formally these are sets with extra structure given by a binary operation (e.g. \(\mathbb{R}\) with \(+\)), but they arose historically (and crop up across maths today) as a way to understand symmetry.
8.1 Motivational examples - Symmetries
Before even giving the definition of a group, we’ll look at several examples of symmetries of objects, so that the formal definition will make more sense when we come to it.
Exactly what we mean by a “symmetry” will vary from example to example, and sometimes there’s more than one sensible notion for the same object, so rather than giving a general definition, we’ll clarify what we mean in each example, and the common features should become clear.
8.1.1 Permutations of a set
Let us consider the set of three elements. Imagine them arranged in a line:

Figure 8.1: three points on a line
We can rearrange them, putting them in a different order. For example, we could swap the two elements furthest to the right:

Figure 8.2: the three points above but with the second and third swapped
This leaves us with exactly the same picture, so we’ll regard this as a “symmetry” in this context.
Now let’s label the elements and put both pictures next to each other to see how the elements have been permuted.
Figure 8.3: showing how we permuted the elements
This picture (Figure 8.3) brings to mind the function \(f:\{1,2,3\}\to\{1,2,3\}\) defined by \(\{(1,1),(2,3),(3,2)\}\) (i.e. \(f(1)=1,f(2)=3\) and \(f(3)=2\)).
Or if we cyclically permuted the elements as follows: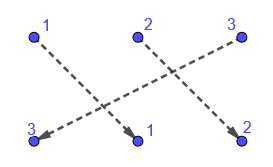
Figure 8.4: a cyclic permutation
this (Figure 8.4) would correspond to the function \(f:\{1,2,3\}\to\{1,2,3\}\) defined by \(\{(1,2),(2,3),(3,1)\}\) (i.e. \(f(1)=2, f(2)=3\) and \(f(3)=1\)).

Figure 8.5: not a permutation
gives a different pattern. Therefore we need the function \(f\) to be bijective.
Let \(X\) be a set. A permutation of the set \(X\) is a bijection \(f:X\to X\).
Let’s look in more detail at the permutations of a set \(X=\{1,2,3\}\) with three elements. It’s easy to check that there are just six of these, which we’ll denote by \(e,f,g,h,i,j\): see Figure 8.6, where we just show the position the three elements end up.
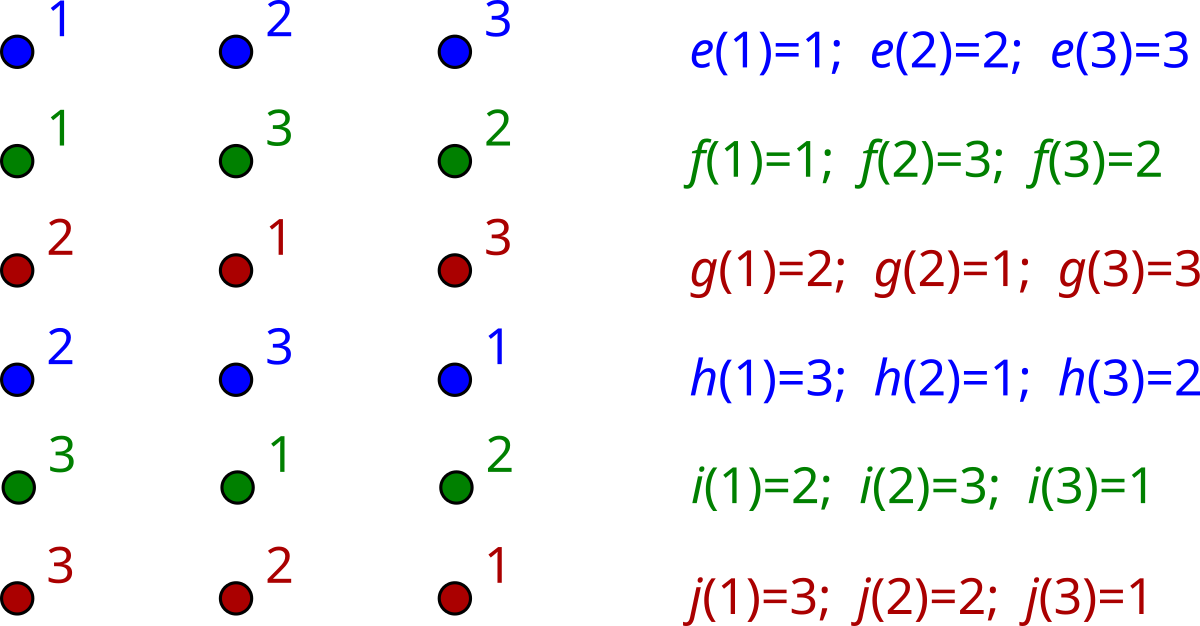
Figure 8.6: the six permutations of three elements
Notice that the function \(e\) is the identity function, and likewise it is called the identity permutation.
Now we can look at what happens when we perform one permutation followed by another. For example, if we do \(f\) (swap the two elements furthest to the right) and then \(g\) (swap the two elements that are now furthest to the left), then we are just taking the composition \(g\circ f\) of the two functions. This gives \(g(f(1))=g(1)=2\), \(g(f(2))=g(3)=3\) and \(g(f(3))=g(2)=1\), so \(g\circ f =i\).
For simplicity, we’ll leave out the composition symbol \(\circ\) and write \(gf\) instead of \(g\circ f\). Let’s see what \(fg\) is: \(f(g(1))=f(2)=3\), \(f(g(2))=f(1)=1\) and \(f(g(3))=f(3)=2\), so \(fg=h\).
When we come to define groups, we’ll think of “composition” as an operation to combine permutations or other kinds of symmetry (if \(f\) and \(g\) are symmetries of an object, then \(gf\) is the symmetry “do \(f\) and then \(g\)”), much as ``multiplication’’ is an operation to combine numbers. In fact we’re using pretty much the same notation: compare \(gf\) for permutations with \(xy\) for numbers. Let’s explore this analogy further with permutations of a set \(X\).
Note that since the composition of two bijections is a bijections, we have that the composition of two permutations is a permutation. This is similar to axioms (A1) and (A7).
We have seen that composition of functions is associative (see Proposition 6.17 ), hence if \(a,b,c\) are permutation, we have \(a(bc)=(ab)c\). This is similar to axioms (A2) and (A8).
We always have an identity permutation, \(e:X\to X\) defined by \(e(x)=x\) for all \(x\in X\). Let \(f\) be any other permutation of \(X\), then for all \(x\in X\) we have \[ef(x)=e(f(x))=f(x)=f(e(x))=fe(x),\] i.e. \(ef=f=fe\). This is similar to axioms (A4) and (A10).
We know that a bijective function is invertible, so for all permutation \(f:X\to X\), there exists \(f^{-1}\) such that \(ff^{-1}=e=f^{-1}f\). This is similar to axioms (A5) and (A11).
[You can check in the permutations of \(\{1,2,3\}\) that \(e^{-1}=e; f^{-1}=f; g^{-1}=g; h^{-1}=i; i^{-1}=h\) and \(j^{-1}=j\)]
Note that we can’t have anything similar to axioms (A3) or (A9) as we have seen an example of two permutations \(f,g\) of \(\{1,2,3\}\) such that \(fg\neq fg\).
8.1.2 Symmetries of polygons
Consider a regular \(n\)-sided polygon (for example, if \(n=3\) an equilateral triangle, or if \(n=4\) a square). Examples of symmetries are:
A rotation through an angle of \(2\pi/n\) (an \(n\)th of a revolution).
A reflection in a line that goes through the centre of the polygon and one of its vertices.
There are many ways to make precise what we mean by a symmetry. For example, considering the polygon as a subset \(X\) of \(\mathbb{R}^2\), we could look at bijections \(f:X\to X\) that preserve distance: i.e., such that the distance between \(f(x)\) and \(f(y)\) is the same as the distance between \(x\) and \(y\). It’s not hard to see that this implies that \(f\) must send vertices to vertices, and moreover must send adjacent vertices to adjacent vertices. To keep things simple, we’ll use this as our definition of a symmetry:
Note that for \(n=3\), every pair of vertices is adjacent, so in that case every permutation of the vertices is a symmetry, and so we are just looking at permutations of a set of three elements as in the last section.
In the case \(n=4\), we have a square. Let’s label the vertices as follows:
Figure 8.7: the four vertices labelled
Figure 8.8: rotating the square
While if we reflect in the line of symmetry going from top right to bottom left (let’s call this symmetry \(g\)) we get (Figure 8.9):
Figure 8.9: reflecting the square
However the following does not represent a symmetry as vertices \(1\) and \(2\) have not remained adjacent (Figure 8.10):
Figure 8.10: not a symmetry
As with permutations, we can compose symmetries together and get a new symmetry. In fact, the analogues of (A1)/(A7), (A2)/(A8), (A4)/(A10) and (A5)/(A11) all hold (Prove that the composition of two bijections that preserves adjacency is a bijection that preserves adjacency, and that the inverse of a function that preserve adjacency is a function that preserves adjacency.)
Let’s look at what happens when we compose the symmetries \(f\) and \(g\) (Figure 8.11).
Figure 8.11: composing the two previous symmetries
We see that \(gf\) is a reflection in the horizontal line of symmetry while \(fg\) is a reflection in the vertical line of symmetry. So here again we have \(gf\neq fg\).
8.1.3 Symmetries of a circle
We can look at bijections from a circle to itself that preserve distances between points. It’s not too hard to see that these symmetries are either rotations (through an arbitrary angle) or reflections (in an arbitrary line through the centre).
Again, if \(f\) and \(g\) are symmetries, then usually \(fg\neq gf\).
8.1.4 Symmetries of a cube
We can look at the eight vertices of a cube, and define a symmetry to be a permutation of the set of vertices that preserves adjacency (as we did with a polygon). There are \(48\) symmetries: most are either rotations or reflections, but there is also the symmetry that takes each vertex to the opposite vertex.
8.1.5 Rubik’s Cube
A Rubik’s cube has \(54\) coloured stickers (\(9\) on each face), and we could define a “symmetry” to be a permutation of the stickers that we can achieve by repeatedly turning faces (as one does with a Rubik’s cube). It turns out that there are \(43,252,003,274,489,856,000\) symmetries. Again we can compose symmetries (do one sequence of moves and then another), and every symmetry has an inverse symmetry.
8.2 Formal definition
We want to formalize the structure of symmetries of the kind we looked at in the last section. First of all noticed that in all cases we looked at combining two permutations/symmetries to get a third. We can formalize this as follows.
The word “binary” refers to the fact that the function takes two inputs \(x\) and \(y\) from \(G\). (Technically speaking, it takes one input from \(G\times G\).)
We’ll usually write \(x\star y\) instead of \(\star(x,y)\).
Let \(X\) be a non-empty set. Composition \(\circ\) is a binary operation on the set \(G\) of permutations of a set \(X\).
Addition \(+\) is a binary operation on the set \(\mathbb{R}\) (or on \(\mathbb{Z}\), or on \(\mathbb{Q}\)).
Multiplication and subtraction are also binary operations on \(\mathbb{R}\), \(\mathbb{Q}\) or \(\mathbb{Z}\).
Intersection and unions are binary operations on the set of subsets of \(\mathbb{R}\).
Note that in the definition of a binary operation, the function \(\star\) maps to \(G\), so if we have a definition of \(x\star y\) so that \(x\star y\) is not always in \(G\), then this is not a binary operation on \(G\) (we say that \(G\) is not closed under \(\star\)). Also, the domain of \(\star\) is \(G\times G\), so \(x\star y\) needs to be defined for all pairs of elements \(x,y\).
Subtraction is not a binary operation on \(\mathbb{Z}_+\) since, for example, \(4-7=-3\notin \mathbb{Z}_+\). So \(\mathbb{Z}_+\) is not closed under subtraction (it is closed under addition).
Division is not a binary operation on \(\mathbb{Z}\) since, for example, \(1/2\notin \mathbb{Z}\).
Division is not a binary operation on \(\mathbb{Q}\) since \(x/y\) is not defined when \(y=0\). (But division is a binary operation on the set \(\mathbb{Q}\setminus\{0\}\) of non-zero rational numbers).
For a general binary operation, the order of the elements \(x,y\) matters: \(x\star y\) is not necessarily equal to \(y\star x\).
Some examples and non-example of commutative binary operations
Addition and multiplication are commutative binary operations on \(\mathbb{R}\) (axioms (A3) and (A9) ).
Subtraction is not commutative on \(\mathbb{R}\) since, for example, \(2-1=1\) but \(1-2=-1\).
Composition is not a commutative operation on the set of permutations of the set \(\{1,2,3\}\).
Bearing in mind the analogies we drew between some of the axioms of \(\mathbb{R}\) and the compositions of permutations/symmetries, we’ll now define a group.
A group \((G,\star)\) is a set \(G\) together with a binary operation \(\star:G\times G\to G\) satisfying the following properties (or “axioms”):
(Associativity) For all \(x,y,z\in G\), \[ (x\star y)\star z=x\star(y\star z). \]
(Existence of an identity element) There is an element \(e\in G\) (called the identity element of the group) such that, for every \(x\in G\), \[x\star e=x=e\star x.\]
(Existence of inverses) For every \(x\in G\), there is an element \(x^{-1}\in G\) (called the inverse of \(x\)) such that \[x\star x^{-1}=e=x^{-1}\star x.\]
Strictly speaking, the group consists of both the set \(G\) and the operation \(\star\), but we’ll often talk about “the group \(G\)” if it’s clear what operation we mean, or say “\(G\) is a group under the operation \(\star\)”. But the same set \(G\) can have several different group operations, so we need to be careful.
If \(X\) is a set, \(S(X)\) is the set of all permutations of \(X\) (i.e., bijective functions \(X\to X\)), and \(f\circ g\) is the composition of bijections \(f\) and \(g\), then \(\left(S(X),\circ\right)\) is a group.
Note that in this example, there are two sets involved (\(X\) and the set \(S(X)\) of permutations). It is the set \(S(X)\) that is the group, not \(X\) (we haven’t defined a binary operation on \(X\)).
The set of all symmetries of a regular \(n\)-sided polygon is a group under composition, as is the set of all symmetries of a cube, or a Rubik’s cube.
These examples, and similar ones, of symmetry groups, are the motivation for the definition of a group, but there are some other familiar examples of sets of numbers with arithmetical operations that fit the definition.
Here we explore some sets and associated operations and check if they are a group or not.
We have \((\mathbb{R},+)\) is a group. [by axioms (A2),(A4),(A5)]. Similarly \((\mathbb{Z},+)\) and \((\mathbb{Q},+)\) are groups.
The set \(\mathbb{Z}_+\) is not a group under addition, since it doesn’t have an identity element [\(0\notin \mathbb{Z}_+\)]. Note \(\mathbb{Z}_{\geq 0}\) is still not a group (under addition), as although it has the identity element \(0\), no integer \(n>0\) has an inverse (since for any \(n\in \mathbb{Z}_+\), \(-n \notin \mathbb{Z}_{\geq 0}\)).
We have \((\mathbb{R}\setminus\{0\},\cdot)\) is a group [by axioms (A8),(A10) and (A11)]. Similarly \((\mathbb{Q}\setminus\{0\},\cdot)\) is a group.
We have \((\mathbb{R},\cdot)\) is not a group, since \(0\) does not have an inverse.
We have \(\mathbb{R}\) is not a group under subtraction, since associativity fails: \((x-y)-z=x-y-z\), but \(x-(y-z)=x-y+z\), and so these are different whenever \(z\neq 0\).
Matrices are another source of examples.
Let \(M_n(\mathbb{R})\) be the set of \(n\times n\) matrices with real entries. Then \(M_n(\mathbb{R})\) is a group under (matrix) addition.
\(M_n(\mathbb{R})\) is not a group under matrix multiplication, since not every matrix has an inverse. However, the set of invertible \(n\times n\) matrices is a group under multiplication.
We’ve stressed that \(x\star y\) and \(y\star x\) are typically different in symmetry groups. But in the examples coming from addition and multiplication of integers, they are the same.
The word “abelian” was introduced in the 1880s by German mathematician Heinrich Weber (1842 - 1913). He derived the name from the Norwegian mathematician Niels Henrik Abel (1802 - 1829) who studied the permutation of solutions of polynomials. Very loosely speaking he showed in 1824 that for a given polynomial if the permutation of the roots form an Abelian group then the polynomial can be solved in radicals (i.e. involving \(+,-,\cdot,\div\) and \(n\)-th roots only). You can learn more about this in the fourth year course Galois Theory (named after French mathematician Évariste Galois, 1811 - 1832).
Even in a non-abelian group, \(x\star y=y\star x\) may hold for some elements \(x\) and \(y\), in which case we say that \(x\) and \(y\) commute. For example, the identity commutes with every other element. However for the group to be abelian it must hold for all elements.
The group \(S(X)\) of permutations of a set \(X\) is non-abelian if \(X\) has at least three elements, since if \(x,y,z\in X\) are three distinct elements, \(f\) is the permutation that swaps \(x\) and \(y\) (and fixing all other elements), \(g\) is the permutation that swaps \(y\) and \(z\), then \(f\circ g\neq g\circ f\).
More generally, symmetry groups are typically non-abelian (although sometimes they are). In particular, the symmetry group of a regular \(n\)-sided polygon (where \(n\geq 3\)) is non-abelian.
\((\mathbb{R},+)\) is abelian by axiom (A3).
\((\mathbb{R}\setminus\{0\},\cdot)\) is abelian by axiom (A9).
\(M_n(\mathbb{R})\) is an abelian group under matrix addition.
If \(n\geq 2\), then the set of invertible \(n\times n\) real matrices is a non-abelian group under matrix multiplication, since for example \[\begin{pmatrix}1&1\\0&1\end{pmatrix}\begin{pmatrix}0&1\\1&0\end{pmatrix} =\begin{pmatrix}1&1\\1&0\end{pmatrix}\] but \[\begin{pmatrix}0&1\\1&0\end{pmatrix}\begin{pmatrix}1&1\\0&1\end{pmatrix} =\begin{pmatrix}0&1\\1&1\end{pmatrix}.\]
Often, especially when we’re dealing with abstract properties of general groups, we’ll simplify the notation by writing \(xy\) instead of \(x\star y\), as though we’re multiplying. In this case we’ll say, for example, “Let \(G\) be a multiplicatively-written group”.
Note that this is purely a matter of the notation we use for the group operation: any group can be “multiplicatively-written” if we choose to use that notation, so if we prove anything about a general multiplicatively-written group, it will apply to all groups, no matter what the group operation is.
Of course, if we’re looking at something like the group of real numbers under addition, it would be incredibly confusing to write this multiplicatively, so in cases like that, where multiplication already has some other meaning, or where there’s already another standard notation for the group operation, we’ll tend not to use multiplicative notation.
Notice that in a multiplicatively-written group, the associativity axiom says \[(xy)z=x(yz),\] and from this it follows easily (by induction, for example) that any product such as \(wxyz\) has a unique meaning: we could bracket it as \((wx)(yz)\) or \((w(xy))z\) or \(w((xy)z)\) or any of the other possible ways, and because of associativity they would all give the same element.
8.3 Elementary consequences of the definition
Throughout this section, \(G\) will be a multiplicatively written group. Remember that being “multiplicatively written” is purely a matter of notation, so everything will apply to any group.
A familiar idea from elementary algebra is that if you have some equation (say involving \(a,b,x\in \mathbb{R}\)) such as \[ax=bx\] then, as long as \(x\neq 0\), you can “cancel” the \(x\) to deduce that \(a=b\). Formally, we multiply both sides by \(x^{-1}\) (which exists by axiom (A11)).
A similar principle applies in a group, because of the fact that elements all have inverses, with one complication caused by the fact that the group operation may not be commutative.
Since multiplying on the left and on the right are in general different, so we need to decide which is appropriate.
Let \(a,b,x\) be elements of a multiplicatively written group \(G\). If \(ax=bx\), then \(a=b\).
Multiply on the right by \(x^{-1}\): \[\begin{align*} ax=bx&\Rightarrow (ax)x^{-1}=(bx)x^{-1}\\ &\Rightarrow a(xx^{-1})=b(xx^{-1})\\ &\Rightarrow ae=be\\ &\Rightarrow a=b. \end{align*}\]
□
Let \(a,b,x\) be elements of a multiplicatively written group \(G\). If \(xa=xb\), then \(a=b\).
Multiply on the left by \(x^{-1}\): \[\begin{align*} xa=xb&\Rightarrow x^{-1}(xa)=x^{-1}(xb)\\ &\Rightarrow (xx^{-1})a =(xx^{-1})b\\ &\Rightarrow ea=eb\\ &\Rightarrow a=b. \end{align*}\]
□
This simple principle has some nice consequences that make studying groups easier. One is that the defining property of identity element \(e\) is enough to identify it: no other element has the same property.
Let \(a,x\) be elements of a multiplicatively written group. If \(ax=a\) then \(x=e\). Similarly, if \(xa=a\) then \(x=e\).
If \(ax=a\) then \(ax=ae\). By “left cancellation”, we can cancel \(a\) to deduce \(x=e\). Similarly, if \(xa=a\) then \(xa=ea\), so by “right cancellation” we can cancel \(a\) to deduce \(x=e\).
□
A similar proof shows that an element of a group can only have one inverse.
Let \(x,y\) be elements of a multiplicatively written group. If \(xy=e\) then \(x=y^{-1}\) and \(y=x^{-1}\).
If \(xy=e\) then \(xy=xx^{-1}\), and so, by left cancellation \(y=x^{-1}\). Similarly, if \(xy=e\) then \(xy=y^{-1}y\), and so by right cancellation \(x=y^{-1}\).
□
This means that, to prove that one element \(x\) of a group is the inverse of another element \(y\), we just need to check that their product (either way round: \(xy\) or \(yx\)) is equal to the identity. Here are some examples of useful facts that we can prove like this:
Let \(x\) be an element of a multiplicatively written group. Then the inverse of \(x^{-1}\) is \(x\): \((x^{-1})^{-1}=x\).
By uniqueness of inverses, we just need to check that \(xx^{-1}=e\), which is true.
□
Let \(x,y\) be elements of a multiplicatively written group. Then the inverse of \(xy\) is \((xy)^{-1}=y^{-1}x^{-1}\).
By uniqueness of inverses, we just need to check that \((xy)(y^{-1}x^{-1})=e\). But \[(xy)(y^{-1}x^{-1})=((xy)y^{-1})x^{-1}=(x(yy^{-1}))x^{-1}=(xe)x^{-1}=xx^{-1}=e.\]
□
Make sure you understand how each step of the previous proof follows from the definition of a group, and in particular how we have used the associative property. The notes will be less explicit about this in future proofs, leaving out brackets.
Next, some notation. If \(x\in G\), we write write \(x^2\) for the product \(xx\) of \(x\) with itself, \(x^3\) for the product \(x(x^2)\) (which is the same as \((x^2)x\) by associativity), and so on.
Note that for \(n=-1\) we also have a meaning for \(x^n\), since \(x^{-1}\) is notation we use for the inverse of \(x\).
We extend this even further by defining \(x^{-n}\) to be \((x^n)^{-1}\) if \(n>0\) (which gives us a meaning for \(x^n\) for any non-zero integer \(n\), positive or negative) and defining \(x^0\) to be the identity element \(e\) (so that we now have a meaning for \(x^n\) for every \(n\in \mathbb{Z}\).
We call \(x^n\) the \(n\)th power of \(x\).To justify why this is a sensible notation, let us see what happens when we multiply powers. First:
If \(n>0\) then \(x^{-n}=(x^{-1})^n\).
By definition, \(x^{-n}=(x^n)^{-1}\). To prove this is the same as \((x^{-1})^n\) we just have to show \((x^{-1})^nx^n=e\), by uniqueness of inverses. But \[(x^{-1})^nx^n=x^{-1}\cdots x^{-1}x^{-1}xx\cdots x= x^{-1}\cdots x^{-1}ex\cdots x=x^{-1}\cdots x^{-1}x\cdots x=\cdots =e,\] cancelling each \(x^{-1}\) with an \(x\).
□
If \(x\) is an element of a multiplicatively written group \(G\), and \(m\) and \(n\) are integers, then \[(x^m)(x^n)=x^{m+n}.\]
Let us fix \(n\in \mathbb{Z}\) and prove it is true for all \(m\in \mathbb{Z}\).
We first prove this by induction for when \(m\geq 0\). It is true when \(m=0\) since \[(x^0)(x^n)=e(x^n)=x^n.\] Suppose it is true for \(m=k-1\) [that is \((x^{k-1})(x^n)=x^{k-1+n}\)]. We show it is true for \(m=k\). We have \[(x^k)(x^n)=\left(x(x^{k-1})\right)(x^n)=x\left((x^{k-1}(x^n)\right)=x(x^{k+n-1})=x^{k+n}.\] So by induction it is true for all \(m\geq 0\).
If \(m<0\), and \(y=x^{-1}\), then by the lemma \((x^m)(x^n)=(y^{-m})(y^{-n})\) which is equal to \(y^{-(m+n)}=x^{m+n}\) by applying what we’ve already proved with \(y\) in place of \(x\).□
We’ve already proved the formula \((xy)^{-1}=y^{-1}x^{-1}\). What about \((xy)^n\) for other values of \(n\)? In a non-abelian group, there is no simple formula. In particular:
8.4 Dihedral Groups
As we study group theory, it will be useful to have a supply of examples of groups to think about. Of course, no single example will be ideal for everything, but some are more helpful than others. Some of the more “arithmetic” groups, such as \((\mathbb{Z},+)\) and \((\mathbb{R}\setminus\{0\},\times)\), have the advantage of being very familiar, but the disadvantage of being rather untypical because they’re abelian. If you have a “standard example” that you like to think about, then it will be much less misleading if it’s non-abelian.
A good first family of examples are the “dihedral groups”, which are the symmetry groups of regular polygons, and are non-abelian, but still fairly uncomplicated. In the next section we will look at a second important family of examples, the “symmetric groups”.
Let \(X\) be a regular \(n\)-sided polygon, with vertices labelled anticlockwise \(1,2,\dots,n\). Recall that by a symmetry of \(X\) we mean a permutation of the vertices that takes adjacent vertices to adjacent vertices.
For example, we can send vertex \(1\) to any other vertex by an appropriate rotation. If \(f\) is a symmetry sending vertex \(1\) to vertex \(i\), then, since it preserves adjacency, it must send vertex \(2\) to one of the two vertices adjacent to vertex \(i\), and once we know \(f(1)\) and \(f(2)\), then \(f(3)\) is determined as the other vertex adjacent to \(f(2)\), and so on around the polygon for \(f(4),\dots,f(n)\).
So the total number of symmetries is \(2n\) (since there are \(n\) choices for \(f(1)\) and for each of these there are two choices for \(f(2)\)). This explains the following choice of notation.
Let’s fix some notation for two particular symmetries.
We set \(a\in D_{2n}\) to be a rotation anticlockwise through an angle of \(2\pi/n\). We set \(b\in D_{2n}\) to be a reflection in the line through vertex \(1\) and the centre of the polygon.
So \[ a(1)=2, a(2)=3, \ldots, a(n-1)=n, a(n)=1, \] and \[ \ldots, b(n-1)=3, b(n)=2, b(1)=1, b(2)=n, b(3)=n-1, \ldots \]
Figure 8.12: The symmetries a and b on \(D_8\)
Figure 8.13: The symmetries a and b on \(D_{10}\)
Now consider the symmetries \(a^i\) and \(a^ib\) for \(0\leq i<n\). These both send vertex \(1\) to vertex \(1+i\), but \(a^i\) sends vertices \(2,3,\dots,n\) to the vertices following anticlockwise around the polygon, whereas \(a^ib\) sends them to the vertices following clockwise around the polygon. So all of these symmetries are different, and every symmetry is of this form, and so every element of \(D_{2n}\) can be written in terms of \(a\) and \(b\).
We have \(D_{2n}=\{e,a,a^2,\dots,a^{n-1},b,ab,a^2b,\dots,a^{n-1}b\}\).
Let \(G\) be a group with a finite number of elements: its multiplication table (often also called the Cayley table) has one row and one column for each element of the group, and the entry in row \(x\) and column \(y\) is the product \(xy\). So the table displays the group operation.
The Cayley table for \(D_6 = \{e,a,a^2,b,ab,a^2b\}\) is as follows:
| \(e\) | \(a\) | \(a^2\) | \(b\) | \(ab\) | \(a^2b\) | |
| \(e\) | \(e\) | \(a\) | \(a^2\) | \(b\) | \(ab\) | \(a^2b\) |
| \(a\) | \(a\) | \(a^2\) | \(a^3\) | \(ab\) | \(a^2b\) | \(a^3b\) |
| \(a^2\) | \(a^2\) | \(a^3\) | \(a^4\) | \(a^2b\) | \(a^3b\) | \(a^4b\) |
| \(b\) | \(b\) | \(ba\) | \(ba^2\) | \(b^2\) | \(bab\) | \(ba^2b\) |
| \(ab\) | \(ab\) | \(aba\) | \(aba^2\) | \(ab^2\) | \(abab\) | \(aba^2b\) |
| \(a^2b\) | \(a^2b\) | \(a^2ba\) | \(a^2ba^2\) | \(a^2b^2\) | \(a^2bab\) | \(a^2ba^2b\) |
Arthur Cayley was an English mathematician (1821 - 1895) who gave the first abstract definition of a finite group in 1854. It is around then that he showed that a group is determined by its multiplication table (i.e., its Cayley table), and gave several examples of groups that were not symmetric groups. However, at the time the mathematical community did not pursue this further, preferring to stick to studying the concrete symmetric groups. It wasn’t until 1878 when he re-introduced his definition that other mathematicians refined it and an agreed formal definition of a group emerged.
As we can see in the Cayley graph above, we have expressions such as \(ba\) or \(a^{-1}\) appearing, but they are not in our list of standard form for elements. So, we must be able to work out how to write elements such as \(ba\) or \(a^{-1}\) into standard form.
There are three basic rules that let us easily do calculations.
We have \(a^n=e\).
This is clearly true, as it just says that if we repeat a rotation through an angle of \(2\pi/n\) \(n\) times, then this is the same as the identity.
Note that this means that \(a(a^{n-1})=e\) and so by uniqueness of inverses \[a^{-1}=a^{n-1},\] which allows us to write any power (positive or negative) of \(a\) as one of \(e,a,\dots,a^{n-1}\).
We have \(b^2=e\).
This is clearly true, as repeating a reflection twice gives the identity.
This implies, by uniqueness of inverses again, that \(b^{-1}=b\), and so any power of \(b\) is one of \(e\) or \(b\).
What about \(ba\)? Well \(a(1)=2\) and \(b(2)=n\), so \(ba(1)=n\), similarly \(ba(2)=n-1\) and so the other vertices follow clockwise. This is the same as \(a^{n-1}b\), or \(a^{-1}b\).
We have \(ba=a^{n-1}b=a^{-1}b\).
We’ll see that these three rules allow us to simplify any expression.
For example, \[ba^{-1}=ba^{n-1}=baa^{n-2}=a^{-1}ba^{n-2}=a^{-1}baa^{n-3}=a^{-1}a^{-1}ba^{n-3}=\dots=a^{-n+1}b=ab,\] where we repeatedly “swap” a \(b\) with an \(a\) or \(a^{-1}\), changing the \(a\) into \(a^{-1}\) or the \(a^{-1}\) into \(a\).
We get the following rules for multiplying expressions in standard form.
Fix \(n\in \mathbb{Z}\). In \(D_{2n}\), for \(0\leq i,j<n\),
\[\begin{align*} a^{i}a^{j}&=\begin{cases}a^{i+j}&\text{ if } i+j<n\\a^{i+j-n}&\text{ if } i+j\geq n\end{cases}\\ a^{i}(a^{j}b)&=\begin{cases}a^{i+j}b&\text{ if } i+j<n\\a^{i+j-n}b&\text{ if } i+j\geq n\end{cases}\\ (a^{i}b)a^{j}&=\begin{cases}a^{i-j}b&\text{ if } i-j\geq0\\a^{i-j+n}b&\text{ if } i-j<0\end{cases}\\ (a^{i}b)(a^{j}b)&=\begin{cases}a^{i-j}&\text{ if } i-j\geq0\\a^{i-j+n}&\text{ if } i-j<0\end{cases} \end{align*}\]You are encouraged to practice some calculations with the dihedral group, especially with \(n=3\) and \(n=4\), as we’ll frequently be using these as examples.
We rewrite The Cayley table for \(D_6 = \{e,a,a^2,b,ab,a^2b\}\) (check the calculation yourself):
| \(e\) | \(a\) | \(a^2\) | \(b\) | \(ab\) | \(a^2b\) | |
| \(e\) | \(e\) | \(a\) | \(a^2\) | \(b\) | \(ab\) | \(a^2b\) |
| \(a\) | \(a\) | \(a^2\) | \(e\) | \(ab\) | \(a^2b\) | \(b\) |
| \(a^2\) | \(a^2\) | \(e\) | \(a\) | \(a^2b\) | \(b\) | \(ab\) |
| \(b\) | \(b\) | \(a^2b\) | \(ab\) | \(e\) | \(a^2\) | \(a\) |
| \(ab\) | \(ab\) | \(b\) | \(a^2b\) | \(a\) | \(e\) | \(a^2\) |
| \(a^2b\) | \(a^2b\) | \(ab\) | \(b\) | \(a^2\) | \(a\) | \(e\) |
The cancellation properties which we previously found have a nice interpretation in terms of Cayley tables:
The left cancellation proposition just says that all the entries in each row are different: if two entries \(xy\) and \(xz\) in row \(x\) are the same, then \(xy=xz\) and so \(y=z\). Similarly the right cancellation property says that all the entries in each column are different. This can be a useful method for deducing information about a group from a partial multiplication table.
Observe that these hold with the Cayley table above.8.5 Symmetric Groups and Cycles
We have already met symmetric groups, but not with that name. A symmetric group is just the group of all permutations of a set. We’ll only really consider finite sets, although the definition makes sense for any set.
Let \(X\) be a set. The symmetric group on \(X\) is the group \(S(X)\) of all permutations of \(X\) (i.e., bijective functions \(f:X\to X\)), with composition as the group operation.
The symmetric group \(S_n\) of degree \(n\) is the group of all permutations of the set \(\{1,2,\dots,n\}\) of \(n\) elements.
Let’s think of ways of describing permutations. Of course, we could just say what \(f(i)\) is for each value of \(i\), and so, for example, refer to the element \(f\) of \(S_6\) with \(f(1)=3\), \(f(2)=6\), \(f(3)=1\), \(f(4)=4\), \(f(5)=2\) and \(f(6)=5\).
This is quite hard to read, and one easy way to set out the information in a more easily readable form is to use a “double row” notation with \(1,2,\dots,n\) along the top row, and \(f(1),f(2),\dots,f(n)\) along the bottom row.
For example, if \(f\) is the element of \(S_6\) described above, then we could write \[f=\begin{pmatrix}1&2&3&4&5&6\\3&6&1&4&2&5\end{pmatrix}.\]
But there’s an even more compact method, that is also much more convenient for understanding group theoretic aspects of permutations.
Let \(k\) and \(n\) be positive integers with \(k\leq n\). A \(k\)-cycle \(f\) in \(S_n\) is a permutation of the following form. There are \(k\) distinct elements \(i_1,i_2,\dots,i_k\in\{1,2,\dots,n\}\) such that \[f(i_1)=i_2, f(i_2)=i_3, \dots, f(i_{k-1})=i_k,f(i_k)=i_1\] and \(f(i)=i\) for \(i\not\in\{i_1,i_2,\dots,i_k\}\). (So \(f\) “cycles” the elements \(i_1,i_2,\dots,i_k\) and leaves other elements unmoved.)
Such an \(f\) is denoted by \(f=(i_1,i_2,\dots,i_k)\).
We call \(k\) the length of this cycle.In \(S_8\), the \(6\)-cycle \[g=(2,7,8,5,6,3)\] has \[g(2)=7,g(7)=8,g(8)=5,g(5)=6,g(6)=3,g(3)=2,g(1)=1\text{ and }g(4)=4,\] or, written in double row notation, \[\begin{pmatrix} 1&2&3&4&5&6&7&8\\1&7&2&4&6&3&8&5\end{pmatrix}.\] The notation \((2,7,8,5,6,3)\) would also denote an element of \(S_9\) with \(g(9)=9\), so this notation doesn’t specify which symmetric group we’re looking at, although that is rarely a problem.
Note that the \(6\)-cycle \((7,8,5,6,3,2)\) is exactly the same permutation as \(g\), so the same cycle can be written in different ways (in fact, a \(k\)-cycle can be written in \(k\) different ways, as we can choose to start the cycle with any of the \(k\) elements \(i_1,i_2,\dots,i_k\)).Transposition comes from the Latin trans meaning “across, beyond” and positus meaning “to put”. A transposition takes two elements and put them across each other, i.e. swap position.
Of course, not every permutation is a cycle. For example, the permutation \[f=\begin{pmatrix}1&2&3&4&5&6\\3&6&1&4&2&5\end{pmatrix}\] that we used as an example earlier is not. However, we can write it as a composition \[f=(1,3)(2,6,5)\] of two cycles. These two cycles are “disjoint” in the sense that they move disjoint set of elements \(\{1,3\}\) and \(\{2,5,6\}\), and this means that it makes no difference which of the two cycles we apply first. So also \[f=(2,6,5)(1,3).\]
A set of cycles in \(S_n\) is disjoint if no element of \(\{1,2,\dots,n\}\) is moved by more than one of the cycles.
Every element of \(S_n\) is may be written as a product of disjoint cycles.
We give a constructive proof, that is we give a method which will write any \(f \in S_n\) as such a product.
We’ll write down a set of disjoint cycles by considering repeatedly applying \(f\) to elements of \(\{1,2,\dots,n\}\), starting with the smallest elements.
So we start with \(1\), and consider \(f(1),f^2(1),\dots\) until we reach an element \(f^k(1)\) that we have already reached. The first time this happens must be with \(f^k(1)=1\), since if \(f^k(1)=f^l(1)\) for \(0<l<k\) then \(f^{k-1}(1)=f^{l-1}(1)\), and so we’d have repeated the element \(f^{l-1}(1)\) earlier. So we have a cycle \[(1,f(1),f^2(1),\dots,f^k(1)).\]
Now we start again with the smallest number \(i\) that is not involved in any of the cycles we’ve already written down, and get another cycle \((i,f(i),\dots, f^s(i))\) for some \(s\).
We keep repeating until we’ve dealt with all the elements of \(\{1,2,\dots,n\}\).□
This will probably be clearer if we look at an example.
Consider the element \[f=\begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 2&5&1&9&7&6&3&4&8\end{pmatrix}\] of \(S_9\) written in double row notation. To write this as a product of disjoint cycles, we start with \(1\), and calculate \[f(1)=2,f(2)=5,f(5)=7,f(7)=3,f(3)=1,\] so we have a \(5\)-cycle \((1,2,5,7,3)\).
The smallest number we haven’t yet dealt with is \(4\), and \[f(4)=9,f(9)=8,f(8)=4,\] so we have a \(3\)-cycle \((4,9,8)\).
The only number we haven’t dealt with is \(6\), and \[f(6)=6,\] so finally we have a \(1\)-cycle \((6)\).
So \[f=(1,2,5,7,3)(4,9,8)(6)\] as a product of disjoint cycles. Since \(1\)-cycles are just the identity permutation, we can (and usually will) leave them out, and so we can write \[f=(1,2,5,7,3)(4,9,8).\]
Since the order in which we apply disjoint permutations doesn’t matter, we could write the cycles in a different order, or we could start each cycle at a different point. So, for example, \[f=(9,8,4)(5,7,3,1,2)\] is another way of writing the same permutation as a product of disjoint cycles.It’s very easy to read off the product of permutations written in disjoint cycle notation, just by using the method in the proof of Theorem 8.25.
Let \[f=(1,5,3,4)(2,6,7)\] and \[g=(3,4,8,1,2,5)\] be elements of \(S_8\) written in disjoint cycle notation. Let’s calculate \(fg\) and \(gf\). \[fg=(1,5,3,4)(2,6,7)(3,4,8,1,2,5),\] but of course these are not disjoint cycles. So we start with \(1\) and calculate where it is sent by performing the permutation \(fg\) repeatedly:
- \(1\) is sent to \(2\) by \((3,4,8,1,2,5)\), which is sent to \(6\) by \((2,6,7)\), which is not moved by \((1,5,3,4)\). So \(fg(1)=6\).
- \(6\) is not moved by \((3,4,8,1,2,5)\). It is sent to \(7\) by \((2,6,7)\), which is not moved by \((1,5,3,4)\). So \(fg(6)=7\).
- \(7\) is not moved by \((3,4,8,1,2,5)\). It is sent to \(2\) by \((2,6,7)\), which is not moved by \((1,5,3,4)\). So \(fg(7)=2\).
- \(2\) is sent to \(5\) by \((3,4,8,1,2,5)\), which is not moved by \((2,6,7)\) and is sent to \(3\) by \((1,5,3,4)\). So \(fg(2)=3\).
- \(3\) is sent to \(4\) by \((3,4,8,1,2,5)\), which is not moved by \((2,6,7)\), and sent to \(1\) by \((1,5,3,4)\). So \(fg(3)=1\).
- So we’ve completed our first cycle \((1,6,7,2,3)\).
- \(4\) is sent to \(8\) by \((3,4,8,1,2,5)\), which is not moved by \((2,6,7)\) or \((1,5,3,4)\). So \(fg(4)=8\).
- \(8\) is sent to \(1\) by \((3,4,8,1,2,5)\), which is not moved by \((2,6,7)\) and sent to \(5\) by \((1,5,3,4)\). So \(fg(8)=5\).
- \(5\) is sent to \(3\) by \((3,4,8,1,2,5)\), which is not moved by \((2,6,7)\) and sent to \(4\) by \((1,5,3,4)\). So \(fg(5)=4\).
- So we’ve completed another cycle \((4,8,5)\).
- We’ve now dealt with all the numbers from \(1\) to \(8\), so \(fg=(1,6,7,2,3)(4,8,5)\) as a product of disjoint cycles.
Symmetric groups were one of the first type of groups to emerge as mathematicians studied the permutation of roots of equations in the 1770s. This was before the formal abstract definition of a group was introduced - around 100 years later in the 1870s.
8.6 Order of a group and of elements
With those two main examples in mind, we now explore some more properties of groups.
The order of a group \(G\), denoted \(|G|\), is the cardinality of the set \(G\).
Similarly, we say a group \(G\) is finite if the set \(G\) is finite, and infinite otherwise.We have seen that \(|D_{2n}| = 2n\) (justifying our notation).
We have \(|(\mathbb{Z},+)|\) is infinite.
We have \(|(\{-1,1\},\cdot)|=2\).
We have \(|S_n|=n!\).
We’ll count the permutations of \(\{1,2,\dots,n\}\). Let \(f\in S_n\). Since \(f(1)\) can be any of the elements \(1,2,\dots,n\), there are \(n\) possibilities for \(f(1)\). For each of these, there are \(n-1\) possibilities for \(f(2)\), since it can be any of the elements \(1,2,\dots,n\) except for \(f(1)\). Given \(f(1),f(2)\), there are \(n-2\) possibilities for \(f(3)\), since it can be any of the elements \(1,2,\dots,n\) except for \(f(1)\) and \(f(2)\). And so on. So in total there are \[n(n-1)(n-2)\cdots2\cdot 1=n!\] permutations of \(\{1,2,\dots,n\}\).
□
Let \(x\) be an element of a multiplicatively-written group \(G\). Then:
If \(x^n=e\) for some \(n\in \mathbb{Z}_+\), then the order of \(x\), and denoted \(\operatorname{ord}(x)\) (or \(\operatorname{ord}_G(x)\) if it may be unclear what group \(G\) we’re referring to) is \(\operatorname{ord}(x)=\min\{n\in \mathbb{Z}_+:x^n=e\}\), i.e. the least positive integer \(n\) such that \(x^n=e\). [Note this is well defined by the Well Ordering Principle.]
If there is no \(n\in \mathbb{Z}_+\) such that \(x^n=e\), then we say that \(x\) has infinite order and write \(\operatorname{ord}(x)=\infty\) (or \(\operatorname{ord}_G(x)=\infty\)).
The order of a \(k\)-cycle in the symmetric group \(S_n\) is \(k\).
It is clear that if we repeat a \(k\)-cycle \((i_1,i_2,\dots,i_k)\) \(k\) times, each element \(i_j\) is sent back to itself (and if we repeat it \(l<k\) times, then \(i_1\) is sent to \(i_{l+1}\neq i_1\)).
□
In fact, one benefit of disjoint cycle notation in \(S_n\) is that it makes it easy to calculate the order of a permutation.
If \(f\) is the product of disjoint cycles of lengths \(k_1,k_2,\dots,k_r\), then \[\operatorname{ord}(f)=\operatorname{lcm}(k_1,k_2,\dots,k_r).\]
Consider when \(f^k\) is the identity permutation. For \(f^k(j_i)=j_i\) when \(j_i\) is one of the numbers involved in the \(k_i\)-cycle, we need \(k_i\) to divide \(k\). But if \(k_i\) divides \(k\) for all \(i\), then this applies to all the numbers moved by \(f\). So the smallest such \(k\) is the lowest common multiple of \(k_1,\dots,k_r\).
□
We’ll now see what we can say about the powers of an element of a group if we know its order, starting with elements of infinite order.
Let \(x\) be an element of a group \(G\) with \(\operatorname{ord}(x)=\infty\). Then the powers \(x^i\) of \(x\) are all distinct: i.e., \(x^i\neq x^j\) if \(i\neq j\) are integers.
Suppose \(x^i=x^j\). Without loss of generality we’ll assume \(i\geq j\). Then for \(n=i-j\geq0\), \[x^n=x^{i-j}=x^i(x^j)^{-1}=(x^i)(x^i)^{-1}=e,\] but since \(\operatorname{ord}(x)=\infty\) there is no positive integer \(n\) with \(x^n=e\), so we must have \(n=0\) and so \(i=j\).
□
If \(x\) is an element of a finite group \(G\), then \(\operatorname{ord}(x)<\infty\).
If \(\operatorname{ord}(x)=\infty\) then the previous proposition tells us that the elements \(x^i\) (for \(i\in\mathbb{Z}\)) are all different, and so \(G\) must have infinitely many elements.
□
In fact, we’ll see later that the order \(|G|\) of a finite group severely restricts the possible (finite) orders of its elements. Next for elements of finite order.
Let \(x\) be an element of a group \(G\) with \(\operatorname{ord}(x)=n<\infty\).
For an integer \(i\), \(x^i=e\) if and only if \(i\) is divisible by \(n\).
For integers \(i,j\), \(x^i=x^j\) if and only if \(i-j\) is divisible by \(n\).
\(x^{-1}=x^{n-1}\).
The distinct powers of \(x\) are \(e,x,x^2,\dots,x^{n-1}\).
- Firstly, if \(i\) is divisible by \(n\), so that \(i=nk\) for some integer \(k\), then \[x^i=x^{nk}=(x^n)^k=e^k=e,\] since \(x^n=e\).
Conversely, suppose that \(x^i=e\). We can write \(i=nq+r\) with \(q,r\in\mathbb{Z}\) and \(0\leq r<n\) (by Theorem 5.2 ). Then \[e=x^i=x^{nq+r}=(x^n)^qx^r=e^qx^r=x^r.\] But \(n\) is the least positive integer with \(x^n=e\) and \(x^r=e\) with \(0\leq r<n\), so \(r\) can’t be positive, and we must have \(r=0\). So \(i\) is divisible by \(n\).
\(x^i=x^j\) if and only if \(x^{i-j}=x^i(x^j)^{-1}=e\), which by a.) is the case if and only if \(i-j\) is divisible by \(n\).
Take \(i=n-1\), \(j=-1\). Then \(i-j=n\) is divisible by \(n\), and so \(x^{n-1}=x^{-1}\) by b.
For any integer \(i\), write \(i=nq+r\) for \(q,r\) integers with \(0\leq r<n\). Then \(i-r\) is divisible by \(n\), and so \(x^i=x^r\) by \((2)\). So every power of \(x\) is equal to one of \(e=x^0,x=x^1,x^2,\dots, x^{n-1}\). Conversely, If \(i,j\in\{0,1,\dots,n-1\}\) and \(i-j\) is divisible by \(n\), then \(i=j\), and so by b.) the elements \(e,x,\dots,x^{n-1}\) are all different.
□
If we know the order of an element of a group, then we can work out the order of any power of that element.
Let \(x\) be an element of a group \(G\), and \(i\) an integer.
If \(\operatorname{ord}(x)=\infty\) and \(i\neq 0\), then \(\operatorname{ord}(x^i)=\infty\). (If \(i=0\), then \(x^i=e\), and so \(\operatorname{ord}(x^i)=1\)).
If \(\operatorname{ord}(x)=n<\infty\), then \[\operatorname{ord}(x^i)=\frac{n}{\gcd(n,i)}.\]
Suppose \(i>0\). If \(\operatorname{ord}(x^i)=m<\infty\), then \(x^{im}=(x^i)^m=e\) with \(im\) a positive integer, contradicting \(\operatorname{ord}(x)=\infty\). Similarly, if \(i<0\) then \(x^{-im}=e\) with \(-im\) a positive integer, again giving a contradiction. So in either case \(\operatorname{ord}(x^i)=\infty\).
Since \(\gcd(n,i)\) divides \(i\), \(n\) divides \(\frac{ni}{\gcd(n,i)}\), and so \[(x^i)^{{n}/{\gcd(n,i)}}=x^{{ni}/{\gcd(n,i)}}=e.\]
□
9 Linking groups together
We linked sets to each other by considering subsets, functions between sets, and Cartesian products of sets. In a related way, in this section we look at appropriate ideas of “subgroups”, functions between groups and direct products of groups.
9.1 Subgroups
\(\ \)
The group \((2\mathbb{Z},+)\) is a subgroup of \((\mathbb{Z},+)\).
If \(n\) is a positive integer, then the group \((n\mathbb{Z},+)\) is a subgroup of \((\mathbb{Z},+)\).Here’s a simple description of what needs to be checked for a subset to be a subgroup.
Let \(G\) be a multiplicatively written group and let \(H\subseteq G\) be a subset of \(G\), Then \(H\) is a subgroup of \(G\) if and only if the following conditions are satisfied.
(Closure) If \(x,y\in H\) then \(xy\in H\).
(Identity) \(e\in H\).
(Inverses) If \(x\in H\) then \(x^{-1}\in H\).
We don’t need to check associativity, since \(x(yz)=(xy)z\) is true for all elements of \(G\), so is certainly true for all elements of \(H\). So the conditions imply \(H\) is a group with the same operation as \(G\).
If \(H\) is a group, then (Closure) must hold. By uniqueness of identity and inverses, the identity of \(H\) must be the same as that of \(G\), and the inverse of \(x\in H\) is the same in \(H\) as in \(G\), so (Identity) and (Inverses) must hold.□
If \(H,K\) are two subgroups of a group \(G\), then \(H\cap K\) is also a subgroup of \(G\).
We check the three properties in the theorem.
If \(x,y\in H\cap K\) then \(xy\in H\) by closure of \(H\), and \(xy\in K\) by closure of \(K\), and so \(xy\in H\cap K\).
\(e\in H\) and \(e\in K\), so \(e\in H\cap K\).
If \(x\in H\cap K\), then \(x^{-1}\in H\) since \(H\) has inverses, and \(x^{-1}\in K\) since \(K\) has inverses. So \(x^{-1}\in H\cap K\).
□
9.2 Cyclic groups and cyclic subgroups
An important family of (sub)groups are those arising as collections of powers of a single element.
Given a (multiplicatively-written) group \(G\) and an element \(x\in G\), we’ll define \(\langle x\rangle\) to be the subset \(\{x^i:i\in\mathbb{Z}\}\) of \(G\) consisting of all powers of \(x\).
It is easy to check that:
The set \(\langle x\rangle\) is a subgroup of \(G\).
We need to check the conditions of Theorem 9.3.
If \(x^i,x^j\) are powers of \(x\), then \(x^ix^j=x^{i+j}\) is a power of \(x\), so \(\langle x\rangle\) is closed.
We have \(e=x^0\) is a power of \(x\), so \(e\in\langle x\rangle\).
If \(x^i\in\langle x\rangle\), then \((x^i)^{-1}=x^{-i}\in\langle x\rangle\), so \(\langle x\rangle\) is closed under taking inverses.
□
The following explicit description of \(\langle x\rangle\) follows immediately from Propositions 8.31 and 8.33.
If \(\operatorname{ord}(x)=\infty\) then \(\langle x\rangle\) is infinite with \(x^i\neq x^j\) unless \(i=j\).
If \(\operatorname{ord}(x)=n\) then \(\langle x\rangle=\{e,x,\dots,x^{n-1}\}\) is finite, with \(n\) distinct elements.This example shows that there may be more than one possible choice of generator. However, not every element is a generator, since, for example, \(\langle 0\rangle=\{0\}\) and \(\langle 2\rangle = 2\mathbb{Z} \neq \mathbb{Z}\).
Every cyclic group is abelian.
Suppose \(G=\langle x\rangle\) is cyclic with a generator \(x\). Then if \(g,h\in G\), \(g=x^i\) and \(h=x^j\) for some integers \(i\) and \(j\). So \[gh=x^ix^j=x^{i+j}=x^jx^i=hg,\] and so \(G\) is abelian.
□
Of course, this means that not every group is cyclic, since no non-abelian group is. But there are also abelian groups, even finite ones, that are not cyclic.
Let \(G\) be a finite group with \(|G|=n\). Then \(G\) is cyclic if and only if it has an element of order \(n\). An element \(x\in G\) is a generator if and only if \(\operatorname{ord}(x)=n\).
Suppose \(x\in G\). Then \(|\langle x\rangle|=\operatorname{ord}(x)\), and since \(\langle x\rangle\leq G\), \(\langle x\rangle=G\) if and only if \(\operatorname{ord}(x)=|\langle x\rangle|=|G|=n\).
□
Every subgroup of a cyclic group is cyclic.
Let \(G=\langle x\rangle\) be a cyclic group with generator \(x\), and let \(H\leq G\) be a subgroup.
If \(H=\{e\}\) is the trivial subgroup, then \(H=\langle e\rangle\) is cyclic. Otherwise, \(x^i\in H\) for some \(i\neq0\), and since also \(x^{-i}\in H\) since \(H\) is closed under taking inverses, we can assume \(i>0\).
Let \(m\) be the smallest positive integer such that \(x^m\in H\). We shall show that \(H=\langle x^m\rangle\), and so \(H\) is cyclic.
Certainly \(\langle x^m\rangle\subseteq H\), since every power of \(x^m\) is in \(H\). Suppose \(x^k\in H\) and write \(k=mq+r\) where \(q,r\in\mathbb{Z}\) and \(0\leq r<m\). Then \[x^r=x^{k-mq}=x^k(x^m)^q\in H,\] since \(x^k\in H\) and \(x^m\in H\). But \(0\leq r<m\), and \(m\) is the smallest positive integer with \(x^m\in H\), so \(r=0\) or we have a contradiction. So \(x^k=(x^m)^q\in\langle x^m\rangle\). Since \(x^k\) was an arbitrary element of \(H\), \(H\subseteq\langle x^m\rangle\).□
9.3 Group homomorphism and Isomorphism
After studying sets, we looked at how functions allows us to go from one set to another. A group is a set with some extra structure, and so to learn about groups we want to consider functions between groups which take account of this structure somehow.
A “group homomorphism” is a function between two groups that links the two group operations in the following way.
If we have a group homomorphism, there are certain things we can deduce:
Let \(\varphi:G\to H\) be a homomorphism, let \(e_G\) and \(e_H\) be the identity elements of \(G\) and \(H\) respectively, and let \(x\in G\). Then
\(\varphi(e_G)=e_H\),
\(\varphi(x^{-1})=\varphi(x)^{-1}\),
\(\varphi(x^i)=\varphi(x)^i\) for any \(i\in\mathbb{Z}\).
We go through all three statements.
We have \(\varphi(e_G)=\varphi(e_Ge_G)=\varphi(e_G)\varphi(e_G)\), so by uniqueness of the identity \(\varphi(e_G)=e_H\).
We have \(e_H=\varphi(e_G)=\varphi(xx^{-1})=\varphi(x)\varphi(x^{-1})\), so by uniqueness of inverses \(\varphi(x^{-1})=\varphi(x)^{-1}\).
This is true for positive \(i\) by a simple induction (it is true for \(i=1\), and if it is true for \(i=k\) then \[\varphi(x^{k+1})=\varphi(x^k)\varphi(x)=\varphi(x)^k\varphi(x)=\varphi(x)^{k+1},\] so it is true for \(i=k+1\)). Then by b.) it is true for negative \(i\), and by a.) it is true for \(i=0\).
□
As we have seen, bijective functions allows us to treat two sets of the same cardinality as essentially the same sets, just changing the name of the elements. A similar story occurs with groups. Suppose \(G=\langle x\rangle=\{e,x,x^2\}\) and \(H=\langle y\rangle=\{e,y,y^2\}\) are two cyclic groups of order \(3\). Strictly speaking they are different groups, since (for example) \(x\) is an element of \(G\) but not of \(H\). But clearly they are “really the same” in some sense: the only differences are the names of the elements, and the “abstract structure” of the two groups is the same. To make this idea, of two groups being abstractly the same, precise, we introduce the idea of an isomorphism of groups.
Homomorphism comes from the Greek homo to mean “same” and morph to mean “shape”. Isomorphism comes from the Greek iso to mean “equal” (and morph to mean “shape”).
A homomorphism is a map between two groups that keeps the same shape, i.e. preserves the group operation (but not necessarily anything else), while an isomorphism is a map between two groups that have equal shape (it preserves the group operation and many other useful properties as we will see below).Next we’ll prove some of the easy consequences of the definition.
Let \(\varphi:G\to H\) be an isomorphism between (multiplicatively-written) groups. Then \(\varphi^{-1}:H\to G\) is also an isomorphism.
Since \(\varphi\) is a bijection, it has an inverse function \(\varphi^{-1}\) that is also a bijection.
Let \(u,v\in H\). Since \(\varphi\) is a bijection, there are unique elements \(x,y\in G\) with \(u=\varphi(x)\) and \(v=\varphi(y)\). Then \[\varphi^{-1}(uv)=\varphi^{-1}\left(\varphi(x)\varphi(y)\right) = \varphi^{-1}\left(\varphi(xy)\right)=xy=\varphi^{-1}(u)\varphi^{-1}(v),\] and so \(\varphi^{-1}\) is an isomorphism.□
Because of this Proposition, the following definition makes sense, since it tells us that there is an isomorphism from \(G\) to \(H\) if an only if there is one from \(H\) to \(G\).
Let \(G,H,K\) be three groups. If \(G\) is isomorphic to \(H\) and \(H\) is isomorphic to \(K\), then \(G\) is isomorphic to \(K\).
Let \(\varphi:G\to H\) and \(\theta:H\to K\) be isomorphisms. Then the composition \(\theta\varphi:G\to K\) is a bijection and if \(x,y\in G\) then \[\theta\left(\varphi(xy)\right)=\theta\left(\varphi(x)\varphi(y)\right) =\theta\left(\varphi(x)\right)\theta\left(\varphi(y)\right),\] and so \(\theta\varphi\) is an isomorphism.
□
Let \(\varphi:G\to H\) be an isomorphism between (multiplicatively-written) groups, let \(e_G\) and \(e_H\) be the identity elements of \(G\) and \(H\) respectively, and let \(x\in G\). Then
\(\varphi(e_G)=e_H\),
\(\varphi(x^{-1})=\varphi(x)^{-1}\).
\(\varphi(x^i)=\varphi(x)^i\) for every \(i\in\mathbb{Z}\).
\(\operatorname{ord}_G(x)=\operatorname{ord}_H\left(\varphi(x)\right)\).
The first three statements follows directly from Proposition 9.13 since an isomorphism is an homomorphism.
For the last statement, by a.) and c.), we have \(x^i=e_G\Leftrightarrow\varphi(x)^i=e_H\), and so \(\operatorname{ord}_G(x)=\operatorname{ord}_H\left(\varphi(x)\right)\).□
To prove that two groups are isomorphic usually requires finding an explicit isomorphism. Proving that two groups are not isomorphic is often easier, as if we can find an “abstract property” that distinguishes them, then this is enough, since isomorphic groups have the same “abstract properties”. We’ll make this precise, and prove it, with some typical properties, after which you should be able to see how to give similar proofs for other properties, just using an isomorphism to translate between properties of \(G\) and of \(H\).
Let \(G\) and \(H\) be isomorphic groups. Then \(|G|=|H|\).
This follows just from the fact that an isomorphism is a bijection \(\varphi:G\to H\).
□
Let \(G\) and \(H\) be isomorphic groups. If \(H\) is abelian then so is \(G\).
Suppose that \(\varphi:G\to H\) is an isomorphism and that \(H\) is abelian. Let \(x,y\in G\). Then \[\varphi(xy)=\varphi(x)\varphi(y)=\varphi(y)\varphi(x)=\varphi(yx),\] since \(\varphi(x),\varphi(y)\in H\), which is abelian. Since \(\varphi\) is a bijection (and in particular injective) it follows that \(xy=yx\). So \(G\) is abelian.
□
Let \(G\) and \(H\) be isomorphic groups. If \(H\) is cyclic then so is \(G\).
Suppose \(\varphi:G\to H\) is an isomorphism and \(H=\langle y\rangle\) is cyclic. So every element of \(H\) is a power of \(y\). So if \(g\in G\) then \(\varphi(g)=y^i\) for some \(i\in\mathbb{Z}\), and so \(g=\varphi^{-1}(y)^i\). So if \(x=\varphi^{-1}(y)\) then every element of \(G\) is a power of \(x\), and so \(G=\langle x\rangle\).
□
If \(n\in \mathbb{Z}_+\), we write \(C_n\) to mean a (multiplicatively-written) cyclic group of order \(n\).
This notation is sensible since a cyclic group can only be isomorphic to another cyclic group of the same order, and since two cyclic groups of the same order are isomorphic.We can use this proposition to show that there exists groups of the same order which are not isomorphic. Consider the groups \(C_8\) and \(D_8\), both have order \(8\), however we have seen \(D_8\) is not abelian, and hence not cyclic.
This again highlights that a group is a set with a binary operation: a bijection exists between the sets \(C_8\) and \(D_8\), but it does not preserve the group operations.Let \(G\) and \(H\) be isomorphic groups and \(n\in \mathbb{Z}\cup \{\infty\}\). Then \(G\) and \(H\) have the same number of elements of order \(n\).
By Proposition 9.18, an isomorphism \(\varphi:G\to H\) induces a bijection between the set of elements of \(G\) with order \(n\) and the set of elements of \(H\) with order \(n\).
□
The idea of isomorphism gives an important tool for understanding unfamiliar or difficult groups. If we can prove that such a group is isomorphic to a group that we understand well, then this is a huge step forward.
The following example of a group isomorphism was used for very practical purposes in the past.
The logarithm function \[\log_{10}:(\mathbb{R}_+,\cdot)\to(\mathbb{R},+)\] is an isomorphism from the group of positive real numbers under multiplication to the group of real numbers under addition (of course we could use any base for the logarithms). It is a bijection since the function \(y\mapsto 10^y\) is the inverse function, and the group isomorphism property is the familiar property of logarithms that \[\log_{10}(ab)=\log_{10}(a)+\log_{10}(b).\] Now, if you don’t have a calculator, then addition is much easier to do by hand than multiplication, and people used to use “log tables” to make multiplication easier. If they wanted to multiply two numbers, they would look up the logarithms, add them and then look up the “antilogarithm”.
In group theoretic language they were exploiting the fact that there is an isomorphism between the “difficult” group \((\mathbb{R}_+,\cdot)\) and the “easy” group \((\mathbb{R},+)\).9.4 Direct Product
In this section we’ll study a simple way of combining two groups to build a new, larger, group. We will do that by generalising the idea of the Cartesian product of two sets (Definition 6.1).
The direct product \(H\times K\) of groups is itself a group.
Associativity of \(H\times K\) follows from associativity of \(H\) and \(K\), since if \(x,x',x''\in H\) and \(y,y',y''\in K\), then \[\begin{align*} \left((x,y)(x',y')\right)(x'',y'')&=(xx',yy')(x'',y'')\\ &=(xx'x'',yy'y'')\\ &=(x,y)(x'x'',y'y'')\\ &=(x,y)\left((x',y')(x'',y'')\right). \end{align*}\]
If \(e_H\) and \(e_K\) are the identity elements of \(H\) and \(K\), then \((e_H,e_K)\) is the identity element of \(H\times K\), since if \(x\in H\) and \(y\in K\), then \[(e_H,e_K)(x,y)=(e_Hx,e_Ky)=(x,y)=(xe_H,ye_K)=(x,y)(e_H,e_K).\]
The inverse of \((x,y)\in H\times K\) is \((x^{-1},y^{-1})\), since \[(x,y)(x^{-1},y^{-1})=(xx^{-1},yy^{-1})=(e_H,e_K) =(x^{-1}x,y^{-1}y)=(x^{-1},y^{-1})(x,y).\]□
Notice that for all aspects of the group structure, we simply apply the corresponding idea in the first coordinate for \(H\) and in the second coordinate for \(K\). This is generally how we understand \(H\times K\), by considering the two coordinates separately, and if we understand \(H\) and \(K\), then \(H\times K\) is easy to understand. For example, it is easy to see that, for any \(i\in\mathbb{Z}\) and any \((x,y)\in H\times K\), \[(x,y)^i=(x^i,y^i),\] so also taking powers in a direct product is just a matter of taking powers of the coordinates separately.
Here are some very easy consequences of the definition.
Let \(H\) and \(K\) be (multiplicatively-written) groups, and let \(G=H\times K\) be the direct product.
\(G\) is finite if and only if both \(H\) and \(K\) are finite, in which case \(|G|=|H||K|\).
\(G\) is abelian if and only if both \(H\) and \(K\) are abelian.
If \(G\) is cyclic then both \(H\) and \(K\) are cyclic.
We go through all three statements.
This is just a familiar property of Cartesian products of sets (that was left as an exercise).
Suppose \(H\) and \(K\) are abelian, and let \((x,y),(x',y')\in G\). Then \[(x,y)(x',y')=(xx',yy')=(x'x,y'y)=(x',y')(x,y),\] and so \(G\) is abelian.
Suppose \(G\) is abelian, and \(x,x'\in H\), then \[(xx',e_K)=(x,e_K)(x',e_K)=(x',e_K)(x,e_K)=(x'x,e_K),\] and considering the first coordinates, \(xx'=x'x\), and so \(H\) is abelian. Similarly \(K\) is abelian.
- Suppose \(G\) is cyclic, and \((x,y)\) is a generator, so that every element of \(G\) is a power of \((x,y)\). Let \(x'\in H\). Then \((x',e_K)\in G\), so \((x',e_K)=(x,y)^i=(x^i,y^i)\) for some \(i\in\mathbb{Z}\), and so \(x'=x^i\). So every element of \(H\) is a power of \(x\), so \(H=\langle x\rangle\) is cyclic. Similarly \(K\) is cyclic.
□
Let \(H\) and \(K\) be (multiplicatively-written) groups, and \(x\in H\), \(y\in K\) elements with finite order. Then \((x,y)\in H\times K\) has finite order equal to the lowest common multiple \[\operatorname{lcm}\left(\operatorname{ord}_H(x),\operatorname{ord}_K(y)\right).\]
Let \(i\in\mathbb{Z}\). Then \((x,y)^i=(e_H,e_K)\) if and only if \(x^i=e_H\) and \(y^i=e_K\), which is the case if and only if \(i\) is divisible by both \(\operatorname{ord}_H(x)\) and by \(\operatorname{ord}_K(y)\). The least positive such \(i\) is \(\operatorname{lcm}\left(\operatorname{ord}_H(x),\operatorname{ord}_K(y)\right)\), and so this is the order of \((x,y)\).
□
We can now decide precisely when the direct product of cyclic groups is cyclic.
Let \(H=C_n\) and \(K=C_m\) be finite cyclic groups. Then \(C_n\times C_m\) is cyclic if and only if \(\gcd(n,m)=1\).
Let \((x,y)\in H\times K\). Then \(\operatorname{ord}_H(x)\leq |H|\) and \(\operatorname{ord}_K(y)\leq |K|\). So by Proposition 9.26, \[\operatorname{ord}_{H\times K}(x,y)=\operatorname{lcm}\left(\operatorname{ord}_H(x),\operatorname{ord}_K(y)\right) \leq\operatorname{ord}_H(x)\operatorname{ord}_K(y)\leq |H||K|,\] where the first inequality is an equality if and only if \(\operatorname{ord}_H(x)\) and \(\operatorname{ord}_K(y)\) are coprime, and the second inequality is an equality if and only if \(H=\langle x\rangle\) and \(K=\langle y\rangle\).
Since \(|H\times K|=|H||K|\), \(H\times K\) is cyclic if and only if it has an element of order \(|H||K|\), which by the argument above is true if and only if \(\gcd\left(\operatorname{ord}_H(x),\operatorname{ord}_K(y)\right)=1\).□
Since cyclic groups of the same order are isomorphic, the last theorem says that \[C_m\times C_n\cong C_{mn}\] if and only if \(\gcd(m,n)=1\).
Felix Klein, German mathematician (1849 - 1925) applied ideas from group theory to geometry, which led to the emergence of transformation groups. These were some of the first example of infinite groups (beyond the groups \((\mathbb{R},+)\), \((\mathbb{R}\setminus\{0\},\times)\), which weren’t really studied as groups). Klein wrote about the Klein 4-group, although he called it Vierergruppe (meaning “four-group”), as it is the smallest group which is not cyclic.
\(C_2\times C_3\cong C_6\)
\(C_2\times C_9\cong C_{18}\)
\(C_{90}\cong C_2\times C_{45}\cong C_2\times (C_9\times C_5)\)
We can clearly extend the definition of a direct product of two groups to three, four or more groups and make sense of things like \(G\times H\times K\), which would be a group whose elements are the ordered triples \((x,y,z)\) with \(x\in G\), \(y\in H\) and \(z\in K\).
We can then write the last example as \[C_{90}\cong C_2\times C_9\times C_5.\]
More generally, if \(n=p_1^{r_1}p_2^{r_2}\dots p_k^{r_k}\), where \(p_1,p_2,\dots,p_k\) are distinct primes, then \[C_n\cong C_{p_1^{r_1}}\times C_{p_2^{r_2}}\times\dots\times C_{p_k^{r_k}},\] so that every finite cyclic group is isomorphic to a direct product of groups with order powers of primes.
We’ll finish this section with a different example of a familiar group that is isomorphic to a direct product.
\((\mathbb{R}\setminus\{0\},\times)\cong(\mathbb{R}_{>0},\times)\times\left(\{1,-1\},\times\right)\).
Define a map \[\varphi:\mathbb{R}_{>0}\times\{1,-1\}\to\mathbb{R}\setminus\{0\}\] by \(\varphi(x,\varepsilon)=\varepsilon x\). This is clearly a bijection, and \[\varphi\left((x,\varepsilon)(x'\varepsilon')\right) =\varphi(xx',\varepsilon\varepsilon')=\varepsilon\varepsilon'xx' =(\varepsilon x)(\varepsilon'x')=\varphi(x,\varepsilon)\varphi(x',\varepsilon'),\] so that \(\varphi\) is an isomorphism.
□
10 Modular arithmetic and Lagrange
We finish this course by linking several threads together. We will explore the important Lagrange’s theorem of group theory (which actually was first formulated long before group theory was developed). We will then see how this theorem has applications to the study of the integers (which was one of our earlier threads). First though, we need to take a step back and explore the concept of partitioning a set, and saying when objects are “basically the same”.
10.1 Equivalence relations and partition of sets
There are many situations in maths where we have different objects that we want to “consider the same”, often because they share a desired property. The requirement that two objects are exactly equal is often too restrictive, so we generalise this concept to be broader (this theory is applied to many branches of mathematics).
A relation \(\sim\) on a nonempty set \(X\) is a subset \(R\subseteq X\times X\). We say \(x\) is related to \(y\), denoted by \(x\sim y\), when \((x,y)\in R\).
A relation \(\sim\) is reflexive if for all \(x\in X\), \(x\sim x\).
A relation \(\sim\) is symmetric if for all \(x,y\in X\) we have \(x\sim y\) implies \(y\sim x\).
A relation \(\sim\) is transitive if for all \(x,y,z\in X\), if \(x\sim y\) and \(y\sim z\) then \(x\sim z\).
We use the notation \(x\not\sim y\) to say \(x\) is not related to \(y\).
We negate the above three properties to say that:
A relation \(\sim\) is not reflexive if there exists \(x\in X\) such that \(x\not\sim x\).
A relation \(\sim\) is not symmetric if there exists \(x,y\in X\) such that \(x\sim y\) and \(y\not\sim x\).
A relation \(\sim\) is not transitive if there exists \(x,y,z\in X\), such that \(x\sim y\) and \(y\sim z\) and \(x\not\sim z\).
A relation \(\sim\) on a nonempty set \(X\) is an equivalence relation if it is reflexive, symmetric and transitive.
In such case we read \(x\sim y\) as “\(x\) is equivalent to \(y\)”.
Reflexive comes from the Latin re meaning “back” and flectere meaning “to bend”. This gave rise to words like “reflect” (where an object is bent back through a mirror) and “reflection”. A relationship is reflexive if it reflects every element (i.e., every element is in relation with itself).
Symmetric comes from the Greek sun meaning “together with” and metron meaning “a measure”. Given a point “together with a distance (from a line of symmetry)”, then you have found the image of the point using that symmetry.
We’ve seen the word transitive before ( (O2) ) - transitive comes from the Latin trans meaning “across, beyond” and the verb itus/ire meaning “to go”. A transitive relationship is one where knowing \(x\sim y\) and \(y\sim z\) allows us to go from \(x\) beyond \(y\) all the way to \(z\).
Equivalence comes from the Latin oequus meaning “even, level” and valere meaning “to be strong, to have value”. Two elements are equivalent if they are level (i.e., equal) in their value. One can be substituted for the other (notice this has the same roots as the word equal).Since we claim that equivalence relations are a generalisation of \(=\), let us show that \(=\) is indeed an equivalence relation. Define a relation \(\sim\) on \(\mathbb{R}\) via \(x\sim y\) if and only if \(x=y\). We show \(\sim\) is an equivalence relation.
Let \(x\in \mathbb{R}\). Since \(x=x\), we have \(x\sim x\). This is true for all \(x\in\mathbb{R}\), hence \(\sim\) is reflexive.
Let \(x,y\in \mathbb{R}\) be such that \(x\sim y\). By definition, this means \(x=y\), which means \(y=x\), i.e. \(y\sim x\). This is true for all \(x,y \in\mathbb{R}\), hence \(\sim\) is symmetric.
Let \(x,y,z\in \mathbb{R}\) be such that \(x\sim y\) and \(y\sim z\). This means \(x=y\) and \(y=z\), so \(x=y=z\), i.e. \(x=z\). So \(x\sim z\). This is true for all \(x,y,z \in\mathbb{R}\), hence \(\sim\) is transitive.
Since \(\sim\) is reflexive, symmetric and transitive, we have that \(\sim\) is an equivalence relation.Notice how in the above example each distinct equivalence class did not intersect each other. This is true in general.
Suppose \(\sim\) is an equivalence relation on a (nonempty) set \(X\). Then for any \(x,y\in X\), \([x]\neq[y]\) if and only if \([x]\cap[y]=\emptyset.\)
Take \(x,y\in X\).
\(\Rightarrow\)). First, we will show that if \([x]\neq[y]\) then \([x]\cap[y]=\emptyset\) by using the contrapositive. That is will prove that if \([x]\cap [y]\not=\emptyset\), then \([x]=[y]\).
So suppose that \([x]\cap[y]\not=\emptyset\). Then there exists some \(z\in[x]\cap[y]\). Hence, \(z\in[x]\), so \(z\sim x\). Similarly, \(z\in[y]\), so \(z\sim y\). Since \(\sim\) is symmetric, we have that \(x\sim z\). Since \(\sim\) is transitive, we have that \(x\sim y\). Now, choose \(w\in[x]\). Then \(w\sim x\), and since \(x\sim y\) and \(\sim\) is transitive, we have that \(w\sim y\). Hence, \(w\in[y]\). Since \(w\in[x]\) is arbitrary, we have that \([x]\subseteq [y]\). Similarly, we can show that, for any \(w\in[y]\), we have \(w\in[x]\), so \([y]\subseteq[x]\). Hence \([x]=[y].\)
\(\Leftarrow\)). Second, we will show that if \([x]\cap[y]=\emptyset\) then \([x]\not=[y]\) by using the contrapositive. So we will show that if \([x]=[y]\), then \([x]\cap[y]\not=\emptyset\).
So suppose that \([x]=[y]\). Since \(\sim\) is reflexive, we know that \(x\in[x]\). Hence, \(x\in[x]=[x]\cap[y]\), so \([x]\cap[y]\not=\emptyset.\)
Summarising, we have that \([x]\not=[y]\) if and only if \([x]\cap[y]=\emptyset.\)□
The above set-up leads us to the following definition which breaks a set into “parts”.
A partition of a non-empty set \(X\) is a collection \(\{A_i: i\in I \}\) of non-empty subsets of \(X\) such that
\(\forall\,x\in X\), \(\exists\,i\in I\) such that \(x\in A_i\), and
\(\forall\,x\in X\) and \(\forall\,i,j\in I\), if \(x\in A_i\cap A_j\), then \(A_i=A_j\ \).
The above two conditions can be rephrased as follows:
\(X = \bigcup_{i\in I} A_i\), and
\(A_i \cap A_j \neq \emptyset\) if and only if \(A_i = A_j\).
The above remark and Proposition 10.4 suggests a strong link between equivalence relations and partitions of sets, as we explore in the next two theorems.
Suppose \(\sim\) is an equivalence relation on a (non-empty) set \(X\). Then \[\Pi=\left\{[x]:\ x\in X\right\}\] is a partition of \(X\).
Take \(a\in X\). Then \(a \in [a]\in\Pi\). Hence, every element of \(X\) is in one of the equivalence classes in \(\Pi\). Furthermore, by Proposition 10.4 we have that \([x]\neq[y]\) if and only if \([x]\cap[y]=\emptyset.\), i.e. (by the contrapositive) \([x]\cap[y]\neq\emptyset\) if and only if \([x]=[y]\) as required.
□
Furthermore, given a partition of a set, we can construct an equivalence relation.
Suppose \(\Pi=\{A_i:\ i\in I\ \}\) is a partition of a (nonempty) set \(X\), for some indexing set \(I\). For \(x,y\in X\), define \(x\sim y\) if and only if there exists an \(i\in I\) such that \(x,y\in A_i\). Then \(\sim\) is an equivalence relation on \(X\).
We show \(\sim\) is reflexive. Take \(x\in X\). Since \(\Pi\) is a partition of \(X\), there exists some \(i\in I\) such that \(x\in A_i\). Hence, \(x\sim x\).
We show \(\sim\) is symmetric. Suppose \(x,y\in X\) such that \(x\sim y\). Then there exists some \(i\in I\) such that \(x,y\in A_i\). It follows that \(y,x\in A_i\), so \(y\sim x\).
We show \(\sim\) is transitive. Suppose that \(x,y,z\in X\) are such that \(x\sim y\) and \(y\sim z\). Then there exists some \(i\in I\) such that \(x,y\in A_i\) and there exists some \(j\in I\) such that \(y,z\in A_j\). Hence, we have that \(y\in A_i\) and \(y\in A_j\). Since \(\Pi\) is a partition, we must have that \(A_i = A_j\). It follows that \(x,z\in A_i\), so \(x\sim z\).
Summarising, we have that \(\sim\) is an equivalence relation on \(X\).□
Let us take the previous example further. Define a relation \(\sim\) on \(\mathbb{Z}\) via \(x\sim y\) if and only if either \(x=y\) or \(xy>0\). This is an equivalence relation. We have that \(\sim\) partitions \(\mathbb{Z}\) into three sets, \([-1]=\mathbb{Z_{-}}\), \([0]=\{0\}\) and \([1]=\mathbb{Z}_{+}\).
We will construct \(\mathbb{Q}\) from \(\mathbb{Z}\) by partitioning the set \(\mathbb{Z} \times \mathbb{Z}_+\).
We define the relation \(\sim\) on \(\mathbb{Z} \times \mathbb{Z}_+\) via \((a,b) \sim (c,d)\) if and only if \(a\cdot d=b\cdot c\). We check this is an equivalence relation.:
Let \((a,b) \in \mathbb{Z} \times \mathbb{Z}_+\). Since \(a\cdot b=b\cdot a\), we have that \((a,b) \sim (a,b)\) and \(\sim\) is reflexive.
Let \((a,b),(c,d) \in \mathbb{Z} \times \mathbb{Z}_+\) be such that \((a,b) \sim (c,d)\). Then we have \(a\cdot d=b\cdot c\), which can be re-written as \(c\cdot b=d\cdot c\), so \((c,d) \sim (a,b)\) and \(\sim\) is symmetric.
Let \((a,b), (c,d), (f,g) \in \mathbb{Z} \times \mathbb{Z}_+\) be such that \((a,b) \sim (c,d)\) and \((c,d) \sim (f,g)\). Then we have \(a\cdot d=b\cdot c\) and \(c\cdot g=d\cdot f\). Multiplying the first equation by \(g\) we get \(adg=cbg\), and using the second equation we can write it as \(adg=bdf\). Since we have \(d \neq 0\) (as \(d\in \mathbb{Z}_+\)) we can divide through to give \(ag=bf\) which means that \((a,b)\sim (f,g)\) and \(\sim\) is transitive.
Therefore \(\sim\) is reflexive, symmetric and transitive, and so it is an equivalence relation.
We define elements of \(\mathbb{Q}\), which we denote \(\frac{a}{b}\) to be the equivalence classes \([(a,b)]=\{(a,b),(2a,2b),\dots\}\).
We will not try to summarise the interesting 2019 article by Amir Asghari on the history of equivalence relation (separating the definition from when the notion was first used), but we would recommend it as something worth reading just to showcase how ideas can be used before they are formalised, and how the mathematics we do today is different from how mathematics used to be done. The full reference is Asghari, A. Equivalence: an attempt at a history of the idea. Synthese 196, 4657–4677 (2019). https://doi.org/10.1007/s11229-018-1674-2
10.2 Congruences and modular arithmetic
We now use our work on equivalence classes to partition \(\mathbb{Z}\). Recall that for any two integers \(a,n \in \mathbb{Z}\), \(n\neq 0\), there exists a quotient \(q\) and a remainder \(r\) such that \(a=nq+r\). Sometimes we only care about the remainder \(r\), which leads us into the following definition.
Let \(n\in\mathbb{Z}_+\). Define a relation on \(\mathbb{Z}\) via \(a\sim b\) if and only if \(a\equiv b\ \pmod{n}\). Then \(\sim\) is an equivalence relation.
Exercise.
□
Using Theorem 5.2, we can see that, given an integer \(n\), every integer \(a\) is congruent modulo \(n\) to a unique \(r\) such that \(0\leq r <n\). I.e, we partition \(\mathbb{Z}\) into exactly \(n\) congruence classes modulo \(n\) given by \([0],[1],\dots,[n-1]\) where \[[r] = \{a\in\mathbb{Z}:a\equiv r \pmod{n}\} = r+n\mathbb{Z}.\]
We write \(\mathbb{Z}/n\mathbb{Z}\) for the set of congruence classes module \(n\).
If we’re clear that we’re considering \([r]\) as an element of \(\mathbb{Z}/n\mathbb{Z}\) we’ll often simply write \(r\).Both addition and multiplication make sense modulo \(n\), by the following theorem, which is very useful in computations.
Fix \(n\in\mathbb{Z}_+\). Suppose that \(a,b,c,d\in\mathbb{Z}\) are such that \(a\equiv c\ \pmod{n}\) and \(b\equiv d\ \pmod{n}\). Then \[a+b\equiv c+d\ \pmod{n} \qquad\text{and}\qquad ab\equiv cd\ \pmod{n}.\]
By assumption, we have that \(n\mid a-c\) and \(n\mid b-d\). Hence, for some \(x,y\in\mathbb{Z}\), we have that \(a-c=nx\) and \(b-d=ny\). It follows that \[(a+b)-(c+d)=(a-c)+(b-d)= nx+ny=n(x+y).\] Since \(x+y\in\mathbb{Z}\), this means that \(n\mid((a+b)-(c+d))\), so \(a+b\equiv c+d\ \pmod{n}.\) Further, since \(a=c+nx\) and \(b=d+ny\), we have that \[ab=(c+nx)(d+ny)=cd+n(cy+dx+nxy)\] so \(ab-cd=n(cy+dx+nxy)\). Since \(cy+dx+nxy\) is an integer, we have that \(n\mid ab-cd\), so \(ab\equiv cd\ \pmod{n}.\)
□
Another consequence of Theorem 10.10 is that we can “shift” the congruence classes by a given constant \(c\in \mathbb{Z}\), i.e. the congruence classes can be given by \([c],[c+1],\dots,[c+n-1]\).
We have \((\mathbb{Z}/n\mathbb{Z},+)\) is an abelian group.
Addition on \(\mathbb{Z}/n\mathbb{Z}\) is a well-defined binary operation by Theorem 10.10. Addition \(\pmod{n}\) is associative, since \[([a]+[b])+[c]=[a+b+c]=[a]+([b]+[c]).\] The identity element is \([0]\) since \[[a]+[0]=[a]=[0]+[a]\] for any \(a\in\mathbb{Z}\). The inverse of \([a]\) is \([-a]\), since \[[a]+[-a]=[0]=[-a]+[a].\] So \((\mathbb{Z}/n\mathbb{Z},+)\) is a group. It is abelian since \([a]+[b]=[a+b]=[b+a]\) for all \(a\) and \(b\).
□
In fact, it is a cyclic group, since the following is clear.
\((\mathbb{Z}/n\mathbb{Z},+)=\langle 1\rangle\).
Since \((\mathbb{Z}/n\mathbb{Z},+)\) is cyclic, it is isomorphic to \(C_n = \langle x \rangle\). The isomorphism is \(\varphi:(\mathbb{Z}/n\mathbb{Z},+)\to C_n\) defined by \(\varphi(i) = x^i\).
This means that cyclic groups are particularly simple to understand if we know a generator, as the group operation is just addition of exponents: in a cyclic group \(G=\langle x\rangle\), \(x^ix^j=x^{i+j}\), so the group operation in an infinite cyclic group is “just like” addition of integers, and the group operation in a finite cyclic group of order \(n\) is “just like”” addition of integers \(\pmod{n}\).However, \((\mathbb{Z}/n\mathbb{Z},\times)\) is not a group, since although it is associative and has an identity element \([1]\), not every element has an inverse. For example, \([0]\) never has an inverse, and in \(\mathbb{Z}/4\mathbb{Z}\), \([2]\) does not have a multiplicative inverse.
In \(\mathbb{Z}/n\mathbb{Z}\), \([a]\) has a multiplicative inverse if and only if \(\gcd(a,n)=1\).
If \(\gcd(a,n)=1\) then Theorem 5.7 there exists \(s,t\in\mathbb{Z}\) such that \(as+nt=1\) for some . So \[as\equiv 1-nt\equiv 1\pmod{n},\] so \([a][s]=[1]\) in \(\mathbb{Z}/n\mathbb{Z}\), and so \([s]\) is a multiplicative inverse of \([a]\).
Conversely, if \(\gcd(a,n)=h>1\), and if \(as\equiv 1\pmod{n}\), then \(1=as+nq\) for some \(q\in\mathbb{Z}\). But \(h\) divides both \(a\) and \(n\), so it divides \(as+nq\). But no integer \(h>1\) divides \(1\). So there is no \(s\) such that \([s]\) is a multiplicative inverse of \(a\).□
Note that the first part of the proof is constructive and allows us to solve some congruence equations.
Find \(x \in \mathbb{Z}\) such that \(4x = 3 \pmod{7}\).
We find the inverse of \([4]\) in \(\mathbb{Z}/7\mathbb{Z}\) (which exists since \(\gcd(4,7)=1\)). We find \(s,t \in \mathbb{Z}\) such that \(4s+7t=1\). We have that
| \(k\) | \(s_k\) | \(t_k\) | Calculation | \(q_k\) | \(r_k\) |
|---|---|---|---|---|---|
| \(0\) | \(0\) | \(1\) | - | - | - |
| \(1\) | \(1\) | \(0\) | \(7=4\cdot 1+3\) | \(1\) | \(3\) |
| \(2\) | \(0-1\cdot1=-1\) | \(1-0\cdot 1=1\) | \(4=3\cdot1+1\) | \(1\) | \(1\) |
| \(3\) | \(1-(-1)\cdot1=2\) | \(0-1\cdot1 = -1\) | \(3=1\cdot3+0\) | \(3\) | \(0\) |
so \(s=2\) and \(t=-1\). So \([2]\) is the inverse of \([4]\) in \(\mathbb{Z}/7\mathbb{Z}\).
Multiply both side of \(4x \equiv 3\pmod{7}\) by \(2\), we get \(x \equiv 2\cdot 4x \equiv 2\cdot 3\equiv 6\pmod{7}\).
We can also look at solving a system of simultaneous congruence equations.
Let \(m,n\in\mathbb{Z}_+\) be co-prime. For any \(a,b\in\mathbb{Z}\), \(\exists\,x\in\mathbb{Z}\) such that \[x\equiv a\ \pmod{m} \qquad\text{ and }\qquad x\equiv b\ \pmod{n}.\] Furthermore, this \(x\) is unique modulo \(mn\). That is for \(x'\in\mathbb{Z}\), we have that \[x'\equiv a\ \pmod{m} \qquad\text{ and } \qquad x'\equiv b\ \pmod{n}\] if and only if \[x'\equiv x\ \pmod{mn}.\]
We will prove the existence of \(x\) and leave the uniqueness of \(x\) modulo \(mn\) as an exercise.
Since \(\gcd(m,n)=1\), by Theorem 5.7 we know that there exist \(s,t\in\mathbb{Z}\) such that \(ms+nt=1\). Then \[1\equiv ms+nt\equiv nt\ \pmod{m}\] and \[1\equiv ms+nt\equiv ms\ \pmod{n}.\] So let \(x=msb+nta\in \mathbb{Z}\). Then \[x\equiv msb+nta \equiv nta\equiv 1\cdot a\equiv a\ \pmod{m}\] and \[x\equiv msb+nta \equiv msb\equiv 1\cdot b\equiv b\ \pmod{n}.\]□
The above theorem is often known as the Chinese Remainder Theorem. An example of this theorem was first discussed by Sun Zi (Chinese mathematician, around 400-460) in his text Sunzi suanjing (Sun Zi’s Mathematical Manual). While Sun Zi came to the correct solution he posed in his text using the methods we would use nowadays, there is no sign that he developed a general method. Instead it was Qin Jiushao (Chinese mathematician, 1202-1261) who wrote in his text “Shushu Jiuzang” how to solve simultaneous linear congruent equations. The origin of the name “Chinese Remainder Theorem” is unclear; it arose in the west some time after a 1852 article by Wiley on the history of Chinese mathematics (however, he did not use this term).
Note that the above proof is a constructive proof, that is, it gives a way to find \(x\).
We want to find \(x\in \mathbb{Z}\) such that \(x\equiv 4\ \pmod{5}\) and \(x\equiv 7\ \pmod{8}\).
We have that \(\gcd(5,8)=1\), so we set \(x=msb+nta\), where \(a=4, m=5, b=7, n=8\) and \(s,t\) are such that \(gcd(5,8)=5s+8t\). We have that
| \(k\) | \(s_k\) | \(t_k\) | Calculation | \(q_k\) | \(r_k\) |
|---|---|---|---|---|---|
| \(0\) | \(0\) | \(1\) | - | - | - |
| \(1\) | \(1\) | \(0\) | \(8=5\cdot 1+3\) | \(1\) | \(3\) |
| \(2\) | \(0-1\cdot1=-1\) | \(1-0\cdot 1=1\) | \(5=3\cdot1+2\) | \(1\) | \(2\) |
| \(3\) | \(1-(-1)\cdot1=2\) | \(0-1\cdot1 = -1\) | \(3=2\cdot1+1\) | \(1\) | \(1\) |
| \(4\) | \(-1-2\cdot1 = -3\) | \(1-(-1)\cdot 1=2\) | \(2=1\cdot2+0\) | \(2\) | \(0\) |
One can use induction and the Fundamental Theorem of Arithmetic to prove the following generalisation of Theorem 10.14:
Let \(r\in\mathbb{Z}_+\) with \(r\ge 2\), and let \(m_1,\ldots,m_r\in\mathbb{Z}_+\) be pairwise co-prime, that is \(\gcd(m_i,m_j)=1\) for \(i,j\in\mathbb{Z}\) with \(1\le i\le r\), \(1\le j\le r\) and \(i\neq j\). Then for any \(a_1,\ldots,a_r\in\mathbb{Z}\), there exists some \(x\in\mathbb{Z}\) such that \[ x\equiv a_i\ \pmod{m_i} \] for all \(i\in\mathbb{Z}\) with \(1\le i\le r\). Further, this \(x\) is unique modulo \(m_1 m_2\cdots m_r\).
One can also think about combining all these methods together to solve simultaneous congruent equation where the coefficient in front of \(x\) is not \(1\).
10.3 Lagrange’s theorem
Let \(G=D_{2n}\) be the dihedral group of order \(2n\), and consider the orders of elements. Every reflection has order \(2\), which divides \(|G|\). The rotation \(a\) has order \(n\), which divides \(|G|\). Every other rotation \(a^i\) has order \(n/\gcd(n,i)\), which divides \(|G|\). In this section we’ll show that this is a general phenomenon for finite groups. In fact, we’ll prove a more general fact about orders of subgroups (of course, this includes the case of the order of an element \(x\), since \(\operatorname{ord}(x)\) is equal to the order of the cyclic subgroup \(\langle x\rangle\) generated by \(x\)).
The theorem in question is named after Joseph-Louis Lagrange, an Italian mathematician ( 1736 - 1813 ), who proved a special case of the theorem in 1770 (long before abstract group theory existed).
Let \(G\) be a finite group, and \(H\leq G\) a subgroup. Then \(|H|\) divides \(|G|\).
The idea of the proof is to partition the set \(G\) into subsets, each with the same number of elements as \(H\), so that \(|G|\) is just the number of these subsets times \(|H|\).
The set of left cosets partition \(G\).
For any group \(G\) and subgroup \(H \leq G\), \(\{xH:x\in G\}\) is a partition of the set \(G\).
Clearly property 1 is satisfied: \(G = \cup_{x\in G} xH\) because any \(x=xe\in xH\). So we just need to check property 2, that for \(x,y\in G\) we have \(xH\cap yH\neq\emptyset\) if and only if \(xH=yH\).
Suppose \(xH\cap yH\neq\emptyset\), and choose \(g\in xH\cap yH\). Then \(g=xa=yb\) for some \(a,b\in H\), so that \(x=yba^{-1}\). If \(h\in H\) then \(xh=y(ba^{-1}h)\in yH\) since \(ba^{-1}h\in H\). So every element of \(xH\) is in \(yH\). Similarly every element of \(yH\) is in \(xH\), so that \(xH=yH\).□
Given that we have a partition on the set \(G\), we can construct an equivalence relation on the set \(G\) and say \(x\sim_H y\) if and only if there exists \(z\) such that \(x,y \in zH\). With a bit of work, we can show that this is the same as saying \(x, y\in G\) are equivalent (with respect to/modulo \(H\)) if and only if \(y^{-1}x \in H\) [you can check this is an equivalence relation].
Compare this with the (infinite) group \(G=(\mathbb{Z},+)\) and (infinite) subgroup \(H = (n\mathbb{Z},+)\). We partitioned \(\mathbb{Z}\) using \(n\mathbb{Z}\) and defined an equivalence relation \(a\equiv b \pmod{n}\) if and only if \(a-b\in n\mathbb{Z}\).Next we verify that each left coset has the same cardinality.
Let \(H\leq G\) and \(x\in G\). Then there is a bijection \(\alpha:H\to xH\), so that \(|xH|=|H|\).
Define \(\alpha\) by \(\alpha(h)=xh\). Then \(\alpha\) is surjective, since by definition every element of \(xH\) is of the form \(xh=\alpha(h)\) for some \(h\in H\). But also \(\alpha\) is injective, since if \(h,h'\in H\) then \[\alpha(h)=\alpha(h')\Rightarrow xh=xh'\Rightarrow h=h'.\]
□
Everything so far works for possibly infinite \(H,G\), but now for finite \(G\) (and hence \(H\)) we can put everything together to prove Lagrange’s Theorem.
Suppose that \(k\) is the number of distinct left cosets \(xH\). By the two previous lemmas, the cosets partition \(G\) and each coset contains \(|H|\) elements. So the number of elements of \(G\) is \(k|H|\).
□
Let \(G=D_6\) again, but let \(H=\langle b\rangle=\{e,b\}\) be the cyclic subgroup generated by \(b\). Then
\(eH=\{e,b\}=bH\);
\(aH=\{a,ab\}=abH\);
\(a^2H=\{a^2,a^2b\}=a^2bH\),
You may have seen the word index (Latin for “pointer”) in the context of summation (e.g., \(\sum_{i=1}^3 i^2\), where \(i\) is the index). In group theory, there are many time where one might want to do \(\sum_{i=1}^{|G:H|}\). Here, the index is telling us how many terms are in our sum.
Let \(G\) be a finite group with \(|G|=n\). Then for any \(x\in G\), the order of \(x\) divides \(n\), and so \(x^n=e\).
By Lagrange’s Theorem, the order of the cyclic subgroup \(\langle x\rangle\) divides \(n\). But the order of this subgroup is just \(\operatorname{ord}(x)\), so \(\operatorname{ord}(x)\) divides \(n\), and so \(x^n=e\).
□
10.4 Some applications of Lagrange’s theorem
Lagrange’s Theorem gives most information about a group when the order of the group has relatively few factors, as then it puts more restrictions on possible orders of subgroups and elements.
Let’s consider the extreme case, when the order of the group is a prime \(p\), and so the only factors are \(1\) and \(p\).
Let \(p\) be a prime and \(G\) a group with \(|G|=p\). Then
\(G\) is cyclic.
Every element of \(G\) except the identity has order \(p\) and generates \(G\).
The only subgroups of \(G\) are the trivial subgroup \(\{e\}\) and \(G\) itself.
Let \(x\in G\) with \(x\neq e\). Then \(\operatorname{ord}(x)\) divides \(|G|=p\) by Corollary 10.20, and \(\operatorname{ord}(x)\neq1\) since \(x\neq e\). So \(\operatorname{ord}(x)=p\). So the cyclic subgroup \(\langle x\rangle\) generated by \(x\) has order \(p\), and so must be the whole of \(G\). This proves a.) and b.).
Let \(H\leq G\). Then by Theorem 10.15 \(|H|\) divides \(|G|=p\), and so \(|H|=1\), in which case \(H\) is the trivial subgroup \(\{e\}\), or \(|H|=p\), in which case \(H=G\).□
If \(p\) is prime and \(P\) and \(Q\) are two subgroups of a group \(G\) with \(|P|=p=|Q|\), then either \(P=Q\) or \(P\cap Q=\{e\}\).
If \(P\cap Q\neq\{e\}\) then choose \(x\in P\cap Q\) with \(x\neq e\). By the previous theorem, \(x\) generates both \(P\) and \(Q\), so \(P=\langle x\rangle=Q\).
□
Now some other simple general consequences of Lagrange’s Theorem.
Let \(G\) be a group and \(H\),\(K\) two finite subgroups of \(G\) with \(|H|=m\), \(|K|=n\) and \(\gcd(m,n)=1\). Then \(H\cap K=\{e\}\).
Recall that the intersection of two subgroups is itself a subgroup, so that \(I=H\cap K\) is a subgroup both of \(H\) and of \(K\). Since it’s a subgroup of \(H\), Lagrange’s Theorem implies that \(|I|\) divides \(m=|H|\). But similarly \(|I|\) divides \(n=|K|\). So since \(\gcd(m,n)=1\), \(|I|=1\) and so \(I=\{e\}\).
□
Let \(G\) be a group with \(|G|=4\). Then either \(G\) is cyclic or \(G\) is isomorphic to the Klein \(4\)-group \(C_2\times C_2\). In particular there are just two non-isomorphic groups of order \(4\), both abelian.
By Corollary 10.20 the order of any element of \(G\) divides \(4\), and so must be \(1\), \(2\) or \(4\).
If \(G\) has an element of order \(4\) then it is cyclic.
If not, it must have one element (the identity \(e\)) of order \(1\) and three elements \(a,b,c\) of order \(2\). So \(a^{-1}=a\), \(b^{-1}=b\) and \(c^{-1}=c\).
Consider which element is \(ab\). If \(ab=e\) then \(b=a^{-1}\), which is false, since \(a^{-1}=a\). If \(ab=a\) then \(b=e\), which is also false. If \(ab=b\) then \(a=e\), which is also false. So \(ab=c\).
Similarly \(ba=c\), \(ac=b=ca\) and \(bc=a=cb\), and \(G\) is isomorphic to the Klein \(4\)-group.□
We’ll finish this section with some other results about groups of small order that we won’t prove. These are easier to prove with a bit more theory, which are all proved in the third year Group Theory unit.
Let \(p\) be an odd prime. Then every group of order \(2p\) is either cyclic or isomorphic to the dihedral group \(D_{2p}\).
Let \(p\) be a prime. Every group of order \(p^2\) is either cyclic or isomorphic to \(C_P\times C_p\) (and so in particular is abelian).
However there are non-abelian groups of order \(p^3\) for every prime \(p\). The dihedral group \(D_8\) is one example for \(p=2\).
There are five groups of order \(8\) up to isomorphism. Three, \(C_8\), \(C_4\times C_2\) and \(C_2\times C_2\times C_2\), are abelian, and two, the dihedral group \(D_8\) and another group \(Q_8\) called the quaternion group are non-abelian.
The first few orders not dealt with by the general theorems above are \(12\), \(15\), \(16\) and \(18\). It turns out that are five non-isomorphic groups of order \(12\), every group of order \(15\) is cyclic, there are fourteen non-isomorphic groups of order \(16\), and five of order \(18\).
The number of non-isomorphic groups of order \(2^n\) grows very quickly with \(n\). There are \(49,487,365,422\) (nearly fifty billion) non-isomorphic groups of order \(1024=2^{10}\).
10.5 Applications to number theory
We now use some of the tools from group theory to look back at questions linked to modular arithmetic.
It is worth noting that much of the following theory predates and motivated the development of abstract group theory, in particular the study of Abelian groups (from 1800). Alongside Symmetry groups and Transformation groups (which we did not explore), Abelian groups were concrete examples of groups that drove this development.
First, recall that \((\mathbb{Z}/n\mathbb{Z},\cdot)\) is not a group as some elements (such as \([0]\)) do not have a multiplicative inverse (recall Proposition 10.13). Let us define the following group.
\((U_n,\cdot)\) is an abelian group.
Suppose \([a],[b]\in U_n\), so \(\gcd(a,n)=1=\gcd(b,n)\). Then \(\gcd(ab,n)=1\) and so \([ab]\in U_n\) and \(U_n\) is closed under multiplication.
Since \[([a][b])[c]=[abc]=[a]([b][c])\] multiplication on \(U_n\) is associative.
\([1]\) is an identity element, since \([1][a]=[a]=[a][1]\) for any \(a\).
If \([a]\in U_n\), so \(\gcd(a,n)=1\), then \(as+nt=1\) for integers \(s,t\), and \(\gcd(s,n)=1\). So \([s]\in U_n\) is an inverse of \([a]\).
So \(U_n\) is a group under multiplication. It is abelian since \([a][b]=[ab]=[b][a]\) for all \(a,b\in\mathbb{Z}\).□
The notation \(U\) stands for “units”. In Algebra 2, you’ll see that a unit is an element which has a multiplicative inverse, so \(U_n\) is the group of units of \(\mathbb{Z}/n\mathbb{Z}\).
Similar links can be made with \((\mathbb{R},+)\) and \((\mathbb{R}\setminus\{0\},\cdot)\) or with \((\mathbb{Z},+)\) and \((\{-1,1\},\cdot)\).Unlike \((\mathbb{Z}/n\mathbb{Z},+)\), \((U_n,\times)\) is not always cyclic (although it sometimes is).
We can now apply Lagrange’s theorem to \(U_n\) to get an important number theory result.
Let \(p\) be a prime and \(a\) an integer not divisible by \(p\). Then \[a^{p-1}\equiv 1\pmod{p}.\]
We’ll apply Corollary 10.20 to the group \(G=U_p\). Since \(p\) is prime, \(U_p=\{[1],[2],\dots,[p-1]\}\) has order \(p-1\), and if \(a\) is not divisible by \(p\) then \([a]\in U_p\). So by Corollary 10.20, \[[a]^{p-1}=[1]\] in \(U_p\), or in other words \[a^{p-1}\equiv 1\pmod{p}.\]
□
This simplifies calculating powers of integers modulo a prime:
Pierre de Fermat, French lawyer and government official (1601 - 1665) worked on several number theory problems alongside his job. He wrote the above theorem however he did not write down a proof for fear it would be too long - he certainly was not aware of group theory tools that would have provided a short proof.
There is a generalization to powers modulo \(m\) where \(m\) is not prime, but the statement is a bit more complicated, since \(U_m\) is not just \(\{[1],[2],\dots,[m-1]\}\). So first, let’s introduce some standard notation for the order of this group.
Let \(m>0\) and \(a\) be integers with \(\gcd(a,m)=1\). Then \[a^{\varphi(m)}\equiv1\pmod{m}.\]
Apply Corollary 10.20 to the group \(G=U_m\). The condition \(\gcd(a,m)=1\) means that \([a]\in U_m\), and \(|U_m|=\varphi(m)\), so the corollary gives \[[a]^{\varphi(m)}=[1]\] in \(U_m\), or in other words \[a^{\varphi(m)}\equiv1\pmod{m}.\]
□
Leonhard Euler, Swiss mathematician (1707 - 1783), wrote down a proof of Fermat’s Little Theorem in 1736 (nearly a 100 year after Fermat wrote down the statement). He then extended Fermat’s theorem to all cases. While he used modular arithmetic notation as we do today, it wasn’t until 1801 that Gauss revisited the proof and gave a shorter and simpler version using group theory ideas.
Many of the groups \(U_n\) are direct products in disguise.
Let \(m,n\) be positive integers with \(\gcd(m,n)=1\). Then \[U_{mn}\cong U_m\times U_n.\]
Define a map \[\varphi:U_{mn}\to U_m\times U_n\] by \(\varphi([a]_{mn})=([a]_m,[a]_n)\) (where we use subscripts such as \([a]_m\) to indicate a congruence class\(\pmod{n}\)). This makes sense, since if \(\gcd(a,mn)=1\), then \(\gcd(a,m)=1\) and \(\gcd(a,n)=1\).
By Theorem 10.14, we know given \(a \in \mathbb{Z}/m\mathbb{Z}\) and \(b \in \mathbb{Z}/n\mathbb{Z}\) there exists \(x\in \mathbb{Z}/mn\mathbb{Z}\) such that \(\varphi(x)=(a,b)\). Furthermore, \(x\) is unique in \(\mathbb{Z}/mn\mathbb{Z}\). Hence \(\varphi\) is bijective [for all \(([a]_m,[b]_n)\in U_m\times U_n\), there exists a unique \([x]\in U_{mn}\) such that \(\varphi([x]_{mn})=([a]_m,[b]_n)\) ]
Since \(\varphi\) is bijective, and \[\varphi([a]_{mn}[a']_{mn})=([aa']_m,[aa']_n) =([a]_m,[a]_n)([a']_m,[a']_n)=\varphi([a]_{mn})\varphi([a']_{mn}),\] \(\varphi\) is an isomorphism.□
We have an immediate corollary
If \(\gcd(m,n)=1\) then \(\varphi(mn)=\varphi(m)\varphi(n)\).
11 Taming infinity
In Chapter 7 we saw the definition of cardinality, to be precise, for sets \(A\) and \(B\), we defined \(|A|=|B|, |A|\leq |B|\) and \(|A|<|B|\), with a focus on finite sets. In this chapter, we will see that there are different sizes of infinity.
11.1 Countable
We first notice that there are some infinite sets where we can “count” the elements.
In essence a countable set is an infinite set where we can enumerate the elements, \(x_1, x_2, x_3, \dots\) where \(x_i=f(i)\) for \(i\in\mathbb{Z}_+\).
Note that some texts in literature say that a set if countable if it is finite or if there exists a bijective function \(f:\mathbb{Z}_+\to X\), and when there exists a bijective function \(f:\mathbb{Z}_+\to X\), these texts say \(X\) is countably infinite. However, in this course, a countable set must be infinite (it makes some theorems easier to state).
Combining the definition of countability with the definition of cardinality, we have that \(X\) is a countable set if and only if \(|X|=|\mathbb{Z}_+|\).We show that the set of positive even integers is countable.
Let \(2\mathbb{Z}_+=\{2x: x\in\mathbb{Z}_+ \}\) and define \(f:\mathbb{Z}_+\to 2\mathbb{Z}_+\) by \(f(x)=2x\), for all \(x\in\mathbb{Z}_+\). To see that \(f\) is injective, suppose that \(x,y\in\mathbb{Z}_+\) such that \(f(x)=f(y)\). Then \(2x=2y\), so \(x=y\), showing that \(f\) is injective.
To see that \(f\) is surjective, take \(a\in \mathbb{Z}_+\). Then \(a=2x\), for some \(x\in\mathbb{Z}_+\), and hence \(a=2x=f(x)\). Hence, \(f\) is surjective. This shows that \(f\) is bijective. Therefore, \(A\) is countable.
Similarly, the set of odd positive integers, \(\{2x-1: x\in\mathbb{Z}_+\}\), can be shown to be countable.Let \(X\) and \(Y\) be two sets such that \(|X|=|Y|\). If \(X\) is countable, then \(Y\) is countable.
Let \(|X|=|Y|\) and suppose that \(X\) is countable. Then \(|X|=|\mathbb{Z}_+|\) so \(|Y|=|X|=|\mathbb{Z}_+|\). Hence \(|Y|\) is countable.
□
Every infinite set contains a countable subset.
Non-examinable. It is beyond the scope of this course.
□
While the statement seems intuitive, proving this result is outside the scope of this course. It involves using the Axiom of Choice, which says given a countable number of non-empty sets, we can choose one element from each set.
Interestingly, some research is done into how many theorems are true independent of the Axiom of Choice (and therefore would be true if we did not assume the Axiom of Choice to be true.)Let \(X\) be a subset of \(\mathbb{Z}_+\). Then \(X\) is either finite or countable.
If \(X\) is finite then we are done. So suppose \(X\) is infinite. We have an injective map \(g:X\to \mathbb{Z}_+\) given by \(g(x)=x\), so \(|X|\le |\mathbb{Z}_+|\). On the other hand, we know that \(X\) contains a countable subset \(A\). Hence, there exists a bijective map \(h:\mathbb{Z}_+\to A\). Now, define \(f:\mathbb{Z}_+\to X\) by \(f(n)=h(n)\), for all \(n\in\mathbb{Z}_+\). Then \(f\) is an injective map from \(\mathbb{Z}_+\) into \(X\). Hence, \(|\mathbb{Z}_+|\le|X|\). So by Theorem 7.8, we have that \(|X|=|\mathbb{Z}_+|\). It follows that \(X\) is countable.
□
Suppose \(X\) is an infinite set. Then \(X\) is countable if and only if there exists an injective \(f:X\to \mathbb{Z}_+\).
We prove both directions separately.
(\(\Rightarrow\)) First, suppose that \(X\) is countable. Then there exists a bijection \(f:X\to \mathbb{Z}_+\). Since \(f\) is bijective, it is injective.
(\(\Leftarrow\)) Second, suppose there exists such an injective \(f:X\to \mathbb{Z}_+\). Then \(|X|=|f[X]|\), and \(f[X] \subseteq \mathbb{Z}_+\). Since \(X\) is not finite and \(|X|=|f[X]|\), \(f[X]\) is not finite. Hence, \(f[X]\) is countable. Therefore, we must have that \(X\) is countable.
Summarising, \(X\) is countable if and only if there exists an injective \(f:X\to \mathbb{Z}_+\).□
Let \(X\) be a set and let \(A,B\subseteq X\). Suppose that \(A\) is a countable set and that \(B\) is a nonempty finite set disjoint from \(A\) (\(A\cap B=\emptyset\)). Then \(A\cup B\) is countable.
Since \(A\) is countable, there exists an injective map \(f:A\to\mathbb{Z}_+\). Since \(B\) is finite we have that \(B=\{b_1,\ldots,b_m\}\), for some \(m\in\mathbb{Z}_+\), where \(|B|=m\). Now, define \(g:A\cup B\to\mathbb{Z}_+\) by \[g(x)=\begin{cases} i,&\text{if $x=b_i$,}\\ f(x)+m,&\text{if $x\in A$}.\end{cases}\] We claim that \(g\) is injective. To see this, take \(x,y\in A\cup B\) such that \(x\not=y\). If \(x,y\in B\), then \(x=b_i\) and \(y=b_j\) for some \(i,j\in\mathbb{Z}_+\) such that \(i\le m\), \(j\le m\) with \(i\not=j\). Hence, we have that \(g(x)=i\not=j=g(y)\). If \(x\in B\) and \(y\in A\), then \(x=b_i\) for some \(i\in\mathbb{Z}_+\) with \(i\le m\). Hence, we have that \(g(x)=i<m+1\le g(y)\). If \(x,y\in A\), then \(f(x)\not=f(y)\) since \(x\not=y\) and \(f\) is injective. So \(g(x)=f(x)+m+1\not=f(y)+m+1=g(y)\). It follows that \(g\) is injective.
Since \(A\subseteq A\cup B\) and \(A\) is infinite, \(A\cup B\) is infinite. Since \(g:A\cup B\to\mathbb{Z}_+\) is injective and \(A\cup B\) is infinite, \(A\cup B\) is countable.□
The above proof was popularised by David Hilbert (Prussian mathematician, 1862-1943) with what is now called the “Hilbert hotel”, where there is always room for another guest:
The Hilbert hotel has countably many rooms,
labelled \(1,2,3,\ldots\) (so for each number in \(\mathbb{Z}_+\), there is a room with that number). One night, the hotel is full,
and another potential guest arrives at the hotel looking for a room. The manager says, no problem! Then the manager announces
to the guests that every guest is to move to the next room (so the guests in room \(n\) move to room \(n+1\)). Thus all the guests
still have rooms, and room 1 has been made available to the new arrival.
We have that \(\mathbb{Z}_+\times \mathbb{Z}_+\) is countable.
First we note that \(\mathbb{Z}_+\times \mathbb{Z}_+\) is infinite as \(\mathbb{Z}_+\times \{1\}=\{(n,1): n \in \mathbb{Z}_+\} \subseteq \mathbb{Z}_+\times \mathbb{Z}_+\), and \(\mathbb{Z}_+\times \{1\}\) is countable (using the bijection \(f:\mathbb{Z}_+\to \mathbb{Z}_+\times \{1\}\) defined by \(f(n)=(n,1)\)).
We define \(f:\mathbb{Z}_+\times \mathbb{Z}_+ \to \mathbb{Z}_+\) by \(f((a,b)) = 2^a3^b \in \mathbb{Z}_+\). Suppose \(f((a_1,b_1))=f((a_2,b_2))\), then \(2^{a_1}3^{b_1}=2^{a_2}3^{b_2}=n\). Note that \(n\geq 2\) (since \(a_1\geq 1\)), so by the Fundamental Theorem of Arithmetic, \(n\) is expressed uniquely as a product of primes. That is \(a_1=a_2\) and \(b_1=b_2\), so \((a_1,b_1)=(a_2,b_2)\). Hence \(f\) is injective and \(\mathbb{Z}_+\times \mathbb{Z}_+\) is infinite, so \(\mathbb{Z}_+\times \mathbb{Z}_+\) is countable.□
There are many proofs of this theorem. Above we presented one that uses the Fundamental Theorem of Arithmetic. Below we outline the idea of another proof that doesn’t use the Fundamental Theorem of Arithmetic. We leave the rigorous details as an exercise.
We arrange the elements of \(\mathbb{Z}_+\times\mathbb{Z}_+\) in a grid: \[\begin{array}{ccccc} (1,1)&(1,2)&(1,3)&(1,4)&\cdots\\ (2,1)&(2,2)&(2,3)&(2,4)&\cdots\\ (3,1)&(3,2)&(3,3)&(3,4)&\cdots\\ (4,1)&(4,2)&(4,3)&(4,4)&\cdots\\ \vdots&\vdots&\vdots&\vdots \end{array}\] We order the elements of this grid along the cross-diagonals: \[(1,1);\ (1,2),\ (2,1);\ (1,3),\ (2,2),\ (3,1); \ldots\] So we want to construct a function \(f:\mathbb{Z}_+\times \mathbb{Z}_+\to \mathbb{Z}_+\) such that \(f((1,1))=1, f((1,2))=2, f((2,1))=3, \dots\). We leave it an exercise to find a general formula for \(f((n,m))\) and show that \(f\) is injective.
The following lemma lists the basic properties of countable sets.
Suppose that \(X\) is a countable set.
if \(A\subseteq X\), then \(A\) is either finite or countable.
if \(A\subseteq X\) and \(A\) is finite, then \(X\setminus A\) is countable.
there exists \(B\subseteq X\) such that \(B\) and \(X\setminus B\) are countable.
if \(f:C\to X\) is injective, then \(C\) is either a finite set or a countable set.
Exercise.
□
Using the above lemma, and the fact that \(\mathbb{Z}_+\times\mathbb{Z}_+\) is countable, we can deduce:
We have that \(\mathbb{Q}_+\), \(\mathbb{Q}\) and \(\mathbb{Z}\) are all countable. In particular \(|\mathbb{Z}_+|=|\mathbb{Z}|=|\mathbb{Q}|\).
Let \(X\) and \(Y\) be countable sets. Then
\(X\times Y\) is countable.
if \(X\cap Y=\emptyset\), then \(X\cup Y\) is countable.
Exercise.
□
Note that by repeated application of the above lemma, we can see that for countable \(X\) and for any \(n\in\mathbb{Z}_+\), we have \(X^n = X\times X \times X \times \dots \times X\) (the Cartesian product of \(n\) copies of \(X\)) is countable.
Let \(\{A_n: n\in\mathbb{Z}_+ \}\) be a (countable) collection of countable sets that are pairwise disjoint (i.e. \(A_i\cap A_j = \emptyset\) for all \(i\neq j\)). Then \(\bigcup\limits_{n\in\mathbb{Z}_+}A_n\) is countable.
First, note that since \(A_1\) is countable, we have that it is infinite. Since \(A_1\subseteq\bigcup\limits_{n\in\mathbb{Z}_+}A_n\), we know that \(\bigcup\limits_{n\in\mathbb{Z}_+}A_n\) is also infinite. We now construct an injective \(g:\bigcup\limits_{n\in\mathbb{Z}_+}A_n\to\mathbb{Z}_+\times\mathbb{Z}_+\).
For each \(n\in\mathbb{Z}_+\), enumerate the elements of \(A_n\) as \(a_{n,1},a_{n,2},a_{n,3},\ldots\). Now, define \(g:\bigcup\limits_{n=1}^{\infty}A_n\to\mathbb{Z}_+\times\mathbb{Z}_+\) by \[g(a_{m,k})=(m,k),\] for all \(a_{m,k}\in\bigcup\limits_{n=1}^{\infty}A_n\). To see that \(g\) is injective, suppose that \(g(a_{m,k})=g(a_{s,t})\) for some \(m,k,s,t\in\mathbb{Z}_+\). Then \((m,k)=(s,t)\), so \(m=s\), \(k=t\), and hence \(a_{m,k}=a_{s,t}\). It follows that \(g\) is injective. Hence, we have an injective function from \(\bigcup\limits_{n=1}^{\infty} A_n\) into a countable set. Since \(\bigcup\limits_{n=1}^{\infty}A_n\) is infinite, it follows that \(\bigcup\limits_{n=1}^{\infty}A_n\) is countable.□
11.2 Uncountable
Having explored the countable sets, we look at whether there exists sets that are not finite and not countable.
An uncountable set is one where we can not enumerate its elements.
We note that the cardinality of \(\mathbb{Z}_+\) separates finite, countable and uncountable sets. Indeed we leave it as an exercise to show that:
\(X\) is finite if and only if \(|X|<|\mathbb{Z}_+|\);
\(X\) is countable if and only if \(|X|=|\mathbb{Z}_+|\);
\(X\) is uncountable if and only if \(|X|>|\mathbb{Z}_+|\).
We will prove that the set \((0,1)=\{x\in\mathbb{R}:0<x<1\}\) is uncountable. First we need to set up some notation. Let us assume that every real numbers between \(0\) and \(1\) has a decimal expansion of the form \[0.a_1a_2a_3\cdots=\sum_{k\in\mathbb{Z}_+}a_k 10^{-k}\] with \(0\leq a_k \leq 9\) for each \(k\in\mathbb{Z}_+\).
Note however that this representation is not unique. Indeed, we have \(0.99999\dots = 1\), and in general let \(0<\alpha<1\) have decimal expansion \(0.a_1a_2a_3\dots a_N99999\dots\). That is, there exists \(\mathbb{Z}_+\) such that \(a_N\neq 9\) and \(a_n=9\) for all \(n>N\). Then, using the results \[\sum_{k\in\mathbb{Z}_+}10^{-k}=\frac{10^{-1}}{1-10^{-1}}=\frac19.\] We have: \[\begin{align*} 0.a_1a_2a_3\dots a_N999\dots &=\sum_{k\in\mathbb{Z}_+}a_k\cdot 10^{-k}\\ &= \sum_{k=1}^{N}a_k\cdot 10^{-k}+\sum_{k\in\mathbb{Z}_+, k>N}9\cdot 10^{-k}\\ &= \sum_{k=1}^{N}a_k\cdot 10^{-k}+10^{-N}\cdot9\cdot\sum_{k\in\mathbb{Z}_k}10^{-k}\\ &= \sum_{k=1}^{N}a_k\cdot 10^{-k}+10^{-N}\\ &= 0.a_1a_2a_3\dots a_{N-1}b_N, \end{align*}\] where \(b_N=a_N+1\).
Therefore, we will take for granted that every \(\alpha \in \mathbb{R}\) such that \(0<\alpha<1\) can be uniquely expressed as \(0.a_1a_2a_3....\) with \(0\leq a_k \leq 9\) and \(\neg(\exists N\in\mathbb{Z}_+ \text{ so that } \forall n\in\mathbb{Z}_+,\ n>N\implies a_n=9).\) (i.e., \(\forall N \in \mathbb{Z}_+, \exists n\in\mathbb{Z}_+, n>N \text{ so that } a_n\neq 9\)).
The interval \((0,1)=\{x\in\mathbb{R}: 0<x<1 \}\) is uncountable.
We know the interval \((0,1)\) is infinite, since \(f:\mathbb{Z}\to(0,1)\) defined by \(f(k)=10^{-k}\) is easily shown to be injective.
For the sake of contradiction, suppose \((0,1)\) is countable. Thus we can enumerate the elements of \((0,1)\) as \(\alpha_1,\alpha_2,\alpha_3,\ldots\). Write each \(\alpha_k\) as a decimal expansion as described above: \[\alpha_k=0.a_{k1}a_{k2}a_{k3}\cdots\] where \(0\leq a_{ki} \leq 9\) and \(\neg(\exists N\in\mathbb{Z}_+ \text{ so that } \forall n\in\mathbb{Z}_+,\ n>N\implies a_n=9).\) For each \(k\in\mathbb{Z}_+\), set \[b_k=\begin{cases} 1&\text{if $a_{kk}\not=1$,}\\2&\text{if $a_{kk}=1$.}\end{cases}\] Set \(\beta=0.b_1b_2b_3\cdots\). Thus \(\beta\in\mathbb{R}\) with \(0<\beta<1\) and \(\neg(\exists N\in\mathbb{Z}_+ \text{ so that } \forall n\in\mathbb{Z}_+,\ n>N\implies a_n=9).\) Hence by assumption, \(\beta=\alpha_m\) for some \(m\in\mathbb{Z}_+\). But \(b_m\not=a_{mm}\), contradicting the uniqueness of the representation of \(\beta\) as a decimal expansion not ending in an infinite sequence of 9s. Thus the assumption that the interval \((0,1)\) is countable leads to a contradiction, so \((0,1)\) must be uncountable.□
The above theorem is sometimes referred to as Cantor’s diagonalisation argument. While it was not the first proof that Cantor published to show \((0,1)\) is uncountable, it showcases a technique that was used subsequently in many other proofs by other mathematicians.
We have that \(\mathbb{R}\) is uncountable.
Since \((0,1)\subseteq \mathbb{R}\), we have \(|(0,1)|\leq |\mathbb{R}|\). Since \((0,1)\) is uncountable, we have \(|\mathbb{Z}_+|<|(0,1)|\leq |\mathbb{R}|\). Hence \(\mathbb{R}\) is uncountable.
□
While we have shown \(|(0,1)|\leq |\mathbb{R}|\), the following theorem shows that in fact \(|(0,1)|=|\mathbb{R}|\).
There is a bijection between the interval \((0,1)\) and \(\mathbb{R}\).
Exercise.
□
In a way, this highlight another difference between \(\mathbb{R}\), \(\mathbb{Q}\) and \(\mathbb{Z}\). In \(\mathbb{R}\) we can have a bounded subset which is uncountable. However \(\mathbb{Q}\) a bounded subset is either finite or countable, while in \(\mathbb{Z}\) a bounded subset must be finite.
Recall that we have shown that given any \(a,b,c,d\in \mathbb{R}\) such that \(a<b\) and \(c<d\) there exists a bijection \(f:(a,b)\to (c,d)\). In particular if we take \(c=0,d=1\) we have that \(|(0,1)|=|(a,b)|\) for all \(a,b \in \mathbb{R}\) such that \(a<b\). No matter how “small” (length wise) we take \((a,b)\) to be, as a set it is extremely large, i.e. uncountable. If we combine this with the fact that if \(X\) is countable then \(X^n\) is countable for all \(n\in \mathbb{Z}_+\), we have strange results like “for any \(n\in\mathbb{Z}_+\), \(|\mathbb{Q}^n|<\left|\left(0,\frac1n\right)\right|\)”.
Since we have shown \(|\mathbb{Z}|<|\mathbb{R}|\), a natural question is “does there exists a set \(A\) such that \(|\mathbb{Z}|<A<|\mathbb{R}|\)”. This was one of the 23 problems set by Hilbert at the turn of the 20th Century, and is known as the continuum hypothesis. It turns out that this is a subtle question without a yes/no answer: G"odel and Cohen showed that the two statements “the continuum hypothesis is true” and “the continuum hypothesis is false” are both consistent with the standard (ZFC) axioms of mathematics.
11.3 Power sets
We finish this section by showing that there are infinitely many different types of infinities.
We have the following examples:
\(\mathcal{P}(\emptyset)=\{\emptyset\}\), so \(|\mathcal{P}(\emptyset)|=1\).
\(\mathcal{P}(\{1,2\})=\{\emptyset,\{1\},\{2\},\{1,2\}\},\) so \(|\mathcal{P}(\{1,2\})|=4=2^2\).
\(\mathcal{P}(\{1,2,3\})=\{\emptyset,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}\}.\) So \(|\mathcal{P}(\{1,2,3\})|=8=2^3\).
Note that, for any nonempty set \(X\), we know that \(\emptyset, X\) are distinct subsets of \(X\). Hence, we have that \(|\mathcal{P}(X)|\ge 2\). We have the following two results, whose proofs are left as an exercise.
Suppose that \(A\) is a finite set with \(|A|=n\) for some \(n\in\mathbb{Z}_{\geq 0}\). Then \(|\mathcal{P}(A)|=2^n\).
Exercise.
□
Let \(A,B\) be sets. Then
\(A\subseteq B\) if and only if \(\mathcal{P}(A)\subseteq\mathcal{P}(B).\)
\(\mathcal{P}(A)\cup\mathcal{P}(B)\subseteq\mathcal{P}(A\cup B)\).
\(\mathcal{P}(A)\cap\mathcal{P}(B)=\mathcal{P}(A\cap B).\)
Exercise.
□
Let \(X\) be a set. Then \(|X|<|\mathcal{P}(X)|.\)
Suppose \(X=\emptyset\). Then \(|X|=0<1=|\mathcal{P}(X)|.\)
So suppose \(X\) is nonempty, and define \(f:X\to\mathcal{P}(X)\) by \(f(x)=\{x\}\), for all \(x\in X\). We show that \(f\) is injective. Let \(x_1,x_2\in X\) be such that \(f(x_1)=f(x_2)\). Then \(\{x_1\}=\{x_2\}\). Hence, we have that \(x_1=x_2\). Therefore, \(f\) is injective, so \(|X|\le|\mathcal{P}(X)|.\)
Next, we use contradiction to show that there exists no bijection between \(X\) and \(\mathcal{P}(X)\). Suppose there exists such a bijection \(g:X\to\mathcal{P}(X).\) Note that for every \(x\in X\), \(g(x)\in \mathcal{P}(X)\) means \(g(x)\subseteq X\). Define \[A=\{x\in X: x\not\in g(x)\} .\] Then \(A\) is a subset of \(X\), so \(A\in\mathcal{P}(X).\) Furthermore, since \(g\) is bijective, there exists some \(z\in X\) such that \(g(z)=A\). By the definition of \(A\), we have \(z\in A\) if and only if \(z\not\in g(z)=A\), which is a contradiction (namely \(z\in A \iff z\not\in A\)). Therefore, our assumption that there exists a bijection \(g:X\to\mathcal{P}(X)\) is false. So \(|X|\neq |\mathcal{P}(X)|.\)
It follows that \(|X|<|\mathcal{P}(X)|.\)□
The above theorem is sometimes known as Cantor’s theorem. For a finite set, the result is clear, and Cantor re-used the diagonalisation method to prove the above for infinite set.
We have:
\(\mathcal{P}(\mathbb{Z}_+)\) is uncountable.
\(|\mathcal{P}(\mathbb{R})|>|\mathbb{R}|\), i.e. there are different type of uncountability.
We can extend on our last bullet point to see that \(|\mathbb{R}|<|\mathcal{P}(\mathbb{R})|<|\mathcal{P}(\mathcal{P}(\mathbb{R}))|<|\mathcal{P}(\mathcal{P}(\mathcal{P}(\mathbb{R})))|<....\), i.e. there are infinitely many different type of infinities.