5 Granger-okság tesztelése a magyar születési mutatók és különböző gazdasági-társadalmi változók között
A magyar születési mutatók és az ismert szakirodalom alapján a velük valamilyen kapcsolatban álló gazdasági-társadalmi indikátorok közötti összefüggések feltárását végzem el a következőkben. Amint azt a dolgozat elméleti megfontolásait tartalmazó fejezetében már kifejtettem érdemes mindhárom születési mutatóval elvégezni a vizsgálatot, miután eltérő eredményekre juthatunk a választás függvényében.
Miután előzetesen nem tartom kizártnak, hogy a vizsgált változók kölcsönösen hassanak egymásra (például a munkanélküliség befolyásolhatja a szülési hajlandóság, majd a szülési hajlandóság megemelkedése számos csatornán keresztül hatást fejthet ki a munkanélküliségre), így a vektor autoregresszív modelleket készítek, amelyeken Granger-oksági tesztekkel ellenőrzöm a kapcsolat fennállásának hipotézisét.
5.1 Alkalmazott módszertan általános bemutatása
Az ebben a fejezetben alkalmazott modellek első lépése, hogy készíteni kell egy vektor-autoregresszív modellt (VAR), amelyen oksági tesztet végzünk. A VAR-modellekben több idősor együttesen szerepel, és alapesetben valamennyien endogén változói a modellnek, tehát a mutatók egyes időpontokhoz tartozó értékei a modellben kerülnek meghatározásra és nem külsőleg kerülnek be. A modell elkészítéséhez a benne foglalt változók körén túl egy késleltetési paraméter (p) meghatározása szükséges. A modell tartalmilag egy olyan rendszer felépítését jelenti, ahol minden változó legutolsó p darab értékeinek sorozata hatással van saját magára és minden más változó tárgyévének meghatározására. Tehát a modellben minden változó t-edik évi értéke úgy határozódik meg, hogy az összes változó p évet visszamenő értékének hatásainak eredőjét vesszük. Fontos azt megjegyezni, hogy egy változó értékére t-edik évben nem lehet hatással más változók t-edik évi értéke14. A modell becslésnek azonban feltétele, hogy a bevont változók mind stacionerek legyenek, így előtte megfelelő számú differenciálással el kell érni.
Az így felállított modelleken hajtottam végre a Granger-oksági teszteket. A teszt nem más, mint egy F-próba melynek nullhipotézise, hogy a vizsgált okozati változóra a modell becslése alapján felírt egyenletben oksági tényezőként tesztelt változó minden késleltetett értékéhez tartozó paraméter értéke nem különbözik szignifikánsan a nullától. Granger-értelemben vett okság akkor áll fenn, ha ez a nullhipotézis elutasításra kerül, melynek interpretálása, hogy az eredményváltozóként tesztelt mutató jövőbeli értékére vonatkozóan csökken a bizonytalanság a magyarázó változó jelen, illetve múltbeli értékeinek ismeretében. A dolgozat eredményeinek megfelelően a helyen kezeléséhez szükséges hangsúlyozni, hogy a Granger-okság fennállása nem abban értelemben jelent kauzalitást, hogy a magyarázó változó valóban a kiváltó ok lenne a függő változó elváltozásában, csupán azt, hogy időben változása megelőzi azt, így előrejelzésében hasznosnak bizonyul. Ezzel azonban már meghaladja a korreláció interpretálhatóságát, miután az ok-okozati viszonyban betöltött szerepek identifikálhatóvá válnak.
Az így elvégzett F-próbák csak késleltetett hatások eredményének megítélésére alkalmasak. Az egyidejű Granger-okság fennállásának tesztelése azon alapul, hogy a modellben endogén módon meghatározódó idősorok valós értéküktől vett eltéréseik mutatnak-e együttmozgást. Ebből következik, hogy míg az általános Granger-okság feltárja a kauzalitás irányát, addig az egyidejű Granger-okság szimmetrikus. Mindazonáltal fennállása esetén elméleti megfontolásból az okozat szerepét nem nyilvánítanám a születési indikátorokra, mivel a fogantatásnak időben biztosan korábban kellett megtörténnie.
5.2 Az alkalmazott módszertan esetspecifikus tulajdonságainak bemutatása
Az teszt elvégzésének első lépése tehát az idősorok stacionerré alakítása megfelelő transzformációval. Amennyiben egy változó integráltságának foka kettő volt, azonban logdifferenciázott idősora stacioner, úgy a változó logdifferenciázott transzformációját használtam fel a modellek elkészítéséhez, az interpretálhatóság egyszerűsítése érdekében, illetőleg mivel ekkora az idősor hossza csak eggyel csökken, nem kettővel, ami a rövidebb idősorok esetében kritikus jelentőségű. A második lépés a modellben szerepeltetett változók körének megválasztása. A VAR-modellekkel kapcsolatosan általánosan az a gyakorlati probléma, hogy rengeteg paramétert tartalmaznak. Az együtthatók számára vonatkozóan korlátozásokat nem tartalmazó modellek előrejelzés tekintetében is rosszul teljesítenek, de a bennük keletkező magas mértékű multikollinearitás az értelmezést is bonyolítja, míg alacsony késleltetés mellett a paraméterek becslése torzítottá válik (Maddala, 2004). Mivel nem tartom kizártnak a vizsgált változóknak csak hosszú távon érvényesülő hatásuknak létét, így modelljeim elkészítése során egyszerre mindig csak az egyik születési indikátort, illetve csak az egyik gazdasági-társadalmi változót vonom be, szem előtt tartva, hogy ezzel a confounding15 problémájába futhatok bele. Minden esetben olyan vektor-autoregresszív modelleket alkalmaztam, melyek a magyarázóváltozókhoz tartozó paramétereken túl konstanst is tartalmaztak.
Harmadik lépés a késleltetés rendjének megfelelő megválasztása. Ez tradicionálisan valamely információs kritérium teljes modellen számított értéke alapján történik. Jelen dolgozatban mindegyik változó párosításra elkészítem az összes lehetéséges késleltetési struktúrával felírható VAR-modellt, majd ezek között szelektálok.
A következőkben az alábbi terminológiát szeretném alkalmazni: jelölje y modellben szereplő születési indikátor differenciázott idősorát, x a bevont társadalmi-gazdasági változó stacionerré transzformált idősorát, az ahhoz tartozó transzformáció jele legyen d, illetőleg p a VAR-modell késleltetésének rendje.
A lefuttattot modelleken szűrést hajtok végre. Adott p késleltetést y magyarázásának céljából relevánsnak tekintem az alábbi feltételek fennállása esetén: (1) a modellben endogén módon meghatározódó y reziduumaiból számított Akaike-féle információs kritérium16 p késleltetésig minimális, és (2) a p paraméterrel rendelkező VAR-modellben az x Granger-értelemben nem oka y-nak nullhipotézissel rendelkező F-próba ezen hipotézise 5%-os szignifikancia szinten elutasításra kerül. Ezzel analóg módon határozom meg x magyarázásához releváns késleltetéseket, tehát a modellben szereplő x hibatagiból számított AIC legyen az addig a késleltetésig előfordultak között a legkisebb és legyen ilyen késleltetés mellett y Granger-értelemben oka x-nek 5%-os szignifikanciaszinten. Az egyidejű okság fennállásáról döntést az alábbi módon határozom meg: a legnagyobb x magyarázásához vagy y magyarázásához relevánsnak tekintett késleltetési struktúra mellett a modellben meghatározódó y és x hibatagjainak együttmozgására vonatkozó teszt p-értéke amennyiben 5%-os szignifikancia szint alatt van úgy egyidejű Granger-okság meglétét állapítom meg. Az itt ismertetett módszertant a 11. ábrán egy példával szemléltetem. Az ábrán megjelenített eredmény értelmezéséhez fontos megjegyezni, hogy mivel a házasságkötések számának idősorának integráltsági foka egy, így differenciázott idősorát alkalmaztam a VAR-modellek előállításhoz, csak úgy, mint a teljes termékenységi arányszám esetében.
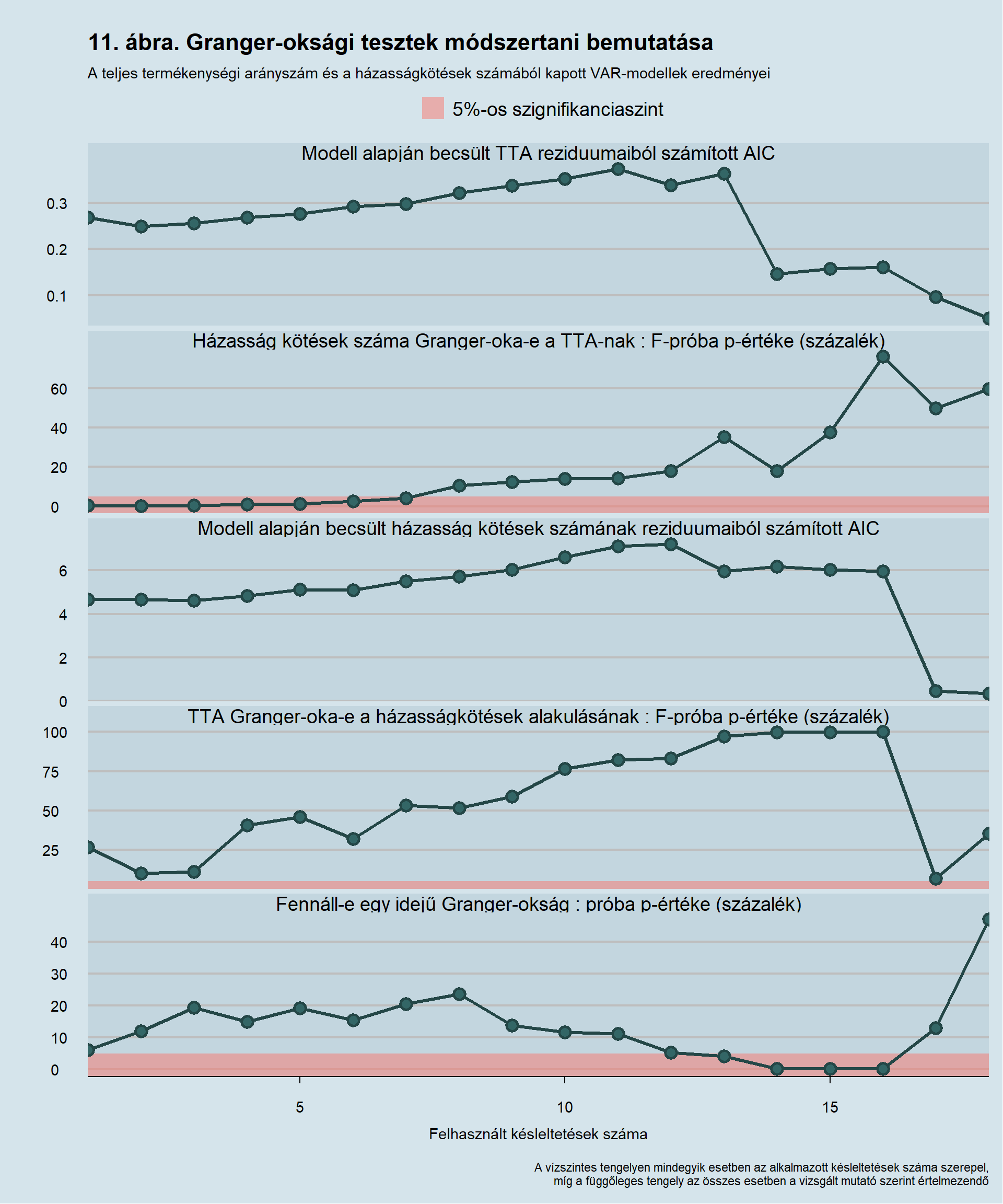
A 11. ábra eredményei alapján a házasságkötések száma Granger-értelemben oka a teljes termékenységi arányszámnak egy és kettő késleltetés mellett. Az itt ismertetett módszertani eljárás alapján más oksági kapcsolat nincsen ebben a párosításban. A 11. ábra utolsó blokkjának vízszintes tengelyén látható, hogy összesen 18 lehetséges késleltetési struktúra mellett kerültek VAR-modellek futtatásra. Ennek oka, hogy a vektor-autoregresszív modellek paramétereinek száma még két bevont változó esetén is néggyel nő minden egyes késleltetéssel és ezenfelül még két konstanst is tartalmat. Ismeretes, hogy lineáris modellek becslésének feltétele, hogy a megfigyelések száma meghaladja a becsült paraméterek számát. Ezért még a leghosszabb vizsgált idősorok esetén is (mind a házasságkötések számának, mind a teljes termékenységi arányszámnak közölt hiánytalan idősora 1960-ban indult) maximum 18 késleltetés mellett becsülhető a modell, de még olyankor sem érdemes komoly következtetéseket levonni belőle.
5.3 Modellbecslés és hipotézis vizsgálat
Az előbb bemutatott módszertan alapján a születési mutatókat az összes gazdasági-társadalmi indikátorral párosítottam és elvégeztem az oksági teszteket. Az eredményeket az 5-7. táblázat tartalmazza, míg az x változók pontos leírást a függelék F1, F2. F3 táblázata mutatja be.
| d | max p | x›y | x›y | x-y | |
|---|---|---|---|---|---|
| Activs | ld | 18 | 3 | ||
| NominalWage | ld | 18 | |||
| RealIncome | 1 | 18 | |||
| Consumption | 1 | 18 | 14, 15, 16, 17 | van | |
| GDP1960 | 1 | 18 | |||
| GDPCAP1960 | 1 | 18 | 1, 14 | van | |
| Saving | 1 | 6 | |||
| HouseholdDebt | ld | 6 | 3, 4 | ||
| PensionPublic | ld | 4 | |||
| FamilyBenefits | 1 | 4 | 1 | ||
| Marriage | 1 | 18 | 1, 2 | ||
| UnemploymentM | ld | 5 | 3 | ||
| UnemploymentT | ld | 5 | 3, 5 | 3 | van |
| UnemploymentW | ld | 5 | |||
| P90P10 | ld | 2 | 2 | ||
| PovertyRate017 | ld | 2 | |||
| PovertyRate66 | ld | 2 | |||
| PovertyRate1865 | ld | 2 | |||
| PovertyRateTot | ld | 2 | 2 | ||
| Gini | ld | 2 | 2 | ||
| MDeprivationT | 0 | 3 | |||
| MDeprivation018 | 0 | 3 | 3 | ||
| MDeprivation1865 | 0 | 3 | |||
| HousesTotal | 1 | 18 | 13 | ||
| HousesRate | 1 | 18 | 13 | ||
| CaesareanSections | ld | 3 | |||
| Crime | 1 | 16 | 16 | van | |
| CriminalYoung | 1 | 16 | 11 | ||
| CriminalAdult | 1 | 16 | 9, 11, 12, 13, 15 | 16 | van |
| CriminalTotal | 1 | 16 | 9, 11, 12, 13, 15 | van |
Megjegyzés: d: bevont gazdasági-társadalmi változón alkalmazott differenciázások száma (ld = logdifferenciázás); max p: maximális késleltetést tartalmazó VAR-modell, amely még megbecsülhető; x → y: a bevont gazdasági-társadalmi változó Granger-oka-e y-nak, és ha igen, akkor milyen késleltetési struktúrával rendelkező VAR-modellben; y → x: a bevont gazdasági-társadalmi változónak Granger-oka-e x, és ha igen, akkor milyen késleltetési struktúrával rendelkező VAR modellben; x-y: van-e egyidejű Granger-okság a két változó között.
| d | max p | x›y | y›x | x-y | |
|---|---|---|---|---|---|
| Activs | ld | 18 | 18 | van | |
| NominalWage | ld | 18 | 15 | ||
| RealIncome | 1 | 18 | |||
| Consumption | 1 | 18 | 18 | ||
| GDP1960 | 1 | 18 | 17, 18 | van | |
| GDPCAP1960 | 1 | 18 | 17 | van | |
| Saving | 1 | 6 | 6 | van | |
| HouseholdDebt | ld | 6 | 4 | ||
| PensionPublic | ld | 4 | |||
| FamilyBenefits | 1 | 4 | 3, 4 | ||
| Marriage | 1 | 18 | 1, 2, 12, 17 | ||
| UnemploymentM | ld | 5 | 3 | ||
| UnemploymentT | ld | 5 | 3, 4, 5 | van | |
| UnemploymentW | ld | 5 | |||
| P90P10 | ld | 2 | 2 | ||
| PovertyRate017 | ld | 2 | |||
| PovertyRate66 | ld | 2 | |||
| PovertyRate1865 | ld | 2 | |||
| PovertyRateTot | ld | 2 | 2 | ||
| Gini | ld | 2 | 2 | ||
| MDeprivationT | 0 | 3 | |||
| MDeprivation018 | 0 | 3 | |||
| MDeprivation1865 | 0 | 3 | |||
| HousesTotal | 1 | 18 | 2, 6, 13 | 1, 2 | |
| HousesRate | 1 | 18 | 2, 6, 13 | 1, 2 | |
| CaesareanSections | ld | 3 | |||
| Crime | 1 | 16 | |||
| CriminalYoung | 1 | 16 | 11, 12, 16 | van | |
| CriminalAdult | 1 | 16 | 9, 10, 11, 12, 13, 14, 15, 16 | van | |
| CriminalTotal | 1 | 16 | 9, 10, 11, 12, 13, 14, 15 |
Megjegyzés: a táblázat fejléceiben szereplő jelölések teljesen azonos tartalmat jelölnek, mint a 5. táblázatban.
| d | max p | x›y | y›x | x-y | |
|---|---|---|---|---|---|
| Activs | ld | 18 | 18 | van | |
| NominalWage | ld | 18 | 16 | ||
| RealIncome | 1 | 18 | |||
| Consumption | 1 | 18 | 17, 18 | ||
| GDP1960 | 1 | 18 | 18 | van | |
| GDPCAP1960 | 1 | 18 | 14 | van | |
| Saving | 1 | 6 | |||
| HouseholdDebt | ld | 6 | 3, 4 | ||
| PensionPublic | ld | 4 | |||
| FamilyBenefits | 1 | 4 | 3, 4 | ||
| Marriage | 1 | 18 | 1, 2, 12, 17 | 2 | |
| UnemploymentM | ld | 5 | 3 | ||
| UnemploymentT | ld | 5 | 3, 4, 5 | ||
| UnemploymentW | ld | 5 | 5 | ||
| P90P10 | ld | 2 | 2 | ||
| PovertyRate017 | ld | 2 | |||
| PovertyRate66 | ld | 2 | |||
| PovertyRate1865 | ld | 2 | |||
| PovertyRateTot | ld | 2 | 2 | ||
| Gini | ld | 2 | 2 | ||
| MDeprivationT | 0 | 3 | |||
| MDeprivation018 | 0 | 3 | |||
| MDeprivation1865 | 0 | 3 | |||
| HousesTotal | 1 | 18 | 2, 6, 13 | 1, 2 | |
| HousesRate | 1 | 18 | 2, 6, 13 | 1, 2 | |
| CaesareanSections | ld | 3 | |||
| Crime | 1 | 16 | |||
| CriminalYoung | 1 | 16 | 11, 12 | ||
| CriminalAdult | 1 | 16 | 9, 10, 11, 12, 13, 14, 15 | ||
| CriminalTotal | 1 | 16 | 9, 10, 11, 12, 13, 14, 15 | 15, 16 | van |
Megjegyzés: a táblázat fejléceiben szereplő jelölések teljesen azonos tartalmat jelölnek, mint a 5. táblázatban.
5.4 Az eredmények értelmezése és következtetések levonása
Az előzőekben közölt táblázatokban szereplő eredmények természetesen interpretálást igényelnek, illetve további vizsgálatot igényelnek. A vektor-autoregresszív modellek paramétereinek vizsgálata helyett az impulzus válaszfüggvényeket vetem elemzés alá azokon a helyeken, ahol szükséges. Az impulzus válaszfüggvény (IRF) azt mutatja be, hogy egy tárgyalt változónak a modellből származó reziduumainak szórásának egyenértékű sokk hatására miként reagál az egész rendszer, így a hatások előjele is megjelenítésre kerül.
A 5-7. táblázatok első néhány sorában a 20. századi natalizmus legfontosabb indokaihoz tartozó proxy változók találhatóak, nevezetesen, hogy szülessen minél több gyermek, akik dolgozni képesek, növelve a gazdaság méretét. Az évenkénti teljes születésszám és a gazdaságilag aktívak számának idősorából 18-as késleltetés mellett készített vektor-autoregresszív modellben a születésszám hatása tűnik ki az aktívak számának növekedési ütemére. A tesztek eredményeit azonban az értelmezések megkezdése előtt a VAR-modellek inverz gyökeinek ellenőrzésével kell megerősíteni. Ebben az esetben éppen azzal állunk szemben, hogy található egynél nagyobb gyök is a VAR (p=18) modellben, így a benne foglalt kapcsolat nem stabil. Amit esetleg érdemes megnézni az a VAR (18) modell becsült egyenletei. Az aktívak számára megbecsült egyenletben szereplő születésszám késleltetett értékeihez tartozó koefficiensek értékét a 7. tábláztat ismerteti.
| Késleltetések száma | Béta |
|---|---|
| 1 | -4.1e-06 |
| 2 | -4.4e-06 |
| 3 | -5.0e-07 |
| 4 | -4.0e-06 |
| 5 | -1.8e-06 |
| 6 | -4.9e-06 |
| 7 | -6.0e-07 |
| 8 | -6.0e-07 |
| 9 | -1.6e-06 |
| 10 | -2.9e-06 |
| 11 | -7.0e-07 |
| 12 | -8.0e-07 |
| 13 | -1.7e-06 |
| 14 | -3.0e-06 |
| 15 | -6.0e-07 |
| 16 | -1.2e-06 |
| 17 | -2.0e-07 |
| 18 | -5.0e-06 |
A 8. táblázatban látható eredményekből nem szabad azonban azt a következtetést levonni, hogy a születendő gyermekek számának növekedése egyértelműen csökkenti a gazdaságilag aktívak számát. Ezek a paraméterek ugyanis bár mind negatívak, 0-hoz nagyon közeliek, továbbá mivel a kapcsolat nem stabil értékei torzítottak lehetnek. Ebből sokkal inkább arra érdemes csupán következtetni, hogy a születések száma mértékében nem akkora, hogy annak változása valóban érezhető legyen a gazdaságilag aktívak számában, mivel semmilyen kisebb késleltetési struktúra mellett nem találtunk Granger-okságot, ez pedig nem értelmezett. Ily módon a natalizmus azon indoka, hogy a születésszám növelésével növelhető a gazdaság mérete bár nem cáfolandó, de feltehetőleg a munkaerőpiac más gazdasági tényezőin keresztül hatékonyabb eredmény érhető el. Legalábbis az ezen modellel vizsgálható 18 éves időintervallumban bizonyosan.
A következő eredmény, amit ki szeretnék emelni a fogyasztás hatása a születésszámra. Ahogyan az a 5-7. táblázatokban olvasható, a fogyasztás 1960-as bázisviszonyszámának differenciázott értékéből becsültem a vektor-autoregresszív modelleket és a 17-18-as késleltetés mellett találtam releváns hatást. Bár a gazdasági-társadalmi indikátorok születési mutatóra gyakorolt hatását érdemes volna a teljes termékenységi ráta alapján értékelni, megtisztítva így a hatásmechanizmust, én most a teljes születési mutatón prezentálom, a befogadható interpretáció céljából. Továbbá szeretném bevezetni a kumulált impulzus válaszfüggvény (CIRF) fogalmát, mely az IRF kumulált értékeit tartalmazza. A fogyasztásban bekövetkező sokk lecsapódását mutatja be a 12. ábra. A VAR-modellben alkalmazott késleltetések száma 17.
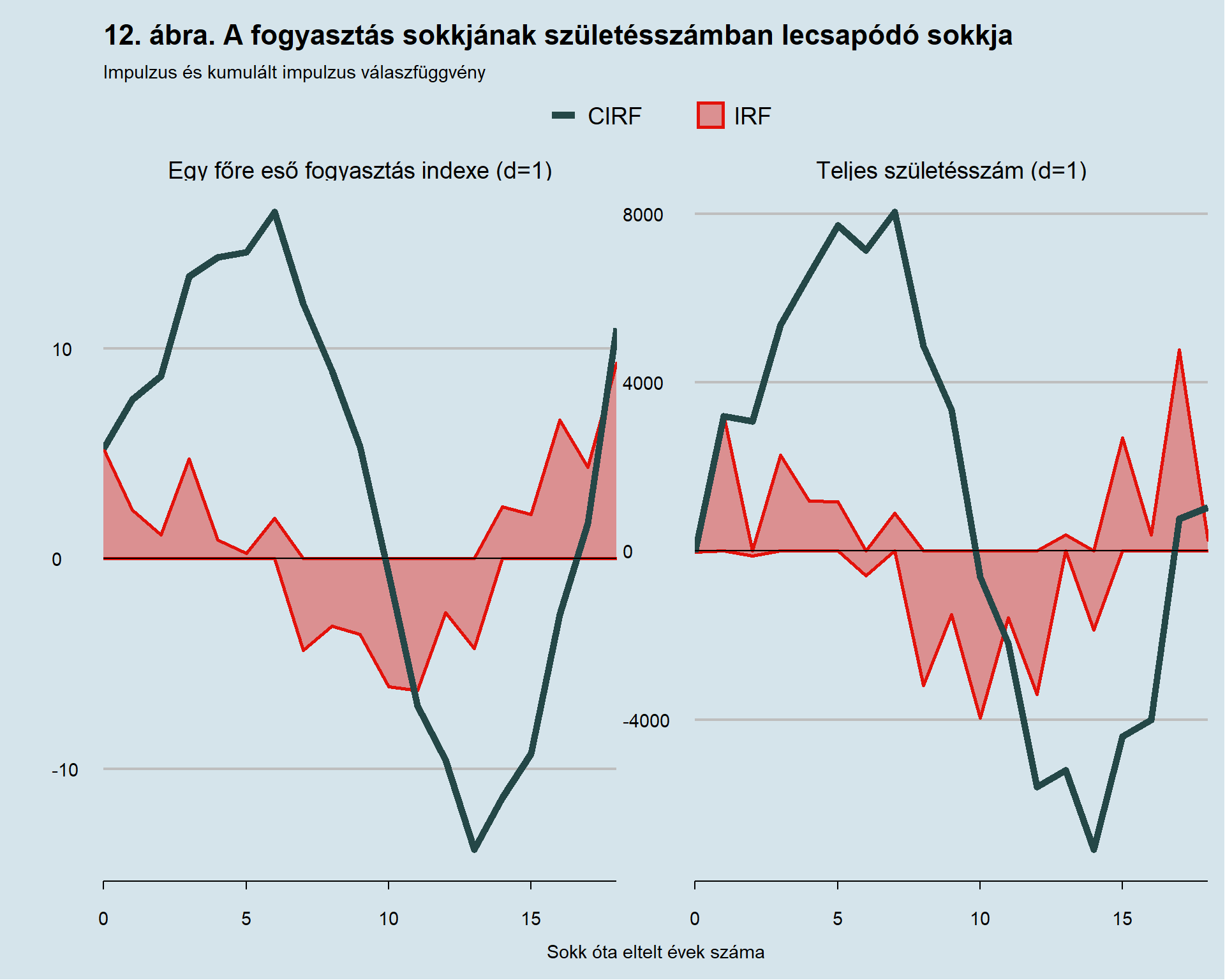
A 12. ábrán az látszik, hogy a teljes születésszám növekménytagja követi a fogyasztás indexének növekménytagját a modell által becsült rendszerben. A termékenységi ráta helyett az évenkénti összes születésszám felhasználása mellett azért döntöttem, mert így a születésszámnál látott CIRF a bekövetkezett sokk, illetőleg annak lecsengésének hatása a születendő gyermekek számára nettó mértékben értelmezhető. A 12. ábrán az impulzus válaszfüggvények ciklikus mivoltát nem kívánom megragadni, így az ábrán látható eredményeknek a sokkot követően 6. évig terjedő intervallumára kívánok fókuszálni, amíg a fogyasztás indexének növekménytagjához tartozó kumulált impulzus válaszfüggvény monoton növekvő. Ezen a ponton a fogyasztás indexének differenciázott értékéhez tartozó CIRF értéke 16,50, míg a teljes születésszám növekménytagjának CIRF értéke 7135,45. Kihasználva, hogy bázisviszonyszámok időben vett relatív növekedésinek sorozata láncviszonyszám, meghatározható17, hogy átlagosan évi 2,5 százalékponttal nagyobb növekedés a fogyasztásban 7135,45-tel eredményez több gyermeket 6 év alatt (2018-ben összesen 89807 gyermek született, így ez egy egészen magas hatásnak nyilvánítható). A GDP-re kivetítve nem kívánom külön elvégezni az értelemzést, mivel az már eleve tartalmazza a fogyasztást.
A háztartások adósságállományának változása mind a termékenységi arányszám, mind a teljes évenkénti születésszám esetében relevánsnak mutatkozott 3, illetve 4 késleltetés mellett, mint következmény. Jelen esetben a termékenységi arányszámban bekövetkező sokk hatását kívánom bemutatni, mivel a népesség teljes számára mindkét indikátort robosztusnak tekintem. A TTA sokkjának hatását a 13. ábrán prezentálom.
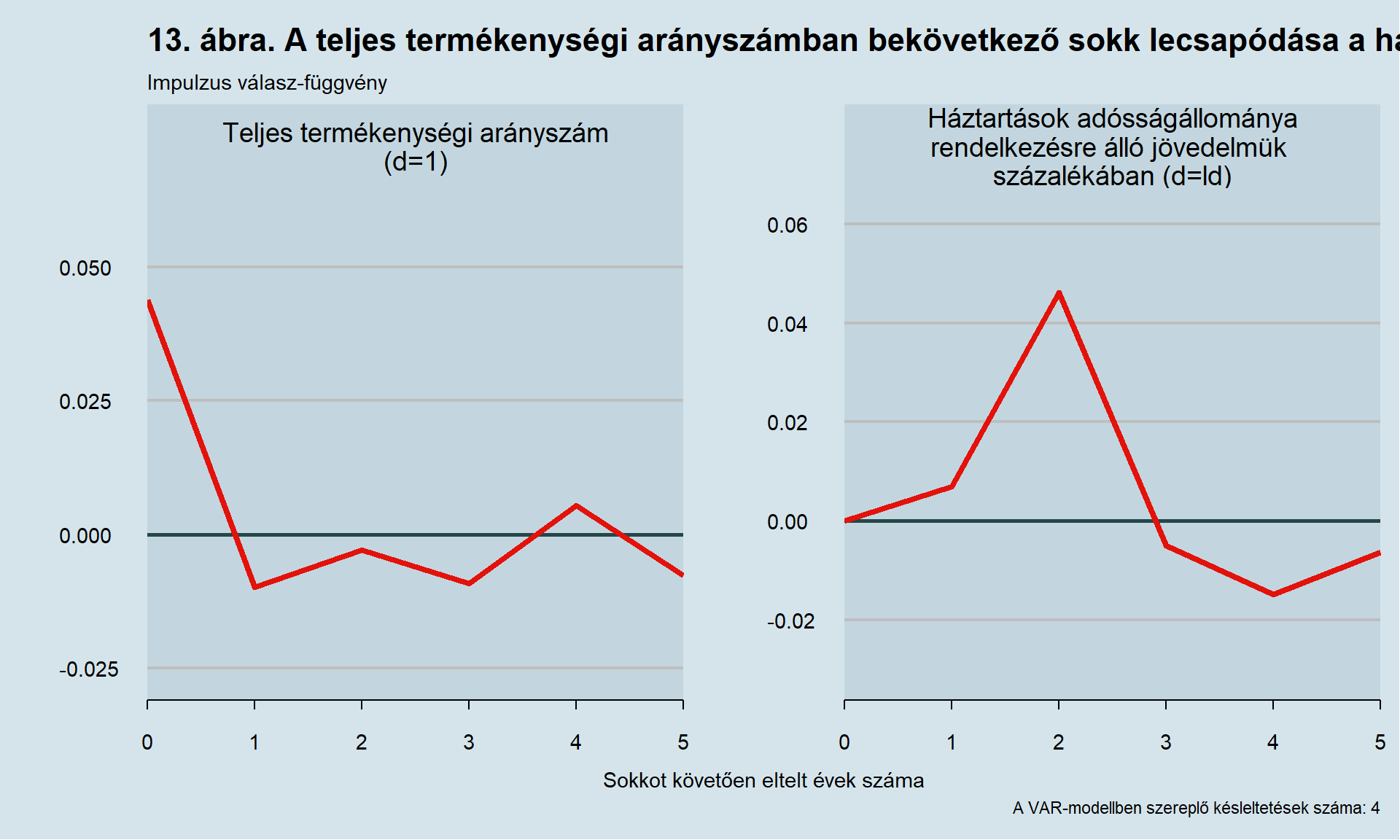
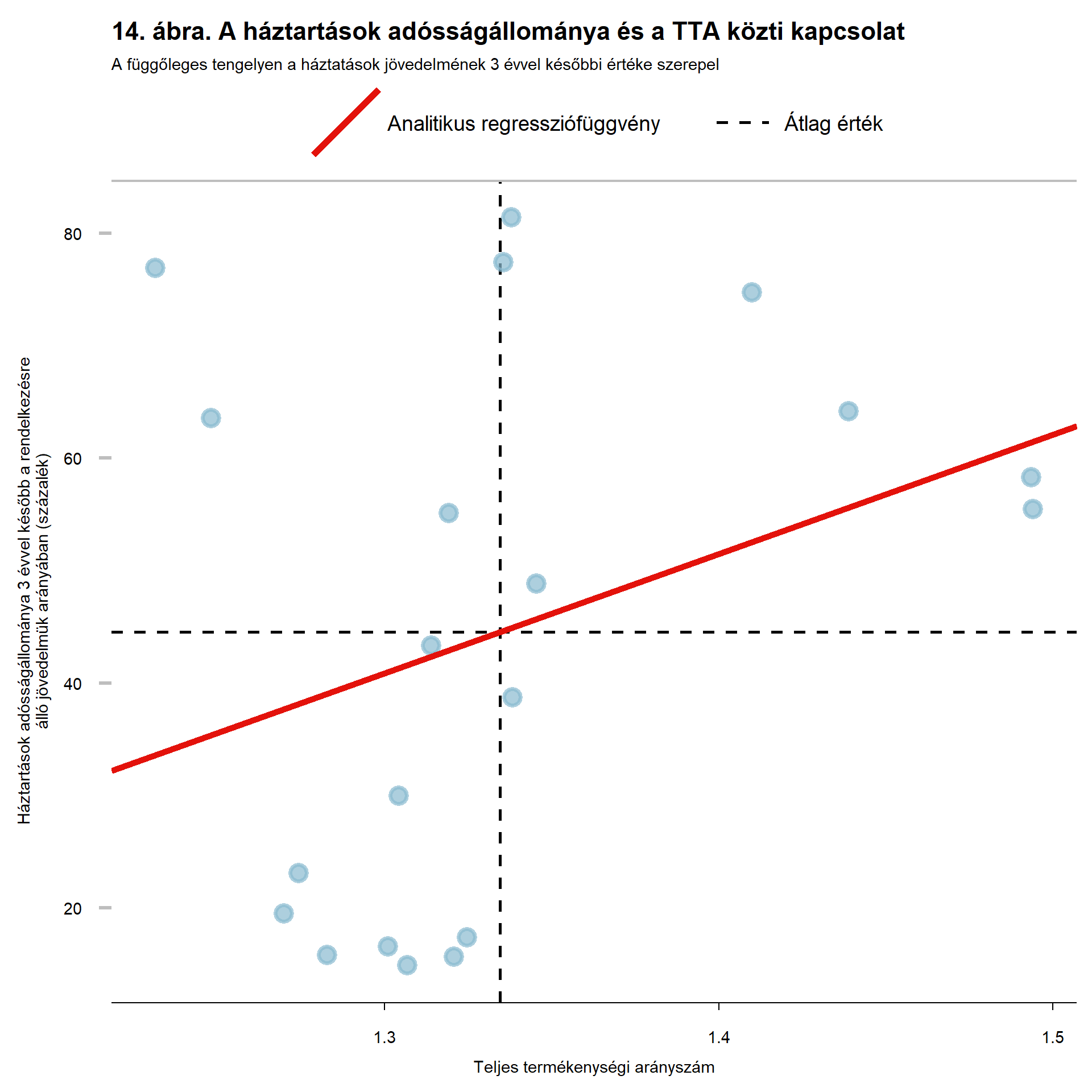
A 13. ábrán az látszik, hogy míg a sokk bekövetkezését követően a háztartások adósságállománya megemelkedett, a TTA növekedésének hirtelen mérséklődése után csökkenésnek indult, de mindezt késéssel. A 14. ábrának vízszintes tengelyére a teljes termékenységi arányszámot, míg függőleges tengelyére a háztartások elérhető jövedelmük arányában mért adósságállományuk három évvel későbbi értékét tüntettem fel, ezzel bemutatva, hogy valóban látszik arra tendencia, hogy késve ugyan, de az adósságállomány emelkedik a termékenységi arányszám növekedésével.
Annak hipotézise, hogy az állam által fizetett nyugdíjak GDP százalékában mért mértéke és a születési indikátor között bármilyen kapcsolat is fennállna ebben az elemzésben elutasításra került. Nem látszódik nyoma annak, hogy a termékenységi ráta változása az elmúlt évtizedekben érdemben befolyásolta volna a nyugdíjak mértékét, vagy fordítva. Mivel ez a hipotézis távol-keleti fejlődő országok mintájára lett megfogalmazva, így ez nem is túl meglepő.
A családtámogatások mértéke egy késleltetés mellet releváns a TTA-ra nézve, azonban semelyik másik születési indikátorra. Ehhez fontos megjegyezni, hogy a családtámogatások mértéke a GDP százalékában kifejezve idősor első értéke 1999, így csak az elmúlt két évtized alakulására alapul a modell, amikor is a három születési indikátor valóban már távolodásnak indult egymástól, ahogyan az az 1. ábrán látszik, így az eltérő eredmény logikus. Ami viszont meglepő, hogy a családtámogatások mértéken előjele ebben a VAR (p=1) modellben negatív, egészen pontosan -0,16. Ez azonban tekintetbe véve, hogy a GDP százalékának értékében kifejezett növekménytagról van szó továbbra is alacsony érték, de negatív.
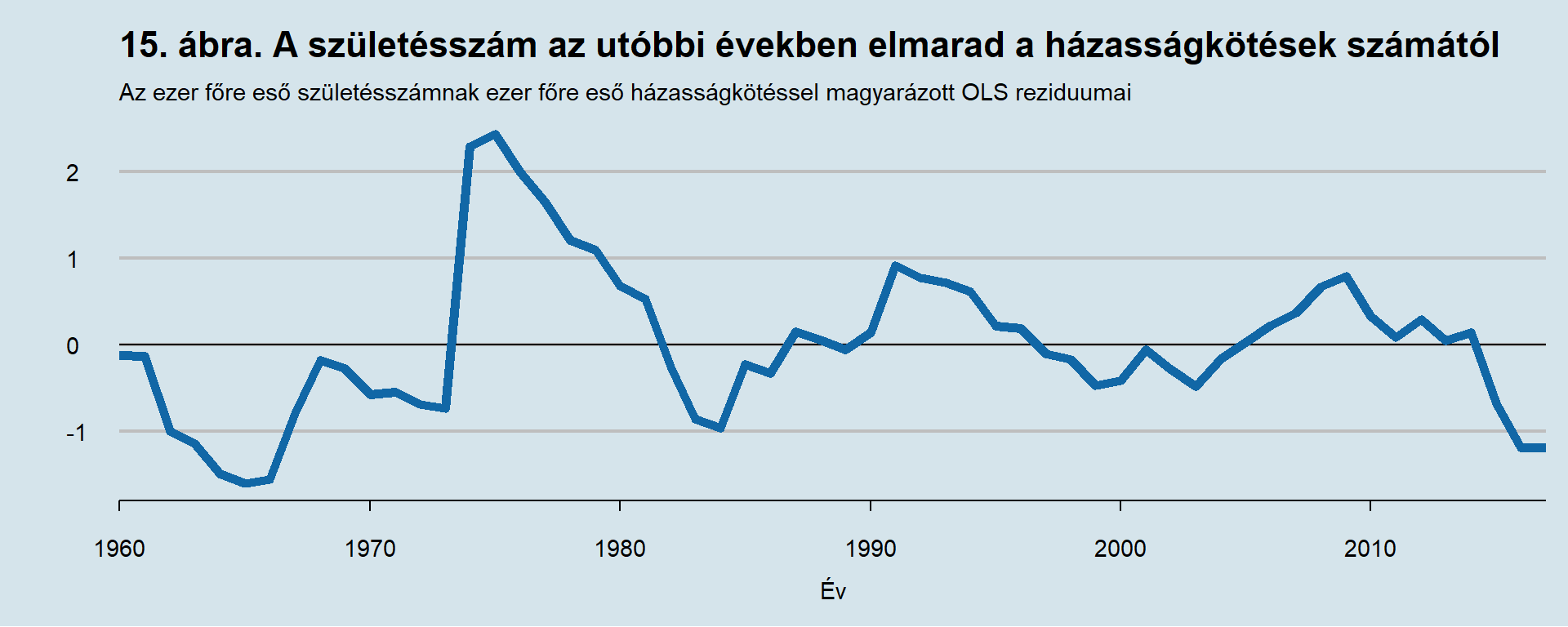
A házasságkötések számának alakulása számos késleltetési struktúra mellett releváns. Mivel ez is 1000 főre eső értékben kifejezve található meg a KSH honlapján, így a könnyű interpretáció érdekében az ezer főre eső születésszámmal párosított VAR (p=17) modellt vizsgáltam meg részletesen. Az impulzus válaszfüggvények olyannyira együtt mozognak, hogy azok bemutatása helyett érdemesnek gondoltam inkább kointegrációs tesztet futtatni és bemutatni annak az eredményét. A korábbi fejezetben leírt tesztekkel teljesen azonosan jártam el, a Granger-okság tesztelése után ismeretes, hogy a két idősor integráltságának foka megegyezik, így a teszt elvégezhető. A házasságkötések számát használtam fel regresszornak és a modell kimentett hibatagja valóban stacioner, tehát a házasságkötések száma és a születésszám között fennáll hosszú távú kapcsolat. A 15. ábrán az OLS hibatagját jelenítem meg, melyen látszik, hogy az ezer főre eső születésszám az utolsó évtizedben növekedni kezdett az ezer főre eső házasságkötések számából adódó egyensúlyi értékéhez képest.
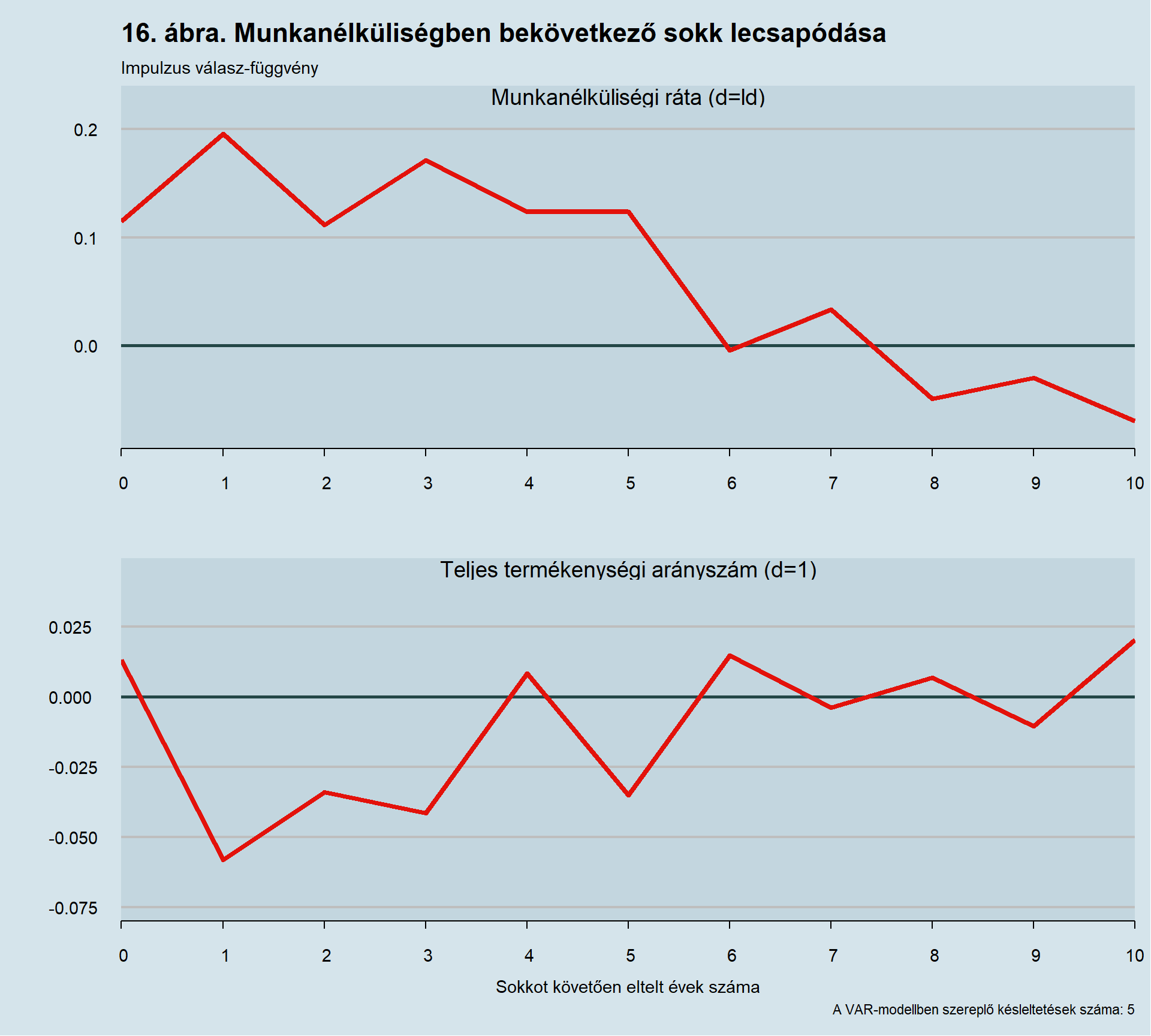
A munkanélküliségnek az eltérő mutatókon való futása eltérő eredményeket eredményezett. Ennek oka, ahogyan azt Kornai János is írja, hogy a szocialista rendszer leváltása után még a munkanélküliek nyilvántartásához szükséges intézmények sem állnak fenn (Kornai, 2012). Így a munkanélküliségről szóló idősorok mindössze 1999-ben indulnak és ahogyan az az 1. ábrán látható az utolsó évtizedben eltávolodásnak indul egymástól a három születési indikátor.
A kihagyott változó okozat lehetséges torzítás elkerüléséért az 5-ös késleltetésű VAR-modellt vizsgálom meg. Az impulzus válaszfüggvények a 16. ábrán láthatók, amin látható, hogy a munkanélküliség és a termékenységi arányszám között negatív irányú kapcsolat áll fenn.
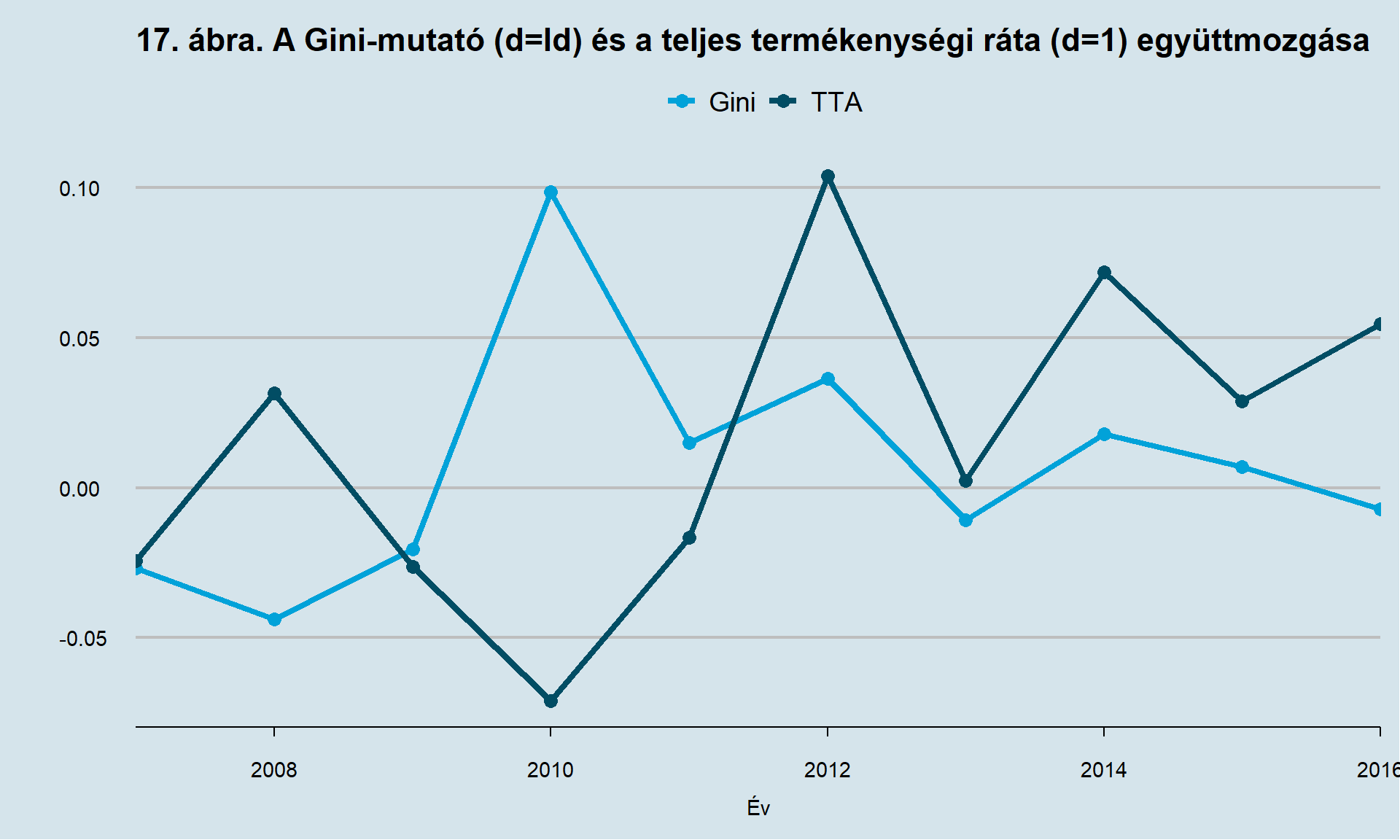
Az egyenlőtlenség é szegénység indikátorait a Gini-mutató előzetesen tesztelése során relevánsnak mutatkozása okán emeltem be az elemzésbe. Ebben az esetben az idősorok még a munkanélküliségi statisztikákénál is rövidebbel hasonló okok miatt, így mindössze 1, 2, illetve 3 késleltetés mellett van lehetőség modellt futtatni rajtuk. Bár több esetben releváns magyarázatnak bizonyulnak érdemes szem előtt tartani, hogy csak a legutolsó évek megfigyelései, mind a tesztek eredményei erősségei nagyon gyengék, mind a hamis regresszió gyanúja erős. A pozitív irányú kapcsolat fennállásának lehetőségét a 17. ábra szemlélteti. Sajnálatos módon ennyire rövid idősorok közötti együttmozgásból a gyanún túl nem lehet többet mondani, illetve mivel nem kerül rögzítésre az anya jövedelmi helyzete a gyermek világra hozatalakor, így olyan adatbázis sem elérhető, amelyből ezzel a hipotézissel kapcsolatban többet lehetne állítani.
A császármetszések számával kapcsolatban szintén elmondható, hogy Granger-értelemben semmilyen oksági kapcsolat nem állapítható meg, így az erre megfogalmazott hipotézis elvetésre kerül, bár itt is meg kell jegyezni, hogy nagyon rövid az elérhető idősor hossza.
A bűnözési statisztikákkal kapcsolatosan pedig éppen ellentétes irányú Granger-okság beazonosítására került sor, mint ahogyan a hipotézisben fel lett állítva. Miután a bűnelkövetők száma főben van megadva, illetőleg az évenkénti összes születésszámmal 16-os késleltetés mellett oda-vissza hatás látható, így ennek a modellnek a részleteit elemzem elsőként. Mindazonáltal ebben a modellben az inverz gyökök értékei között találni egynél nagyobbat, ami a kapcsolat instabilságára utal, így a 16-os késleltetéssel rendelkező modell helyett a 12-eset közlöm, ahol már rendben van ez a stabilitási feltétel. Ennek a modellnek az impulzus függvényeit tartalmazza a 18. ábra.
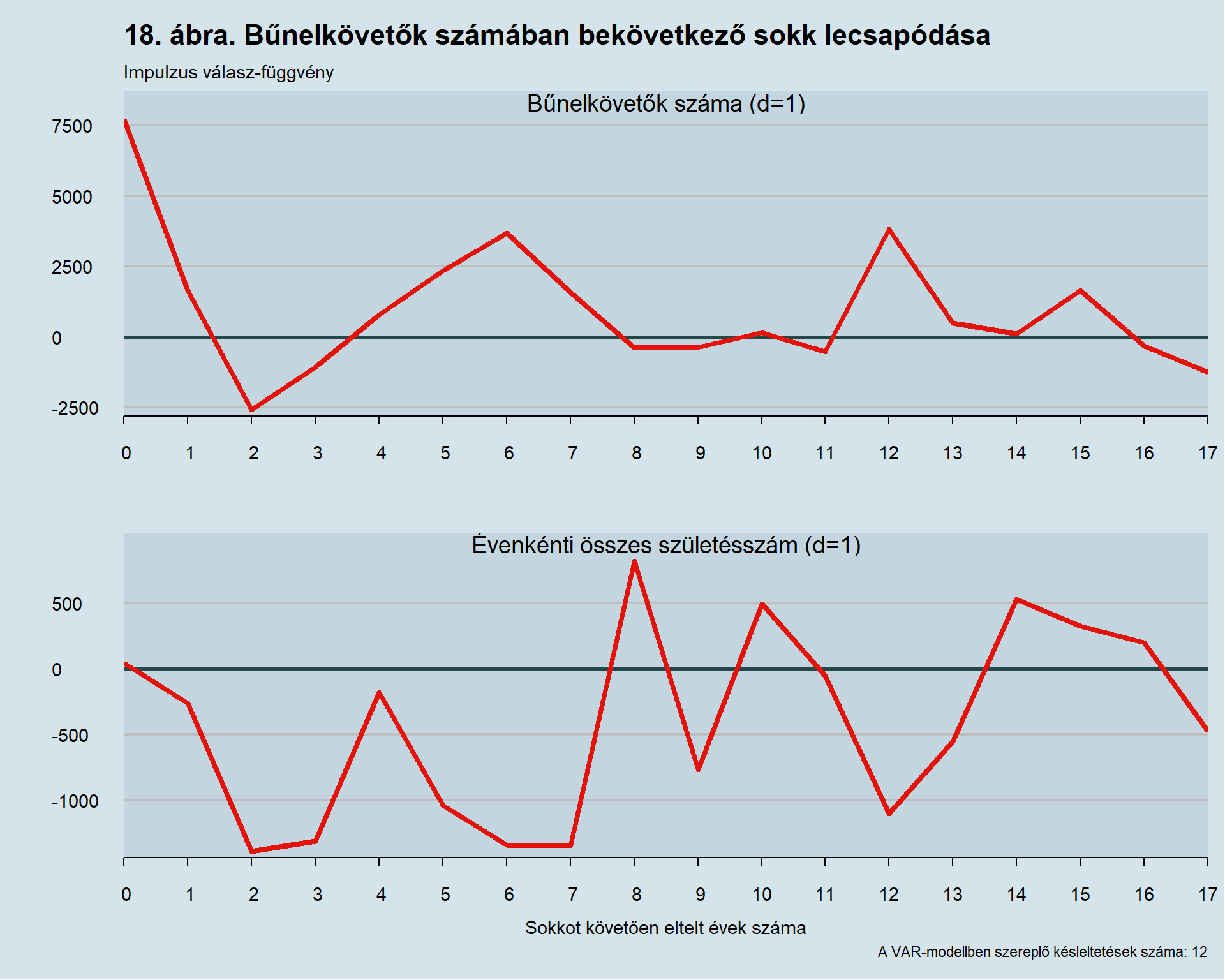
A 18. ábrán megjelenített rendszer értelmezéséből zajosan tűnik, hogy pontosan hogyan is hat a bűnelkövetők száma a születésszámra. Ennek egyszerűsítésének céljából kiszámítottam, hogy a modellben a születések számára becsült egyenletben a bűnözők számának késleltetett értékeihez tartozó paraméterek összege -0,43, tehát végeredményben a bűnözők számának növekedése a születésszám csökkenésének előrejelzője. Fontos továbbra is hangsúlyozni, hogy a Granger-okság pusztán időbeni megelőzést jelent, amely alapján a jövőre vonatkozó bizonytalanság csökkenthető, az, hogy ez milyen csatornákon keresztül valósul meg, az ezekkel a tesztekkel és eredményekkel nem tűnik ki. Mindazonáltal az eredetileg feltett hipotézis vektor-autoregresszív modellek segítségével nem tesztelhető, mert a maximális késleltetési szám azt nem teszi lehetővé.
5.4.1 A modellek korlátai
Ahogyan azt a VAR modellek módszertanánál is ismertettem ezen elemzés egyik legfontosabb problémája, hogy a modellek számos együtthatót tartalmaznak, ami jelentősen bekorlátozza a segítségükkel vizsgálható időintervallum terjedelmét. Még a Magyarországra elérhető legkorábbra visszamenő statisztikák esetében is mindössze 16 év késleltetetten jelentkező hatásainak vizsgálatára van lehetőség. Hazánk esetében pedig az ilyen 1960-ig visszamenő idősoroknak meglehetősen híján vagyunk.
5.4.2 Az eredmények lehetséges kiterjesztése
Három fontos eredményt tartok kiemelni, mely napjainkban a gazdasági folyamatainak megítélése szempontjából kulcstényezővé válhatnak. A születési indikátorok alakulását döntő mértékben befolyásolja a fogyasztás és a munkanélküliség alakulása. Napjainkban a COVID-19 terjedése okán bevezetett rendelkezések valószínűsíthetően csökkenteni fogják az elmúlt évek gazdasági növekedését, felemelik a munkanélküliség szintjét. Jelen tanulmány írásakor a Federal Reserve Bank of St Louis nyilatkozataiban nem tartja kizártnak a munkanélküliségnek akár 30%-ra való felugrását (The Economist, 2020, c). Az általam végzett számítások alapján a munkanélküliségi ráta 0,2%-os változása okoz 0,05 egységnyi csökkenést a termékenységi arányszámban. Egy ilyen drasztikus munkanélküliség bekövetkezése tehát elképzelhetetlen csökkenését okozná a születésszámnak. Az előző eredmény egyszerű felszorzása alapján körülbelül 2,5 egységgel csökkentené a termékenységi arányszámot, ami nyilván egy nem értelmezhető eredmény nem is állítom, hogy ez így alakulna, a modell a „betanulása” során egyszer sem találkozhatott a munkanélküliség hirtelen 10-szeresére ugrásával.
Hasonlóan elmondható ez a fogyasztás előrejelzésén. A The Economist legutolsó előrejelzése szerint nem kizárt a GDP 9%-os esése 2020-ban az Euro övezetben (The Economist, 2020, a). Amennyiben a GDP felhasználási oldalról való megközelítés értelmében nem történik szerkezeti átalakulás, tehát a fogyasztás is 9%-kal esne, úgy a következő 6 év alatt jelentheti 15.000 gyermek megszületésének elmaradását is. Ez pedig a napjainkban a nyugdíjrendszer fenntarthatóságához köthető diskurzusnak is csak egy újabb impulzust jelentene. Ezentúl meg kell jegyezni, hogy az egészségügyi, illetve oktatási rendszerben szereplők fluktúációja is a koronavírus járvány okozta válság hozadéka lehet az elkövetkezendő években. Bár ennek az ellenkezőjét feltételezi előrejelzések azon halmaza, mely egy következő „baby-boomot” vetít előre a kijárási korlátozások bevezetéséből fakadóan (The Economist, 2020. április 2).
Ennek a szimultaneitás problémájának modellezési vonzata az oka, termesztésen elképzelhető olyan eset, hogy a születésszám hirtelen megugrása egy gazdasági vagy társadalmi mutatót már a tárgyalt évben befolyásol. Ennek vizsgálati módszerét a későbbiekben fejtem ki.↩
Az „egybemosódás” problémája, azaz elképzelhető, hogy a magyarázó változó azért, tűnik okának az eredményváltozónak, mert van egy harmadik változó, amely mindkettőnek oka.↩
Mivel VAR-modellek egyenleteire vonatkozó AIC mutatót ismereteim szerint semmilyen szoftver nem közöl, így ezeknek számítása az egyenletek hibatagjainak lekérése után az 𝑅𝑆𝑆𝑝×exp[(𝑘𝑝+1)/𝑛] képlet alapján történt, ahol 𝑅𝑆𝑆𝑝 a p késleltetést tartalmazó modell hibatagjaink négyzetösszege, 𝑘𝑝 pedig a p késleltetést tartalmazó modellben az y változóra felírt egyenletben szereplő együtthatók száma és n az idősor hossza.↩
(((16,50+100)/100)^1/6−1)×100↩