Capítulo 6 Clustering
En apartados anteriores hemos vimos cómo clasificar objetos en función de alguna característica de interés (por ejemplo, discriminar los clientes susceptibles de ser morosos de los que no). Ese tipo de tareas se denominan de segmentación «supervisada» porque, de entrada, ya tenemos una variable (en este caso la «morosidad») en función de la cual queremos clasificar los objetos.
En otras ocasiones quizá queramos encontrar grupos (por ejemplo, grupos de clientes), sin ninguna característica predefinida. Es decir, ¿pueden dividirse los clientes de manera natural en diversos grupos? Esta idea de agrupar los datos en categorías «no supervisadas» se denomina clustering. Existen dos métodos de clustering:
Jerárquicos:
Aglomerativos (bottom up): construyen los grupos por agregación a partir de los individuos considerados uno a uno.
Disociativos (top down): parten del conjunto total de individuos y los dividen en grupos más pequeños.
No jerárquicos: formación de nuevos clústers fusionando o dividiendo los existentes sin seguir un orden jerárquico. Por ejemplo, k-means.
6.1 Clustering jerárquico
La tabla 6.1 muestra la frecuencia en la adquisición de cuatro productos por parte de cinco clientes. Utilizando esta información vamos a intentar crear segmentos de clientes que tengan un comportamiento similar.
| Producto_1 | Producto_2 | Producto_3 | Producto_4 | |
|---|---|---|---|---|
| Cliente_1 | 2 | 3 | 4 | 6 |
| Cliente_2 | 1 | 3 | 5 | 4 |
| Cliente_3 | 5 | 6 | 4 | 6 |
| Cliente_4 | 8 | 8 | 9 | 9 |
| Cliente_5 | 7 | 9 | 8 | 8 |
A partir de la tabla de datos, calculamos la distancia entre todos los pares de individuos utilizando la distancia euclidiana.
\[d(X, Y) = \sqrt{(X_{b} - X_{a})^2 + (Y_{b} - Y_{a})^2}\]
Por ejemplo, la distancia entre los clientes 1 y 2 será la siguiente:
\[d(C_{1}, C_{2}) = \sqrt{(2 - 1)^2 + (3 - 3)^2 + (4 - 5)^2 + (6 - 4)^2} = \sqrt{6} = 2,45\]
El resultado se muestra en una matriz simétrica.
data_dist = dist(data, method = "euclidean")
data_dist## Cliente_1 Cliente_2 Cliente_3 Cliente_4
## Cliente_2 2.449490
## Cliente_3 4.242641 5.477226
## Cliente_4 9.746794 10.723805 6.855655
## Cliente_5 9.000000 9.848858 5.744563 2.000000La distancia más reducida es la existente entre los clientes 4 y 5, que conforman el primer cluster con una distancia entre ellos de 2.
Figure 6.1: Primer cluster
Ahora hemos de recalcular la tabla de distancias. Las distancias entre los clientes 1, 2 y 3 continúan siendo las mismas, pero hemos de determinar la distancia entre estos clientes y el cluster {4,5}. Hay diversas maneras de hacerlo. Una forma es la denominada single link o nearest neigbor, según la cual elegimos la distancia al elemento más cercano dentro del cluster. Por ejemplo, la distancia entre el cliente 1 y el cluster {4,5} será de 9, la distancia que había entre los clientes 1 y 5, porque la distancia entre los clientes 1 y 4 era mayor, de 9,7.
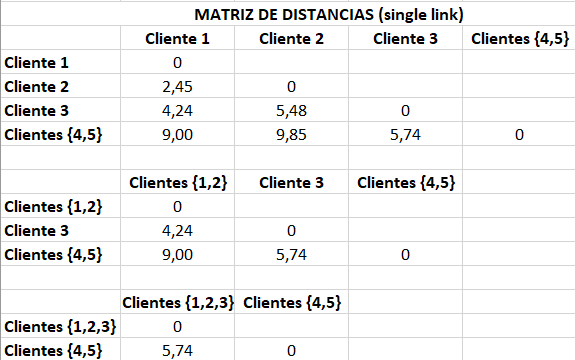
Figure 6.2: Matrices de distancias
La gráfica muestra los sucesivos recalculos de las distancias hasta agrupar a todos los clientes. El código para hacerlo con R y generar el dendograma es el siguiente.
cluster_clients = hclust(data_dist, method="single")
plot(cluster_clients, hang=-1)
Veamos un segundo ejemplo. En este caso utilizaremos un dataset que viene en R con datos de delicuencia en Estados Unidos.
data("USArrests")
summary(USArrests)## Murder Assault UrbanPop Rape
## Min. : 0.800 Min. : 45.0 Min. :32.00 Min. : 7.30
## 1st Qu.: 4.075 1st Qu.:109.0 1st Qu.:54.50 1st Qu.:15.07
## Median : 7.250 Median :159.0 Median :66.00 Median :20.10
## Mean : 7.788 Mean :170.8 Mean :65.54 Mean :21.23
## 3rd Qu.:11.250 3rd Qu.:249.0 3rd Qu.:77.75 3rd Qu.:26.18
## Max. :17.400 Max. :337.0 Max. :91.00 Max. :46.00Generamos un dendrograma jerárquico aglomerativo con método de agrupación average. En este caso la distancia de un individuo a un cluster no es la distancia al individuo más cercano, sino la distancia media a todos los miembros del cluster. A diferencia del ejemplo anterior, en este caso no hemos calculado las distancias por separado, sino que todo el proceso está agrupado en una única función.
crim <- hclust(dist(USArrests), "average")
plot(crim, hang=-1)
Veamos, por ejemplo, los datos de Iowa y New Hampshire que aparecen como dos estados muy similares en la parte derecha del dendrograma.
## Murder Assault UrbanPop Rape
## Iowa 2.2 56 57 11.3
## New Hampshire 2.1 57 56 9.5O los datos de Illinois y New York, que también aparecen como estados similares.
## Murder Assault UrbanPop Rape
## Illinois 10.4 249 83 24.0
## New York 11.1 254 86 26.1Dividimos el dendrograma en cuatro clusters y los marcamos en color rojo.
plot(crim)
rect.hclust(crim, k = 4, border = "red")
6.2 Clustering no jerárquico (k-means)
Veremos un ejemplo de creación de clusters no jerárquicos con el método k-means. Utilizaremos el paquete cluster sobre un dataset disponible en R.
library(cluster) # Llamamos al paquete
data(ruspini) # Descargamos los datos
plot(ruspini) # Representamos los datos en un diagrama de dispersión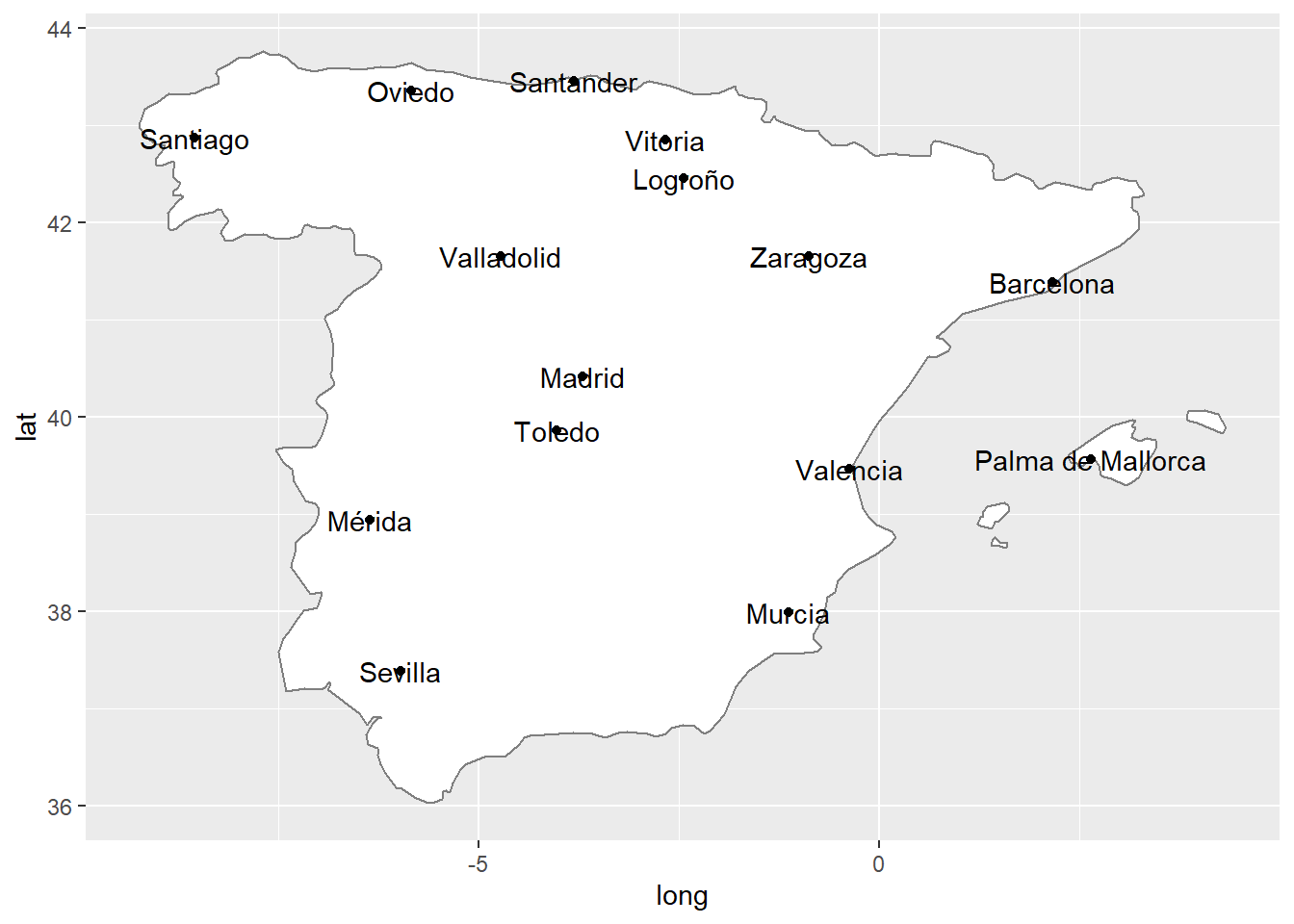
set.seed(7) # Inicio aleatorio
k <- kmeans(ruspini, centers = 4) # Creamos 4 clusters (podemos optar por otra cantidad)
g1 <- plot(ruspini, col = k$cluster) # Representamos los clusters con diversos colores
points(k$centers, cex=2, col=11, pch=19) # Representamos los centroides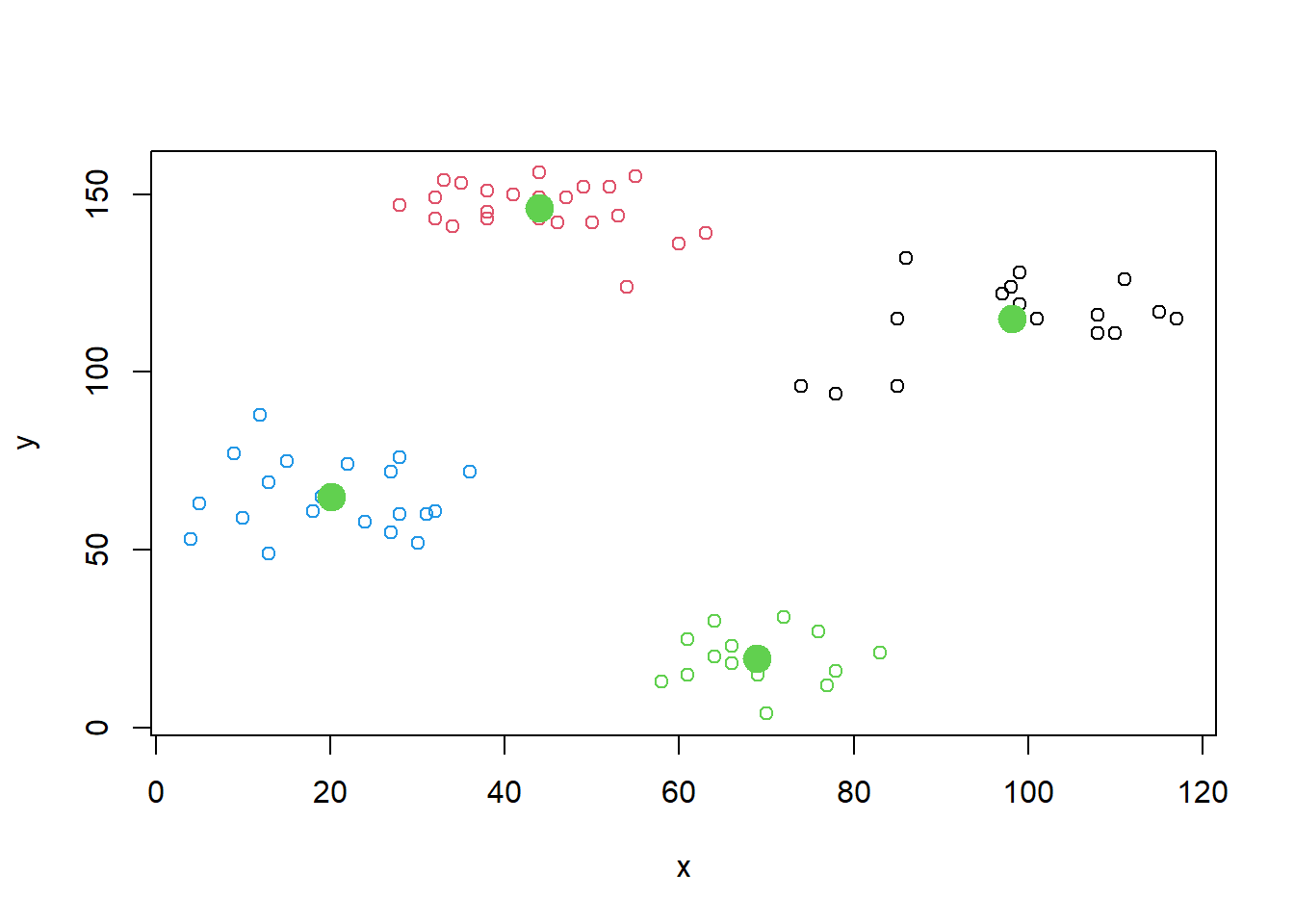
Utilizaremos de nuevo los datos de delicuencia de un caso anterior para ilustrar un segundo ejemplo de clustering no jerárquico.
k2 <- kmeans(scale(USArrests), 4)
# Medias de las variables en cada cluster
aggregate(USArrests, by=list(cluster=k2$cluster), mean)## cluster Murder Assault UrbanPop Rape
## 1 1 3.60000 78.53846 52.07692 12.17692
## 2 2 5.65625 138.87500 73.87500 18.78125
## 3 3 10.81538 257.38462 76.00000 33.19231
## 4 4 13.93750 243.62500 53.75000 21.41250# Representación gráfica
library(factoextra)
fviz_cluster(k2, data = USArrests,
palette = c("#00AFBB","#2E9FDF", "#E7B800", "#FC4E07", "#E495A5"),
main = "Agrupación de estados por criminalidad")
6.3 Ejercicio 6. Agrupación de los clientes de un centro comercial
Un centro comercial ha recopilado los datos de 40 clientes. Para cada uno de ellos tiene, además del nombre, su edad, sus ingresos (en miles de euros) y el número de visitas anuales.
A partir de estos datos, calcula la distancia euclidiana entre todos los clientes. A continuación, crea un dendrograma jerárquico aglomerativo utilizando el método de agrupación “average”. Divide el dendrograma en 3 clústers.
¿Quién es el cliente con un comportamiento más parecido al de Liam? ¿Y el más similar a Maria?
| Edad | Ingresos | Visitas | |
|---|---|---|---|
| Abril | 40 | 29 | 31 |
| Aina | 21 | 30 | 73 |
| Aleix | 20 | 21 | 66 |
| Alex | 22 | 17 | 76 |
| Arlet | 53 | 33 | 4 |
| Arnau | 37 | 20 | 13 |
| Biel | 23 | 18 | 94 |
| Bruno | 58 | 20 | 15 |
| Carla | 21 | 33 | 81 |
| Chloe | 42 | 34 | 17 |
| Claudia | 20 | 37 | 75 |
| Emma | 25 | 24 | 73 |
| Enzo | 22 | 20 | 79 |
| Eric | 24 | 20 | 77 |
| Hugo | 67 | 19 | 14 |
| Jan | 21 | 15 | 81 |
| Jana | 49 | 33 | 14 |
| Julia | 35 | 24 | 35 |
| Laia | 35 | 28 | 61 |
| Leo | 31 | 17 | 40 |
| Lia | 30 | 34 | 73 |
| Liam | 35 | 19 | 99 |
| Lucas | 30 | 19 | 72 |
| Lucia | 54 | 28 | 14 |
| Marc | 19 | 15 | 39 |
| Maria | 23 | 29 | 87 |
| Marti | 35 | 18 | 6 |
| Martina | 46 | 25 | 5 |
| Mateo | 52 | 23 | 29 |
| Max | 35 | 21 | 35 |
| Mia | 31 | 25 | 73 |
| Nil | 23 | 16 | 77 |
| Noa | 60 | 30 | 4 |
| Ona | 29 | 28 | 82 |
| Pau | 64 | 19 | 3 |
| Paula | 18 | 33 | 92 |
| Pol | 20 | 16 | 6 |
| Roc | 35 | 23 | 98 |
| Sara | 36 | 37 | 26 |
| Sofia | 45 | 28 | 32 |