Capítulo 2 Estadística descriptiva y visualización de datos

2.1 Distribuciones de frecuencias

El primer paso para el estudio estadístico de una muestra es su ordenación y presentación en una tabla de frecuencias.

En el sentido más amplio, hacer una inferencia implica describir en forma parcial o completa un fenómeno o un objeto físico. Se encuentra poca dificultad cuando se dispone de mediciones descriptivas apropiadas y significativas, pero éste no es siempre el caso. Por ejemplo, podríamos caracterizar una persona si usamos su estatura, peso, color de cabello y ojos, así como otras mediciones descriptivas de la fisonomía de la persona. Identificar un conjunto de mediciones descriptivas para caracterizar una pintura al óleo sobre tela sería un trabajo comparativamente más difícil. Caracterizar una población formada por un conjunto de mediciones es también muy difícil. En consecuencia, un preludio necesario para una discusión de hacer inferencias es la adquisición de un método para caracterizar un conjunto de números. Las caracterizaciones deben ser significativas para que el conocimiento de las mediciones descriptivas haga posible que visualicemos con claridad el conjunto de números. Además, requerimos que las caracterizaciones tengan significación práctica para que el conocimiento de las mediciones descriptivas de una población se pueda usar para resolver un problema práctico, no estadístico (Walkerly, Mendenhall, and Scheaffer 2010).

Los hallazgos numéricos de un estudio deben presentarse de manera clara, concisa y de tal manera que un observador pueda obtener rápidamente una idea de las características esenciales de los datos. A lo largo de los años se ha descubierto que las tablas y los gráficos son formas especialmente útiles de presentar datos, ya que a menudo revelan características importantes como el rango, el grado de concentración y la simetría de los dato (Ross 2020)

Investigar : diagrama de tallos y hojas

2.2 Diagramas de barras e Histogramas

Supongamos que tenemos una muestra de tamaño \(n\), y cada observación estaará representada por la variable estadística \(x\) con valores \(x_1, x_2, . . . , x_n\), en esta muestra los valores repetidos toman los valores distintos, sin pérdida de generalidad, de \(x_1, x_2, . . . , x_k\). En primer lugar hay que ordenar los diferentes valores que toma la variable estadística (normalmente orden creciente).

2.2.1 Tabla de frecuencias de una variable discreta y diagrama de barras

La diferencia entre el valor mayor y menor que toma la variable se conoce como recorrido, o rango. En el caso de variables discretas, generalmente, un mismo valor de la variable aparecerá repetido más de una vez (es decir \(k < n\)). De forma que el siguiente paso es la construcción de una tabla en la que se indiquen los valores posibles de la variable y su frecuencia de aparición:

Frecuencia absoluta \(n_i\): Definida como el número de veces que aparece repetido el valor en cuestión de la variable estadística en el conjunto de las observaciones realizadas. Si \(n\) es el número de observaciones (o tamaño de la muestra), las frecuencias absolutas cumplen las propiedades:

\[0 \le {n_i} \le n;\quad i = 1,2,...,k\]

\[\sum\limits_{i = 1}^k {{n_i}} = {n_1} + {n_2} + ... + {n_k} = n\]

Frecuencia relativa \(f_i\): cociente entre la frecuencia absoluta y el número de observaciones realizadas \(n\):

\[{f_i} = \frac{{{n_i}}}{n}\]

Cumpliéndose las propiedades:

\[0 \le f_i \le 1\] \[\sum\limits_{i = 1}^k {{f_i}} = {f_1} + {f_2} + ... + {f_k} = 1\]

Esta frecuencia relativa se puede expresar también en tantos por cientos del tamaño de la muestra, para lo cual basta con multiplicar por 100:

\[\left( \% \right){x_i} = 100 \times {f_i}\]

Frecuencia absoluta acumulada \(N_i\): Suma de las frecuencias absolutas de los valores inferiores o igual a \(x_i\), o número de medidas por debajo, o igual, que \(x_i\). Evidentemente la frecuencia absoluta acumulada de un valor se puede calcular a partir de la correspondiente al anterior:

\[{N_i} = {n_i} + {N_{i - 1}}\]

\[{N_m} = {n_1} + {n_2} + ... + {n_m} = \sum\limits_{i = 1}^m {{n_i}}\]

\[{N_1} = {n_1}\]

\[{N_k} = n\]

\[{n_1} = {N_1} \le {N_2} \le ... \le {N_k} = n\]

Frecuencia relativa acumulada \(F_i\): es el cociente entre la frecuencia absoluta acumulada y el número de observaciones. Coincide además con la suma de las frecuencias relativas de los valores inferiores o iguales a \(x_i\)

\[{F_i} = \frac{{{N_i}}}{n} = \frac{{\sum\nolimits_{m = 1}^i {{n_m}} }}{n} = \sum\limits_{m = 1}^i {\frac{{{n_m}}}{n}} = \sum\limits_{m = 1}^i {{f_i}}\]

Y cumple:

\[{F_m} = {f_1} + {f_2} + ... + {f_m} = \sum\limits_{i = 1}^m {{f_i}}\] \[{f_1} = {F_1} \le {F_2} \le ... \le {F_k} = 1\]

La siguiente tabla muestra cada uno de los ítems anteriores:

\(i\)	Valores de la variable estadística \(x_i\)	Frecuencia absoluta \(n_i\)	Frecuencia relativa \(f_i\)	Frecuencia absoluta acumulada \(N_i\)	Frecuencia relativa acumulada \(F_i\)
\(1\)	\(x_1\)	\(n_1\)	\(f_1\)	\(N_1\)	\(F_1\)
\(2\)	\(x_2\)	\(n_2\)	\(f_2\)	\(N_2\)	\(F_2\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(k\)	\(x_k\)	\(n_k\)	\(f_k\)	\(N_k\)	\(F_k\)

2.2.1.1 Construcción del diagrama de barras

Cuando se trate de frecuencias absolutas o de frecuencias relativas, se realizará la representación por medio del llamado diagrama de frecuencia, que consiste en colocar en el eje horizontal los valores \(x_i\), que toma la variable y levantando en cada punto un segmento vertical de longitud igual a la frecuencia correspondiente.

El gráfico de frecuencias absolutas difiere del gráfico de frecuencias relativas sólo en la escala del eje de las ordenadas.

Ejemplo 2.1 Supongamos que el número de hijos de una muestra de 20 familias es el siguiente: (Gorgas, Cardiel, and Zamorano 2009)

2	1	1	3	1	2	5	1	2	3
4	2	3	2	1	4	2	3	2	1

Escribiendo estos datos en :

n_hijos <- c(2, 1, 1, 3, 1, 2, 5, 1, 2, 3, 4, 2, 3, 2,1, 4, 2, 3, 2, 1)

El tamaño de la muestra es \(n = 20\), el número de valores posibles es \(k = 5\), es decir, todos los datos se pueden clasificar en \(5\) valores que toma variable y el recorrido es \(5 - 1 = 4\). La tabla de frecuencias queda expresada como:

\(i\)	\(x_i\)	\(n_i\)	\(f_i\)	\(N_i\)	\(F_i\)
1	1	6	0,30	6	0,30
2	2	7	0,35	13	0,65
3	3	4	0,20	17	0,85
4	4	2	0,10	19	0,95
5	5	1	0,05	20	1,00
		20	1,00

Para construir una tabla de frecuencias para una variable discreta basta con el uso de varias funciones y luego concatenarlas en una tabla.

f_abs <- table(n_hijos) # frecuencia absoluta

f_abs

## n_hijos
## 1 2 3 4 5 
## 6 7 4 2 1

El diagrama de barras para estos datos usando la función \(barplot()\):

barplot(f_abs,
        main = "Diagrama de barras para el número de hijos", # Título principal
        xlab = "Número de hijos x",  # Título eje x
        ylab = "Frecuencia absoluta n", # Título eje y
        col = topo.colors(5)) # Color de barras

2.2.1.2 Función empírica de distribución acumulada

Las frecuencias acumuladas pueden definirse como funciones sobre todos los números reales:

\(F(x)\) = fracción (o porcentaje) de los datos que son menores o iguales que \(x\).

\[F\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {0\quad \quad \quad \quad x < {x_m}}\\ {{F_m}\quad {x_m} \le x < {x_{m + 1}}}\\ {1\quad \quad \quad \quad x \ge {x_k}} \end{array},\quad m = 1,2,...,k} \right.\]

La función de distribución acumulada \(F(x)\) para el ejemplo del número de hijos por familia queda expresado como:

\[F\left( x \right) = \left\{ {\begin{array}{*{20}{c}} 0\\ {0.30}\\ {0.65}\\ {0.85}\\ {0.95}\\ 1 \end{array}\quad \begin{array}{*{20}{c}} {x < 1}\\ {1 \le x < 2}\\ {2 \le x < 3}\\ {3 \le x < 4}\\ {4 \le x < 5}\\ {x \ge 5} \end{array}} \right.\]

fda <- ecdf(n_hijos) # se usa la función ecdf (Empirical Cumulative Distribution Function)
plot(fda,
     main = "Función emprírica de distribución acumulada para el número de hijos",
     ylab = "F(x)",
     xlab = "Número de hijos")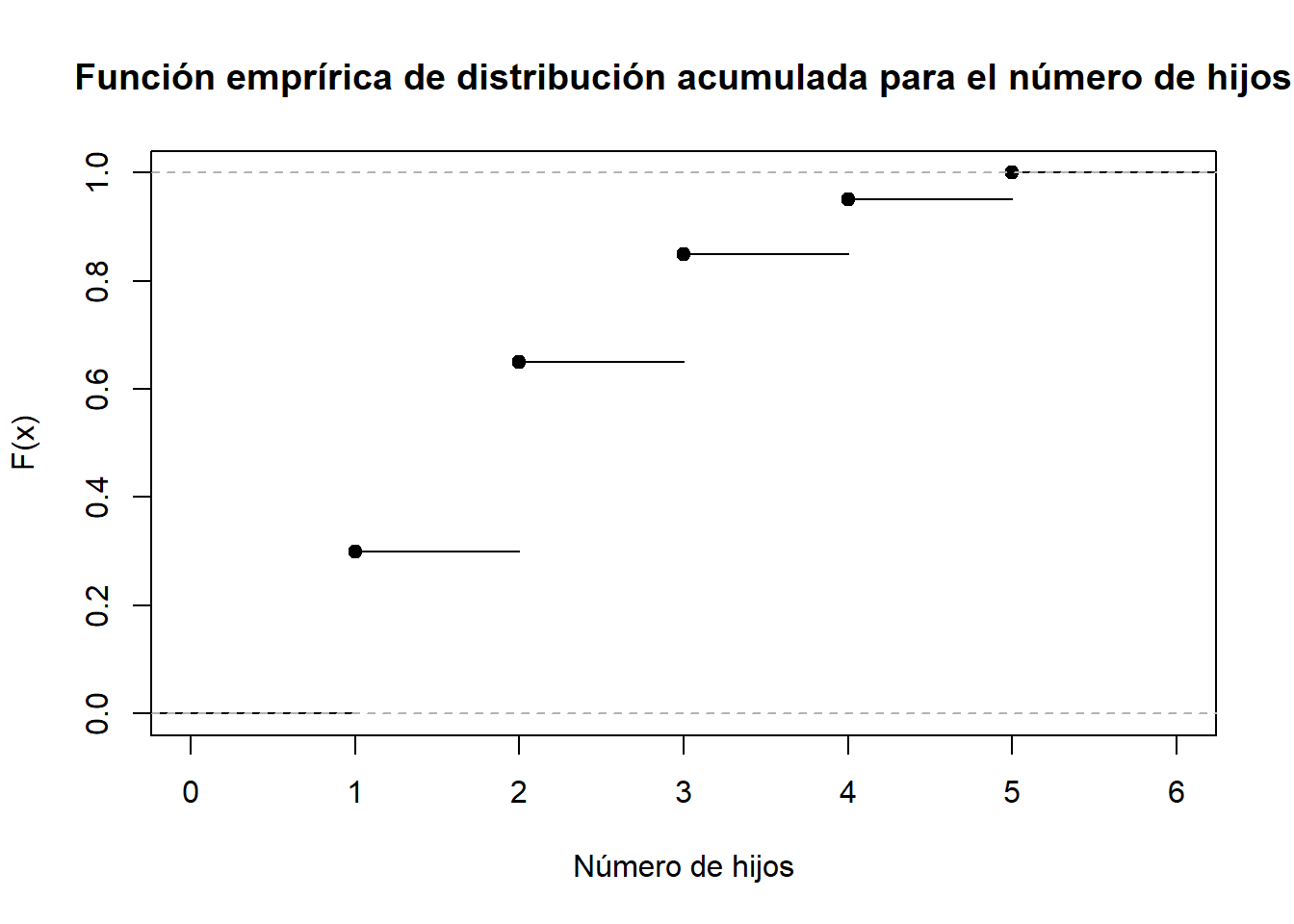

2.2.2 Tabla de frecuencias de una variable continua e Histogramas

Cuando el número de valores distintos que toma la variable estadística es demasiado grande o la variable es continua no es útil elaborar una tabla de frecuencias como la vista anteriormente. En estos casos se realiza un agrupamiento de los datos en intervalos y se hace un recuento del número de observaciones que caen dentro de cada uno de ellos. Dichos intervalos se denominan intervalos de clase, y al valor de la variable en el centro de cada intervalo se le llama marca de clase. Normalmente se trabaja con intervalos de amplitud constante. La tabla de frecuencias resultante es similar a la vista anteriormente. La tabla se construye con los siguientes ítems:

Rango(R): también llamado recorrido de los datos. Esto es, la diferencia entre el mayor y el menor de los valores que toma la variable.

\[Rango = \max ({x_i}) - \min ({x_i})\]

Número de Clases (k): número de intervalos de clase en que se van a agrupar los datos. Dicho número se debe situar normalmente entre 5 y 20, dependiendo del caso. En general el número será más grande cuanto más datos tenga la muestra. Una regla que a veces se sigue es elegir \(k\) como el entero más próximo a \(\sqrt{n}\). Sin embargo, se es más frecuente usar la Regla de Sturges:

\[k = 1 + 3.332 \times \log (n)\]

Amplitud (A): dividir el recorrido entre el número de intervalos para determinar la amplitud (constante) de cada clase.

\[A \cong \frac{R}{k}\]

Límites inferiores (LI) y superiores (LS): el extremo superior de cada intervalo ha de coincidir con el extremo inferior del siguiente. Ocasionalmente algunas observaciones coinciden con alguno de los extremos y para evitar esa ambiguedad en la clasificación dse asigna a los extremos de los intervalos una cifra decimal más que las medidas de la muestra. Una convención recomendada comúnmente usada \([LI , LS)\) (el límite inferior no pertenece a él, pero sí, su límite superior) ó \((LI , LS]\) ((el límite inferior pertenece a él y no su límite superior).

\[L{I_1} = Min({x_i})\] \[L{S_1} = L{I_1} + A\]

Generalizando,

\[L{I_i} = L{S_{i - 1}}\;;\;i > 1\] \[L{S_i} = L{I_i} + A\]

Marcas de Clase (C): valor medio entre los límites inferior y superior de cada intervalo de clase.

\[{C_i} = \frac{{L{I_i} + L{S_i}}}{2}\]

Para determinar la frecuencia asociada con cada intervalo, deben contarse los datos que pertenecen a cada uno; las definiciones de las frecuencias dadas para variables discretas siguen vigentes para el caso de variables continuas, lo mismo que sus propiedades.

Número de clase \(k_i\)	Límite Inferior \(LI_i\)	Límite superior \(LS_i\)	Marca de Clase \(C_i\)	Frecuencia Absoluta \(n_i\)	Frecuencia Relativa \(f_i\)	Frecuencia Absoluta Acumulada \(N_i\)	Frecuencia Relativa Acumulada \(F_i\)
1	\(LI_1\)	\(LS_1\)	\(C_1\)	\(n_1\)	\(f_1\)	\(N_1\)	\(F_1\)
2	\(LI_2\)	\(LS_2\)	\(C_2\)	\(n_2\)	\(f_2\)	\(N_2\)	\(F_2\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(k\)	\(LI_k\)	\(LS_k\)	\(C_k\)	\(n_k\)	\(f_k\)	\(N_k\)	\(F_k\)

Ejemplo 2.2 Los datos que se presentan a continuación corresponden a los tiempos de atención (en minutos) de pacientes en el servicio de urgencias de un hospital:

13,1	7,1	14,8	19	10,2	18	19,8	15	17,3	10,8	22,3	14,5	17,1
14,9	12	14	18,4	10,2	15,8	16,5	15	17,6	4,2	13,4	21,2	14,7
13,8	21	14,3	11,1	18,9	8,3	16,6	11,2	20,2	14,4	13,5	18,2	12,4
17	26,7	15,5	22	12,9	17,9	7,4	18	19,8	16	21,2

En se podría escribir de la forma:

t_atencion <- c(13.1,7.1,14.8,19,10.2,18,19.8,15,17.3,10.8,22.3,14.5,17.1,
                14.9,12,14,18.4,10.2,15.8,16.5,15,17.6,4.2,13.4,21.2,14.7,
                13.8,21,14.3,11.1,18.9,8.3,16.6,11.2,20.2,14.4,13.5,18.2,12.4,
                17,26.7,15.5,22,12.9,17.9,7.4,18,19.8,16,21.2)

Los datos iniciales son:

Tamaño de la muestra \(n = 50\)

Valor máximo \(Max = 26,7\)

valor mínimo \(Min = 4,2\)

Rango \(R = 22,5\)

Número de clases \(k \cong 7\)

Amplitud \(A = 3,214\)

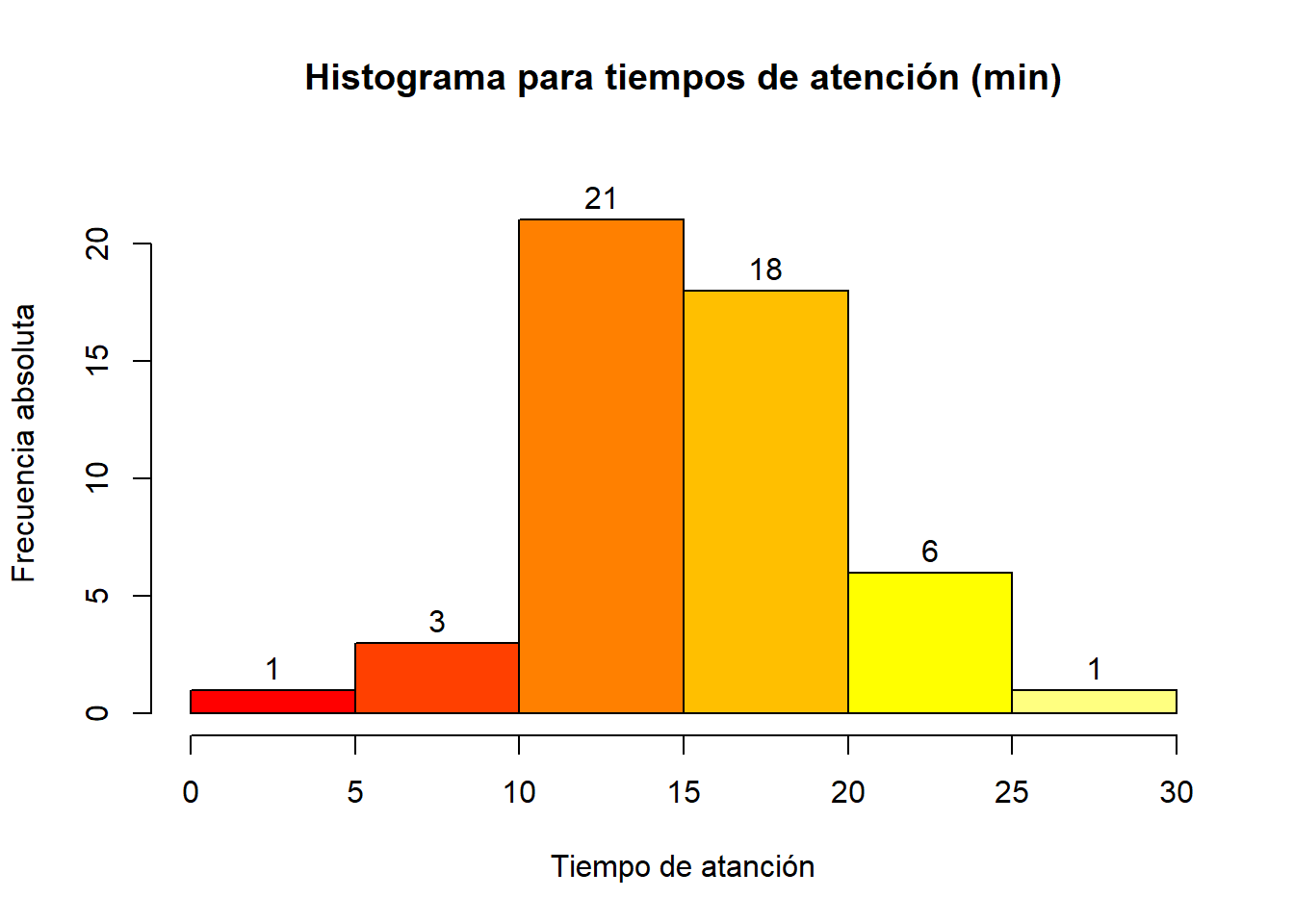
Una forma sencilla de mostrar los resultados de una tabla de frecuencias en \(R\) es usando la función hist() del paquete graphics falseando el argumento plot como sigue:

hist(t_atencion, plot = F)

## $breaks
## [1]  0  5 10 15 20 25 30
## 
## $counts
## [1]  1  3 21 18  6  1
## 
## $density
## [1] 0.004 0.012 0.084 0.072 0.024 0.004
## 
## $mids
## [1]  2.5  7.5 12.5 17.5 22.5 27.5
## 
## $xname
## [1] "t_atencion"
## 
## $equidist
## [1] TRUE
## 
## attr(,"class")
## [1] "histogram"

Un paquete que nos ayuda a construir la tabla de frecuencias para estos datos es el de agricolae(), para esto instale el paquete con la función install.packages(“agricolae”) y luego active con library() como sigue:

library(agricolae)

La tabla de frecuencias se elabora a partir de los datos del histograma generado por la función hist() en conjunto la función table.freq() perteneciente al paquete agricolae()

his_t_atencion <- hist(t_atencion, plot=F)
tf_t_atencion <- table.freq(his_t_atencion)
tf_t_atencion

##   Lower Upper Main Frequency Percentage CF CPF
## 1     0     5  2.5         1          2  1   2
## 2     5    10  7.5         3          6  4   8
## 3    10    15 12.5        21         42 25  50
## 4    15    20 17.5        18         36 43  86
## 5    20    25 22.5         6         12 49  98
## 6    25    30 27.5         1          2 50 100

Si lo que se desea es visualizar el histograma con todos los elemneto como título, color, etc, una alternativa sería:

hist(t_atencion,
     main = "Histograma para tiempos de atención (min)", # título de la gráfica
     ylab = "Frecuencia absoluta",# título del eje "y"
     xlab = "Tiempo de atanción", # título del eje "x"
     labels = T,                  # mostrar las etiquetas de las barras
     col= heat.colors(6),         # colores usando paleta heat.colors()
     ylim = c(0, 23)              # ajuste de límites en "y" para mostrar las etiquetas
     )

2.3 Diagrama de torta (pie o circular)

Un gráfico circular se usa a menudo para indicar frecuencias relativas cuando los datos no son de naturaleza numérica. Se construye un círculo y luego se corta en diferentes sectores; uno para cada tipo distinto de valor de datos. La frecuencia relativa de un valor de dato viene indicada por el área de su sector, siendo esta área igual al área total del círculo multiplicada por la frecuencia relativa del valor de dato (Ross 2020).

Ejemplo 2.3 Los siguientes datos relacionan los diferentes tipos de cáncer que afectan a los 200 pacientes más recientes dianosticados en una clínica especializada en cáncer:

Tipo de cáncer	No. Casos
Pulmón	42
Seno	50
Colon	32
Próstata	55
Melanoma	9
Vejiga	12

Una tabla de frecuencias de este tipo debe ordenarse para tener claridad sobre qué elementos o categorías tienen mayor participación sobre el total de la muestra, por ejemplo, los casos de cáncer de próstata reprentan el 27.5% de todos los casos, mientras que los de melanoma representan el 4.5%, por tanto ordenamos la tabla (preferiblemnte en orden descendente):

Tipo de cáncer	No. Casos
Próstata	55
Seno	50
Pulmón	42
Colon	32
Vejiga	12
Melanoma	9

En se deben escribir los dos vectores, uno para el tipo de cáncer y otro para el número de casos de la forma:

tc <- c("Próstata", "Seno", "Pulmón", "Colon", "Vejiga", "Melanoma")
nc <- c(55,50,42,32,12,9)

pie(x = nc,                   # frecuencias absolutas
    labels = tc,              # categorías tipo de cáncer
    main = "Número de casos por tipo de cáncer diagnosticado (n=200)",
    col =  terrain.colors(6), # color de los segmentos
    clockwise = T)            # sentido horario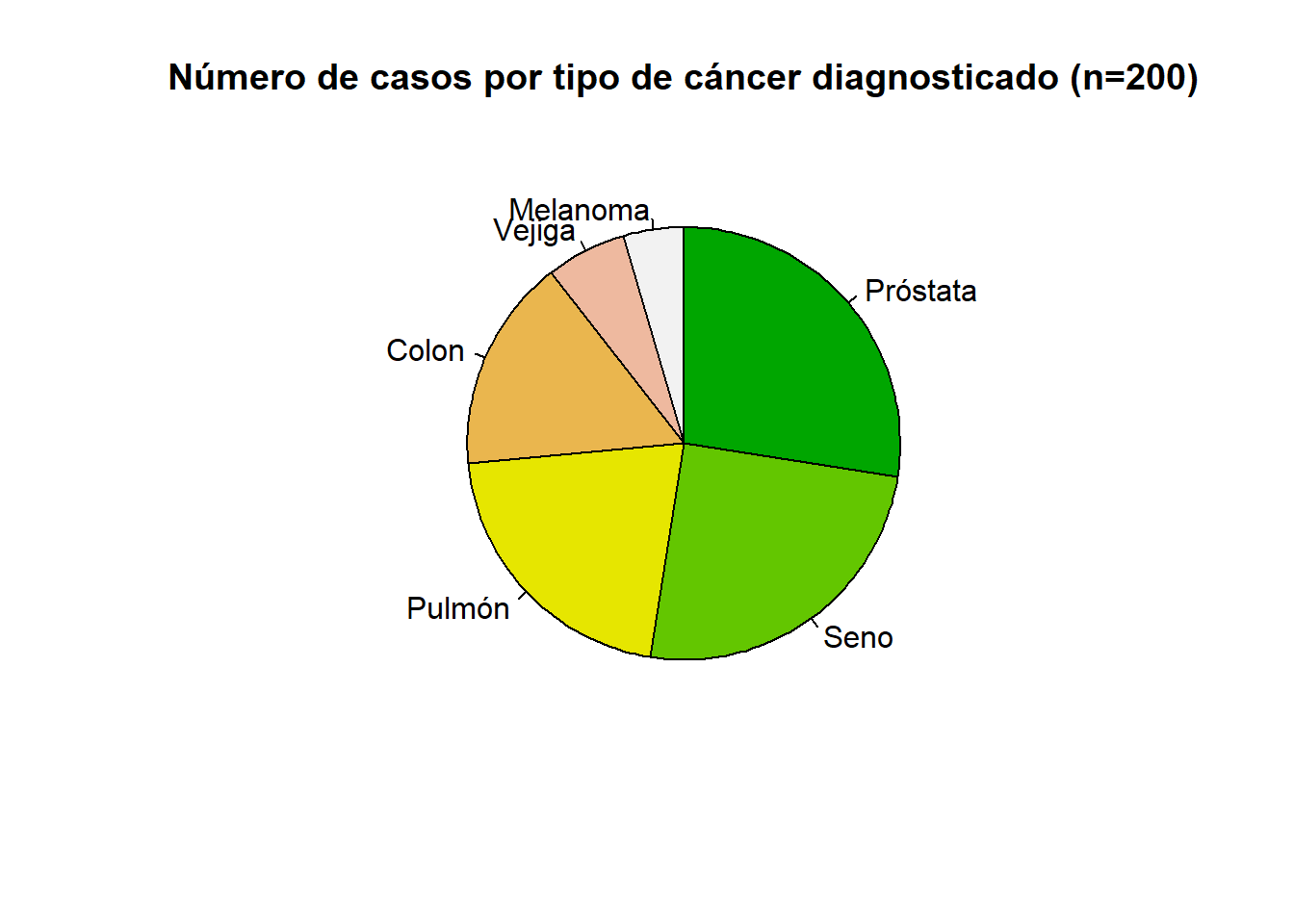

Una alternativa con un poco más de elaboración, pero más estética sería agregando etiquetas y leyendas como sigue:

#install.packages("scales") #paquete con funciones para dar formato a los datos.
library(scales) #activación del paquete

Estimamos las frecuencias relativas:

frecR_nc <- percent(nc/sum(nc)) # se divide entre el total de datos, 
# la función percent() le da formato de porcentaje.

Luego elaboramos el diagrama de torta, ubicando como etiquetas las frecuencias relativas y agregando la leyenda.

pie(x = nc,
    labels = frecR_nc,        # frecuencias relativas
    main = "Número de casos por tipo de cáncer diagnosticado (n=200)",
    col =  terrain.colors(6), # color de los segmentos
    clockwise = T)            # sentido horario

legend(x = "right", #ubicación de la leyenda
       y = tc, # leyenda de tipo de cáncer
       fill = terrain.colors(6), # color de la leyenda, debe coincidir con color de segmentos
       cex = 1, #tamaño de la letra
       title = "Tipo de cáncer")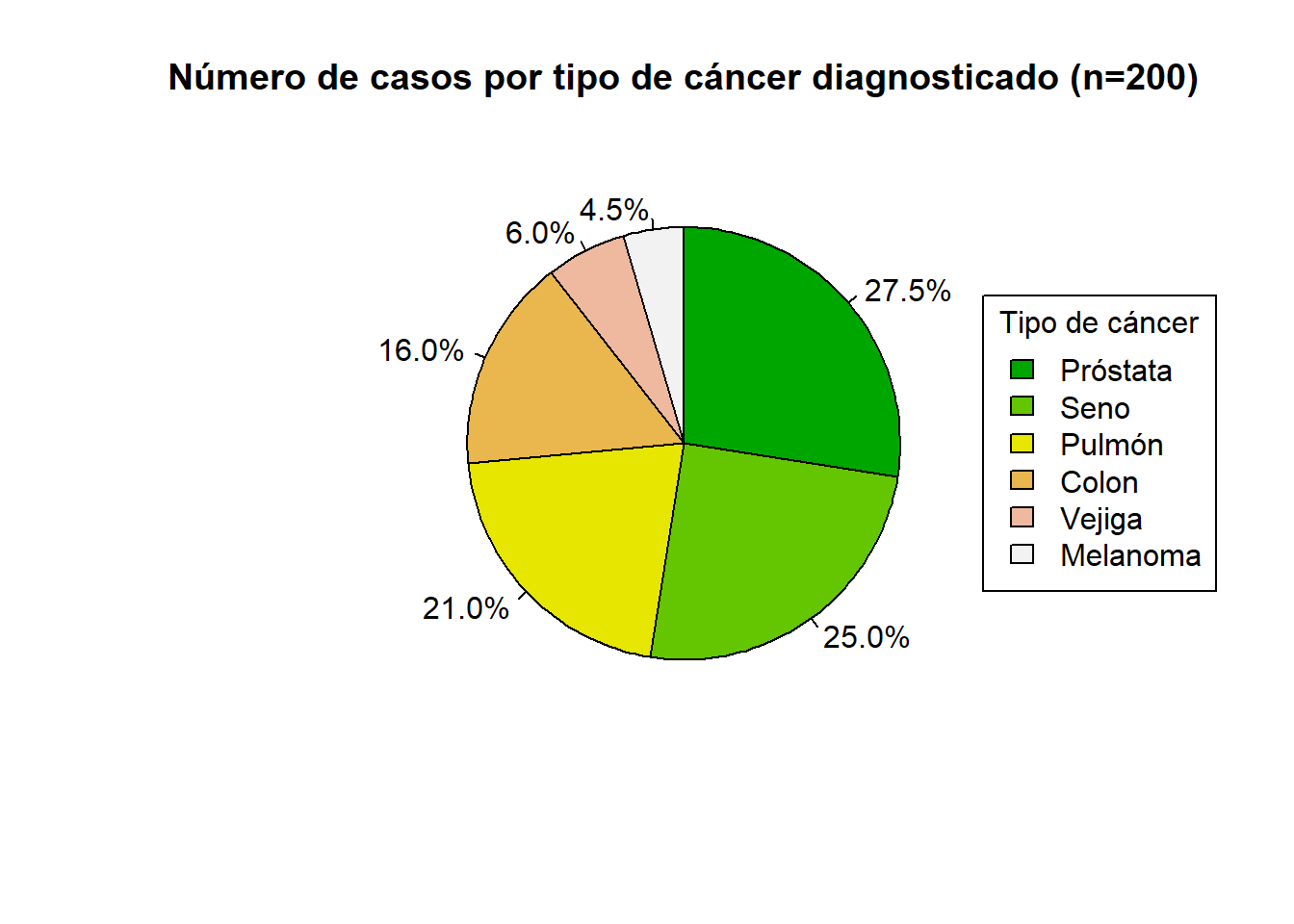

Investigar : ¿Cómo elaborar un diagrama de torta manualmente?

2.4 Diagrama de dispersión

A veces los elementos de una población pueden tener algunos valores asociados entre sí. Por ejemplo, imagine que elige una muestra aleatoria de días y determine el promedio de la temperatura y de la humedad para cada día. Cada día la población proporciona dos valores, la temperatura y la humedad. Por tanto, la muestra aleatoria constaría de pares de números. Si las precipitaciones también se midieran todos los días, la muestra constaría de tripletes. En principio, se podría medir todos los días cualquier número de cantidades, lo que produciría una muestra en la que cada elemento representa una lista de números. Los datos para cada elemento que constan de más de un valor se llaman datos multivariados. Cuando cada elemento es un par de valores, se dice que los datos son bivariados.

Uno de los resúmenes gráficos más útiles por los datos bivariados numéricos es el diagrama de dispersión. Si los datos constan de pares arreglados \((x_l, y_1)\),… , \((x_n, y_n)\), entonces un diagrama de dispersión se construye sólo al trazar cada punto en un sistema coordenado bidimensional (Navidi 2006)

Ejemplo 2.4 Construya un diagrama de dispersión para las variables de longitud y ancho del pétalo de la tabla de datos Iris del paquete datasets

R contiene múltiples repositorios de datos para explorar y analizar, uno de esos es la base de datos Iris del paquete datasets que contien datos sobre medidas (en centímetros) de las variables largo y ancho del sépalo y largo y ancho del pétalo, respectivamente, para 50 flores de cada una de las 3 especies de iris: setosa, versicolor y virginica.

Para trabajar con este tipo de datos es necesario activar el paquete usando la función \(library()\) como se muestra a continuación (la función \(head()\) se usa para mostrar los primeros 10 registros de la tabla)

library(datasets)
head(iris,10)

##    Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1           5.1         3.5          1.4         0.2  setosa
## 2           4.9         3.0          1.4         0.2  setosa
## 3           4.7         3.2          1.3         0.2  setosa
## 4           4.6         3.1          1.5         0.2  setosa
## 5           5.0         3.6          1.4         0.2  setosa
## 6           5.4         3.9          1.7         0.4  setosa
## 7           4.6         3.4          1.4         0.3  setosa
## 8           5.0         3.4          1.5         0.2  setosa
## 9           4.4         2.9          1.4         0.2  setosa
## 10          4.9         3.1          1.5         0.1  setosa

plot(x = iris$Petal.Length,   # Longitud del pétalo
     y = iris$Petal.Width,    # Ancho del pétalo
     main = "Dispersión de la longitud y el ancho del pétalo", 
     xlab = "Longitud (cm)",  # Título eje x
     ylab = "Ancho (cm)",     # Título eje y
     pch=19)                  # Tipo de punto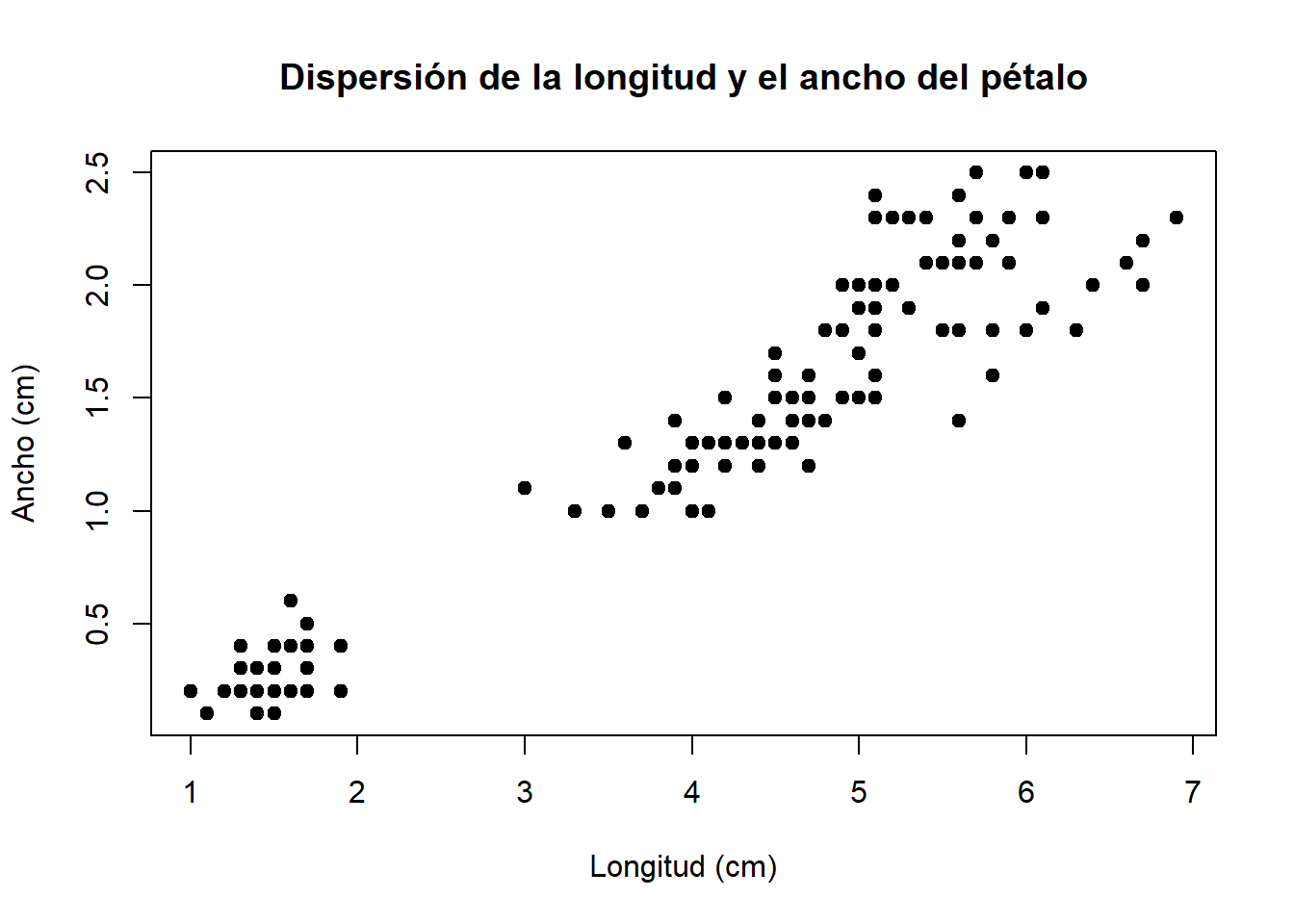

Una dato importante que se podría representar en esta gráfica es saber qué puntos correspnden a cada especie, para lo cual se agrega el argumento de \(col\) que permitirá clasificar los puntos de cada especie por color y agregar una leyenda con la función \(legend()\) para indicar a qué color pertenece cada especie.

plot(x = iris$Petal.Length,   # Longitud del pétalo
     y = iris$Petal.Width,    # Ancho del pétalo
     main = "Dispersión de la longitud y el ancho del pétalo", 
     xlab = "Longitud (cm)",  # Título eje x
     ylab = "Ancho (cm)",     # Título eje y
     col = rainbow(3)[iris$Species], # Color de los puntos
     pch=19)                  # Tipo de punto

legend(x = "topleft", 
       legend = c("Setosa", "Versicolor", "Virginica"), # nombre de las especies
       fill = c("red", "green", "blue"),               # color de las especies
       title = "Especie")                               # título de la leyenda

Referencias

Gorgas, Javier, Nicolás Cardiel, and Jaime Zamorano. 2009. Estadística básica Para Estudiantes de Ciencias. Madrid: Universidad Complutense de Madrid.

Navidi, William. 2006. Estadı́stica Para Ingenieros. 519.5 N325. McGraw Hill Interamericana.

Ross, Sheldon M. 2020. Introduction to Probability and Statistics for Engineers and Scientists. Academic press.

Walkerly, D, W Mendenhall, and R Scheaffer. 2010. “Estadística Matemática Con Aplicaciones (7 Ma Edición).” México, DF: Cencage Learning.