Rozdział 4 Procesy stochastyczne, modelowanie szeregów czasowych
4.1 Procesy stacjonarne
4.1.1 Stacjonarność kowariancyjna
Proces stochastyczny jest stacjonarny w sensie szerokim (jest stacjonarny kowariancyjnie), gdy dwa wektory zmiennych losowych pochodzących z tego procesu \(\left(Y_t, Y_{t+1}, ... Y_{t+r}\right)\) i \(\left(Y_{t+s}, Y_{t+s+1}, ... Y_{t+s+r}\right)\) mają takie same średnie, wariancje i kowariancje dla dowolnych wartości \(t\), \(r\) i \(s\).
Mówiąc intuicyjnie: proces stochastyczny jest stacjonarny, gdy niezależnie od okna czasowego mamy takie same średnie, wariancje i autokorelacje.
W stacjonarnym procesie brak trendu i brak sezonowości.
4.1.2 Stacjonarność ścisła
Proces stochastyczny jest stacjonarny w sensie ścisłym, gdy dwa wektory zmiennych losowych \(\left(Y_t, Y_{t+1}, ... Y_{t+r}\right)\) i \(\left(Y_{t+s}, Y_{t+s+1}, ... Y_{t+s+r}\right)\) mają taki sam rozkład dla dowolnych wartości \(t\), \(r\) i \(s\).
Używa się też określenia stacjonarność silna.
W porównaniu ze stacjonarnością szeroką, wymagane są nie tylko takie same średnie, wariancje i autokorelacje, ale wszystkie inne charakterystyki, np. momenty wyższych rzędów, asymetria, kurtoza, itp.
4.1.3 Przykład procesu stacjonarnego
Przykładem procesu stacjonarnego, w którym występuje autokorelacja, jest następujący proces:
\[ y_t = \alpha + \phi y_{t-1} + \varepsilon_t; \:\:\: 0 < \phi < 1;\:\:\: \varepsilon_t \sim \mathcal{N}\left(0, \sigma_\varepsilon^2\right) \tag{4.1} \]
Średnia w tym procesie to \(\alpha/(1-\phi)\), wariancja to \(\sigma_\varepsilon^2/(1-\phi^2)\), a autokorelacja rzędu k to \(\phi^k\).
Symulacja:
# pojedynczy szereg
T <- 100
alpha <- 2
phi <- 0.8
sigma_eps <- 0.5
yt <- numeric(T)
yt[1] <- alpha/(1-phi)
for (t in 2:T) {
yt[t] <- alpha + phi*yt[t-1] + rnorm(1, 0, sigma_eps)
}
plot(yt, type="l")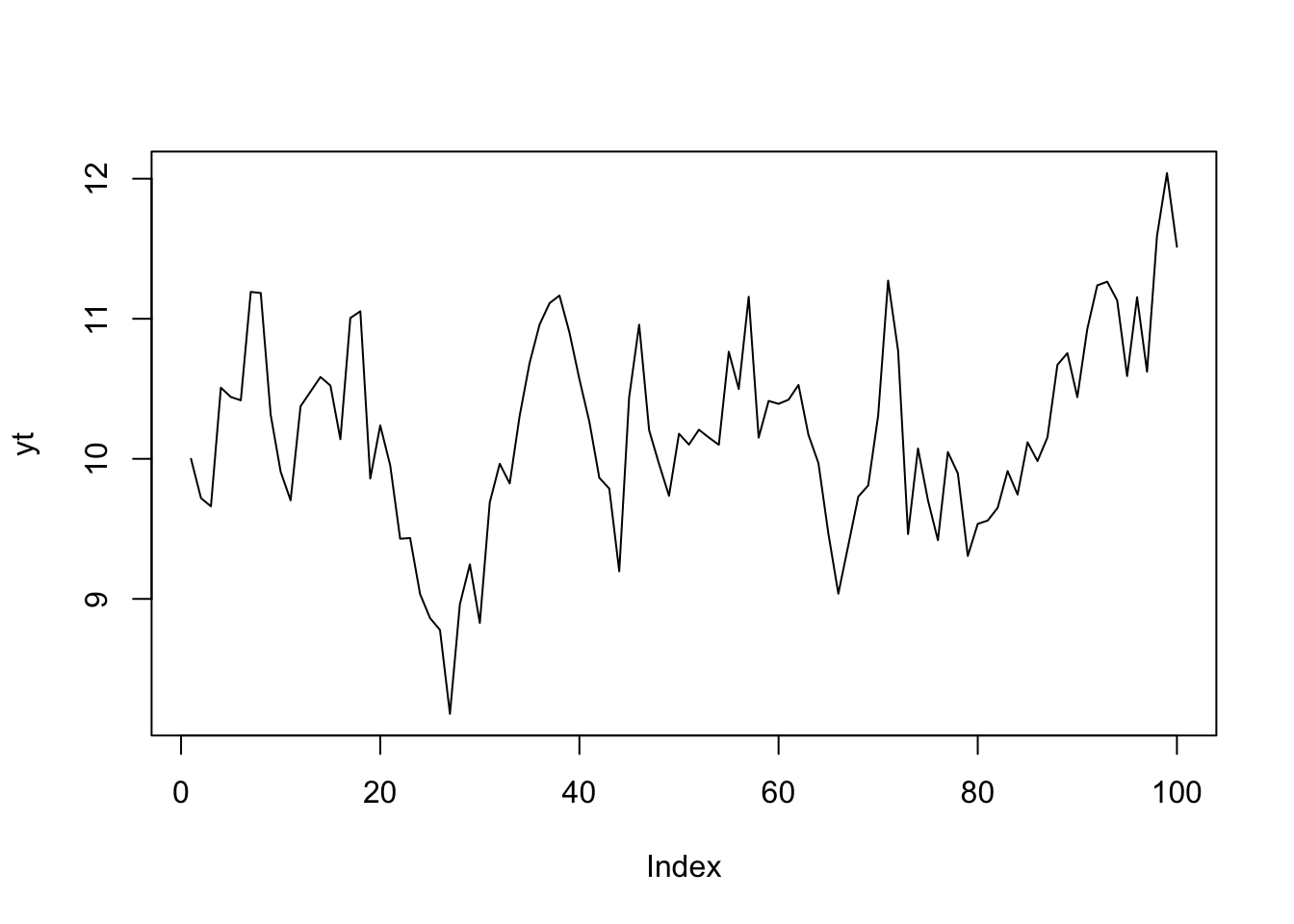
# wiele szeregów plus wykresy pudełkowe
nsim <- 1e3
w <- replicate(nsim,{
yt <- numeric(T)
yt[1] <- alpha/(1-phi) + rnorm(1, 0, 1) * sigma_eps/sqrt(1-.8^2)
for (t in 2:T) {
yt[t] <- alpha + phi*yt[t-1] + rnorm(1, 0, .5)
}
yt}
)
boxplot(t(w), pch='.')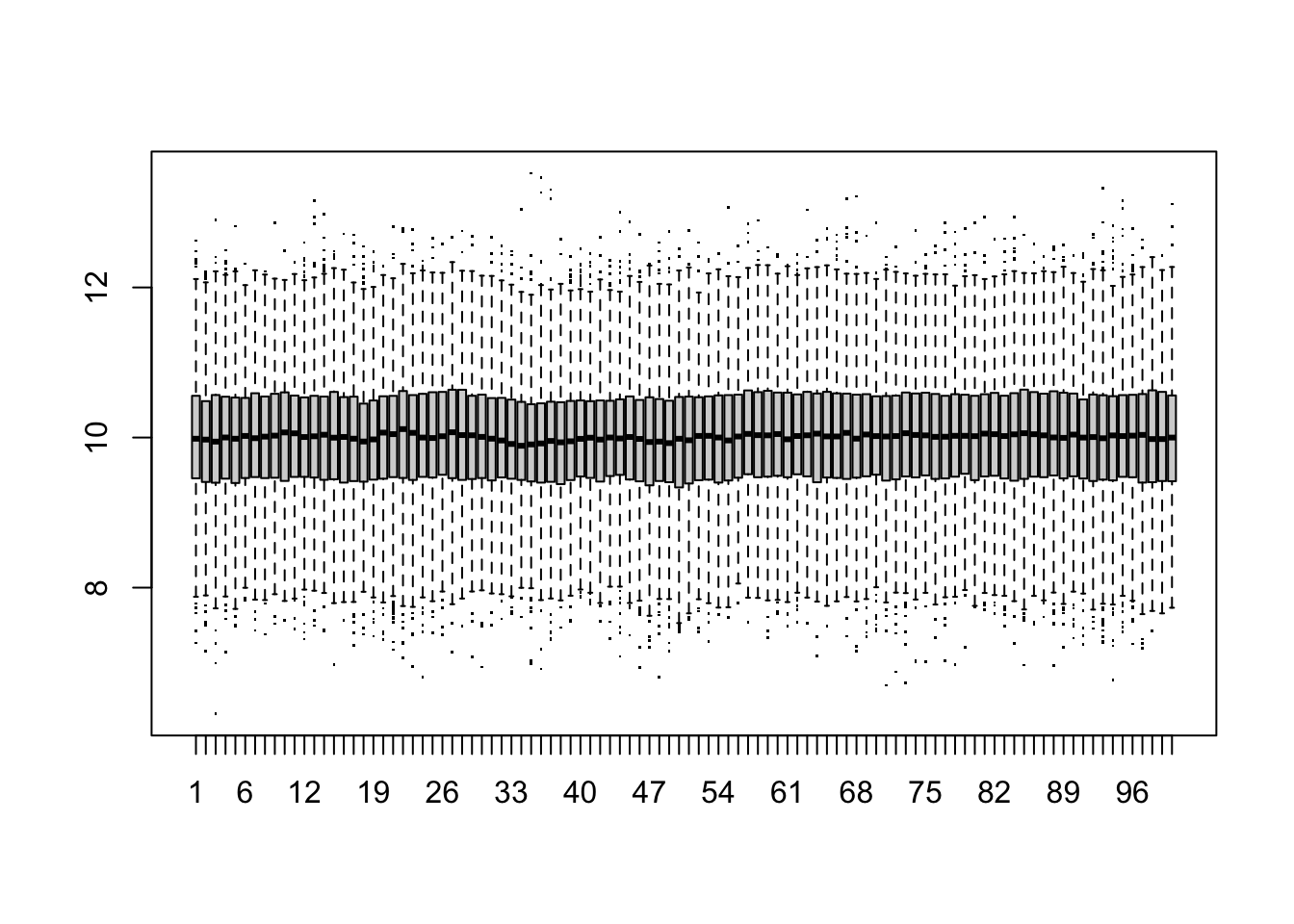
4.1.4 Biały szum
Białym szumem najczęściej określa się proces stacjonarny, w którym średnia wynosi zero, wariancja jest stała, a zmienne \(Y_s\) i \(Y_t\) są niezależne dla wszystkich \(s \ne t\).
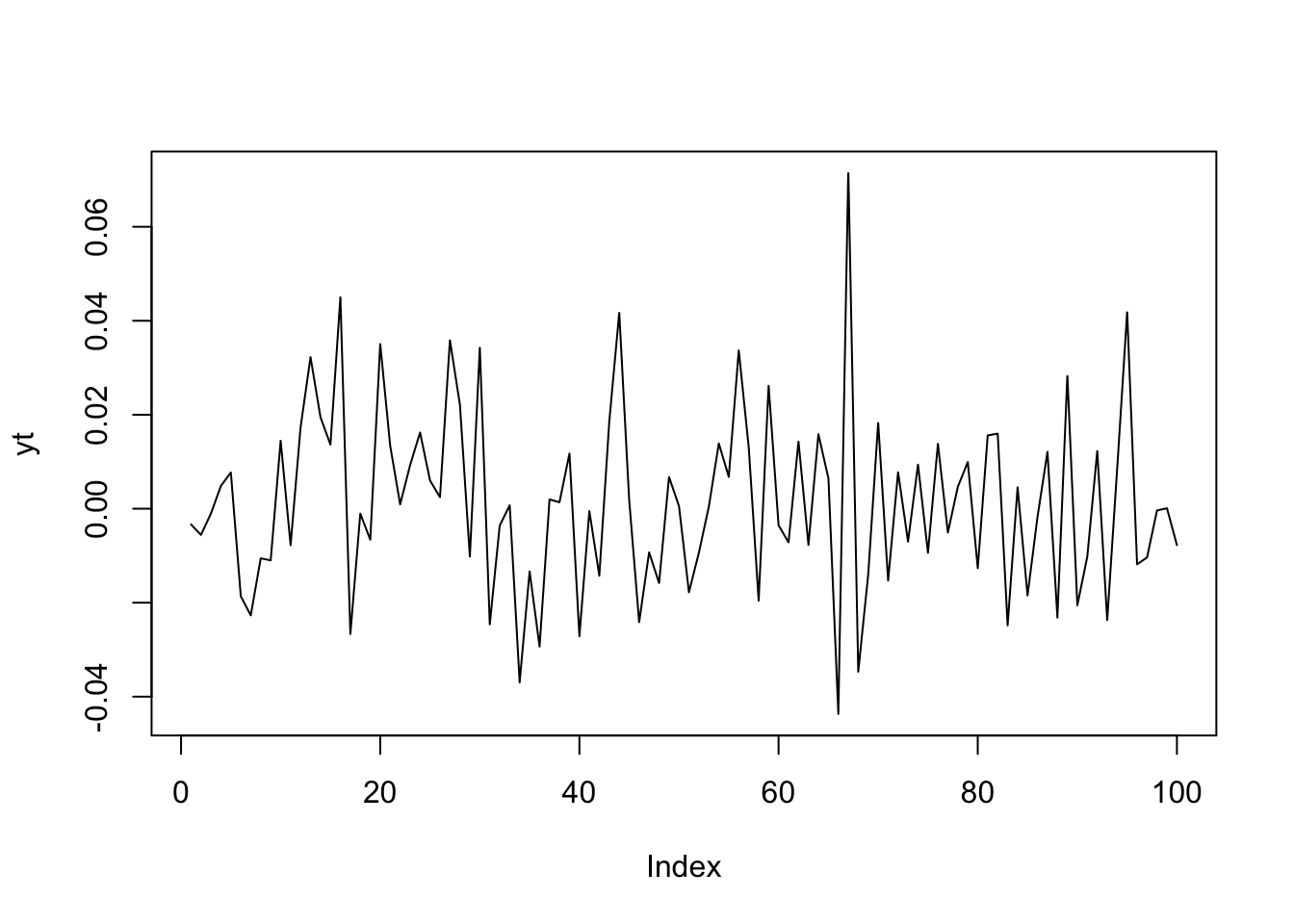
4.1.5 Ścisły biały szum
Ścisły biały szum to biały szum, w którym rozkład zmiennych \(Y_t\) jest normalny (jest rozkładem Gaussa):
\[ y_t = \varepsilon_t; \:\:\: \varepsilon_t \sim \:\text{i.i.d.}\:\mathcal{N}\left(0, \sigma_\varepsilon^2\right) \tag{4.2}\]
# wiele szeregów plus wykresy pudełkowe
nsim <- 1e3
w <- replicate(nsim,{
yt <- rnorm(T, 0, sigma_eps)
yt}
)
boxplot(t(w), pch='.')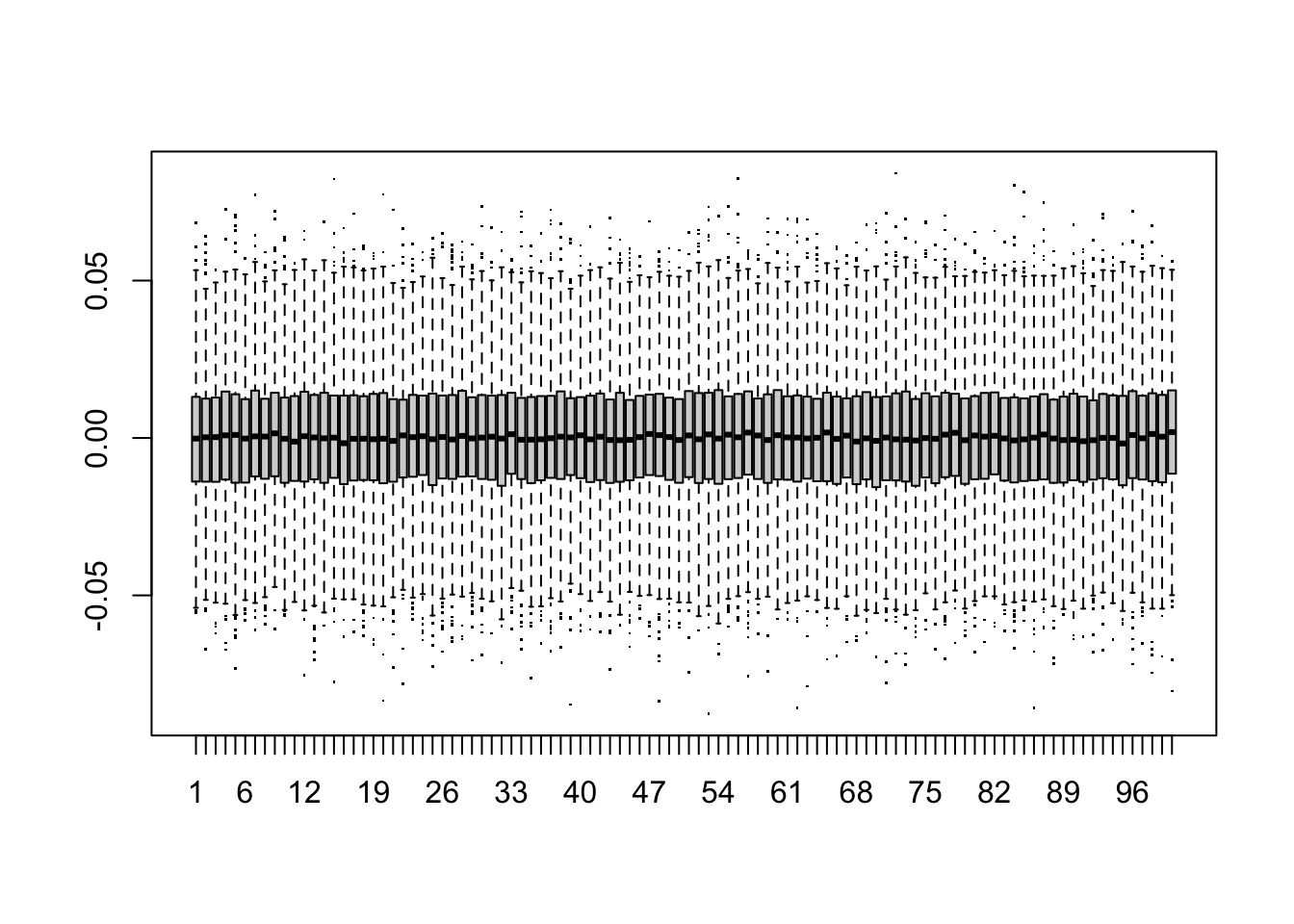
4.1.6 Przesunięty biały szum
Przesunięty biały szum (czasem, niekoniecznie poprawnie: „białym szumem z dryftem”) to proces stacjonarny, bez autokorelacji ze średnią inną niż zero.
Przykład przesuniętego białego szumu:
\[ y_t = \alpha + \varepsilon_t; \:\:\: \varepsilon_t \sim \mathcal{N}\left(0, \sigma_\varepsilon^2\right) \tag{4.3}\]
4.2 Proces błądzenia losowego
Błądzeniem losowym (ang. random walk) nazywa się proces, w którym przyrosty są białym szumem lub przesuniętym białym szumem (w tym drugim przypadku mówimy o błądzeniu losowym z dryftem).
Przykład błądzenia losowego:
\[ y_t = y_{t-1} + \varepsilon_t; \:\:\: \varepsilon_t \sim \mathcal{N}\left(0, \sigma_\varepsilon^2\right) \tag{4.4}\]
Przykład błądzenia losowego z dryftem:
\[ y_t = \alpha + y_{t-1} + \varepsilon_t; \:\:\: \varepsilon_t \sim \mathcal{N}\left(0, \sigma_\varepsilon^2\right) \tag{4.5}\]
Symulacja:
# pojedynczy szereg
T <- 100
alpha <- 0.1
phi <- 1
sigma_eps <- 0.5
yt <- numeric(T)
yt[1] <- 0
for (t in 2:T) {
yt[t] <- alpha + phi*yt[t-1] + rnorm(1, 0, sigma_eps)
}
plot(yt, type="l")
# wiele szeregów i wykresy pudełkowe
nsim <- 1e3
w <- replicate(nsim,{
yt <- numeric(T)
yt[1] <- 0
for (t in 2:T) {
yt[t] <- alpha + phi*yt[t-1] + rnorm(1, 0, sigma_eps)
}
yt}
)
boxplot(t(w), pch='.')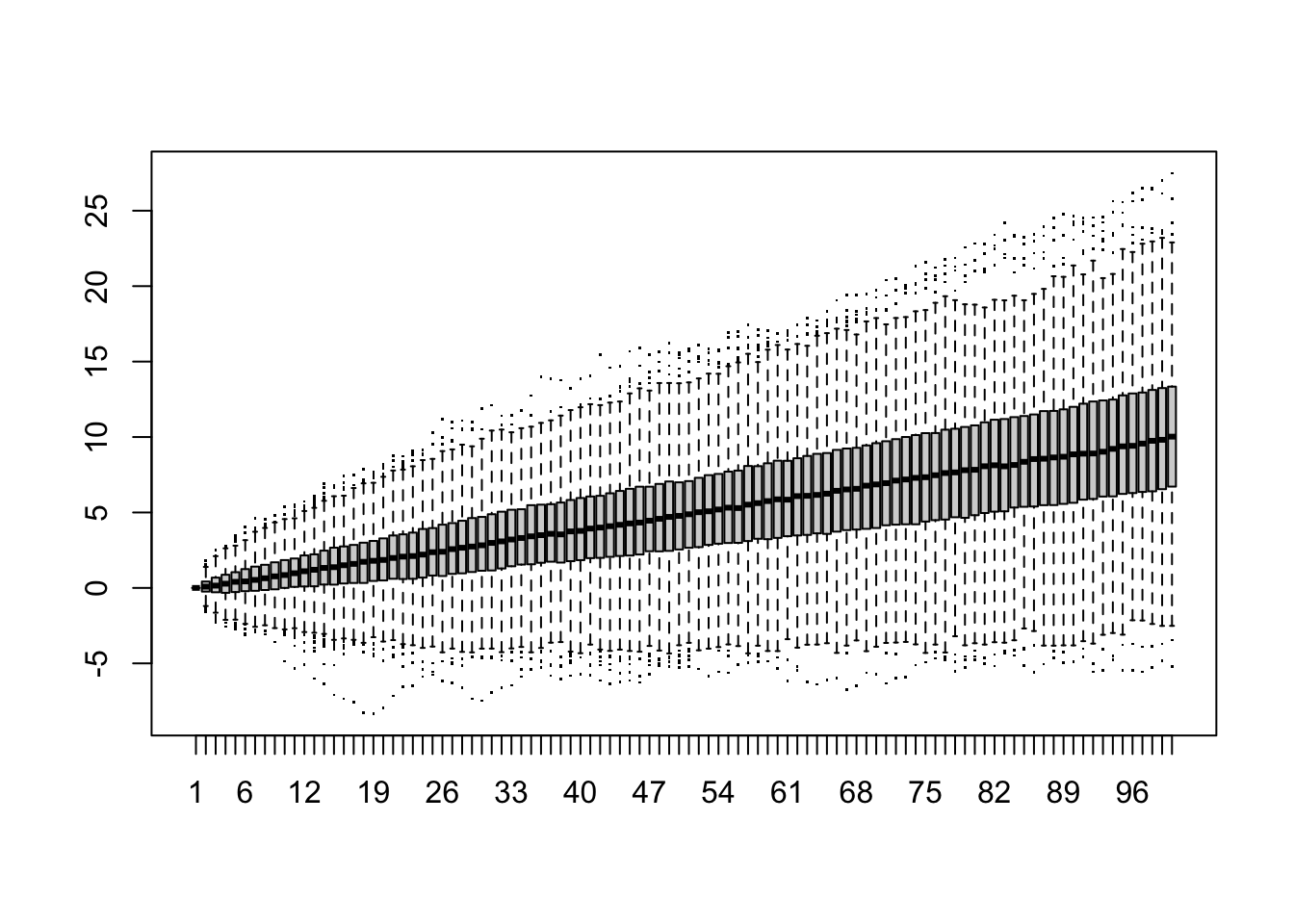
4.3 Procesy zintegrowane, procesy z pierwiastkiem jednostkowym
Proces zintegrowany (stopnia 1, I(1)) to taki proces, który po jednokrotnym różnicowaniu (obliczeniu różnic i stworzeniu w ten sposób procesu pochodnego) staje się stacjonarny. Ponieważ przyrosty w takim procesie są stacjonarne, proces taki nazywa się też przyrostostacjonarnym (ang. difference stationary).
Proces zintegrowany stopnia k (I(k)) wymaga k-krotnego różnicowania, żeby stać się stacjonarnym.
Proces stochastyczny z pierwiastkiem jednostkowym to proces, dla którego przynajmniej jeden z pierwiastków w wielomianie charakterystycznym jego modelu autoregresyjnego (AR) wynosi 1.
Pojęcia procesu z pierwiastkiem jednostkowym i procesu zintegrowanego są pokrewne, ale nie tożsame. Na przykład proces z pierwiastkiem jednostkowym po różnicowaniu może być niestacjonarny ze względu na heteroskedastyczność.
Proces błądzenia losowego jest procesem zintegrowanym I(1) i ma pojedynczy pierwiastek jednostkowy.
Inne przykłady procesów z pierwiastkiem jednostkowym:
\[y_t = y_{t-1} - 0{,}2y_{t-2} + \varepsilon_t \tag{4.6}\]
\[y_t = 1{,}5y_{t-1} - 0{,}5y_{t-2} + \varepsilon_t \tag{4.7}\]
\[y_t = 2y_{t-1} - y_{t-2} + \varepsilon_t \tag{4.8}\]
Pierwsze dwa procesy mają pojedynczy pierwiastek jednostkowy, trzeci z nich ma podwójny pierwiastek jednostkowy.
Symulacja:
# pojedynczy szereg
T <- 100
phi1 <- 2
phi2 <- -1
sigma_eps <- 0.5
yt <- numeric(T)
yt[1] <- 0
yt[2] <- 0
for (t in 3:T) {
yt[t] <- alpha + phi1*yt[t-1] + phi2*yt[t-2] + rnorm(1, 0, sigma_eps)
}
plot(yt, type="l")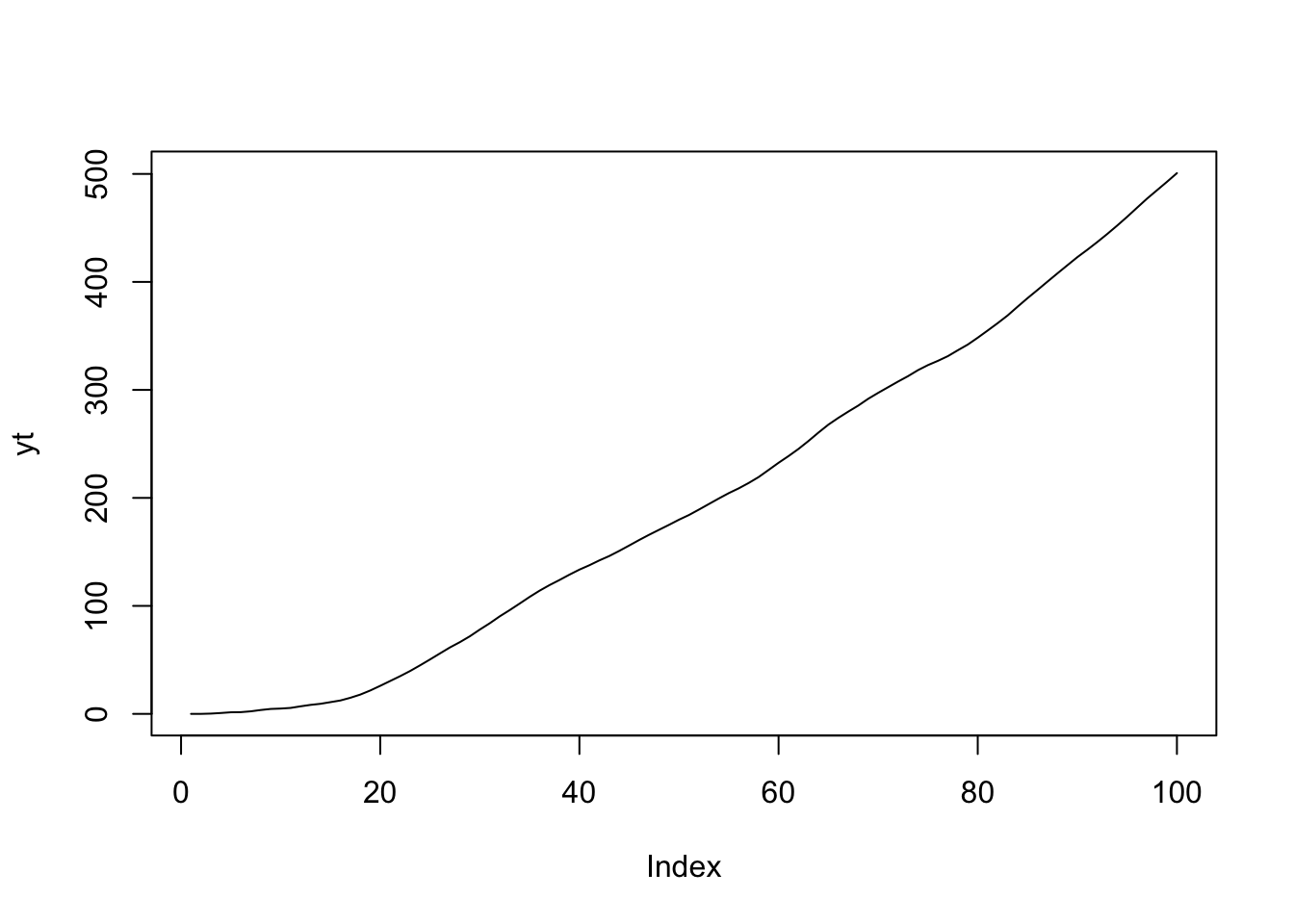
# wiele szeregów i wykresy pudełkowe
nsim <- 1e3
w <- replicate(nsim,{
yt <- numeric(T)
yt[1] <- 0
yt[2] <- 0
for (t in 3:T) {
yt[t] <- alpha + phi1*yt[t-1] + phi2*yt[t-2] + rnorm(1, 0, sigma_eps)
}
yt}
)
boxplot(t(w), pch='.')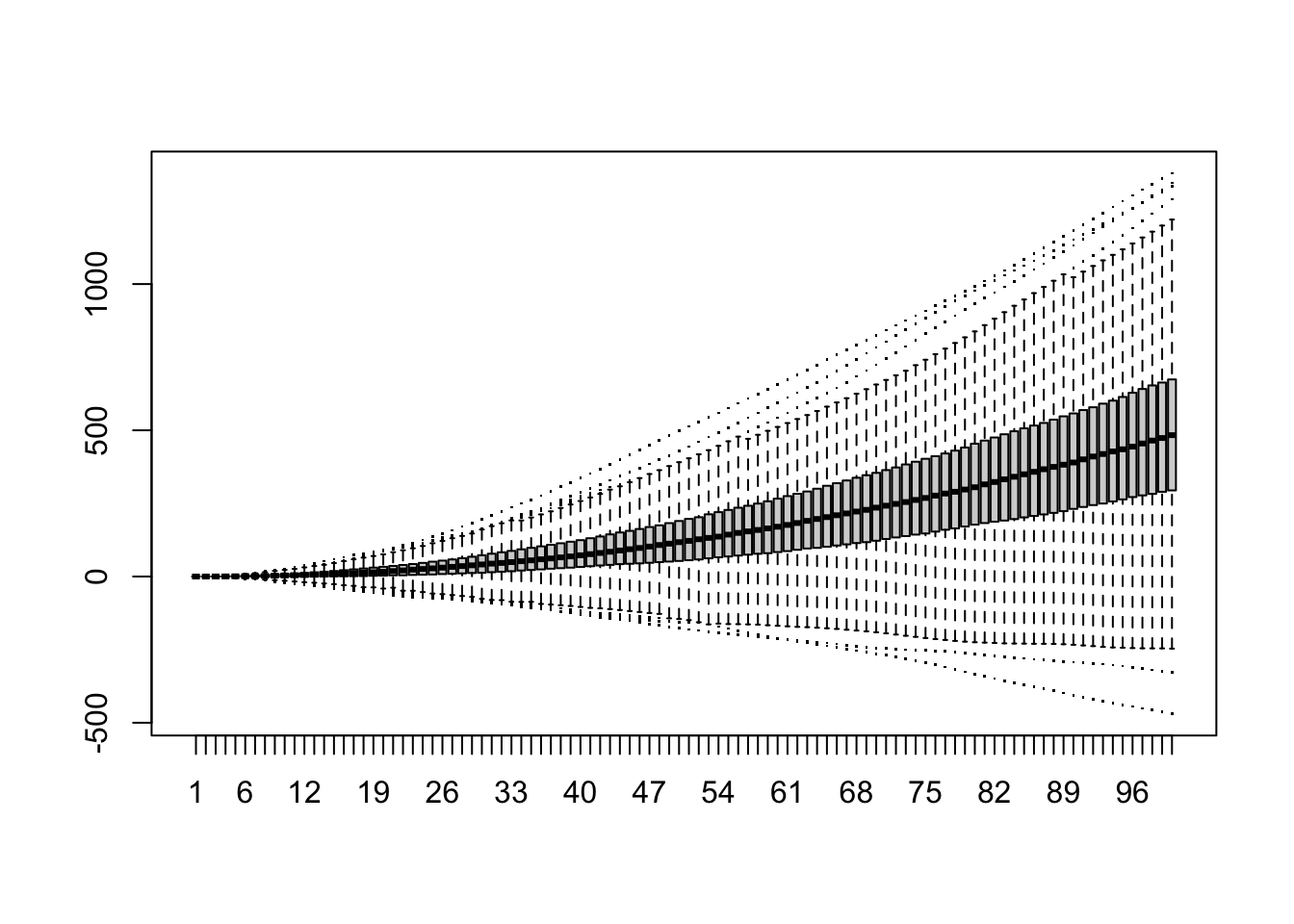
4.4 Proces z trendem deterministycznym
Proces z trendem deterministycznym to taki proces, którego wzór zawiera komponent będący funkcją czasu, czyli np.:
\[y_t = f(t) + ... + \varepsilon_t\]
Proces, który po eliminacji trendu jest stacjonarny nazywany jest procesem trendostacjonarnym (ang. trend stationary).