Rozdział 7 Współczynnik Giniego

Współczynnik Giniego to miara stosowana często do oceny stopnia koncetracji dochodów lub majątku.

7.1 Definicja i pierwszy wzór

Jeżeli mamy szereg szczegółowy posortowany rosnąco, współczynnik Giniego możemy wyznaczyć na podstawie następującego wzoru:

\[\begin{equation} G = {\frac {\sum _{i=1}^{n}(2i-n-1)x_{(i)}}{{n^{2}}{\overline {x}}}}, \tag{7.1} \end{equation}\]

gdzie \(n\) to łączna liczba obserwacji, \(i\) to indeks kolejnej obserwacji przyjmujący wartości od 1 do \(n\), \(\overline{x}\) to średnia wartość cechy X (np. dochodu, majątku), \(x_{(i)}\) to dochód \(i\)-tej obserwacji (np. \(i\)-tej osoby, gospodarstwa domowego) dla obserwacji posortowanych rosnąco.

Współczynnik Giniego przyjmuje wartość zerową w sytuacji, gdy zmienna X nie jest w ogóle zróżnicowana (tzn. przykładowo, dla zmiennej dochód, wszyscy zarabiają tyle samo). Gini zbliża się do jedności, gdy występuje maksymalna koncentracja zmiennej X (dla dochodów -- jedna osoba "zgarnia" cały dochód, dochody pozostałych są równe zero).

Współczynnik Giniego dla Polski wynosi...

7.2 Interpretacja graficzna i drugi wzór

Współczynnik Giniego ma swoją interpretację graficzną opartą na tzw. krzywej Lorenza.

## [1] 34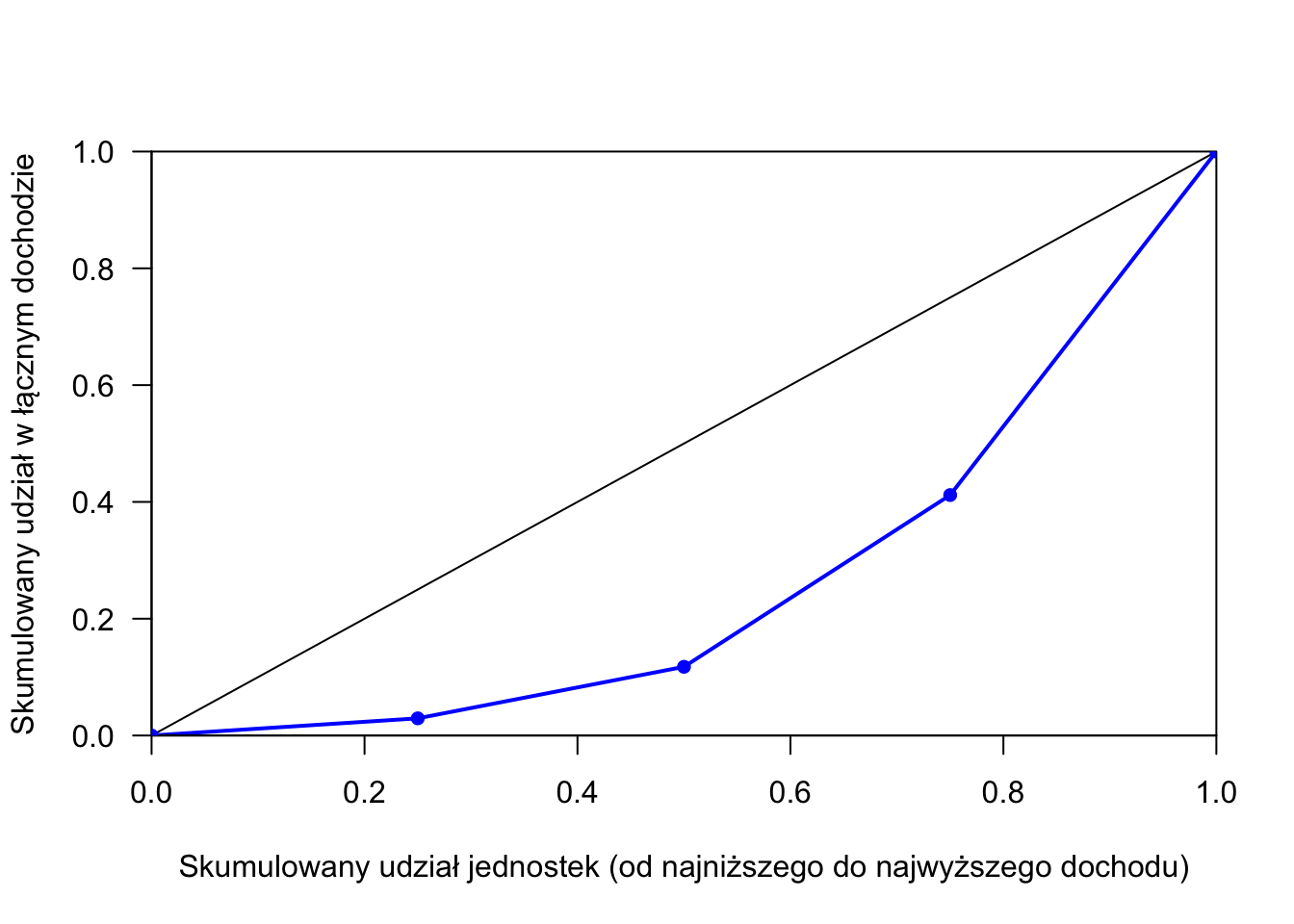

Rysunek 7.1: Przykładowa krzywa Lorenza dla czteroosobowej grupy o dochodach równych 1, 3, 10 i 20

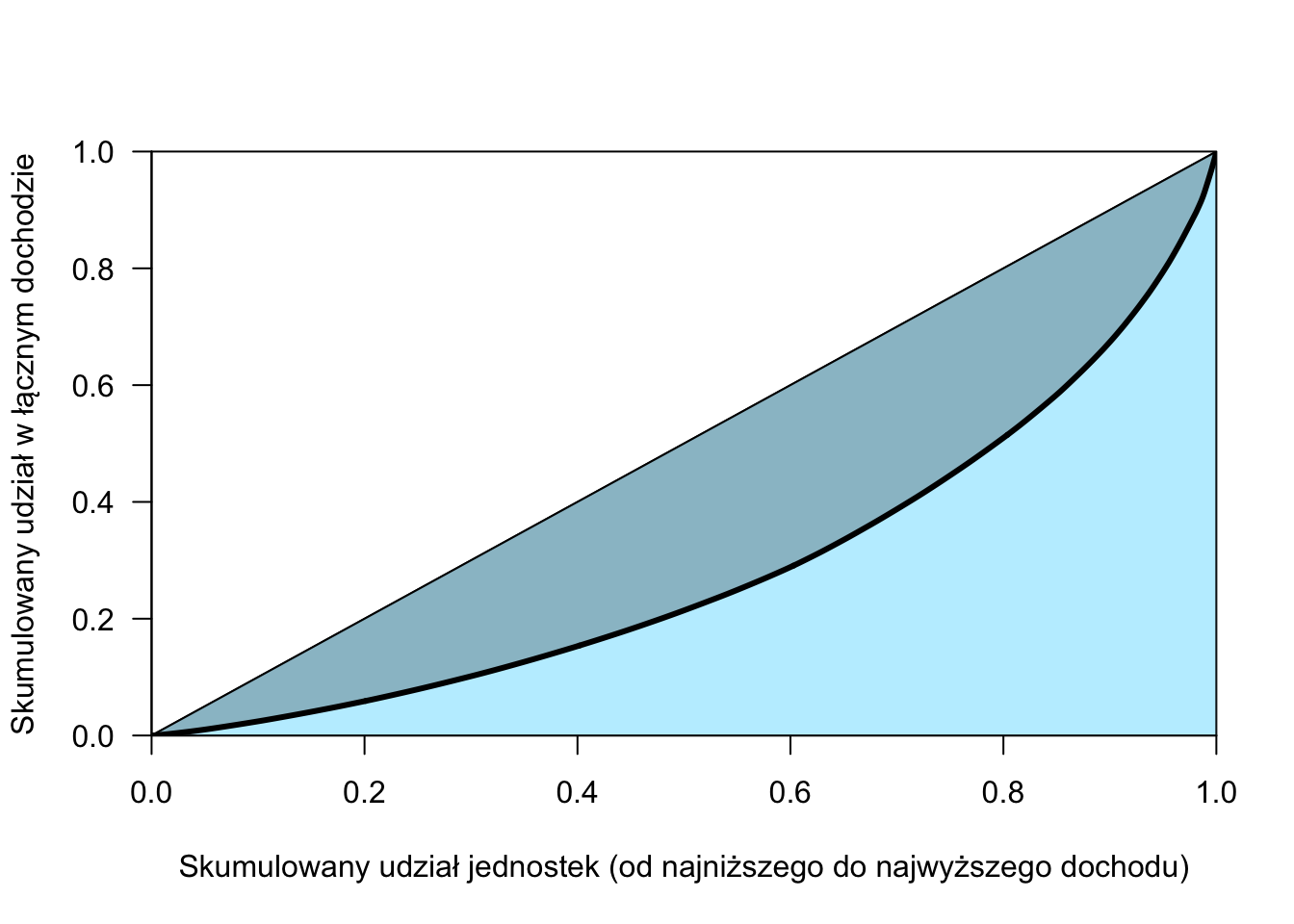
Rysunek 7.2: Współczynnik Giniego to stosunek ciemniejszego obszaru do całego niebieskiego trójkąta