12.1 Teste T
O teste t-independente é uma ferramenta estatística utilizada para testar hipóteses. Nesse contexto, ele avalia duas hipóteses mutuamente excludentes: a hipótese nula (H0) e a hipótese alternativa (H1).
A decisão sobre qual hipótese é mais plausível baseia-se no valor de p obtido pelo teste, comparado ao nível de significância (α), que é previamente estabelecido. O nível de significância mais comumente adotado é de 5% (0,05).
Se o valor de p for maior que 0,05, não rejeitamos a hipótese nula (H0). Por outro lado, se o valor de p for menor ou igual a 0,05, rejeitamos a H0 e aceitamos a hipótese alternativa (H1).
Considere dois grupos independentes, denominados A e B. As hipóteses testadas no contexto de um teste t-independente são formuladas da seguinte forma:
H0: A média do grupo A é igual à média do grupo B H1: A média do grupo A é diferente da média do grupo B
Esse procedimento permite avaliar se há evidências suficientes para concluir que as médias dos dois grupos diferem de forma significativa, considerando os dados observados.
Vamos utilizar um banco de dados proveniente do tutorial: https://fernandafperes.com.br/blog/teste-t-independente/
Essa tabela traz informações sobre notas de diversos alunos segundo gênero, tipo de escola e posição na sala de aula. Vamos utilizar um teste T para compreender a relação entre notas de História e Biologia e a posição dos alunos na sala.
12.1.1 Checando os pressupostos
Os dois principais pressupostos de um teste t (t de Student) são:
Normalidade dos Dados: Assume-se que as distribuições dos dados em cada grupo são aproximadamente normais. Isso é especialmente importante para amostras pequenas. Esse pressuposto pode ser verificado por testes de normalidade (como Shapiro-Wilk ou Kolmogorov-Smirnov) ou por inspeção visual (histogramas ou gráficos Q-Q).
Homogeneidade de Variâncias: Presume-se que as variâncias dos dois grupos são iguais (ou homogêneas). Esse pressuposto é avaliado com testes como o teste de Levene ou o teste de Bartlett. Caso esse pressuposto seja violado, uma versão alternativa do teste t (como o teste t de Welch) pode ser utilizada.
Para checar a normalidade usaremos para isso o pacote tidyverse, para separação dos grupos, e o pacote rstatix para aplicar o teste de Shapiro (função shapiro_test) a cada grupo e nota.
## # A tibble: 4 × 4
## Posicao_Sala variable statistic p
## <chr> <chr> <dbl> <dbl>
## 1 Frente Nota_Biol 0.985 0.993
## 2 Frente Nota_Hist 0.894 0.0759
## 3 Fundos Nota_Biol 0.900 0.0686
## 4 Fundos Nota_Hist 0.917 0.131O teste de Shapiro-Wilk tem como hipóteses: H0: os dados seguem a distribuição normal H1: os dados não seguem a distribuição normal. Se o valor p>0.05, não vamos rejeitar a hipótese H0, ou seja, vamos considerar que todos apresentam distribuição normal.
Para verificarmos a homogeneidade de variâncias, que pode ser avaliada pelo teste de Levene.
Para a nota de Biologia:
## Warning in leveneTest.default(y = y, group = group, ...): group coerced to factor.## Levene's Test for Homogeneity of Variance (center = mean)
## Df F value Pr(>F)
## group 1 1.0359 0.3169
## 30Para a nota de História:
## Warning in leveneTest.default(y = y, group = group, ...): group coerced to factor.## Levene's Test for Homogeneity of Variance (center = mean)
## Df F value Pr(>F)
## group 1 14.292 0.0006954 ***
## 30
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1O teste de Levene apresenta as hipóteses: H0: os grupos apresentam variâncias homogêneas H1: os grupos não apresentam variâncias homogêneas. Para a nota de Biologia, p> 0.05, logo consideraremos que os grupos apresentam variâncias homogêneas. Para a nota de História p <0.05, logo podemos considerar que o pressuposto da homogeneidade de variâncias foi violado.Nós poderemos seguir com o teste-t, mas deveremos usar um teste-t com correção para essa violação da homogeneidade, a correção de Welch.
12.1.2 Teste T
Realizamos primeiramente um teste T para as notas de Biologia segundo posição dos alunos na sala. Especificamos var.equal=TRUE para indicar que as variâncias são homogêneas nesse caso.
##
## Two Sample t-test
##
## data: Nota_Biol by Posicao_Sala
## t = 4.6027, df = 30, p-value = 7.136e-05
## alternative hypothesis: true difference in means between group Frente and group Fundos is not equal to 0
## 95 percent confidence interval:
## 1.411664 3.663630
## sample estimates:
## mean in group Frente mean in group Fundos
## 6.520000 3.982353Encontramos um p<0.05, logo vamos rejeitar a H0.
Adaptando para essa situação, teremos:
H0: média das notas de biologia do grupo Frente =média das notas de biologia do grupo Fundos
H1: média das notas de biologia do grupo Frente ≠média das notas de biologia do grupo Fundos
Assim, vamos considerar que os dois grupos apresentam notas de biologia que são, em média, estatisticamente diferentes.
Agora, realizaremos um teste T para as notas de História. Vamos especificar var.equal=FALSE, pois as variâncias não são homogêneas. Isso nos ajuda a aplicar o teste de Welch.
##
## Welch Two Sample t-test
##
## data: Nota_Hist by Posicao_Sala
## t = 1.5737, df = 19.909, p-value = 0.1313
## alternative hypothesis: true difference in means between group Frente and group Fundos is not equal to 0
## 95 percent confidence interval:
## -0.3860238 2.7546513
## sample estimates:
## mean in group Frente mean in group Fundos
## 5.466667 4.282353Encontramos um valor de p de 0,1313, ou seja, devemos aceitar H0. No caso da nota de História, não temos evidências para afirmar que as médias dos grupos Frente e Fundos são estatisticamente diferentes.
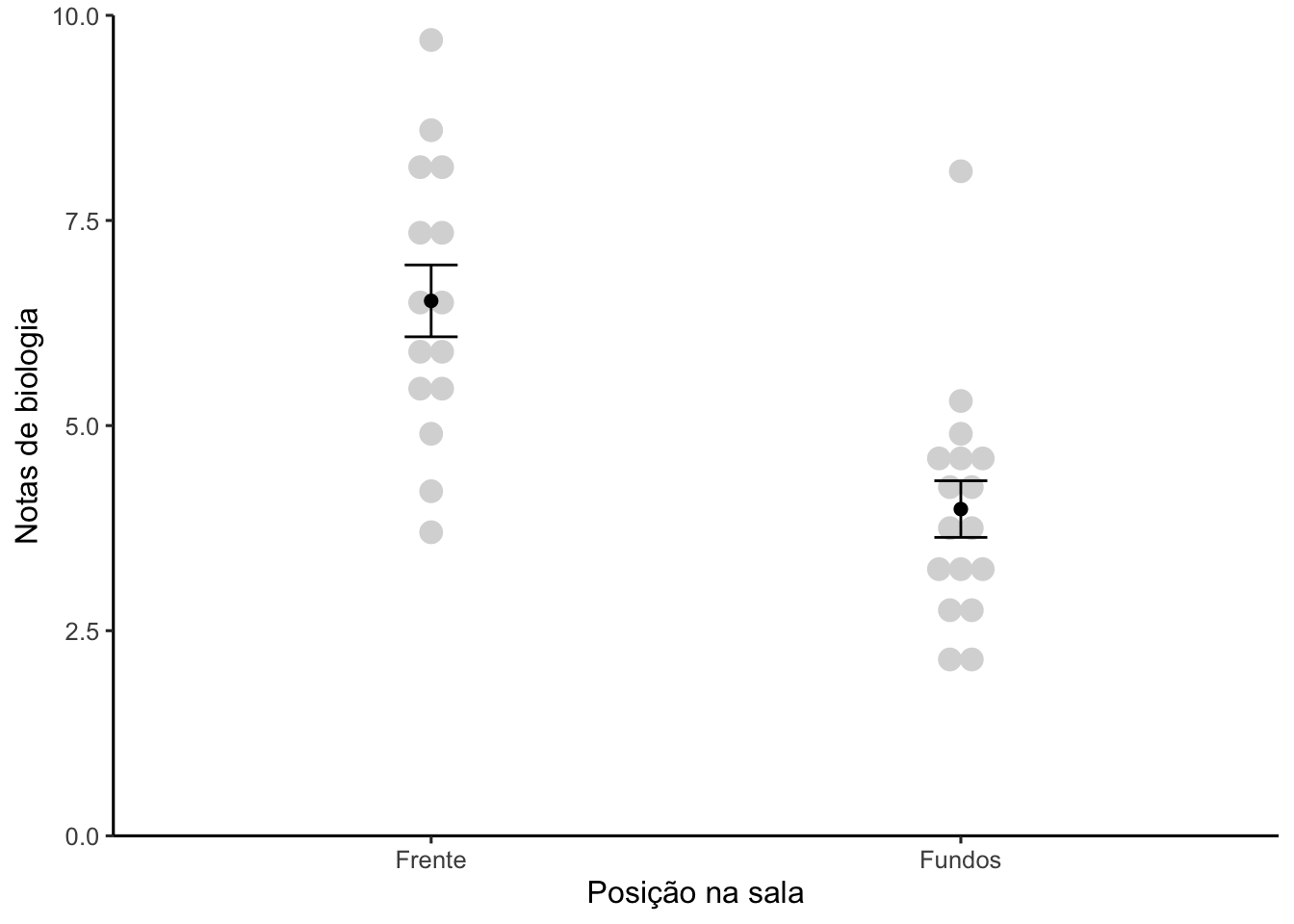
12.1.3 Representação
Por fim, podemos utilizar um gráfico para representar o teste T.
aula%>%ggplot(aes(x = Posicao_Sala, y = Nota_Biol)) +
geom_dotplot(binaxis = "y", stackdir = "center",
fill="#D8D8D8", color="#D8D8D8", dotsize = 0.8)+
geom_point(stat = "summary", fun = "mean", size = 2) +
geom_errorbar(stat = "summary", fun.data = "mean_se", width = 0.1)+
ylab("Notas de biologia") +
xlab("Posição na sala") +
scale_y_continuous(limits=c(0,10), expand = c(0,0)) +
theme_classic(base_size=12)## Bin width defaults to 1/30 of the range of the data. Pick better value with `binwidth`.