Chapter 9 Effekte und Kontraste

9.1 Effektgrößen in der ANOVA

Ähnlich wie beim Zweistichproben-t-Test ist es möglich, bei der ANOVA Effektgrößen zu definieren. Es gibt mehrere solher Effektgrößen wobei wir uns im folgenden mit dem sogenannten Eta-squared \(\eta^2\) beschäftigen werden. Bei jeder signifikanten ANOVA ist logischerweise die Effektgröße von Relevanz, da diese der ausschlaggebende Faktor war, der zum signifikanten Ergebnis geführt hat, neben der Stichprobengröße und dem ausgewählten \(\alpha\)-Fehler. Allgemein ist das \(\eta^2\) folgendermaßen definiert:

\(\eta^2=\frac{QS_{Effekt}}{QS_{tot}}\)

Man erkennt, dass das \(\eta^2\) aus einem Quotienten berechnet wird, wobei im Nenner die totale Quadratsumme und im Zähler der Effekt des jeweiligen Faktors steht. Folglich repräsentiert Eta-squared denjenigen Anteil an der Gesamtvarianz \(QS_{tot}\), welcher durch einen bestimmten Faktor erklärt wird \(QS_{Effekt}\) (die Interpretation von Eta-squared ähnelt also der Interpretation des Determinationskoeffizienten). Bei der einfaktoriellen ANOVA ist die Bestimmung der Effektgröße relativ simpel:

\(\eta^2=\frac{QS_{zw}}{QS_{tot}}\)

Man setzt die Quadratsumme zwischen die Gruppen ins Verhältnis zur totalen Quadratsumme. Dadurch erhält man denjenigen Anteil an der totalen Variation, die durch die Variation zwischen den Gruppen aufgeklärt wird. Hieran erkennt man auch, dass \(\eta^2\) minimal 0 sein kann und niemals größer als 1 sein kann (theoretisch gesehen kann sie auch nicht 1 sein, da es ansonsten keine signifikante ANOVA geben kann). Bei der zweifaktoriellen ANOVA gibt es mehrere \(\eta^2\) für jeden Faktor und die Interaktionzwischen den Faktoren, die man folgendermaßen berechnet:

\(\eta^2_{A}=\frac{QS_{A}}{QS_{tot}}\) \(\eta^2_{B}=\frac{QS_{B}}{QS_{tot}}\) \(\eta^2_{AxB}=\frac{QS_{AxB}}{QS_{tot}}\)

Man hat bei diesen Effektgrößen jedoch bemerkt, dass die Effektgröße eines Faktors in der zweifaktorielen bzw. - allgemeiner - in der mehrfaktoriellen ANOVA stets von den Effektgrößen der anderen Faktoren abhängt. Folglich ist die Interpretation der Effektgröße eines Faktors nur im Kontext der anderen Faktoren möglich. Deshalb hat man das partielle Eta-Squared erstellt, bei welchem die Effektgröße eines Faktors so berechnet wird, dass die totale Variation vorher um den Effekt der anderen Faktoren und ihre Interaktionen bereinigt wurde:

\(\eta^2_{A}=\frac{QS_{A}}{QS_{A}+QS_{inn}}\) \(\eta^2_{B}=\frac{QS_{B}}{QS_{B}+QS_{inn}}\) \(\eta^2_{AxB}=\frac{QS_{AxB}}{QS_{AxB}+QS_{inn}}\)

Das partielle \(\eta^2\) gibt den durch den Faktor erklärten Anteil an der Gesamtvarianz an, nachdem die Varianz um den Effekt der anderen Faktoren bereinigt wurde.

9.2 Kontraste

9.2.1 Einführung

Nach einer signifikanten ANOVA könnte man sich dafür interessieren, auf welche Weise sich Mittelwerte voneinader unterscheiden. Mit Hilfe von Kontrasten ist es möglich, anwenderspezifische Mittelwertsunterschiede zwischen Gruppen zu testen. Es ist nicht nur möglich zu untersuchen, ob eine Gruppe sich deutlich von den anderen Gruppen unterscheidet, man kann darüber hinaus auch bestimmte Trends mit Kontrasten untersuchen. Beispielsweise könnte man vielleicht untersuchen, ob die Effektivität eines Medikaments einem linearen Trend folgt, also dass mit einer höheren Dosis die Effektivität ansteigt. Man unterscheidet bei Kontrasten zwischen einfachen und komplexen Kontrasten: Bei einfachen Kontrasten werden nur zwei Gruppen miteinander verglichen, während bei komplexen Kontrasten mehr als zwei Gruppen miteinander verglichen werden.

9.2.2 Kontrast \(\psi\)

Die Kontrastgleichung sieht folgendermaßen aus: \(\psi=c_{1}\mu_{1}+...+c_{k}\mu_{k}\)

Ein Kontrast ist folglich die gewichtete Summe der Gruppenmittelwerte, wobei die Gewichtung mit Hilfe von sogenantnen Kontrastkoeffizienten \(c_{k}\) für die zusätzlich gilt: \(c_{1}+...+c_{k}=0\). Die Nullhypothese bei Kontrasten ist stets \(H_{0}:\psi=0\), d.h. es wird gegen die Nullhypothese getestet, dass der Kontrast in der Population Null ergibt. Die Hauptschwierigkeit bei Kontrasten besteht darin, von dem Kontrast, welchen wir untersuchen möchten (z.B. einen linearen Trend überprüfen), zu den konkreten Kontrastkoeffizienten zu kommen. Später in diesem Kapitel wird dies an mehreren Beispielen behandelt. Es ist möglich, merhere Kontraste gleichzeitig zu testen. Dabei spricht man von sogenannten orthogonalen Kontrasten wenn die beiden Kontrasten zwei nicht-redundante Hypothesen testen. Damit ist gemeint, dass die beiden Kontraste keine inhaltlich überlappenenden Aussagen überprüfen. Wenn ein Faktor aus K Gruppen besteht, ist es möglich, K-1 orthogonale Kontraste zu testen. Wenn jedoch mehr als K-1 Kontraste getestet werden, so werden unweigerlich einzelne Kontraste redundante Informationen enthalten. Wir haben einmal gelernt, dass bei einer multiplen Anwendung eines Tests die sogenannte Bonferroni-Korrektr angewendet wird um den \(\alpha\)-Fehler in den einzelnen Tests zu kontrollieren. Dies gilt auch für Kontraste. Der Vorteil orthogonaler Kontraste ist die Tatsache, dass durch die Bonferroni-Korrektur keine Teststärke verlorengeht, da die Kontraste inhaltlich nicht überlappen. Wenn jedoch redundante Kontraste zusätzlich getestet werden, geht Teststärke verloren durch die Bonferroni-Korrektur, da die individuellen Tests ünnötigerweise konservativer werden. Zwei Kontraste sind dann orthogonall, wenn die Kreuzprouduktsumme der Koeffizienten Null ergibt: \(c_{1}d_{1}+...+c_{k}+d_{k}=0\). Im Folgenden werden anhand von einem Beispiel mehrere Kotnraste getestet.

9.2.3 Beispiel

Stellen wir uns vor, wir möchten die allgemeine Fitness von Vegetariern, Veganern und Fleischessern untersuchen. Dabei erfassen wir auf einer Skala von 1-10 die Fitness \(n=10\) Probanden aus den jeweiligen Gruppen und erhalten folgende Mittelwerte:

Fleischesser: \(\mu_{1}= 3\)

Vegetarier: \(\mu_{2}=4.5\)

Veganer: \(\mu_{3}=8\)

Die einfaktorielle ANOVA war signifikant und wir haben als zusätzliche Information \(MQS_{inn}=15\).

9.2.4 Vergleich einer Gruppe gegen die restlichen Gruppen

Wir möchten nun untersuchen, ob die mittlere allgemeine Fitness der Veganer sich von den Vegetariern und Fleischessern unterscheidet. Dabei müssen wir die Kontrastkoeffizienten so gewichten, dass sie zum einen in der Summe Null ergeben und zum anderen die Verhältnisse zwischen den drei Gruppen berücksichtigen. Genauer gesagt müssen wir beachten, dass wennn wir die Gruppe der Veganer gegen den Rest vergleichen, theoretisch gesehen eine Gruppe von 10 Personen gegen die restlichen 20 getestet werden. Folglich müssen wir dieses Ungleichgewicht mit in unserer Rechnung einbauen. Bei einem Gruppenvergleich von einer Gruppe gegen den Rest gilt i.d.R. folgendes Verhältnis (bei einem balancierten Design):

\(\mu_{1}=\frac{\mu_{2}+....+\mu_{k}}{K-1}\)

Übertragen auf unser Beispiel würden wir folgendes Verhältnis erhalten: \(\mu_{3}=\frac{\mu_{1}+\mu_{2}}{2}\). Wenn wir diese Gleichung nach Null auflösen würden wir folgendes Resultat erhalten: \(\mu_{3}-0.5\cdot \mu_{1}- 0.5\cdot \mu_{2}=0\). Nun haben wir die Kontrastkoeffizienten für unseren Gruppenvergleich gefunden und zwar 1 für \(\mu_{3}\), -0.5 für \(\mu_{1}\) und -0.5 für \(\mu_{2}\). Nun können wir \(\psi\) berechnen nach der obigen Formel:

\(\hat{\psi}=1\cdot 8 - 0.5\cdot 3 - 0.5\cdot 4.5=4.25\)

Als nächstes müssen wir den Standardfehler der Kontrast-Schätzer nach folgender Formel bestimmen:

\(s_{\hat{\psi}}=\sqrt{(\frac{MQS_{inn}}{n_{Gruppe}})\cdot \sum_{k}c_{k}^2}\)

Für unser Beispiel würden wir folgendes Ergebnis erhalten: \(s_{\hat{\psi}}=\sqrt{\frac{15}{10}\cdot (1^2+(-0.5)^2+(-0.5^2))}=\sqrt{1.5\cdot 1.5}=1.5\)

Im letzten Schritt bestimmen wir die t-Prüfgröße für den Kontrast und erhalten:

\(t=\frac{\hat{\psi}}{s_{\hat{\psi}}}=\frac{4.25}{1.5}=2.83\)

Da die t-Prügröße extremer ist als 1.96 (\(\alpha\)-Fehler=0.05) wird die Nullhypothese verworfen, d.h. die allgemeine Fitness der Veganer unterscheidet sich in der Population von den Vegetariern und Fleischessern.

9.2.5 Einfaches Testen

Möglicherweise interessieren wir uns nur dafür, ob sich Veganer von Fleischessern unterscheiden. In diesem Fall geben wir den Mittelwert für die Vegetarier den Kontrastkoeffizient Null, da uns in diesem Kontrast dieser Mittelwert nicht interessiert. Da die Gruppengrößen bei diesem einfachen Vergleich identisch sind, besteht folgendes Verhältnis unterder Nullhypothese:

\(\mu_{3}=\mu_{1}+0\cdot \mu_{2}\) Daraus folgt folgender Kontrast: \(\hat{\psi}=1\cdot \mu_{3}+0\cdot \mu_{2}-1\cdot \mu_{1}= 1\cdot 8-0\cdot 4.5-1\cdot 3=5\)

Als Standardfehler erhalten wir: \(s_{\hat{\psi}}=\sqrt{\frac{15}{10}\cdot (1^2+0^2+(-1)^2)}=\sqrt{3}=1.732\)

Unsere t-Prüfgröße für diesen Kontrast beträgt folglich: \(t=\frac{\hat{\psi}}{s_{\hat{\psi}}}= \frac{5}{\sqrt{3}}=2.887\)

Da die t-Prüfgröße extremer ist als 1.96, wird die Nullhypothese verworfen, d.h. die allgemeine Fitness der Veganer unterscheidet sich in der Population von den Vegetariern und Fleischessern.

Möglicherweise habt ihr bei den beiden Kontrasten gemerkt, dass sie sich inhaltlich etwas überlappen. Wenn man die Kreuzproduktsumme der beiden Kontrastkoeffizienten berechnet, erhält man folgendes Ergebnis \(1\cdot 1+0\cdot (-0.5)+(-1)\cdot (-0.5)=1.5\). Da die Kreuzproduktsumme nicht Null ergeben hat, bedeutet dies, dass die beiden Kontraste nicht orthogonal zueinander sind und inhaltlich redundante Informationen erhalten.

9.2.6 Trendtests

Wie bereits vorhin erwähnt ist es möglich Trendverläufe von Gruppen zu untersuchen. Stellene wir uns vor, wir möchten den Effekt eines Medikaments in unterschiedlichen Dosen untersuchen und erhalten folgende Mittelwerte für \(n=10\) Probanden pro Dosisgruppe:

100mg: \(\mu_{1}=1.5\)

200mg: \(\mu_{2}=3\)

300mg: \(\mu_{3}=4.5\)

Im Folgendne werden wir überprüfen, ob die Effektivität des Medikaments einem linearen oder logarithmischen Trend folgt. Die mittlere Quadratsumme beträgt \(MQS_{inn}=60\)

9.2.6.1 linearer Trendtest

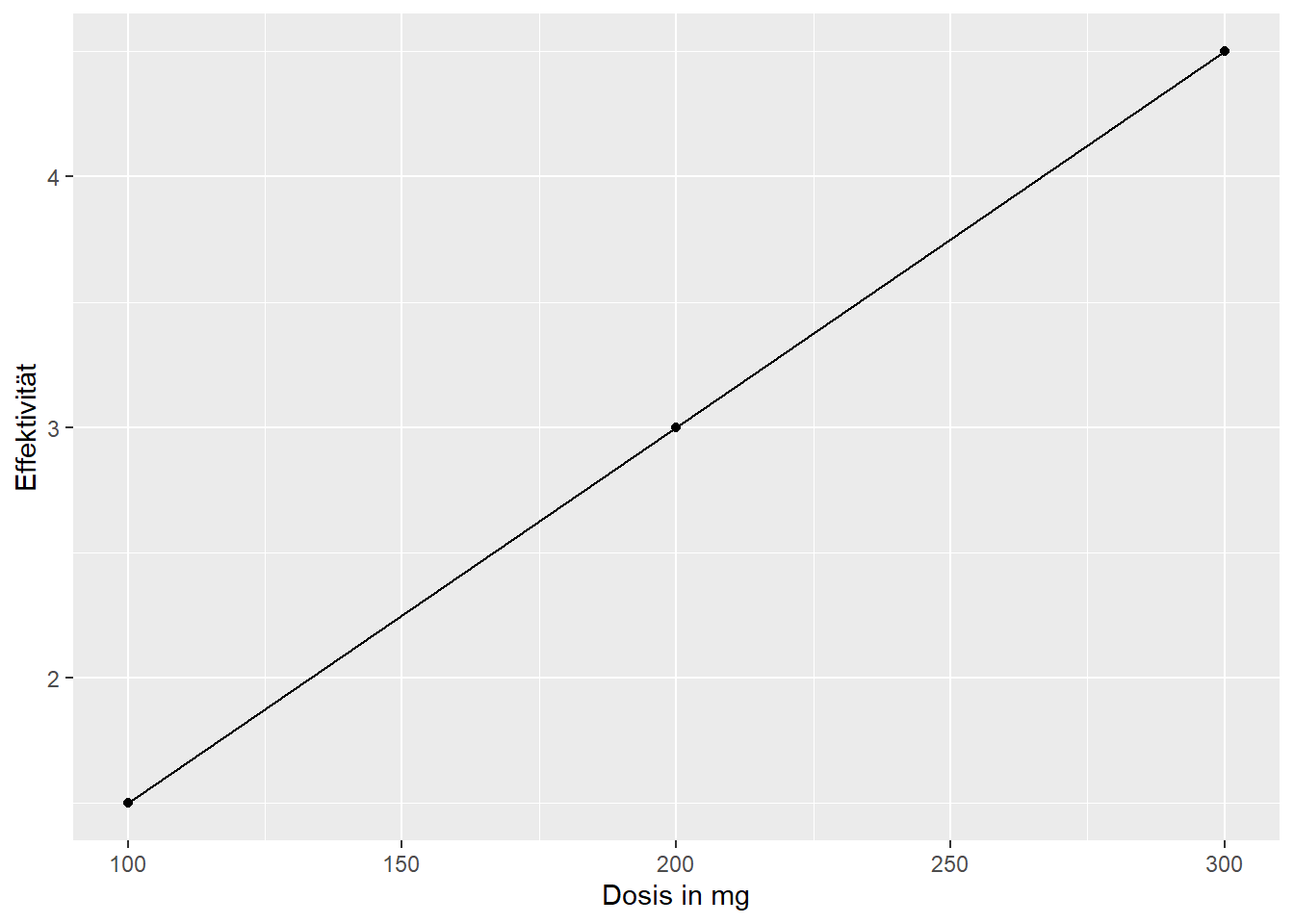
Man erkennt bereits an der visuellen Darstellung, dass die Effektivität des Medikaments eindeutig einem linearen Trend folgt. Gehen wir erstmal jedoch davon aus, dass wir uns nicht sicher sind. Um nun die Kontrastkoeffizienten für den linearen Trendtest zu erhalten, müssen wir folgendes Verhältnis aufstellen:

\(\mu_{3}-\mu_{2}=\mu_{2}-\mu_{1}\) Wenn die Abstande auf der x-Achse zwischen den Gruppen konstant ist, was in unserem Beispiel der Fall ist, da immer 100 mg hinzugefügt wird, sollte dieses Verhältnis in der Effektivität zwischen den drei Gruppen bestehen, wenn diese tatsächlich einem linearen Trend folgt. Es gibt mehrere Verhältnisse in einer linearen Beziehung zwischen zwei Variablen. Beispielsweise kann man auch folgendes Verhätlnis aufstellen: \(\mu_{3}-\mu_{1}=2(\mu_{2}-\mu_{1})\). Foglich kann es dazu kommen, dass mit unterschiedlichen Kontrastkoeffizienten die gleiche inhaltliche Hypothese getestet wird. Dieser Umstand hat jedoch keine Auswirkungen auf die Signifikanzaussage der Kontraste. Wenn wir die erste Formel nun nach Null auflösen, erhalten wir folgende Kontrastgleichung unter der Nullhypothese:

\(\mu_{1}-2\cdot \mu_{2}+\mu_{3}=0\)

Mit diesen Kontrastkoeffizienten können wir nun den Kontrast auf Signifikanz testen.

1.) Berechnung \(\hat{\psi}=1.5-2\cdot 3+ 4.5=0\) (lol)

2.) Berechnung des Standardfehlers der Kontraste: \(s_{\hat{\psi}}=\sqrt{\frac{60}{10}\cdot (1^2+(-2)^2+1^2)}=\sqrt{36}=6\)

3.) Berechnung der t-Prüfgröße: \(t=\frac{0}{6}=0\)

Da die t-Prüfgröße nicht extremer als 1.96 ist, wird die Nullhypothese beibehalten, d.h. die Effektivität des Medikaments folgt einem linearen Trend. Möglicherweise seid ihr jetzt ein bisschen verwirrt, da wir die Nullhypothese beibehalten haben, jedoch trotzdem behaupten, dass die Effektivität einem linearen Trend folgt. Um diesen Umstand zu verstehen, müssen wir uns folgendes vor Augen führen: Die Nullhypothese sagt, dasss der Kontrast in der Population Null ergibt (\(H_{0}: \psi=0\)). In unserer Aufgabe haben wir definiert, dass bei einer linearen beziehung folgendes gelten wird \(\mu_{1}-2\cdot \mu_{2}+\mu_{3}=0\). Dementsprechend bedeutet in unserem Fall ein Kontrast von Null, dass die Mittelwerte einem linearen Trend folgen. Wenn wir die Nullhypothese verworfen hätten würde dies bedeuten, dass unsere Werte einem nichtlinearen Trend folgen, den wir nicht genauer definieren können.

Beim Vergleich einer Gruppe mit mehreren Gruppen hat die Nullhypothese besagt, dass sich die Mittelwerte nicht voneinander unterscheiden und somit folgendes gelten muss:\(\mu_{3}-0.5\cdot \mu_{1}- 0.5\cdot \mu_{2}=0\). Da die t-Prüfgröße jedoch signifikant war, bedeutet dies, dass sich die Mittelwerte in der Population voneinander unterscheiden (mit einer bestimmten Irrtumswahrscheinlichkeit). Ihr müsst stets darauf achten, was die Nullhypothese inhaltlich aussagt bei den Kontrasten, da in Abhängigkeit davon entweder die Null- oder Alternativhypothese das erwünschte Ergebnis ist.

9.2.7 logarithmischer Trendtest

Es ist auch möglich, die Mittelwerte auf alternative Verteilungen zu Testen, wie beispielsweise einem logarithmischen Verlauf. Stellen wir uns vor, wir hätten als Mittelwerte statt den oben genannten Werten folgende Werte erhalten:

100 mg: \(\mu_{1}=4.61\)

200 mg: \(\mu_{2}=5.3\)

300 mg: \(\mu_{3}=5.7\)

Die Idee zur Überprüfung des logarithmischen Trend ist, dass man die Mittelwerte exponiert, damit der Einfluss durch den logarithmus naturalis auf den Kurvenverlauf ausgeglichen wird. Das Resultat wäre in dem Fall eine gerade. Folglich kann man testen, ob ein Mittelwertsverlauf logarithmisch ist, indem man überprüft, ob die Exponentialwerte der MIttelwerte einem linearen Trend folgt. Unsere Kontrastgleichung sieht also folgendermaßen aus:

\(\hat{\psi}=1\cdot e^{\mu_{1}}-2\cdot e^{\mu_{2}}+1\cdot e^{\mu_{3}}=1\cdot e^{4.61}-2\cdot e^{5.3}+1\cdot e^{5.7}=-1.32\)

Im nächsten Schritt berechnen wir den Standardfehler: \(s_{\hat{\psi}}=\sqrt{\frac{60}{10}\cdot (1^2+(-2)^2+1^2)}=6\)

Zuletzt wird die t-Prügröße berechnet: \(t=\frac{-1.32}{6}=-0.22\)

Da die t-Prüfgröße im Betrag nicht extremer als 1.96 ist, wird die Nullhypothese beibehalten, d.h. die Mittelwerte folgen einem logarithmischen Trend in der Population (mit einer bestimmten Irrtumswahrscheinlichkeit). Es ist auch möglich mit Hilfe mehrerer Kontraste eine einzige Hypothese zu überprüfen. Ein grundlegendes Verständnis von Kontrasten und ihrem Zustandekommen können einem vor allem in der Forschung sehr dienlich sein. Falls ihr jedoch nicht weiter wisst, gibt es auch Kontraspläne, in welchem für bestimmte Fälle die Kontrastkoeffizienten angegeben werden.

9.3 Kontrastkodierung und Effektkodierung

Im Folgenden weichen wir vom Thema Kontraste abweichen und beschäftigen uns mit einem besonderen Fall der multiplen Regression und zwar wenn wir einen kategorialen Prädiktor haben. Das Problem bei einem kategorialen Prädiktor ist die Tatsache, dass dieser keine intervallskalierte Variable darstellt und dementsprechend die Abstände zwischen den kodierten Gruppen nicht konstant ist. Als Lösung für dieses Problem gibt es die Kontrastkodierung. Um es kurzzufassen wird bei der Kontraskodierung eine Gruppe der kategorialen Variable zur Referenzgruppe \(b_{0}\). Die restlichen Gruppen werden in insgesamt K-1 dichotome Variablen unterteilt, wobei jeder dieser Variablen nur dann den Wert 1 annimmt, wenn man die jeweilige Gruppe betrachtet. Die Regressionsgewichte \(b_{j}\)dieser dichotomen Variablen \(D_{j}\) stehen dabei für die Differenz der Gruppenvariable vom Referenzgruppenmittelwert. Am ende haben wir dann folgende Gleichung: \(y=b_{0}+b_{1}D_{1}+....+b_{j}D_{j}\). Bei der Effektkodierung ist \(b_{0}\) der Gesamtmittelwert und \(b_{j}\) die Abweichungen der Grupenmittelwerte vom Gesamtmittelwert. Die ursprüngliche Referenzkategorie hat auf den ursprünglich dichotomen Variablen nun die Ausprägung -1.