Chapter 6 Lab 4 - 04/11/2022
In questa lezione vedremo:
- la stima kernel della densità
- come gestire i valori mancanti (NA) presenti in un data frame;
- come ottenere e rappresentare graficamente la funzione di ripartizione empirica;
- come fittare una distribuzione teorica a un campione di dati.
6.1 Data frame con valori mancanti
Per questo laboratorio useremo un nuovo set di dati disponibile nel file posteitit.csv. Si procede quindi con l’importazione dei dati come mostrato nel laboratorio 2 (Sezione @ref(#dataimport)) facendo però attenzione al fatto che la colonna dei prezzi contiene dei valori mancanti indicati con NA. Sarà quindi necessario ad andare a specificare NA nell’apposita cella denominata na della finestra che compare quando si usa l’opzione Import Dataset - From Excel. L’oggetto di tipo data frame e denominato posteit verrà quindi creato:
library(readxl)
posteit <- read_excel("data/posteit.xlsx", na = "NA")Come si può notare l’opzione na = "NA" è quella che si occupa di interpretare le stringhe "NA" come valori mancanti.
Controlliamo la struttura del data frame usando il seguente codice
str(posteit)## tibble [1,213 × 2] (S3: tbl_df/tbl/data.frame)
## $ Date : POSIXct[1:1213], format: "2017-01-10" "2017-01-11" ...
## $ PSTadj: num [1:1213] 4.71 4.72 4.68 4.73 4.65 ...dal cui output si nota che la variabili che contiene il prezzo del titolo posteit (PSTadj) è di tipo num (i.e. variabili quantitative continue). Attenzione: se la variabile è codificata come chr vuol dire che c’è stato un problema con l’import dei dati! Provate a ripetere l’operazione.
Inoltre la funzione summary può essere utilizzata per ottenere le principali statistiche descrittive per ogni variabile contenuta nel data frame:
summary(posteit)## Date PSTadj
## Min. :2017-01-10 00:00:00 Min. : 4.461
## 1st Qu.:2018-03-20 00:00:00 1st Qu.: 5.518
## Median :2019-06-04 00:00:00 Median : 7.213
## Mean :2019-06-01 19:15:05 Mean : 7.414
## 3rd Qu.:2020-08-13 00:00:00 3rd Qu.: 8.966
## Max. :2021-10-20 00:00:00 Max. :12.555
## NA's :3Si mette in evidenza che la variabile PSTadj presenta tre valori mancanti indicati come NA (not available, non disponibili), ovvero tre giorni per i quali il prezzo non è disponibile.
Si noti che in presenza di valori mancanti in un vettore per calcolare ad esempio la media o la mediana (così come altre statistiche descrittive) è necessario includere l’opzione na.rm = TRUE:
mean(posteit$PSTadj, na.rm = TRUE)## [1] 7.413583median(posteit$PSTadj, na.rm = TRUE)## [1] 7.212518In questo caso il numero di osservazioni utilizzate per il calcolo degli indici è pari a 1210 e non 1213.
Al fine di identificare in quali giorni sono presenti i dati mancanti viene usata la funzione is.na che restituisce, per ogni elemento in un vettore, TRUE o FALSE a seconda che l’elemento sia mancante oppure no. Si vede ad esempio che i primi 6 valori di posteit$PSTadj, recuperabili con head() sono non mancanti (FALSE).
head(is.na(posteit$PSTadj))## [1] FALSE FALSE FALSE FALSE FALSE FALSEPer andare a visualizzare i valori mancanti (quelli per cui la condizione is.na restituisce TRUE) si utilizza il metodo di selezione per condizione visto nel laboratorio 1 (sezione 3.2):
posteit[is.na(posteit$PSTadj), ] #solo le righe con NA, tutte le colonne## # A tibble: 3 × 2
## Date PSTadj
## <dttm> <dbl>
## 1 2017-01-27 00:00:00 NA
## 2 2020-08-20 00:00:00 NA
## 3 2021-08-27 00:00:00 NAUna possibile soluzione consiste nell’eliminare i valori mancanti e creare un nuovo data frame contenente solo i valori non mancanti. In alternativa, invece di creare un nuovo data frame, è possibile sostituire i valori mancanti dentro posteit con un valore come ad esempio la media o la mediana dei valori non mancanti:
#si selezionano le righe con valori di PSTadj non mancanti &
#si seleziona la seconda colonna dei prezzi
posteit[is.na(posteit$PSTadj) , 2] =
median(posteit$PSTadj, na.rm = TRUE)
summary(posteit)## Date PSTadj
## Min. :2017-01-10 00:00:00 Min. : 4.461
## 1st Qu.:2018-03-20 00:00:00 1st Qu.: 5.520
## Median :2019-06-04 00:00:00 Median : 7.213
## Mean :2019-06-01 19:15:05 Mean : 7.413
## 3rd Qu.:2020-08-13 00:00:00 3rd Qu.: 8.965
## Max. :2021-10-20 00:00:00 Max. :12.555Si noti che ora posteit non ha valori mancanti.
Dopo aver eliminato i dati mancanti è possibile ora procedere con il calcolo dei rendimenti logaritmici così come descritto nella Sezione ??. Un nuovo oggetto di nome logret viene quindi creato:
logret = diff(log(posteit$PSTadj))6.2 KDE
Il grafico della stima kernel della densità (KDE) si può ottenere usando le funzioni plot e density:
plot(density(logret))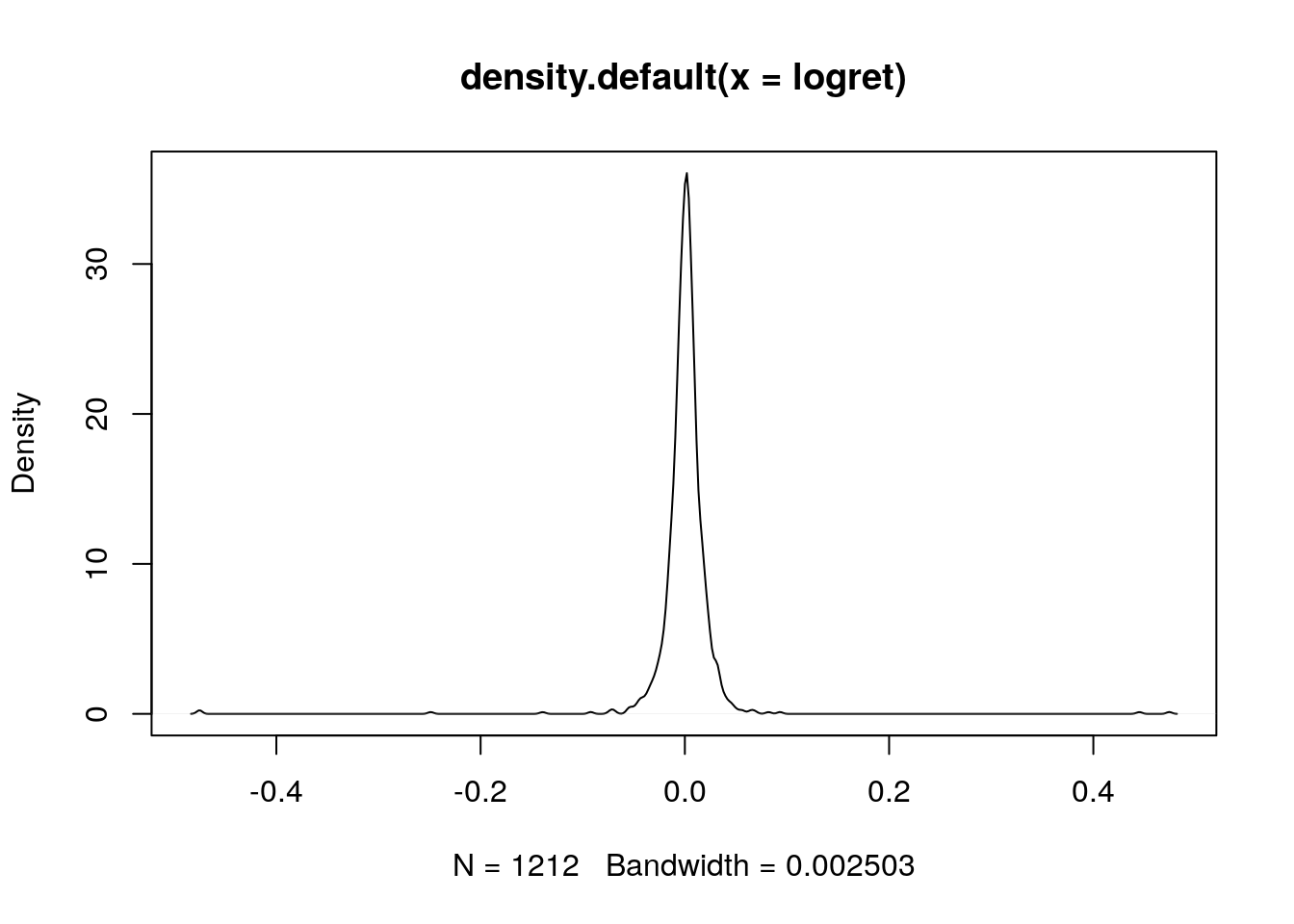
Si nota una distribuzione molto concentrata su 0 e con code molto lunghe (valori estremi) a destra e sinistra.
Si noti che R di default sceglie il miglior valore per l’ampiezza di banda (bandwidth, riportato in basso a destra nel grafico). Con l’obiettivo di studiare l’effetto dell’ampiezza di banda sul grafico finale della KDE, possiamo ad esempio raddopiarne il valore utilizzando l’opzione adjust:
# Raddoppio il parametro di bandwidth
plot(density(logret,adjust = 2))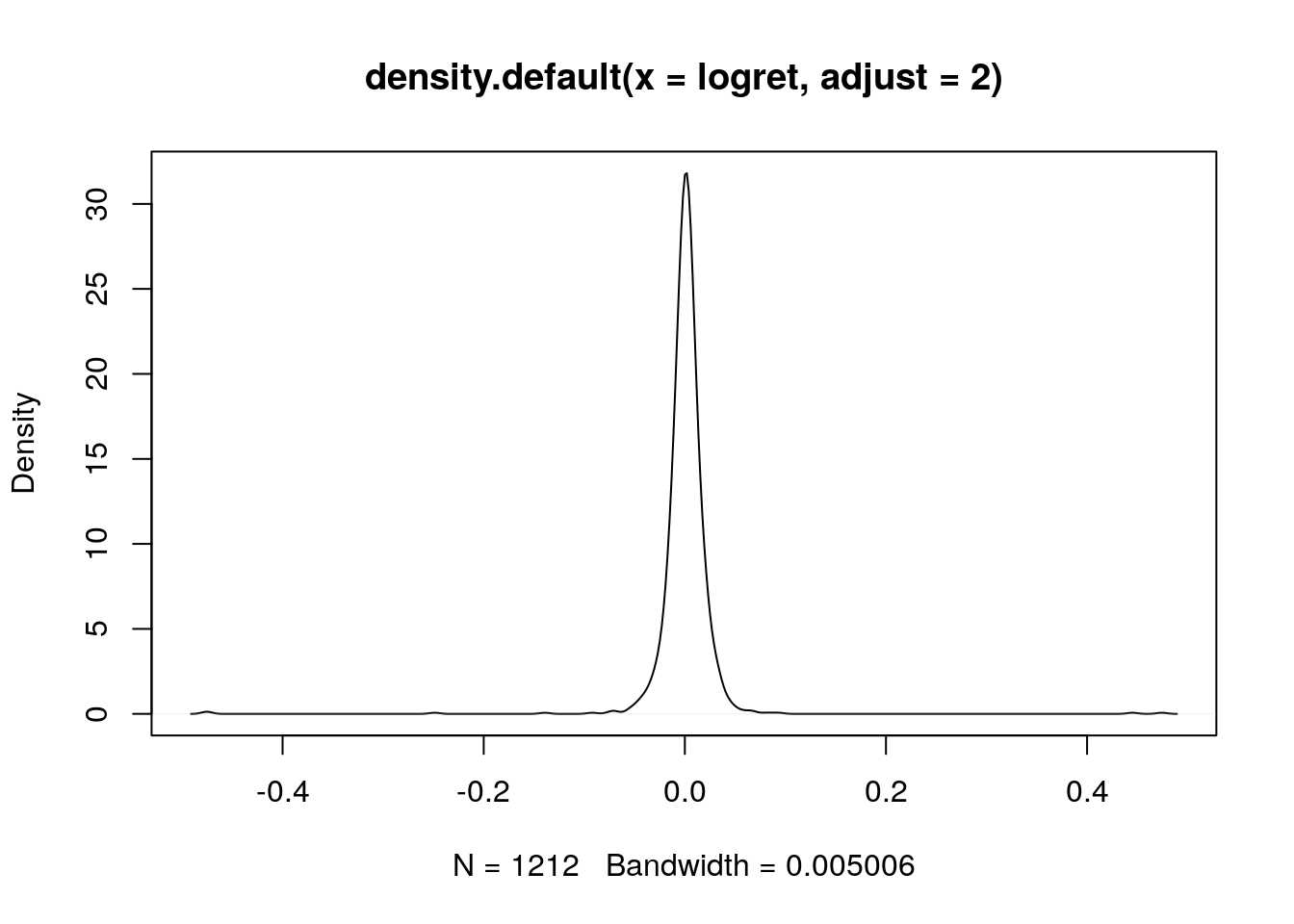
La costante moltiplicativa definita con adjust viene applicata al valore dell’ampiezza di banda scelta automaticamente da R. Quando l’ampiezza di banda raddoppia la curva è più liscia. Se invece l’ampiezza viene dimezzata
plot(density(logret,adjust=0.5))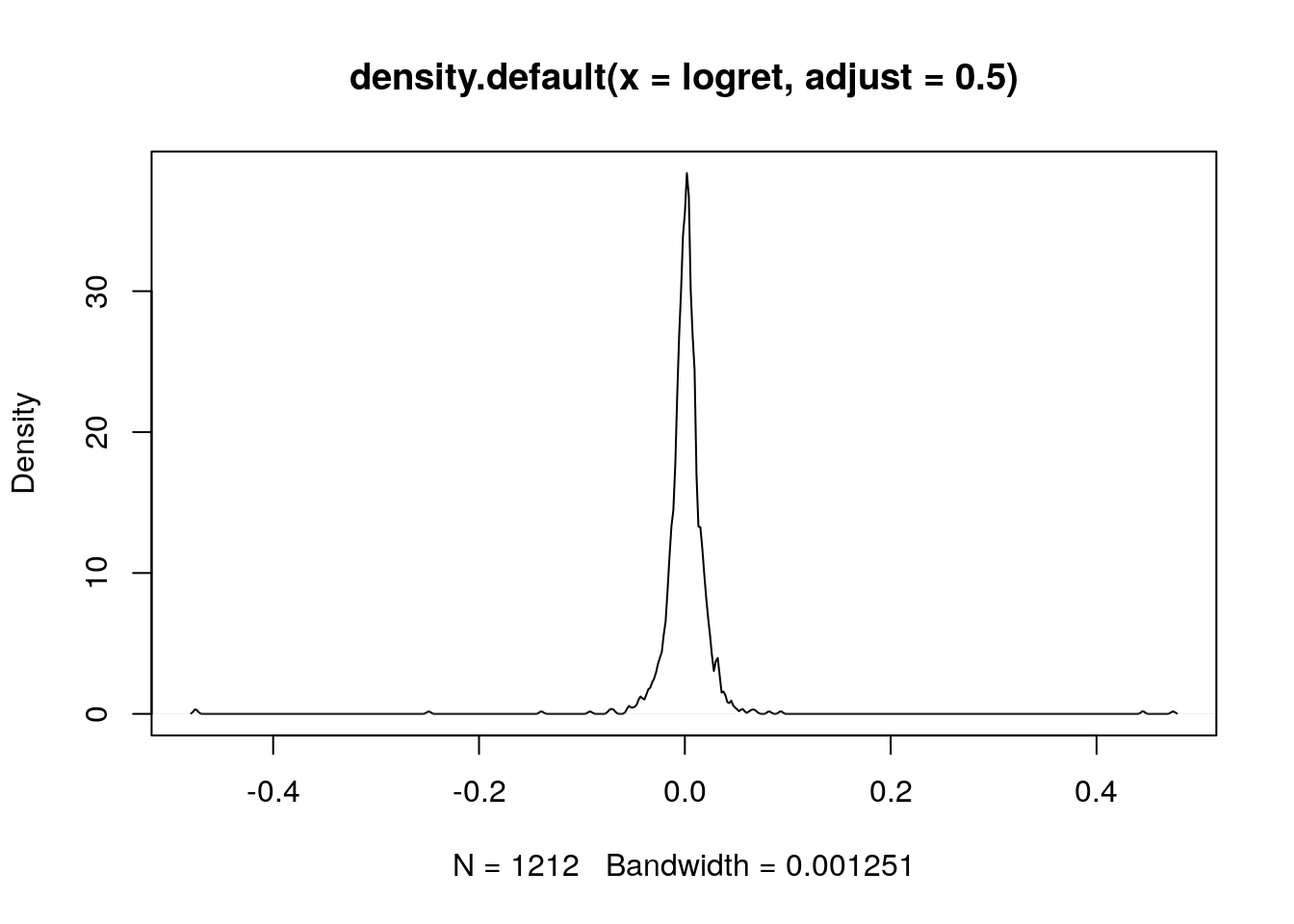
la KDE finale mostra più dettagli ed è meno liscia (più variabile).
E’ anche possibile mostrare insieme l’istogramma e la linea della KDE:
hist(logret,
freq = F, ylim = c(0,35))
lines(density(logret))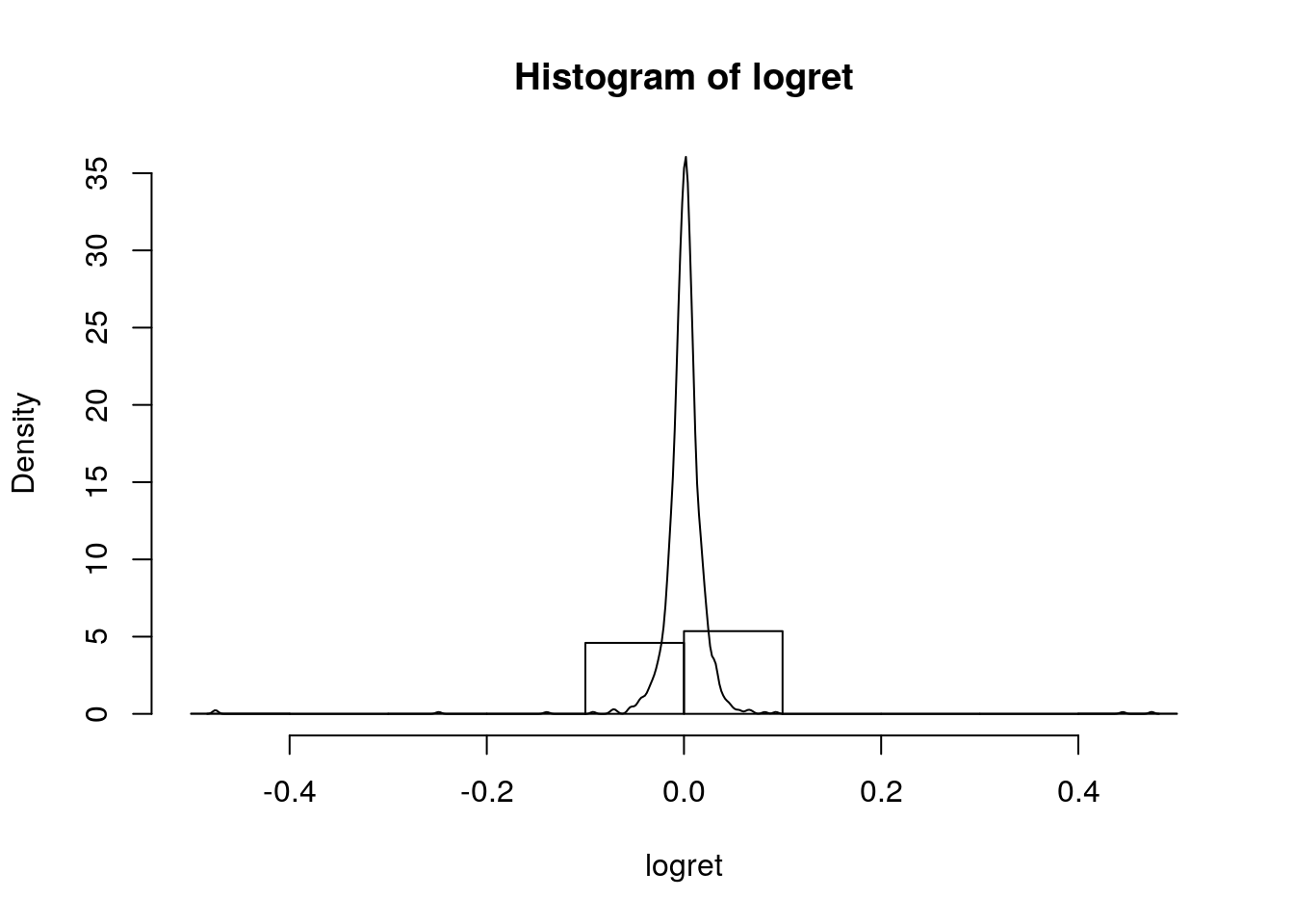
L’argomento freq=F serve per poter rappresentare sull’asse delle y le densità di frequenza invece delle frequenze assolute. In questo modo l’istogramma e la KDE sono comparabili e possono essere rappresentati insieme sullo stesso grafico.
6.3 Funzione di ripartizione empirica
La funzione di ripartizione empirica (ECDF) restituisce la proporzione di valori in un vettore di dati minori o uguali ad un dato numero reale \(y\). La ECDF è definita da \[ F_n(y)=\frac{\sum_{i=1}^n \mathbb I(Y_i\leq y)}{n} \] dove \(\mathbb I(\cdot)\) è la funzione indicatarice che vale uno se \(Y_i\leq y\) o zero altrimenti (di fatto si calcola il rapporto tra il numero totale di osservazioni \(\leq y\) ed il totale \(n\) delle osservazioni).
In R la ECDF si può ottenere salvando l’output della funzione ecdf in un nuovo oggetto qui di seguito denominato myecdf (qualsiasi nome può essere scelto per il nuovo oggetto):
myecdf = ecdf(logret)L’oggetto myecdf appartiene alla classe function è può essere utilizzato come una normale altra funzione. In questo caso la funzione, valutata in un certo valore reale, restituirà la proporzione di valori uguali o inferiori al valore scelto. Ad esempio, utilizzando -0.22:
myecdf(-0.22) ## [1] 0.002475248si ottiene che il 0.25% dei log-rendimenti è minore o uguale a -0.22. Di conseguenza
(1-myecdf(-0.22))*100## [1] 99.75248è la percentuale di valori maggiori di -0.22. In maniera simile
myecdf(0)## [1] 0.4628713restituisce la proporzione di log-rendimenti negativi (i.e. casi di diminuzione nel prezzo) o uguali a zero.
Si ricordi che il numero utilizzato in input della funzione myecdf può essere qualsiasi numero reale. Ovviamente per il caso in esame ci si aspetta che la ECDF valutata in un numero inferiore a -0.4760486 sia 0 e che sia 1 per qualsiasi valore superiore a 0.4743245. Ad esempio:
myecdf(1000)## [1] 1La ECDF può essere rappresentata graficamente usando la funzione plot:
plot(myecdf)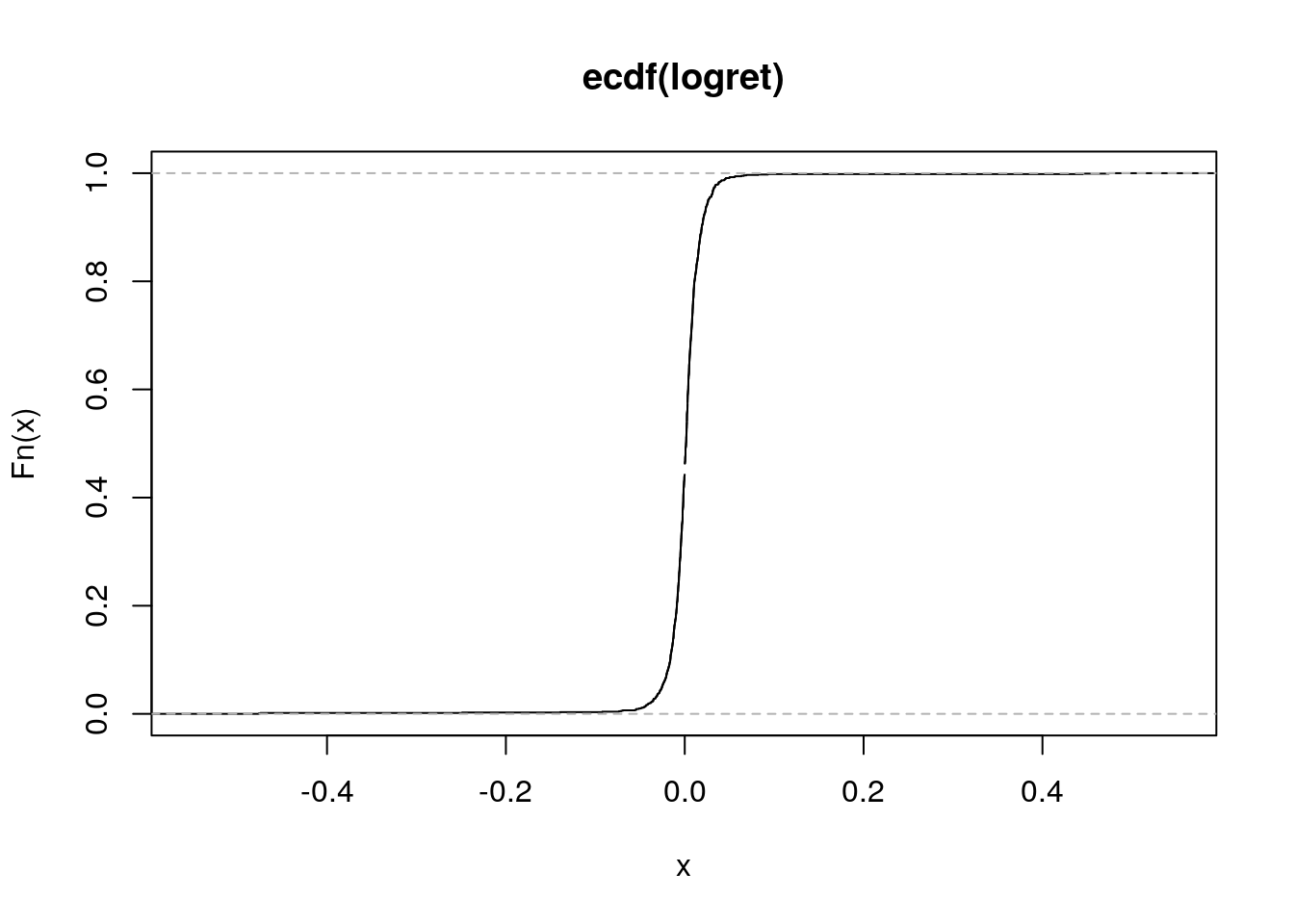
L’asse delle x si riferisce all’intervallo da \(-\infty\) a \(+\infty\); ovviamente vengono visualizzati i valori compresi tra il minimo e il massimo di logret rappresentando essi l’intervallo di interesse. Sull’asse delle y vengono riportati i valori della ECDF, e quindi proporzioni comprese tra 0 e 1.
Analizzando il grafico è possibile ottenere, per qualsiasi valore sull’asse delle x, il corrispondente valore della ECDF. Per una migliore visualizzazione dell’andamento della ECDF è opportuno fare uno zoom sui valori mostrati sull’asse delle x:
plot(myecdf, xlim = c(-0.001, +0.001))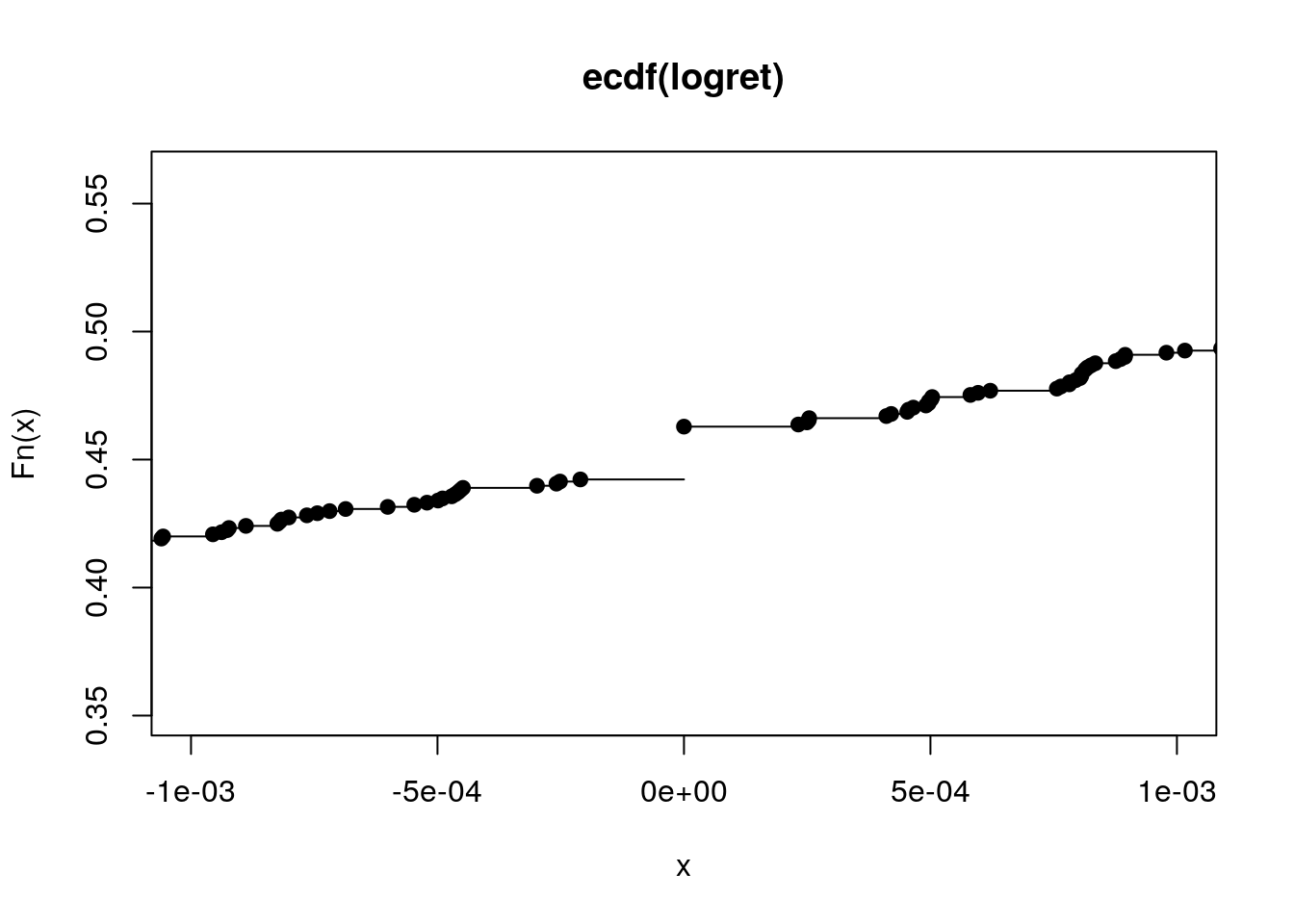
Dal grafico è evidente che la ECDF è definita per tutti i valori reali (anche quelli non osservati nel campione) ed è una funzione non decrescente. E’ inoltre una funzione a gradini: in particolare, i gradini sono localizzati in corrispondenza dei valori inclusi nel vettore logret La pendenza della ECDF fornisce importanti informazioni circa la distribuzione analizzata: una curva molto pendenza indica poca variabilità dei dati, mentre una curva con poca pendenza indica una distribuzione caratterizzata da maggiore variabilità.
6.4 Fittare una distribuzione teorica ai dati
Si intende fittare ai dati un modello teorico, la cui funzione di densità di probabilità (PDF) sia nota (e.g. distribuzione Normale o t di Student). I parametri della distribuzione teorica sono stimati tramite il metodo della massima verosimiglianza (ML).
Questo tipo di analisi può essere svolto in R utilizzando la funzione fitdistr contenuta nella libreria MASS. Quest’ultima è già disponibile nella release base di R e non è necessario installarla (ma solo caricarla con library(MASS)). Gli input della funzione fitdistr sono: i dati e il modello teorico da fittare ai dati (si veda ?fitdistr per l’elenco dei modelli teorici disponibili). Si consideri in prima battuta la distribuzione Normale.
library(MASS)
fitN = fitdistr(x=logret, densfun="normal")
fitN## mean sd
## 0.0008095993 0.0323746397
## (0.0009299372) (0.0006575649)L’output di fitN fornisce le stime di massima verosimiglianza per i due parametri della Normale (la media \(\mu\) e la varianza \(\sigma^2\)) con i corrispondenti standard error forniti in parentesi che rappresentano una misura di accuratezza delle stime. Nel caso di modello Normale, la stima ML della media \(\mu\) è data dalla media campionaria \(\bar x=\frac{\sum_{i=1}^n x_i}{n}\), mentre la stima ML della varianza è data dalla varianza campionaria non corretta \(s^2 =\frac{\sum_{i=1}^n (x_i-\bar x)^2}{n}\).
Si noti nel pannello in alto a destra che l’oggetto fitN è di tipo list (un nuovo tipo di oggetto che, come una scatola, può contenere al suo interno altri oggetti) contenente 5 oggetti il cui nome può essere ottenuto come segue:
names(fitN)## [1] "estimate" "sd" "vcov" "n" "loglik"Per estrarre un generico elemento da una lista si utilizza il simbolo del dollaro; per esempio per estrarre da fitN l’oggetto che contiene le stime dei parametri si usa il seguente codice:
fitN$estimate #vettore delle stime## mean sd
## 0.0008095993 0.0323746397fitN$estimate[1] #prima stima## mean
## 0.0008095993fitN$estimate[2] #seconda stima## sd
## 0.03237464Un’altra distribuzione continua che può essere fittata ai dati è la distribuzione t standardizzata \(t_\nu^{std}(\mu,\sigma^2)\). Si noti che in questo caso i parametri sono tre: media \(\mu\), sd \(\sigma\) e gradi di libertà \(\nu\) (df). Si procede analogamente a prima andando a specificare "t" per l’argomento densfun:
fitT = fitdistr(logret, densfun="t")## Warning in dt((x - m)/s, df, log = TRUE): NaNs produced## Warning in log(s): NaNs produced
## Warning in log(s): NaNs produced
## Warning in log(s): NaNs produced
## Warning in log(s): NaNs produced## Warning in dt((x - m)/s, df, log = TRUE): NaNs produced## Warning in log(s): NaNs produced## Warning in dt((x - m)/s, df, log = TRUE): NaNs produced
## Warning in dt((x - m)/s, df, log = TRUE): NaNs produced## Warning in log(s): NaNs produced
## Warning in log(s): NaNs produced
## Warning in log(s): NaNs produced
## Warning in log(s): NaNs produced
## Warning in log(s): NaNs produced
## Warning in log(s): NaNs produced
## Warning in log(s): NaNs produced
## Warning in log(s): NaNs produced## Warning in dt((x - m)/s, df, log = TRUE): NaNs produced
## Warning in dt((x - m)/s, df, log = TRUE): NaNs producedfitT## m s df
## 0.0012310830 0.0101193875 2.5484985213
## (0.0003621179) (0.0003916357) (0.2235071834)6.5 AIC e BIC
Quale è il miglior modello per i dati considerati? Per confrontare i due modelli fittati ai dati si può utilizzare il valore della funzione di log verosimiglianza (incluso con il nome loglik nell’output della funzione fitdistr): si andrà a preferire il modello con il valore più elevato di loglik.
fitN$loglik## [1] 2437.867fitT$loglik ## [1] 3325.392In questo caso la distribuzioen di t ha un valore più elevato della funzione di log verosimiglianza. Una conclusione simile si ottiene analizzando il valore della devianza che rappresenta un indice di misfit da minimizzare (più piccola la devianza, migliore il fit). La devianza è definita come \[\text{deviance} = -2*\text{loglikelihood}\]
-2*fitN$loglik## [1] -4875.734-2*fitT$loglik ## [1] -6650.784Anche in questo caso il modello t è da preferire. Ricordiamo però che esso è caratterizzato da un numero maggiore di parametri da stimare (ed è quindi da considerarsi come un modello più complesso). Per confrontare due modelli tenendo in considerazione anche la loro complessità è possibile utilizzare due indici: Akaike Information Criterion (AIC) e Bayes information criterion (BIC). Essi penalizzano la bontà di adattamento per il numero di parametri da stimare. Essi sono così definiti: \[ AIC = \text{deviance}+2p \]
\[ BIC = \text{deviance}+\log(n)p \] dove \(p\) è il numero di parametri da stimare (2 per la Normale e 3 per la t) e \(n\) la numerità del campione di dati. I termini \(2p\) e \(\log(n)p\) sono le penali legate alla complessità del modello. Entrambi gli indici AIC e BIC seguono il criterio smaller is better.
I due indici possono essere calcolati utilizzando le funzioni AIC e BIC come segue:
AIC(fitN)## [1] -4871.734AIC(fitT)## [1] -6644.784BIC(fitN)## [1] -4861.534BIC(fitT)## [1] -6629.484Confrontando i valori di AIC e BIC si preferisce il modello t.
6.6 Grafico della PDF della VC Normale
Si intende confrontare il grafico della stima Kernel della densità (KDE) ottenuta dai dati con la funzione di densità della vc Normale fittata ai dati e riportata nella seguente formula (dove i parametri \(\mu\) e \(\sigma^2\) sono sostituiti dalle corrispondenti stime di massima verosimiglianza): \[ \hat f(x)=\frac{1}{\sqrt{2\pi s^2}}e^{-\frac{1}{s^2}(x-\bar x)^2} \]
La PDF della VC Normale è implementata in R tramite la funzione dnorm(x,mean,sd) (si veda ?dnorm).
Si inizia rappresentando graficamente la KDE (stima della PDF) data da
plot(density(logret))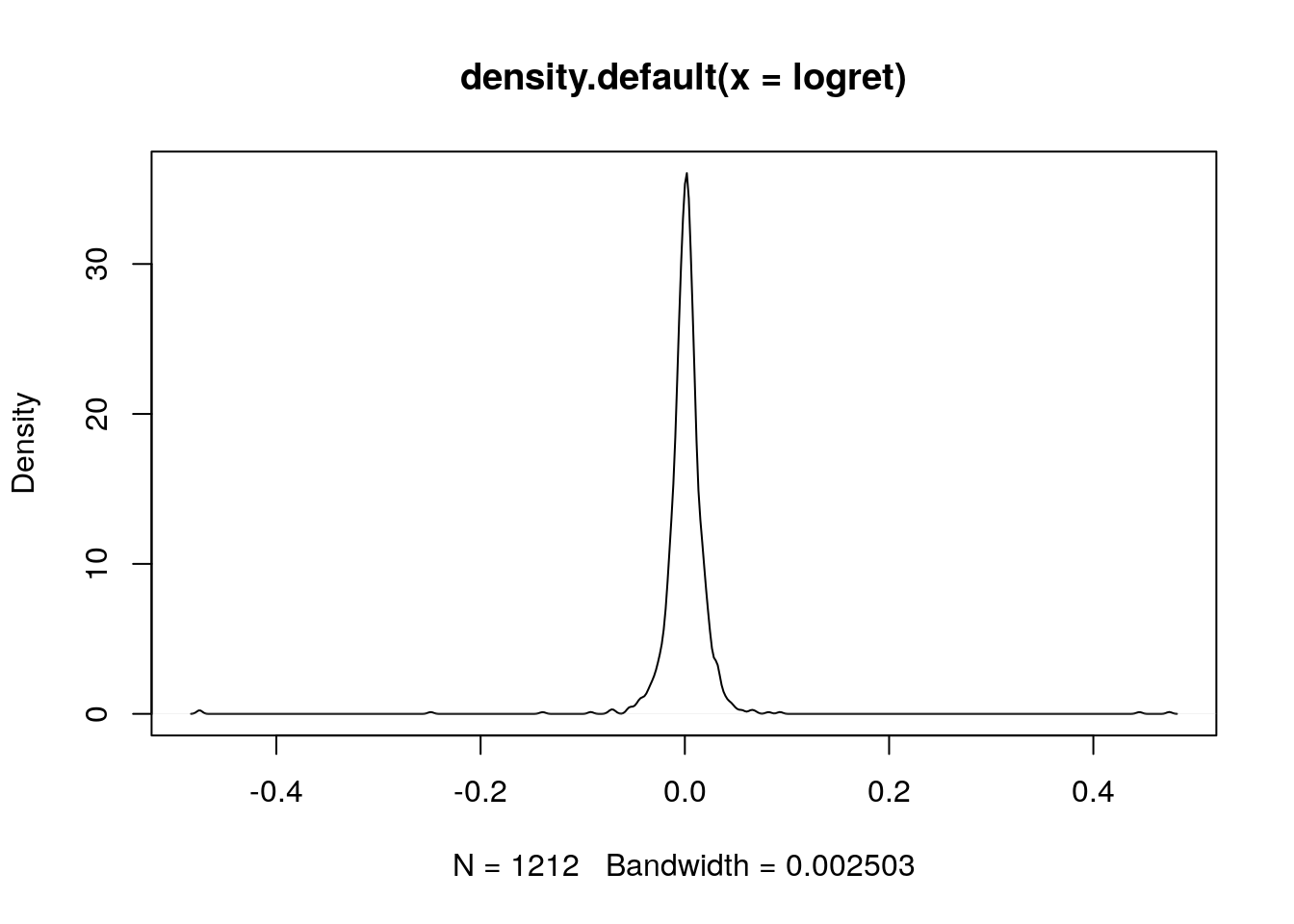
Si noti che i valori sull’asse delle x sono indicativamente compresi tra -0.5 e +0.5. Andremo quindi a costruire una sequenza regolare di 1000 valori tra -0.5 e +0.5 utilizzando la funzione seq:
xseq = seq(from=-0.5,to=+0.5, length=1000)
#parte iniziale della sequenza
head(xseq)## [1] -0.500000 -0.498999 -0.497998 -0.496997 -0.495996 -0.494995#parte finale della sequenza
tail(xseq)## [1] 0.494995 0.495996 0.496997 0.497998 0.498999 0.500000Per ognuno di questi valori nel vettore xseq andremo a valutare la funzione di densità \(f(x)\) della Normale stimata nella sezione precedente (i cui parametri sono stimati con il metodo della massima verosimiglianza).
Data la sequenza di valori per cui calcolare la PDF siamo ora pronti ad utilizzare la funzione dstd utilizzando le stime ML dei parametri contenute in fitN:
dens = dnorm(xseq,
mean = fitN$estimate[1],
sd = fitN$estimate[2])Il grafico finale si ottiene come segue:
plot(density(logret),
ylim = c(0,80))
lines(xseq,dens,col="orange")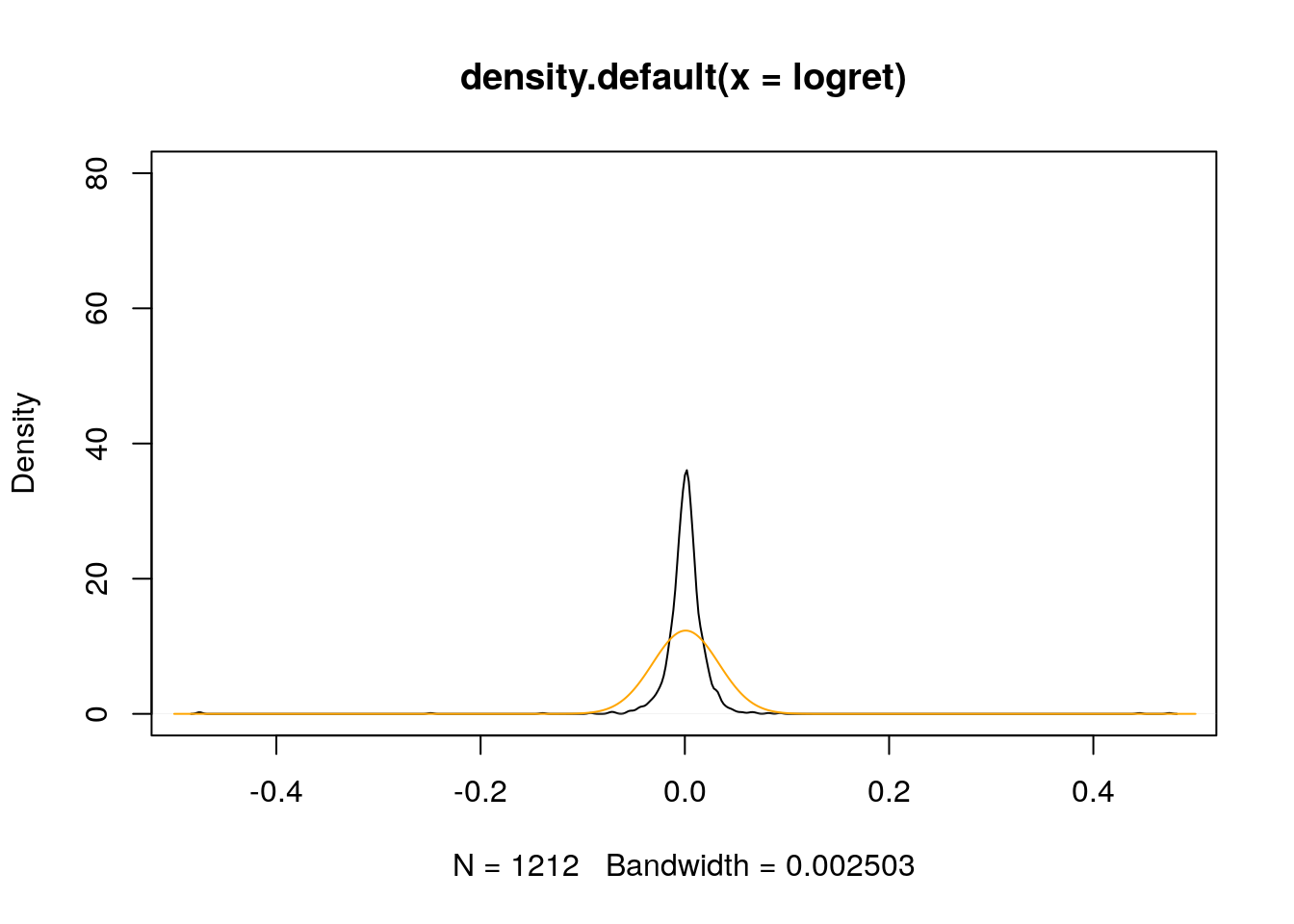
Si noti che la densità della Normale è molto diversa da quella empirica. Ciò significa che il modello Normale non è adatto per i dati osservati (e infatti il modello t è preferibile).
6.7 Esercizi Lab 4
6.7.1 Esercizio 1
Le serie giornalerie dei prezzi per il periodo dal 2012-11-09 al 2017-11-09 per il titolo ENI sono disponibili nel file E.xlsx. Importare i dati in R.
Calcolare i rendimenti lordi e rappresentarne graficamente la distribuzione con un istogramma a cui aggiungere anche la KDE. Commentare il grafico.
Calcolare l’indice di asimmetria e curtosi. Commentare i valori.
Calcolare la funzione di ripartizione empirica in corrispondenza del valore 1. Interpretare il valore ottenuto. Rappresentare inoltre graficamente la funzione di ripartizione empirica.
Stimare la distribuzione Normale e t di Student che meglio si adatta ai dati. Quale dei due modelli (Normale e t) è preferibile in termini di devianza, AIC e BIC?
Rappresentare graficamente la distribuzione dei dati con una KDE a cui vengono aggiunte la funzione di densità delle vc Normale fittata al punto precedente.
Quale è il valore della PDF (fittata ai dati) per la VC Normale\(x=0.9\)?
6.7.2 Esercizio 2
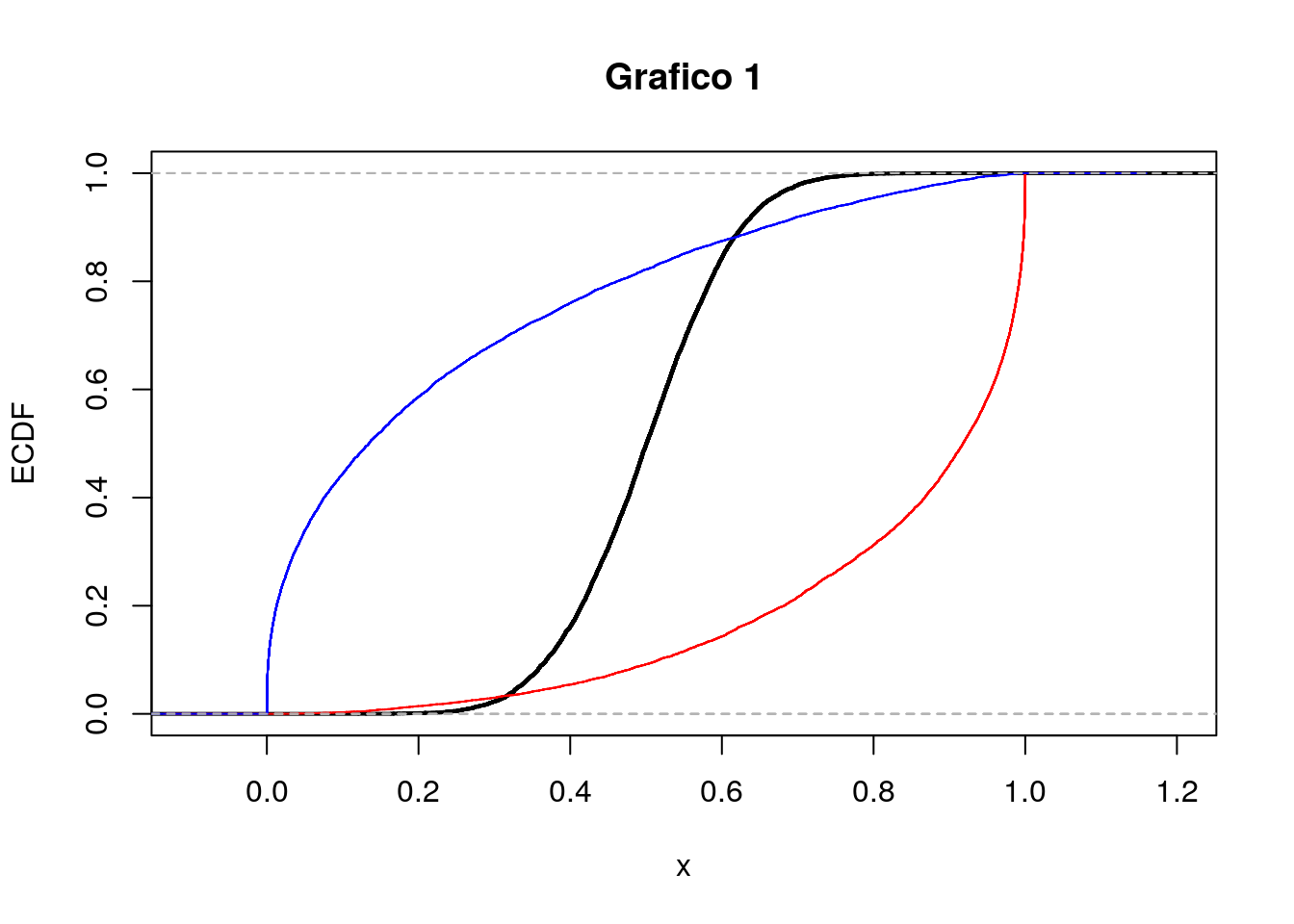
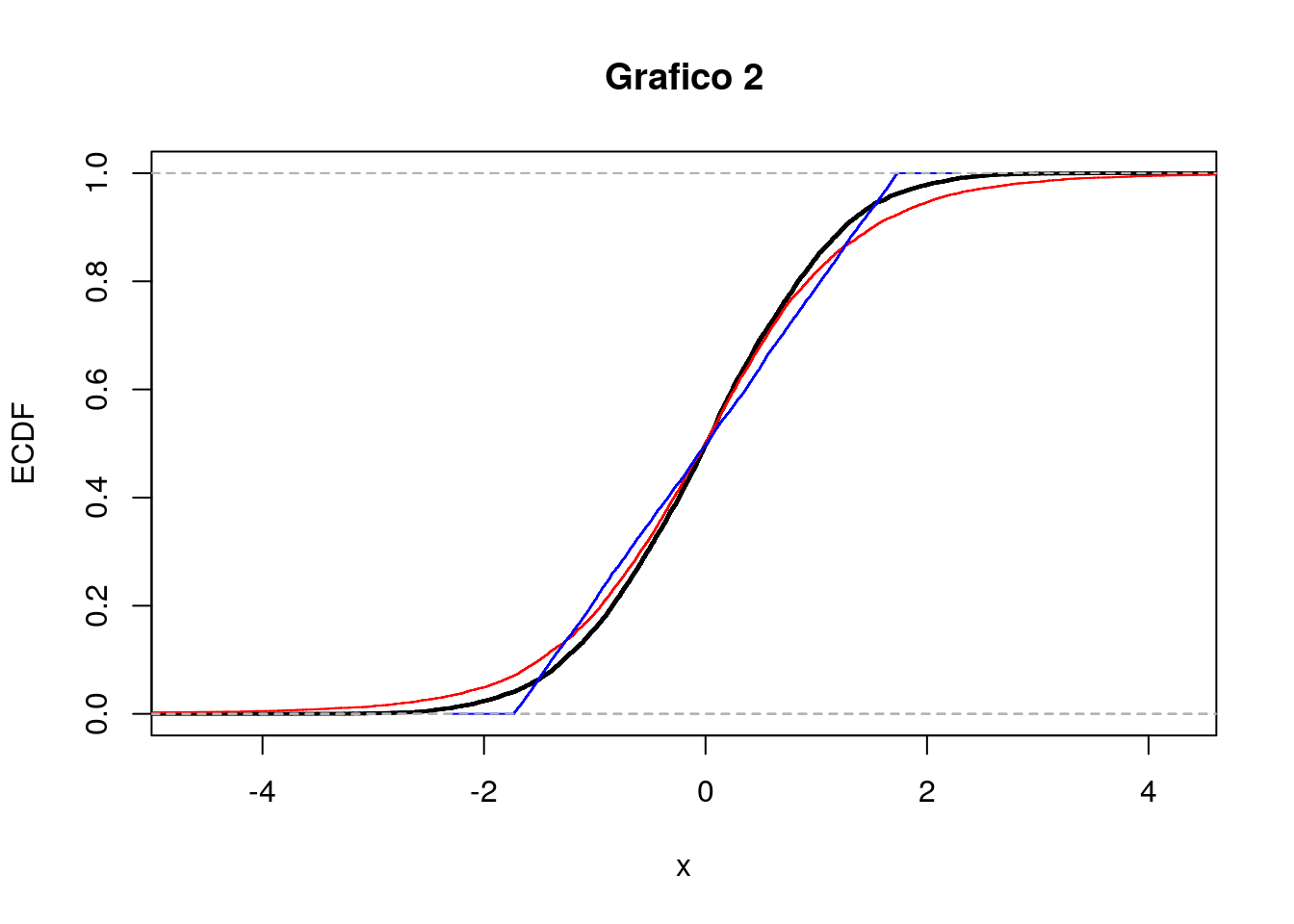
- Si considerino i due seguenti grafici (A e B). Entrambi riportano le stime kernel della densità per tre distribuzioni empiriche (curva nera, rossa e blu). In merito al grafico A cosa si può commentare circa la simmetria delle distribuzioni? E per il grafico B cosa si può dire circa la kurtosi?
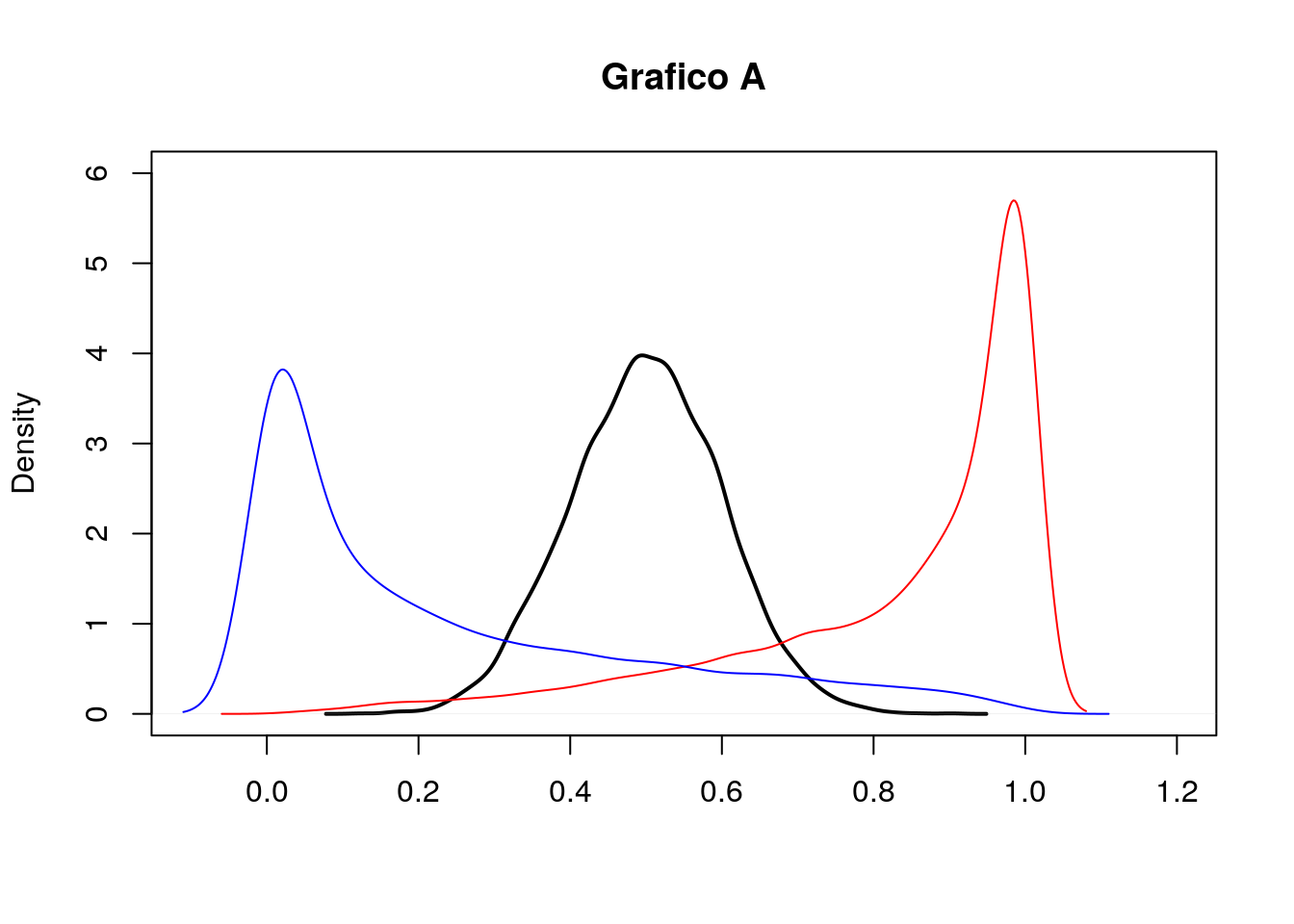
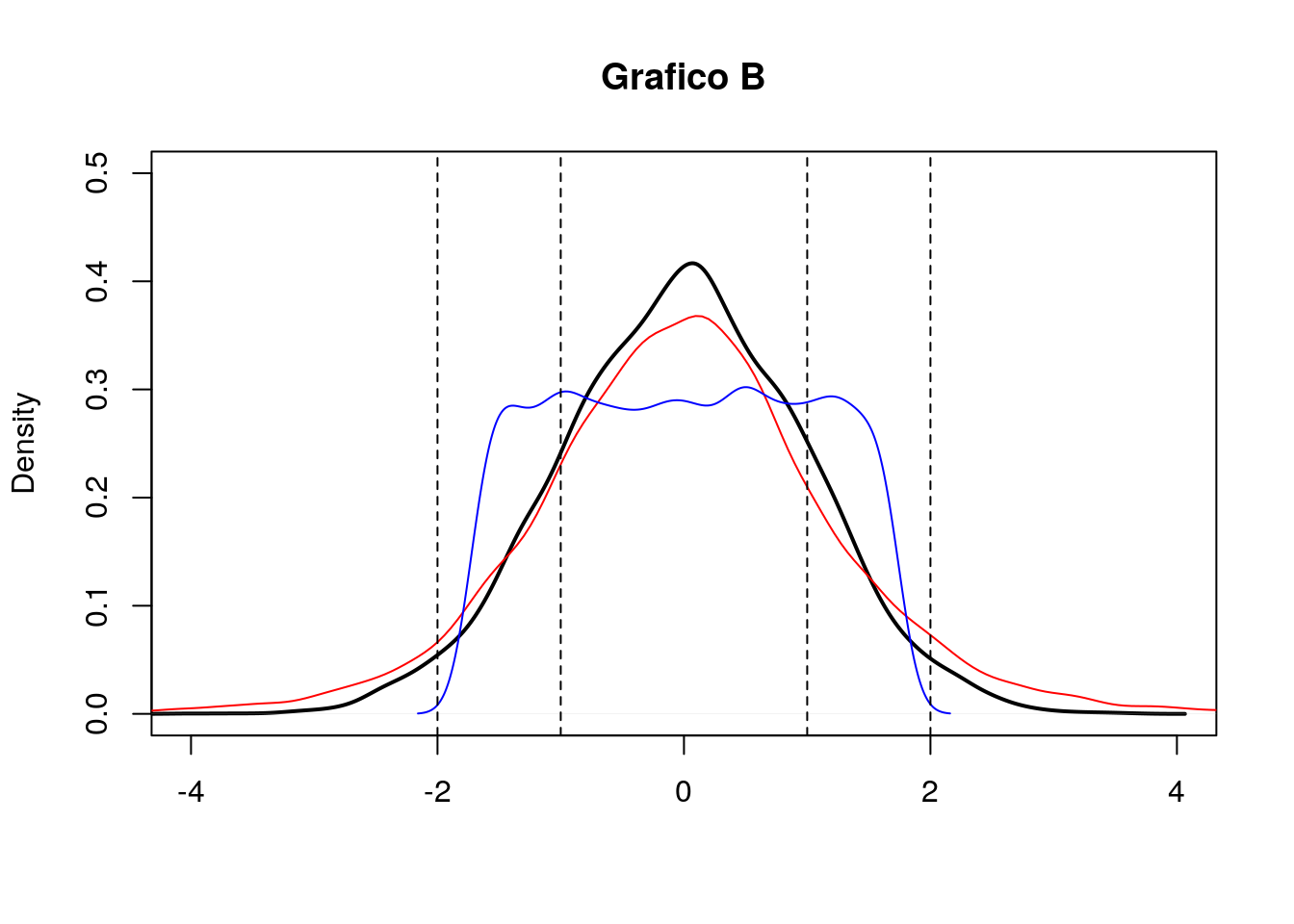
- Si considerino ora i due seguenti grafici (grafico 1 e 2) che riportano le funzioni di ripartizioni empiriche (EDF). Il grafico 1 si riferisce alle distribuzioni riportate nel grafico A o a quelle del grafico B? Motivare.
