Chapter 34: notational system for design
9 p.51
NSD = notational system for design
34.1 graphic notation
9 p.51
- \(X\): treatment or exposure to an agent or an event of interest
- \(P\): placebo, i.e. blank treatment or exposure, or standard treatment, or exposure as an active control
- \(O\): observation or process of measurement
- \(R\): randomization, i.e. random assignment of research subjects to separate treatment or exposure groups
- subscript
- \(_g\): groups
- \(_k\): kinds of treatments, exposures, or placebos
- \(_t\): time or sequential order
https://tex.stackexchange.com/questions/591882/citation-within-a-latex-figure-caption-in-rmarkdown
(ref:rudolph) *nice* cite: [@Lam94].
(ref:campbell1963) *nice* cite: [@campbell1963].
(ref:campbell1963) ([@campbell1963]
(ref:campbell1963) \ [@campbell1963]
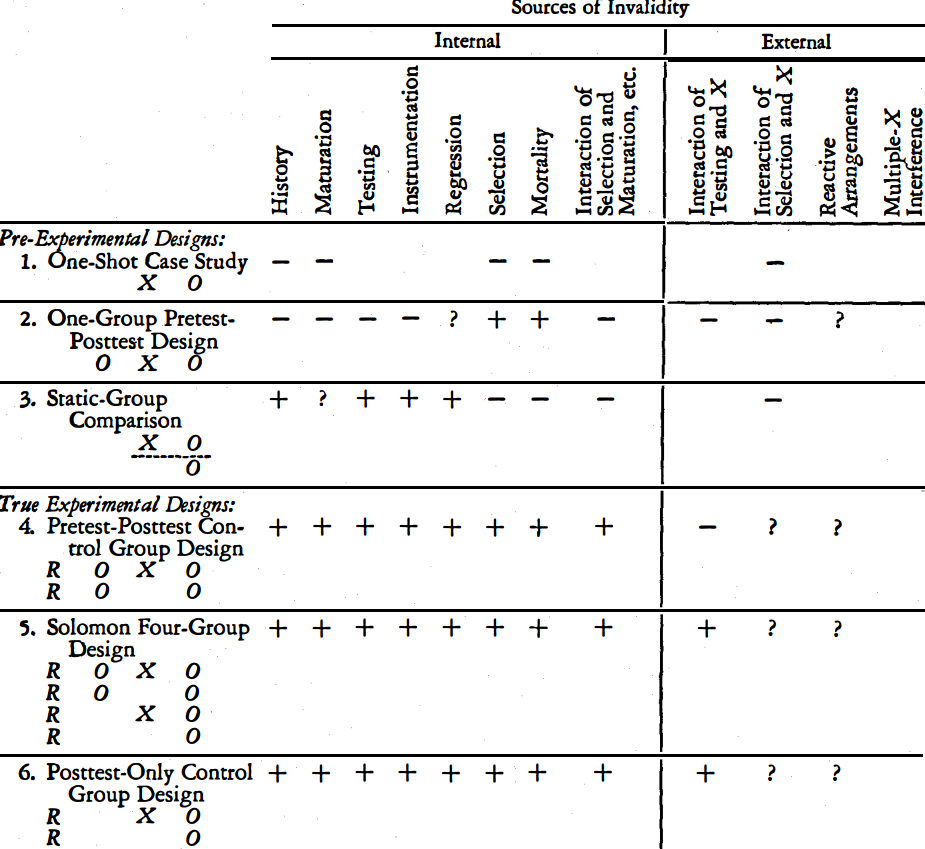
Fig. 24.1: pre- and true experimental designs ( 5 p.8)
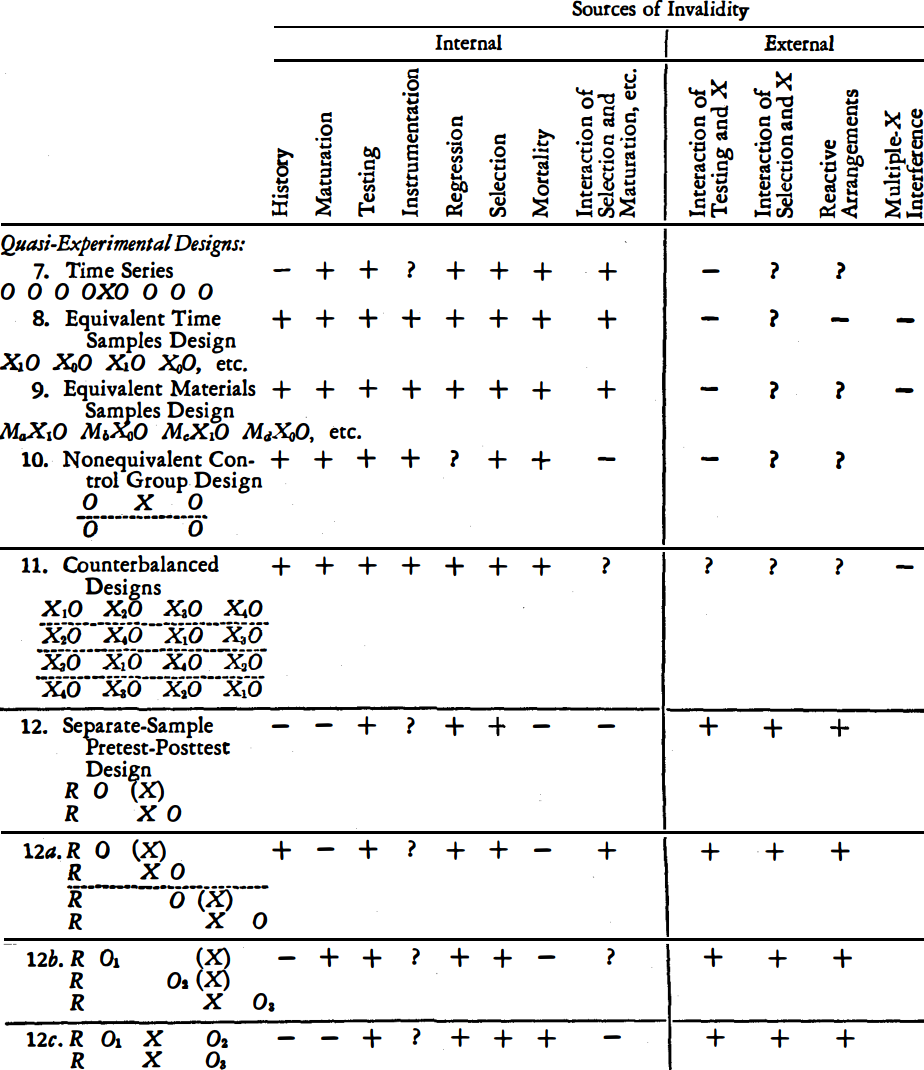
Fig. 30.2: quasi-experimental designs ( 5 p.40)
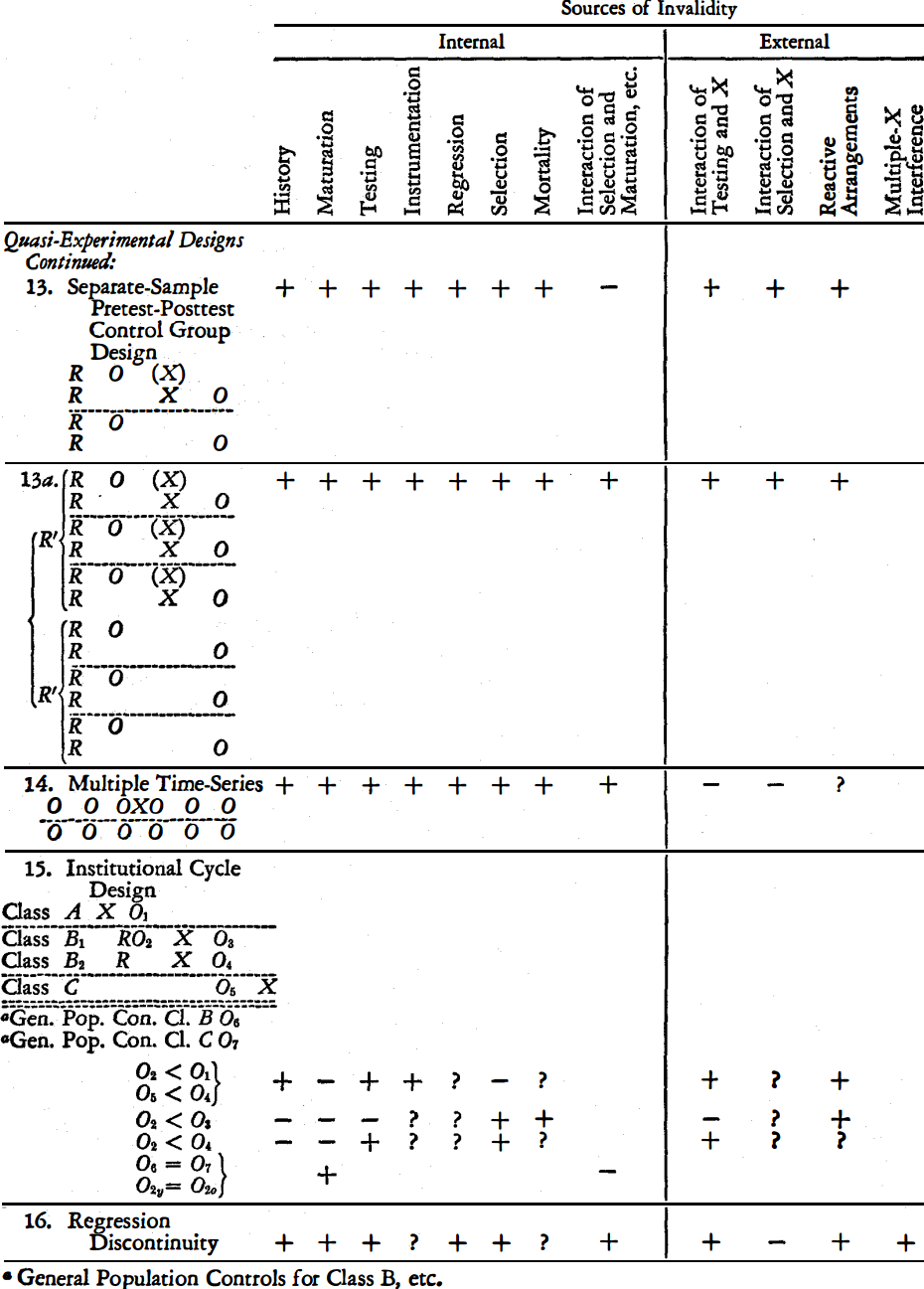
Fig. 17.1: quasi-experimental designs continued ( 5 p.56)
34.2 pre-experimental design
5 p.6
34.2.2 one-group pretest-posttest design
\[ \begin{array}{ccc} O & X & O \end{array} \] paired \(t\) test
9 p.62
\[ \begin{array}{ccc} O & X & O \\ O_{t} & X & O_{t} \\ O_{0} & X & O_{1} \end{array} \]
\[ \begin{array}{ccc} O & X & O \\ O_{gt} & X_{g} & O_{gt} \\ O_{10} & X & O_{11} \end{array} \]
34.3 true experimental design
5 p.13
34.3.1 posttest-only control group design
basic experimental design
two-sample \(t\) test
9 p.53
\[ \begin{array}{ccc} R & X & O\\ R & & O \end{array} \] or, with a placebo or an active control, \[ \begin{array}{ccc} R & X & O\\ R & P & O \end{array} \]
\[ \begin{array}{ccc} R & X_{g} & O_{gt}\end{array} \]
\[ \begin{array}{ccc} R & X_{g}=X_{1}=X & O_{gt}=O_{11}\\ R & X_{g}=X_{2}=\emptyset & O_{gt}=O_{21} \end{array} \] or, with a placebo or an active control \[ \begin{array}{ccc} R & X_{g}=X_{1}=X & O_{gt}=O_{11}\\ R & X_{g}=X_{2}=P & O_{gt}=O_{21} \end{array} \]
\[ \begin{array}{ccc} R & X & O_{11}\\ R & & O_{21} \end{array} \] or, with a placebo or an active control \[ \begin{array}{ccc} R & X & O_{11}\\ R & P & O_{21} \end{array} \]
\[ \begin{array}{ccc} R & X_{g} & O_{gt}\\ R & X & O_{11}\\ R & P & O_{21} \end{array} \]
\[ \begin{array}{ccc} R & X & O\\ R & X_{g} & O_{gt}\\ R & X & O_{11}\\ R & P & O_{21} \end{array} \]
34.3.2 pretest-posttest control group design
\[ \begin{array}{cccc} R & O & X & O\\ R & O_{gt} & X_{g} & O_{gt}\\ R & O_{10} & X & O_{11}\\ R & O_{20} & & O_{21} \end{array} \]
34.3.3 Solomon four-group design
9 p.52
Solomon 4-group design = pretest-posttest + posttest-only control group design
\[ \begin{array}{cccc} R & O_{gt} & X_{g} & O_{gt}\\ R & O_{10} & X & O_{11}\\ R & O_{20} & & O_{21}\\ R & & X & O_{31}\\ R & & & O_{41} \end{array} \]
\[ \begin{array}{cccc} R & O & X & O\\ R & O_{gt} & X_{g} & O_{gt}\\ R & O_{10} & X & O_{11}\\ R & O_{20} & & O_{21}\\ R & & X & O_{31}\\ R & & & O_{41} \end{array} \]
34.4 quasi-experimental design
5 p.34
34.5 correlational and ex post facto designs
5 p.64
34.6 graphic notation, advanced
9 p.74
- \(X\): treatment or exposure to an agent or an event of interest
- \(P\): placebo, i.e. blank treatment or exposure, or standard treatment, or exposure as an active control
- \(O\): observation or process of measurement
- \(R\): randomization, i.e. random assignment of research subjects to separate treatment or exposure groups
- subscript
- \(_g\): groups
- \(_k\): kinds of treatments, exposures, or placebos
- \(_t\): time or sequential order
- \(V\): variable(s)
- \(B(V)\): blocking by the variable(s)
- \(M(V)\): matching by the variable(s)
- \(S(V)\): stratifying by the variable(s)
- \(L(V/L)\): limiting to the level(s) of the variable(s)
- \(M^{*}\): research material(s) selected
- \(-\): cohort