Chapter 3 Generalized Linear Models

The first class of models we will study in this class are generalized linear models. I am operating under the assumption that your previous classes have covered Frequentist and Bayesian approaches to linear models in sufficient detail.

3.1 Motivation

Generalized linear models were introduced to resolve many of the limitations that arise from linear models — perhaps most importantly, the heteroskedasticity that arises naturally from Poisson and binomial/Bernoulli response models.

In the beforetimes, when there was software to fit linear models but not generalized linear models, folks used a variety of hacks to deal with the fact that various types of data are intrinsically heteroskedsatic. For example, if $Y$ is a count we generally expect that $\operatorname{Var}(Y) \ge \mathbb E(Y)$ (for Poisson data, there is equality). One approach is to transform the data to be homoskedastic, i.e., we could use the model \[ g(Y_i) = X_i^\top \beta + \epsilon_i \] for some transformation $g(\cdot)$, with $\mathbb E(\epsilon_i) = 0$ and $\operatorname{Var}(\epsilon_i) = \sigma^2$. Usually, we would take $g(y)$ to be a variance stabilizing transformation.

Exercise 3.1 Suppose that $Y \sim \operatorname{Poisson}(\lambda)$. Using the expansion \[ g(y) \approx g(\lambda) + (y - \lambda) \, g'(\lambda) \] find a transformation $g(\cdot)$ such that the variance of $g(Y)$ is approximately constant.

Exercise 3.2 Explain some of the deficiencies of the model from the previous exercise. For example: how does the interpretation of $\beta$ change vis-a-vis the linear model?

The framework of generalized linear models allows for the same ideas underlying linear models to be extended to other response types (count, discrete, non-negative, etc) without resorting to the contortions of Exercise 3.1.

3.2 Generalized Linear Models

The class of generalized linear models assumes that we are working with a dependent variable $Y_i$ that has a distribution in an exponential dispersion family.

Definition 3.1 (Exponential Dispersion Family) A family of distributions $\{f(\cdot ; \theta, \phi) : \theta \in \Theta, \phi \in \Phi\}$ is an exponential dispersion family if we can write \[ \begin{aligned} f(y; \theta, \phi) = \exp\left\{\frac{y\theta - b(\theta)}{\phi} + c(y; \phi)\right\}, \end{aligned} \] for some known functions $b(\cdot)$ and $c(\cdot, \cdot)$. The parameter $\theta$ is referred to as the canonical parameter of the family and $\phi$ is referred to as the dispersion parameter.

Exercise 3.3 Show that the following families are types of exponential dispersion families, and find the corresponding $b, c, \theta, \phi$.

$Y \sim \operatorname{Normal}(\mu, \sigma^2)$
$Y = Z / N$ where $Z \sim \operatorname{Binomial}(N, p)$
$Y \sim \operatorname{Poisson}(\lambda)$
$Y \sim \operatorname{Gam}(\alpha, \beta)$ (parameterized so that $\mathbb E(Y) = \alpha / \beta$).

Using this definition, we can define the class of generalized linear models.

Definition 3.2 (Generalized Linear Model) Suppose that we have $\mathcal D= \{(Y_i, x_i) : i = 1,\ldots, N\}$ (with the $x_i$’s regarded as fixed constants). We say that the $Y_i$’s follow a generalized linear model if:

$Y_i$ has density/mass function \[ f(y_i \mid \theta_i, \phi / \omega_i) = \exp\left\{ \frac{y_i \, \theta_i - b(\theta_i)}{\phi / \omega_i} + c(y_i ; \phi / \omega_i) \right\} \] where the coefficients $\omega_1, \ldots, \omega_N$ are known. This is referrred to as the stochastic component of the model.
For some known (invertible) link function $g(\mu)$ we have \[ g(\mu_i) = x_i^\top\beta \] where $\mu_i = \mathbb E(Y_i \mid \theta_i, \phi / \omega_i)$. This is referred to as the systematic component of the model. The term $\eta_i = x_i^\top\beta$ is known as the linear predictor.

Exercise 3.4 (GLM Moments) Suppose that $Y \sim f(y; \theta, \omega / \omega)$ for some exponential dispersion family. Show that

$\mathbb E(Y \mid \theta, \phi / \omega) = b'(\theta)$; and
$\operatorname{Var}(Y \mid \theta, \phi / \omega) = \frac{\phi}{\omega} b''(\theta)$.

Hint: The log-likelihood is given by \[ \log f = \frac{y\theta - b(\theta)}{\phi / \omega} + c(y, \phi / \omega). \] Use the score equations \[ \begin{aligned} \mathbb E\{s(y; \theta, \phi / \omega) \mid \theta, \phi / \omega\} &= \boldsymbol{0} \qquad \text{and} \\ \operatorname{Var}\{s(y; \theta, \phi / \omega) \mid \theta, \phi / \omega\} &= -\mathbb E\{\dot s(y; \theta, \phi / \omega)\}, \end{aligned} \] to derive the result, where \[ \begin{aligned} s(y; \theta, \phi / \omega) = \frac{\partial}{\partial \theta} \log f \qquad \text{and} \quad \dot s (y; \theta, \phi / \omega) = \frac{\partial^2}{\partial \theta \partial \theta^\top} \log f \end{aligned} \] are the gradient and Hessian matrix of $\log f$ with respect to $\theta$.

From Exercise 3.4 we immediately have \[ \theta_i = (b')^{-1}(\mu_i) = (b')^{-1}\{g^{-1}(x_i^\top\beta)\} \] provided that $b'$ and $g$ both have an inverse. Note a GLMs are heteroskedastic models, as $\operatorname{Var}(Y \mid \theta, \phi / \omega)$ depends on $\mathbb E(Y_i \mid \theta, \phi / \omega)$. In particular, we have \[ \operatorname{Var}(Y \mid \theta, \phi / \omega) = \frac{\phi}{\omega} b''(\theta) = \frac{\phi}{\omega} b''\{(b')^{-1}(\mu)\} = \frac{\phi}{\omega} V(\mu). \] The function $V(\mu) = b''\{(b')^{-1}(\mu)\}$ is sometimes called the variance function of the GLM.

Exercise 3.5 Show the following.

For the Poisson regression model, $V(\mu) = \mu$.
For the binomial proportion regression model, $V(\mu) = \mu(1 - \mu)$.

Exercise 3.6 Argue (informally) that there exists an inverse function for $b'(\theta)$ provided that $\operatorname{Var}(Y \mid \theta, \phi) > 0$ for all $(\theta, \phi)$.

Exercise 3.7 To convince yourself of the correctness of Exercise 3.4, use the results to compute the mean and variance of the $\operatorname{Normal}(\mu, \sigma^2)$ and $\operatorname{Gam}(\alpha, \beta)$ distributions.

Exercise 3.8 To specify a GLM we must choose the so-called link function $g(\mu)$. A convenient choice (for reasons we will discuss later) is $g(\mu) = (b')^{-1}(\mu)$. This is known as the canonical link. By definition this gives the model \[ f(y_i \mid x_i, \omega_i, \theta, \phi) = \exp\left\{ \frac{y_i x_i^\top \beta - b(x_i^\top \beta)}{\phi / \omega_i} + c(y_i ; \phi / \omega_i) \right\}, \] i.e., we use the exponential dispersion family with $\theta_i = x_i^\top\beta$.

Show $Y \sim \operatorname{Normal}(\mu, \sigma^2)$ has the identity as the canonical link $g(\mu = mu)$.
Show $Y \sim \operatorname{Poisson}(\lambda)$ has the log-link as the canonical link $g(\mu) = \log \mu$.
Show that $Y = Z / n$ with $Z \sim \operatorname{Binomial}(n, p)$ has the logit link as the canonical link $g(\mu) = \log\{\mu / (1 - \mu)\}$.
Show that $Y \sim \operatorname{Gam}(\alpha,\beta)$ has the inverse as the canonical link $g(\mu) = -1/\mu$.
The canonical link for gamma GLMs (while commonly used in some fields) is used far less than for other types of GLMs, for one very good reason. What is that reason?

3.3 Fitting GLMs in `R`

We can fit GLMs in R via maximum likelihood by using the glm command; generally, fitting a GLM will look like this

my_glm <- glm(
  response ~ predictor_1 + predictor_2 + and_so_forth,
  data = my_data,
  family = my_family
)

The family argument tells R which type of GLM to fit: we will mostly use family = binomial for logistic regression or family = poisson for Poisson regression. It is also possible to change the link function with the family command; for example, doing family = binomial("probit") corresponds to fitting a binomial GLM using the probit link $g(\mu) = \Phi^{-1}(\mu)$ where $\Phi(z)$ is the cdf of a standard normal distribution (more on specific settings for link functions later). You can get information on all the options by running ?glm in the R console.

The easiest way to fit a GLM in the Bayesian paradigm is probably to use the rstanarm package in R.

install.packages("rstan")
install.packages("rstanarm")

After installing the package we can fit GLMs using something like this:

my_glm <- rstanarm::stan_glm(
  response ~ predictor_1 + predictor_2 +  and_so_forth, 
  data = my_data,
  family = my_family
)

The rstanarm package will use a “default” prior that places independent normal priors on the $\beta_j$’s, but this can be changed; see ?rstanarm::stan_glm for details on the priors that are available. The default priors are designed to give reasonable answers across a wide variety of problems encountered in practice.

3.4 Example: Logistic Regression

A particular case of a GLM takes \[ Y_i = Z_i / n_i \qquad \text{where} \qquad Z_i \sim \operatorname{Binomial}(n_i, p_i). \] When used with the canonical link of Exercise 3.8 we arrive at the logistic regression model \[ p_i = \frac{\exp(x_i^\top \beta)}{1 + \exp(x_i^\top \beta)}. \] Defining $\operatorname{logit}(p) = \log\{p / (1 - p)\}$, we equivalently can express the model as \[ \operatorname{logit}(p_i) = x_i^\top\beta. \]

3.4.1 What the Coefficients Represent

Exercise 3.9 Suppose we fit a logistic regression model $\operatorname{logit}(p_i) = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2}.$ Logistic regression models are often interpreted in terms of odds ratios; the odds of success of observational unit $i$ relative to $i'$ is given by \[ \frac{\operatorname{Odds}(Y_i = 1 \mid X_i)}{\operatorname{Odds}(Y_{i'} = 1 \mid X_{i'})} = \frac{\Pr(Y_i = 1 \mid X_i) \, \Pr(Y_{i'} = 0 \mid X_{i'})} {\Pr(Y_i = 0 \mid X_i) \, \Pr(Y_{i'} = 1 \mid X_{i'})} \] Show that, if $X_i$ and $X_{i'}$ are identical except that $X_{i2} = X_{i'2} + \delta$, then the odds ratio is given by $e^{\beta_2 \delta}$. That is shifting a covariate by $\delta$ has a multiplicative effect on the odds of success, inflating the odds by a factor of $e ^{\beta_2\delta}$.

3.4.2 Bernoulli Regression: The Challenger Shuttle Explosion

On January $28^{\text{th}}$, 1986, the space shuttle Challenger broke apart just after launch, taking the lives of all seven crew members. This example is taken from an article by Dalal et al. (1989), which examined whether the incident should have been predicted, and hence prevented, on the basis of data from previous flights. The cause of failure was ultimately attributed to the failure of a crucial shuttle component know as the O-rings; these components had been tested prior to the launch to see if they could hold up under a variety of temperatures.

The dataset Challenger.csv consists of data from test shuttle flights. This can be loaded using the following commands.

library(tidyverse)

f <- str_c("https://raw.githubusercontent.com/theodds/",
           "SDS-383D/main/Challenger.csv")

challenger <- read.csv(f) %>%
  drop_na() %>%
  mutate(Fail = ifelse(Fail == "yes", 1, 0))

head(challenger)

##   FlightNumber Temperature Pressure Fail nFailures Damage
## 1            1          66       50    0         0      0
## 2            2          70       50    1         1      4
## 3            3          69       50    0         0      0
## 4            5          68       50    0         0      0
## 5            6          67       50    0         0      0
## 6            7          72       50    0         0      0

Our Goal: The substantive question we are interested in is whether those in charge of the Challenger launch should have known that the launch was dangerous and delayed it until more favorable weather conditions. In fact, engineers working on the shuttle had warned beforehand that the O-rings were more likely to fail at lower temperatures.

Our Model: To help answer our substantive question, we will consider a model for whether an O-Ring failure occurred on a given flight ($Y_i = 1$ if an O-ring failed, $Y_i = 0$ otherwise) given the temperature $\texttt{temp}_i$. The most general model we could use would be $p_i = f(\texttt{temp}_i)$ for some function $f(\cdot)$; there is nothing wrong with this per-se, but it is useful to consider a model with a more interpretable structure \[ \operatorname{logit}(p_i) = \beta_0 + \beta_{\text{temp}} \times \text{temp}_i. \] In R we can fit the this model by maximum likelihood as follows.

challenger_fit <- glm(
  Fail ~ Temperature,
  data = challenger,
  family = binomial
)

A Bayesian version can also be fit as follows.

challenger_bayes <- rstanarm::stan_glm(
  Fail ~ Temperature,
  data = challenger,
  family = binomial
)

Using the Bayesian version, let’s plot the samples of the function \[ f(\texttt{temp}) = \{1 + \exp(-\beta_0 - \beta_1 \texttt{temp})\}^{-1}. \] We select $200$ of the $4000$ posterior samples at random for display purposes. I highly encourage you to step through this code on your own to understand what each line does.

## For Reproducibility
set.seed(271985)

## Converts the rstanarm object to a matrix
beta_samples <- as.matrix(challenger_bayes)

## Some Colors
pal <- ggthemes::colorblind_pal()(8)

## Set up plotting region
plot(
  x = challenger$Temperature, 
  y = challenger$Fail, 
  ylab = "Failure?",
  xlab = "Temperature",
  type = 'n'
)

## A function for adding estimate
plot_line <- function(beta, col = 'gray') {
  plot(function(x) 1 / (1 + exp(-beta[1] - beta[2] * x)), 
       col = col, add = TRUE, xlim = c(40, 90), n = 200)
}

## Apply plot_line for a random collection of betas
tmpf <- function(i) plot_line(beta_samples[i,])
tmp <- sample(1:4000, 200) %>% lapply(tmpf)

## Get the Bayes estimate of the probability
tempgrid <- seq(from = 40, to = 90, length = 200)
bayes_est <- predict(challenger_bayes, 
  type = 'response', 
  newdata = data.frame(Temperature = tempgrid)
)
lines(tempgrid, bayes_est, col = pal[3], lwd = 4)

## Adding the observations
points(
  x = challenger$Temperature, 
  y = challenger$Fail, 
  pch = 20, 
  col = pal[4]
)

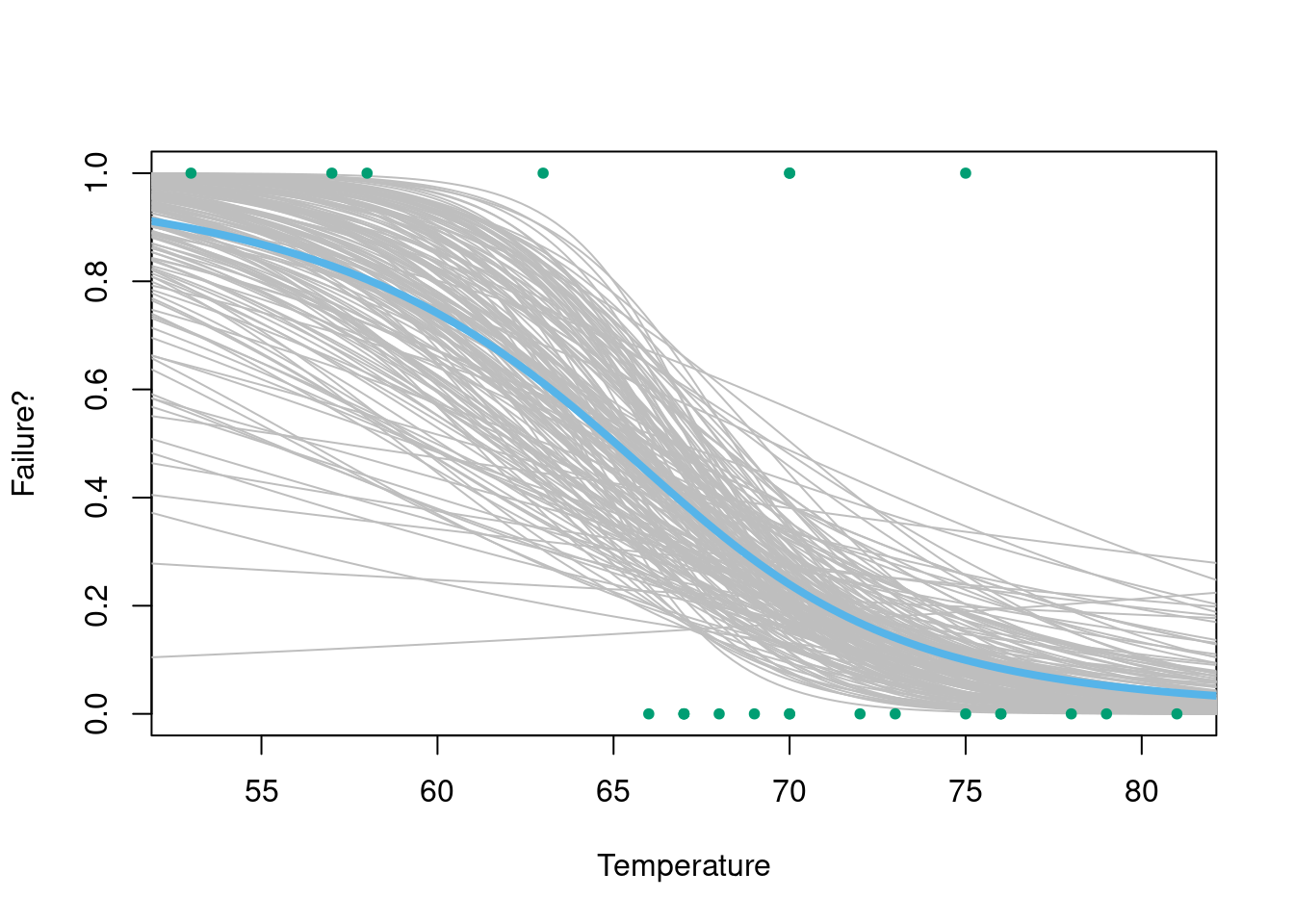
Figure 3.1: Posterior samples of the probability of failure.

Samples are given in Figure 3.1. We see that our Bayesian robot believes that it is extremely unlikely that lower temperatures are associated with a higher chance of failure and, indeed, that in most cases the failure of the O-rings is basically a foregone conclusion. On the day of the launch, the temperature was forecast to be 30 degrees, well below any of the experimental data. While we should always be wary of extrapolating beyond the range of our data, our robot would have made the following prediction for the probability of failure.

predict(challenger_bayes, 
        newdata = data.frame(Temperature = 30), 
        type = 'response')

##         1 
## 0.9862516

Hence, our model believes that an O-ring failure was a virtual certainty.

Exercise 3.10 Extract the posterior mean of $\beta_1$ from the model and interpret this estimate in terms of the impact of a 10-degree decrease in temperature on the odds of failure.

Exercise 3.11 Repeat the above analysis using the maximum likelihood approach. Rather than plotting the samples from a posterior, however, given a 95% pointwise confidence band. Note the function predict(..., type = 'response', se.fit = TRUE) will be useful. The type = 'response' tells predict that you want to get a probability; by default it gives the linear predictor $x^\top\beta$ instead.

Optionally: You can make the prediction on the scale of the linear predictor and transform the interval to the probability scale. This is probably the better strategy since $x^\top\beta$ will typically be closer to a normal distribution than $\operatorname{logit}^{-1}(x^\top\beta)$.

3.5 Example: Poisson Log-Linear Models

Another particular case of the generalized linear model takes \[ Y_i \sim \operatorname{Poisson}(\mu_i) \qquad \text{where} \qquad \log(\mu_i) = x_i^\top\beta. \] This is referred to as a Poisson log-linear model. Equivalently, we have $\mu_i = \exp(x_i^\top \beta)$.

3.5.1 What the Coefficients Represent

Exercise 3.12 Suppose we fit a Poisson log-linear model $\log(\mu_i) = \beta_0 + \beta_{i1} X_{i1} + \beta_{i2} X_{i2}$. Show that a change in $X_{i2}$ by $\delta$ units, holding $X_{i1}$ fixed, results in a multiplicative effect on the mean: \[ \mu_{\text{new}} = e^{\beta_2\delta} \mu_{\text{old}} \]

3.5.2 Poisson Log-Linear Regression: The Ships Dataset

This example is taken from Section 6.3.2 of McCullaugh and Nelder (1989). We consider modeling the rate of reported damage incidents of certain types of cargo-carrying ships. The data is available in the package and can be loaded as follows.

ships <- MASS::ships
head(ships)

##   type year period service incidents
## 1    A   60     60     127         0
## 2    A   60     75      63         0
## 3    A   65     60    1095         3
## 4    A   65     75    1095         4
## 5    A   70     60    1512         6
## 6    A   70     75    3353        18

The variable type refers to the type of vessel, year to year in which the vessel was constructed, period to the period of time under consideration, and service to the number of months of service of all vessels of this type. The response of interest, incidents, refers to the total number of damage incidents which occurred during the period across all vessels constructed in year year and of type type; the reason for this pooling is that it is assumed that incidents occur according to a Poisson process with no ship-specific effects (possibly a dubious assumption, but it is all we can do with the data we have been given).

We are interested in three questions:

Do certain types of ships tends to have higher numbers of incidents, after controlling for other factors?
Were some periods more prone to other incidents, after controlling for other factors?
Did ships built in certain years have more accidents than others?

One possible choice of model we could use is a Poisson log-linear model of the form $\texttt{incidents}_i \sim \operatorname{Poisson}(\mu_i)$ with \[ \log \mu_i = \beta_0 + \beta_{\texttt{service}} \cdot \texttt{service}_i + \beta_{\texttt{type}}\cdot\texttt{type}_i + \beta_{\texttt{period}} \cdot \texttt{period}_i + \beta_{\texttt{year}} \cdot \texttt{year}_i. \] This model is fine, but we actually have more information about how to incorporate service: consider two ships, one of which was at service for 6 months and the other for a year, but which are otherwise identical. If the incidents really follow a homogeneous Poisson process, we would expect that the second shipe has twice as many incidents as the first, on average. If this is the case, we should prefer the model \[ \log \mu_i = \beta_0 + \log (\texttt{service}_i) + \beta_{\texttt{type}}\cdot\texttt{type}_i + \beta_{\texttt{period}} \cdot \texttt{period}_i + \beta_{\texttt{year}} \cdot \texttt{year}_i. \] Equivalently, we have $\mu_i = \texttt{service}_i \cdot \eta_i$ where $\eta_i$ does not depend on $\texttt{service}_i$, giving the desired effect: doubling $\texttt{service}_i$ will double the mean. The term $\log(\texttt{service}_i)$ is called an offset; terms of this nature are very common in Poisson GLMs.

We can fit this model by maximum likelihood as follows.

ships_glm <- glm(
  incidents ~ type + factor(period) + factor(year),
  family = poisson,
  offset = log(service),
  data = dplyr::filter(ships, service > 0)
)

print(summary(ships_glm))

## 
## Call:
## glm(formula = incidents ~ type + factor(period) + factor(year), 
##     family = poisson, data = dplyr::filter(ships, service > 0), 
##     offset = log(service))
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.6768  -0.8293  -0.4370   0.5058   2.7912  
## 
## Coefficients:
##                  Estimate Std. Error z value Pr(>|z|)    
## (Intercept)      -6.40590    0.21744 -29.460  < 2e-16 ***
## typeB            -0.54334    0.17759  -3.060  0.00222 ** 
## typeC            -0.68740    0.32904  -2.089  0.03670 *  
## typeD            -0.07596    0.29058  -0.261  0.79377    
## typeE             0.32558    0.23588   1.380  0.16750    
## factor(period)75  0.38447    0.11827   3.251  0.00115 ** 
## factor(year)65    0.69714    0.14964   4.659 3.18e-06 ***
## factor(year)70    0.81843    0.16977   4.821 1.43e-06 ***
## factor(year)75    0.45343    0.23317   1.945  0.05182 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 146.328  on 33  degrees of freedom
## Residual deviance:  38.695  on 25  degrees of freedom
## AIC: 154.56
## 
## Number of Fisher Scoring iterations: 5

From this we see that there is substantial evidence for the relevance of all variables. There is quite strong evidence for an effect of period, with a period of 75 being associated with more incidents. Similarly, it seems that incidents are particularly low for ships operating in year 60 relative to other years. Finally, there is evidence for differences across types of ships, with (for example) B having fewer incidents than A.

Exercise 3.13 Fit this function using stan_glm, then try out the plot function for stanreg objects. Describe your results.

Exercise 3.14 A problem with Poisson log-linear models is that they impose the restriction $\mathbb E(Y_i) = \operatorname{Var}(Y_i)$ so that the variance is completely constrained by the mean. Count data is referred to as overdispersed if $\operatorname{Var}(Y_i) > \mathbb E(Y_i)$.

Consider the model $Y \sim \operatorname{Poisson}(\lambda)$ (given $\lambda$) and $\lambda \sim \operatorname{Gam}(k, k/\mu)$. Find the mean and variance of $Y$. Is $Y$ overdispersed?
Show that $Y$ marginally has a negative binomial distribution with $k$ failures and success probability $\mu / (k + \mu)$; recall that the negative binomial distribution has mass function \[ f(y \mid k, p) = \binom{k + y - 1}{y} p^y (1 - p)^k. \]
The following data is taken from Table 14.6 in Categorical Data Analysis, 3rd edition, by Alan Agresti.
```
poisson_data <- data.frame(
  Response = 0:6,
  Black = c(119,16,12,7,3,2,0),
  White = c(1070,60,14,4,0,0,1)
)
knitr::kable(poisson_data, booktabs = TRUE)
```
Response Black White

0 119 1070

1 16 60

2 12 14

3 7 4

4 3 0

5 2 0

6 0 1

The data is from a survey of 1308 people in which they were asked how many homicide victims they know. The variables are response, the number of victims the respondent knows, and race, the race of the respondent (black or white). The question is: to what extend does race predict how many homicide victims a person knows?

Fit a Poisson model of the form $g(\mu_i) = \beta_0 + \beta_1 \, \texttt{black}_i$ where $\texttt{black}_i$ is the indicator that an individual is black. Does the Poisson model fit well?
Compute an estimate of the variance for the two groups using a negative binomial model. How does this compare to (i) the Poisson estimate of the variance and (ii) the empirical estimate of the variance for the two groups?

Response	Black	White
0	119	1070
1	16	60
2	12	14
3	7	4
4	3	0
5	2	0
6	0	1

3.6 The Likelihood of a GLM

GLMs are fit in R using likelihood based inference. The likelihood function for a GLM, given data $\mathcal D= \{(Y_i, X_i) : i = 1, \ldots, N\}$ is given by \[ L(\beta, \phi) = \prod_{i = 1}^N \exp\left\{ \frac{Y_i \theta_i - b(\theta_i)}{\phi / \omega_i} + c(Y_i; \phi / \omega_i) \right\}, \] where we define $\theta_i \equiv (b')^{-1}(\mu_i)$ and $\mu_i \equiv g^{-1}(X_i^\top\beta)$. We can then derive the score function $s(\beta, \phi) = \frac{\partial}{\partial \beta} \log L(\beta,\phi)$ as \[ s(\beta,\phi) = \sum_{i=1}^N \frac{\partial}{\partial\beta} \frac{Y_i \theta_i - b(\theta_i)}{\phi / \omega_i} + c(Y_i ; \phi / \omega_i). \] Again, we will write $\frac{\partial}{\partial\beta} F(\beta)$ for the gradient of $F$ and $\frac{\partial^2}{\partial\beta\partial\beta^\top} F(\beta)$ for the Hessian matrix.

Exercise 3.15 Using the chain rule $\frac{\partial}{\partial\beta} = \frac{\partial}{\partial \theta} \times \frac{\partial \theta}{\partial\mu} \times \frac{\partial \mu}{\partial\beta}$, show that \[ s(\beta, \phi) = \sum_{i=1}^N \frac{\omega_i (Y_i - \mu_i) X_i}{\phi V(\mu_i) g'(\mu_i)}. \] Show also that, for the canonical link, we have $g'(\mu_i) = V(\mu_i)^{-1}$ so that this reduces to \[ s(\beta, \phi) = \sum_{i=1}^N \frac{\omega_i (Y_i - \mu_i) X_i}{\phi}. \] Hint: recall that $\frac{d}{dx}g^{-1}(x) = \frac{1}{g'\{g^{-1}(x)\}}$.

Exercise 3.16 We define the Fisher Information to be \[ \mathcal I(\beta, \phi) = -\mathbb E\left\{ \frac{\partial^2}{\partial\beta\partial\beta^\top} \log L(\beta, \phi) \mid \beta, \phi \right\}. \] The Fisher information plays an important role in inference for GLMs. The ``observed’’ Fisher information is also used, \[ \mathcal J(\beta,\phi) = -\frac{\partial^2}{\partial\beta\partial\beta^\top} \log L(\beta, \phi). \] In addition to being easier to evaluate, using $\mathcal J$ has been argued to be the right-thing-to-do. In any case, show that \[ \langle \mathcal J(\beta,\phi)\rangle_{jk} = \frac{1}{\phi} \sum_{i=1}^N X_{ij} X_{ik} \left\{ \frac{\omega_i}{V(\mu_i) g'(\mu_i)^2} - \frac{\omega_i (Y_i - \mu_i)}{g'(\mu_i)} \left( \frac{\partial}{\partial \mu_i} \frac{1}{V(\mu_i) g'(\mu_i)} \right) \right\} \] and \[ \langle \mathcal I(\beta,\phi) \rangle_{jk} = \frac{1}{\phi}\sum_{i=1}^N X_{ij} X_{ik} \frac{\omega_i}{V(\mu_i) g'(\mu_i)^2} \] where $\langle A \rangle_{ij}$ denotes the $(i,j)^{\text{th}}$ element of the matrix $A$. Show also that $\mathcal I(\beta,\phi) = \mathcal J(\beta,\phi)$ when the canonical link is used.

From the above exercise, notice that the Fisher information has the familiar form \[ \mathcal I^{-1} = \phi (X^\top D X)^{-1} \] where $D$ is a diagonal matrix with entries $\omega_i / \{V(\mu_i) g(\mu_i)^2\}$. Similarly, we can write $\mathcal J^{-1} = \phi(X^\top \widetilde D X)^{-1}$ for some diagonal matrix $\widetilde D$. Compare this with the linear model, which has inverse Fisher information $\mathcal I^{-1} = \sigma^2 (X^\top X)^{-1}$.

3.7 Aside: Likelihood-Based Inference

In this section, we will briefly refresh our memories on the theory underlying likelihood methods. For simplicity, consider data $\mathcal D= \{Z_i : i = 1, \ldots, N\}$ with $Z_i$’s iid according to some density $f(z \mid \theta_0)$ where $\{f(\cdot \mid \theta : \theta \in \Theta)\}$ is a family of distributions satisfying some (unstated) regularity conditions. We define the log-likelihood, score, and Fisher information with the equations \[ \ell(\theta) = \sum_{i = 1}^N \log f(Z_i \mid \theta), \quad s(\theta) = \frac{\partial}{\partial \theta} \ell(\theta), \quad \text{and} \quad \mathcal I(\theta) = - \mathbb E\left\{ \frac{\partial^2}{\partial \theta \partial \theta^\top} \ell(\theta) \mid \theta \right\}. \] The following identities are fundamental to likelihood inference \[ \mathbb E\{s(\theta) \mid \theta\} = \boldsymbol{0}, \qquad \text{and} \qquad \operatorname{Var}\{s(\theta) \mid \theta\} = \mathcal I(\theta). \] We will study three types of methods for constructing inference procedures from the likelihood: Score methods, Wald methods, and likelihood ratio (LR) methods.

Exercise 3.17 Using the multivariate central limit theorem, show that \[ s(\theta_0) \stackrel{{}_{\bullet}}{\sim}\operatorname{Normal}\{0, \mathcal I(\theta_0)\}, \] but only if we plug in the true value $\theta_0$ Note: this asymptotic notation means that $X \stackrel{{}_{\bullet}}{\sim}\operatorname{Normal}(\mu, \Sigma)$ if-and-only-if $\Sigma^{-1/2}(X - \mu) \to \operatorname{Normal}(0, \mathrm{I})$ in distribution.

Exercise 3.18 Using Taylor’s theorem, we have \[ s(\theta_0) = s(\widehat \theta) - \mathcal J(\theta^\star)(\theta_0 - \widehat \theta) = -\mathcal J(\theta^\star)(\theta_0 - \widehat\theta). \] where $\theta^\star$ lies on the line segment connecting $\theta_0$ and $\widehat\theta$. Now, assume that we know somehow that $\widehat\theta$ is a consistent estimator of $\theta_0$. Show that \[ \widehat \theta \stackrel{{}_{\bullet}}{\sim}\operatorname{Normal}(\theta_0, \mathcal I(\theta_0)^{-1}). \] Note: you do not need to give a completely rigorous proof. In particular, you can assume that, if $\theta_N \to \theta_0$, then $\frac{1}{N} \mathcal J(\theta_N) \to i(\theta_0)$ where \[ i(\theta_0) = -\mathbb E\left\{ \frac{\partial^2}{\partial\theta\partial\theta^\top} \log f(Z_i \mid \theta) \right\} = \mathcal I(\theta_0) / N. \]

Exercise 3.19 Consider the Taylor expansion \[ \ell(\theta_0) = \ell(\widehat\theta) + s(\widehat\theta)^\top (\theta_0 - \widehat \theta) - \frac{1}{2} (\theta_0 - \widehat \theta)^\top \mathcal J(\theta^\star) (\theta_0 - \widehat\theta) \] where $\theta^\star$ lies on the line segment connecting $\widehat\theta$ and $\theta_0$. Using Exercise 3.18, show that \[ -2\{\ell(\theta_0) - \ell(\widehat\theta)\} \to \chi^2_P. \] in distribution, where $P = \dim(\theta)$. Recall here that the $\chi^2_P$ distribution is the distribution of $\sum_{i=1}^P U_i^2$ where $U_1,\ldots,U_P \stackrel{\text{iid}}{\sim}\operatorname{Normal}(0,1)$.

Exercise 3.18 provides the basis for “Wald” methods, while Exercise @ref{exr:notes-glm-score} provides the basis for “score” methods, and Exercise @ref{ex:notes-glm-lrt} provides the basis for “likelihood ratio” (LR) methods.

More generally one can show, using the same sorts of Taylor expansions used above, the following result.

Theorem 3.1 (Wilk's Theorem) Suppose that $\{f_{\theta,\eta} : \theta \in \Theta, \eta \in H\}$ is a parametric family satisfying certain regularity conditions. Consider the null hypothesis $H_0: \eta = \eta_0$, let $\widehat \theta_0$ denote the MLE obtained under the null model, and let $(\widehat \theta, \widehat \eta)$ denote the MLE under the unrestricted model. Then, if $(\theta_0, \eta_0)$ denote the values of the parameters that generated the data (so that $H_0$ is true) then \[ -2\{\ell(\widehat \theta_0, \eta_0) - \ell(\widehat \theta, \widehat \eta)\} \stackrel{{}_{\bullet}}{\sim} \chi^2_{D} \] where $D = \dim(\eta)$, as the amount of data tends to $\infty$.

The statement of the result above is deliberately vague; the regularity conditions are unstated, and what it means for the “amount of data” to tend to $\infty$ is not made precise. If our data is of the form $\mathcal D= \{(X_i, Y_i) : i = 1,\ldots,N\}$ then taking $N \to \infty$ will suffice, but there are other situations where the result will hold even if $N$ is fixed (with the data “tending to infinity” in other ways). An example in which this is the case is analysis of contingency tables, where $N$ denotes the number of cells. Another important requirement to get a result like this is that we should have the dimension of the parameters fixed, which is sometimes not the case even for old-school GLMs.

The above result will let us do things like perform hypothesis tests and construct confidence intervals.

Note: It is also possible to extend the score method to the case with parameter constraints, but we don’t have time to do so. My experience is that, for the most part, LR methods tend to be better than score methods (both are better than Wald methods), although this isn’t universally true. Notice that LR methods require fitting both a constrained and unconstrained model. It turns out that score methods only require fitting the constrained model, which can occasionally be useful if the unconstrained model is difficult to fit.

3.8 Likelihood-Based Inference for GLMs

Bayesian inference for GLMs is quite straight-forward — just fit the model with stan_glm, get the posterior samples, and interpret the results as you normally would.

For Frequentist inference, we can use likelihood-based methods to do things like conduct hypothesis tests. A convenient quantity to use is the deviance of a GLM.

Definition 3.3 (Deviance of a GLM) Let $\mathcal D= \{(Y_i, X_i) : i = 1 ,\ldots, N\}$ be modeled with a GLM in the exponential dispersion family with canonical parameters $\theta_i = (b')^{-1}(\mu_i) = (b')^{-1}(g^{-1}(X_i^\top\beta))$. Let $\theta = (\theta_1, \ldots, \theta_N)$ and let $\widehat \theta = (\widehat \theta_1, \ldots, \widehat \theta_N)$ be the MLE of the $\theta$’s under our model. We define the saturated model as the model which has a separate parameter for all unique values of $x$ in $\mathcal D$: \[ f(y \mid x, \phi / \omega) = \exp\left\{ \frac{y \theta_x - b(\theta_x)}{\phi/\omega} + c(y;\phi/\omega). \right\}. \] The residual deviance of a model is defined by \[ D = -2 \phi\left\{\ell(\widehat \theta) - \ell(\widehat \theta_x) \right\} \] where $\ell(\theta) = \sum_{i=1}^N \dfrac{\omega_i(Y_i\theta_i - b(\theta_i))}{\phi}$ is the log-likelihood of $\theta$. The scaled deviance is $D^\star = D / \phi$. Note: if $\phi$ is unknown, we generally replace $\phi$ with an estimate $\widehat \phi$ given by \[ \widehat \phi = \frac{1}{N-P} \sum_{i=1}^N \frac{\omega_i (Y_i - \widehat \mu_i)^2}{V(\widehat \mu_i)}. \]

Exercise 3.20 Show that the quantity \[ \widetilde \phi = \frac{1}{N} \sum_i \frac{\omega_i (Y_i - \mu_i)^2}{V(\mu_i)} \] is unbiased for $\phi$. We don’t use $\widetilde\phi$ because we don’t know the $\mu_i$’s, so the modified denominator in $\widehat\phi$ compensates for the “degrees of freedom” used to estimate $\beta$.

In words: the scaled deviance is the LRT statistic for comparing the model with the saturated model which has the maximal number of model parameters in the GLM.

If it were up to me, I would only ever talk about the scaled deviance, since the scaled deviance is interpretable as an LRT statistic. Unfortunately, the software output of R returns the deviance, and $D \ne D^\star$. Conveniently, however, $D = D^\star$ for the Poisson and Binomial GLMs.

What is the deviance good for? The deviance is commonly used for two purposes.

It can be used as a goodness-of-fit statistic, testing to see whether the model under consideration would be rejected in favor of the saturated model. From a modern perspective, this might be construed as a test of the parametric model against a nonparametric alternative, without making any smoothness assumptions on $\theta_x$. This is a little bit tricky, however, since the saturated model has $P = N$ parameters, so the usual asymptotics (where $N$ is large relative to $P$) do not apply. In certain situations, however, one can show that $D^\star \stackrel{{}_{\bullet}}{\sim}\chi^2_{N-P}$, as would be suggested by a naive application of Theorem 3.1.
If model $\mathcal M_0$ is a submodel of $\mathcal M_1$ then the LRT statistic for comparing these models is $D^\star_0 - D^\star_1$. Under very weak conditions, we have $D^\star_0 - D^\star_1 \stackrel{{}_{\bullet}}{\sim}\chi^2_K$ where $K$ is the difference in the number of parameters between the two models.

For example, we can easily perform the LRT in Theorem 3.1 using the anova function.

anova(ships_glm, test = "LRT")

## Analysis of Deviance Table
## 
## Model: poisson, link: log
## 
## Response: incidents
## 
## Terms added sequentially (first to last)
## 
## 
##                Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
## NULL                              33    146.328              
## type            4   55.439        29     90.889 2.629e-11 ***
## factor(period)  1   20.786        28     70.103 5.135e-06 ***
## factor(year)    3   31.408        25     38.695 6.975e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

This table gives an analysis of deviance, which should feel quite similar to the analysis of variance that you are already familiar with.

The NULL residual deviance gives the deviance of an intercept-only model.
The type residual deviance gives the deviance of a model with type and an intercept.
The period residual deviance gives the deviance of a model with type, period, and an intercept.
The year residual deviance gives the deviance of a model with all terms included in the model.
The columns Df and Deviance give the degrees of freedom and the LRT statistic that compares the model including all terms up-to-and-including the current line with the model including all terms up-to-but-not-including the current line. For example, the Deviance corresponding to factor(period) tests a model with terms ~ intercept + type against a model with terms ~ intercept + type + period.

The results of the analysis of deviance point clearly to the relevance of the individual terms. Unlike the output of summary, this provides the likelihood ratio test rather than Wald tests for the parameters, and the different variables have been helpfully grouped together (i.e., we have a single term of type with four degrees of freedom, rather than four separate coefficients).

The last residual deviance for the full model is $38.695$, with a (naive) null distribution of $\chi^2_{25}$. This corresponds to a $P$-value of

pchisq(38.695, df = 25, lower.tail = FALSE)

## [1] 0.0395148

This gives some evidence that the model lacks fit, and the model could be disproved in favor of the saturated model. As mentioned above, however, the deviance may not be close to a $\chi^2_{N-P}$ distribution in this case. For Poisson data, the key is that the individual counts for each observation should be largeish. But

print(ships$incidents)

##  [1]  0  0  3  4  6 18  0 11 39 29 58 53 12 44  0 18  1  1  0  1  6  2  0  1  0
## [26]  0  0  0  2 11  0  4  0  0  7  7  5 12  0  1

Hence, use of the deviance in this situation as a goodness of fit test seems questionable.

We can also construct likelihood-based confidence intervals for the parameters. If I want a confidence interval for (say) $\beta_1$, I can get one by inverting the test $H_0: \beta_1 = \beta_{01}$ to get a confidence set \[ \{\beta_{01} : \text{The LRT fails to reject $H_0: \beta_0 = \beta_{01}$}\}. \] If the LRT has Type I error rate $\alpha$ for all $\beta_{01}$ then the above set is guaranteed to be a $100(1 - \alpha)\%$ confidence set. This is implemented in R with the function confint:

confint(ships_glm)

## Waiting for profiling to be done...

##                        2.5 %      97.5 %
## (Intercept)      -6.84305161 -5.98968373
## typeB            -0.88135891 -0.18353080
## typeC            -1.37649167 -0.07452031
## typeD            -0.67151807  0.47524605
## typeE            -0.14346972  0.78520455
## factor(period)75  0.15339419  0.61740478
## factor(year)65    0.40752296  0.99512708
## factor(year)70    0.48728088  1.15369754
## factor(year)75   -0.01234169  0.90386446

In general, you should use anova and confint rather than the output of summary.

Lastly, rather than doing sequential tests like anova does, you can do a “leave-one-out” test using drop1 as follows.

drop1(ships_glm, test = "LRT")

## Single term deletions
## 
## Model:
## incidents ~ type + factor(period) + factor(year)
##                Df Deviance    AIC    LRT  Pr(>Chi)    
## <none>              38.695 154.56                     
## type            4   62.365 170.23 23.670 9.300e-05 ***
## factor(period)  1   49.355 163.22 10.660  0.001095 ** 
## factor(year)    3   70.103 179.97 31.408 6.975e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

This tests each model term under the assumption that the other terms are in the model.

Exercise 3.21 Try these ideas out on the Challenger dataset. How do your conclusions differ (nor not differ) from the Bayesian analysis?