15 K-medoides
15.1 Algoritmo:
Asignar aleatoreamente un número, del \(1\) a \(K\) a cada observación. Estos funcionan como asignaciones iniciales para las observaciones.
Iterar hasta que las asignaciones dejen de cambiar:
2.1. Para cada uno de los $K$ conglomerados, calcular el medoide del conglomerado. El $k$-ésimo medoide del grupo es el vector de las $p$ medias de características para las observaciones en el $k$-ésimo grupo.
2.2. Asignar cada observación al conglomerado cuyo medoide es el más cercano (donde más cercano se define utilizando la distancia euclidiana).15.1.3 Paso 3: entrenar un modelo en los datos
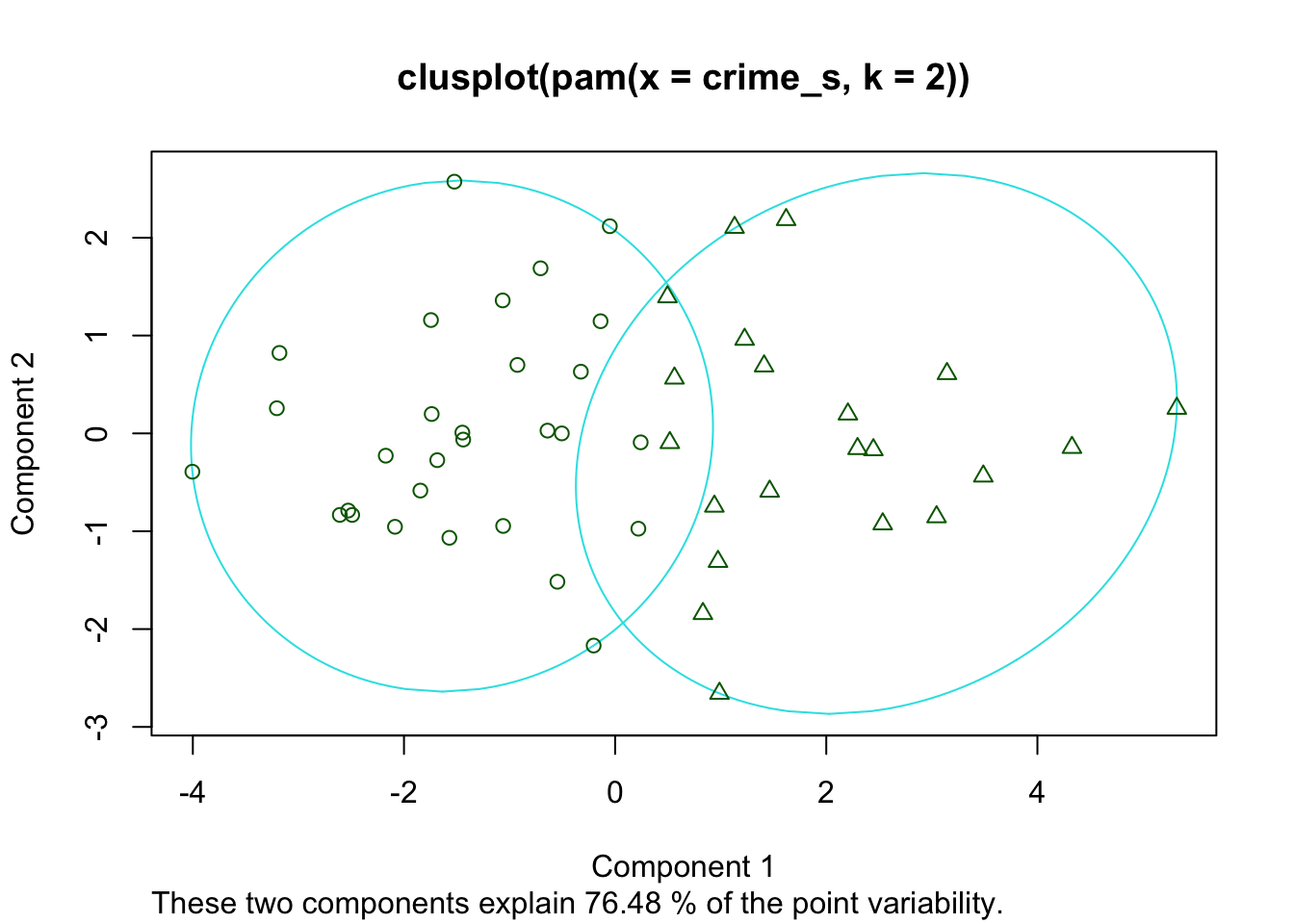
Los pasos anteriores son los mismos realizados en kmeans. Ahora ajustamos un kmedoides: