2 Deep Dive into Linear Algebra
2.1 Definition of Vector Space
Definition: A vector space consists of a set V along with 2 operations “+” (addition) and “*” (scalar multiplication) subject to 10 properties
Example: $L = $ Show L forms a vector under the operations vector addition and vector scalar multiplication.
(i) let →a,→bϵL
∴
\vec{b} = \begin{bmatrix} x_{2} \\ y_{2} \end{bmatrix} = \begin{bmatrix} x_{2} \\ 5y_{2} \end{bmatrix} = \begin{bmatrix} 1 \\ 5 \end{bmatrix}x_{2}
\Rightarrow \vec{a} + \vec{b} = \begin{bmatrix} 1 \\ 5 \end{bmatrix}x_{1} + \begin{bmatrix} 1 \\ 5 \end{bmatrix}x_{2} = \begin{bmatrix} 1 \\ 5 \end{bmatrix}(x_{1}+x_{2}) \epsilon L
(ii) commutative: \vec{a}+\vec{b} = \vec{b}+\vec{a}
(iii) let \vec{c} \epsilon L \therefore(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) by associativity of vector (+)
(iv) zero vector: let x=y=0 \therefore \begin{bmatrix} 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 5 * 0 \end{bmatrix}
(v) additive inverse: let \vec{d} = \begin{bmatrix} -x_{1} \\ -5x_{1} \end{bmatrix} \epsilon L
\therefore \vec{a} + \vec{d} = \begin{bmatrix} x_{1} \\ 5x_{1} \end{bmatrix} + \begin{bmatrix} -x_{1} \\ -5x_{1} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
\therefore the additive inverse of \vec{a} is in L
(vi) let c \epsilon \mathbb{R}; c \vec{a} = c\begin{bmatrix} x_{1} \\ 5x_{1} \end{bmatrix} = cx_{1}\begin{bmatrix} 1 \\ 5 \end{bmatrix} \epsilon L
\therefore closed under scalar multiplication
(vii) (c_{1}+c_{2})\vec{a} = c_{1}\vec{a} + c_{2}\vec{a} by distributive property of scalar multiplication
(viii) c_{1}(\vec{a}+\vec{b}) = c_{1}\vec{a} + c_{1}\vec{b} by distributive property of vector (+)
(ix) (c_{1}c_{2})\vec{a} = c_{1}(c_{2}\vec{a}) by associativity of scalar multiplication
(x) 1\vec{a} = \vec{a}
Extend to \mathbb{R^{n}}
I. \mathbb{R^{2}} (entire space)
II. Any line through origin
III. \vec{0} (trivial space)
Other kinds of vector spaces:
Example: let P_{2} = \begin{Bmatrix}a_{0}+a_{1}x+a_{2}x^{2} | a_{0},a_{1},a_{2} \epsilon \mathbb{R^{2}}\end{Bmatrix} Show P_{2} is a vector space under the operations for addition and multiplication by a constant.
All axioms are easy to check. I’ll show a few.
Closure under addition:
let f(x), g(x) \epsilon P_{2} \therefore f = a_{0}+a_{1}x+a_{2}x^{2}
g = b_{0}+b_{1}x+b_{2}x^{2}
\Rightarrow f+g= (a_{0}+b_{0})+(a_{1}+b_{1})x+ (a_{2}+b_{2})x^{2} \epsilon P_{2}
therefore closed under addition
Closure under scalar multiplication:
let c \epsilon \mathbb{R} \Rightarrow cf = c(a_{0}+a_{1}x+a_{2}x^{2})
= ca_{0}+ca_{1}x+ca_{2}x^{2} \epsilon P_{2} therefore closed under scalar multiplication
Zero element:
let a_{0}=a_{1}=a_{2}=0 \therefore h(x)=0 \epsilon P_{2} and 0 + f(x) = f(x)
Subspaces
General polynomial space P_{n}=\begin{Bmatrix}a_{0}+a_{1}x+a_{n}x^{n} | n \epsilon \mathbb{N}, a \epsilon \mathbb{R^{2}}\end{Bmatrix}
P_{k} is a subspace of P_{n} for 0 \leq k \leq n
Example: let f(x) = 3x^{2}+2x+1
f(x) \epsilon P_{n} for n \geq 2, f(x) does not span P_{1}
Calculus Operations:
Example: V=\begin{Bmatrix}y^{'} + y | y^{'} + y = 0\end{Bmatrix} homogeneous ODE
Closure under addition: let f,g \epsilon V
\therefore f^{'}+f=0, g^{'}+g=0 by definition
\frac{d}{dx}[f+g]+f+g
=\frac{df}{dx} + \frac{dg}{dx} + f + g
=(\frac{df}{dx} + f) + (\frac{dg}{dx} + g)
= 0 + 0
= 0 \therefore f+g \epsilon V
Closure under scalar multiplication: let c \epsilon \mathbb{R}
\frac{d}{dx}[cf] + cf
=c\frac{df}{dx} + cf
=c(\frac{df}{dx} + f)
=c * 0
=0 \therefore cf \epsilon V
Zero element: let h=0
\therefore \frac{dh}{dx} + h = 0+0=0 \therefore \vec{0} \epsilon V
Yes, this forms a vector space
Examples of Vector Space Rules:
Closure under Addition:
let\ A, B \in V \therefore A= \left[ \begin{array}{cc} a_1 & 0 \\ 0 & a_2 \end{array} \right], \ \ B= \left[ \begin{array}{cc} b_1 & 0 \\ 0 & b_2 \end{array} \right]
\Rightarrow A + B = \left[ \begin{array}{cc} a_1+b_1 & 0+0 \\ 0+0 & a_2+b_2 \end{array} \right] = \left[ \begin{array}{cc} a_1+b_1 & 0 \\ 0 & a_2+b_2 \end{array} \right] \in V
Closure under Scalar Multiplication:
let\ c \in \mathbb{R} \therefore cA= c\left[ \begin{array}{cc} a_1 & 0 \\ 0 & a_2 \end{array} \right] = \left[ \begin{array}{cc} ca_1 & c\times0 \\ c\times0 & ca_2 \end{array} \right] = \left[ \begin{array}{cc} ca_1 & 0 \\ 0 & ca_2 \end{array} \right] \in V
Zero Element:
let\ A=B=0\therefore \left[ \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right] \in V
Example: V=set of singular matrices. Is it a vector space? NO
let\ A= \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right],\ B= \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right]
A,B\in V\ by\ def^{(n)};\ but, A+B=\left[\begin{array}{cc}1 & 0 \\0 & 1\end{array}\right] \notin V
therefore not closed, therefore not a vector space
Complex Numbers
Example: V=\Bigg\{\left[\begin{array}{cc}1 & 0 \\0 & 1\end{array}\right]\Bigg|\ a,b\in \mathbb{C},\ a+b=0\Bigg\}
Is this a Vector Space? YES
Closure under Addition:
let\ A, B \in V \therefore A= \left[\begin{array}{cc}0 & a_1 \\a_2 & 0\end{array}\right], \ \ B= \left[\begin{array}{cc}0 & b_1 \\b_2 & 0\end{array}\right]
a_1 + a_2=0,\ \ b_1 + b_2=0,\ \ \therefore \ a_1 + a_2 + b_1 + b_2=0
\Rightarrow A + B = \left[\begin{array}{cc}0+0 & a_1+b_1 \\a_2+b_2 & 0+0\end{array}\right] = \left[\begin{array}{cc}0 & a_1+b_1 \\a_2+b_2 & 0\end{array}\right]\in V
Closure under Scalar Multiplication:
let\ c \in \mathbb{C} \therefore c=c_1 + c_2i\ where\ i=\sqrt{-1}
\therefore cA= (c_1+c_2i)\left[\begin{array}{cc}a_1 & 0 \\0 & a_2\end{array}\right]
=c_1\left[\begin{array}{cc}0 & a_1 \\a_2 & 0\end{array}\right] +c_2i\left[\begin{array}{cc}0 & a_1 \\a_2 & 0\end{array}\right]
=\left[\begin{array}{cc}0 & c_1a_1 \\c_1a_2 & 0\end{array}\right] +\left[\begin{array}{cc}0 & c_2ia_1 \\c_2ia_2 & 0\end{array}\right]
=\left[\begin{array}{cc}0 & ca_1 \\ca_2 & 0\end{array}\right]\in V
Zero Element: let\ A=B=0\therefore \left[ \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right] \in V
Subspaces & Spanning Sets
Subspaces of \mathbb{R}^{3}:
- point(\overrightarrow{0})
- line through origin
- plane through origin
- \mathbb{R}^{3}
Subspace:
A subspace W of a vector space V is another vector space contained within V; W must be closed under linear combinations
Span:
Let S = \{\overrightarrow{s_1},\overrightarrow{s_2},...,\overrightarrow{s_n}\}; the span of S, denoted span\{S\} is the set of all linear combinations.
\therefore span\{S\} = \{c_1\overrightarrow{s_1}+...+c_n\overrightarrow{s_n}|c_i\in \mathbb{R},\overrightarrow{s_i}\in S\}
Example: let\ \hat{i}=\left[\begin{array}{c}1 \\0 \\0\end{array}\right],\ \hat{j}=\left[\begin{array}{c}0 \\1 \\0\end{array}\right],S=\{\hat{i},\hat{j}\}
\therefore span(S)=\{c_1\hat{i}+c_2\hat{j}|c_i,c_2\in \mathbb{R}\}
\Rightarrow xy-plane, z=0
Example: span\Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right],\left[\begin{array}{c}0 \\1 \\0\end{array}\right],\left[\begin{array}{c}0 \\0 \\1\end{array}\right]\Bigg\}=\mathbb{R}^{3}
Example: span\Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right],\left[\begin{array}{c}2 \\0 \\0\end{array}\right],\left[\begin{array}{c}3 \\0 \\0\end{array}\right],\left[\begin{array}{c}4 \\0 \\0\end{array}\right]\Bigg\}=\Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right]c\ \Bigg|\ c\in \mathbb{R}\Bigg\} = x-axis (line)
Example: span\Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right],\left[\begin{array}{c}0 \\0 \\1\end{array}\right],\left[\begin{array}{c}5 \\0 \\5\end{array}\right]\Bigg\}=\Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right]c_1+\left[\begin{array}{c}0 \\0 \\1\end{array}\right]c_2+\left[\begin{array}{c}5 \\0 \\5\end{array}\right]c_3\ \Bigg|\ c_1, c_2, c_3\in \mathbb{R}\Bigg\}
5\left[\begin{array}{c}1 \\0 \\0\end{array}\right]+5\left[\begin{array}{c}0 \\0 \\1\end{array}\right]=\left[\begin{array}{c}5 \\0 \\5\end{array}\right], \therefore \Bigg\{\left[\begin{array}{c}1 \\0 \\0\end{array}\right]c_1+\left[\begin{array}{c}0 \\0 \\1\end{array}\right]c_2\ \Bigg|\ c_1, c_2\in \mathbb{R}\Bigg\} = xz-plane
Solutions to Assorted Problems:
1.17(p. 92-93)
- f(x)=0
- \left[\begin{array}{cccc}0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0\end{array}\right]
1.22(p. 93)
- let \overrightarrow{a}, \overrightarrow{b} \in S
\therefore \overrightarrow{a}=\left[\begin{array}{c}x_1 \\y_1 \\z_1\end{array}\right] so that x_1+y_1+z_1=1 \overrightarrow{b}=\left[\begin{array}{c}x_2 \\y_2 \\z_2\end{array}\right] so that x_2+y_2+z_2=1\\But, \overrightarrow{a}+\overrightarrow{b}=\left[\begin{array}{c}x_1+x_2 \\y_1+y_2 \\z_1+z_2\end{array}\right] and\\(x_1+x_2)+(y_1+y_2)+(z_1+z_2)=(x_1+y_1+z_1)+(x_2+y_2+z_2)=1+1=2\not= 1, \therefore \overrightarrow{a}+\overrightarrow{b}\notin S, \therefore Not Closed, \therefore Not Vector Space
1.23
S=\{a+bi|a,b\in \mathbb{R}\}
2.2 Linear Independence, Basis, Dimension
Linear Independence
Definition: A set of vectors \{ \vec{v_1}, ... ,\vec{v_n} \} is linearly independent if none of its elements is a linear combinations of the other elements in the set. Otherwise, the set is linearly dependent
Example 1: { \Biggl\{ \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}}, {\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}}, {\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}}, {\begin{bmatrix} -2 \\ 3 \\ 5 \end{bmatrix} \Biggl\} }
Note: { -2 \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}} + 3 {\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}} + 5 {\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}} = {\begin{bmatrix} -2 \\ 3 \\ 5 \end{bmatrix} }
\therefore \vec{v_4} is a linear combination of \vec{v_1},\vec{v_2},\vec{v_3} , and we say S is linearly dependent
Example 2: { \biggl\{ \begin{bmatrix} 1 \\ 0 \end{bmatrix}}, {\begin{bmatrix} 0 \\ 3\end{bmatrix} \biggl\} }
\because c_1\vec{v_1} \neq \vec{v_2} for any c \in R, the set is linearly independent
Theorem: \{ \vec{v_1}, ... ,\vec{v_n} \} is linearly independent if and only if c_1\vec{v_1} + ... + c_n\vec{v_n} = \vec{0} only when c_1 = c_2 = ... = c_n = 0
- This provides a way to test for linear independence
Example 3: Use the previous theorem to show { \biggl\{ \begin{bmatrix} 40 \\ 15 \end{bmatrix}}, {\begin{bmatrix} -50 \\ 25 \end{bmatrix} \biggl\} } are linearly independent.
c_1\begin{bmatrix} 40 \\ 15 \end{bmatrix} + c_2\begin{bmatrix} -50 \\ 25 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
\therefore I. 40c_1 - 50c_2 = 0
- 15c_1 + 25c_2 = 0 c_1 = c_2 = 0
Basis
Example 1: { \biggl\{ \begin{bmatrix} 2 \\ 3 \end{bmatrix}}, {\begin{bmatrix} -1 \\ 2\end{bmatrix}, \begin{bmatrix} 0 \\ 5\end{bmatrix} \biggl\} }
Since this set has 3 vectors in \mathbb{R^{2}}, the set is linearly dependent.
Example 2: { \{ \begin{bmatrix} 2 \\ 3 \\ 7 \end{bmatrix}}, {\begin{bmatrix} -1 \\ 2 \\10 \end{bmatrix}, \begin{bmatrix} 0 \\ 5 \\ -3\end{bmatrix} \} }
Since this set has 3 vectors in \mathbb{R^{3}},need to test for linear independence.
{ c_1 \begin{bmatrix} 2 \\ 3 \\ 7 \end{bmatrix} + c_2 \begin{bmatrix} -1 \\ 2 \\10 \end{bmatrix} + c_3 \begin{bmatrix} 0 \\ 5 \\ -3\end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}}
\left[ \begin{array}{rrr|r} 2 & -1 & 0 & 0 \\ 3 & 2 & 5 & 0 \\ 7 & 10 & -3 & 0 \end{array} \right] \longrightarrow \left[ \begin{array}{rrr|r} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right]
This matrix is in RREF form, \therefore the only solution is c_1=c_2=c_3=0, \therefore the vectors are linearly independent.
Example 3: { \{ 8+3x+3x^2, x+2x^2,2+2x+2x^2,8-2x+5^2 \} } Is this set a basis of P_{2}
\begin{bmatrix} 8 & 0 & 2 & 8 \\ 3 & 1 & 2 &-2 \\ 3& 2 & 2 & 5 \end{bmatrix}
\therefore No, since any basis of P_2 requires exactly 3 functions, and we have 4.
Dimension
Defintion: The minimum number of elements required to span a given vector space V.
- Notation: dim(V) “dimension of V
Let V be a vector space. V is called finite-dimensional if dim(V) = n < \infty
Examples:
dim(\mathbb R^{6}) = 6
dim(M_{2\times2}) = 4
dim(P_2) = 3
Let V = {\begin{bmatrix} a & c \\ b & d \end{bmatrix}| a,b,c,d \in \mathbb C }
Assume entries are complex-valued and scalars are real-valued, \therefore dim(V) = 8
Theorem: In any finite dimensional vector space, any 2 bases have the same # of elements.
Note: Some vector spaces are infinite dimensional
Example: Let V be the set of all functions of 1 variable
\therefore V = \{ f(x) | x \in \mathbb R \} , \therefore dim(V) = \infty
Examples from III.2: 2.17 V = \Biggl\{ \begin{bmatrix} x \\ y \\ z \\w \end{bmatrix} \Biggl| \space x-w+z = 0 \Biggl\}
Basis: x + z = w, \therefore x,z are free; y is also free since it is unrestricted
\therefore V = \Biggl\{ \begin{bmatrix} 1\\0\\0\\1\end{bmatrix}x+ \begin{bmatrix} 0\\1\\0\\0\end{bmatrix}y + \begin{bmatrix} 0\\0\\1\\1\end{bmatrix}z \space \Biggl| \space x,y,z \in \mathbb R \Biggl\} \longrightarrow V = span \Biggl\{ \begin{bmatrix} 1\\0\\0\\1\end{bmatrix}, \begin{bmatrix} 0\\1\\0\\0\end{bmatrix}, \begin{bmatrix} 0\\0\\1\\1\end{bmatrix} \Biggl\} Thus, \Biggl\{ \begin{bmatrix} 1\\0\\0\\1\end{bmatrix}, \begin{bmatrix} 0\\1\\0\\0\end{bmatrix}, \begin{bmatrix} 0\\0\\1\\1\end{bmatrix} \Biggl\} is a basis of V, which means that V is a 3D subspace of \mathbb R^4, and dim(V) = 3 as it has 3 elements in basis
Fundamental Subspaces
Let A be n\times m. There are 4 associated vector spaces with A.
I. Column space: span of the columns of A
Row space: span of the rows of A
Null space (will learn in later topics)
Left Null Space (will learn in later topics)
Row space:
The row space of a matrix is the span of the rows in the matrix; the dimension of row space is called the row rank
- Notation: rowspace(A)
Example: Let A = \begin{bmatrix} 2&3\\4&6 \end{bmatrix}. What is the rowspace? rowspace(A) = \{ c_1\begin{bmatrix} 2&3 \end{bmatrix} + c_2 \begin{bmatrix} 4&6 \end{bmatrix}| \space c_1,c_2 \in \mathbb R \} = span\{\begin{bmatrix} 2&3 \end{bmatrix}, \begin{bmatrix} 4&6 \end{bmatrix} \} = span\{\begin{bmatrix} 2&3 \end{bmatrix}\}, \space \because \space 2\begin{bmatrix} 2&3 \end{bmatrix} = \begin{bmatrix} 4&6 \end{bmatrix} \because \space dim(rowspace(A)) = 1 \longrightarrow \space \therefore rank(A) = 1
Column space:
The column space of a matrix is the span of the columns in the matrix; the dimension of column space is called the column rank
- Notation: colspace(A)
Example: colspace(A) = \biggl\{ c_1\begin{bmatrix} 2\\4 \end{bmatrix} + c_2 \begin{bmatrix} 3\\6 \end{bmatrix}|c_1,c_2 \in \mathbb R \biggl\} = span \biggl\{\begin{bmatrix} 2\\4 \end{bmatrix}, \begin{bmatrix} 3\\6 \end{bmatrix} \biggl\}
= span \biggl\{\begin{bmatrix} 2\\4 \end{bmatrix} \biggl\}, \space \because \space \frac{3}{2} \begin{bmatrix} 2\\4 \end{bmatrix} = \begin{bmatrix} 3\\6 \end{bmatrix} \because \space dim(colspace(A)) = 1 \longrightarrow \space \therefore rank(A) = 1
Theorem: In any n\times m matrix the row rank and column rank are equal.
- Comment - the rank of a matrix is its row rank or column rank
Example: B = \begin{bmatrix} 1&3&7\\2&4&12 \end{bmatrix} \space \therefore B^T = \begin{bmatrix} 1&2\\3&4\\7&12 \end{bmatrix}
- Comments:
- (A^T)^T = A
- (A^T)^T = A
- rowspace(A) = colspace(A^T)
- rowspace(A) = colspace(A^T)
Example: Let A = \begin{bmatrix} 1&3&7\\2&3&8\\0&1&2\\4&0&4\end{bmatrix}. Determine a basis for colspace(A)
\therefore A^T = \begin{bmatrix} 1&2&0&4\\3&3&1&0\\7&8&2&4 \end{bmatrix}\underset{\overset{-7I +III}{\longrightarrow}}{\overset{-3I+II}{\longrightarrow}} \begin{bmatrix} 1&2&0&4\\0&-3&1&-12\\0&-6&2&-24 \end{bmatrix} \underset{-2II +III}{\longrightarrow} \begin{bmatrix} 1&2&0&4\\0&-3&1&-12\\0&0&0&0 \end{bmatrix} = RREF(A^T)
Theorem: Let A be n\times m, RREF(A^T) = RREF(A)^T
Thus, RREF(A) = \begin{bmatrix} 1&0&0 \\2&-3&0\\0&1&0\\4&-12&0 \end{bmatrix}, \space \therefore basis(colspace(A)) = \Biggl\{ \begin{bmatrix} 1 \\2\\0\\4 \end{bmatrix}, \begin{bmatrix} 0 \\-3\\1\\-12 \end{bmatrix} \Biggl\}
Theorem(3.13): For any linear system with n unknowns, m equations, and matrix of coefficiencts A, then:
- rank(A) = r
- the vector space of solutions has dimensions n-r
are equivalent statements.
Corollary(3.14): Let A be n\times n. Then:
- (i) rank(A) = n
- (ii) A is non-singular
- (iii) rows of A are linearly independent
- (iv) columns of A are linearly independent
- (v) associated linear system has 1 solution
are equivalent statements.
Solutions to Assorted Problems:
2.21(a): Let V = \{ f(x) = a_0+a_1x+a_2x^2+a_3x^3 | a_i \in \mathbb R, f(7) = 0 \}
f(7) = 0, \therefore a_0+7a_1+7^{2}a_2+7^{3}a_3 = 0 \longrightarrow a_0=-7a_1-7^{2}a_2-7^{3}a_3
\therefore there are 3 free variables, and dim(V)=3
2.21(d): V = \{ f(x) = a_0+a_1x+a_2x^2+a_3x^3 | a_i \in \mathbb R, f(7) = 0, f(5) = 0, f(3) = 0, f(1) = 0 \}
a_0+7a_1+7^{2}a_2+7^{3}a_3 = 0
a_0+5a_1+5^{2}a_2+5^{3}a_3 = 0
a_0+3a_1+3^{2}a_2+3^{3}a_3 = 0
a_0+1a_1+1a_2+1a_3 = 0
\therefore there are 0 free variables because of 4 pivots, \therefore dim(V)=0
2.22: V = span \{ cos^2\theta,sin^2\theta,cos2\theta,sin2\theta \} | dim(V) = ? cos^2\theta+sin^2\theta=1 \longrightarrow sin^2\theta=1-cos^2\theta cos2\theta = 2cos^2\theta-1 sin2\theta = 2sin\theta cos\theta \therefore span\{ cos^2\theta,1-cos^2\theta, 2cos^2\theta-1, sin2\theta \} \therefore The basis of the span of the space can be written as \{ cos^2\theta,1, sin2\theta \}, and dim(V)=3
More Examples - 1
span \{ 1,x,x^2 \} = P_2 and \{1,x,x^2 \} is a basis of P_2
More Examples - 2
M_{2\times2} = \biggl\{ \begin{bmatrix} a&c\\b&d \end{bmatrix} \biggl| \space a,b,c,d \in \mathbb R \biggl\}
dim(M_{2\times2}) = 4, since basis(M_{2\times2}) = \biggl\{ \begin{bmatrix} 1&0\\0&0 \end{bmatrix},\begin{bmatrix} 0&1\\0&0 \end{bmatrix},\begin{bmatrix} 0&0\\1&0 \end{bmatrix},\begin{bmatrix} 0&0\\0&1 \end{bmatrix} \biggl\}
More Examples - 3 V = \biggl\{ \begin{bmatrix} a&c\\b&d \end{bmatrix} \biggl| \space a,b,c,d \in \mathbb C \biggl\} dim(V) = 4, since basis(V) = \biggl\{ \begin{bmatrix} 1&0\\0&0 \end{bmatrix},\begin{bmatrix} 0&1\\0&0 \end{bmatrix},\begin{bmatrix} 0&0\\1&0 \end{bmatrix},\begin{bmatrix} 0&0\\0&1 \end{bmatrix},\begin{bmatrix} i&0\\0&0 \end{bmatrix},\begin{bmatrix} 0&i\\0&0 \end{bmatrix},\begin{bmatrix} 0&0\\i&0 \end{bmatrix},\begin{bmatrix} 0&0\\0&i \end{bmatrix} \biggl\}
2.3 Orthogonal Matrices, Change of Basis
Orthogonal Vector
Definition: Two vectors \vec{x} and \vec{y} are orthogonal if \vec{x} \cdot \vec{y} = 0 Note: This is equivalent to \vec{x} perpendicular to \vec{y}
For example: Let S = {\vec{v}_{1}, ...., \vec{v}_{n}} we say the set S is an orthogonal set is \vec{x}_{i} \cdot \vec{x}_{j} = 0, i \neq j
Example: S = {\hat{i}, \hat{j}, \hat{k}}
\hat{i} = \begin{bmatrix} 1\\ 0\\ 0 \\ \end{bmatrix} \hat{j} = \begin{bmatrix} 0\\ 1\\ 0 \\ \end{bmatrix} \hat{k} = \begin{bmatrix} 0\\ 0\\ 1 \\ \end{bmatrix}
\hat{i} \cdot \hat{j} = 0 \hat{j} \cdot \hat{k} = 0 \hat{i} \cdot \hat{k} = 0
So Set S is an orthogonal set of vectors
Orthogonal Vector
Definition: An orthogonal set of vectors that each vector is a unit vector.
Example: \hat{u} = \frac{1}{5} \begin{bmatrix} 3\\ 4\\ \end{bmatrix} = \begin{bmatrix} \frac{3}{5}\\ \frac{4}{5}\\ \end{bmatrix} ||\hat{u}|| = \sqrt{\frac{3}{5}^{2} + \frac{4}{5}^{2}} = 1
Orthogonal Matrix
Let \hat{q}_{1}, ..., \hat{q}_{n} be an orthonormal set, if (i) \hat{q}_{i} \cdot \hat{q}_{j}, i \neq j (ii) ||\hat{q}_{i}|| = 1
Then Q = \begin{bmatrix} \\\ \hat{q}_{1} && \hat{q}_{2} && \hat{q}_{3} .... \hat{q}_{n}\\\\\end{bmatrix} is an orthogonal matrix.
Example: \hat{u} = \begin{bmatrix} cos\theta && -sin\theta\\ sin\theta && cos\theta\\ \end{bmatrix}, show Q is an orthogonal matrix:
\hat{q}_{1} \cdot \hat{q}_{2} = cos\theta(sin\theta) = sin\theta(cos\theta) = 0 ||\hat{q}_{1}|| \cdot ||\hat{q}_{2}|| = \sqrt{cos^{2}\theta + sin^{2}\theta} = 1
Orthonormal Basis
Theorem: Let S = {\hat{v}_{1}, ... , \hat{v}_{n}} is an orthonormal basis Then for each \hat{x} \epsilon V, \hat{x} = (\hat{x} \cdot \hat{v}_{1}) \hat{v}_{1} + ... + (\hat{x} \cdot \hat{v}_{n}) \hat{v}_{n}
Example: If S = {\hat{v}_{1}, ... , \hat{v}_{n}}, \hat{v}_{1} = \begin{bmatrix} 0\\ 1\\0 \end{bmatrix}, \hat{v}_{2} = \begin{bmatrix} -\frac{4}{5}\\ 0\\ \frac{3}{5} \end{bmatrix}, \hat{v}_{3} = \begin{bmatrix} \frac{3}{5}\\ 0\\\frac{4}{5} \end{bmatrix}
Show that S is an orthogonal basis.
Steps:
1. Check if S is a basis
A = \begin{bmatrix} 0 & -\frac{4}{5} & \frac{3}{5} \\ 1 & 0 & 0 \\ 0 & \frac{3}{5} & \frac{4}{5} \\ \end{bmatrix}\rightarrow \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\\ \end{bmatrix}
There are three pivots, so S is a basis
2. Check if it is an orthogonal matrix
\hat{v}_{1} \cdot \hat{v}_{2} = 0
\hat{v}_{1} \cdot \hat{v}_{3} = 0
\hat{v}_{2} \cdot \hat{v}_{3} = 0
It is an orthogonal set of matrix
3. Check if it is normal (magnitude = 1)
||\hat{v}_{1}|| = \sqrt{0^{2} + 1^{2} + 0^{2}} = 1
||\hat{v}_{2}|| = \sqrt{(-\frac{4}{5})^{2} + \frac{3}{5}^{2}} = 1
||\hat{v}_{3}|| = \sqrt{\frac{3}{5}^{2} + \frac{4}{5}^{2}} = 1
2.4 Projection and Change of Basis
How to construct orthonormal or orthonormal basis:
Projection:
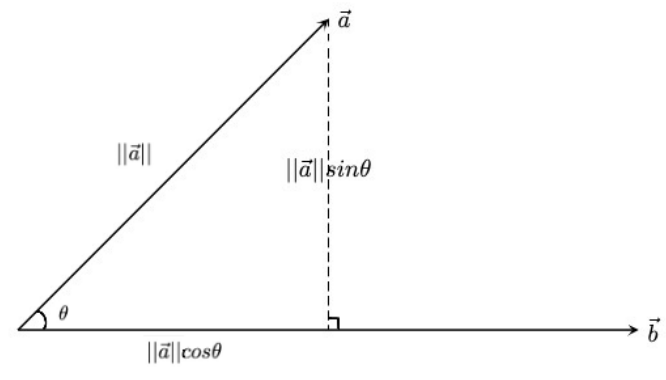
orthogonal projection of \overrightarrow{a} onto \overrightarrow{b} (proj_{\overrightarrow{b}}\overrightarrow{a})
Magnitude of projection vector (component of projection)
||proj_{\overrightarrow{b}}\overrightarrow{a}|| = ||\overrightarrow{a}||cos\theta
In addition, realize that \overrightarrow{a}\cdot\overrightarrow{b} = ||\overrightarrow{a}||||\overrightarrow{b}||cos\theta
\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{||\overrightarrow{b}||} = ||\overrightarrow{a}||cos\theta
||proj_{\overrightarrow{b}}\overrightarrow{a}|| = \frac{\overrightarrow{a}\cdot\overrightarrow{b}}{||\overrightarrow{b}||}
Projection vector (unit vector in direction of \overrightarrow{b} scaled by component)
proj_{\overrightarrow{b}}\overrightarrow{a} = (\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{||\overrightarrow{b}||}) \frac{\overrightarrow{b}}{||\overrightarrow{b}||} = (\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{||\overrightarrow{b}||^2})\overrightarrow{b}
Projection into Subspaces:
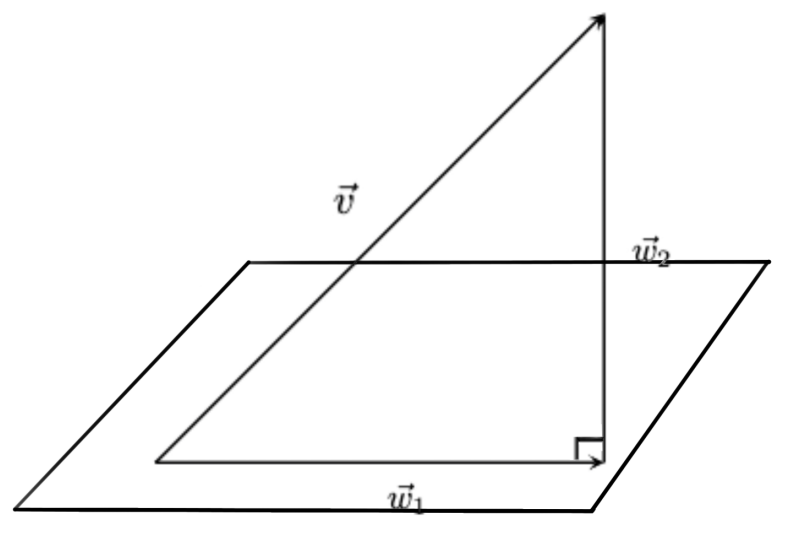
Let V be a vector space with subspace w, \overrightarrow{w}, \overrightarrow{v}\in \overrightarrow{v}
Theroem: If V is a vector space and W is a subspace of V then for each \overrightarrow{v} \in V
\overrightarrow{v} =\overrightarrow{w}_1 + \overrightarrow{w}_2 where \overrightarrow{w}_1\in W and \overrightarrow{w}_2\perp W
How to determine \overrightarrow{w}_1 and \overrightarrow{w}_2?
Theorem: Let W be a finite dimensional subspace of a vector space V. If {\overrightarrow{u}_1,…, \overrightarrow{u}_n} is an orthonormal basis of W and \overrightarrow{x} \in V then proj_{W}\overrightarrow{x} = \frac{\overrightarrow{x} \cdot \overrightarrow{v}_1}{||\overrightarrow{v}_1||^2}\overrightarrow{v}_1 + ...+ \frac{\overrightarrow{x} \cdot \overrightarrow{v}_n}{||\overrightarrow{v}_n||^2}\overrightarrow{v}_n
Example:
Let V = \mathbb{R}^3 and W = span{\begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix}, \begin{bmatrix} -\frac{4}{5} \\ 0 \\ \frac{3}{5} \\ \end{bmatrix}}. Compute proj_{W}\overrightarrow{x} where \overrightarrow{x} = <1,1,1>
\therefore proj_{W}\overrightarrow{x} = (<1,1,1>\cdot <0,1,0>) \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} + (<1,1,1> \cdot <-\frac{4}{5},0,\frac{3}{5}>)\begin{bmatrix} -\frac4{5} \\ 0 \\ \frac{3}{5} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} + \begin{bmatrix} \frac{4}{25} \\ 0 \\ -\frac{3}{25} \\ \end{bmatrix} = \begin{bmatrix} \frac{4}{25} \\ 1 \\ -\frac{3}{25} \\ \end{bmatrix}
proj_{W}\overrightarrow{x} = \overrightarrow{w}_1
\therefore \overrightarrow{w}_2 = \overrightarrow{x} - proj_{W}\overrightarrow{x} = \begin{bmatrix} \frac{21}{25} \\ 0 \\ \frac{28}{25} \\ \end{bmatrix}
Key Result
Theorem: Every finite dimensional vector space has an orthonormal basis.
Proof: We will proceed by constructing an algorithmic solution:
The Gram-Schmidt Process:
*Goal: Given a basis of a vector space construct an orthonormal basis.
Let {\overrightarrow{u}_1,…, \overrightarrow{u}_n} be any basis and {\overrightarrow{v}_1,…, \overrightarrow{v}_n} be the desired orthonormal basis.
\overrightarrow{v}_1 = \overrightarrow{u}_1
Let \overrightarrow{w}_1 = span{\overrightarrow{v}_1}
\therefore \overrightarrow{v}_2 = \overrightarrow{u}_2 - proj_{w_1}\overrightarrow{u}_2
\therefore \overrightarrow{v}_2 = \overrightarrow{u}_2 - \frac{\overrightarrow{u}_2 \cdot \overrightarrow{v}_1}{||\overrightarrow{v}_1||^2}\overrightarrow{v}_1
Let \overrightarrow{w}_2 = span{\overrightarrow{v}_1, \overrightarrow{v}_2}
\therefore \overrightarrow{v}_3 = \overrightarrow{u}_3 - proj_{w_2}\overrightarrow{u}_3
\therefore \overrightarrow{v}_3 = \overrightarrow{u}_3 - \frac{\overrightarrow{u}_3 \cdot \overrightarrow{v}_1}{||\overrightarrow{v}_1||^2}\overrightarrow{v}_1 - \frac{\overrightarrow{u}_3 \cdot \overrightarrow{v}_2}{||\overrightarrow{v}_2||^2}\overrightarrow{v}_2
…
Continue in this fashion up to \overrightarrow{v}_n
Example:
Use the Gram-Schmidt process to transform the basis \overrightarrow{u}_1 = <1,1,1>, \overrightarrow{u}_2 = <0,1,1>, \overrightarrow{u}_3 = <0,0,1>
\overrightarrow{v}_1 = \overrightarrow{u}_1 = <1,1,1>
\overrightarrow{v}_2 = \overrightarrow{u}_2 - proj_{\overrightarrow{w_1}}\overrightarrow{u}_2
\overrightarrow{v}_2 = <0,1,1> - \frac{\overrightarrow{u}_2 \cdot \overrightarrow{v}_1}{||\overrightarrow{v}_1||^2}\overrightarrow{v}_1
\overrightarrow{v}_2 = <0,1,1> - \frac{2}{3}<1,1,1>
\overrightarrow{v}_2 = <0,1,1> - <\frac{2}{3},\frac{2}{3},\frac{2}{3}>
\overrightarrow{v}_2 = <-\frac{2}{3},\frac{1}{3},\frac{1}{3}>
\overrightarrow{v}_3 = \overrightarrow{u}_3 - proj_{w_2}\overrightarrow{u}_3
\overrightarrow{v}_3 = \overrightarrow{u}_3 - \frac{\overrightarrow{u}_3 \cdot \overrightarrow{v}_1}{||\overrightarrow{v}_1||^2}\overrightarrow{v}_1 - \frac{\overrightarrow{u}_3 \cdot \overrightarrow{v}_2}{||\overrightarrow{v}_2||^2}\overrightarrow{v}_2
\overrightarrow{v}_3 = <0,0,1> - \frac{1}{3}<1,1,1> - \frac{1}{2}<-\frac{2}{3},\frac{1}{3},\frac{1}{3}>
\overrightarrow{v}_3 = <0,-\frac{1}{2},\frac{1}{2}>
\therefore \overrightarrow{v}_1, \overrightarrow{v}_2, \overrightarrow{v}_3 orthogonal (not orthonormal)
Normalize => unit vectors
\overrightarrow{v}_1 => \frac{1}{||\overrightarrow{v}_1||}\overrightarrow{v}_1 = <\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}> Repeat for \overrightarrow{v}_2,\overrightarrow{v}_3