5 Machine Learning - Classificação

A Classificação é uma área do Machine Learning que como o próprio nome diz classifica em classes as observações a partir de variáveis preditivas, por exemplo, em uma classe binária, as observações serão classificadas em 0 ou 1.

5.1 Base de dados

A base de dados utilizada para aplicação dos algoritmos de classificação são de observações obtidos no seguinte endereço:

https://archive.ics.uci.edu/

As amostras são de pacientes do Dr.William H.Wolberg do Hospitais da Universidadede Wisconsin, Madison, Wisconsin, EUA. As amostras foram coletadas periodicamente conforme os casos ocorriam. O banco de dados possui um total de 699 observações e 11 variáveis, destas variáveis foi excluída a variável de identificação do paciente. As variaveis são descritas adiante, onde a variável classe será a variável que queremos prevê, e as demais são as variáveis explicativas, conforme é mostrado a seguir:

Espessura de aglomerado 1-10
Uniformidade do tamanhoda célula 1-10
Uniformidade da forma celular 1-10
Adesão marginal 1-10
Tamanho de célula epitelial única 1-10
Núcleos nus 1-10
Cromatina Suave 1-10
Nucléolos normais 1-10
Mitoses 1-10
Classe (2 para benigno, 4 para maligno)

Os algoritmos de classificação serão treinados e posteriormente será submetida a base de dados de teste para verificar o desempenho dos algoritmos. Deseja-se prever o diagnostico do paciente, sendo 2 para a classe benigna e 4 para a classe maligna, conforme segue:

2: Não Câncer (Tumor benigno);
4: Câncer (Tumor maligno).

5.2 Análise exploratória

Antes de seguir com a abordagem e aplicação dos modelos de Machine Learning é imprescindível que seja realizada uma análise exploratória dos dados.

5.2.1 Preparação dos dados

Comece carregando o banco de dados, onde header = TRUE significa que a primeira linha do arquivo deve ser interpretada como os nomes das colunas e sep = indica o tipo de separador de colunas.

dados = read.csv("Cancer_Wisconsin.csv", header = T, sep = ";")

5.2.2 Pacotes utilizados

Carregando os pacotes que serão utilizados ao longo da análise, são eles, tidymodels para uso dos algoritmos de Machine Learning, corrplot e Hmisc para verificar a correlação, knitr e kableExtra para geração de tabelas.

library(tidymodels)
library(corrplot)
library(Hmisc)
library(knitr)
library(kableExtra)

Para visualizar as primeiras linhas dos dados utiliza-se o comando a seguir.

dados %>% head()

O pipe (%>%) usa o valor resultante do lado esquerdo como primeiro argumento da função do lado direito, conhecido também como operador de encadeamento. A função glimpse() retorna as primeiras observações e o tipo das variáveis.

glimpse(dados)

## Rows: 699
## Columns: 11
## $ Nº.Ident             <int> 1000025, 1002945, 1015425, 1016277, 1017023, 1017…
## $ Espessura_aglomerado <int> 5, 5, 3, 6, 4, 8, 1, 2, 2, 4, 1, 2, 5, 1, 8, 7, 4…
## $ Uni.tamanho_celula   <int> 1, 4, 1, 8, 1, 10, 1, 1, 1, 2, 1, 1, 3, 1, 7, 4, …
## $ Uni.forma_celular    <int> 1, 4, 1, 8, 1, 10, 1, 2, 1, 1, 1, 1, 3, 1, 5, 6, …
## $ Adesao_marginal      <int> 1, 5, 1, 1, 3, 8, 1, 1, 1, 1, 1, 1, 3, 1, 10, 4, …
## $ T.celula_epitelial   <int> 2, 7, 2, 3, 2, 7, 2, 2, 2, 2, 1, 2, 2, 2, 7, 6, 2…
## $ nucleos_nus          <int> 1, 10, 2, 4, 1, 10, 10, 1, 1, 1, 1, 1, 3, 3, 9, 1…
## $ cromatina_suave      <int> 3, 3, 3, 3, 3, 9, 3, 3, 1, 2, 3, 2, 4, 3, 5, 4, 2…
## $ nucleolos_normais    <int> 1, 2, 1, 7, 1, 7, 1, 1, 1, 1, 1, 1, 4, 1, 5, 3, 1…
## $ mitoses              <int> 1, 1, 1, 1, 1, 1, 1, 1, 5, 1, 1, 1, 1, 1, 4, 1, 1…
## $ classe               <int> 2, 2, 2, 2, 2, 4, 2, 2, 2, 2, 2, 2, 4, 2, 4, 4, 2…

A primeira coluna dos dados não é necessária para a análise, pode-se exclui-lá do conjunto de dados.

dados$Nº.Ident = NULL

A variável resposta classe precisa ser transformada em fator, utilizando o comando as_factor obtêm-se essa transformação.

dados$classe = factor(dados$classe)

Após transformar a variável classe em fator pode-se confirmar a alteração executando novamente o comando abaixo.

glimpse(dados)

## Rows: 699
## Columns: 10
## $ Espessura_aglomerado <int> 5, 5, 3, 6, 4, 8, 1, 2, 2, 4, 1, 2, 5, 1, 8, 7, 4…
## $ Uni.tamanho_celula   <int> 1, 4, 1, 8, 1, 10, 1, 1, 1, 2, 1, 1, 3, 1, 7, 4, …
## $ Uni.forma_celular    <int> 1, 4, 1, 8, 1, 10, 1, 2, 1, 1, 1, 1, 3, 1, 5, 6, …
## $ Adesao_marginal      <int> 1, 5, 1, 1, 3, 8, 1, 1, 1, 1, 1, 1, 3, 1, 10, 4, …
## $ T.celula_epitelial   <int> 2, 7, 2, 3, 2, 7, 2, 2, 2, 2, 1, 2, 2, 2, 7, 6, 2…
## $ nucleos_nus          <int> 1, 10, 2, 4, 1, 10, 10, 1, 1, 1, 1, 1, 3, 3, 9, 1…
## $ cromatina_suave      <int> 3, 3, 3, 3, 3, 9, 3, 3, 1, 2, 3, 2, 4, 3, 5, 4, 2…
## $ nucleolos_normais    <int> 1, 2, 1, 7, 1, 7, 1, 1, 1, 1, 1, 1, 4, 1, 5, 3, 1…
## $ mitoses              <int> 1, 1, 1, 1, 1, 1, 1, 1, 5, 1, 1, 1, 1, 1, 4, 1, 1…
## $ classe               <fct> 2, 2, 2, 2, 2, 4, 2, 2, 2, 2, 2, 2, 4, 2, 4, 4, 2…

Uma maneira de verificar a existência de dados faltantes é usando a função complete.cases() que retorna os casos completos e a exclamação ! funciona como o operador de negação, que retorna o contrário do que foi solicitado, neste caso é retornado as observações faltantes.

sum(!complete.cases(dados))

## [1] 16

No banco de dados é observado um total de 16 observações faltantes. Essa observações faltantes serão tratadas adiante utilizando o pacote recipes do tidymodels, pois este processo só poderá ser aplicado aos dados de treinamento.

Pode-se obter algumas medidas descritivas usando a função summary

summary(dados)

##  Espessura_aglomerado Uni.tamanho_celula Uni.forma_celular Adesao_marginal 
##  Min.   : 1.000       Min.   : 1.000     Min.   : 1.000    Min.   : 1.000  
##  1st Qu.: 2.000       1st Qu.: 1.000     1st Qu.: 1.000    1st Qu.: 1.000  
##  Median : 4.000       Median : 1.000     Median : 1.000    Median : 1.000  
##  Mean   : 4.418       Mean   : 3.134     Mean   : 3.207    Mean   : 2.807  
##  3rd Qu.: 6.000       3rd Qu.: 5.000     3rd Qu.: 5.000    3rd Qu.: 4.000  
##  Max.   :10.000       Max.   :10.000     Max.   :10.000    Max.   :10.000  
##                                                                            
##  T.celula_epitelial  nucleos_nus     cromatina_suave  nucleolos_normais
##  Min.   : 1.000     Min.   : 1.000   Min.   : 1.000   Min.   : 1.000   
##  1st Qu.: 2.000     1st Qu.: 1.000   1st Qu.: 2.000   1st Qu.: 1.000   
##  Median : 2.000     Median : 1.000   Median : 3.000   Median : 1.000   
##  Mean   : 3.216     Mean   : 3.545   Mean   : 3.438   Mean   : 2.867   
##  3rd Qu.: 4.000     3rd Qu.: 6.000   3rd Qu.: 5.000   3rd Qu.: 4.000   
##  Max.   :10.000     Max.   :10.000   Max.   :10.000   Max.   :10.000   
##                     NA's   :16                                         
##     mitoses       classe 
##  Min.   : 1.000   2:458  
##  1st Qu.: 1.000   4:241  
##  Median : 1.000          
##  Mean   : 1.589          
##  3rd Qu.: 1.000          
##  Max.   :10.000          
##

Observa-se que a média retornada não é um número inteiro, pois os dados estão em uma escala ordinal de 1 a 10, portanto a mediana será utilizada para a imputação dos valores faltantes, além disso, podemos notar pelo o conjunto de gráficos na Figura 5.1 que os dados não são simétricos.

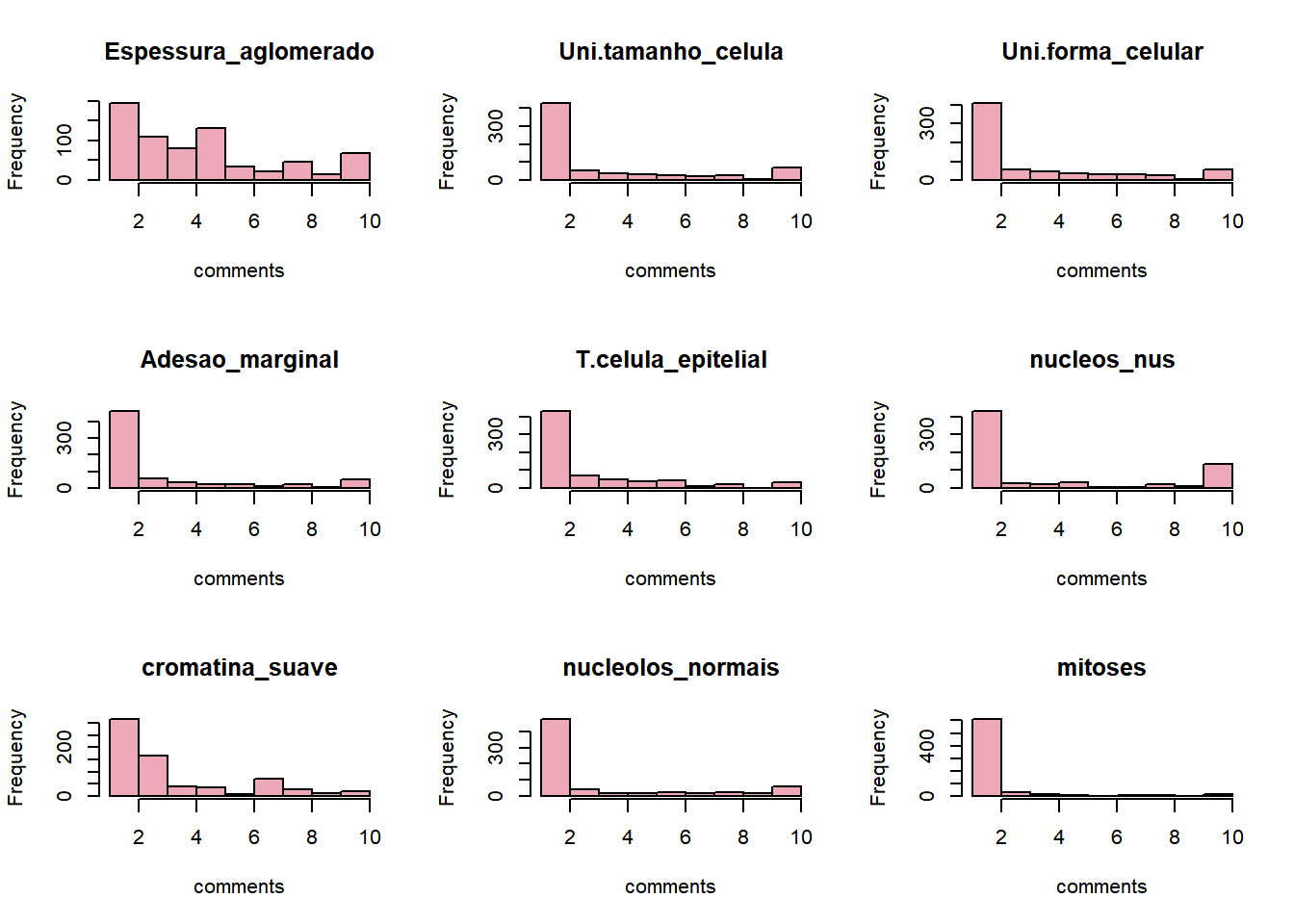
Figure 5.1: Histograma das variáveis preditoras.

Outra verificação necessária é avaliar o quanto as variáveis estão correlacionadas.

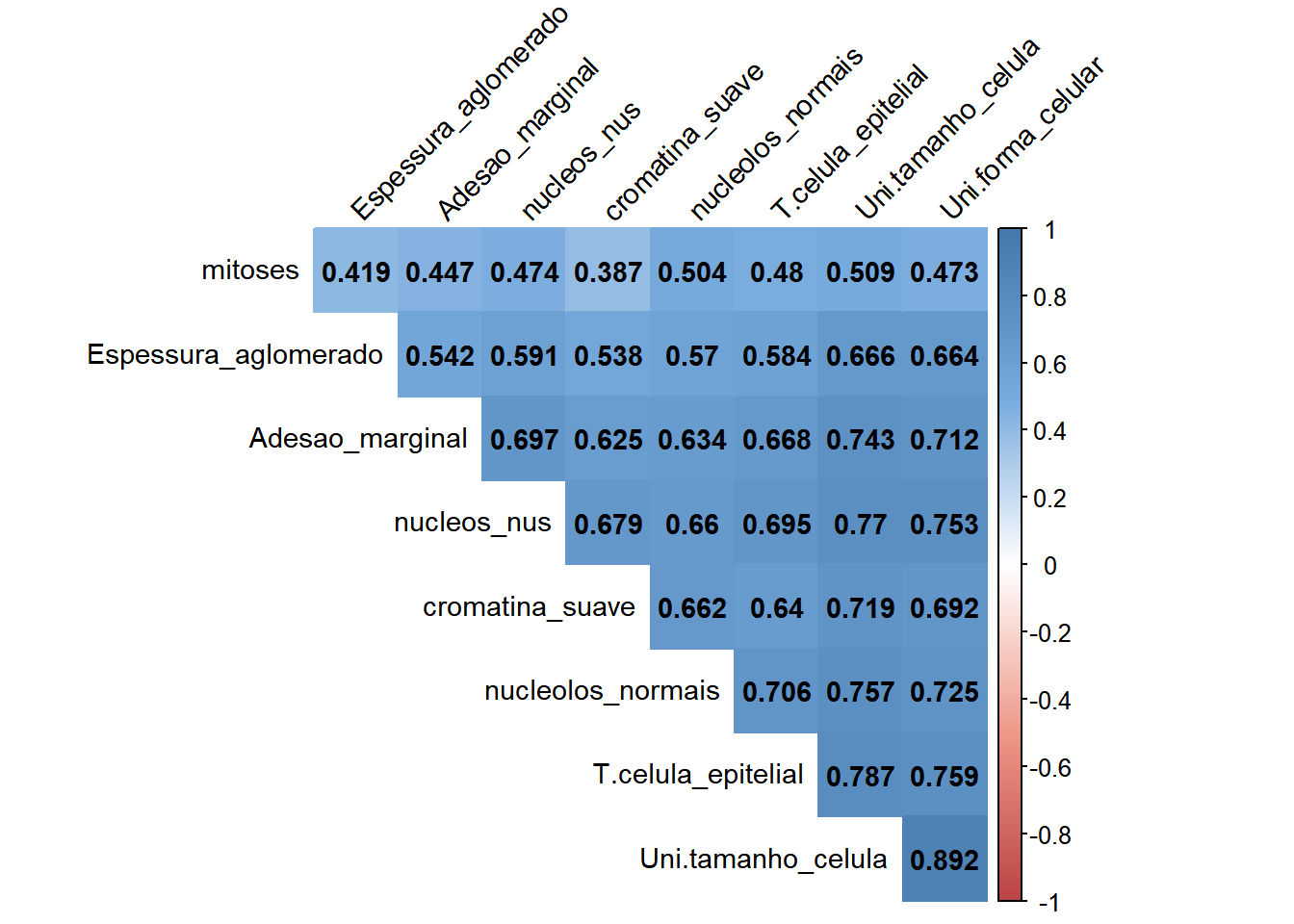
Figure 5.2: Correlação entre as variáveis preditoras.

Conforme pode ser observado na Figura 5.2 não existe nenhuma variável com correlação maior ou igual a 0.90. Outra verificação importante que deve ser feita no conjunto de dados é verificar o balanceamento desses dados em relação a variável de interesse classe.

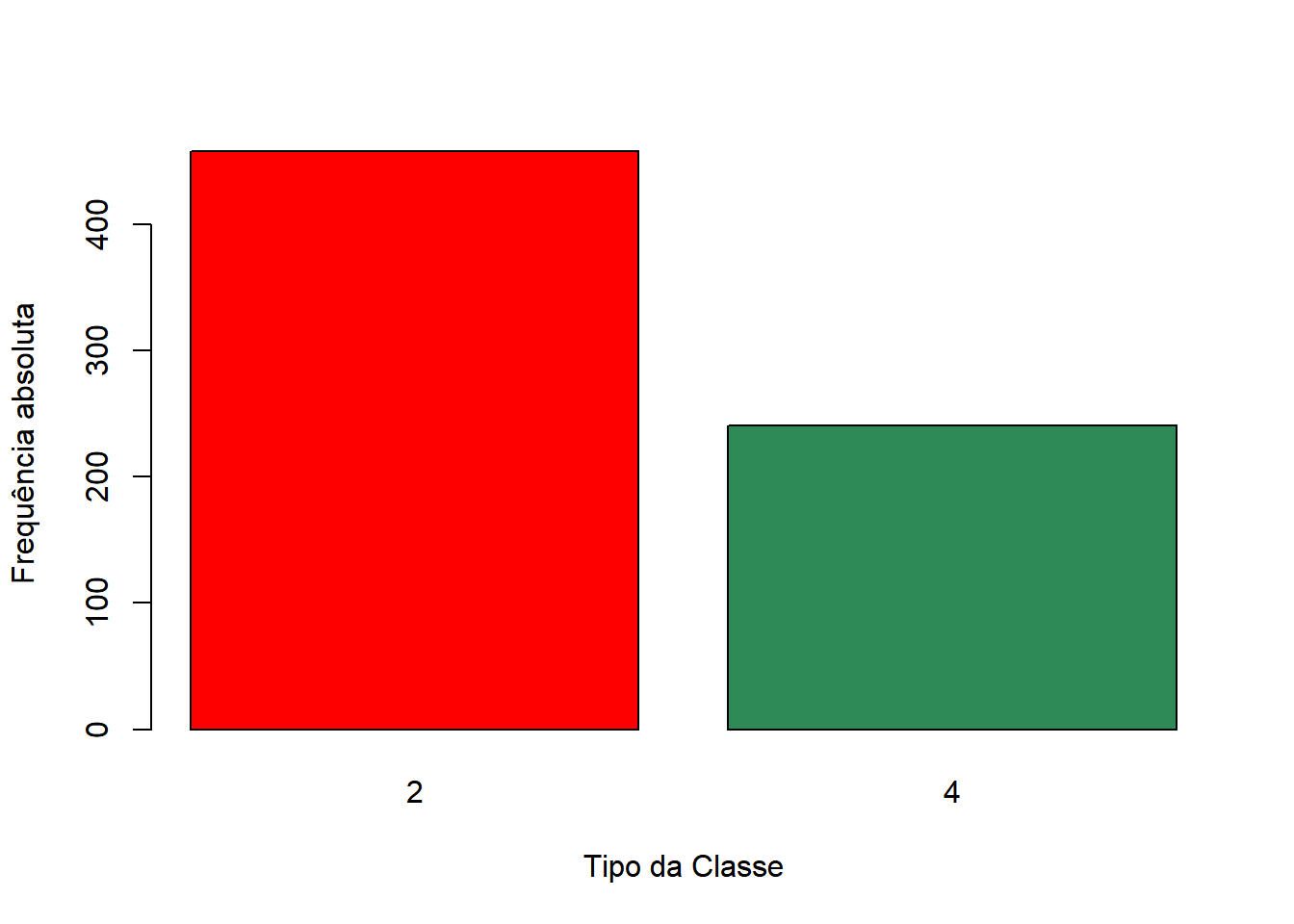
Figure 5.3: Visualização do comportamento dos dados em relação a variável Classe.

Observa-se na Figura 5.3 que a quantidade de observações da classe 2 é quase o dobro das observações da classe 4. Portanto, será necessário estratificar os dados em relação a variável classe ao realizar a divisão entre treinamento e teste.

5.3 Árvore de decisão

Decision trees (Árvores de decisão) é uma algoritmo de classificação e regressão de dados. A formação de uma árvore de decisão é composta por nós, ramos e folhas. Os nós raizes são as regiões onde se localiza os testes lógicos de separação de dados para tomada de decisão e são divididos em nó raiz (ou nó pai) e nós filhos (ou de tomada de decisão), onde geralmente é gerado uma sub-árvore. Os ramos fazem uma conexão entre os nós raiz e os nós filhos. Nas folhas se localizam os rótulos ou valores. Dessa forma o algoritmo percorre a árvore e tomada a decisão a partir dos atributos mais relevantes, na Figura 5.4 pode-se visualizar uma ilustração de como algoritmos de árvores de decisão funciona.

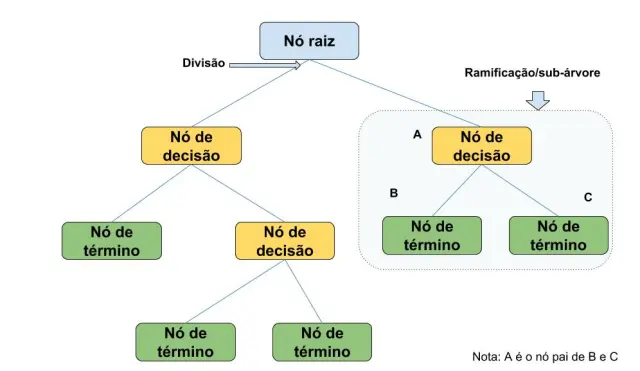
Figure 5.4: Esquema de um algoritmo de árvore de decisão.

Fonte: https://www.vooo.pro/insights/

A aplicação de qualquer método de aprendizagem de máquina, consiste em utilizar uma base de dados, sendo esta divida em treinamento e teste. O primeiro passo é treinar o algoritmo avaliar seu desempenho nos dados de treinamento, selecionar o melhor modelo segundo a métrica utilizada e em seguida testar o modelo que obtiver o melhor desempenho.

5.3.1 Divisão dos dados

Primeiro, é realizado a divisão do conjunto de dados em treino e teste. O argumento strata usa amostragem estratificada para criar a reamostragem e faz um balanceamento dos dados de modo a equilibrar a quantidade de observações do atributo classe (0 - para tumor benigno, 1 - para tumor maligno) nos conjuntos de treinamento e teste.

set.seed(1234)
divisao <- initial_split(dados, strata = classe)
divisao

## <Analysis/Assess/Total>
## <523/176/699>

O conjunto de dados é dividido em aproximadamente 75% dos dados para treinamento e 25% para teste, abaixo e carregado os dados para treino e teste respectivamente. Fixa-se uma semente set.seed() para que os resultados não se altere a cada execução. Sendo assim, as observações que farão parte da base de dados de treino e teste serão as mesmas, independentemente de quantas vezes o código seja executado.

data_treino <- training(divisao) 
data_teste <- testing(divisao)

Os dados de treinamento serão usados para ajustar o modelo e seus parâmetros, e os dados de teste serão usados para avaliar o desempenho do modelo final.

5.3.2 Pré - processamento

pre_recipe <- recipe(classe ~ ., data = data_treino) %>% 
  step_impute_median(all_predictors())

Primeiramente a função recipe () recebe a variável resposta classe em relação a todas as demais variáveis explicativas (.) e atribui-se os dados de treinamento. A função step_impute_median() substitui os dados faltantes do conjunto de dados pela a sua mediana. Não foi utilizado nenhum tipo de normalização/padronização dos dados pois ambas as variáveis explicativas estão em uma mesma escala de medida.

A função step_impute_knn() também existente no pacote é útil quando existe muitos dados faltantes e a alternativa e tirá-los do conjunto de dados. Neste caso optou-se pela imputação do valores faltantes pela mediana pois existia apenas 16 observações faltantes no conjunto de dados inteiro.

Observe que a receita foi salva em um objeto chamado pre_recipe que será utilizada por todos os algoritmos de classificação.

5.3.3 Validação cruzada

A validação cruzada V-fold (também conhecida como validação cruzada k-fold) divide aleatoriamente os dados em grupos V de tamanho aproximadamente iguais (chamados “dobras”). A técnica de validação cruzada usa reamostragem para comparar e selecionar os melhores modelos. O vfold_cv() já divide por padrão em 4 partes v = 4.

set.seed(1243)
val_set <- vfold_cv(data_treino, v = 4, strata = classe)

5.3.4 Definição do modelo

Define-se o modelo que será utilizado, nesse caso o algoritmo de árvore de decisão, decision_tree() que recebe os argumentos cost_complexity que determina o parâmetro de custo/complexidade do modelo e min_n um número inteiro para o número mínimo de pontos de dados em um nó que são necessários para que o nó seja dividido ainda mais. Para ambos os argumentos cost_complexity e min_n atribui-se a função tune() do pacote tune que significa que os valores serão ajustados pelo pipeline, ou seja, será escolhido o modelo que apresentar o melhor resultado.

tree_model <- decision_tree(cost_complexity = tune(), 
                           min_n = tune()) %>%
  set_engine("rpart") %>% 
  set_mode("classification")

A função set_engine() e set_mode() define o pacote que será utilizado para o ajuste, e o modelo respectivamente. O pipe (%>%) é o operador de encadeamento que é utilizado para separar e organizar funções dentro de funções, de maneira que simplificará o código.

Após a definição do modelo é criado o fluxo de trabalho workflow().

tree_workflow <- workflow() %>% 
  add_model(tree_model) %>% 
  add_recipe(pre_recipe)

O modelo add_model() e o pré-processamento add_recipe() são colocados dentro de um workflow() e salvo em um objeto chamado tree_workflow.

5.3.5 Treinamento

Nessa etapa é realizado o treinamento do modelo, onde o fluxo de trabalho criado anteriormente é salvo em um objeto chamado tree_trained e é adicionado a função tune_grid() onde é adicionado a validação cruzada salva no objeto val_set.

tree_trained <- tree_workflow %>% 
  tune_grid(
    val_set,
    grid = 10,
    control = control_grid(save_pred = TRUE),
    metrics = metric_set(roc_auc)
  )

O argumento grid define a quantidade de combinações de parâmetros do modelo que será treinado, a função control_grid() armazena as informações do treinamento para serem avaliadas posteriormente. Em metric_set() define-se as métricas que serão utilizadas na avaliação dos modelos.

tree_trained %>% show_best("roc_auc")

## # A tibble: 5 × 8
##   cost_complexity min_n .metric .estimator  mean     n std_err .config          
##             <dbl> <int> <chr>   <chr>      <dbl> <int>   <dbl> <chr>            
## 1   0.00000000602    18 roc_auc binary     0.962     4 0.00624 Preprocessor1_Mo…
## 2   0.00000258       33 roc_auc binary     0.961     4 0.00635 Preprocessor1_Mo…
## 3   0.00000000941    39 roc_auc binary     0.960     4 0.00565 Preprocessor1_Mo…
## 4   0.000122         24 roc_auc binary     0.959     4 0.00587 Preprocessor1_Mo…
## 5   0.000000169      26 roc_auc binary     0.959     4 0.00587 Preprocessor1_Mo…

Utilizando a função show_best() e definindo a métrica utilizada é possível visualizar os modelos gerados. Caso deseje visualizar todos os modelos gerados independente da métrica utlizada use collect_metrics(), conforme código abaixo.

tree_trained %>%
collect_metrics() %>% 
  print(n = Inf)

5.3.6 Seleção do melhor modelo

Observa-se que o melhor modelo obteve uma AUC de 0.962. Usando a função select_best() define-se a métrica e é mostrado o melhor modelo.

tree_best_tune <- select_best(tree_trained, 'roc_auc')
final_tree_model <- tree_model %>% 
  finalize_model(tree_best_tune)
tree_best_tune

## # A tibble: 1 × 3
##   cost_complexity min_n .config              
##             <dbl> <int> <chr>                
## 1   0.00000000602    18 Preprocessor1_Model10

O Modelo 10 obteve o melhor resultado usando a métrica de Curva Roc, escolhe-se então esse modelo como modelo final e aplica-se os dados de teste ao modelo.

5.3.7 Aplicando os dados de teste ao modelo

Na etapa final é criado o novo fluxo de trabalho e é submetido os dados de teste ao modelo escolhido a partir dos dados de treinamento. É adicionado em add_recipe() o pré-processamento dos dados criado no início, em add_model() é adicionado o modelo final. A função last_fit() indica que é último ajuste a ser realizado.

previsoes <-  workflow() %>% 
  add_recipe(pre_recipe) %>% 
  add_model(final_tree_model) %>% 
  last_fit(divisao)

Usando collect_predictions() visualizamos as predições salva no objeto previsoes.

previsoes %>% collect_predictions()

## # A tibble: 176 × 7
##    id               .pred_2 .pred_4  .row .pred_class classe .config            
##    <chr>              <dbl>   <dbl> <int> <fct>       <fct>  <chr>              
##  1 train/test split  0.979   0.0210     1 2           2      Preprocessor1_Mode…
##  2 train/test split  0.979   0.0210     3 2           2      Preprocessor1_Mode…
##  3 train/test split  0.979   0.0210     5 2           2      Preprocessor1_Mode…
##  4 train/test split  0.979   0.0210     8 2           2      Preprocessor1_Mode…
##  5 train/test split  0.979   0.0210     9 2           2      Preprocessor1_Mode…
##  6 train/test split  0.979   0.0210    10 2           2      Preprocessor1_Mode…
##  7 train/test split  0.979   0.0210    12 2           2      Preprocessor1_Mode…
##  8 train/test split  0.0556  0.944     19 4           4      Preprocessor1_Mode…
##  9 train/test split  0.105   0.895     21 4           4      Preprocessor1_Mode…
## 10 train/test split  0.105   0.895     26 4           4      Preprocessor1_Mode…
## # … with 166 more rows

Esse resultado podem ser visualizado atráves de uma matriz de confusão (Figura 5.5), onde é possível avaliar a quantidade de previsões certas e erradas que o modelo obteve.

previsoes %>% collect_predictions() %>% 
  conf_mat(truth = classe,
           estimate = .pred_class, dnn = c("Previsto", "Real")) %>% 
  autoplot(type = "heatmap") +
  scale_fill_gradient(low = "pink3", high = "cyan4")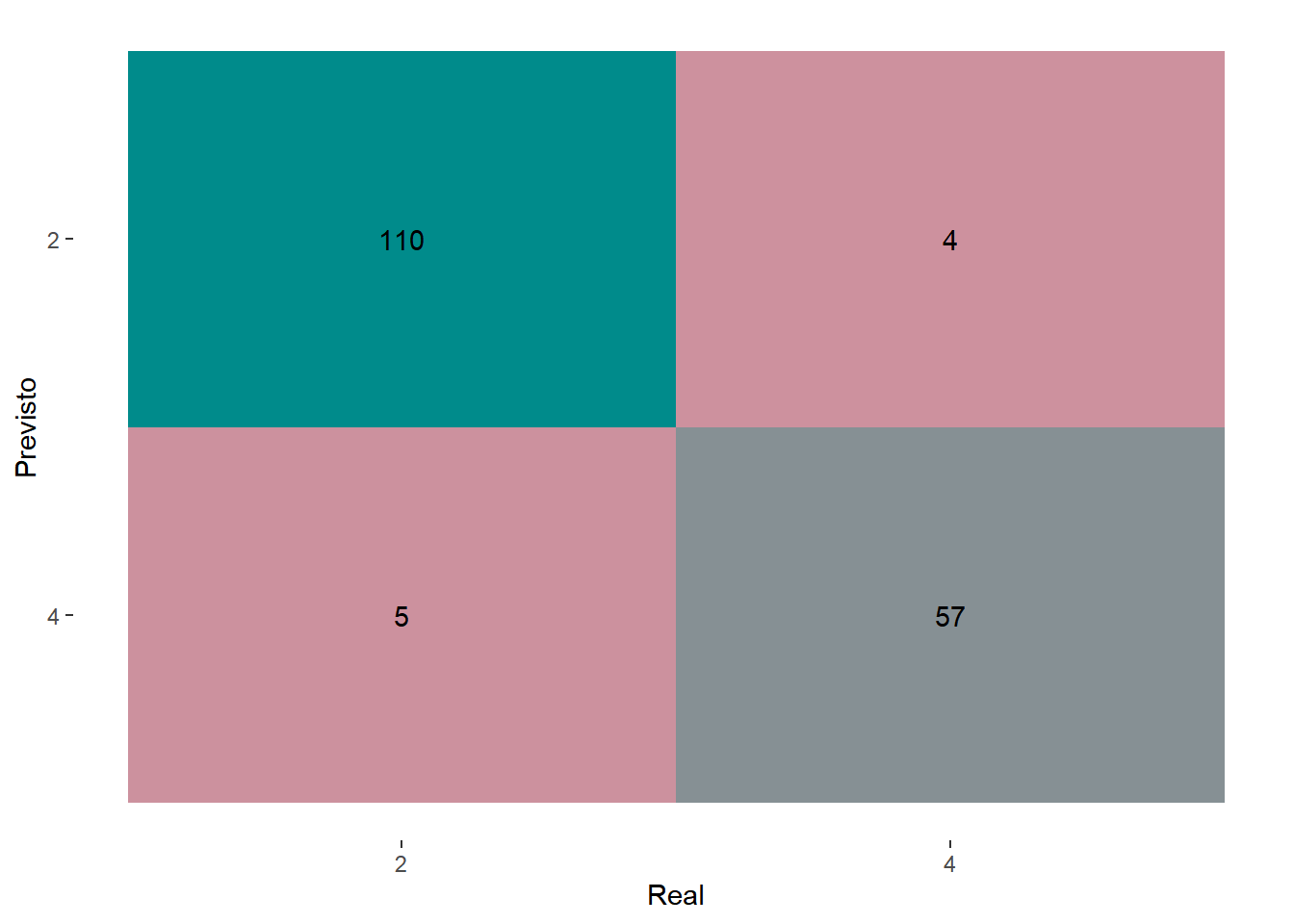

Figure 5.5: Matriz de confusão para o algoritmo de árvore de decisão.

Pode-se também visualizar o resultado final atráves de uma Curva Roc (Figura 5.6) usando a função roc_curve() e pedindo o autoplot().

previsoes %>% collect_predictions() %>%
  roc_curve(classe, .pred_2) %>% 
  autoplot()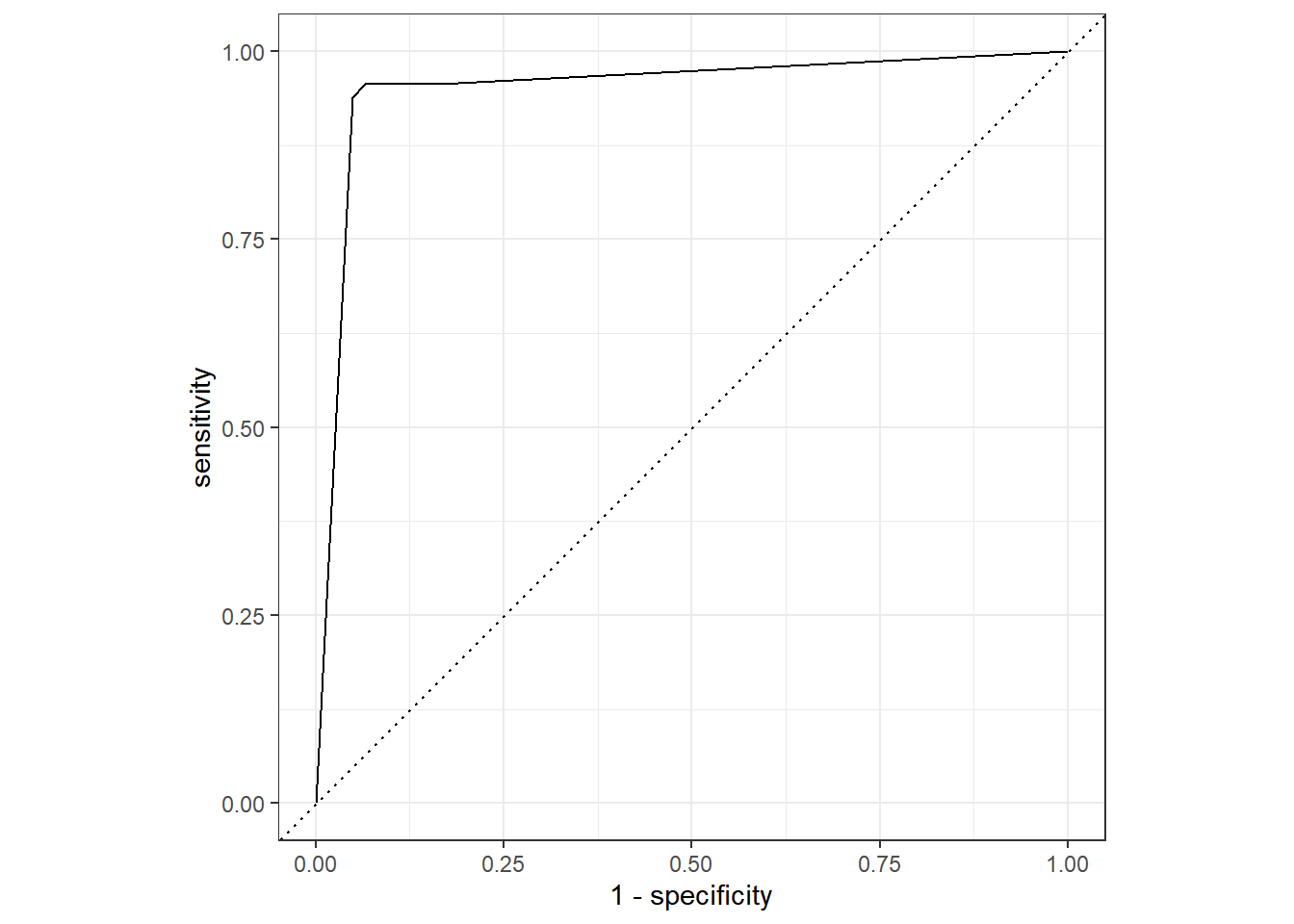

Figure 5.6: Desempenho do algoritmo Árvore de decisão nos dados de teste.

Quanto maior for a distância entre a curva e a linha, melhor é o desempenho do algoritmo. Como podemos visualizar o desempenho do modelo foi satisfatório. É possível obter o valor da AUC para o dados de teste usando novamente a função show_best() nos dados de teste.

previsoes %>% show_best("roc_auc")

## # A tibble: 1 × 7
##   .workflow  .metric .estimator  mean     n std_err .config             
##   <list>     <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
## 1 <workflow> roc_auc binary     0.951     1      NA Preprocessor1_Model1

Obtendo a AUC do modelo nos dados de teste de outra maneira.

previsoes %>% collect_predictions() %>% 
  roc_auc(classe, .pred_2)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 roc_auc binary         0.951

Comparando o valor da AUC tanto nos dados de treinamento como de teste, observa-se um desempenho similar.

O processo de aplicação do algoritmo de Machine Learning para o demais modelos seguem a mesma lógica do que foi apresentado para o modelo de árvore de decisão, a única mudança que ocorre é na definição do modelo.

5.4 Random Forest

O algoritmo Random Forest é formado por várias árvores de decisão, geralmente treinados com o método de bagging, que gera um conjunto de dados por amostragem bootstrap, a ideia principal do método é criar combinações de modelos que aumentem o resultado final.

O modelo de Random Forest tanto pode ser utilizado para classificação como para regressão. Um dos principais benefícios do algoritmo é a possibilidade de se trabalhar com um grande conjunto de dados de maior dimensão.

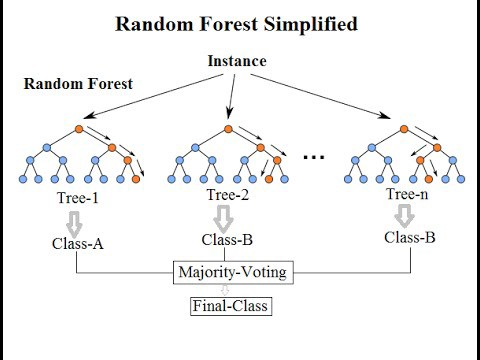
Figure 5.7: Exemplo do funcionamento do algoritmo Random Forest.

Fonte: https://estatsite.com.br/

Diferentemente da árvore de decisão, o funcionamento do Random Forest consiste no crescimento de várias árvores, onde cada árvore fornece uma classificação de votos para a classe, até chegar ao resultado final, conforme é mostrado na Figura 5.7.

Algoritmos baseaddos em árvore de decisão utilizam a média em regressão e os votos da maioria na classificação para dar uma resposta final.

5.4.1 Definição do modelo

Define-se o modelo que será utilizado, nesse caso é o algoritmo Random Forest rand_forest() que recebe os argumentos mtry que determina o número de preditores que serão amostrados ateatoriamente em cada divisão, trees que determina o número de árvores contidas no conjunto e min_n um número inteiro para o número mínimo de pontos de dados em um nó que são necessários para que o nó seja dividido ainda mais. Para os argumentos mtry e min_n atribui-se a função tune() que significa que os valores serão ajustados pelo pipeline, para trees foi atribuido o total de 1000 árvores.

library(ranger)
rf_model <- rand_forest(mtry = tune(), min_n = tune(), 
                        trees = 1000) %>%
  set_engine("ranger") %>% 
  set_mode("classification")

Após a definição do modelo é criado o fluxo de trabalho workflow(), em add_recipe() adciona o pre_recipe que é a receita criada na parte de pré-processamento feito antes da aplicação do modelo de árvore de decisão mostrado na seção 5.3.

rf_workflow <- workflow() %>% 
  add_model(rf_model) %>% 
  add_recipe(pre_recipe)

5.4.2 Treinamento

Nessa etapa é realizado o treinamento do modelo para o algoritmo Random Forest.

rf_trained <- rf_workflow %>% 
  tune_grid(
    val_set,
    grid = 10,
    control = control_grid(save_pred = TRUE),
    metrics = metric_set(roc_auc)
  )

Observa-se os modelos gerados a partir do algoritmo de Random Forest.

rf_trained %>% show_best("roc_auc")

## # A tibble: 5 × 8
##    mtry min_n .metric .estimator  mean     n std_err .config              
##   <int> <int> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
## 1     4    19 roc_auc binary     0.994     4 0.00207 Preprocessor1_Model01
## 2     2    28 roc_auc binary     0.994     4 0.00214 Preprocessor1_Model09
## 3     5     9 roc_auc binary     0.994     4 0.00199 Preprocessor1_Model07
## 4     1    32 roc_auc binary     0.993     4 0.00250 Preprocessor1_Model04
## 5     6    14 roc_auc binary     0.993     4 0.00216 Preprocessor1_Model06

5.4.3 Seleção do melhor modelo

Usando a função select_best() e defininado a métrica é mostrado o melhor modelo, dentre todos os modelos gerados.

rf_best_tune <- select_best(rf_trained, 'roc_auc')
final_rf_model <- rf_model %>% 
  finalize_model(rf_best_tune)
rf_best_tune

## # A tibble: 1 × 3
##    mtry min_n .config              
##   <int> <int> <chr>                
## 1     4    19 Preprocessor1_Model01

O modelo 1 aprensentou o melhor resultado com uma AUC de 0.994.

5.4.4 Aplicando os dados de teste ao modelo

O código abaixo retorna as predições obtidas para os dados de teste e é salvo em um objeto chamado previsoes.

previsoes <- workflow() %>% 
  add_recipe(pre_recipe) %>% 
  add_model(final_rf_model) %>% 
  last_fit(divisao)

Para visualizar as previsões utiliza-se a função collect_predictions(), onde em classe é mostrado os valores reais e em .pred_class os valores preditos.

previsoes %>% collect_predictions()

## # A tibble: 176 × 7
##    id               .pred_2  .pred_4  .row .pred_class classe .config           
##    <chr>              <dbl>    <dbl> <int> <fct>       <fct>  <chr>             
##  1 train/test split 1       0            1 2           2      Preprocessor1_Mod…
##  2 train/test split 1.00    0.000119     3 2           2      Preprocessor1_Mod…
##  3 train/test split 0.997   0.00329      5 2           2      Preprocessor1_Mod…
##  4 train/test split 1       0            8 2           2      Preprocessor1_Mod…
##  5 train/test split 0.829   0.171        9 2           2      Preprocessor1_Mod…
##  6 train/test split 1       0           10 2           2      Preprocessor1_Mod…
##  7 train/test split 1       0           12 2           2      Preprocessor1_Mod…
##  8 train/test split 0.00307 0.997       19 4           4      Preprocessor1_Mod…
##  9 train/test split 0.361   0.639       21 4           4      Preprocessor1_Mod…
## 10 train/test split 0.354   0.646       26 4           4      Preprocessor1_Mod…
## # … with 166 more rows

Visualizado a matriz de confusão para o modelo escolhido (Figura 5.8).

previsoes %>% collect_predictions() %>% 
  conf_mat(truth = classe,
           estimate = .pred_class, dnn = c("Previsto", "Real")) %>% 
  autoplot(type = "heatmap") +
  scale_fill_gradient(low = "pink3", high = "cyan4")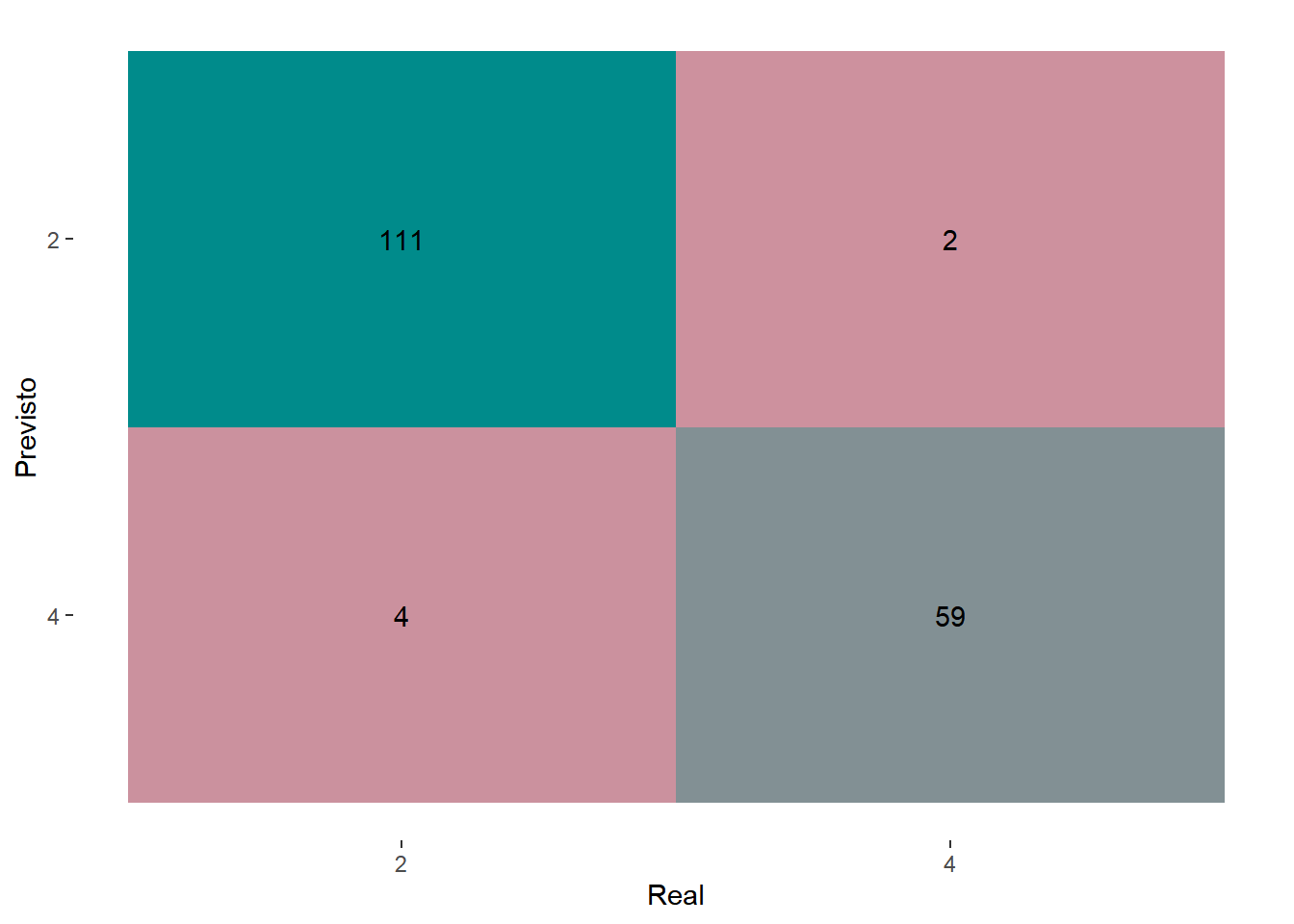

Figure 5.8: Matriz de confusão para o algoritmo de Random Forest.

A seguir tem-se o código que gera a curva Roc, conforme pode ser observado na Figura 5.9, onde é mostrado o desempenho do modelo nos dados de teste.

previsoes %>% collect_predictions() %>%
  roc_curve(classe, .pred_2) %>% 
  autoplot()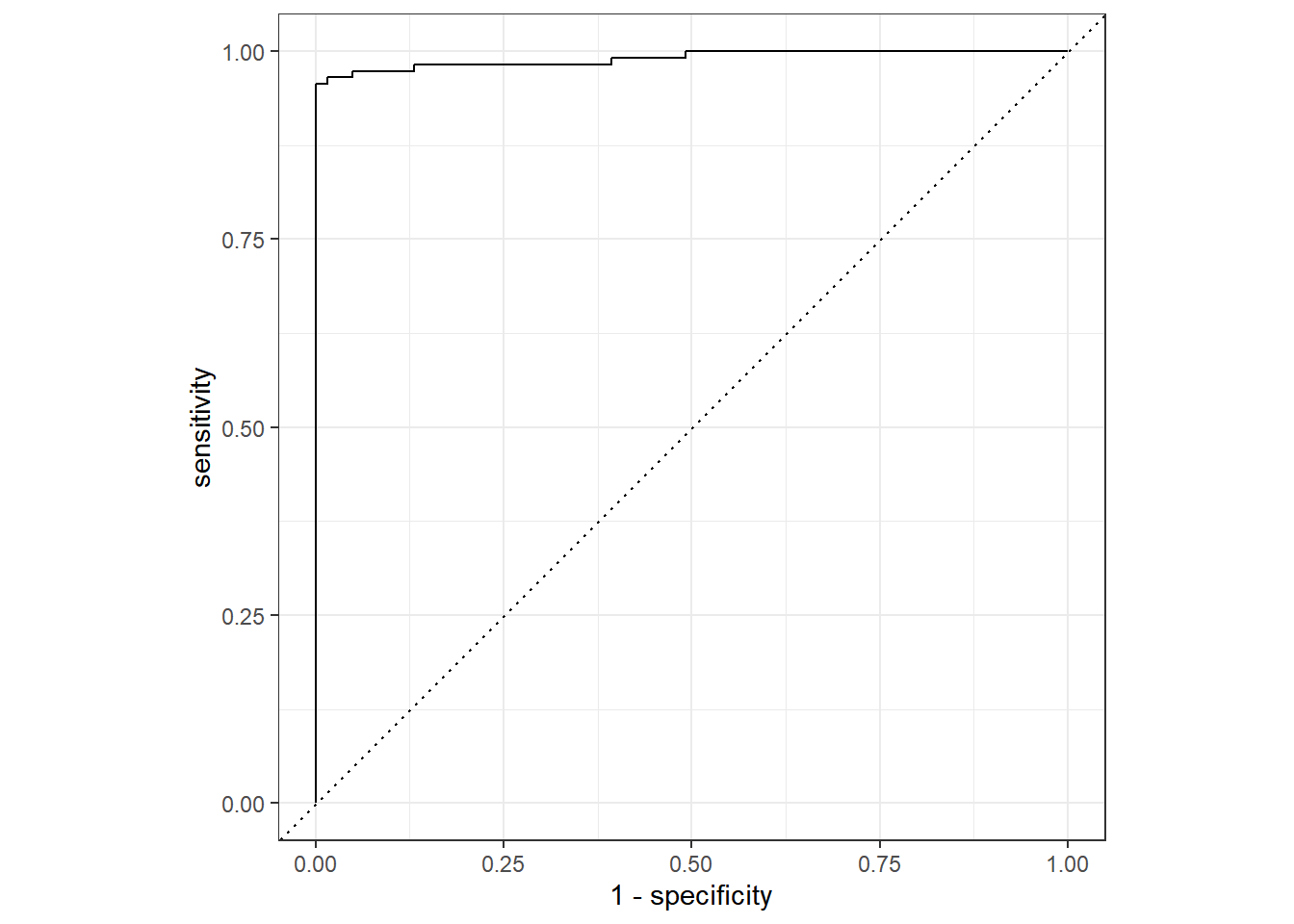

Figure 5.9: Desempenho do algoritmo Random Forest nos dados de teste.

Obtendo a AUC da Curva ROC.

previsoes %>% collect_predictions() %>% 
  roc_auc(classe, .pred_2)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 roc_auc binary         0.991

Observe que o algoritmo Random Forest obteve melhores resultados se comparado com algoritmo de árvore de decisão.

5.5 Aprendizagem baseada em instâncias (KNN)

O K-Nearest Neighbors (KNN) ou simplesmente K vizinhos mais próximos, traduzindo para o português, é um algoritmo que como o próprio nome diz, classifica os novos dados com base em uma medida de similaridade entre seus “vizinhos” mais próximos, ou seja, forma grupos com os atributos que possuem características semelhantes. O KNN faz a comparação das distâncias entre os dados no espaço euclidiano.

A aprendizagem baseada em instâncias é conhecida como sendo uma aprendizagem preguiçosa, a lentidão ocorre à medida que o volume de dados aumenta, tornando a sua escolha impraticável em situações em que as previsões precisam ser feitas rapidamente. É uma algoritmo majoriatariamente utilizado para classificação.

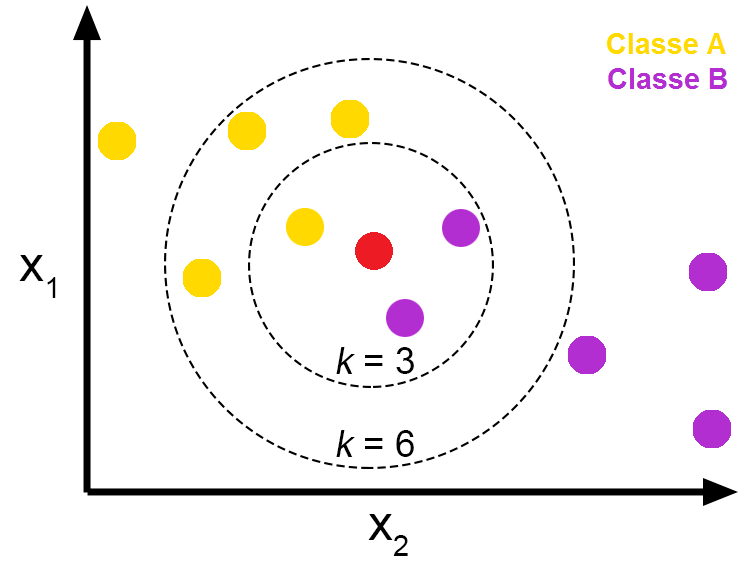
Figure 5.10: Exemplo do funcionamento do algoritmo KNN.

Fonte: https://medium.com/

Conforme mostra a Figura 5.10, o algoritmo KNN pressupõe que itens semelhantes estão próximos um dos outros, então tenta encaixar o novo dado nos conjuntos de seus vizinhos mais próximos em relação a similaridade existe entre eles. O cálculo de distância mais comum é a distância euclidiana, mas outras distâncias podem ser utilizadas.

5.5.1 Definição do modelo

Define-se o modelo que será utilizado, nesse caso é o algoritmo KNN nearest_neighbor() que recebe os argumentos neighbors que determina o número de vizinhos a serem considerados, weight_func usado para ponderar as distâncias entre as amostras. Para ambos os parâmetros atribui-se a função tune() que significa que os valores serão ajustados pelo pipeline.

library(kknn)
knn_model <- nearest_neighbor(neighbors = tune(), 
                             weight_func = tune()) %>%
  set_engine("kknn") %>% 
  set_mode("classification")

Após a definição do modelo é criado o fluxo de trabalho workflow().

knn_workflow <- workflow() %>% 
  add_model(knn_model) %>% 
  add_recipe(pre_recipe)

O modelo add_model() e o pré-processamento add_recipe() são colocados dentro de um workflow() e salvo em um objeto chamado knn_workflow.

5.5.2 Treinamento

Nessa etapa é realizado o treinamento do modelo para o algoritmo KNN.

knn_trained <- knn_workflow %>% 
  tune_grid(
    val_set,
    grid = 10,
    control = control_grid(save_pred = TRUE),
    metrics = metric_set(roc_auc)
  )

Visualização dos resultados usando para métrica de Curva ROC.

knn_trained %>% show_best("roc_auc")

## # A tibble: 5 × 8
##   neighbors weight_func  .metric .estimator  mean     n std_err .config         
##       <int> <chr>        <chr>   <chr>      <dbl> <int>   <dbl> <chr>           
## 1         9 inv          roc_auc binary     0.988     4 0.00632 Preprocessor1_M…
## 2        10 gaussian     roc_auc binary     0.988     4 0.00646 Preprocessor1_M…
## 3        14 epanechnikov roc_auc binary     0.987     4 0.00623 Preprocessor1_M…
## 4        12 cos          roc_auc binary     0.987     4 0.00611 Preprocessor1_M…
## 5        13 triweight    roc_auc binary     0.986     4 0.00565 Preprocessor1_M…

Observa-se o modelos gerados conforme definido na etapa de treinamento.

5.5.3 Seleção do melhor modelo

knn_best_tune <- select_best(knn_trained, 'roc_auc')
final_knn_model <- knn_model %>% 
  finalize_model(knn_best_tune)
knn_best_tune

## # A tibble: 1 × 3
##   neighbors weight_func .config              
##       <int> <chr>       <chr>                
## 1         9 inv         Preprocessor1_Model05

O modelo 5 apresentou melhores resultados com AUC de 0.988, utilizando o algortimo KNN.

5.5.4 Aplicando os dados de teste ao modelo

previsoes <- workflow() %>% 
  add_recipe(pre_recipe) %>% 
  add_model(final_knn_model) %>% 
  last_fit(divisao)

previsoes %>% collect_predictions()

## # A tibble: 176 × 7
##    id               .pred_2 .pred_4  .row .pred_class classe .config            
##    <chr>              <dbl>   <dbl> <int> <fct>       <fct>  <chr>              
##  1 train/test split   1       0         1 2           2      Preprocessor1_Mode…
##  2 train/test split   1       0         3 2           2      Preprocessor1_Mode…
##  3 train/test split   1       0         5 2           2      Preprocessor1_Mode…
##  4 train/test split   1       0         8 2           2      Preprocessor1_Mode…
##  5 train/test split   0.882   0.118     9 2           2      Preprocessor1_Mode…
##  6 train/test split   1       0        10 2           2      Preprocessor1_Mode…
##  7 train/test split   1       0        12 2           2      Preprocessor1_Mode…
##  8 train/test split   0       1        19 4           4      Preprocessor1_Mode…
##  9 train/test split   0.104   0.896    21 4           4      Preprocessor1_Mode…
## 10 train/test split   0.422   0.578    26 4           4      Preprocessor1_Mode…
## # … with 166 more rows

Observa-se as classificações reais dos dados de teste em classe e os valores preditos em .pred_class. Visualiza-se na Figura 5.11 a matriz de confusão para o modelo.

previsoes %>% collect_predictions() %>% 
  conf_mat(truth = classe,
           estimate = .pred_class, dnn = c("Previsto", "Real")) %>% 
  autoplot(type = "heatmap") +
  scale_fill_gradient(low = "pink3", high = "cyan4")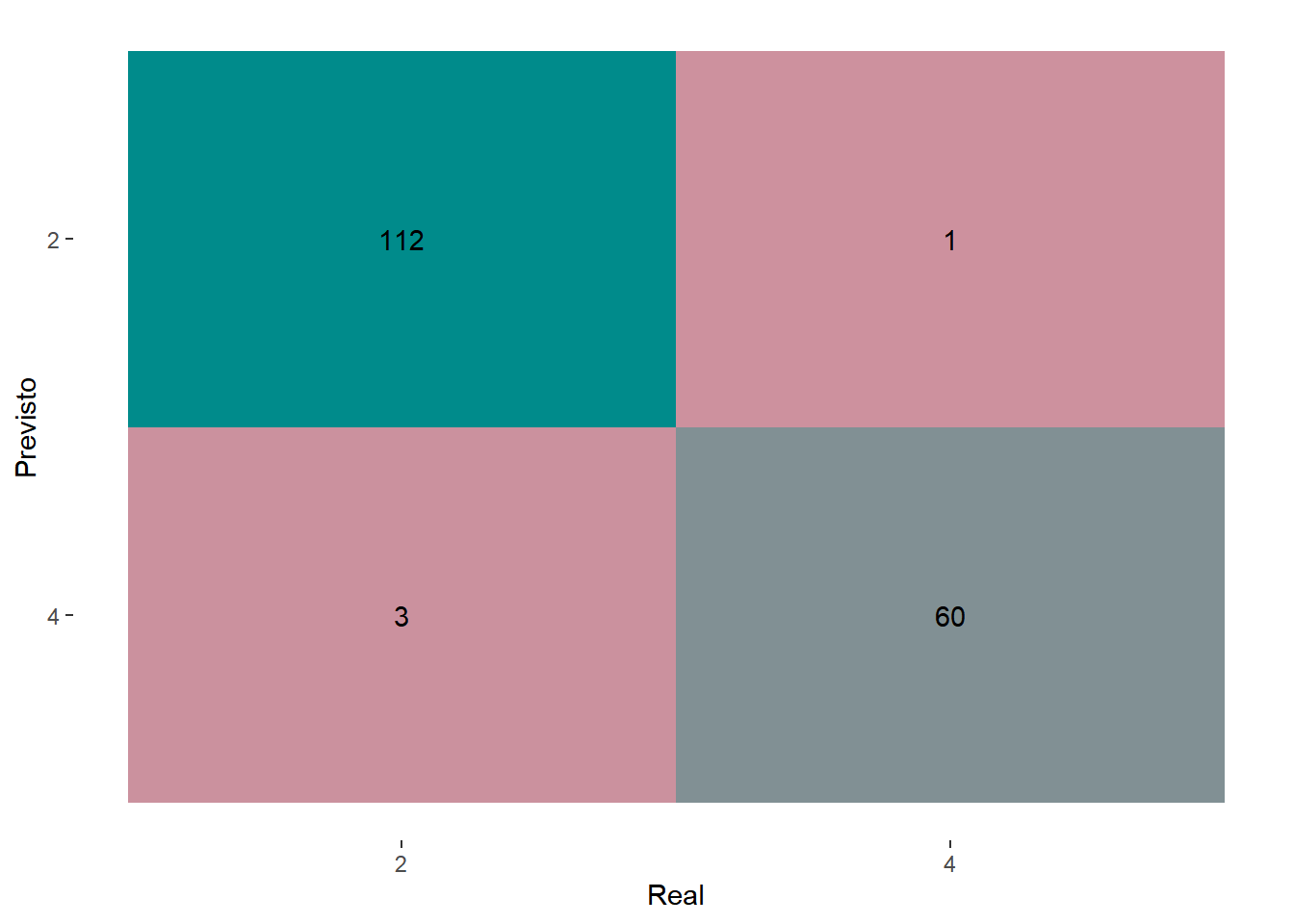

Figure 5.11: Matriz de confusão para o algoritmo KNN.

Visualizando a Curva ROC do modelo aplicado aos dados de teste (Figura 5.12).

previsoes %>% collect_predictions() %>%
  roc_curve(classe, .pred_2) %>% 
  autoplot()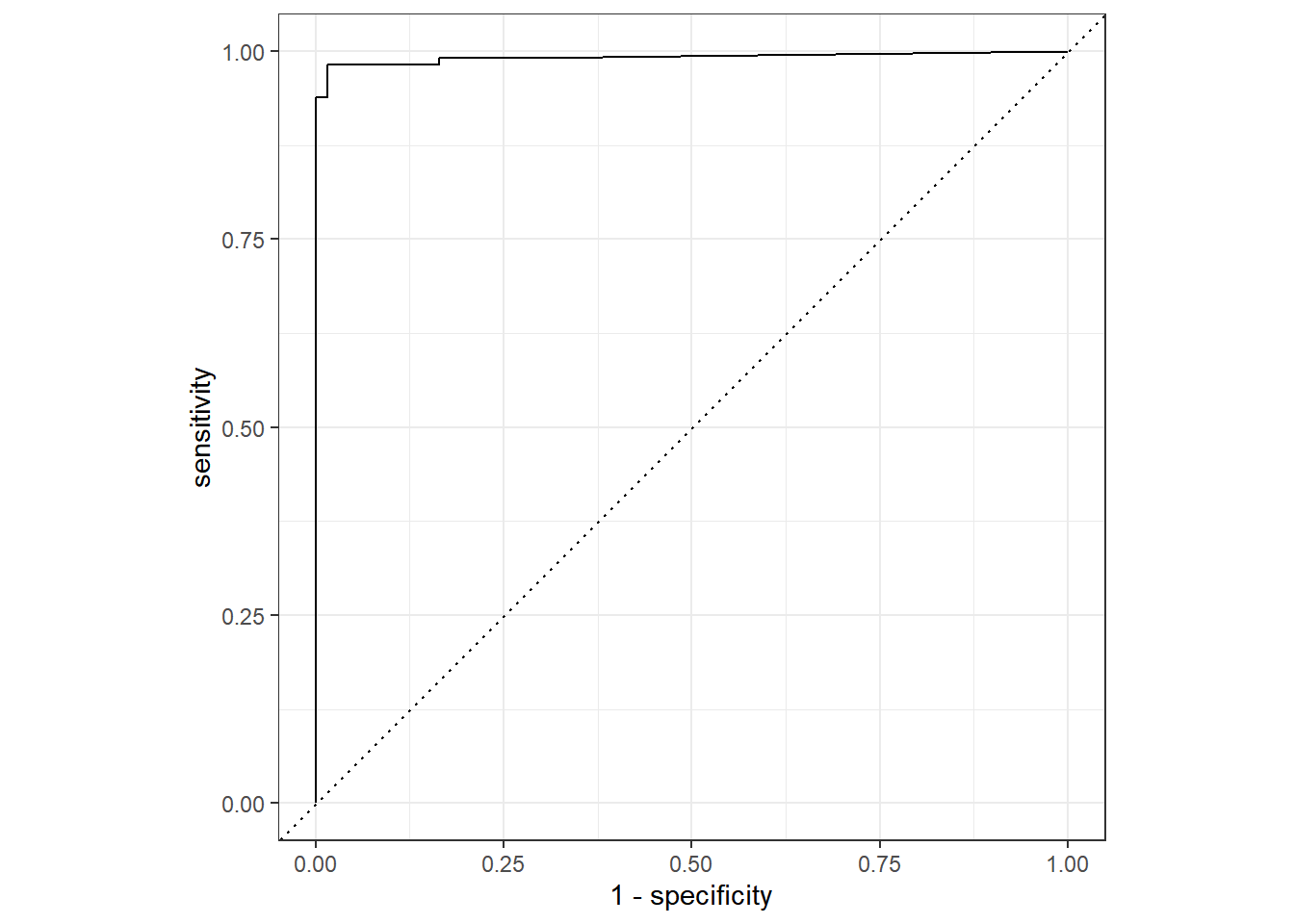

Figure 5.12: Desempenho do algoritmo KNN nos dados de teste.

Obtendo a AUC da Curva ROC para o modelo escolhido.

previsoes %>% collect_predictions() %>% 
  roc_auc(classe, .pred_2)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 roc_auc binary         0.992

Observa-se que os resultados obtidos quando aplicado o modelo gerado pelo algoritmo KNN ao dados de teste, são satisfatórios. O algoritmo KNN teve um desempenho ainda melhor que o algoritmo de árvore de decisão.

5.6 Regressão Logística

A Regressão Logística lida apenas com problemas de classificação, apesar do nome regressão, a Regressão Logística não é um modelo que prevê valores como a Regressão Linear. A utilização da regressão logística é comum na classificação de duas classes, mas ela não se limita apenas a isso.

A Regressão Logística trabalha com conceitos de estatística e probabilidade e seu uso é comum em algoritmos de Machine learning devido criar previsões precisas no que se refere a classificação. A variável resposta deve ser dicotômica ou binária.

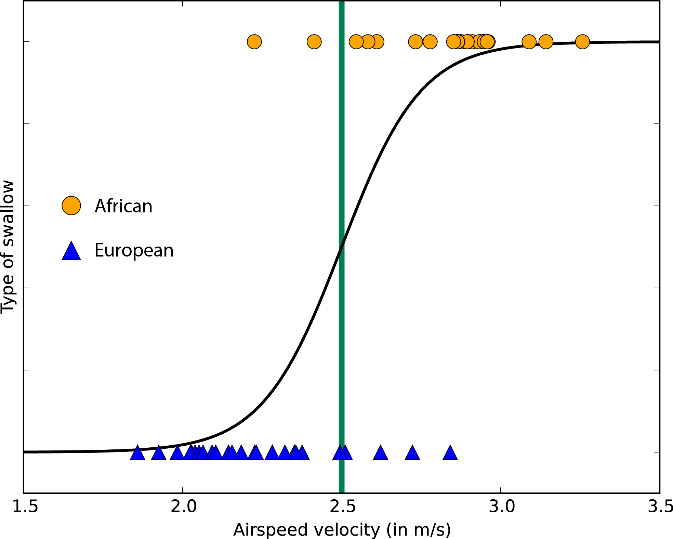
Figure 5.13: Exemplo do funcionamento da Regressão Logística.

Fonte: https://pcodinomebzero.neocities.org/

Conforme mostra a Figura 5.13, diferentemente da regressão linear o gráfico da regressão logística mostra um padrão em S e apresenta valores no intervalo de 0 a 1, ao invés de uma reta linear.

5.6.1 Definição do modelo

Define-se o modelo que será utilizado, nesse caso é o modelo de Regressão Logística logistic_reg() que recebe os argumentos penalty que é o número não negativo que representa a quantidade total de regularização e mixture um número entre zero e um que é a proporção de regularização no modelo. Para ambos os parâmetros atribui-se a função tune() que significa que os valores serão ajustados pelo pipeline.

library(glmnet)
Log_model <- logistic_reg(penalty = tune(),
                          mixture = tune()) %>%
  set_engine("glmnet")

A função set_engine()define o pacote que será utilizado para o ajuste, por se tratar de um modelo apenas de classificação não é necessário definir o tipo do modelo.

Após a definição do modelo é criado o fluxo de trabalho workflow().

Log_workflow <- workflow() %>% 
  add_model(Log_model) %>% 
  add_recipe(pre_recipe)

O modelo add_model() e o pré-procesamento add_recipe() são colocados dentro de um workflow() e salvo em um objeto chamado Log_workflow.

5.6.2 Treinamento

Nessa etapa é realizado o treinamento do modelo para o algoritmo de Regressão Logística.

Log_trained <- Log_workflow %>% 
  tune_grid(
    val_set,
    grid = 10,
    control = control_grid(save_pred = TRUE),
    metrics = metric_set(roc_auc)
  )

Em todos os métodos de aprendizagem utilizaremos a mesma métrica. Usando a função show_best visualiza-se os modelos gerados.

Log_trained %>% show_best("roc_auc")

## # A tibble: 5 × 8
##    penalty mixture .metric .estimator  mean     n std_err .config              
##      <dbl>   <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
## 1 1.02e- 1  0.804  roc_auc binary     0.995     4 0.00130 Preprocessor1_Model08
## 2 1.11e- 2  0.629  roc_auc binary     0.995     4 0.00196 Preprocessor1_Model07
## 3 3.01e- 3  0.985  roc_auc binary     0.995     4 0.00217 Preprocessor1_Model10
## 4 6.04e-10  0.0718 roc_auc binary     0.994     4 0.00197 Preprocessor1_Model01
## 5 3.10e- 4  0.333  roc_auc binary     0.994     4 0.00210 Preprocessor1_Model03

5.6.3 Seleção do melhor modelo

Log_best_tune <- select_best(Log_trained, 'roc_auc')
final_Log_model <- Log_model %>% 
  finalize_model(Log_best_tune)
Log_best_tune

## # A tibble: 1 × 3
##   penalty mixture .config              
##     <dbl>   <dbl> <chr>                
## 1   0.102   0.804 Preprocessor1_Model08

O Modelo 8 apresentou melhores resultados com AUC de 0.995 utilizando o algoritmo de Regressão Logística.

5.6.4 Aplicando os dados de teste ao modelo

Aplicação do modelo nos dados de teste, onde os resultados são salvos em um objeto chamado previsoes.

previsoes <- workflow() %>% 
  add_recipe(pre_recipe) %>% 
  add_model(final_Log_model) %>% 
  last_fit(divisao)

Obtendo as previsões.

previsoes %>% collect_predictions()

## # A tibble: 176 × 7
##    id               .pred_2 .pred_4  .row .pred_class classe .config            
##    <chr>              <dbl>   <dbl> <int> <fct>       <fct>  <chr>              
##  1 train/test split   0.878  0.122      1 2           2      Preprocessor1_Mode…
##  2 train/test split   0.881  0.119      3 2           2      Preprocessor1_Mode…
##  3 train/test split   0.883  0.117      5 2           2      Preprocessor1_Mode…
##  4 train/test split   0.896  0.104      8 2           2      Preprocessor1_Mode…
##  5 train/test split   0.921  0.0791     9 2           2      Preprocessor1_Mode…
##  6 train/test split   0.883  0.117     10 2           2      Preprocessor1_Mode…
##  7 train/test split   0.914  0.0857    12 2           2      Preprocessor1_Mode…
##  8 train/test split   0.130  0.870     19 4           4      Preprocessor1_Mode…
##  9 train/test split   0.312  0.688     21 4           4      Preprocessor1_Mode…
## 10 train/test split   0.543  0.457     26 2           4      Preprocessor1_Mode…
## # … with 166 more rows

Observa-se as classificações reais dos dados de teste em classe e os valores preditos em .pred_class. A Figura 5.14 mostra o resultado na matriz de confusão para o modelo.

previsoes %>% collect_predictions() %>% 
  conf_mat(truth = classe,
           estimate = .pred_class, dnn = c("Previsto", "Real")) %>% 
  autoplot(type = "heatmap") +
  scale_fill_gradient(low = "pink3", high = "cyan4")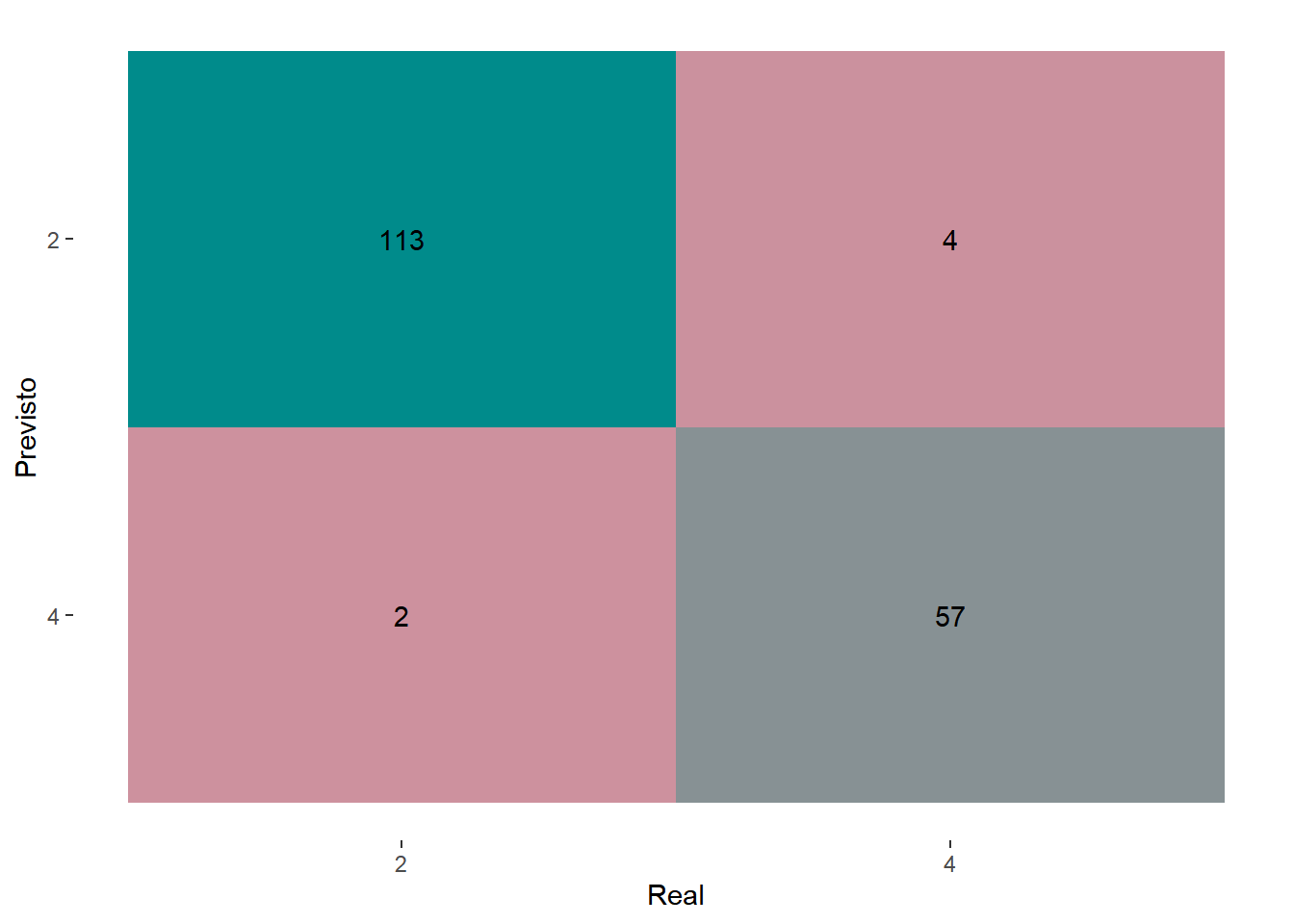

Figure 5.14: Matriz de confusão para o algoritmo de Regressão Logística.

A Figura 5.15 mostra a Curva ROC para o modelo de Regressão Logística.

previsoes %>% collect_predictions() %>%
  roc_curve(classe, .pred_2) %>% 
  autoplot()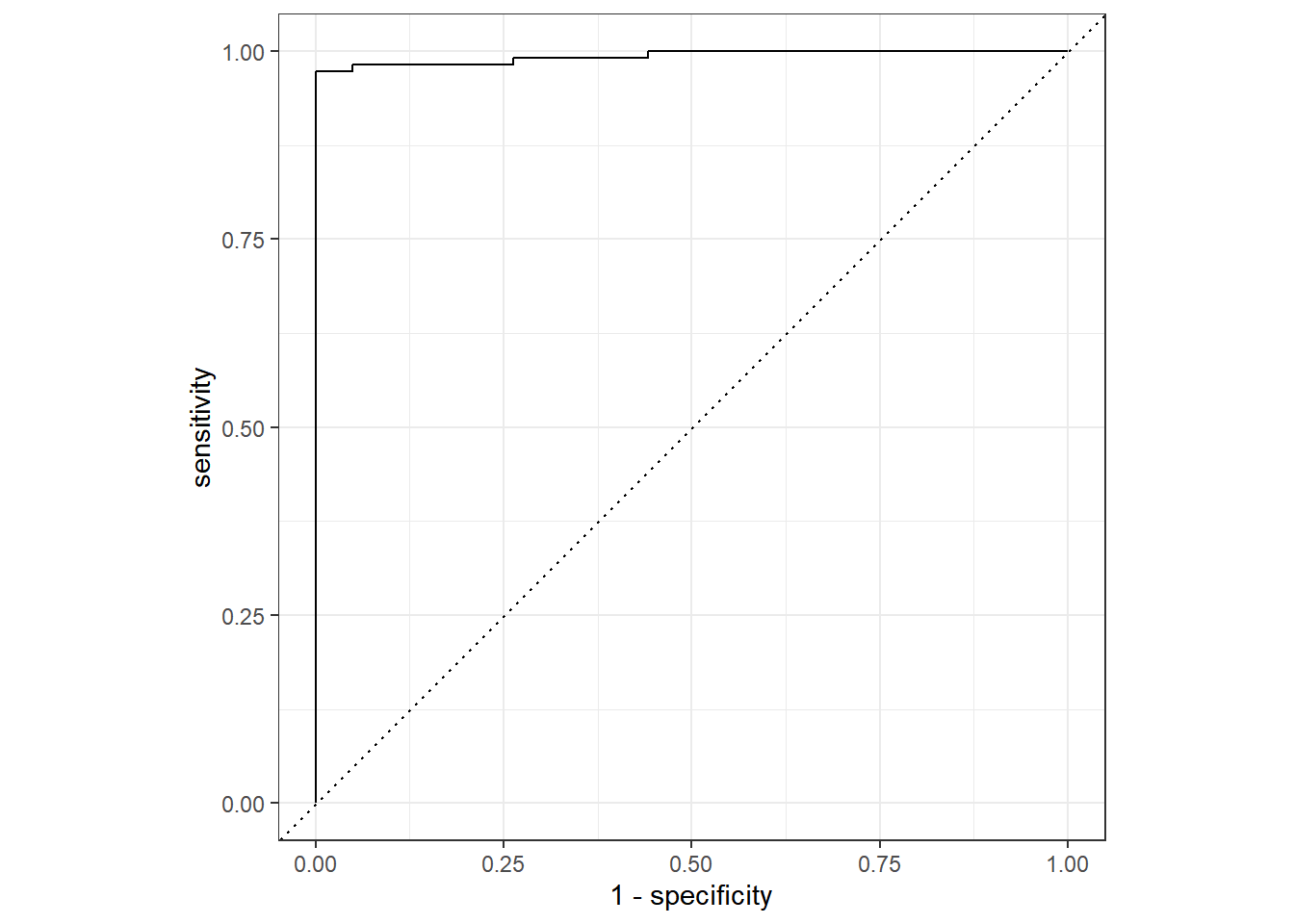

Figure 5.15: Desempenho do algoritmo Regressão Logística nos dados de teste.

Obtendo a AUC da curva ROC para o modelo selecionado.

previsoes %>% collect_predictions() %>% 
  roc_auc(classe, .pred_2)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 roc_auc binary         0.993

O modelo de Regressão Logística teve um resultado semelhante ao algoritmo Random Forest, porém com um desempenho um pouco melhor considerando o valor da AUC. A Tabela 5.1 fornece um resumo dos resultados.

Table 5.1: Resultados da classificação para cada algoritmo, modelo, AUC treino, Erro Padrão e AUC teste.
Algoritmos	Modelo	AUC_treino	Erro	AUC_teste
Árvore de decisão	Modelo 10	0.962	0.00624	0.951
Random Forest	Modelo 1	0.994	0.00207	0.991
Algoritmo KNN	Modelo 5	0.988	0.00632	0.992
Regressão Logística	Modelo 8	0.995	0.00130	0.993

Comparando os resultados dos modelos utilizados, aquele que teve um melhor desempenho com AUC de 0.995 foi algoritmo de Regressão Logística se comparado com os demais modelos. O modelo de Regressão Logística também foi o que generalizou melhor quando aplicado nos dados de teste.