Chapter 4 Inferencias

Antes de comenzar a profundizar en este interesante capítulo y todas las implicaciones que tienen los conceptos que se abordan en el mismo, conviene comprender primero que es una inferencia y los dos tipos principales que distinguiré a lo largo del libro. El acto de inferir consiste en sacar una consecuencia, en concluir algo, a raiz de otra cosa. En el ámbito científico lo que realizamos es una inducción, donde partimos de un caso concreto hacia una generalización. Voy a distinguir dos tipos de inferencia:

Inferencia estadística: Es la que realizamos a través de los análisis estadísticos, partiendo de las asunciones necesarias para su realización. Es decir, si asumimos una “simulación matemática perfecta”“, sin tener en cuenta desviaciones de la misma. Aquí tendríamos a los valores-p e intervalos de confianza.
Inferencia técnica: Es la que realizamos sin cálculos matemáticos, aunque los tengamos en cuenta para llevarla a cabo, y en la que influye todo el conocimiento que tenemos de un campo concreto sobre el que vamos a inferir.

De manera simple, podríamos afirmar que de cualquier investigación relacionada con nuestra profesión, lo que vamos a realizar siempre es una inferencia técnica, no estadística, pues como ya veremos, interpretar los resultados asumiendo ese “modelo matemático perfecto”, teniendo solo en cuenta la pequeña parte de inferencia estadística que realizamos como parte de la investigación, es un grave error que nos llevará a sacar conclusiones desacertadas en una gran cantidad de casos.

4.1 Poblaciones, muestras e individuos

Queremos conocer la estatura media de los habitantes de Alcalá de Henares. Más o menos, Alcalá tiene una población de unos 200000 habitantes. Tenemos un trabajo como falso autónomo en una clínica privada cobrando 600€ brutos por media jornada, y necesitamos nuestro “tiempo libre” para hacer domicilios para poder pagarnos un piso y no morir de hambre. Es decir, no tenemos tiempo libre para estar midiendo a tantas personas, de modo que decidimos seleccionar una pequeña cantidad de las mismas, una muestra de 200 individuos. Los medimos y obtenemos una estatura media de , \(\bar x = 170.5cm\).

Si hemos seguido una buena metodología y el muestreo se ha realizado de forma aleatoria, podremos inferir estadísticamente esta media a la población estadística, que comprendería a todos los sujetos de los cuales hemos extraído nuestra muestra aleatoria, pudiendo calcular un intervalo de confianza al 95% para dicha media, con el fin de estimar la confianza/precisión de nuestra afirmación. Imaginemos ahora que, en lugar de querer estimar la estatura media de la población de Alcalá de Henares, queremos hacerlo de toda la Comunidad de Madrid, pero solo tenemos acceso al listado de habitantes de Alcalá de Henares. En ese caso, ya no podríamos hacer ina inferencia estadística, si no que entraríamos en el campo de la inferencia técnica hacia esa población diana, los habitantes de la Comunidad de Madrid.

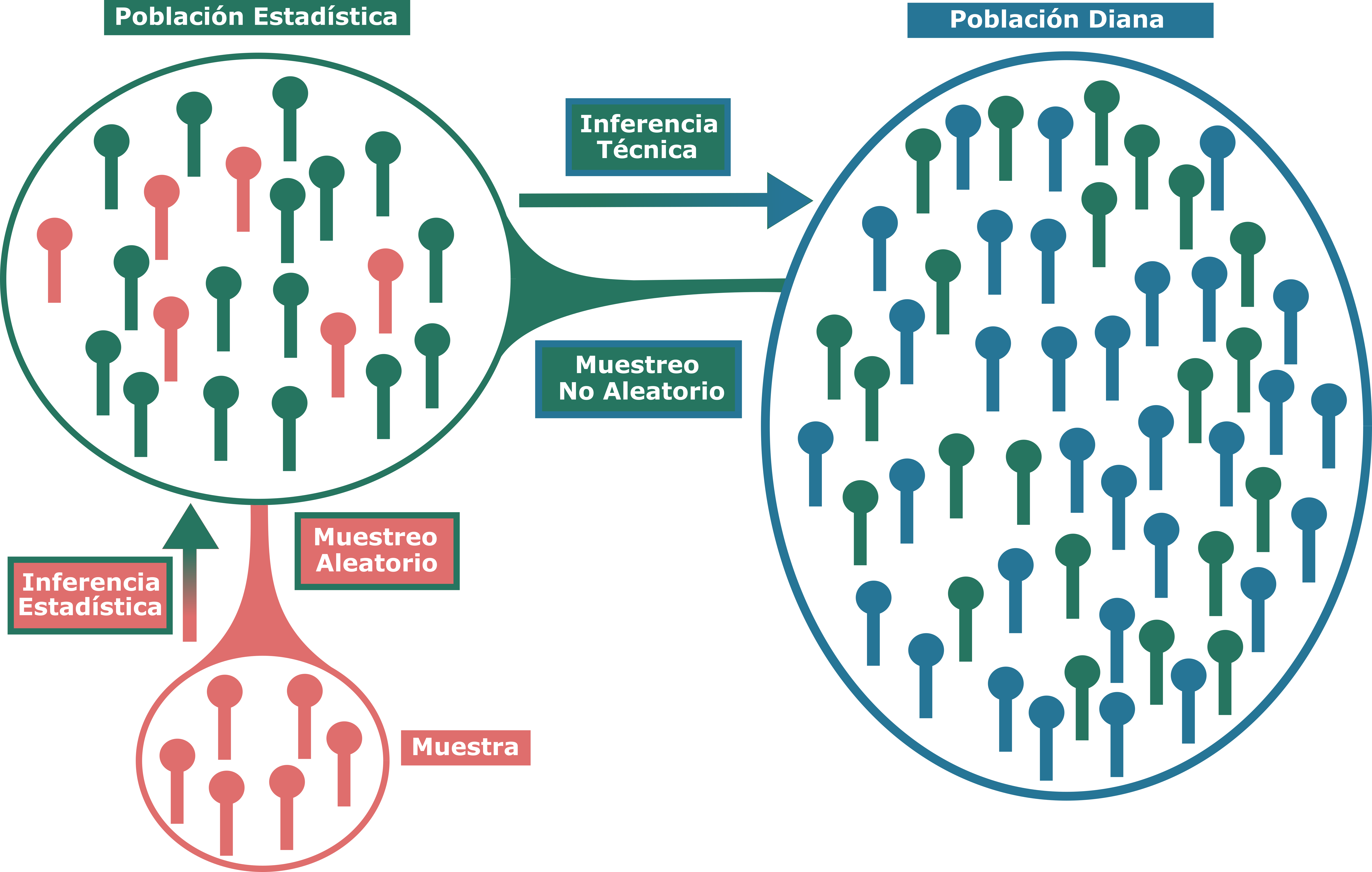
Figure 4.1: Población, muestra e inferencias

La población estadística y la población diana pueden ser la misma, como en el caso donde simplemente queríamos estimar la estatura media de la población de Alcalá y disponíamos del listado de todos sus habitantes para realizar el muestreo aleatorio. La población diana es aquella a la que queremos inferir los resultados de una investigación, mientras que la población estadistica es aquella a la que tenemos acceso real y sobre la que realizamos nuestro muestreo aleatorio. La inferencia estadística como tal, se realiza sobre la población estística y para que tenga sentido a nivel conceptual, requiere de un muestreo aleatorio. En cuanto nos salimos de la población estadística, obligatoriamente lo que vamos a realizar es una inferencia técnica, donde habrá que tener en cuenta en mayor o menos medida los análisis estadísticos, pero no sacar conclusiones basadas íntegramente en ellos.

Existe cierto malentendido con respecto al concepto de muestreo aleatorio y la inferencia estadística en la literatura, con múltiples investigaciones donde, sin llevar a cabo un muestreo aleatorio o disponiendo de toda la población, se calculan valores-p o intervalos de confianza (Williamson 2003). Si bien los datos de dicho artículo son de hace un tiempo y de una revista de Enfermería, actualmente en Fisioterapia, especialmente en los estudios de caracter observacional, se está realizando la misma mala práxis y malinterpretación de la gran mayoría de los resultados de investigación. En casi ningúna publicación con ese tipo de diseño en nuestro campo se utilizan métodos de muestreo probabilísticos, es decir, que implicen una selección aleatoria de los sujetos. Estos suelen ser seleccionados mediante anuncios, boca a boca, y otra serie de muestreos por conveniencia. Pensemos en el caso donde hemos medido a toda la población de Alcalá de Henares, ¿qué sentido tiene calcular un intervalo de confianza para la media muestral? Hemos medido a todos los habitantes, ya tenemos el valor real de la media de estatura de la población de Alcalá, no hay que calcular el grado de precisión/certidumbre asociado a nuestra estimación. Por otro lado, si seleccionamos nosotros a mano una muestra de 100 sujetos, sin aleatorizar de toda la población, y calculamos un intervalo de confianza al 95%, no podremos afirmar literalmente que con un 95% de confianza, el valor de la media muestral se encuentra dentro de dicho intervalo. Si repitiéramos ese experimento infinitas veces, con ese muestreo por conveniencia, es muy probable que el número de veces en que la media se encontrase fuera de dicho intervalo fuese distinto a 0.05, el valor teórico asumiendo algunas consideraciones, entre ellas el muestreo aleatorio. Debemos grabarnos esto en la cabeza, tanto los valores-p como los intervalos de confianza, nos sirven para “cuantificar” el grado de certidumbre que podemos poner en una afirmación, debido a errores aleatorios del muestreo, sin esa aleatorización, matemáticamente carecen de sentido.

¿Significa esto que debemos dejar de reportar valores-p e intervalos de confianza en estudios con muestreos por conveniencia? No del todo, deben reportarse e interpretarse, pero teniendo en cuenta dicha este aspecto que constituye una limitación, el error sería sacar una conclusión exclusivamente basada en dicha estadística inferencial. Otro problema, que nos atañe especialmente en nuestra profesión, son los estudios con pequeños tamaños muestrales. Los problemas derivados de la ausencia de un muestreo probabilístico deben tenerse en mayor consideración con muestras pequeñas. Actualmente en el ámbito de investigación en Fisioterapia está demasiado normalizada la utilización de muestras pequeñas y esto, en estudios observacionales con muestreos por conveniencia, es un factor crucial para su interpretación. Podemos encontrar estudios comparando distintas variables entre sujetos asintomáticos y sujetos con dolor en alguna región corporal, que utilizan muestras de 20, 30, 40, o 50 sujetos por grupo. Es totalmente inapropiado, salvo casos muy concretos, la utilización de muestras tan pequeñas. Una muestra de 100 sujetos (50 asintomáticos y 50 con dolor lumbar), no es un tamaño muestral grande. Este es uno de los factores que, a mi parecer, contribuyen en gran medida a la dificultad de reproducibilidad de los resultados de estudios observacionales en nuestro campo.

4.1.1 El caso particular de los ensayos controlados aleatorizados

Cuando nos encontramos ante un ensayo controlado aleatorizado (ECA), el concepto de muestreo aleatorio puede confundirse con el concepto de asignación aleatoria. Esta confusión puede ser en parte normal, dado que ambos procesos tienen que ver con el error aleatorio que evaluamos con distintos análisis estadísticos, con los valores-p y los intervalos de confianza.

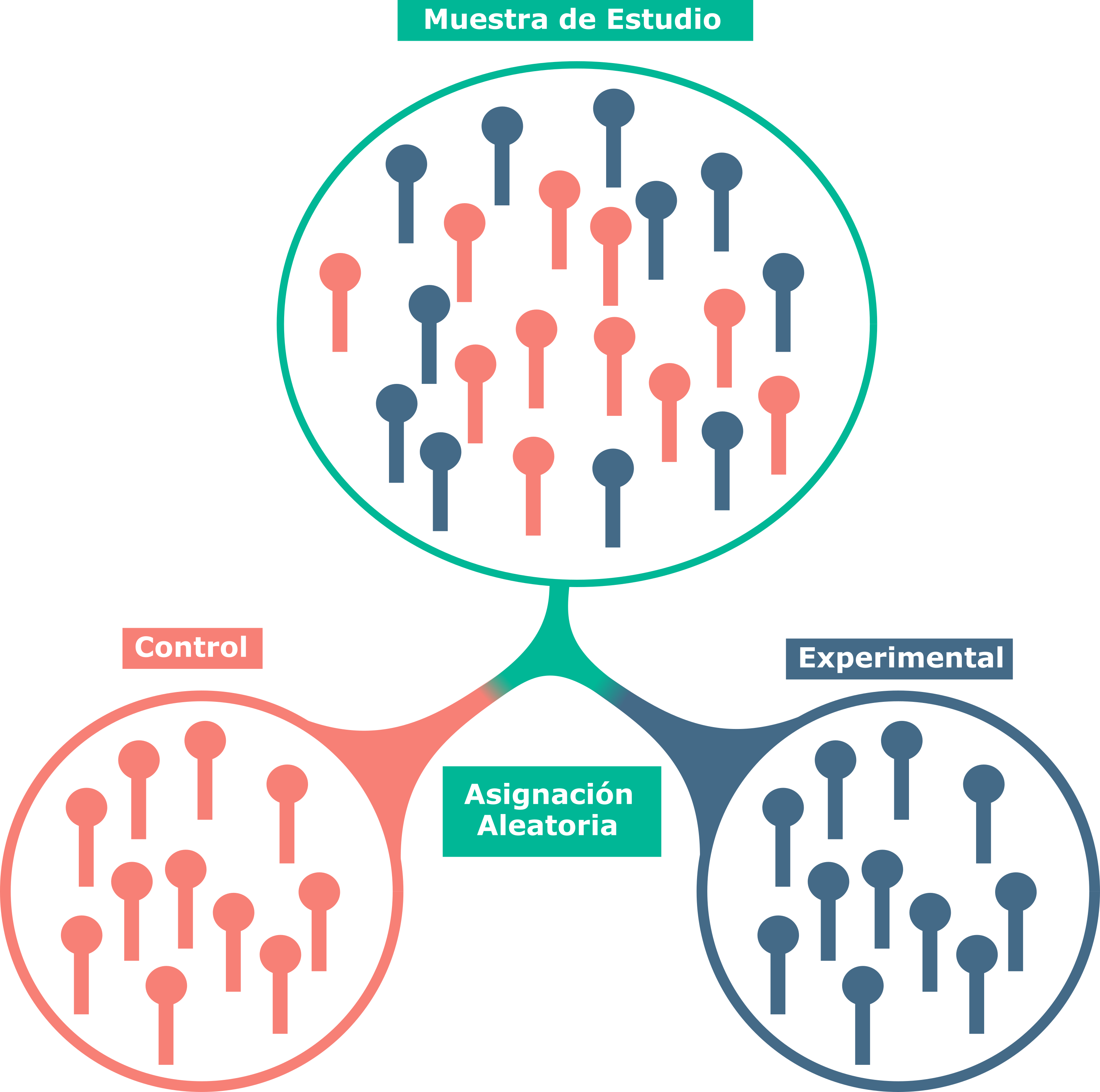
Figure 4.2: Inferencia estadística en un ensayo controlado aleatorizado

Cuando se realiza un ECA, se recluta una muestra de la población estadística (también denominada a veces población accesible o población de estudio), esta sería la fase de muestreo, donde rara vez se utiliza un muestreo probabilístico, suele usarse el muestreo por conveniencia. Una vez reclutada la muestra, se procede con la asignación de los sujetos a cada grupo de intervención (dos en el caso más simple). Este proceso siempre se realiza de manera aleatoria mediante programas de ordenador actualmente, es la asignación aleatoria. Partiendo de las asunciones anteriormente mencionadas para el cálculo de los valores-p y los intervalos de confianza, con respecto a la aleatorización de los muestreos, paso a explicar la interpretación de estos en un ECA de manera simplificada. Al realizar el proceso de asignación aleatoria introducimos un error aleatorio al igual que con los ejemplos de muestreo anteriormente mencionados. Imaginemos que sabemos a priori la mejoría que obtendrá cada sujeto en el dolor con la aplicación de cada una de las dos intervenciones y que cada sujeto podría obtener una y solo una mejoría (en la realidad esto no sería del todo cierto, ya que cada sujeto, debido a múltiples factores, puede obtener distintas mejorías con una determinada intervención, pero lo asumiremos para simplificar el ejemplo), podríamos tener unos datos como los de la Tabla 4.1.

Table 4.1: Mejorías de dolor simuladas para dos tratamientos
Sujeto	Tratamiento A	Tratamiento B
1	2.16	6.45
2	2.65	4.72
3	5.34	4.80
4	3.11	4.22
5	3.19	2.89
6	5.57	7.57
7	3.69	5.00
8	1.10	0.07
9	1.97	5.40
10	2.33	3.05

Si realizamos una asignación aleatoria, de manera cada mitad de los sujetos reciba un tratamiento, podemos obtener por ejemplo lo siguiente:

Tratamiento A: Sujetos 1, 3, 4, 6 y 8; \(\bar x_a = 3.46\)
Tratamiento B: Sujetos 2, 5, 7, 9 y 10; \(\bar x_b = 4.21\)

Estas medias son las que obtendríamos en un caso concreto, pero…¿y si pudieramos repetir el experimento en condiciones identicas más veces? Este punto, el de condiciones idénticas, es por el cual he asumido anteriormente que cada sujeto tenía una sola puntuación para cada terapia. En la vida real, es imposible simular ese experimento en condiciones idénticas con los mismos sujetos, no podemos retroceder en el tiempo. Si repetimos esta asignación aleatoria simulada, por ejemplo 5 veces, podemos obtener los siguientes resultados:

Table 4.2: Asignaciones aleatorias simuladas
Aleatorización	Muestra A	Muestra B	Media A	Media B	Diferencia
1	1,3,4,6,7	2,5,8,9,10	3.974	3.226	0.748
2	2,4,5,9,10	1,3,6,7,8	2.65	4.778	-2.128
3	3,4,6,8,9	1,2,5,7,10	3.418	4.422	-1.004
4	2,3,6,9,10	1,4,5,7,8	3.572	3.726	-0.154
5	1,3,5,7,8	2,4,6,9,10	3.096	4.992	-1.896

En la práctica, no es posible repetir el experimento múltiples veces bajo las mismas condiciones para cuantificar ese error aleatorio derivado del proceso de asignación y poder calcular la media de todas las diferencias medias posibles (infinitas asignaciones aleatorias), que sería la diferencia media real para nuestra muestra. En lugar de eso, lo que se hace es calcular los valores-p e intervalos de confianza, para estimar como de plausible es, bajo el modelo preespecificado de ausencia de diferencias, que hubieramos obtenido una diferencia igual o superior a la observada por azar, debido a la asignación aleatoria. Por tanto, los valores-p e intervalos de confianza tienen su sentido con respecto a la asignación aleatoria, sin embargo, lo que suele interesarnos es inferir los resultados de dicho experimento al conjunto de gente con ese determinado proceso, por ejemplo dolor lumbar. Como ya se ha comentado, normalmente este muestreo inicial no se realiza mediante métodos probabilísticos, es decir, no disponemos de esa población estadística, estamos violando una de las asunciones para el cálculo de los valores-p e intervalos de confianza y es por ello que la inferencia de los resultados de un ECA, más allá de la muestra estudiada, ha de realizarse con cautela, pues se trata de una inferencia técnica y no estadística, por lo que basarse exclusivamente en los resultados de los valores-p e intervalos de confianza, es totalmente inapropiado.

4.2 Técnicas de muestreo

Ya se ha comentado que existen dos grandes grupos que vamos a distinguir de tipos de muestreo, los probabilísticos y los no probabilísticos o por conveniencia. La distinción esencial entre ambos, es que en los primeros si se realiza un muestreo generando números aleatorios mediante un programa de ordenador, mejor dicho, números pseudoaleatorios, ya que actualmente no es posible generar números aleatorios por ordenador, sin entrar en detalles esto implica que llegado a un número de valores, se repetirá, por eso no es realmente una secuencia aleatoria como tal y a estos programas se les llama generadores de números pseudoaleatorios. No obstante, esto no tiene mayor relevancia para los propósitos de este libro o la intepretación de los análisis estadísticos en nuestro campo.

Dentro de los tipos de muestreo probabilístico podemos distinguir varios, no obstante explicaré solamente dos de ellos:

Muestreo aleatorio simple: En este tipo de muestreo cada sujeto tiene la misma probabilidad de ser seleccionado, así como cada grupo n, es decir, si el tamaño muestral es de 30 sujetos, cada combinación de 30 sujetos tiene la misma probabilidad de ser seleccionada.
Muestreo estratificado: En este tipo de muestreo se selecciona una o varias variables, dentro de las cuales se definirán dos o más estratos. Por ejemplo, podemos seleccionar la variable sexo, con dos estrados. Una vez definidos los estratos, se procede a realizar un muestreo aleatorio de sujetos dentro de cada estrato. Esto nos permitiría por ejemplo, sabiendo que en la población estadística hay un 60% mujeres y un 40% hombres, asegurar que en la muestra de estudio esos porcentajes sean los mismos, es decir, que sea representativa para esa variable.

El objetivo al realizar un muestreo, es que la muestra sobre la que vamos a realizar el estudio sea lo más representativa posible de la población hacia la que vamos a inferir los resultados, este sería el concepto de representatividad. Este concepto hace referencia a que la muestra bajo estudio, presente las mismas características que la población a la que se van a inferir sus resultados. Una muestra puede ser representativa para una variable (como en el ejemplo anterior de muestreo estratificado en función del sexo) pero no para otras. En la práctica, nunca vamos a poder asegurar que nuestra muestra sea representativa de la población, es decir, sería un error hablar de “muestra representativa”, ya que casi nunca conocemos los valores de la población y podemos realizar tal afirmación. La mejor manera, sin disponer de conocimiento sobre las características de la población, para asegurar la mayor representatividad posible, es realizar muestreos probabilísticos.

Anteriormente he hecho mucho hincapié con respecto a la importancia de utilizar muestreos probabilísticos. Uniendo esto con el concepto de la representatividad, podemos afirmar que, si consiguiéramos que la muestra de estudio fuese representativa de la población, a expensas del tipo de muestreo utilizado, tendría sentido la interpretación puramente matemática de los distintos análisis, p-valores e intervalos de confianza. No obstante, esto en la práctica real es casi imposible de conseguir y en aquellos casos donde se puede, también se puede hacer un muestreo probabilístico, ya sea estratificado o de otro tipo, de modo que no habría excusa para no hacerlo. Este aspecto simplemente lo nombro para remarcar que, la importancia del muestreo probabilístico no es el azar en si mismo, sino el conseguir una muestra lo más representativa posible de la población.

Por otro lado, tendríamos los muestreos por conveniencia, en los que no se realizaría un reclutamiento mediante secuencias pseudoaleatorias generadas por ordenador. Algunos ejemplos serían:

Carteles solicitando voluntarios.
Selección de muestra accesible (por ejemplo, los jugadores del equipo de natación de la localidad donde vive el investigador).
Boca a boca.

Existe gran variedad de métodos de reclutamiento por conveniencia y, algunos de ellos, requieren mayor cuidado a la hora de interpretar los resultados del estudio. Por ejemplo, hay que tener especial cuidado con realizar reclutamiento por redes sociales (twitter, instagram, facebook…) para estudios que tengan por objetivo pasar una encuesta. Es plausible pensar que las personas que sigan al investigador puedan tener alguna cosa en común con él/ella, que pueda condicionar los resultados de la investigación.

4.3 Técnicas de remuestreo (Bootstrapping)

Para poder realizar algunos análisis determinados y calcular los valores-p e intervalos de confianza, nos basamos en una serie de asunciones, entre ellas, la de normalidad. Es decir, asumimos que el parámetro muestral sigue una distribución normal y en función de ello y otras asunciones calculamos los valores-p. Cuando no se cumple el supuesto de normalidad, existen alternativas como por ejemplo las pruebas no paramétricas. Otra opción, es la utilización de técnicas de remuestreo, más conocidas como bootstrapping, para el cálculo de los intervalos de confianza asociados a un determinado parámetro muestral.

En ausencia de datos para asumir una distribución de probabilidad concreta, la mejor asunción que podemos hacer es que la distribución de dicho parámetro muestral sería la distribución de los datos. Con el bootstrapping lo que se realiza es simular múltiples muestras, partiendo de esa distribución de probabilidad de los datos observados. Los pasos para realizar bootstrapping serían los siguientes:

Paso 1: Medir una muestra.
Paso 2: Generar múltiples muestras (con el mismo tamaño muestral que la original) mediante un remuestreo con reemplazo.
Paso 3: Calcular el parámetro muestral en cada una de dichas muestras.
Paso 4: Construir el intervalo de confianza para dicho parámetro muestral en función de la distribución de los múltiples parámetros calculados.

El paso uno realmente no sería un paso propio del bootstrapping, sino un paso previo necesario para realizar cualquier investigación. En el paso dos se realiza un remuestreo con reemplazo. Si tuvieramos una caja con 30 pelotas, cada una con un número escrito en ella, el muestreo con reemplazo consistiría en seleccionar una de las pelotas, anotar el número adjudicado a la misma y, antes de seleccionar otra pelota, devolver la pelota inicialmente escogida de nuevo a la caja, es decir, siempre que se selecciona una pelota, hay 30 pelotas en la caja. Con una muestra de una investigación sería lo mismo, solo que con sujetos que tienen adjudicado un valor de la/las variable/s bajo estudio. Este paso se hace un número elevado de veces, normalmente 2000, 5000 o incluso 10000 veces.

Se realiza el reemplazo para que no se altere la probabilidad de obtener un determinado valor de una variable. Si por ejemplo, tenemos 10 sujetos y 5 de ellos presentan una estatura de 170cm, si seleccionamos un sujeto y no lo “devolvemos a la caja” al seleccionar el siguiente sujeto, la probabilidad de obtener una estatura de 170cm para el segundo sujeto que seleccionemos es distinta a la del primer sujeto. Esto es importante, pues como se comentaba anteriormente, el objetivo del bootstrapping es utilizar la distribución de los datos observados y por tanto, eso hace necesario el reemplazo, para que dicha distribución se mantenga todas las veces que seleccionamos un sujeto al azar de nuestra muestra.

El paso tres es distinto según los objetivos del estudio, consiste en realizar el análisis estadístico objetivo del estudio en todas las muestras obtenidas con el remuestreo con reemplazo. Por ejemplo, si queremos comparar dos medias, el paso tres consistiría en hayar la diferencia media entre los dos grupos para cada una de las muestras simuladas. Si el objetivo fuese evaluar una asociación con el coeficiente de correlación de Pearson, en el paso tres se calcularía dicho coeficiente para cada una de las muestras simuladas.

Finalmente, en el paso cuatro se construiría el intervalo de confianza del bootstrapping. Existen distintas formas de llevar a cabo este paso, pero nombraré solo tres de ellas:

Método percentil: Este método consiste en utilizar percentiles para calcular un intervalo con X% confianza, es decir, seleccionamos los valores entre los cuales se encontarían el X% de los datos, por ejemplo para el intervalo al 95% de confianza, seleccionariamos los percentiles 2.5 y 97.5, ya que entre ellos estarían el 95% de los valores de los parámetros muestrales de las muestras simuladas, y ellos definirían el intervalo de confianza.
Método sesgos corregido (BC): Es un método similar al de percentil, salvo porque los valores del intervalo de confianza se ajustan, en función del número de valores del parámetro estimado con los remuestreos, que están por debajo del valor observado en la muestra original. Es decir, si el valor de la media observada es de 30, en las sucesivas simuladas con remuestreo los valores caerán por encima o debajo de esa media, sin tener que haber el mismo numero de valores por encima que por debajo, con este método se corrige en función de esa desigualdad, de ese sesgo. En inglés este método se denomina bias-corrected bootstrap.
Método sesgos corregido y acelerado (BCa): En este método, se realiza un ajuste adicional al llevado a cabo en el método de sesgos corredigo, donde además de corregir para los sesgos, se corrige para la asimetría de la curva de distribución del parámetro objeto de estudio en las múltiples muestras simuladas. En inglés este método se denomina bias-corrected and accelerated bootstrap.

En la Tabla 4.3 se muestran los intervalos de confianza al 95% para la media muestral, asumiendo la normalidad y con los métodos percentil y BCa de bootstrapping.

Table 4.3: Ejemplo de intervalos de confianza con bootstrap (2000 muestras de n = 30)
Método	Media	Límite Inferior del IC al 95%	Límite Superior del IC al 95%
Normal	30.65	27.43	33.88
Percentil	30.7	27.76	34.08
BCa	30.7	27.84	34.28

4.4 El método de Montecarlo

El método de Montecarlo recibe su nombre del casino de Montecarlo, debido a la ruleta, un mecanismo simple de generación de números aleatorios. El motivo de explicar este concepto, es porque a lo largo del libro, como se ha podido observar en capítulos anteriores, se utilizará el mismo para simular datos que sirvan para ejemplificar distintos aspectos que se irán abordando.

De forma simplificada, lo que se hace en dichas simulaciones es, partiendo de una distirbución de probabilidad pre-especificada (por ejemplo, la distribución normal) y algunos parámetros (por ejemplo, la media y desviación típica), generar muestras de números pseudoaleatorios. Sería como asumir que tenemos una población infinita de sujetos, con por ejemplo una estatura media de \(\bar x = 170cm\) y una desviación estándar de \(\sigma = 10\), con una distribución normal, y reclutamos una muestra de 30 sujetos mediante un método de muestro probabilístico. De esta forma, se pueden generar gráficos y estadísticos para ejemplificar que pasaría en determinadas situaciones, sin necesidad de realizar el estudio de investigación real. Entre las múltiples utilidades que tiene el método de Montecarlo, cabe destacar la estimación de la potencia estadística, estimación de tamaños muestrales y la evaluación de como determinadas situaciones, como por ejemplo los errores de medición, la dicotomización de una variable continua u otras, afectan a un determinado análisis estadístico.

Por ejemplo, existen ya fórmulas propuestas para el cálculo de la potencia estadística de determinados tests (número de veces que obtendríamos un resultado estadísticamente significativo para un determinado tamaño muestral), como por ejemplo el coeficiente de correlación de Pearson, utilizado para dos variables continuas. Sin embargo, también podemos realizar dicha estimación de la potencia estadística mediante el método de Montecarlo. En este caso, procederíamos de la siguiente manera:

1º. Establecer las asunciones, como por ejemplo una correlación real entre las dos variables de \(r = 0.50\), con un tamaño muestral de \(n = 30\), y una distribución normal para cada una de las dos variables.
2º. Generar un número elevado de muestras aleatorias de 30 sujetos partiendo de las anteriores asunciones, por ejemplo 10000 muestras.
3º. Para cada muestra, calcular el coeficiente de correlación de Pearson y su significación estadística, es decir, el valor-p.
4º. Calcular el número de veces que dicho valor-p es \(p < .05\), dividir dicho número entre 10000 (número total de simulaciones) y multiplicarlo por 100, para hayar el porcentaje de veces que el resultado es estadísticamente significativo, es decir, para hayar la potencia estadística.

Con la fórmula ya descrita, la potencia estadística asociada a la anterior asunción (\(r = 0.50\) y \(n = 30\)) es de \(82.50\%\). Con la simulación mediante el método de Montecarlo, se ha obtenido que en 8251 de las 10000 muestras simuladas, el resultado era estadísticamente significativo, es decir, se ha estimado una potencia estadística del \(82.51\%\), coincidiendo con el primer cálculo basado en la fórmula ya propuesta.

Hay situaciones en las que carece de sentido utilizar el método de Montecarlo para calcular la potencia estimada, como el ejemplo anterior del coeficiente de correlación de Pearson, donde ya disponemos de fórmulas que facilitan la tarea. Sin emargo, cuando se elaboran modelos estadísticos complejos, el método de Montecarlo es tremendamente útil para esta y muchas otras cosas.

4.5 Contraste de hipótesis

Nos encontramos en Escocia en 1710, tenemos una elevada ideología religiosa y acabamos de leer un poco de estadística. Se nos ocurre una idea, probar la existencia de Dios a través de análisis estadísticos. Esto es lo que pensó e intentó John Arbuthnott, un médico escocés (Arbuthnott 1710).

John analizó los nacimientos de niños y niñas de Londres durante 82 años consecutivos, desde 1629 hasta 1710. Estableció la hipótesis de que la probabilidad de que naciera un niño o una niña era la misma, un 50%, ya que en la naturaleza debía haber un equilibrio entre ambos, existiendo una mujer para cada hombre (hipótesis nula).

Observó que, durante los 82 años consecutivos, nacieron más niños que niñas, y calculó la probabilidad de dicho patrón. Asumió que la probabilidad de que en un año nacieran más niños que niñas era del 50%, y partiendo de que los eventos eran independientes, la probabilidad estimada para ese patrón era de \(0.50^{82} = 2.07*10^{-27}\). Puesto que era una probabilidad muy pequeña, rechazó su hipótesis nula de que dicho patrón pudiera explicarse por mero azar.

Arbuthnott concluyó que, dado que los hombres mueren más que las mujeres, porque tienen que salir a buscar su comida poniéndose en peligro, el Creador (Dios) hace uqe nazcan más hombres que mujeres, produciendo ese patrón de baja probabilidad por azar, para compensar dicha perdida y seguir manteniendo el equilibrio de una mujer para cada hombre.

A pesar de que el estudio de Arbuthnott no constituye una prueba a favor de la Divina Providencia como él pretendía, es curioso como el razonamiento probabilístico de contraste de hipótesis se viene utilizando desde hace varios siglos.

4.5.1 Tipos de hipótesis

Actualmente, la mayoría de investigaciones de nuestro campo se basan en el establecimiento a priori de dos hipótesis:

Hipótesis nula (\(H_0\)): Esta sería la hipótesis contraria a la que tienen los investigadores. Normalmente, postula la ausencia de diferencias entre tratamientos, la ausencia de una correlación entre dos variables… Es decir, la ausencia de un efecto. No obstante, no siempre tiene porqué ser así, pudiendo establecerse otras hipótesis nulas, como por ejemplo, una correlación inferior a 0.20, porque consideremos que valores inferiores sean despreciables para el objetivo de la investigación.
Hipótesis alternativa (\(H_1\)): Esta es la hipótesis que tienen los investigadores, que postula la presencia de una diferencia entre tratamientos, de una correlación, etc.

Cuando se establecen a priori dichas hipótesis durante la planificación de una investigación, se asume una dicotomía subyacente, es decir, todo lo que no sea hipótesis nula es la hipótesis alternativa y viceversa. Este hecho suele llevar a una malinterpretación del contraste de hipótesis al analizar los resultados de una investigación, como mostraré más adelante.

Otro concepto que conviene saber es el de hipótesis conceptual e hipótesis operativa. Estos conceptos en verdad son dos formas de presentar las hipotesis nula y alternativa de una investigación, no dos hipótesis distintas. La hipótesis conceptual sería como denominaríamos a la formulación de alguna de las hipotesis (nula o alternativa) en términos no matemáticos, mientras que si hablamos de hipótesis operativa estamos haciendo referencia a una expresión más matemática de las hipotesis alternativa o nula. Por ejemplo, imaginemos que estamos realizando un estudio donde comparamos dos tratamientos (peso muerto vs sentadillas) para ver cual reduce más la intensidad del dolor lumbar, en una escala de 0 (no dolor) a 10 (peor dolor imaginable):

Hipótesis conceptual: El peso muerto es más efectivo que las sentadillas en la reducción de la intensidad del dolor lumbar.
Hipótesis operativa: El peso muerto reduce la media de intensidad del dolor lumbar por encima de 2 puntos, en comparación a las sentadillas.

Como se ha comentado, al establecer las hipótesis alternativa y nula se asume una dicotomía subyacente, es decir, entre ambas se abarca todo el espectro de posibles resultados de la investigación. A continuación muestro tres ejemplos basados en el estudio anterior de comparación de dos ejercicios para dolor lumbar:

Ejemplo 1: \(H_0 = 0\) y \(H_1 \neq 0\).
Ejemplo 2: \(H_0 \le 2\) y \(H_1 > 2\).
Ejemplo 3: \(H_0 \le 0\) y \(H_1 > 0\).