Chapter 3 Teoría de la Probabilidad

3.1 Definición de probabilidad

Antes de comprender el concepto de probabilidad, es necesario comprender otros dos: el suceso y el espacio muestral.

Un suceso sería cualquier resultado posible de un experimento u observación, por ejemplo si tiramos un dado al aire y sale el número 5 en la cara superior, eso sería un suceso.

El espacio muestral sería el conjunto de todos los posibles sucesos de un experimento, en el caso del dado, el espacio muestral sería el siguiente: \(\Omega = \{1, 2, 3, 4, 5, 6\}\).

La probabilidad sería el grado de certidumbre de que pueda ocurrir un determinado suceso aleatorio. Es importante el concepto de suceso aleatorio, que implica que dicho suceso toma sus valores según la ley del azar. Abordaré más en profundidad las implicaciones de esta asunción en el subapartado de muestreo. La probabilidad asociada a un determinado suceso puede tomar valores del 0 al 1, y el sumatorio de las probabilidades asociadas a todos los posibles sucesos de un experimento dado es igual a 1.

La fórmula más sencilla para el cálculo de la probabilidad asociada a un suceso es la de Pascal, donde NCF es el número de casos favorables y NCP es el número de casos posibles: \[P = \frac{NCF}{NCP}\] En el ejemplo del dado, el número de casos favorables de cada suceso, si tiramos el dado una sola vez, es 1, y el número de casos posibles es el espacio muestral, es decir, 6 casos, de forma que cada suceso tiene una probabilidad asociada de 0.1667

Cuando disponemos de todos los datos para poder calcular dicha probabilidad, a esta se la denomina probabilidad exacta. Por el contrario, si no disponemos de todos los datos y estamos haciendo una estimación, hablamos de probabilidad experimental. Por ejemplo, la probabilidad de obtener el número 6 lanzando un dado al aire (no trucado) sería una probabilidad exacta, mientras que la probabilidad de desarrollar cáncer a consecuencia de fumar, sería una probabilidad experimental.

3.1.1 Ley de los grandes números

Imaginemos que no conocemos el numero de casos posibles del lanzamiento de un dado. Otra forma de estimar la probabilidad asociada a, por ejemplo, el suceso de que salga el número 3, sería tirar el dado muchas veces e ir contando cuantas veces sale dicho número, de manera que la probabilidad asociada a dicho suceso, sería la frecuencia relativa del mismo, es decir, número de veces que sale el suceso, es decir, el número de casos favorable para dicho número (NCF), entre el número total de veces que hemos tirado el dado, que sería el número de casos posibles en los que podría haber salido el número 3 (NCP). La ley de los grandes números nos dice que, cuando el número de veces que lanzamos el dado se aproxima al infinito, la frecuencia relativa de dicho suceso es igual a la probabilidad asociada al mismo: \[P(A)=lim_{n \rightarrow \infty}fr(A) \] Es importante grabarse en la memoria la frase “cuando la muestra tiende al infinito”, ya que de lo contrario, podemos terminar realizando malinterpretaciones de probabilidades tanto exactas como experimentales. Seguramente, muchas veces habrás escuchado alguna frase como la siguiente: “La probabilidad de tener dolor de hombro es del 0.40, es decir, 4 de cada 10 personas tienen dolor de hombro”. Esta frase es desacertada, y es un ejemplo de lo que Daniel Kahneman habla en su libro Pensar rápido, pensar despacio de aplicación de la ley de los grandes números a pequeños números. Una afirmación más acertada sería que aproximadamente, de 100000000 sujetos, 40000000 tienen dolor de hombro. No podemos esperar que, de 10 sujetos seleccionados al azar, 4 vayan a tener dolor de hombro porque la prevalencia estimada sea de 0.40.

3.2 Probabilidad condicionada. Teorema de Bayes

3.2.1 Teoría de conjuntos

La teoría de conjuntos es una rama de la lógica matemática que estudia las propiedades y relaciones de los conjuntos. Estas relaciones se pueden representar visualmente mediante los diagramas de Venn. Si por ejemplo, tenemos dos conjuntos A y B, y queremos representar su intersección, el diagrama de Venn correspondiente sería el siguiente:

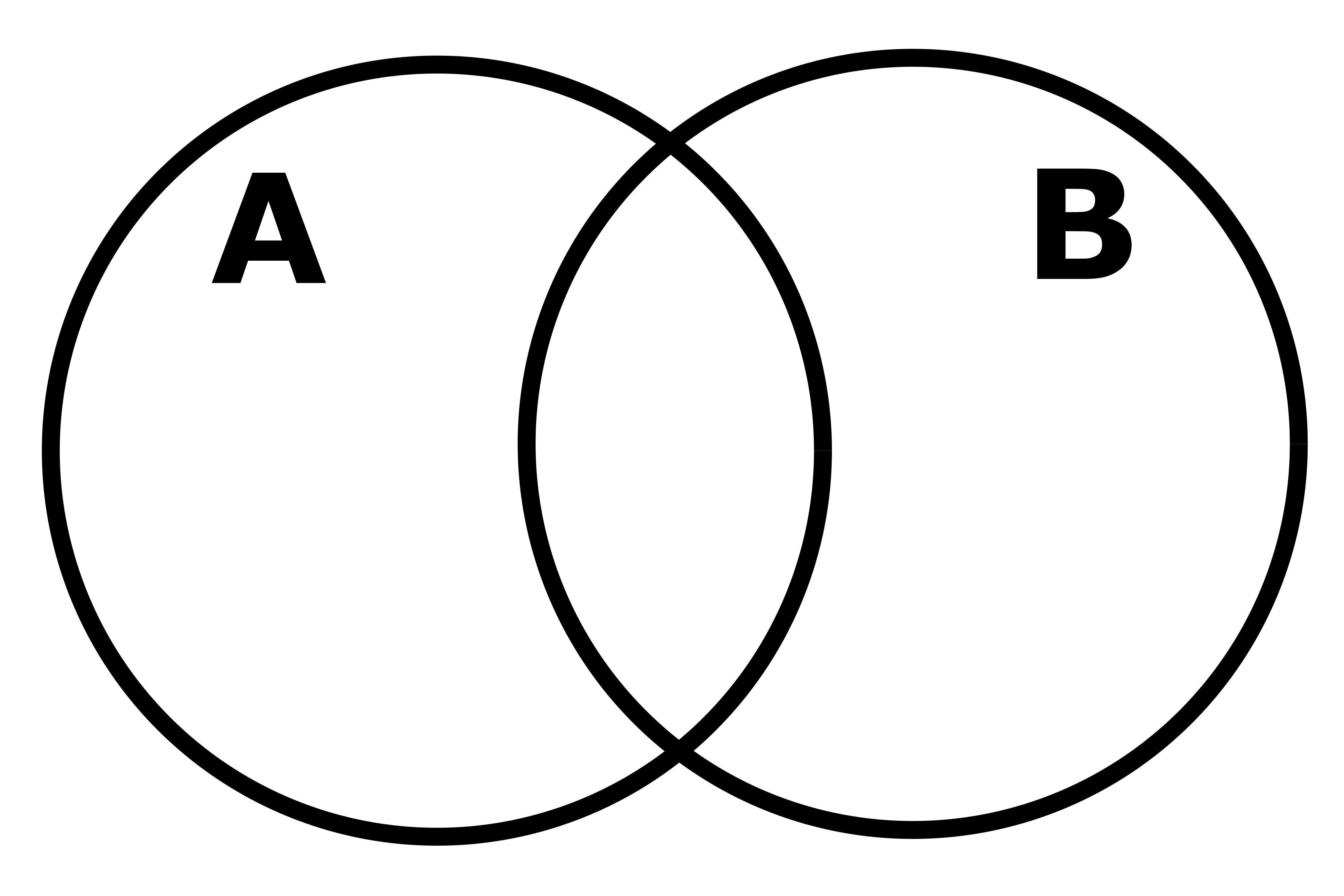
Figure 3.1: Intersección de dos conjuntos

Dentro de cada conjunto dado tenemos una seríe de elementos, que son los que conforman dicho conjunto, por ejemplo: \(A = \{a, b, c, d\}\). Cuando el número de elementos es elevado, se utiliza una notación más compleja, de modo que conviene conocer el significado de algunos símbolos:

\(\in\) : Pertenencia
\(\notin\) : No pertenencia
: Tal que
\(\cup\) : Unión.
\(\cap\) : Intersección.
\(\mathbb {Z}\) : Conjunto de números enteros.
\(\mathbb {N}\) : Conjunto de números naturales.
\(\mathbb{R}\) : Conjunto de números reales.

De esta forma, podríamos definir un conjunto C conformado por x elementos tal que, todos sus elementos X pertenezcan al conjunto de numeros naturales para x menor que 1000: \(C = \{x | x \in \mathbb{Z} \quad \textrm{para} \quad x < 1000\}\).

3.2.2 Operaciones con conjuntos

Se pueden realizar distintas operaciones con conjuntos:

Unión de dos conjuntos: \(C = A \cup B = \{x | x \in A \quad o \quad x \in B\}\)
Intersección de dos conjuntos: \(C = A \cap B = \{x | x \in A \quad y \quad x \in B\}\)
Diferencia de dos conjuntos: \(C = A-B = \{x|x \in A \quad y \quad x \notin B\}\)
Diferencia de dos conjuntos: \(C = B-A = \{x|x \in B \quad y \quad x \notin A\}\)

Hay que tener en cuenta que en las operaciones con conjuntos A-B es distinto de B-A. En la Figura 3.2 se muestran los diagramas de Venn correspondientes a dichas operaciones.

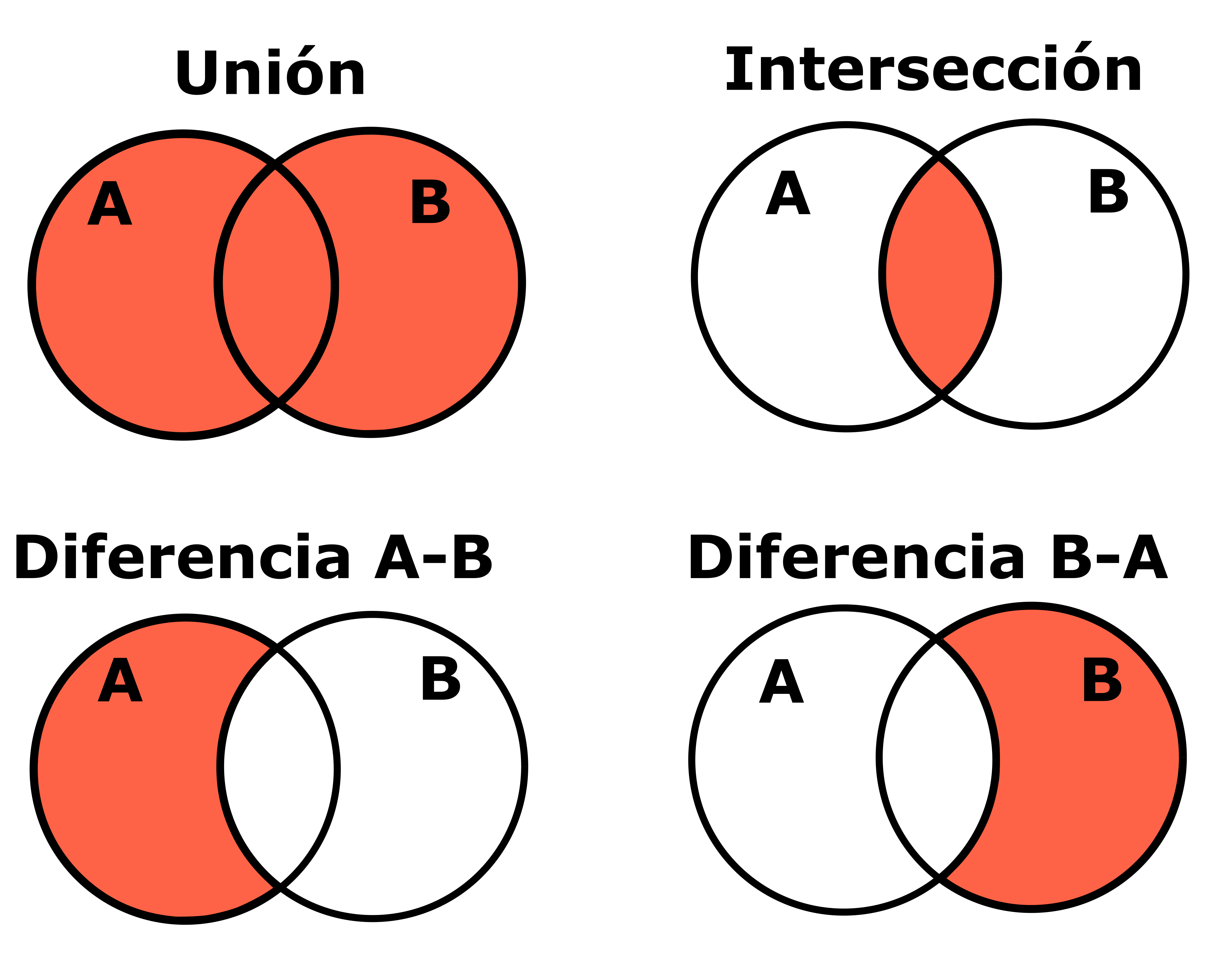
Figure 3.2: Diagramas de Venn para las operaciones con conjuntos

3.2.3 Probabilidad condicionada

Imaginemos que disponemos de una clase de 50 estudiantes de Fisioterapia, en la cual 30 son mujeres y 20 hombres, y además, sabemos que a 30 de dichos estudiantes les gusta la bioestadística y a los otros 20 no, con la siguiente distribución:

Mujeres: A 25 les gusta la bioestadística y a 5 no.
Hombres: A 5 les gusta la estadística y a 15 no.

Conociendo estos datos, nos facilitan un cuestionario anónimo de un estudiante, en el que se refleja que le gusta la bioestadística, ¿cuál sería la probabilidad de que dicho estudiante fuese una mujer? Esto es lo que se conoce como probabilidad condicionada, es decir, la probabilidad de que se de un suceso (ser mujer, B), partiendo de que se haya dado otro (gustar la bioestadística, A), es decir, \(P(B|A)\). Esta probabilidad condicionada, cuando estos dos sucesos son dependientes, es decir, hay una relación entre ellos, se calcula como: \[P(B|A) = \frac {P(A \cap B)}{P(A)}\] Si por el contrario, los sucesos son independientes, es decir, la probabilidad de que suceda uno no depende de que haya sucedido o no el otro, entonces \(P(B|A) = P(B)\). De esto se deriva que dos sucesos son independientes si y solo si: \[P(A \cap B) = P(A) * P(B), \quad ya \quad que, \quad P(B|A) = \frac {P(A \cap B)}{P(A)} = P(B)\] También debemos tener en cuenta que, si dos sucesos son independientes, entonces \(P(A \cup B) = P(A) + P(B)\).

3.2.4 Teorema de Bayes

El teorema de Bayes es una generalización de la fórmula anteriormente mencionada, que tiene en cuenta el conjunto de todos los posibles sucesos \(B_k\) que pueden darse una vez ha sucedido A, para calcular la probabilidad condicionada de un suceso \(B_i\): \[P(B_i|A) = \frac{P(A|B_i)*P(B_i)}{\sum_{k=1}^{n}P(A|B_k)*P(B_k)}\] Por ejemplo, si partimos del diagrama de Venn de la Figura 3.3, podemos apreciar que, una vez ha sucedido W, solo hay tres opciones posibles, es decir \(W = \{A, B, C\}\).

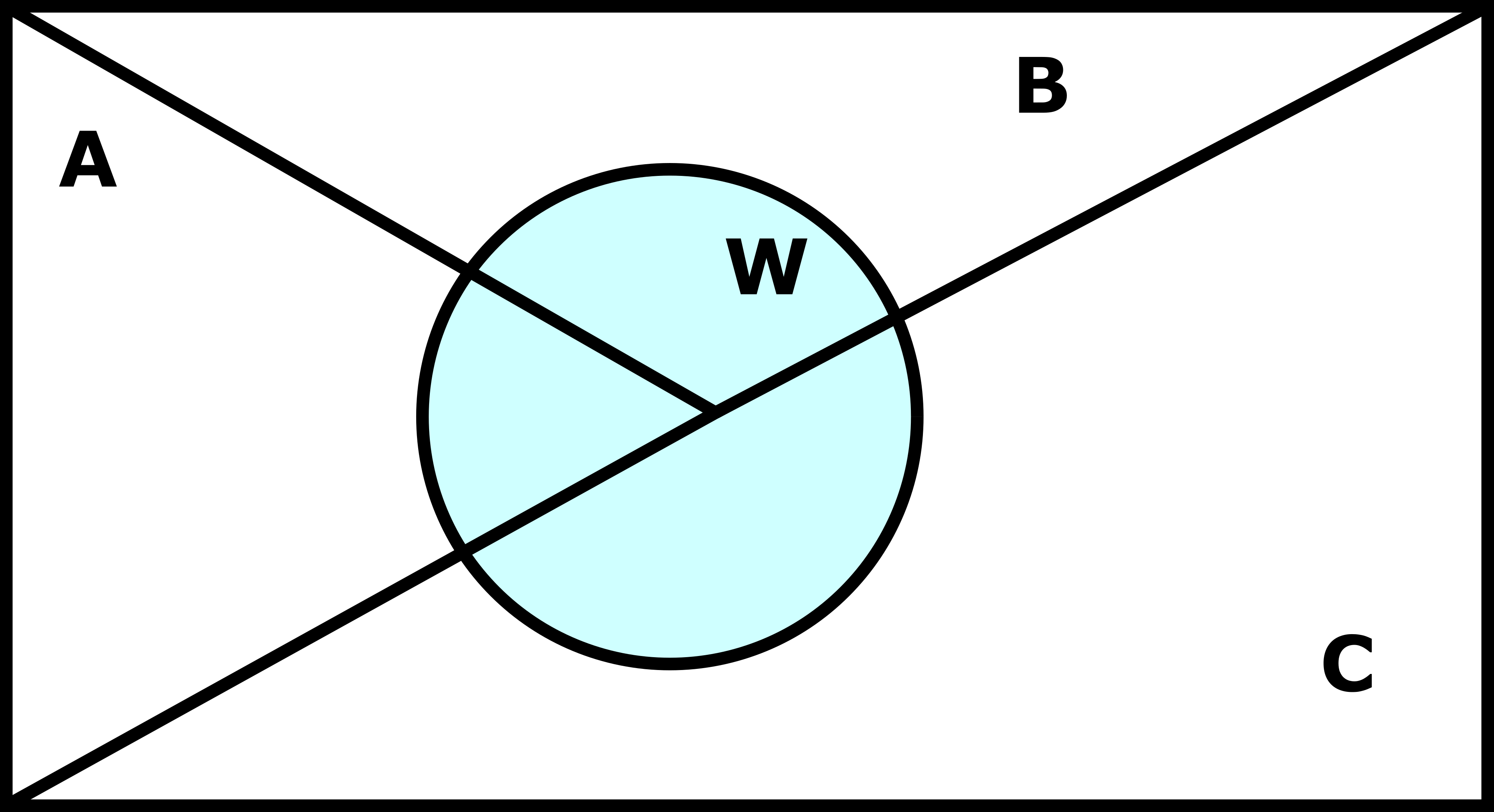
Figure 3.3: Diagramas de Venn para las operaciones con conjuntos

Aplicando el teorema de Bayes, la probabilidad condicionada de A dado W, \(P(A|W)\), quedaría definida como: \[P(A|W) = \frac{P(W|A)*P(A)}{P(W|A)*P(A) + P(W|B)*P(B) + P(W|C)*P(C)}\] Es importante conocer estos conceptos, ya que lo contrario puede llevar a una malinterpretación de los famosos p-valores e intervalos de confianza de la estadística inferencial, como explicaré más adelante.

3.3 Cometiendo errores

Volvamos a nuestra clase de estudiantes de Fisioterapia. Si tuvieramos que estimar que estatura tendría un estudiante escogido de forma aleatoria de dicha clase, la mejor estimación que podríamos hacer es utilizar la media muestral (partiendo de una serie de asunciones). La media muestral de estatura de la clase sería, \(\bar x = 170.50\). Cada vez que seleccionasemos un sujeto de dicha clase, de manera aleatoria, estaríamos cometiendo un error, que sería la diferencia entre la media y el valor obtenido en dicho sujeto, \(E_i = x_i - \bar x\). Imaginemos que realizamos este proceso muchas veces, cada una de ellas seleccionando aleatoriamente un sujeto y calculando su diferencia de estatura con respecto a la media. Si sumamos todos esos errores, el valor obtenido es cero, es decir, los errores se distribuyen aleatoriamente por encima y por debajo de la media. Esto es lo que se conoce como error aleatorio. Estas líneas pueden parecer familiares, y es que, una estimación del error aleatorio asociado a la predicción del valor de un sujeto, en función de la media muestral, es la desviación estandar.

Partamos ahora del supuesto de que, en lugar de tener acceso a la lista de 10 sujetos, tuvieramos solo acceso a un listado con los sujetos 3, 4, 5, 6 y 7. Si ahora realizamos el mismo procedimiento, obtendríamos los siguientes errores:

\(E_3 = 178 - 170.50 = 7.50\)
\(E_4 = 170 - 170.50 = -0.50\)
\(E_5 = 171 - 170.50 = 0.50\)
\(E_6 = 179 - 170.50 = 8.50\)
\(E_7 = 172 - 170.50 = 1.50\)

En este caso, si sumamos los errores cometidos al estimar el valor de esos 5 sujetos, ya no obtenemos un valor de cero, la suma de dichos errores es 17.50. Esto es un ejemplo de un error sistemático, que es aquel que no se cometé a consecuencia del azar, y por tanto no se distribuye por igual por encima y debajo del valor estimado, la media. El error sistemático tiene una dirección prefernte, positivo o negativo. En este caso, el error sistemático se habría producido por esa primera selección prevía de los 5 sujetos.

Es muy importante evitar introducir errores sistemáticos durante el diseño de una investigación, ya que por ejemplo, cuando estámos comparando la efectividad de dos tratamientos, el error sistemático no se pueden separar del posible efecto de la intervención en la mayoría de casos. De forma simple, lo que se hace al comparar esa efectividad, como ya veremos más adelante, es enfrentar la diferencia de medias, con el error aleatorio, y en esa diferencia de medias, iría incluido el error sistemático que metamos por fallos en el diseño (ej. ausencia de enmascaramiento de los evaluadores).

3.4 Distribuciones y funciones de probabilidad

3.4.1 Dispersión de parámetros muestrales

Al igual que cuando tenemos una muestra, se han nombrado estadísticos descriptivos de dispersión de los datos, como la desviación esandar y la varianza, también podemos calcular estadísticos descriptivos de dispersión de distintos parámetros muestrales, como la media. A estos descriptivos, se los denomina errores estándar, y serían un análogo de la desviación estandar, pero para el parámetro muestral, es decir, estos errores estándar están en las mismas unidades que el parámetro muestral para el cual se calculan. Las fórmulas para el cálculo de los errores estándar de distintos estadísticos son tediosas, y carece de sentido por un lado, explicarlas, y por otro, memorizarlas. Utilizaré la media muestral como ejemplo para explicar este concepto, que se aplica por igual a cualquier otro estadístico como un coeficiente de correlación de Pearson.

Imaginemos que tenemos acceso al listado de todos los estudiantes de Fisioterapia de España, un total de 5000. Seleccionamos aleatoriamente a 50 de ellos, y les medimos la estatura, obteniendo una media, \(\bar x_1 = 168.50\). Ahora, sin eliminar a esos sujetos que ya hemos medido previamente, volvemos a repetir el procedimiento, seleccionamos de nuevo de forma aleatoria otros 50 sujetos de los 5000 posibles, y calculamos de nuevo la media, \(\bar x_2 = 173.50\). Debido a errores aleatorios de ese procedimiento de muestreo, las medias de las distintas muestras seleccionadas difieren unas de las otras. Si pudiesemos realizar este procedimiento con todas las combinaciones posibles de sujetos de esos 5000, cogidos de 50 en 50, y calculásemos la desviación estandar de dichas medias, obtendríamos una estimación de su dispersión, esto sería el errror estándar de la media (EE). Sin embargo, en la práctica esto no es viable, y lo que se hace es calcular una estimación del EE en función del valor de la desviación estandar poblacional estimada, y el tamaño de la muestra:

\[EE = \frac{\sigma}{\sqrt n}\] El error estándar asociado a un determinado estadístico nos informa por tanto sobre el error aleatorio asociado a su estimación poblacional. Estos errores estándar se utilizan para el cálculo de los valores-p y de los intervalos de confianza.

3.4.2 Distribución de probabilidad

Las monedas han sido utilizadas desde hace décadas como procedimiento aleatorio de toma de decisiones en el día a día, de modo que comenzaré este apartado con un ejemplo basado en ello. Asumimos que tenemos una moneda equilibrada, sin trucar, y donde obviaremos la posibilidad de que caiga de canto, dada la baja probabilidad estimada de este suceso (Murray, 1993), de forma que la probabilidad de que salga cara o cruz es la misma, 0.50. Si lanzamos la moneda al aire 5 veces, anotamos el número de veces que sale cara, y repetimos este procedimiento 10 veces, podríamos obtener unos resultados como los siguientes:

\[ C = \{3, 3, 2, 3, 1, 3, 2, 2, 4, 2\}\] Podemos calcular las frecuencias absolutas y relativas observadas de cada suceso, que serían:

Table 3.1: Frecuencias del experimento de lanzamiento de una moneda (5 veces) repetido 10 veces
Suceso	Frecuencia absoluta	Frecuencia relativa
0	0	0.0
1	1	0.1
2	4	0.4
3	3	0.3
4	1	0.1
5	0	0.0

Sin embargo, nuestro experimento tiene poca muestra, lo hemos repetido tan solo 10 veces, de modo que la estimación de esas frecuencias relativas puede que no sea del todo precisa. Si repitieramos el experimento un número infinito de veces, por la ley de los grandes números, obtendríamos esa estimación precisa de la frecuencia relativa asociada a cada posible suceso, resultando los siguientes valores:

Table 3.2: Frecuencias relativas del experimento de lanzamiento de una moneda (5 veces) repetido infinitas veces
Suceso	Frecuencia relativa
0	0.03125
1	0.15625
2	0.31250
3	0.31250
4	0.15625
5	0.03125

Estos datos pueden representarse gráficamente, mediante lo que se denomina un histograma, un tipo de gráfico indicado en el caso de variables discretas, en el cual se muestran los posibles sucesos en el eje x y las frecuencias (abdolutas o relativas) asociadas a los mismos en el eje y. El histograma de nuestro experimento, repetido infinitas veces, sería el siguiente:

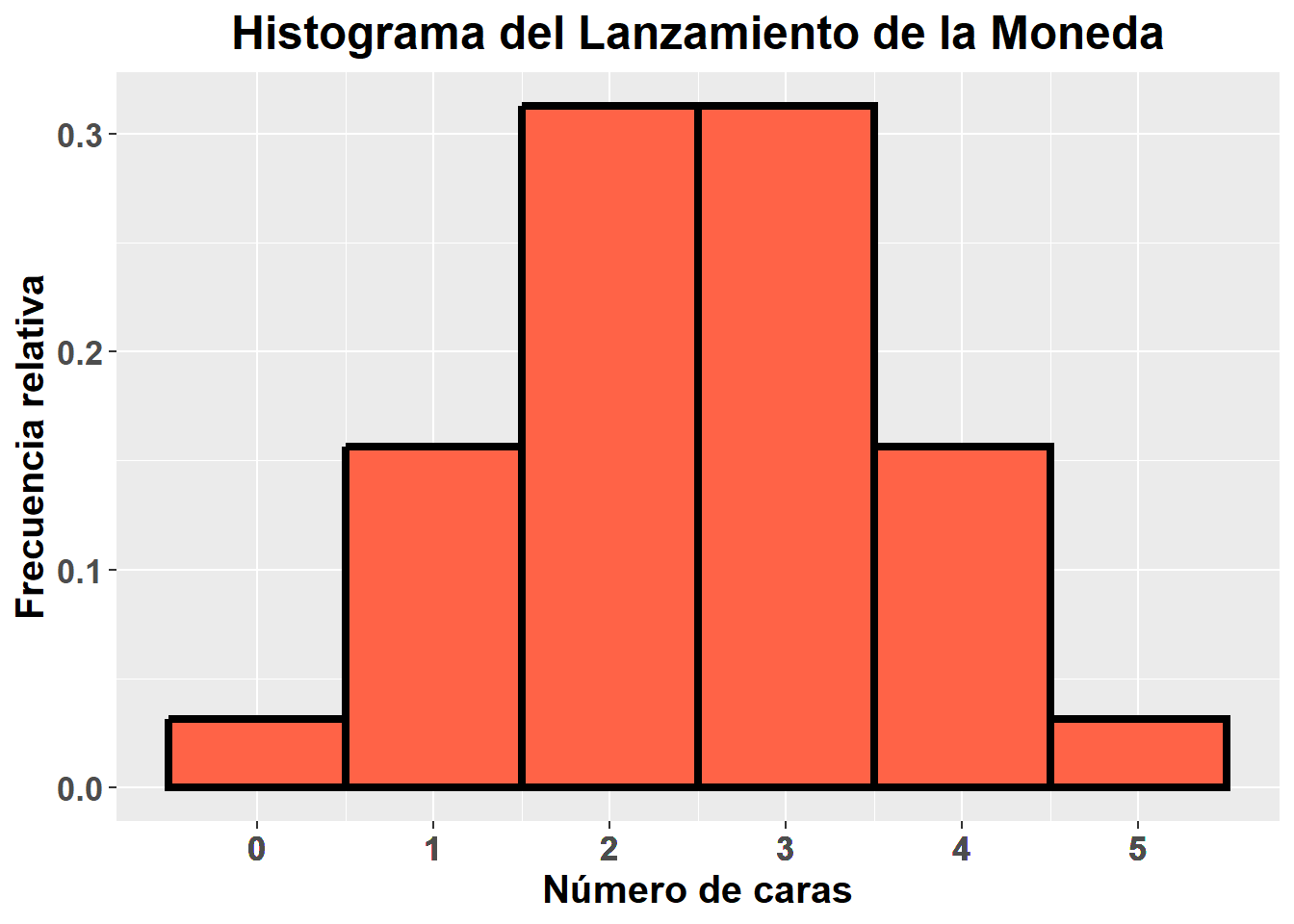Este gráfico resultante es lo que se denomina distribución de probabilidad, debido a que nos indica como se distribuye la probabilidad asociada a cada posible suceso. Existen distintos tipos de distribuciones de probabilidad, este caso concreto estamos ante una distribución de probabilidad binomial. Parece muy tedioso tener que realizar infinitas replicas de nuestro experimento, para poder estimar las probabilidades asociadas a cada posible suceso. Sin embargo, esto no es necesario, gracias a que actualmente ya disponemos de las llamadas funciones de distribución de probabilidad. Estas funciones sirven para calcular la probabilidad de que ocurra un suceso dado, asumiendo una distribución de probabilidad dada. Por ejemplo, la función de distribución de probabilidad binomial sería: \[ P(x = k) = \binom nk p^k(1-p)^{n-k} \] En esta fórmula, se estaría calculando la probabilidad de que el número de “caras”, \(x\) fuese igual a \(k\), es decir \(P(x = k)\), donde:

\(\binom nk\) = Número de combinaciones sin repetición de \(k\) elementos elegidos entre \(n\) elementos posibles. En nuestro ejemplo anterior, \(k\) sería igual a un suceso cualquiera, por ejemplo 3 caras, y \(n\) sería igual al número de veces que se lanzaba el dado, es decir, \(n = 5\) (ver el ¡Curidato! si se quiere ampliar conocimiento en combinaciones y entender la matemática subyacente a la función de distribución binomial).
\(p\) = Probabilidad de que salga el evento que deseamos, en nuestro caso “cara”, que sería 0.50.
\(1-p\) = También se le suele denominar \(q\), y sería la probabilidad de que ocurra el otro evento posible. \(p\) y \(q\) no siempre van a ser iguales, por ejemplo, si tuviesemos una moneda trucada, podríamos tener una probabilidad de que salga cara de 0.30 y una de que salga cruz de 0.70.

Cabe destacar otro concepto, el de valor esperado, \(E(x)\). El valor esperado se define como el número de veces que es más probable que ocurra un evento \(x\), y se calcula multiplicando la probabilidad de dicho evento por el número de veces que repetimos el experimento dado. Por ejemplo, lanzando 5 veces una moneda al aire, el valor esperado de caras sería:

\[ E(C) = 0.5*5 = 2.5 \] Como puede resultar obvio, el número 2.5 no tiene un sentido real, es decir, no podemos obtener “2 caras y media”, esto lo que nos indica es que, como el número de veces que hemos lanzado es impar, existe la misma probabilidad de que salgan 2 caras que de que salgan 3 caras. Es decir, el valor esperado nos habla de que suceso es más probable que ocurra. En otras palabras, si no tenemos más datos y tenemos que apostar 100€ a que sale un número de veces cara lanzando una moneda al aire, lo más sensato es apostar a que saldrá 2 o 3 veces si la lanzamos 5, es decir, apostar a su valor esperado. El valor esperado sería un análogo de la media.

¡Curidato!

Cuando lanzamos una moneda al aire 5 veces, podemos obtener, por ejemplo, la siguiente secuencia de eventos: \(\{C, C, X, C, X\}\), siendo C = cara y X = cruz. Podemos adjudicar una letra a cada una de las 5 veces que lanzamos el dado, \(\{A, B, C, D, E\}\), de manera que en el suceso anteriormente mencionado, habría salido cara en A, B, y D. Si asumimos que tienen que salir dos veces cara, podemos calcular todas las combinaciones posibles de esas 5 letras, tomadas de dos en dos, sin repetir letras y sin importar el orden, es decir siendo AB igual que BA. Estas serían todas las posibles situaciones en que podríamos obtener 2 caras lanzando la moneda al aire 5 veces: \[ \begin{matrix}AB & AC & AD & AE\\ & BC & BD & BE \\ & & CD & CE\end{matrix} \] Resultan un total de 10 posibles combinaciones. Hacer esto a mano, cuando se incrementa el número de posibles letras, es decir, el número de veces que lanzamos la moneda al aire, es un trabajo aurduo. Existe una fórmula para calcular ese número de combinaciones: \[ C_{n,k} = \binom nk = \frac{n!}{k!(n-k)!} \] En esta fórmula, el símbolo “!” hace referencia a las permutaciones sin repetición, que es el número posible de formas en que podemos ordenar un conjunto dado de elementos, donde el orden si importa, es decir, AB es distinto de BA, de modo que si solo tenemos dos letras, solo hay 2 permutaciones posibles. La forma en que se calculan las permutaciones sin repetición es: \[ P_n = n*(n-1)*(n-2)*...*(n-n+1) \\[-8pt] P_2 = 2*1 = 2 \\[-8pt] P_5 = 5*4*3*2*1 = 120 \]

Lanzar una moneda al aire es un suceso independiente, es decir, que salga cara la primera vez no influye en la probabilidad de que salga cara la segunda, de forma que la probabilidad si tiramos una moneda al aire dos veces, de que salga dos veces cara (C), sería \(P(C)*P(C) = 0.50*0.50 = 0.25\). Por tanto, la probabilidad de obtener una secuencia concreta donde salen dos veces cara de 5 lanzamientos sería: \[ P(\{C, X, X, C, X\}) = P(C)*P(X)*P(X)*P(C)*P(X) = \\[-8pt] =P(C)^2*P(X)^3=0.5^2*0.5^3 = 0.03125 \]

Esta es una de las posibles secuencias que podemos obtener en las que al lanzar una moneda al aire, sale dos veces cara. Arriba mostré que en total existen 10 posibles secuencias. Como comenté anteriormente, la probabilidad de que ocurra uno u otro suceso, siendo estos independientes, es igual al sumatorio de sus probabilidades, es decir \(P(A \cup B) = P(A) + P(B)\). Todas las posibles secuencias en las que se obtiene dos caras lanzando 5 veces la moneda tienen la misma probabilidad asociada, de forma que, si queremos calcular la probabilidad de obtener 2 veces cara, sin importar en que lanzamientos las obtenemos, lo único que tenemos que hacer es sumar esa probabilidad 10 veces, o lo que es lo mismo, multiplicar dicha probabiliadd por 10, el número de combinaciones posibles, \(P(C = 2) = 10*0.03125 = 0.3125\). Todo esto que acabo de describir, es el razonamiento que subyace a la fórmula de la distribución de probabilidad binomial mostrada anteriormente, de modo que ya puedes entender porqué se calculan así dichas probabilidades.

- El Príncipe Mestizo

Existen más distribuciones de probabilidad con sus respectivas funciones, cuyo razonamiento matemático subyacente no es de tan fácil visualización como con la distribución binomial. No me explayaré mucho en la explicación de todas las distribuciones, ni mostraré sus funciones salvo para una concreta, la famosa distribución normal.

Retomemos a los estudiantes de Fisioterapia, en este caso, de toda españa. Imaginemos que el la media de peso es de \(\bar x = 68kg\), con una desviación estándar de \(\sigma = 10kg\). Seleccionamos aleatoriamente 10 estudiantes, obteniendo los siguientes valores:

\[c = \{79.25, 76.31, 58.29, 67.26, 67.04, 72.62, 64.45, 63.66, 72.00, 76.55\}\] Como se puede apreciar, la mayoría de valores de peso están próximos a la media y el número de sujetos con valores alejados de la media es menor. Si en lugar de 10 sujetos, seleccionamos 100, esto sería más visual. Siguiendo el mismo razonamiento llevado hasta ahora, podemos elaborar un gráfico que nos muestre la distribución de probabilidad para 100 sujetos dados, salvo que en este caso, al tratarse de una variable continua, no se reflejaría un histograma, si no un gráfico de densidad con una línea: 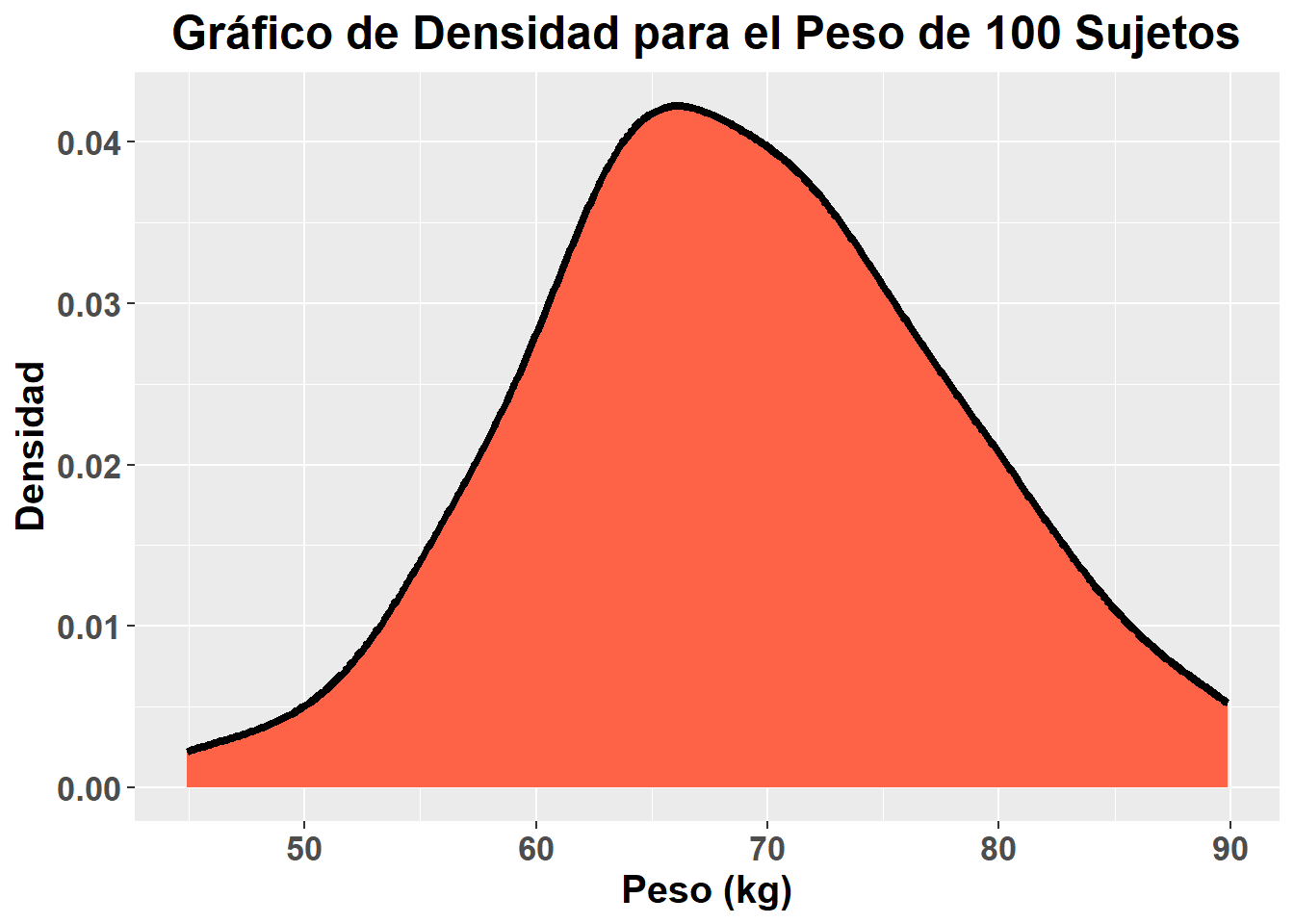Si en lugar de disponer de 100 sujetos, tuvieramos acceso a un número infinito de sujetos, el gráfico de densidad resultante sería el siguiente: 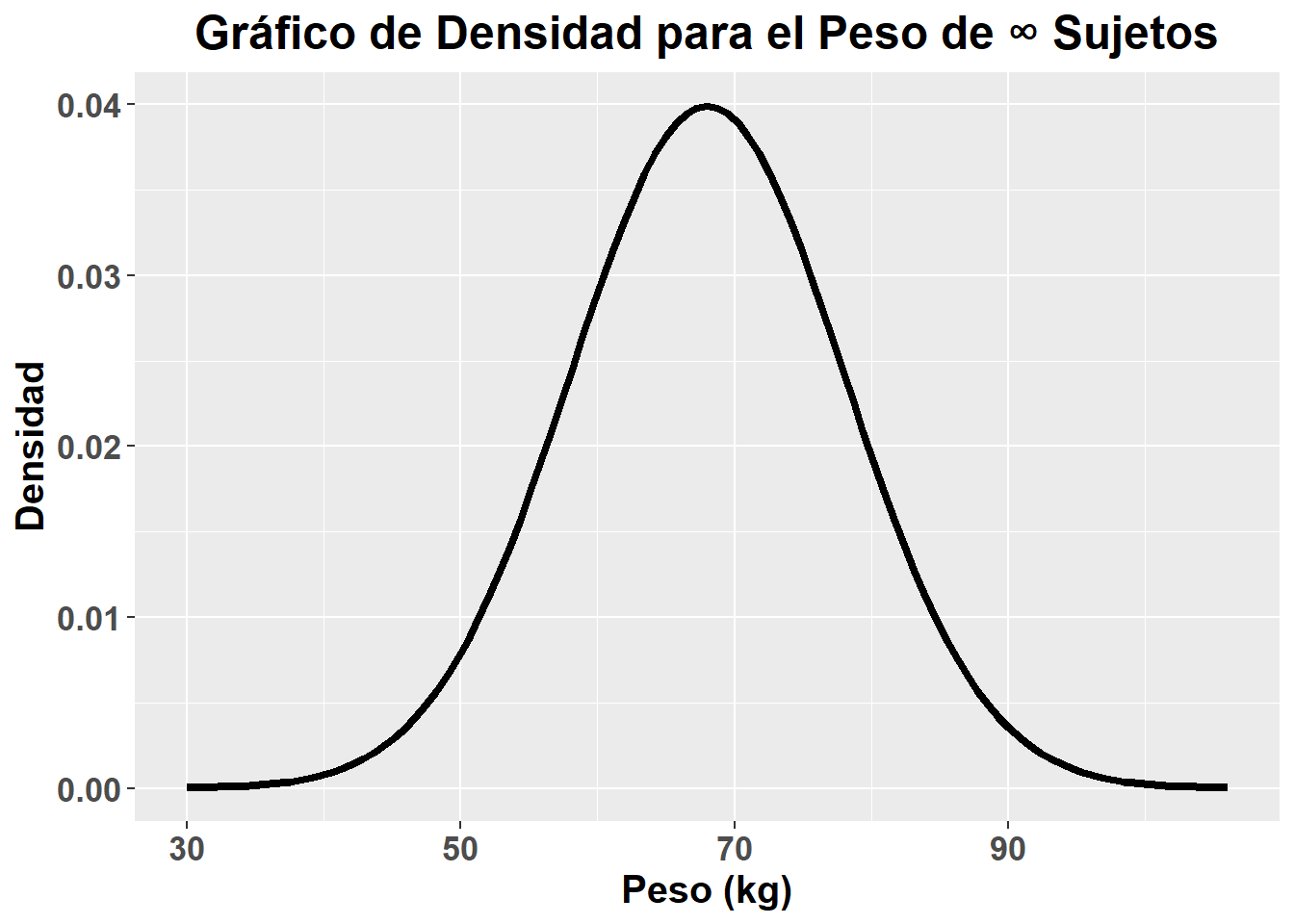Esta distribución mostrada en el gráfico anterior, es una representación de la que sería la distribución de probabilidad normal. UN aspecto que me gustaría aclarar es que esto son datos simulados, en los cuales yo he pre-especificado que distribución de probabilidad quería, es decir, no toda variable cuantitativa continua tiene que presentar una distribución de probabilidad normal. La función de probabilidad de dicha distribución, que nos permite calcular la probabilidad de obtener un determinado valor de peso, seleccionando un sujeto al azar, es la siguiente: \[ f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x - \mu}{\sigma}\right)^2} \] La distribución de probabilidad normal presenta una serie de características, pero para entender mejor alguna de ellas, es necesario conocer antes unos estadísticos descriptivos que faltaban por nombrar, las medidas de forma.

Las medidas de forma sirven para describir, como su propio nombre indica, la forma de la distribución de probabilidad de nuestros datos:

Asimetría: También se la denomina sesgo. Sirve para ver si una de las dos colas de la curva, es decir, los extremos, es más alargada que la otra. Un coeficiente de asimetría igual a cero nos indicaría ausencia de asimetría, un valor < 0 nos indicaría una curva sesgada hacia la izquierda, y uno > 0 una curva sesgada hacia la derecha.
Curtosis: Nos habla del grado de aplanamiento de la curva, tomando como referencia la distribución normal. Un coeficiente de curtosis igual a 0 indica semejanza a la normal, llamándose a esta curva mesocúrtica; un coeficiente < 0 indica una curva más aplanada, llamada platicúrtica; y un coeficiente < 0 indica una curva más puntiaguda, llamada leptocúrtica.

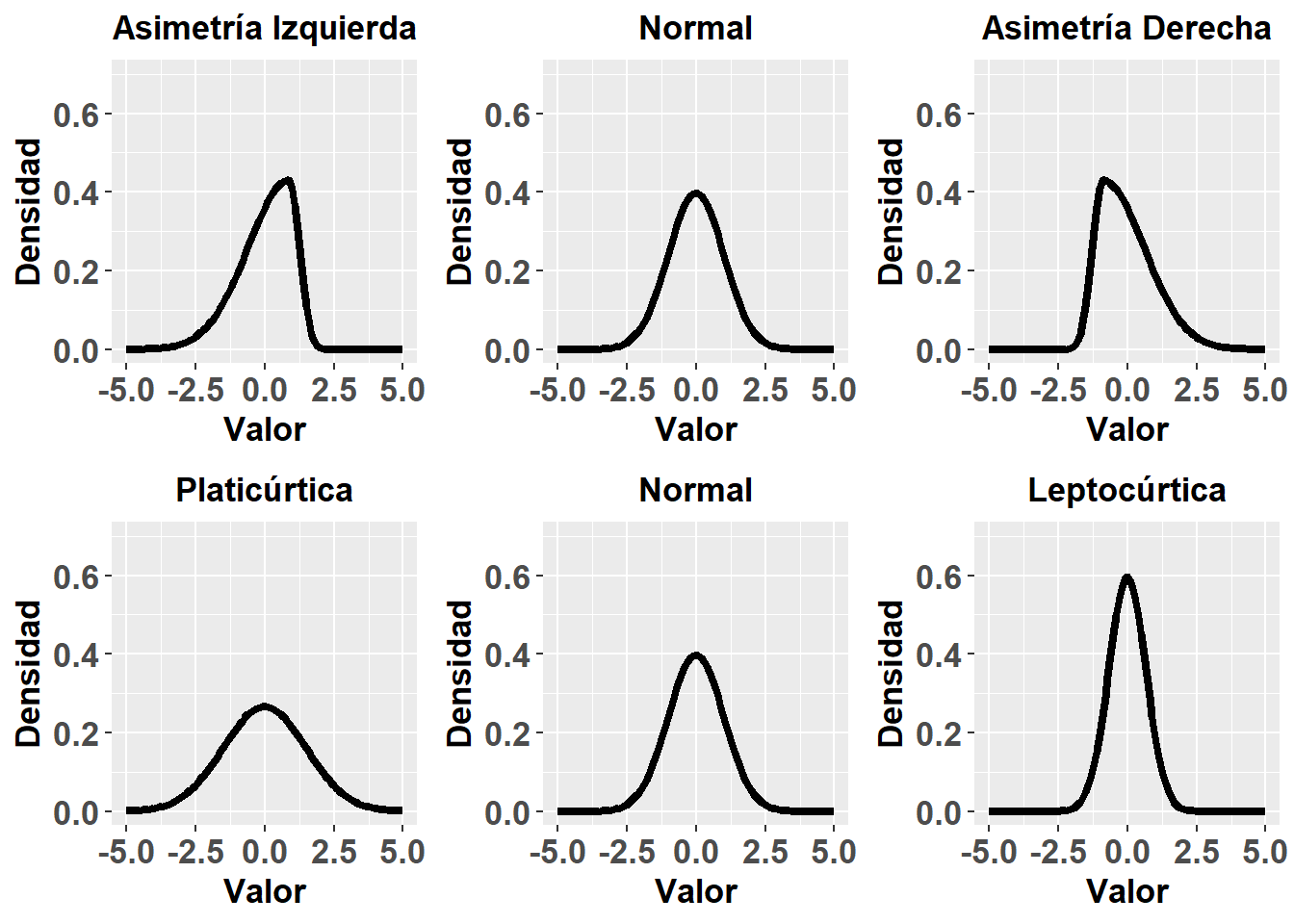Como podemos apreciar en la función de distribución normal, la probabilidad asociada a un determinado valor depende de la media (\(\bar x\)) y desviación estándar (\(\sigma\)) de la población. Antiguamente no se disponía de los ordenadores que tenemos ahora y calcular a mano la probabilidad de nuevo cada vez que cambiaba la media y/o desviación estándar era tedioso. Es por ello que se decidió simplificar la fórmula, mediante lo que se conoce como tipificación, a través del estadístico \(z\)=

\[ z = \frac{x - \mu}{\sigma} \\[-8pt] f(z) = \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}z^2} \]

El proceso de tipificación consiste en mostrar cada valor observado en función del número de desviaciones estándar que se aleja de la media. De esta forma, los cálculos se volvían más sencillos y se podían crear tablas en las que se mostrarán las probabilidades asociadas a determinados valores \(z\), de forma que se pudiera saber la probabilidad asociada a un determinado valor de cualquier población fuese cual fuese su media y desviación estándar. A pesar de que actualmente con el uso de ordenadores, no sería necesaria esa transformación, es importante conocer el concepto de tipificación y del estadístico \(z\), pues el resto de análisis de estadística inferencial que se verán, se realizan calculando probabilidades asociadas a estadísticos similares a \(z\). La distribución normal tipificada tendría por tanto, \(\bar x = 0\) y \(\sigma = 1\), es decir, la media se aleja 0 desviaciones estándar de si misma, y la desviación estándar se aleja 1 desviación estándar de la media.

La curva normal tiene una serie de propiedades que es necesario conocer:

Es simétrica y centrada en la media. Además, la media, la mediana y la moda coinciden. Al ser simétrica, en ambos lados de la media se encuentran el 50% de los valores.
La función tiene una asíntota horizontal, es decir, se aproximará al eje de abscisas (eje x), pero nunca lo tocará. En otras palabras, como se trata de una variable contínua que puede tomar infinitos valores, todos esos valores tienen una probabilidad asociada, aunque esta es despreciable cuando nos alejamos más de \(3\sigma\) de la media.
En función de la desviación estándar podemos decir que:
- \(P(\mu - \sigma < x < \mu + \sigma) = 0.68\). Es decir que entre la media \(\pm\) una desviación estándar se encuentran el 68% de los valores.
- \(P(\mu - 1.645\sigma < x < \mu + 1.645\sigma) = 0.90\).
- \(P(\mu - 1.966\sigma < x < \mu + 1.966\sigma) = 0.95\).
- \(P(\mu - 2.5756\sigma < x < \mu + 2.5756\sigma) = 0.99\).

3.4.3 Otras distribuciones de probabilidad

Existen otras posibles distribuciones de probabilidad, cuyas fórmulas es totalmente innecesario conocer. No obstante, si es necesario conocer el sentido de las mismas, ya que apareceran términos haciendo alusión a ellas en capítulos posteriores.

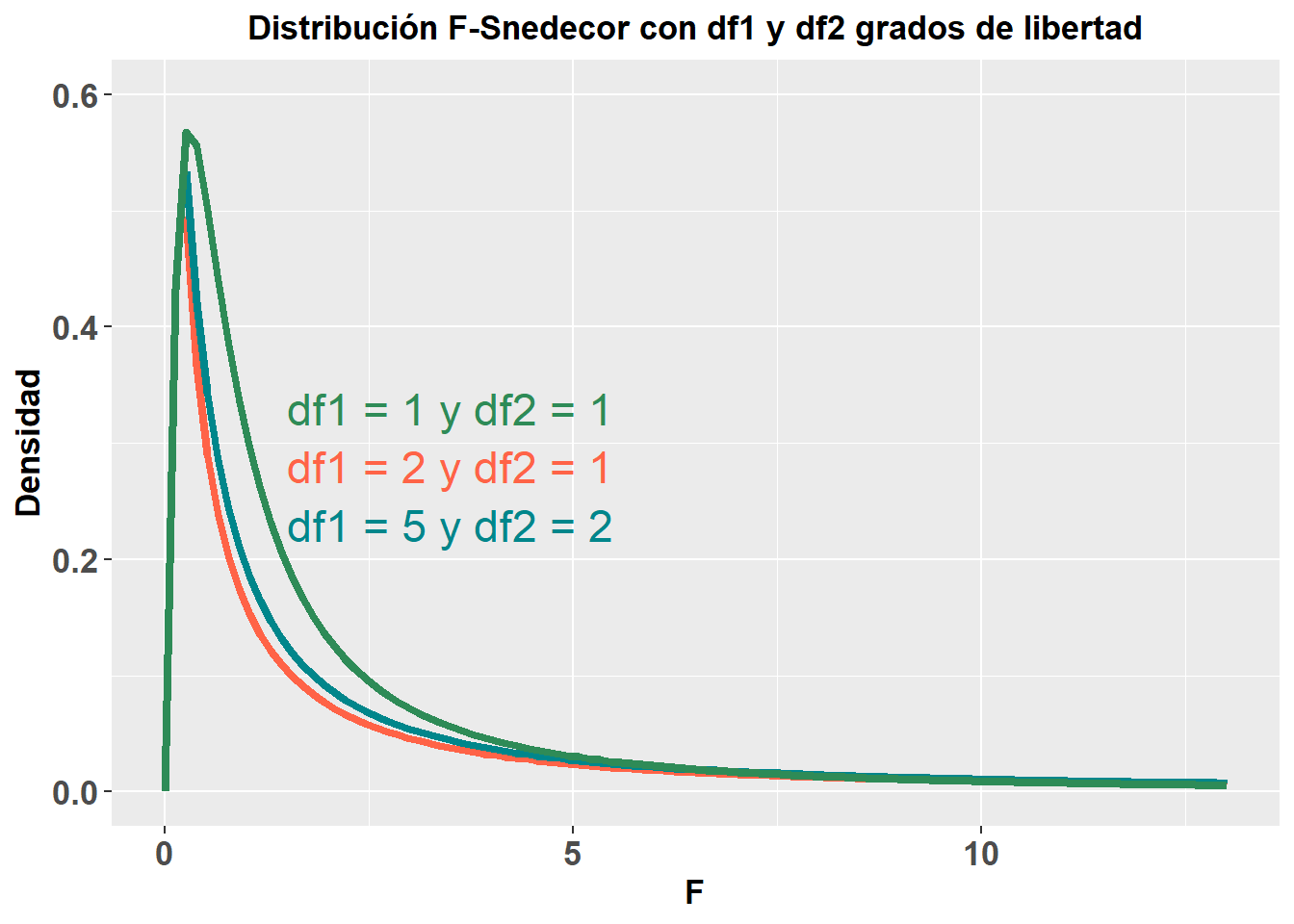
Al igual que cuando he mostrado el valor tipificado \(z\), tenemos otros estadísticos de interpretación similar que se usan para algunos análisis estadísticos. De forma simple, como iremos viendo más adelante en cada análisis, los estadísticos se utilizan para calcular la significación estadística, el famoso valor-p, que veremos en el apartado siguiente. Estos estadísticos siguen distintas distribuciones de probabilidad, pero mostraré solo dos de ellas, ya que son las que más nombraré en los capítulos posteriores de este libro y bastan para entender el concepto de que cada estadístico sigue una determinada distribución, que es en la que nos basamos para estimar ese valor-p. A continuación muestro la distribución chi-cuadrado (\(\chi^2\)) y la distribución F de Snedecor (\(F\)). Estas distribuciones, como puede apreciarse, varían en función de los grados de libertad, aunque no entraré a explicar este punto, ya que no tiene mayor importancia para el objetivo de este libro.

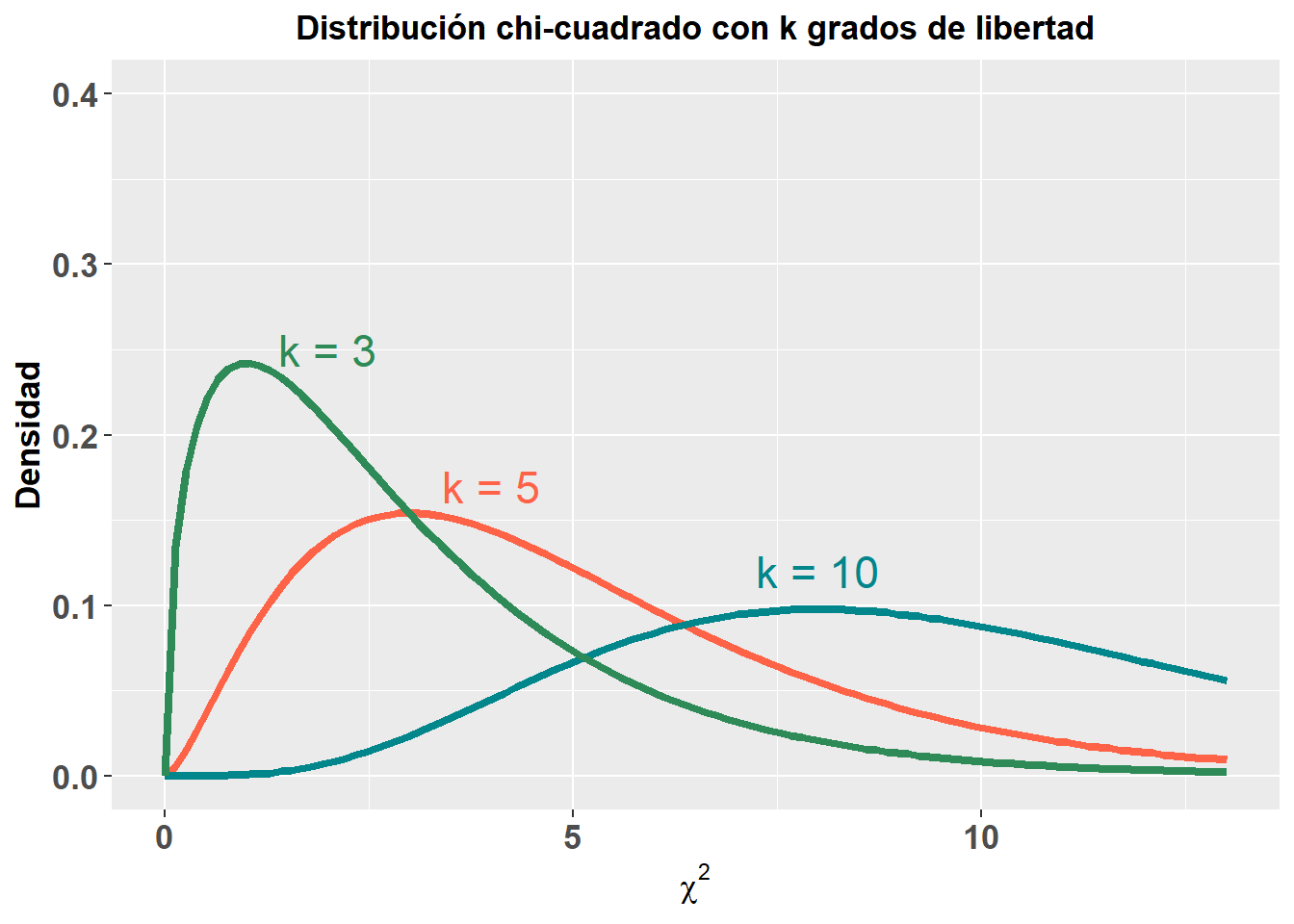
3.5 Definiendo la significación y los intervalos de confianza

Hemos llegado a un momento álgido del libro, quizás uno de los más importantes, pues un mal entendimiento de estos dos conceptos, puede llevar a interpretaciones totalmente alejadas de la realidad de cualquier análisis estadístico y por ende, de cualquier resultado de una investigación científica.

3.5.1 Significación estadística

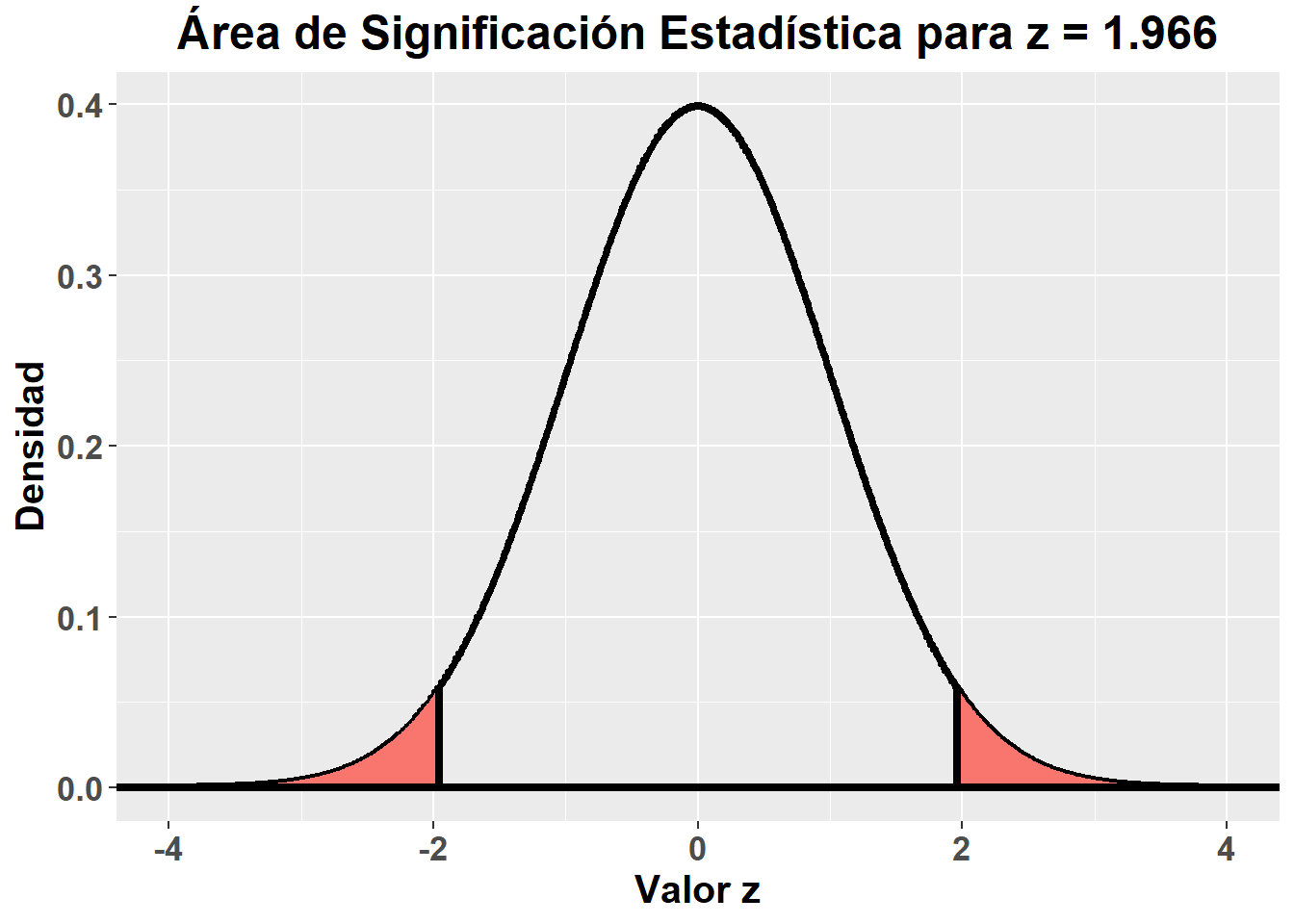
Antes se ha comentado que, por ejemplo, entre la media \(\pm\) 1.966 desviaciones estándar se encontraban el 95% de los valores. Para calcular esa probabilidad acumulada se utilizan las integrales de la función de probabilidad. Por si no se recuerda, con una integral podemos calcular el área bajo una curva. Por ejemplo, para los valores anteriormente mencionados en una curva normal tipificada: \[ P(-1.966 \le z \le 1.966) = \int\limits_{-1.966}^{1.966}f(z)dz = 0.95 \] La significación estadística, más conocida como valor-p, es una probabilidad acumulada, concretamente la probabilidad de obtener un valor igual o más extremo que el valor observado por azar. Normalmente, por ejemplo al comparar dos tratamientos, se parte a priori de que no sabemos que tratamiento será mejor que el otro a la hora de analizar los datos, esto es lo que se denomina, un contraste a dos colas, donde el valor-p asociado a una observación, es el área bajo la curva delimitada por \(\pm\) ese valor observado, como se refleja en el siguiente gráfico de una curva normal tipificada:

Una definición más precisa de la significación estadística (valor-p), según la declaración de la Asociación Americana de Estadística de 2016 (Wasserstein 2016), es la probabilidad, bajo un modelo estadístico especificado, de que un resumen estadístico de los datos (ej. la diferencia de medias muestrales entre dos grupos) fuese igual o más extremo que su valor observado.

Varios puntos de la definición de la significación estadística merecen ser destacados:

Probabilidad acumulada: Este es un punto importante, ya que el valor-p no es la probabilidad de haber obtenido ese valor observado concreto, una mal interpretación que se realiza a menudo.
Modelo estadístico especificado: Cuando se calcula un valor-p, partimos de una serie de asunciones, por ejemplo, en el gráfico anteriormente mostrado, hemos partido de la asunción de que la distribución de probabilidad que seguían los datos era la distribución normal. Otras asunciones que se hacen son con respecto a la tendencia central y la dispersión del estadístico para el que estamos calculando el valor-p. Por ejemplo, el valor-p asociado a un valor de peso de 65.898, asumiendo una distribución normal y \(\bar x = 60\) y \(\sigma = 3\), es de 0.05 (\(z = 1.966\)); mientras que el valor-p asociado a ese mismo valor de peso, asumiendo \(\bar x = 62.618\) y \(\sigma = 2\), es de 0.10 (\(z = 1.64\)). En un estudio de investigación, cuando se reportan valores-p, este modelo especificado normalmente postula la ausencia de efecto, por ejemplo, si comparasemos dos grupos, asumiríamos para calcular el valor-p asociado a una diferencia de medias entre ellos, que la diferencia de medias real es \(\bar x = 0\). Es decir, se asume que la hipótesis nula es cierta, para calcular el valor-p.
Azar: Cualquier valor-p se calcula asumiendo que el azar es el que ha producido la asociación observada, tanto si partimos de la hipótesis nula como cierta, como si no.

3.5.2 Intervalos de confianza

Un concepto íntimamente ligado a la significación estadística es el intervalo de confianza. Un intervalo de confianza con n% de confianza, podría definirse como un rango de valores, bajo un modelo estadístico especificado, entre los cuales se encontraría el valor “real” del parámetro estimado, un n% de veces, si repitieramos el experimento en condiciones identicas un número infinito de veces, donde solo influyera el muestreo aleatorio.

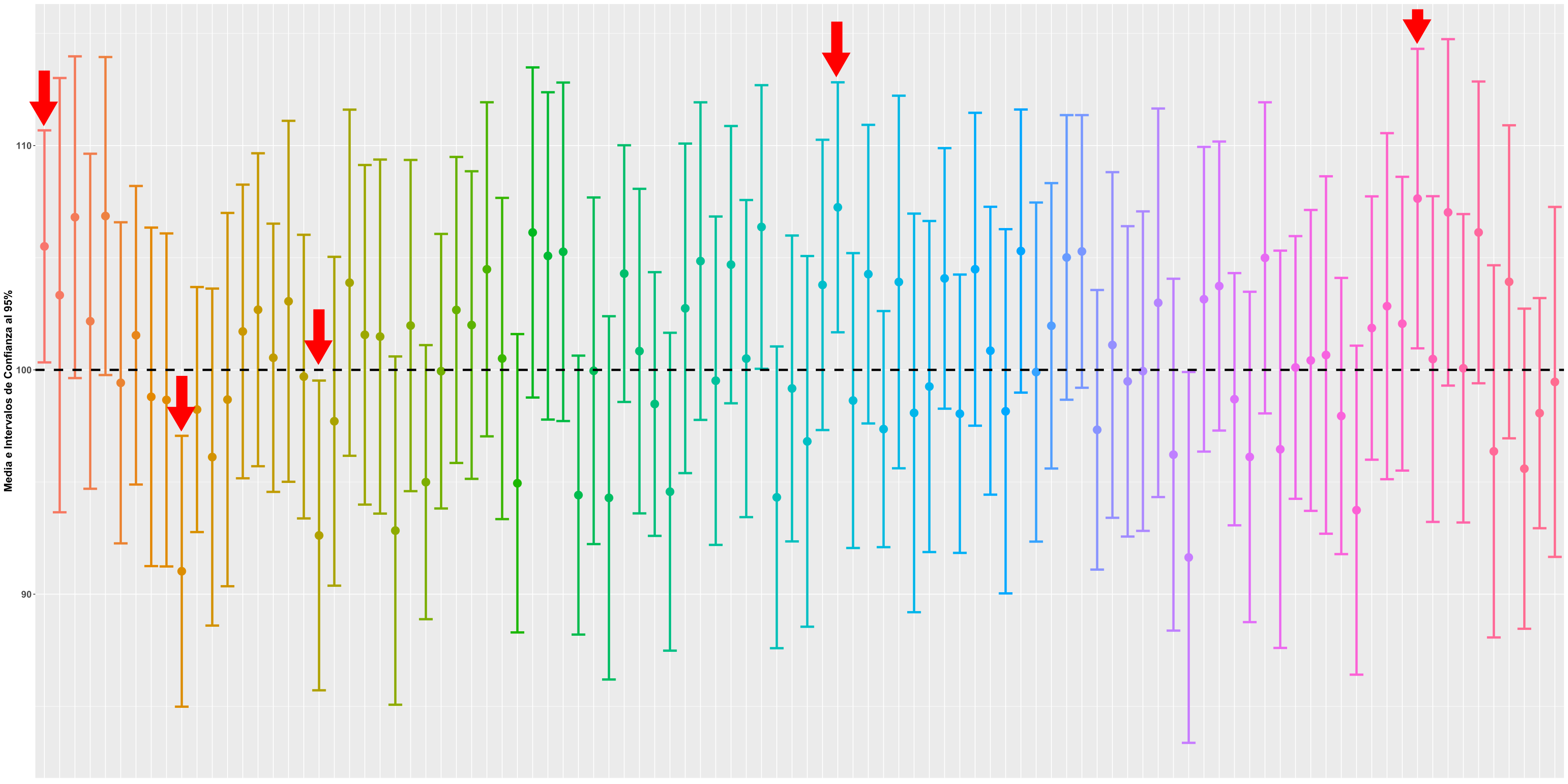
Figure 3.4: Ejemplo Intervalos de Confianza al 95%

En la Figura 3.4 se reflejan 100 simulaciones de medias muestrales seleccionadas de forma aleatoria, con sus respectivos intervalos de confianza al 95%, de una población con una \(\mu = 100\). Como puede apreciarse, en 5 de dichas simulaciones, el intervalo de confianza calculado no contiene la media poblacional, es decir, el valor real del parámetro estimado.

Una malinterpretación habitual que se hace de los intervalos de confianza, es que son un rango de valores entre los cuales se encuentra el valor real del parámetro estimado con una probabiliadd “n”. Esto no es cierto, el valor real, o se encuentra (\(P(x \in IC) = 1\)), o no se encuentra (\(P(x \in IC) = 0\)) dentro de ese rango de valores, no hay posibilidades intermedias de probabilidad.

Existen distintas fórmulas para el cálculo de los intervalos de confianza, algunas de ellas bastante complejas. Mostraré solo la fórmula para el cálculo del intervalo de confianza de una media muestral, para que se entienda en parte la matemática subyacente a este concepto: \[ Intervalo \quad de \quad Confianza = \bar x \pm z_{\alpha/2}EE \\[-8pt] IC \quad al \quad 95\% = \bar x \pm 1.966EE \\[-8pt] IC \quad al \quad 90\% = \bar x \pm 1.645EE \] La fórmula anterior parte de la aasunción de que conocemos la \(\sigma\) poblacional. En ella, \(z_{\alpha/2}\) es el valor del estadístico \(z\) para el cual la probailidad acumulada igual o por encima de dicho valor (positivo o negativo), 1 menos la probabilidad especificada para el intervalo de confianza, por ejemplo, 1-0.95 que sería \(z = 1.966\) como se comentó en las propiedades de la curva normal. Como recordatorio, \(EE\) es el error estándar de la media, calculado a partir de la \(\sigma\) poblacional y el tamaño de la muestra reclutada.

3.6 La asunción de normalidad

Esta asunción es bastante conocida. Casi cualquier persona que haya leido un poco sobre bioestadística, o leido algún artículo de investigación que utilice métodos de análisis de estadística inferencial, se habrá topado con él. Sin embargo, habitualmente se malinterpreta.

La asunción de normalidad hace referencia a la distribución normal del parámetro muestral a estimar, o de los resíduos/errores del modelo (de lo que hablaré más en profundidad en los capítulos de análisis de regresión), pero no hace referencia a la distribución de los datos de nuestro estudio. Es decir, podemos tener una muestra con datos que no sigan una distribución normal, pero cumplirse la asunción de normalidad.

En la Figura 3.5 muestro un ejemplo con una simulación de Montecarlo (que explicaré más adelante). Lo que he hecho, es crear una población simulada con 10000 sujetos, con \(\mu = 30\) y \(\sigma = 8\), con una asimetría derecha, de forma que los datos de dicha población no seguirían una distribución normal. Posteriormente, he simulado 10000 muestreos, cada uno de ellos selecionando aleatoriamente 200 sujetos de dicha población inventada, para calcular la media de cada una de esas 10000 muestras de 200 sujetos. La distribución de dichas medias se muestra en la gráfica de la derecha de la Figura 3.5. Como se puede apreciar, aunque la distribución de los datos se asemeja a una distribución normal, la de las medias muestrales (parámetro muestral), si se aproxima a una distribución normal.

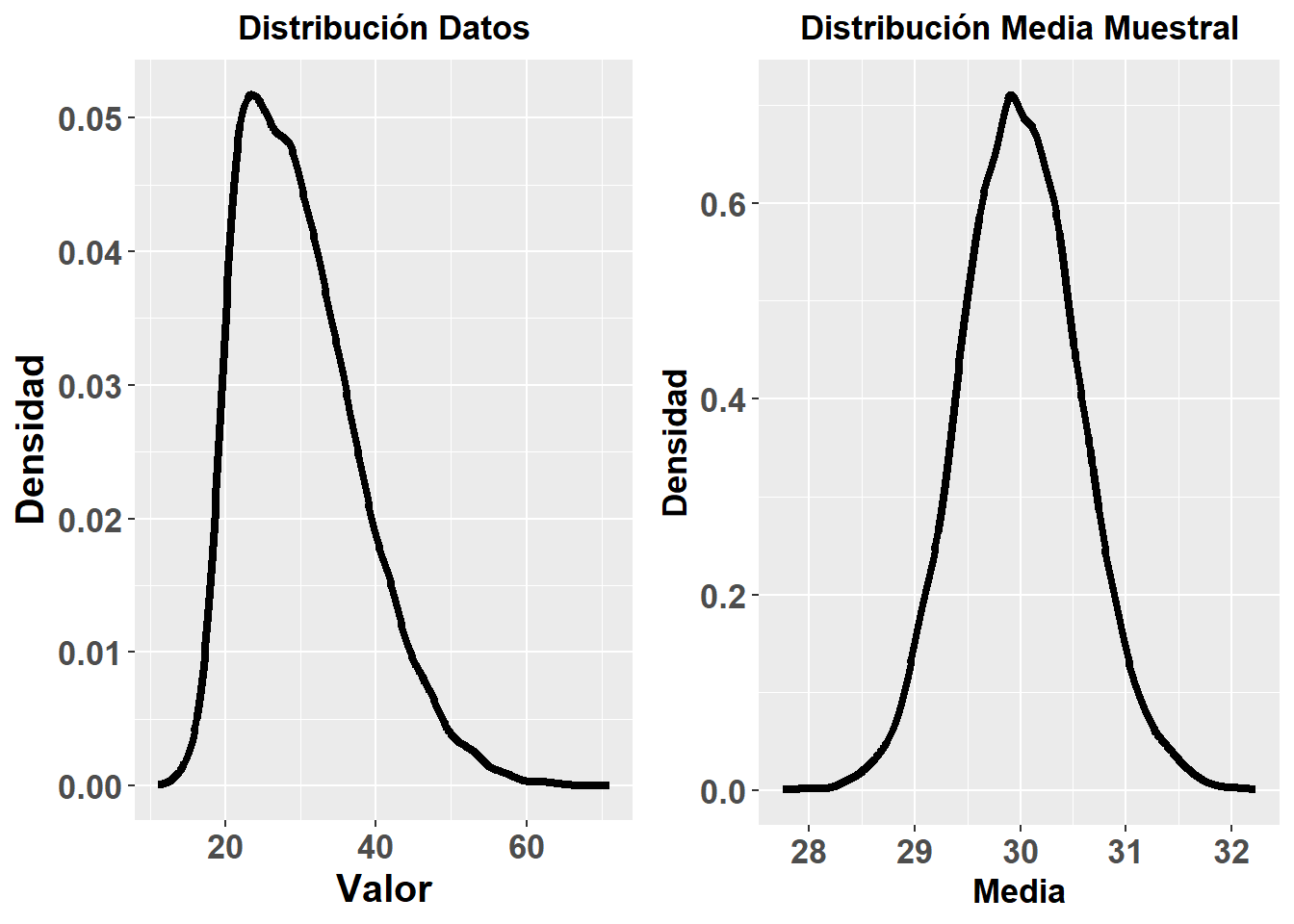
Figure 3.5: Simulación de Montecarlo de la Asunción de Normalidad

La asunción de normalidad suele evaluarse a menudo con dos tests, el de Shapiro-Wilk o el de Kolmogorov-Smirnov. En la práctica, no tenemos acceso a la distribución muestral para poder evaluar directamente la asunción de normalidad. Lo que hacen estos dos tests es evaluar si la distribución de los datos se aproxima a una distribución normal, porque en principio es razonable pensar que, si los datos siguen una distribución normal, entonces el parámetro muestral y los errores del modelo también.

A pesar de su extendido uso, las recomendaciones actuales son no utilizar estos tests para decidir si asumimos el cumplimiento de la asunción de normalidad o no. Ambos tests se basan en el cálculo de nu valor-p, de forma que si este es inferior a 0.05, se asume que no se cumple el supuesto de normalidad, y si este es mayor a 0.05, se asume su cumplimiento. Esta práctica, como veremos más adelante, de dicotomización de decisiones en función de un punto de corte del valor-p es problemática. Por ejemplo, ¿y si el valor-p de un test de Shapiro-Wilk es de 0.049 en una muestra y en otra de 0.053? ¿aceptaríamos en un caso la asunción y en el otro no? Además, en muestras pequeñas, desviaciones considerables de la asunción de normalidad pueden no ser detectadas por ambos tests, por falta de potencia estadística, mientras que en muestras con un elevado tamaño muestral, pequeñas desviaciones pueden resultar en valores-p menores de 0.05. La recomendación actual es hacer evaluar visualmente algunos gráficos y estadísticos de forma en el caso de muestras pequeñas, para no relegar la decisión sobre la asunción de normalidad exclusivamente en un valor-p, y casos con muestras considerables, incluso no tener en cuenta la normalidad de los datos, para establecer si aceptamos la asunción del supuesto de normalidad, ya que podremos asumirla en muchos casos solo por el elevado tamaño muestral.

No es el objetivo de este libro entrar en como se analizan distintos datos para evaluar si aceptamos o no el cumplimiento del supuesto de normalidad. Pero si es necesario comprender que, con una muestra por ejemplo de 10 sujetos por grupo, aceptar el cumplimiento de la asunción de normalidad es muy atrevido, y más atrevido aún hacerlo en función del resultado de la prueba de Shapiro-Wilk o Kolmogorov-Smirnov. Existen otros métodos de análisis estadístico que no requieren del cumplimiento de dicha asunción y que serían más adecuados en muchos de estos casos con muestras pequeñas, dentro de lo que se conocen como métodos robustos. No obstante, como veremos más adelante, estudios con tamaños muestrales tan pequeños son, por lo general, desaconsejables.

3.7 El teorema central límite

El teorema central límite es, desde mi punto de vista, otro de los conceptos que suelen malinterpretarse habitualmente. De forma simplificada, nos dice que a expensas de la distribución poblacional de los datos, la distribución de los parámetros muestrales tenderían a tener una distribución normal cuando el tamaño muestral se aproxima al infinito, algo similar a lo mostrado en la Figura 3.5. La pregunta sería, ¿qué tamaño muestral es lo suficientemente grande como para asumir la distribución normal en función de dicho teorema? Y la respuesta que se suele dar es: 30 sujetos. Esta es la malinterpretación que suele cometerse habitualmente, pensar que el teorema nos habla de 30 sujetos y que, en cualquier situación, podemos aceptar como cierta la asunción de normalidad con \(n\ge 30\). Rand R. Wilcox aporta varios argumentos de porqué aceptar esta afirmación, tal cual, es erróneo y deben tenerse en cuenta otros aspectos a la hora de decidir que análisis estadísticos utilizar en una investigación (Wilcox 2010), aunque este es un aspecto que deben tener en cuenta aquellos que van a realizar los análisis estadísticos de una investigación, que no es el objetivo de este libro.

Algo derivado de esta malinterpretación del teorema central límite, es la creencia de que un tamaño muestral de 30 sujetos es suficiente para cualquier investigación. Este punto si es de especial interés para el propósito de este libro y es por el cual he querido destacar que, el punto de corte generalizado de 30 sujetos, no se sostiene. En multitud de investigaciones un tamaño muestral de 30 sujetos por grupo es totalmente inapropiado y limita notoriamente la confianza que podemos depositar en los resultados de las mismas, como explicaré en el capítulo destinado a tamaños muestrales.

3.8 Significación, azar y teorema de Bayes

El valor-p es la probabilidad de que la asociación observada se haya producido por azar, el valor-p es la probabilidad de que la hipótesis nula sea cierta. Dos afirmaciones, dos mentiras. Estamos ante dos de las mayores malinterpretaciones en el campo de investigación de la Fisioterapia (y no solo, de multitud de ciencias aplicadas). El valor-p no es la probabilidad de la asociación observada se haya producido por azar o de que la hipótesis nula sea cierta, debido a que:

El valor-p es una probabilidad acumulada.
El valor-p se basa siempre en la asunción de que, efectivamente, el azar ha producido la asociación observada. Es decir, asumimos que eso ha pasado para calcular el valor-p.
El valor-p se basa en la asunción de un modelo estadístico especificado, que suele ser de la hipótesis nula, que postula la ausencia de efecto, de modo que partimos de que eso ya ha sucedido, de que es cierto (P = 1), para calcular el valor-p.

Lo que voy a mostrar a continuación es una demostración matemática, a través del teorema de Bayes, de que el valor-p no es la probabilidad de que la hipótesis nula (de que el azar haya operado por sí solo) sea cierta.

Siendo A el efecto observado, B la hipótesis nula, y el valor-p en este caso, la probabilidad de haber obtenido ese efecto observado, dada la hipótesis nula (\(P(A|B)\)), en lugar de una probabilidad acumulada (simplemente para simplificar el entendimiento de la demostración, ya que no altera la veracidad de la misma), y aceptamos que es correcta la afirmación mencionada al inicio de este apartado, entonces: \[ P(A|B)=P(B) \] Esta igualdad debería cumplirse para todo posible suceso \(A_i\), es decir, para cualquier posible efecto observado al hacer ese experimento: \[ P(A_1|B) = P(B) \\[-8pt] P(A_2|B) = P(B) \] Utilizando el teorema de Bayes se puede apreciar por tanto que: \[ P(A_1|B) = P(A_2|B) \\[-8pt] \frac{P(B|A_1)*P(A_1)}{P(B)}=\frac{P(B|A_2)*P(A_2)}{P(B)} \\[-8pt] P(B|A_1)*P(A_1)=P(B|A_2)*P(A_2) \] Como dicha igualdad ha de cumplirse para todo posible \(A_i\), entonces la formula de Bayes para este caso sería: \[ P(A_i|B)= \frac{P(B|A_i)*P(A_i)}{\sum_{i=1}^{n} P(B|A_i)*P(A_i)}=\frac{P(B|A_i)*P(A_i)}{n*P(B|A_i)*P(A_i)}=P(B) \] El número de posibles resultados a obtener en el estudio es infinito, es decir, existen infinitos sucesos \(A_i\) de modo que \(n \rightarrow \infty\). Cuando \(n \rightarrow \infty\), el resultado de la anterior ecuación tiende a cero, \(P(B) \rightarrow 0\). Es decir, la ecuación solo se cumpliría para todos los posibles sucesos \(A_i\) cuando la probabilidad de la hipótesis nula fuese cero, \(P(B) = 0\), es decir, cuando la hipótesis nula no pudiera darse, cuando el azar no pudiera estar actuando por sí solo, lo cual no tiene sentido.