Chapter 2 Introducción
2.1 ¿Qué es una variable?
Imaginemos que contamos el número de calcetines que lleva cada uno de los estudiantes de una clase del grado en Fisioterapia. El estudiante 1 lleva 2 calcetines, el estudiante 2 lleva 2 calcetines, el estudiante 3 lleva 2 calcetines… Todos los estudiantes llevan el mismo número de calcetines, es decir, el número de calcetines no varía, esto es lo que se denomina constante.
Una variable por el contrario, y como su propio nombre indica, si presenta variabilidad en sus valores. Por ejemplo, la estatura y/o peso de los sujetos de esa misma clase. Un dato curioso es el equívoco término de constantes vitales, pues no son realmente constantes, ya que varían.
| Sujeto | Calcetines | Estatura | Peso |
|---|---|---|---|
| 1 | 2 | 167 | 85 |
| 2 | 2 | 169 | 81 |
| 3 | 2 | 178 | 82 |
| 4 | 2 | 170 | 80 |
| 5 | 2 | 171 | 78 |
| 6 | 2 | 179 | 87 |
| 7 | 2 | 172 | 82 |
| 8 | 2 | 164 | 72 |
| 9 | 2 | 167 | 83 |
| 10 | 2 | 168 | 78 |
Esta variabilidad es importante, ya que sin ella, no se podrán realizar los análisis estadísticos orientados a estudiar asociaciones entre variables. No podemos demostrar ni refutar la existencia de una asociación entre dos constantes.
2.2 Tipos de variables
Existen distintas formas de clasificar variables. Por un lado tenndríamos la clasificación en función de la dependencia de cara a los análisis estadísticos:
- Variable independiente: Es aquella cuyo valor no depende de las otras incluidas en los análisis. Por ejemplo, la variable grupo de tratamiento en un ensayo controlado aleatorizado, sería una variable independiente.
- Variable dependiente: Es aquella cuyo valor depende del valor de otra/s variable/s incluidas en el modelo. Por ejemplo, el cambio en la fuerza medido con dinamometría tras aplicar dos intervenciones en un ensayo controlado aleatorizado.
La etiqueta de dependiente/independiente no es fija, es decir, una misma variable podemos definirla como dependiente o independiente en función de como se trate en el análisis estadístico, esto se aprecia facilmente en los análisis de regresión lineal que veremos más adelante.
Imaginemos que el objetivo de un estudio es predecir la fuerza muscular en función del índice de masa corporal (IMC) de una persona. En este caso, el IMC sería la variable independiente y la fuerza la variable dependiente. Sin embargo, en este mismo estudio, podríamos también querer predecir el IMC de una persona en función del volumen de ejercicio físico realizado por semana. En este segundo caso, el IMC pasaría a ser la variable dependiente, y el volumen de ejercicio físico semanal la variable independiente. Por tanto, en función de como se lleven a cabo los análisis, una misma variable puede ser dependiente o independiente.
Otra forma de clasificar una variable es en función de la capacidad de cuantificación de las mismas. Podemos distinguir dos grupos:
- Variable cuantitativa: Es aquella en la que si podemos cuantificar, es decir, adjudicar un número con un sentido real (que si es informativo), a cada valor de dicha variable (ej. estatura, peso, IMC…). Dentro de las variables cuantitativas, podemos distinguir dos subgrupos:
- Continua: Entre dos valores dados de dicha variable, existen infinidad de posibles valores. Por ejemplo, entre 170cm de estatura y 171cm de estatura, podemos tener infinitos valores de estatura, y estos son informativos: 170.1, 170.123, 170.76538, etc.
- Discreta: Entre dos valores dados de dicha variable, no existen infinidad de valores informativos, los valores van “a saltos”, es decir, están restringidos. Por ejemplo, si una variable es el número de hijos de una persona, podemos tener 1 hijo, 2 hijos, 3 hijos… Pero no podemos tener 1.5 hijos, este valor carece de sentido, no es informativo. Otro ejemplo de variable cuantitativa discreta es la frecuencia cardíaca.
- Variable cualitativa: Es aquella en la no se puede adjudicar un número con sentido real. Los números a adjudicados a cada categoría de una varibale cualitative no son informativos de dicha categoría (ej. sexo, género, presencia o no de una patología…).
Cuando tenemos una variable cualitativa, por ejemplo la presencia de una patología, no podemos realizar análisis con palabras (Si / No). Al proceso mediante el cual se adjudica un valor numérico a cada categoría de una variable cualitativa se le denomina codificación. Por ejemplo, podemos codificar la anterior variable como Si = 1, No = 0; de forma que podamos utiliar esos unos y ceros para posteriormente realizar los análisis estadísticos correspondientes.
2.3 Tipos de escalas de medición
La escala de medición hace referencia a la naturaleza de los números contenidos en cada sujeto, es decir, hace referencia a la naturaleza de la variable en cuestión. Dependiendo de la escala de medición, los datos deberan ser analizados de distintas formas. Podemos distinguir varios subgrupos dentro de las variables cuantitativas y cualitativas en función de la escala de medición:
- Variable cuantitativa
- Intervalo: En este tipo de escala de medición, no existe el cero real, si no que se ha establecido un cero por convención, pero ese valor no implica al ausencia de la ariable. Esto hace que si tenga sentido y sea informativo, calcular la diferencia (intervalo) entre dos valores, pero que no tenga sentido calcular la razón entre ellos. Un ejemplo sería la temperatura, donde el cero no implica ausencia de la misma, en este caso tendría sentido restar 20 grados y 40 grados, pero no tendría sentido decir que un objeto con 40 grados tiene el doble de temperatura que uno con 20 grados.
- Razón: En este tipo de escala si existe el cero real, este es informativo e indica la ausencia de dicha variable, teniendo sentido el cálculo de diferencias y razones. Un ejemplo sería el número de habitantes de una ciudad, donde cero indicaría la ausencia de habitantes, y donde si podemos decir que una ciudad tiene el doble de habitantes que otra.
- Variable cualitativa
- Nominal: Las categorías contenidas no presentan un orden, de forma que los números adjudicados en el proceso de codificación solo sirven para distinguir una categoría de otra (ej. sexo, número de tratamientos administrados en un ensayo, ciudades de un país,…).
- Ordinal: En este caso, las categorías contenidas si presentan un orden, de modo que los números adjudicados, además de distinguir unas categorías de otras, nos informan también de la relación ordinal entre las mismas, de modo que se debe tener en cuenta dicho orden a la hora de realizar la codificación. A pesar de existir un orden, y poder afirmar que una categoría está por encima o por debajo de otra, no tiene sentido calcular diferencias entre dichos valores codificados, y por tanto tampoco decir que la diferencia entre dos valores contiguos de dicho orden es la misma que entre los dos valores contiguos siguientes. Un ejemplo sería la Escala de Kendall de fuerza muscular, o la Escala Likert que mida el grado de acuerdo. En ambos casos existe un orden, pero no tendría sentido decir que pasar del 0 al 1 en la Escala Kendall representa lo mismo que pasar del 3 al 4.
2.4 Estadística descriptiva
Cuando tenemos un conjunto de datos, por ejemplo un conjunto de sujetos a los cuales hemos medido una variable como puede ser la fuerza isométrica máxima con un dinamómetro manual, necesitamos algunos estadísticos (medidas) para poder mostrar un resumen de dichos datos que sea informativo para el lector, y que se utilizarán posteriormente para los análisis estadísticos.
Podemos distinguir cuatro subgrupos de medidas:
- Tendencia central.
- Dispersión.
- Posición.
- Forma.
Las medidas de forma se explicarán en el capítulo correspondiente a teoría de la probabilidad.
2.4.1 Tendencia central
Las medidas de tendencia central nos hablan, como su propio nombre indica, del valor hacia el que tienden los datos, un valor ubicado hacia el centro de su distribución. Existen distintas medidas de tendencia central, a continuación se muestran las más comunes:
1. Media aritmética
La media aritmética muestral \((\bar x)\) es la medida de tendencia central más utilizada. Se corresponde con el sumatorio de todos los datos \((x_{i})\), entre el número total de ellos \((n)\). La media puede adquirir un valor que no se corresponda con ninguno de los observados en los distintos sujetos. \[\bar x = \frac{\sum_{i=1}^{n} x_{i}}{n}\] Algunos aspectos que deben ser tenidos en consideración con respecto a la media aritmética son los siguientes:
- La diferencia de dos medias es igual a la media de las diferencias.
- Si a todos los valores de una muestra se les suma un valor k o se multiplican por un valor k, eso es igual que sumarle a la media el valor k o multiplicar la media por el valor k.
- El valor de la media aritmética se ve influenciado por la presencia de valores atípicos, especialmente en muestras pequeñas, así como por la asimetría.
2. Mediana
Si ordenamos todos los valores de una determinada variable, el valor que se encuentra en la mitad, sería la mediana \((M_{e})\). Matemáticamente su valor se representaria como: \[M_{e}= x_{\frac{n+1}{2}}\] A diferencia de la media aritmética:
- La diferencia entre dos medianas no es igual a la mediana de las diferencias. Es decir, teniendo dos grupos A y B, la mediana del grupo A menos la mediana del grupo B, da un valor distinto a la mediana de A-B.
- La mediana no se ve influenciada por valores atípicos, pero si por la asimetría.
La mediana, al igual que la media, no tiene porque corresponderse con un valor observado, esto dependerá del número de valores observados.
3. Moda
La moda absoluta \((M_o)\) es el valor que más veces se repite en la muestra. Al igual que con la mediana, no su valor no se ve influenciado por valores atípicos. Existen diversos aspectos a tener en cuenta sobre la moda, pero la mayoría no son de especial relevancia para los asuntos tratados en este libro, de modo que no se profundizará en ellos. La moda tampoco tiene porque corresponderse con un valor observado en la muestra.
2.4.2 Dispersión
Las medidas de dispersión sirven para cuantificar como se alejan los valores de los distintos sujetos entre sí. Llegando al extremo, de ausencia de dispersión, todos los sujetos tendrían la misma puntuación, y estaríamos en el caso de la constante. Las principales medidas de dispersión son:
- Rango
- Desviación estandar
- Varianza
- Coeficiente de variación
1. Rango
El rango se define como la diferencia entre el valor más pequeño y más grande de un conjunto de datos. No es una medida de dispersión muy útil si se intepreta de manera aislada sin tener en cuenta otras medidas de dispersión.
2. Varianza
La varianza \((\sigma^2)\) es una medida de dispersión muy importante, que aparecera citada en numerosos análisis estadísticos que tienen en cuenta esta medida de dispersión. IMaginemos que tenemos una muestra de 10 sujetos, a los cuales medimos la fuerza isométrica máxima de extensión de rodilla con un dinamómetro manual. En la Tabla 2.2 aparece reflejada una columna con el título de “diferencia”, donde se encuentra la diferencia de cada valor con respecto a la media muestral.Como puede apreciarse, la suma de todas estas dispersiones de cada valor con respecto a la media muestral, da cero. Es por ello que no se puede utilizar esta diferencia bruta como estimador de la dispersión de los datos.
| Sujeto | Fuerza | Diferencia | Cuadrados |
|---|---|---|---|
| 1 | 139 | -12.4 | 153.76 |
| 2 | 145 | -6.4 | 40.96 |
| 3 | 181 | 29.6 | 876.16 |
| 4 | 151 | -0.4 | 0.16 |
| 5 | 153 | 1.6 | 2.56 |
| 6 | 184 | 32.6 | 1062.76 |
| 7 | 159 | 7.6 | 57.76 |
| 8 | 125 | -26.4 | 696.96 |
| 9 | 136 | -15.4 | 237.16 |
| 10 | 141 | -10.4 | 108.16 |
| Estadísticos | Media = 151.4 | Suma = 0 | SS = 3236.4 |
Para solventar este problema, podemos elevar al cuadrado cada una de las diferencias, obteniendo los valores de la columna “cuadrados” de la Tabla 2.2. Si realizamos la suma de estas diferencias al cuadrado, obtenemos un valor distinto de cero, que se denomina suma de cuadrados, en inglés sum of squares (SS). Sin embargo, como puede apreciarse, el valor de SS depende del número de mediciones de las que disponemos, es decir, a mayor número de sujetos mayor valor de SS. Por ello, debemos dividir ese valor entre el tamaño de la muestra, dando lugar al cuadrado medio, en inglés mean square (MS). Este término que puede resultar nuevo, es sinónimo de otro más conocido, la varianza. Es importante conocer los términos SS y MS, pues aparecerán más adelante en múltiples análisis estadísticos. La fórmula para calcular la varianza muestral quedaría definima como: \[\sigma^2 = \frac{SS}{n} =\frac{\sum_{i=1}^{n} (x_{i} - \bar x)^2}{n}\] Esta sería la formula para calcular la varianza de la muestra, sin embargo, normalmente lo que nos interesa calcular es una estimación de la varianza poblacional, de la cual hemos extraido nuestra muestra. La formula para el cálculo de la estimación varianza poblacional difiere ligeramente, quedando así: \[\sigma^2 = \frac{\sum_{i=1}^{n} (x_{i} - \bar x)^2}{n-1}\] Este n-1 es lo que se denomina grados de libertad. No entraré muy en detalle en este concepto, pero si conviene entender su significado ya que aparecerá posteriormente en la mayoría de análisis estadísticos. Como para calcular la \(\sigma^2\) poblacional, se utiliza la media; si partimos de la asunción de que la media poblacional \((\mu)\) tiene un valor fijo (ya que incluye a todos los sujetos que la conforman) que es el de la media muestral \((\bar x)\), ya que la media muestral es un estimador de la media poblacional, pudiendo solo variar las mediciones individuales de cada uno de los sujetos de la muestra \((x_i)\), pero no el valor de la media, y comenzamos a adjudicar valores a cada sujeto según nuestro criterio, cuando hayamos adjudicado valores a todos los sujetos menos 1, el valor que deberemos adjudicar al último sujeto no puede ser a nuestro criterio, ya que como hemos asumido que la media debe permanecer constante, el valor del último sujeto no puede variar libremente, si no que estará restringido a un único valor, en función del valor que hayamos adjudicado al resto de sujetos y del valor de la media. Por tanto, solo n-1 sujetos pueden tomar valores que varien libremente, y por ello a ese número se le donomina grados de libertad. Este es un ejemplo sencillo que puede ayudar a entender este concepto, a pesar de que el cálculo de los grados de libertad utilizados para determinados análisis estadísticos no sean tan intuitivos.
3. Desviación estandar
Un aspecto a tener en cuenta de la varianza, es que no presenta las mismas unidades de medida que la variable para la cual se está calculando, es decir, no podemos afirmar que la varianza anteriormente calculada sean Newtons, ya que hemos elevado al cuadrado las diferencias calculadas. Es por ello que, normalmente, la medida de dispersión reportada en los análisis descriptivos de multitud de estudios de investigación, es la desviación estandar \((\sigma)\). La desviación estandar se calcula como la raiz cuadrada de la varianza, de forma que al invertir el cuadrado, retornamos a las unidades de medida de la variable en cuestión, en este caso Newtons. La formula de la estimación de la desviación estandar poblacional sería: \[\sigma =\sqrt{\frac{\sum_{i=1}^{n} (x_{i} - \bar x)^2}{n-1}}\] 4. Coeficiente de variación
La desviación estandar es la medida de dispersión más utilizada, sin embargo, al estar en las unidades de medida de la variable en cuestión, de modo que se dificulta la comparación de dispersión entre distintas variables.
Podemos tener una muestra con una desviación estandar de 20, donde estemos midiendo en Newtons la fuerza de extensión de rodilla, y otra muestra con una desviación estandar de 0.8, donde estemos midiendo la longitud del dedo anular con una cinta métrica en centímetros, sin embargo, esto no tiene porqué implicar que la primera muestra presente más dispersión de la segunda, ya que no podemos comparar Newtons con centímetros. Por ello, conviene conocer otra medida de dispersión, el coeficiente de variación (CV). El CV refleja el porcentaje que representa la desviación estandar con respecto a la media muestral: \[CV=\frac{\sigma}{\bar x}*100\] El CV, además de facilitarnos la comparación de dispersiones entre distintas variables, también nos permite evaluar mejor si un conjunto de datos presentan mucha o poca dispersión, algo que tendrá especial relevancia en el análisis crítico de estudios de fiabilidad. Como regla simplista, podemos afirmar que un CV mayor del 30% indica ya un grado de dispersión a tener en cuenta, y un CV mayor del 50% indica mucha dispersión.
2.4.3 Posición
Si ordenamos los valores de un conjunto de datos de menor a mayor, las medidas de posición nos informan del puesto que ocupa un determinado valor dentro del conjunto de los datos. El conjunto de medidas de posición podemos denominarlas n-tiles, y consisten en dividir la muestra en porcentajes, para ver que porcentaje de posición ocupa un determinado valor. Las divisiones más conmunmente utilizadas son:
- Percentiles: Dividimos la muestra entre 100, de forma que cada percentil se corresponde con un incremento del 1%.
- Deciles: Dividimos la muestra entre 10, con incrementos del 10% en cada decil. El primer decil se correspondería con el percentil 10.
- Cuartiles: Dividimos la muestra entre 4, con incrementos del 25% en cada quartil. El primer cuartil se correspondería con el percentil 25.
Antes ya se han nombrado algunos valores de percentiles, pero sin especificarlo como tal, es el caso de la mediana, que constituye el percentil 50, y el rango, que denota los percentiles 0 y 100.
En algunos casos, para describir los datos, se suele reportar la mediana como estimador de tendencia central, y el rango intercuartílico, como estimador de la dispersión (aunque aquí lo se haya incluido en el apartado de medidas de posición, por una finalidad meramente organizatiba). El rango intercuartílico es la diferencia entre los valores que se corresponden con el primer y tercer cuartil, es decir, los percentiles 25 y 75.
Aunque es común reportar el rango intercuartílico como medida de dispersión, esto no es del todo acertado. Si solamente disponemos del rango intercuartílico, no podremos saber los valores correspondientes al primer y tercer cuartil. Es por ello que actualmente se recomienda reportar tales valores, en lugar del rango intercuartílico, pues reportando los mismos, el rango si se puede calcular, pero a la inversa no.
Si observamos los datos de la Tabla 2.2, los valores de fuerza correspondientes al primer y tercer cuartil serían: 139.5 y 157.5. Como puede apreciarse, los valores de los percentiles no tienen porque corresponderse con ningún valor observado, ya que eso dependerá del número de datos que compongan la muestra, al igual que sucede con la mediana. No es necesario conocer como se calculan dichos n-tiles en estos casos, su interpretación es la misma aunque no se correspondan con ningún valor observado, y es que, entre los valores correspondientes al primer y tercer cuartil, se estima que se encuentran el 50% de los datos, es decir, el 50% de los sujetos tienen un valor de fuerza que oscila entre 139.5 y 157.5.
2.4.4 Frecuencias
Cuando estamos tratando con variables cualitativas, especialmente con variables nominales, los descriptivos que suelen reportarse son las frecuencias absolutas y relativas porcentuales.
La frecuencia absoluta constituye el número total de sujetos incluidos en una determinada categoría. Por su parte, la frecuencia relativa porcentual hace referencia al porcentaje que representan esos sujetos con respecto al total de la muestra. Por ejemplo, si tenemos una muestra de 50 sujetos y una variable nominal de 3 categorías (A, B y C), los datos se reportarían como: A = 10 (20%), B = 18 (36%), y C = 22 (44%).
2.4.5 ¿Qué estadísticos descriptivos reportar?
Dependiendo del tipo de variable (cuantitativa o cualitativa), la escala de medición y otros factores, es aconsejable reportar unos u otros estadísticos descriptivos:
- Variable cuantitativa:
- Normal: Media y desviación estandar.
- No normal: Mediana y primer y tercer cuartiles.
- Discreta con poca dispersión (ej. Número de hijos/as): Mediana y primer y tercer cuartiles, o incluso frecuencias.
- Variable cualitativa:
- Nominal: Frecuencias absolutas y relativas porcentuales.
- Ordinal: Mediana y primer y tercer cuartiles, salvo si hay pocas categorías, donde es preferible el reporte de frecuencias.
Aparte de estas recomendaciones generales, personalmente tengo algunas preferencias añadidas:
- Reportar el rango siempre:
- En estudios observacionales, ya que aporta información relevante para entender mejor la descripción de la muestra, crucial en estos estudios.
- Cuando se reporten la mediana y cuartiles en casos de no seguir la normalidad. Esta recomendación, aparte de facilitar la interpretación de la descripción de la muestra, ayudará de forma significativa a investigadores posteriores que quieran metaanalizar los datos de dicho estudio, pues ese reporte añadido del rango permite hacer estimaciones más precisas de la media y desviación estandar muestrales, a partir de la mediana y cuartiles.
- Reportar frecuencias absolutas y relativas porcentuales siempre en el caso de variables ordinales, aparte de la mediana y cuartiles, también para facilitar la interpretación.
2.4.6 Diferencia entre parámetros muestrales y valores individuales.
Uno de los errores que suelen cometerse al interpretar los resultados de una investigación, es confundir los parámetros muestrales con los valores individuales. Como ya se ha comentado, la media no tiene porque corresponerse con ningun valor observado, simplemente informa, bajo ciertas circunstancias, hacia que valor tienden los datos de la muestra. Sin embargo, pueden darse situaciones en las que la media no sea nada informativa de los valores individuales, como por ejemplo un conjunto de datos donde la mitad de los sujetos tengan un valor y la otra mitad otro valor, como en la Figura 2.1.
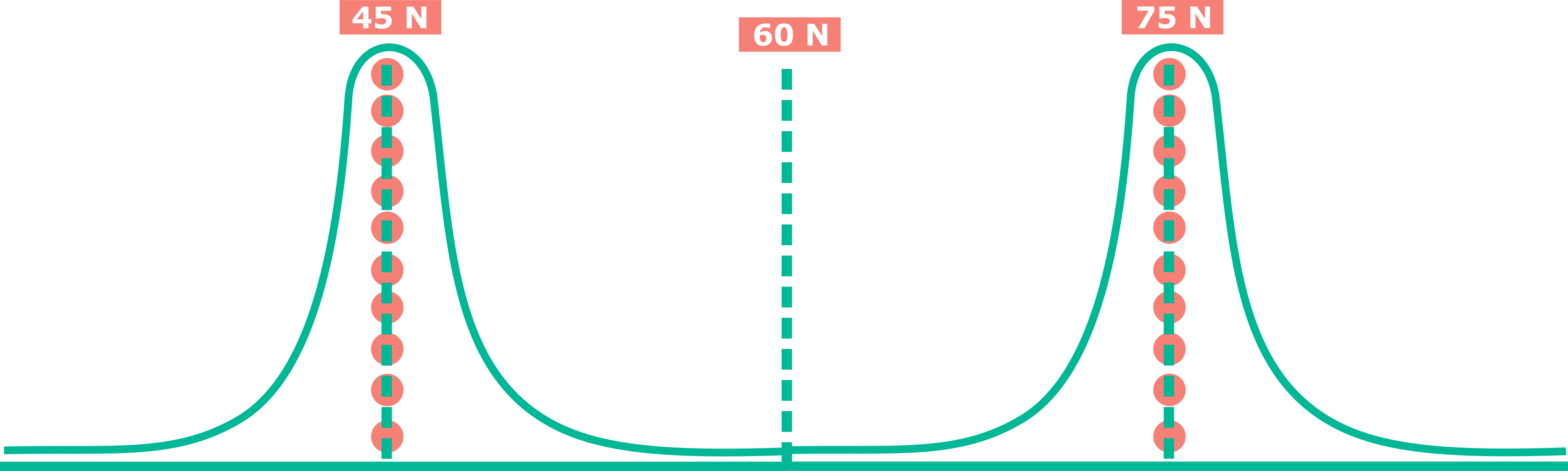
Figure 2.1: Ejemplo de media no informativa
Otro aspecto que debe tenerse en cuenta es la dispersión de los datos, ya que en función de ello, la media será más o menos informativa sobre los valores individuales. Si nos planteamos un extremo, con cero dispersión, volveríamos al caso de la constante, donde la media informa a la perfección de los valores individuales, ya que todos ellos son el mismo. En la Figura 2.2 aparecen dos ejemplos con mayor y menor dispersión.
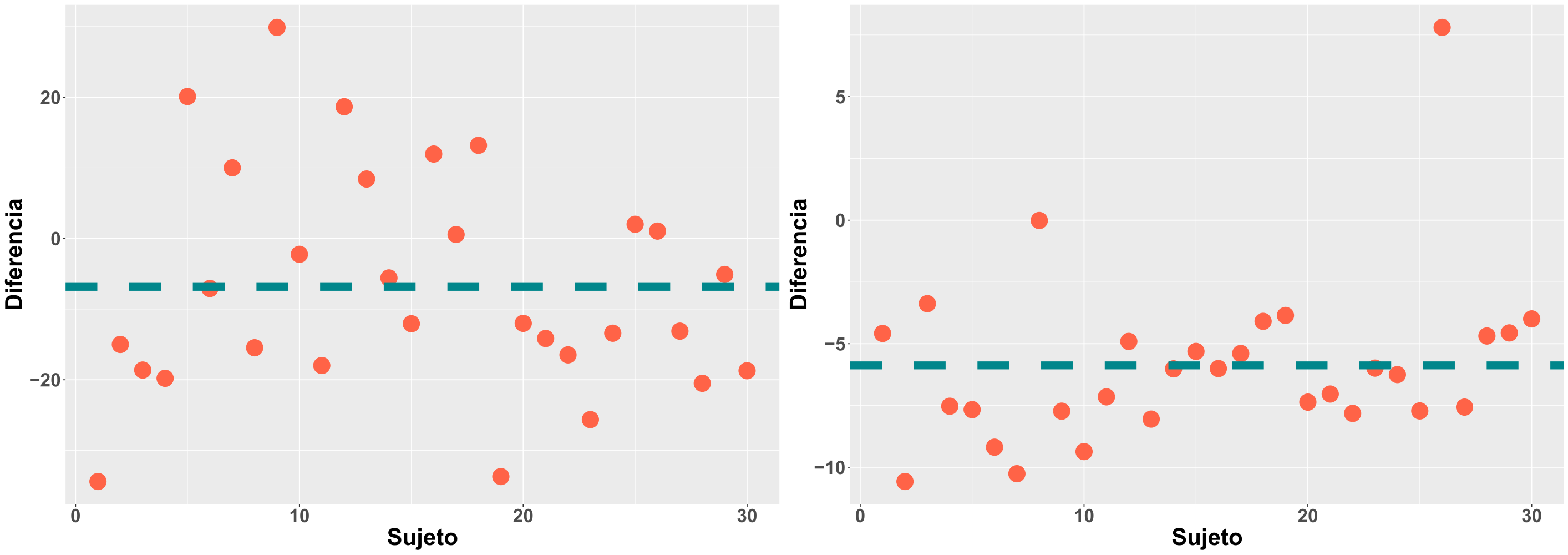
Figure 2.2: Ejemplo dispersión sujetos
Por tanto, es un error inferir directamente el valor de una media, o una difernecia de medias, de una determinada investigación, a la practica clínica con un paciente individual. Realizar esto podría llevarnos a equivocarnos muchas veces en la práctica clínica sobre la respuesta esperada en un determinado paciente con un tratamiento dado, y a desconfiar en la investigación como herramienta de obtención del conocimiento, por una malinterpretación de la misma por nuestra parte.
2.5 Conversión de variables
Cuando disponemos de una variable cuantitativa continua o discreta, podemos convertirla en una variable cualitativa nominal u ordinal, estableciendo puntos de corte de diferenciación de los sujetos. Podemos encontrar ejemplos de esta práctica en estudios que investigan la relación entre la posición adelantada de la cabeza con otras variables (Bokaee 2017, Goodarzi 2017), donde el angulo craneo-vertebral, tomando como referencia para su cálculo el trago de la oreja, la apófisis espinosa de C7 y la horizontal, es decir, una variable cuantitativa continua, se dicotomiza utilizando un punto de corte que suele estar próximo a los 48-50 grados.
A pesar de que esta práctica esta ciertamente extendida dentro de nuestro campo de investigación, mi recomendación es no llevarla a cabo, a no ser de que dispongamos de información relevante que nos oriente a pensar que es una buena idea. Son varios los motivos por los cuales desaconsejo totalmente este tipo de prácticas. En primer lugar, el punto o los puntos de corte utilizados para estas conversiones son totalmente arbitrarios, incluso aunque se afirme que se basan en investigaciones previas, pues estas no suelen utilizar métodos de análisis adecuados ni valorar toda la información pertinente para calcular dichos puntos de corte. Por otro lado, estas prácticas llevan consigo una pérdida de información. Al inicio del libro se nombraba la importancia de la variabilidad, para poder realizar análisis estadísticos. Si dicotomizamos una variable continua, como puede ser el angulo craneo-vertebral, estamos diciendo que el sujeto que tiene 39 grados es igual que aquel que tiene 47 grados (usando un punto de corte de 48 grados), estamos perdiendo información util para distinguir a esos dos sujetos, perdiendo variabilidad. Esta pérdida de información puede llevar consigo a una pérdida de potencia estadística, haciendo más dificil encontrar una determinada asociación entre dos variables si es que esta existe. En tercer lugar, las relaciones objetivo de estudio se van a poder analizar también sin convertir la variable cuantitativa en cualitativa, no hay una necesidad de conversión para estudiar una asociación dada. Por último, y relacionado con el primer punto, la categorización de una variable continua de forma arbitraria puede llevar al investigador a sufrir la “tentación” de probar distintos puntos de corte para categorizar dicha variable, ver que resultados se obtienen con cada punto, y quedarse con el punto que más le interese, sesgando los resultados de la investigación. Aunque debemos partir de una asunción de buena práctica en investigación, lo cierto es que, especialmente en estudios observacionales, cuyo registro previo del proyecto no es necesario para poder publicarlos, no podemos saber si el punto de corte mostrado ha sido elegio a priori o a posteriori de la realización de los análisis.
En resumen, si no se dispone de un motivo de peso, objetivo y justificado con diversos argumentos y datos, no se debe, nunca, categorizar una variable cuantitativa.
2.7 El caso particular de la escala visual analógica
La escala visual analógica (EVA), suele utilizarse bastante dentro del campo de investigación y clínica de la Fisioterapia. El uso más común es para medir la intensidad de dolor. Esta escala consta de una línea horizontal de 10cm de longitud, donde 0 refleja la ausencia de dolor y 10 el peor dolor imaginable. El hecho de que la puntuación obtenida en dicha escala se obtenga midiendo una distancia en centímetros, ha llevado a que se haya generalizado la asunción de que la EVA es una variable cuantitativa continua y se analice como tal. Sin embargo, esto no es del todo cierto.
Si bien la escala en si misma, la recta de 10cm, y el método de medición con una regla o cinta métrica, es decir, la medición de una distancia, es una variable cuantitativa continua, no estamos midiendo una distancia con la EVA, si no que estamos usando dicha distancia para inferir sobre algo subjetivo que no podemos medir directamente de manera objetiva, la intensidad de dolor. ¿Podemos afirmar que una persona con 4cm en la EVA tiene el doble de dolor que una persona con 2cm en la EVA? ¿Podemos decir que es lo mismo un cambio de 1cm a 2cm en la EVA, que un cambio de 6cm a 7cm? En ambos casos la respuesta es no, no tendría sentido hablar de “doble intensidad de dolor”, ni tenemos nada que nos lleve a pensar que esas dos diferencias indican lo mismo.
La EVA debería tratarse como una variable cualitativa ordinal, a pesar de que en el conjunto de investigación en que es utilizada, se trate como continua. No obstante, este es un tema complejo que llevará tiempo cambiar, ya que la tradición de su utilización y análisis como continua está muy instaurada en nuestra sociedad científica.
A pesar de este interesante debate, y sus posibles implicaciones en la interpretación de los resultados ya obtenidos en investigación, de aquí en adelante, seguiremos con la “tradición ya instaurada”, y la EVA será considerada una variable cuantitativa continua en los distintos ejemplos en que se utilice.