4 Day 4 (January 30)

4.1 Announcements

  • Please upload a photo of the signature sheet to Canvas to get 2 magic extra credit points.

  • Please read (and re-read) Ch. 2 and 3 in BBM2L book.

  • Table of distributions in book

  • Activity 2 is posted

4.2 Example with differential equations

  • Motivating data example

    url <- "https://www.dropbox.com/scl/fi/uokqouco07c44cder5vse/Butler-et-al.-Table-1.csv?rlkey=z37llt9dgvs59dw0ee8hnu7uq&dl=1"
df1 <- read.csv(url)
plot(df1$Winter, df1$N, typ = "b", xlab = "Year", ylab = "Population Size", 
ylim = c(0, 300), lwd = 1.5, pch = "*")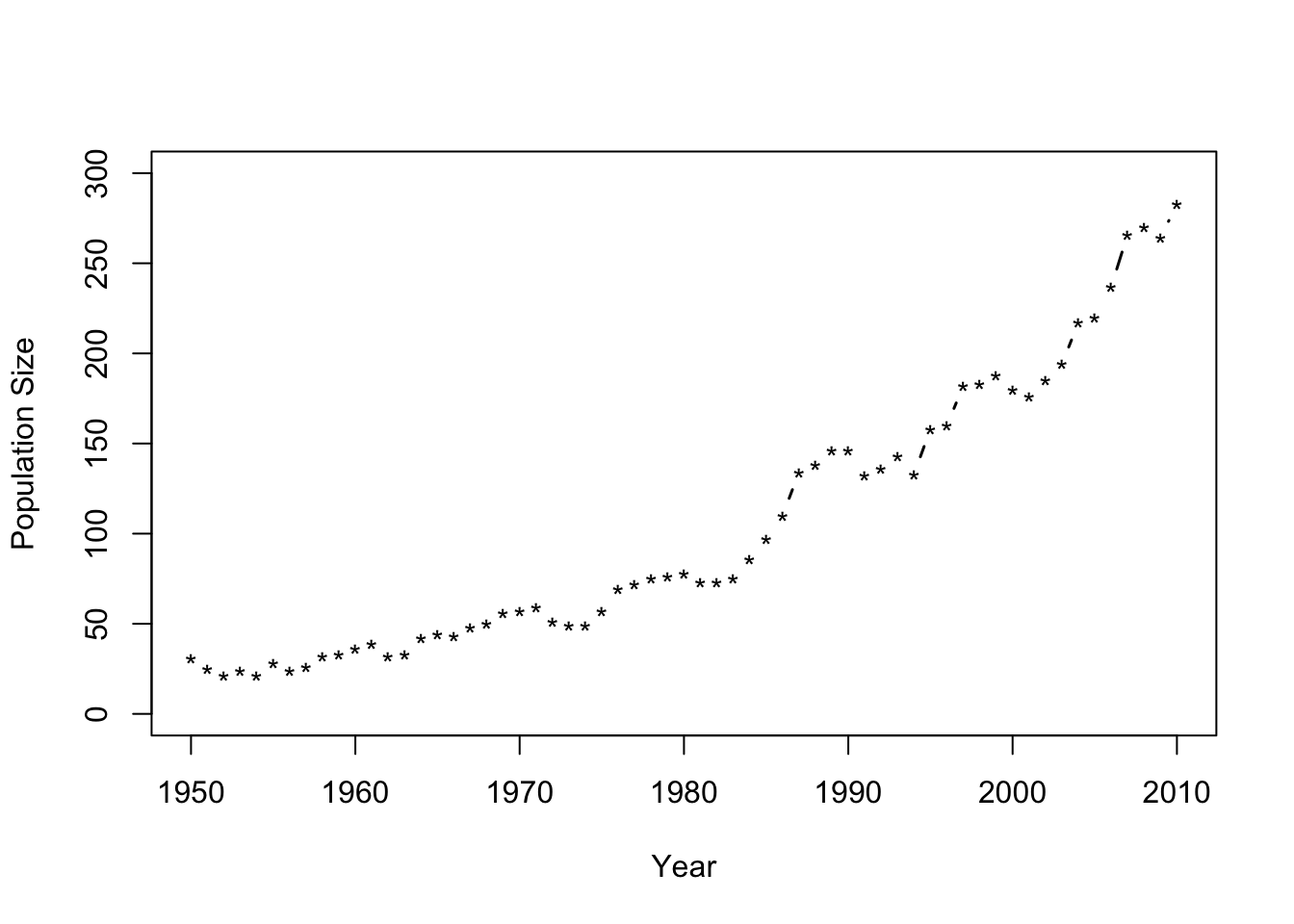

    • Statistical model \[y_t\sim~\text{Poisson}(\lambda(t))\] where \[\lambda(t)=\lambda_{0}e^{\gamma(t-t_0)}\]
      • Assume \(\lambda_0\) is known and equal to the the population size in 1950 (\(\lambda_0 = 31\))
      • We want to obtain the distribtuion of \(\gamma\) given the data \(\mathbf{y}\)
      • What else do we need to fully specify the model? 
K <- 10^6                   # Number of samples to try  
samples <- matrix(,K,2)     # Save samples
lambda0 <- df1$N[1]         # Lambda0
y <- df1$N[-1]              # Data
t <- df1$Winter[-1] - 1950  # Time

for(i in 1:K){
  
  gamma <- runif(1,0,0.1)
  lambda <- lambda0*exp(gamma*t)
  y.sample <- rpois(length(t),lambda)
  
  samples[i,1] <- mean(abs(y-y.sample))
  samples[i,2] <- gamma
}

par(mfrow=c(1,2))
hist(samples[,2],col="grey", main="Prior distribution",xlab=expression(gamma),ylab=expression("["*gamma*"]"),ylim=c(0,100),freq=FALSE,breaks=seq(0,0.1,by=0.005))
hist(samples[which(samples[,1]<30),2],ylim=c(0,100),xlim=range(samples[,2]),col="grey", main="Posterior distribution",xlab=expression(gamma*"|"*bold(y)),ylab=expression("["*gamma*"|"*bold(y)*"]"),freq=FALSE,breaks=seq(0,0.1,by=0.005))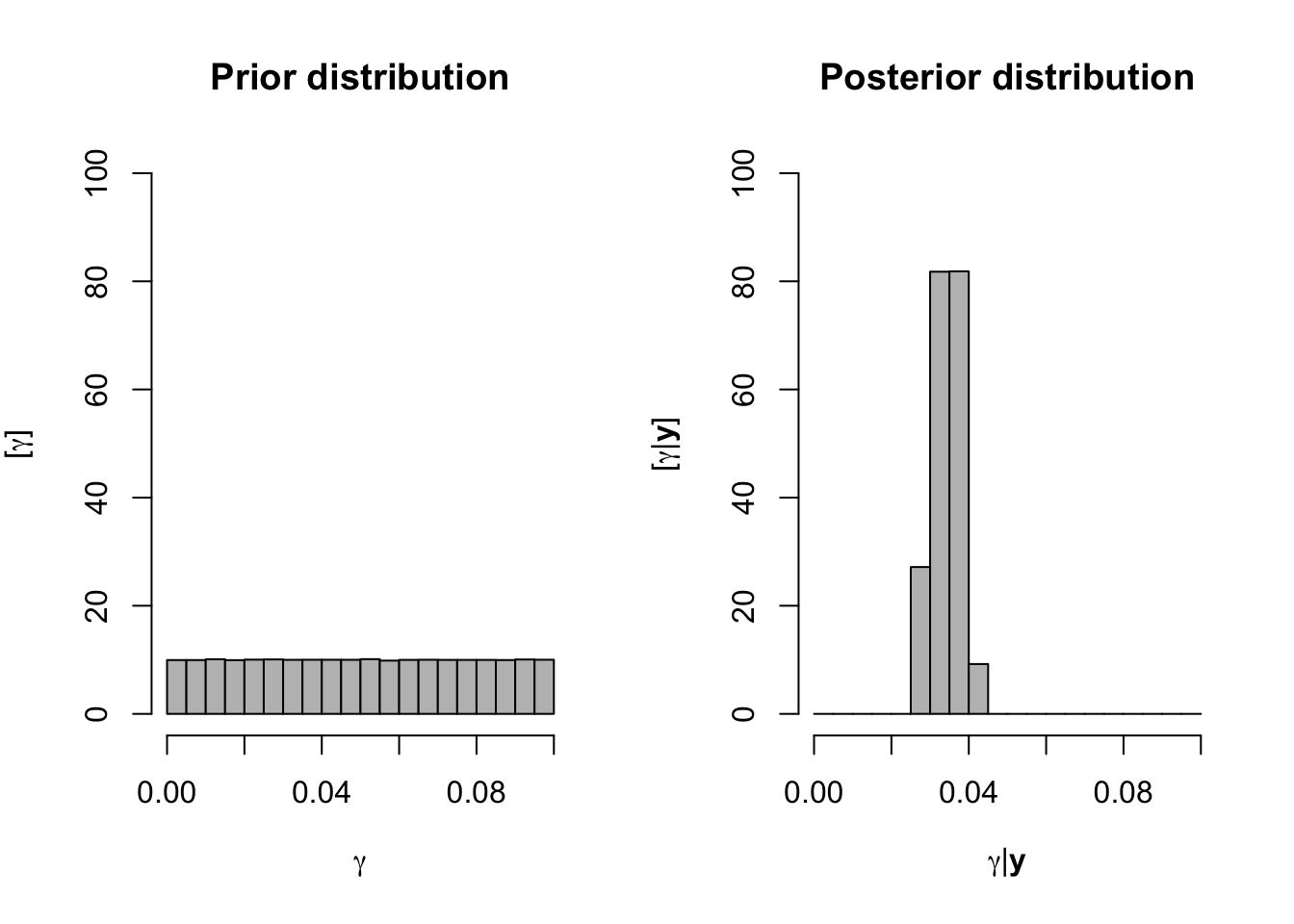

4.3 Building our first statistical model

  • The backstory
  • Building a statistical model using a likelihood-based (classical) approach
    • Specify (write out) the likelihood
    • Select an approach to estimate unknown parameters (e.g., maximum likelihood)
    • Quantify uncertainty in unknown parameters (e.g., using normal approximation, see here)
  • Building a statistical model using a Bayesian approach
    • Specify (write out) the likelihood/data model
    • Specify the parameter model (or prior) including hyper-parameters
    • Select an approach to obtain the posterior distribution
      • Analytically (i.e., pencil and paper)
      • Simulation-based (e.g., Metropolis-Hastings, MCMC, importance sampling, ABC, etc)

4.4 Numerical Integration

  • Why do we need integrals to do Bayesian statistics?

    • Example using Bayes theorem to estimate prevalence rate of rabies
    • Why it is important to keep track of what we are calculating (i.e., clarity in what is being estimated)

  • Numerical approximation vs. analytical solutions

  • Definition of a definite integral \[\int_{a}^b f(z)dz = \lim_{Q\to\infty} \sum_{q=1}^{Q}\Delta q f(z_q)\] where \(\Delta q =\frac{b-a}{Q}\) and \(z_q = a + \frac{q}{2}\Delta q\).

  • Riemann approximation (midpoint rule)\[\int_{a}^b f(z)dz \approx \sum_{q=1}^{Q}\Delta q f(z_q)\] where \(\Delta q =\frac{b-a}{Q}\) and \(z_q = a + \frac{2q - 1}{2}\Delta q\).

  • Using similar approach in R (Adaptive quadrature)

    fn <- function(y){dnorm(y,0,1)}
integrate(f=fn,lower=-4,upper=4,subdivisions=10)
    ## 0.9999367 with absolute error < 4.8e-12