Capítulo 6 Resumindo dados
Com o intuito de identificar padrões nos dados coletados, iremos apresentar algumas funções no R úteis para resumir variáveis de interesse, isto é, iremos discutir como construir tabelas e obter estimativas pontuais, que servem para extrair informação dos dados.
Para apresentar como calcular as medidas de interesse, vamos importar o arquivo seguro saude.txt que contém variáveis referentes a clientes de um seguro de saúde, tais como sexo, imc, número de dependentes, fumante, região, valor das cobranças e se possuía plano de saúde anteriormente. Criem um projeto chamado Resumos. Vale ressaltar que o arquivo possui as seguintes características:
- 99999 foi usado como código para dado faltante,
- , é o indicador de decimal.
#Ativando o pacote
library(readr)
#Importando o arquivo seguro saude.txt
base = read_delim(file = "seguro saude.txt", #nome do arquivo com extensão entre aspas
na = "99999", #código usado para indicar dado faltante
locale = locale(decimal_mark = ",")) #função que controla aspectos do arquivo como o decimal## Rows: 1338 Columns: 8
## ── Column specification ───────────────────────────────────
## Delimiter: " "
## chr (1): fumante
## dbl (7): idade, sexo, imc, num_dep, regiao, cobrancas, plano_anterior
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.#Visualizando o objeto
base## # A tibble: 1,338 × 8
## idade sexo imc num_dep fumante regiao cobrancas plano_anterior
## <dbl> <dbl> <dbl> <dbl> <chr> <dbl> <dbl> <dbl>
## 1 31 2 20.4 0 Não 4 3260. NA
## 2 25 2 26.2 0 <NA> 1 2721. NA
## 3 21 2 36.9 0 Não 2 1917. NA
## 4 59 1 27.7 3 Não 3 14001. NA
## 5 58 2 23.3 0 Não 4 11346. NA
## 6 32 1 23.6 1 Não 3 17626. NA
## 7 50 1 26.2 2 Não 2 10494. NA
## 8 62 1 39.2 0 Não 4 13471. NA
## 9 62 1 33.0 3 Não 2 15612. NA
## 10 39 2 24.5 2 Não 2 6710. 1
## # … with 1,328 more rowsApós a importação do arquivo, iremos transformar em fatores as variáveis qualitativas, seguindo o dicionário da base.
#Transformando a variável sexo em factor
base$sexo = factor(x = base$sexo, #vetor com os valores a serem rotulados
levels = c(1,2), #os valores distintos que aparecem
labels = c("Mulher", "Homem")) #os rótulos dos valores
#Transformando a variável fumante em factor
base$fumante = factor(x = base$fumante)
#Transformando a variável regiao em factor
base$regiao = factor(x = base$regiao,
levels = c(1,2,3,4),
labels = c("Nordeste", "Noroeste", "Sudeste", "Sudoeste"))
#Transformando a variável plano_anterior em factor
base$plano_anterior = factor(x = base$plano_anterior, #vetor com os valores a serem rotulados
levels = c(0,1), #os valores distintos que aparecem
labels = c("Não", "Sim")) #os rótulos dos valores
#Visualizando o objeto
base## # A tibble: 1,338 × 8
## idade sexo imc num_dep fumante regiao cobrancas plano_anterior
## <dbl> <fct> <dbl> <dbl> <fct> <fct> <dbl> <fct>
## 1 31 Homem 20.4 0 Não Sudoeste 3260. <NA>
## 2 25 Homem 26.2 0 <NA> Nordeste 2721. <NA>
## 3 21 Homem 36.9 0 Não Noroeste 1917. <NA>
## 4 59 Mulher 27.7 3 Não Sudeste 14001. <NA>
## 5 58 Homem 23.3 0 Não Sudoeste 11346. <NA>
## 6 32 Mulher 23.6 1 Não Sudeste 17626. <NA>
## 7 50 Mulher 26.2 2 Não Noroeste 10494. <NA>
## 8 62 Mulher 39.2 0 Não Sudoeste 13471. <NA>
## 9 62 Mulher 33.0 3 Não Noroeste 15612. <NA>
## 10 39 Homem 24.5 2 Não Noroeste 6710. Sim
## # … with 1,328 more rows6.1 Analisando dados faltantes
Quando importamos dados, usualmente, fazemos uma avaliação simples e rápida da base, usando funçoes como summary ou str. Estas funções servem, principalmente se o volume de dados disponível é pequeno. Quando lidamos com um volume maior, precisamos de funções que nos permitam avaliar melhor a presença de dados faltantes.
Dentre as diversas possibilidades, vamos discutir o pacote naniar.

6.1.1 A função viss_miss
Um dos primeiros gráficos que usaremos para avaliar a presença de dados faltantes é proveniente da função viss_miss.
#Ativando o pacote
library(package = naniar)
#Visualizando dados faltantes para toda a base
vis_miss(x = base)
O gráfico traz diversas informações sobre dados faltantes. Em cinza ele indica a posição dos dados preenchidos na base e em preto ele indica a posição dos dados faltantes. Além disso, ele nos informa os % de dados presentes e ausentes na base, de um modo global e para cada uma das variáveis isoladamente.
6.1.2 A função gg_miss_var
Uma outra forma de avaliar os dados faltantes, visualmente é por meio da função gg_miss_var.
#Visualizando somente os dados faltantes para toda a base
gg_miss_var(x = base)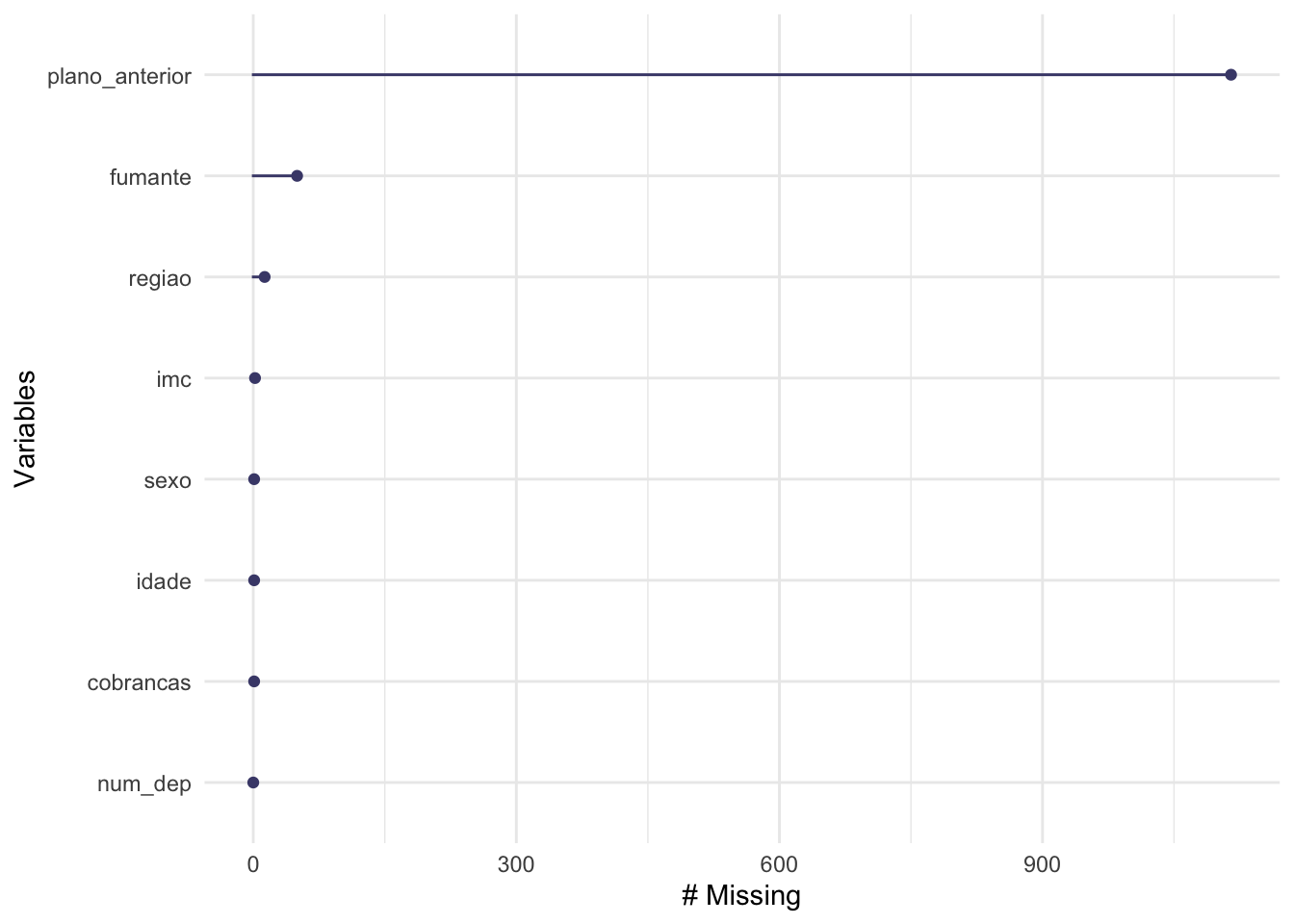
O gráfico traz a quantidade de dados faltantes para cada variável que compõe a base de dados. As variáveis estão ordenadas da que possui o maior quantidade de dados faltantes para a que possui a menor quantidade. É possível avaliarmos os percentuais por variáveis, usando esta visualização, basta modificarmos o argumento show_pct = TRUE.
#Visualizando somente os dados faltantes para toda a base em %
gg_miss_var(x = base,
show_pct = TRUE)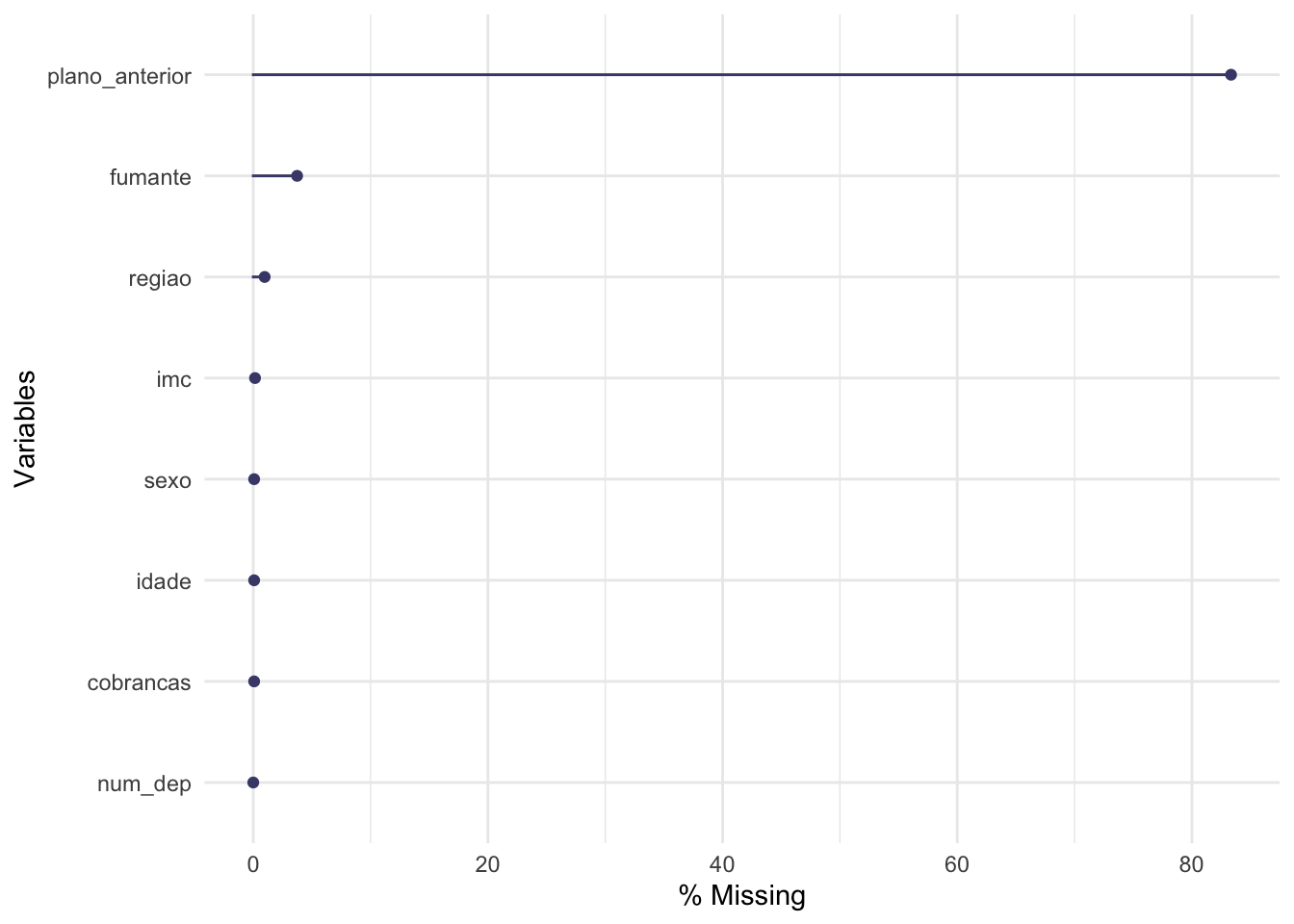
Nós também podemos avaliar os dados faltantes de acordo com as categorias de alguma variável.
#Visualizando somente os dados faltantes para toda a base em % por região
gg_miss_var(x = base,
show_pct = TRUE,
facet = regiao)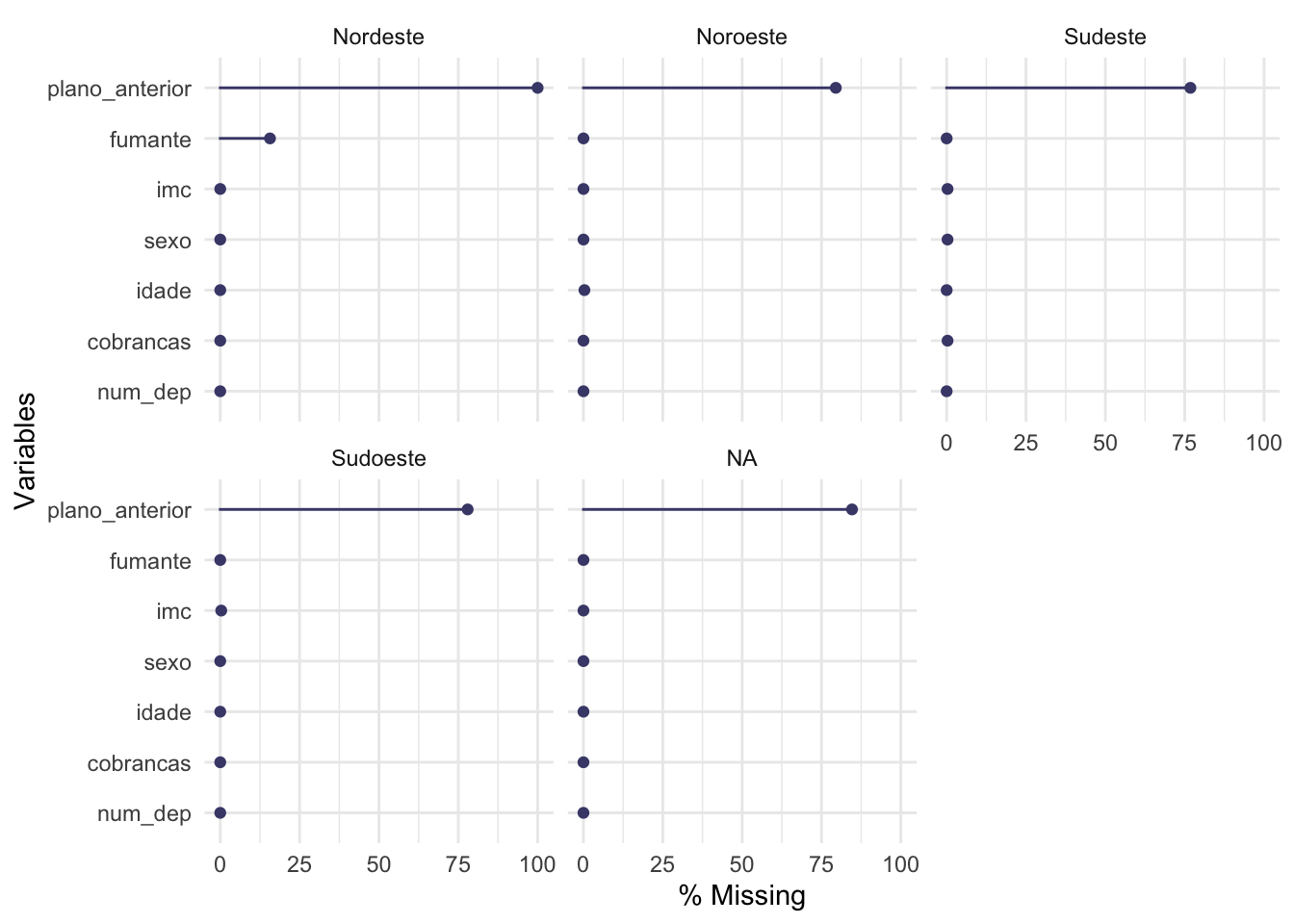
6.1.3 A função gg_miss_upset
Existem gráficos que nos permitem avaliar padrões de omissão de dados, isto é, possíveis combinações de omissões e interseções de omissões entre as variáveis. A função gg_miss_upset é uma boa opção neste cenário.
#Avaliando interações de dados faltantes entre variáveis
gg_miss_upset(data = base)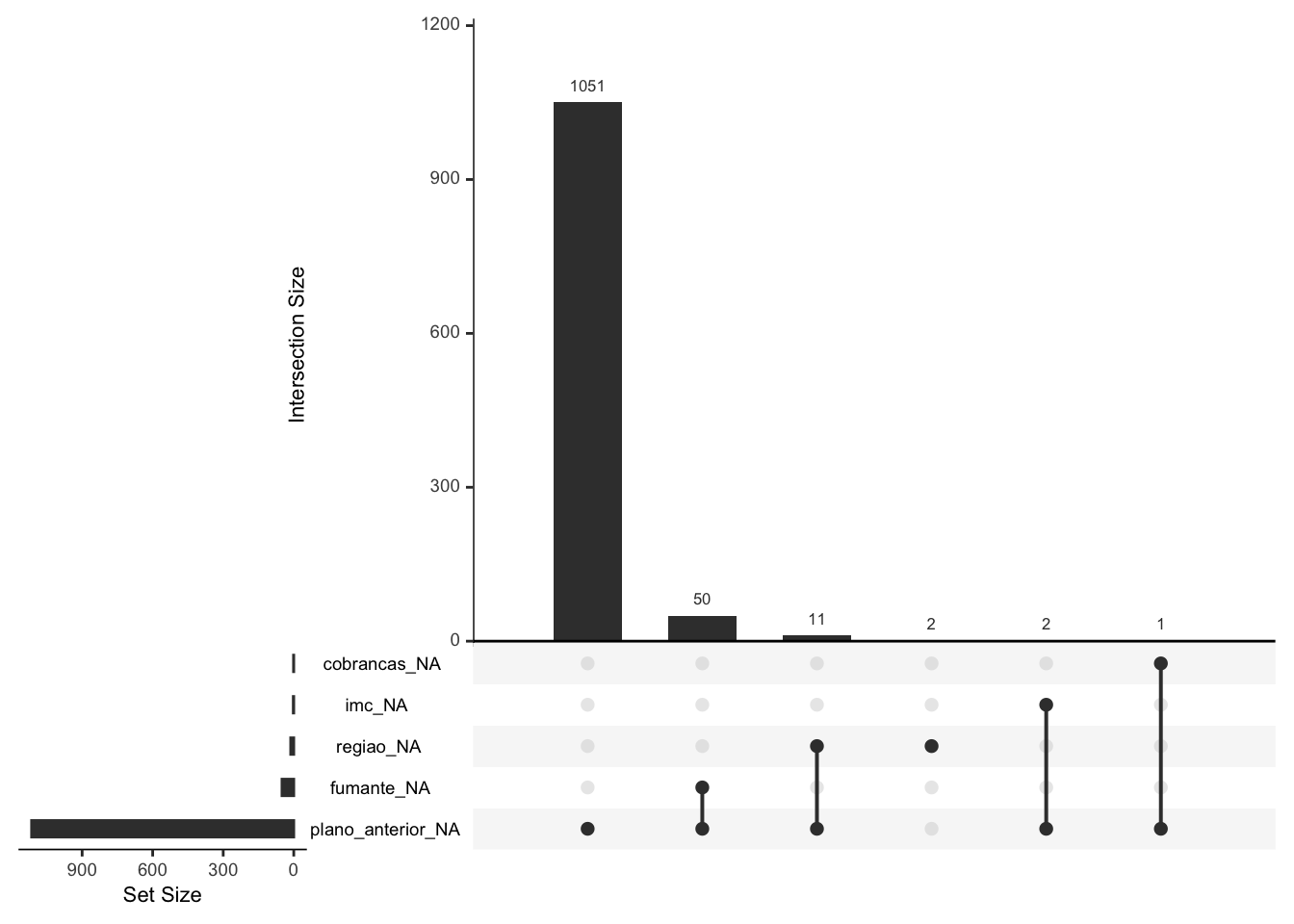
6.1.4 A função miss_var_summary
Se desejarmos explorar os dados faltantes da base de forma numérica podemos recorrer a função miss_var_summary.
#Obtendo quantitativo e o % de dados faltantes para cada variável
base |>
miss_var_summary()## # A tibble: 8 × 3
## variable n_miss pct_miss
## <chr> <int> <dbl>
## 1 plano_anterior 1115 83.3
## 2 fumante 50 3.74
## 3 regiao 13 0.972
## 4 imc 2 0.149
## 5 idade 1 0.0747
## 6 sexo 1 0.0747
## 7 cobrancas 1 0.0747
## 8 num_dep 0 0#Obtendo quantitativo e o % de dados faltantes para cada variável por região
base |>
group_by(regiao) |>
miss_var_summary()## # A tibble: 35 × 4
## # Groups: regiao [5]
## regiao variable n_miss pct_miss
## <fct> <chr> <int> <dbl>
## 1 Sudoeste plano_anterior 251 78.0
## 2 Sudoeste imc 1 0.311
## 3 Sudoeste idade 0 0
## 4 Sudoeste sexo 0 0
## 5 Sudoeste num_dep 0 0
## 6 Sudoeste fumante 0 0
## 7 Sudoeste cobrancas 0 0
## 8 Nordeste plano_anterior 319 100
## 9 Nordeste fumante 50 15.7
## 10 Nordeste idade 0 0
## # … with 25 more rows6.2 Criando tabelas no R
Uma tabela de distribuição de frequências é uma tabela contendo as(os) categorias(valores) ou agrupamento das categorias(valores) de uma determinada variável. Podemos apresentar as frequências absolutas, percentuais e acumuladas.
Existem diversas opções de pacotes para a construção de tabelas no R, aqui vamos explorar o pacote janitor
Para obtermos uma tabela de distribuição de frequências usamos a função tabyl.
6.2.1 Para uma única variável
A seguir, vamos construir uma tabela de distribuição de frequências para a variável região.
#Ativando o pacote
library(janitor)
#Criando uma tabela de distribuição de frequências para a variável regiao
tab1 = base |>
tabyl(var1 = regiao)
#Visualizando o objeto
tab1## regiao n percent valid_percent
## Nordeste 319 0.238415546 0.2407547
## Noroeste 322 0.240657698 0.2430189
## Sudeste 362 0.270553064 0.2732075
## Sudoeste 322 0.240657698 0.2430189
## <NA> 13 0.009715994 NAA função retorna uma tabela contendo a frequência absoluta (n), o percentual (percent) e o percentual considerando somente os dados válidos (valid_percent). É possível apresentar as colunas dos percentuais em formato de percentual, para isso, usaremos as funções adorn_totals e adorn_pct_formatting.
#Transformando as colunas de percentuais em %
tab1 |>
adorn_totals(where = "row") |> #adiciona uma linha com os totais
adorn_pct_formatting() #apresenta os percentuais na escala de 0 a 100 com o símbolo %## regiao n percent valid_percent
## Nordeste 319 23.8% 24.1%
## Noroeste 322 24.1% 24.3%
## Sudeste 362 27.1% 27.3%
## Sudoeste 322 24.1% 24.3%
## <NA> 13 1.0% -
## Total 1338 100.0% 100.0%6.2.2 Para duas variáveis
Estas tabelas, geralmente, são chamadas de tabelas de contingência.
#Criando uma tabela de contingência para região e sexo
tab2 = base |>
tabyl(var1 = sexo,
var2 = regiao)
#Visualizando o objeto
tab2## sexo Nordeste Noroeste Sudeste Sudoeste NA_
## Mulher 158 161 174 159 10
## Homem 161 161 187 163 3
## <NA> 0 0 1 0 0Para retirarmos os dados faltantes, basta usarmos a função filter.
#Criando uma tabela de contingência para região e sexo
tab2 = base |>
tabyl(var1 = sexo,
var2 = regiao,
show_na = FALSE) #calcula a frequência absoluta para os cruzamentos de sexo e regiao
#Visualizando o objeto
tab2## sexo Nordeste Noroeste Sudeste Sudoeste
## Mulher 158 161 174 159
## Homem 161 161 187 163Podemos incluir os percentuais na tabela de contingência. Vale lembrar, que podemos calcular os percentuais por linha, por coluna e pelo total. Os três casos são exemplificados a seguir.
#Melhorando a tabela de contingência
tab2 |>
adorn_percentages(denominator = "row") |> #calcula os % por linha
adorn_pct_formatting(digits = 2) |> #apresenta os percentuais na escala de 0 a 100 com o símbolo %
adorn_ns() #inclui as frequências absolutas na tabela## sexo Nordeste Noroeste Sudeste Sudoeste
## Mulher 24.23% (158) 24.69% (161) 26.69% (174) 24.39% (159)
## Homem 23.96% (161) 23.96% (161) 27.83% (187) 24.26% (163)#Melhorando a tabela de contingência
tab2 |>
adorn_percentages(denominator = "col") |> #calcula os % por coluna
adorn_pct_formatting(digits = 2) |> #apresenta os percentuais na escala de 0 a 100 com o símbolo %
adorn_ns() #inclui as frequências absolutas na tabela## sexo Nordeste Noroeste Sudeste Sudoeste
## Mulher 49.53% (158) 50.00% (161) 48.20% (174) 49.38% (159)
## Homem 50.47% (161) 50.00% (161) 51.80% (187) 50.62% (163)#Melhorando a tabela de contingência
tab2 |>
adorn_percentages(denominator = "all") |> #calcula os % pelo total
adorn_pct_formatting(digits = 2) |> #apresenta os percentuais na escala de 0 a 100 com o símbolo %
adorn_ns() #inclui as frequências absolutas na tabela## sexo Nordeste Noroeste Sudeste Sudoeste
## Mulher 11.93% (158) 12.16% (161) 13.14% (174) 12.01% (159)
## Homem 12.16% (161) 12.16% (161) 14.12% (187) 12.31% (163)6.2.3 Para três variáveis
A seguir, vamos construir uma tabela de contingência para região e sexo, considerando a informação sobre o hábito de fumar dos indivíduos.
#Criando uma tabela de distribuição de frequências para a variável regiao
tab3 = base |>
tabyl(var1 = sexo,
var2 = regiao,
var3 = fumante,
show_na = FALSE)
#Visualizando o objeto
tab3## $Não
## sexo Nordeste Noroeste Sudeste Sudoeste
## Mulher 108 133 138 138
## Homem 105 132 134 126
##
## $Sim
## sexo Nordeste Noroeste Sudeste Sudoeste
## Mulher 26 28 36 21
## Homem 30 29 53 37A função retorna uma lista de tabelas de contingência. Ela calculou a tabela de contingência para não fumantes e depois para os fumantes.
#Melhorando a tabela de contingência
tab3 |>
adorn_percentages(denominator = "col") |> #calcula os % por coluna
adorn_pct_formatting(digits = 2) |> #apresenta os percentuais na escala de 0 a 100 com o símbolo %
adorn_ns() #inclui as frequências absolutas na tabela## $Não
## sexo Nordeste Noroeste Sudeste Sudoeste
## Mulher 50.70% (108) 50.19% (133) 50.74% (138) 52.27% (138)
## Homem 49.30% (105) 49.81% (132) 49.26% (134) 47.73% (126)
##
## $Sim
## sexo Nordeste Noroeste Sudeste Sudoeste
## Mulher 46.43% (26) 49.12% (28) 40.45% (36) 36.21% (21)
## Homem 53.57% (30) 50.88% (29) 59.55% (53) 63.79% (37)6.3 Calculando medidas resumos no R
As medidas resumos são utilizadas como representantes numéricos para o conjunto de dados, as vezes são calculadas considerando todos os dados disponíveis, as vezes parte dos dados disponíveis. A seguir vamos apresentar as principais funções que calculam as medidas de posição e as medidas de dispersão.
6.3.1 Medidas de posição
São as medidas que nos ajudam a entender o posicionamento dos dados. São usadas como representantes únicos de uma variável de interesse. As principais medidas de tendência central são média, moda, mediana, quantis, entre outras.
A seguir, vamos obter a
#Obtendo medidas de posição para variáveis numéricas
base |>
summarise(across(.cols = where(is.numeric),
.fns = list(mean, median)))## # A tibble: 1 × 8
## idade_1 idade_2 imc_1 imc_2 num_dep_1 num_dep_2 cobrancas_1 cobrancas_2
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 NA NA NA NA 1.09 1 NA NAClaramente temos um problema, uma vez que várias medidas retornaram como NA. Isso se deve ao fato de existirem dados faltantes para estas variáveis e a função não foi manipulada de forma adequada. É preciso modificar o argumento na.rm = TRUE.
#Obtendo medidas de posição para variáveis numéricas
base |>
summarise(across(.cols = where(is.numeric),
.fns = list(media = ~mean(.x, na.rm = TRUE),
mediana = ~median(.x, na.rm = TRUE),
Q1 = ~quantile(.x, na.rm = TRUE, probs = .25)),
.names = "{.col}.{.fn}"))## # A tibble: 1 × 12
## idade…¹ idade…² idade…³ imc.m…⁴ imc.m…⁵ imc.Q1 num_d…⁶ num_d…⁷ num_d…⁸ cobra…⁹
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 39.2 39 27 30.7 30.4 26.3 1.09 1 0 13268.
## # … with 2 more variables: cobrancas.mediana <dbl>, cobrancas.Q1 <dbl>, and
## # abbreviated variable names ¹idade.media, ²idade.mediana, ³idade.Q1,
## # ⁴imc.media, ⁵imc.mediana, ⁶num_dep.media, ⁷num_dep.mediana, ⁸num_dep.Q1,
## # ⁹cobrancas.media6.3.2 Medidas de dispersão
O resumo do conjunto de dados por uma única medida representativa de posição central esconde toda a informação sobre a heterogeneidade do conjunto de observações. As medidas de dispersão trazem informações sobre o grau de homogeneidade dos dados.
Principais medidas de dispersão: variância, desvio padrão, desvio absoluto mediano, coeficiente de variação, entre outras.
#Obtendo medidas de posição para variáveis numéricas
base |>
summarise(across(.cols = where(is.numeric),
.fns = list(vari = ~var(.x, na.rm = TRUE),
dp = ~sd(.x, na.rm = TRUE),
dam = ~mad(.x, na.rm = TRUE)),
.names = "{.col}.{.fn}"))## # A tibble: 1 × 12
## idade…¹ idade…² idade…³ imc.v…⁴ imc.dp imc.dam num_d…⁵ num_d…⁶ num_d…⁷ cobra…⁸
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 197. 14.1 17.8 37.2 6.10 6.21 1.45 1.21 1.48 1.47e8
## # … with 2 more variables: cobrancas.dp <dbl>, cobrancas.dam <dbl>, and
## # abbreviated variable names ¹idade.vari, ²idade.dp, ³idade.dam, ⁴imc.vari,
## # ⁵num_dep.vari, ⁶num_dep.dp, ⁷num_dep.dam, ⁸cobrancas.vari6.4 Desafio
- Importe o arquivo Base Desafio.txt (77777 - código para dado faltante).
- Avalie a presença de dados faltantes na base de dados, apresentando os % de dados faltantes por variável.
- Apresente uma tabela de distribuição de frequências para a escolaridade (deixe os percentuais no seguinte formato, por exemplo, 2,3%).
- Apresente uma tabela de contingência para escolaridade e filhos com frequência absoluta e % (na coluna deve aparecer escolaridade e na linha se possui filhos, o % deve ser calculado por coluna).
- Calcule a média, a mediana e o desvio-padrão da renda e dos meses de experiência profissional por cada nível de escolaridade.