2 Cluster analysis
Anàlisis de Classificació
Autors: J.P. Casas-Ruiz & S. Gascón
Aquesta sessió servirà per a posar en pràctica alguns dels mètodes de classificació. Recordeu que els mètodes de classificació tenen com a objectiu classificar un conjunt d’observacions (mostres) en diferents grups més o menys homogenis tenint en compte múltiples descriptors o variables.
Per exemple, podríem utilitzar mètodes de classificació per tal d’agrupar els diferents boscos de Catalunya en funció de la comunitat d’arbres que les constitueixen.
Un altre exemple seria també definir grups de llacunes litorals segons les seves característiques fisicoquímiques (e.g. pH, conductivitat, concentració de diversos nutrients, temperatura, anions i cations, etc).
A l’exemple que farem avui, utilitzarem mètodes de classificació jeràrquica i no jeràrquica per tal d’agrupar diferents punts al llarg d’un riu en funció de la seva comunitat de peixos. Les dades són de 30 punts de mostreig al llarg del riu Doubs, que drena les muntanyes del Jura entre França i Suïssa.
2.1 Preparació de les dades per anàlisis de classificació
Primer de tot, carreguem els packages que serán necessaris per l’anàlisi. És recomanable carregar ade4 abans que vegan per evitar conflictes.
library(ade4)
library(vegan)
library(gclus)
library(cluster)
library(RColorBrewer)
library(labdsv)
library(leaflet)i assignem el directori de treball o projecte. Canvieu el de l’exemple pel vostre.
Carreguem les dades a través de l’arxiu Doubs.Rdata tal i com vam fer a la secció anterior. Recordeu que l’arxiu ha d’estar al directori de treball que hagueu escollit o a la carpeta del projecte en que treballeu. En cas contrari, cal especificar el directori a dins de la funció load():
load(file="Doubs.Rdata")
spe <- spe[-8, ] # Eliminem la fila 8 perquè no té dades
env <- env[-8, ] # Eliminem la fila 8 perquè no té dades
spa <- spa[-8, ] # Eliminem la fila 8 perquè no té dades
latlong <- latlong[-8, ] # Eliminem la fila 8 perquè no té dades
source('hcoplot.R') # aprofitem per carregar un parell de funcions custom que farem servir
source('coldiss.R')La primera matriu que utilitzarem spe conté rangs abundàncies de 27 espècies de peixos. Cada fila correspon a un punt de mostreig, de l’1 al 30, i cada columna correspon al número d’observacions per a cada espècie. Exploreu la matriu per entendre les dimensions i tipus de dades amb les que treballarem. Les funcions str(), summary(), hist(), corr(), o plot() us poden ser útils (veure secció 1 de la guia d’R i RSTudio-part univariant).
2.2 Càlcul matriu de distància o dissimilaritat
Primer de tot ens cal calcular una matriu de distàncies, i per tant ens cal escollir una mesura d’associació. Per a decidir quina mesura utilitzar pot ser útil fer-nos dues preguntes:
Estem tractant amb dades d’abundància d’espècies o dades ambientals?
Les dades són de tipus binàries, quantitatives i/o ordinals?
En el nostre cas, totes les variables són d’abundància de diferents espècies de peixos. Per tant, escollirem una mesura de tipus assimètric per dades (semi)quantitatives, com per exemple la distància de Bray-Curtis.
El segon pas seria preguntar-nos si és necessari dur a terme una transformació o estandardització de les variables (veure “1.4.1.estandardització de les dades” per detalls). Com que totes les nostres variables tenen les mateixes unitats (número d’individus) i no varien massa (de 0 a 5), no seria necessari fer cap transformació del tipus \(log(x+1)\) ni tampoc estandarditzar les dades.
Passem doncs a calcular la matriu de distància de Bray-Curtis de les dades originals:
2.3 Anàlisis de clúster jeràrquic
Un cop tenim la nostra matriu de distàncies, ja podem començar amb l’anàlisi de classificació, que farem utilitzant la funció hclust(). Les anàlisis de classificació de tipus jeràrquic i aglomeratiu es visualitzen normalment a través de dendrogrames. N’heu vist alguns a les sessions teòriques.
Anem a calcular-ne alguns utilitzant els mètodes d’aglomeració més habituals: single linkage, complete-linkage, UPGMA (i.e. average linkage) i Ward.
par(mfrow = c(2, 2))
# Compute single linkage agglomerative clustering
spe.db.single <- hclust(spe.db, method = "single")
plot(spe.db.single,
labels = rownames(spe),
main = "Bray-Curtis - Single linkage")
# Compute complete-linkage agglomerative clustering
spe.db.complete <- hclust(spe.db, method = "complete")
plot(spe.db.complete,
labels = rownames(spe),
main = "Bray-Curtis - Complete linkage")
# Compute UPGMA agglomerative clustering
spe.db.UPGMA <- hclust(spe.db, method = "average")
plot(spe.db.UPGMA,
labels = rownames(spe),
main = "Bray-Curtis - UPGMA")
# Compute Ward’s Minimum Variance Clustering
spe.db.ward <- hclust(spe.db, method = "ward.D2")
plot(spe.db.ward,
labels = rownames(spe),
main = "Bray-Curtis - Ward")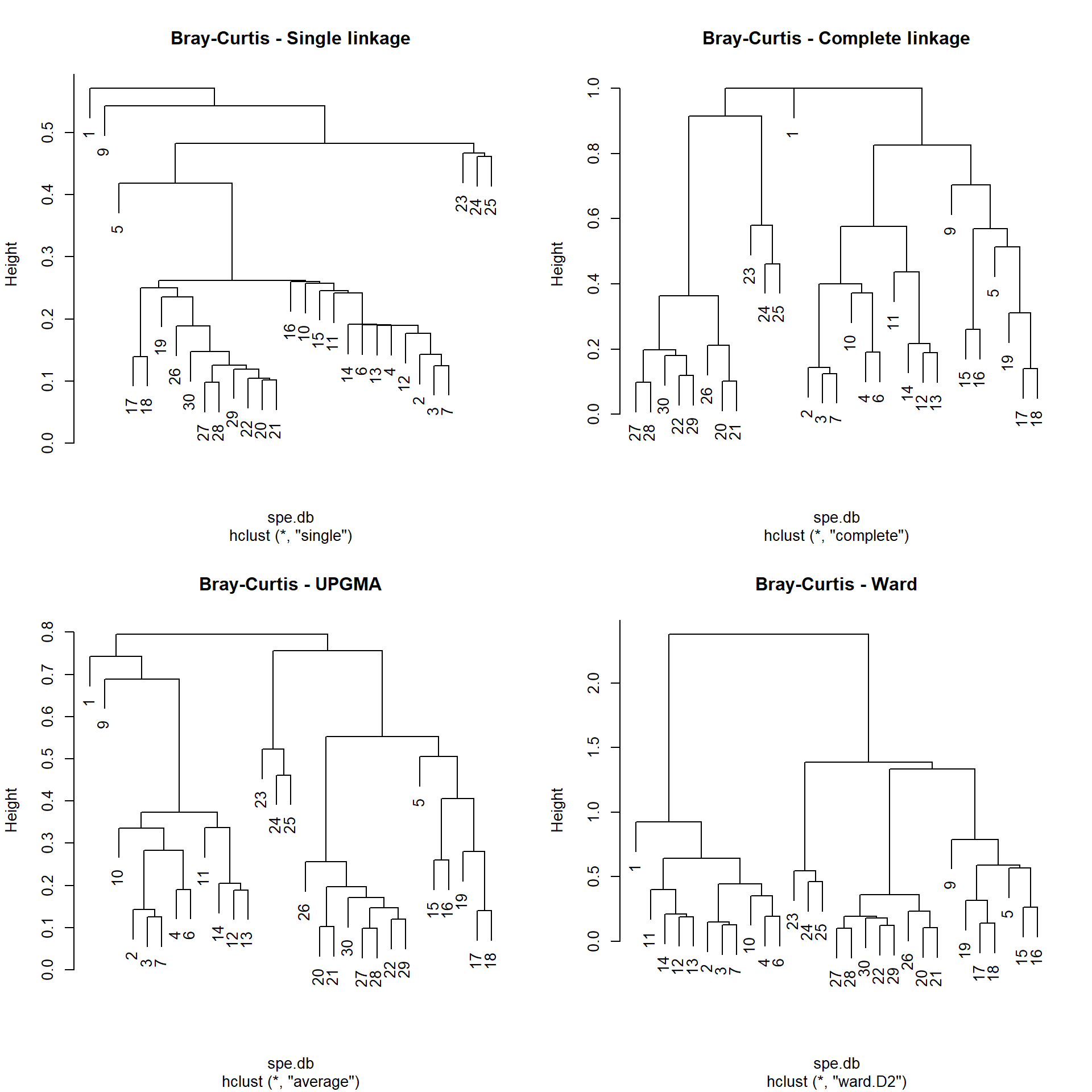
Com podeu veure, obtenim resultats diferents en funció del mètode aglomeratiu emprat. La pregunta és, amb quin d’ells ens quedem? La veritat és que tots ells són vàlids, i qualsevol podria ser adequat en funció del nostre objectiu. Per exemple, si estem explorant les dades, single linkage és útil per identificar gradients, mentres que complete linkage ajuda a identificar discontinuitats.
2.3.1 Comparativa i elecció del millor mètode
Si no tenim cap criteri específic per escollir un mètode aglomeratiu en concret, el que es fa és comparar els diferents dendrogrames a través de la seva distància cofenètica.
La distància cofenètica entre dos objectes en un dendrograma és la distància en què els dos objectes es converteixen en membres del mateix grup. Així doncs, una matriu cofenètica és una matriu que representa les distàncies cofenètiques entre tots els parells d’objectes.
Comparant la matriu de distàncies original (e.g. Bray-Curtis en el nostre cas) i la matriu de distàncies cofenètiques podem tenir una idea de com de fidel és el nostre dendrograma a les dades reals. Per exemple, si punts de mostreig que tenen distàncies de Bray-Curtis molt petites (molta similaritat) apareixen molt allunyades en el dendrograma, voldrà dir que la nostra anàlisis de classificació està lluny de ser òptima.
Per tal de comparar aquestes dues matrius (distància Bray-Curtis i cofenètica) se sol utilizar una anàlisis de correlació (e.g., Pearson, Spearman, Kendall), que en aquest context pren el nom de correlació cofenètica. Es calculen aquestes correlacions per a cada dendrograma i s’escull el que té una correlació cofenètica més elevada.
Anem a calcular les correlacions cofenètiques per als quatre dendrogrames que hem computat més amunt:
# Single linkage clustering
spe.db.single.coph <- cophenetic(spe.db.single)
cor(spe.db, spe.db.single.coph)## [1] 0.5408425# Complete linkage clustering
spe.db.comp.coph <- cophenetic(spe.db.complete)
cor(spe.db, spe.db.comp.coph)## [1] 0.8088618## [1] 0.8249401## [1] 0.7409896Ens quedaríem amb el mètode aglomeratiu UPGMA (average linkage), ja que té la correlació cofenètica més elevada (0.82). Podem concloure que el dendrograma UPGMA és el que manté la relació més estreta amb la matriu de distàncies original.
Alternativament, també podem comparar els dendrogrames a través de la distància de Gower, que es calcula com la suma del quadrats de les diferències entre les distàncies cofenètiques i les distàncies originals (Bray-Curtis en el nostre cas):
## [1] 57.82551## [1] 22.87238## [1] 8.253247## [1] 556.3019En aquest cas, com més gran és la distància de Gower, vol dir que més s’allunya el dendrograma de la matriu de distàncies original. Per tant, ens hem de quedar amb el dendrograma que tingui un valor més baix (de nou UPGMA; 8,25).
NOTA: En general els dos criteris (correlació cofenètica i distància de Gower) solen convergir, però pot passar que donin lloc a conclusions lleugerament diferents. En aquest cas podeu quedar-vos amb els dos, i un cop acabades les anàlisis mirar quin dels dos dóna lloc a resultats més coherents des d’un punt de vista ecològic.
Aquest seria doncs el nostre dendrograma final:

2.3.2 Escollir el nombre de grups
Un cop hem escollit el mètode d’aglomeració i tenim el nostre dendrograma final, el següent pas és decidir a quin nivell fem el tall i amb quants clústers o grups ens quedem.
Hi ha vàries maneres de fer-ho. Es pot fer de manera visual i subjectiva a partir de la forma del dendrograma, o bé a partir de certs criteris com els gràfics de nivel de fusió o els gràfics de Silhouette Widths. Per aquest exemple utilitzarem els gràfics de Silhouette Widths.
Silhouette width és una mesura del grau de pertinença d’un objecte al seu grup o clúster. Es basa en comparar la distància mitjana entre aquest objecte i tots els objectes del seu clúster amb la mateixa mesura calculada per al següent clúster més proper. Els valors poden oscil·lar entre -1 i 1, i valors majors indiquen una més bona classificació d’aquell objecte. Valors negatius solen indicar que l’objecte ha estat assignat en un clúster erroni.
Per a calcular les Silhouette width del nostre dendrograma UPGMA utilitzarem la funció silhouette() del package cluster.
asw <- numeric(nrow(spe))
for (k in 2:(nrow(spe)-1)) {
sil <- silhouette(cutree(spe.db.UPGMA, k=k), spe.db)
asw[k] <- summary(sil)$avg.width
}
k.best <- which.max(asw)
plot(1:nrow(spe), asw, type="h",
main="Silhouette-optimal number of clusters, UPGMA",
xlab="k (number of groups)", ylab="Average silhouette width")
axis(1, k.best, paste("optimum",k.best,sep="\n"), col="red", font=2,
col.axis="red")
points(k.best, max(asw), pch=16, col="red", cex=1.5)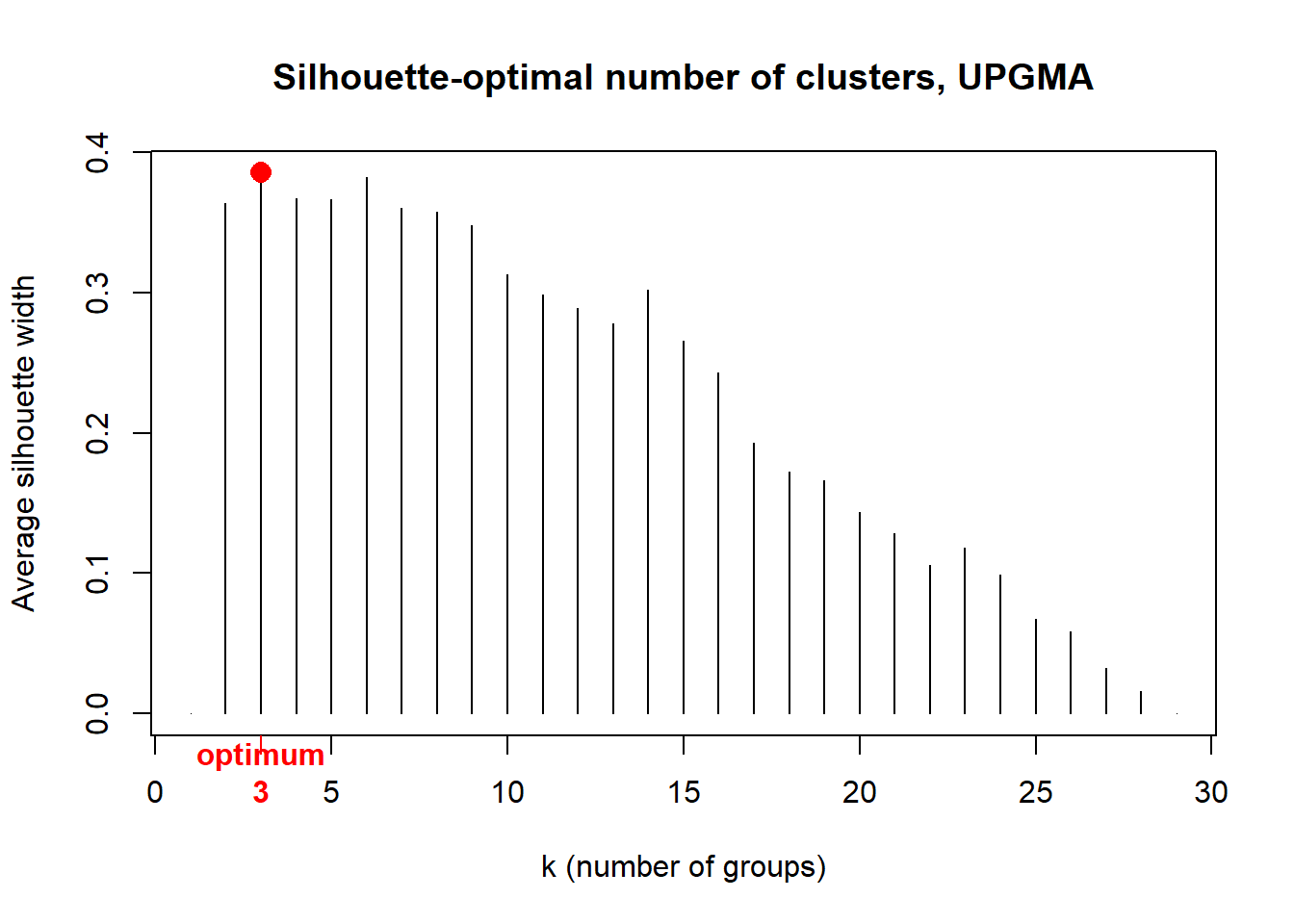
cat("", "Silhouette-optimal number of clusters k =", k.best, "\n",
"with an average silhouette width of", max(asw), "\n")## Silhouette-optimal number of clusters k = 3
## with an average silhouette width of 0.3852207#aquí l'únic que cal anar canviant és el nom del dendrograma que hauríeu explorar, en aquest cas la millor solució era la donada per el mètode Average linkage (UPGMA). "spe.db.UPGMA" és el nom d'aquesta solució. Si voleu mirar les agrupacions que sortirien d'altres solucions cal anar canviant aquest nom pel que correspongui. També podeu canviar la mesura de distància o similitud, en aquest cas només hem provat la distancia Bray-Curtis (spe.db), però si tinguessiu altres opcions haurieu d'anar localitzant i canviant com correspongui aquest nom.D’acord amb aquest criteri, el número òptim de grups o clústers és 3, tot i que també podria ser 6, ja que tenen una Silhouette width molt semblant. Quan hi ha vàries opcions es sol escollir en base al context de l’anàlisi, per exemple, en funció de quina de les opcions té més sentit ecològic.
Com que ara per ara no tenim cap raó per decantar-nos cap a 6 grups, escollirem 3 grups simplement perquè és el número òptim segons el gràfic anterior. Quedar-nos amb 3 grups es correspon amb una alçada de tall d’aproximadament 0.75 (línia vermella discontínua).
plot(spe.db.UPGMA, hang=-1,
labels = rownames(spe),
main = "Bray-Curtis - UPGMA")
#abline(h=0.54, lty=3, col='dark red')
abline(h=0.75, lty=3, col='dark red')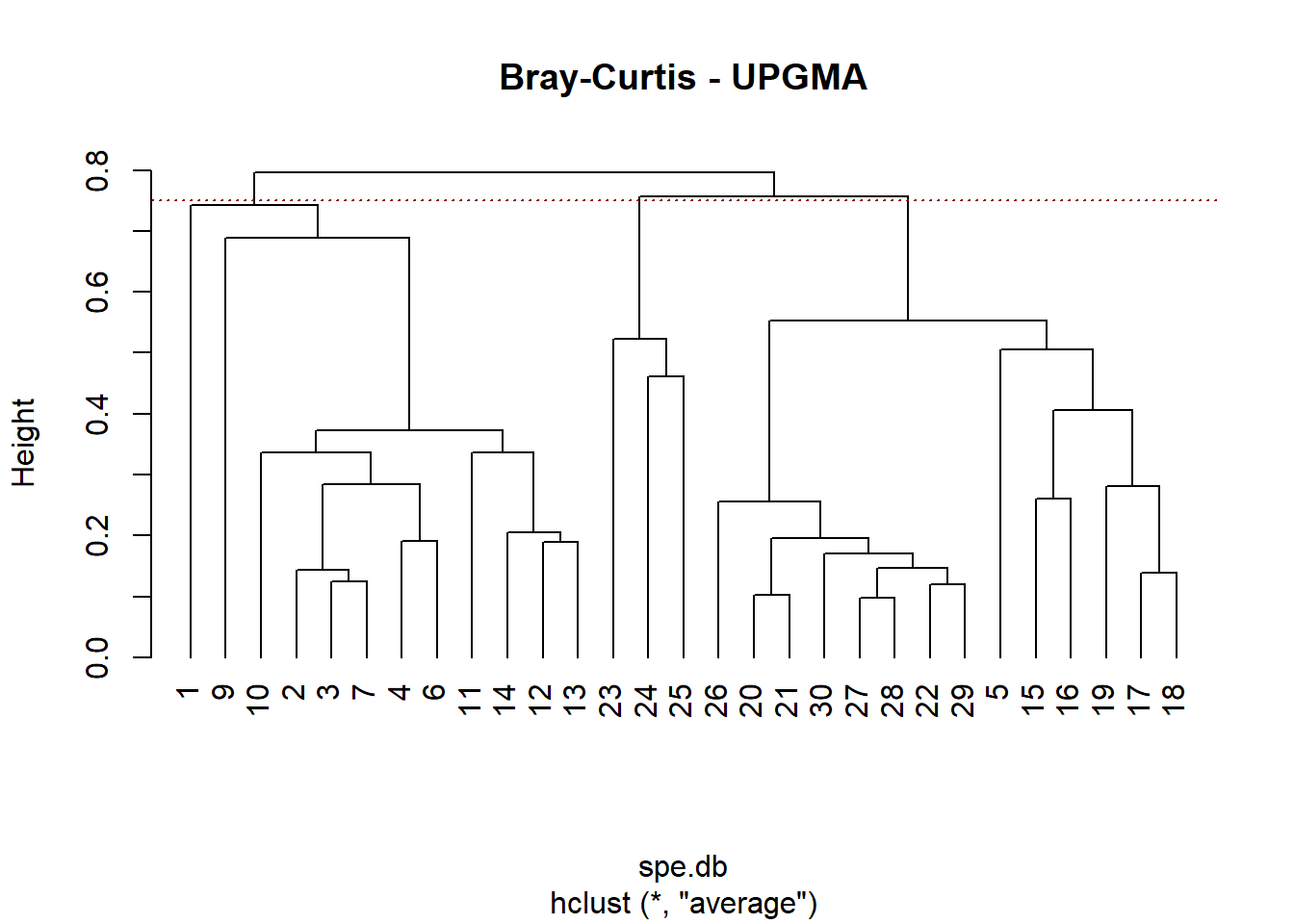
Per fer la separació dels grups més visual, podem reordenar el dendrograma i diferenciar clarament els tres grups.
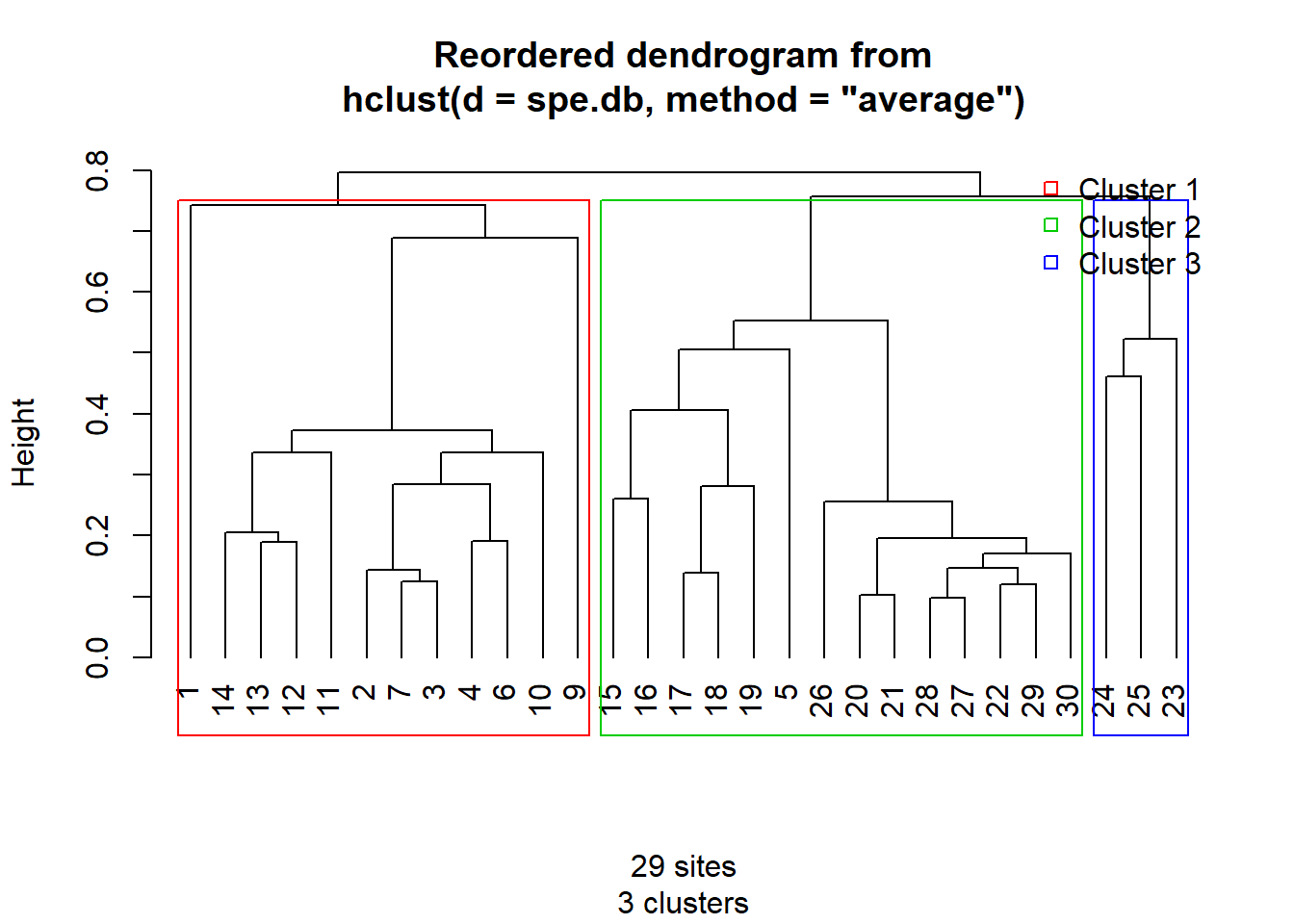
Un cop escollit el número de grups, cal verificar la classificació de les diferents observacions, és a dir, mirar que no s’hagi assignat cap (o almenys no gaires) observacions a un grup equivocat. I això ho podem mirar fàcilment a través d’un Silhouette plot:
# escollim el nombre de grups que abans s'ha seleccionat com a òptim
k <- 3
# Silhouette plot
cutg <- cutree(spe.db.UPGMA, k=k)
sil <- silhouette(cutg, spe.db)
rownames(sil) <- row.names(spe)
plot(sil, main="Silhouette plot - Euclidian - UPGMA",
cex.names=0.8, col=2:(k+1), nmax=100)
Hi ha una observació del grup 2 (punt de mostreig 15) que té una silhouette width negativa, i que per tant no ha quedat ben classificada. Però en general hem aconseguit una classificació molt coherent!
Ara que ja tenim el dendrograma final i els grups definits, podem explorar quines característiques diferencien els tres grups. Una bona manera és fer-ho visual, utilitzant un heat map que mostri la composició de la comunitat de peixos amb els llocs de mostreig ordenats en funció del nostre dendrograma:
spe.dbUPGMAo <- reorder.hclust(spe.db.UPGMA, spe.db)
dend <- as.dendrogram(spe.dbUPGMAo)
or <- vegemite(spe, spe.dbUPGMAo)
# Heat map of the doubly ordered community table, with dendrogram
heatmap(t(spe[rev(or$species)]), Rowv = NA, Colv = dend, col = c("white", brewer.pal(5, "Greens")),
scale = "none", margin = c(4, 4), ylab = "Species (weighted averages of sites)",xlab = "Sites")
par(xpd=NA)
rect(0.122,-0.114,0.362,0.945, border = 2)
rect(0.363,-0.114,0.641,0.945, border = 3)
rect(0.642,-0.114,0.7,0.945, border = 4)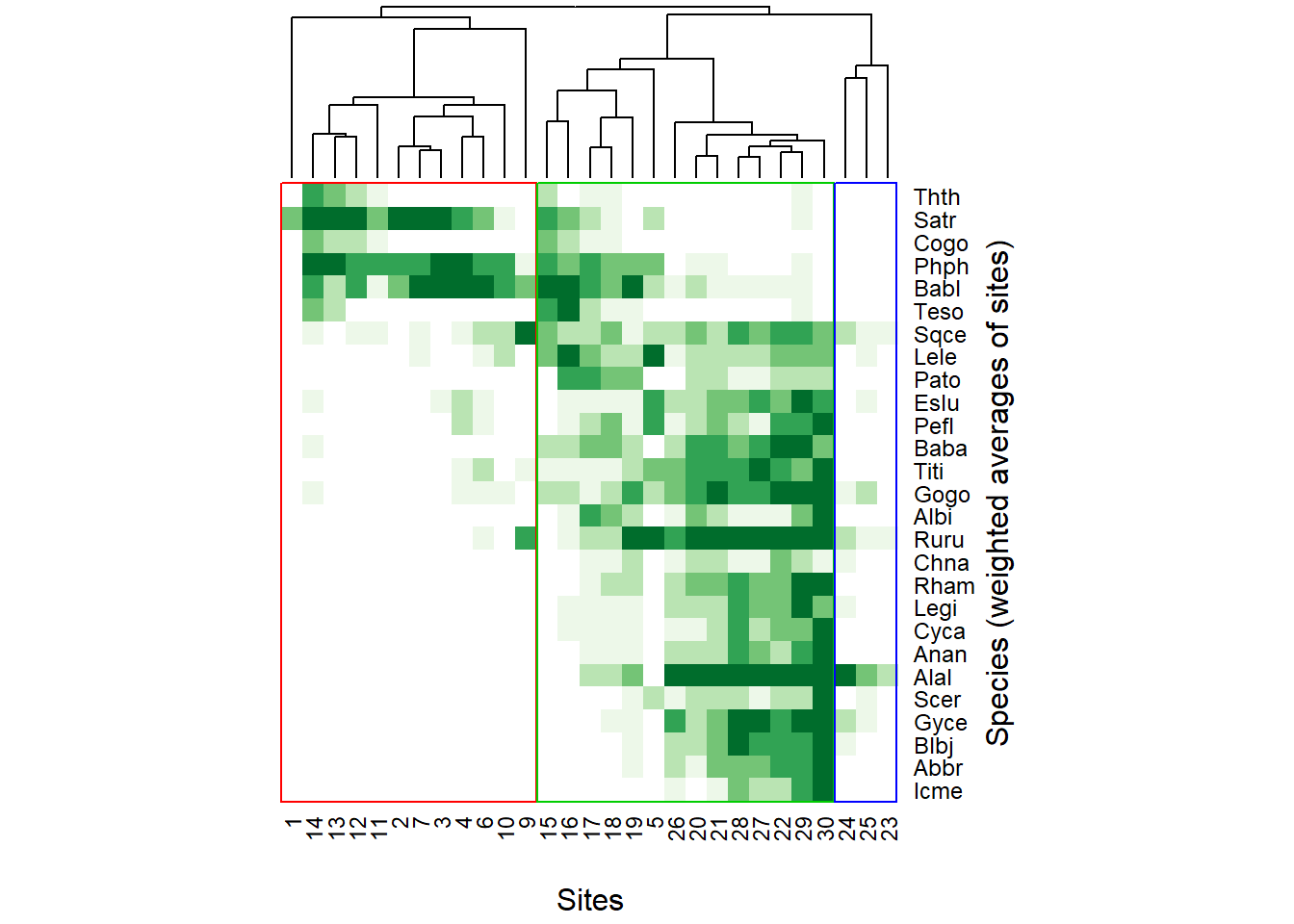
La intensitat de color reflecteix l’abundància de cada espècie per a cada punt de mostreig.
Veieu alguna diferència entre els tres grups? Els grups 1 i 2 (vermell i verd) són molt diferents tant en termes de riquesa d’espècies com de les espècies en concret que habiten el riu, oi?. I després tenim el grup 3 (blau), que agrupa tres punts de mostreig (23-25) amb molt poca diversitat de peixos, i on bàsicament predomina l’espècie Alal.
2.3.3 Visualització dels resultats
Ara podem fer una ullada a com estan distribuïts aquests 3 grups al llarg del riu Doubs.
Per a això utilitzarem la base de dades spa, que conté les coordenades geogràfiques (longitud, latitud) dels punts de mostreig.
Grafiquem els punts i els pintem en funció de l’anàlisi de classificació que hem fet:
plot(spa, asp = 1.5, type = "n", main = "Site Locations", xlab = "x coordinate (km)", ylab = "y coordinate (km)")
# Add a blue line connecting the sites along the Doubs River
lines(spa, col = "light blue")
# Add the site labels
text(spa, row.names(spa), cex = 1)
# Add text blocks
text(68, 20, "Upstream", cex = 1.2, col = "cornflowerblue")
text(15, 35, "Downstream", cex = 1.2, col = "cornflowerblue")
colors <- c(2:4)
text(spa, row.names(spa), cex = 1, col=colors[cutg])
legend('topleft', c('Group 1', 'Group 2', 'Group 3'), fill = 2:4)
Sembla que hi ha dues parts molt diferenciades del riu pel que fa a la seva comunitat de peixos. Per una part el curs alt del riu (punts 1-14), on trobem comunitats de peixos moderadament diverses dominades principalment per les espècies Thth, Satr, Cogo, PhPh, Babl (grup 1, veure heatmap anterior). I per l’altra, la part de curs baix (15-30), amb comunitats molt diverses formades per espècies que generalment no es troben al curs alt del riu (grup 2). Aquestes diferències entre curs alt i baix del riu podrien ser degudes per exemple a canvis en la geomorfologia i temperatura del riu, o també per una diferent influència antròpica. En tot cas ho explorarem més endavant.
Cal destacar els punts classificats com a grup 3 (23-25). Semblen uns punts de mostreig molt particulars i valdria la pena fer-hi un cop d’ull amb més detall. Una bona primera aproximació és agafar un mapa i veure si hi ha alguna cosa al voltant que els pugui fer diferents. Podeu remenar el mapa de sota a veure si hi veieu alguna cosa:
longitude <- latlong$LongitudeE
latitude <- latlong$LatitudeN
site <- as.character(latlong$Site)
background <- addTiles(leaflet())
mymap1 <-
addMarkers(
background,
lng = longitude,
lat = latitude,
label = site,
labelOptions = labelOptions(noHide = TRUE, textOnly = TRUE)
)
mymap1ATENCIÓ: Recordeu que els resultats d’una anàlisis de classificació són altament depenents de la mesura d’associació que haguem escollit, de les transformacions que haguem aplicat a les dades, previ al càlcul de la matriu de distàncies, i del mètode aglomeratiu emprat. Per estar segurs de que el resultat que hem obtingut és robust, es sol repetir l’anàlisi utilitzant mesures d’associació alternatives (e.g. Chord i o Hellinger per dades d’abundància d’espècies) o diferents transformacions de les dades.
Sabríeu repetir l’anàlisi fent servir la distància de la corda (Chord)? Obtenim els mateixos resultats?
2.4 Anàlisis de clúster no jeràrquic (k-means)
Ara mirarem d’analitzar de nou les mateixes dades però utilitzant un mètode de classificació no jeràrquic, l’anàlisi k-means.
k-means té com a objectiu assignar objectes (punts de mostreig en el nostre cas) a un nombre de clústers (k) prèviament definits, de manera que es maximitzi la separació entre aquests clústers al mateix temps que es minimitzen les distàncies dins de cada clúster.
k-means té un particularitat: és un mètode lineal. Això implica que només és compatible amb mesures d’associació mètriques (e.g., Euclidian, Chord, Manhattan, Hellinger). Mesures semi-mètriques com la distància de Bray-Curtis que hem utilitzat abans no serien vàlides.
Per tant, primer ens cal calcular una nova matriu de distàncies diferent a la que teníem, per exemple utilitzant la distància de la corda, que també és adequada per dades d’abundància. La distància de la corda és simplement la distància euclídia sobre dades que han estat prèviament transformades mitjançant la transformació de la corda.
spe.norm <- decostand(spe, "normalize") # transformació de la corda. Aquesta transformació divideix cada valor de la matriu de dades per l'arrel quadrada de la seva suma marginal de quadrats.
spe.ch <- vegdist(spe.norm, "euc") # distància euclídia de les dades transformades
coldiss(spe.ch, byrank=F,diag=T)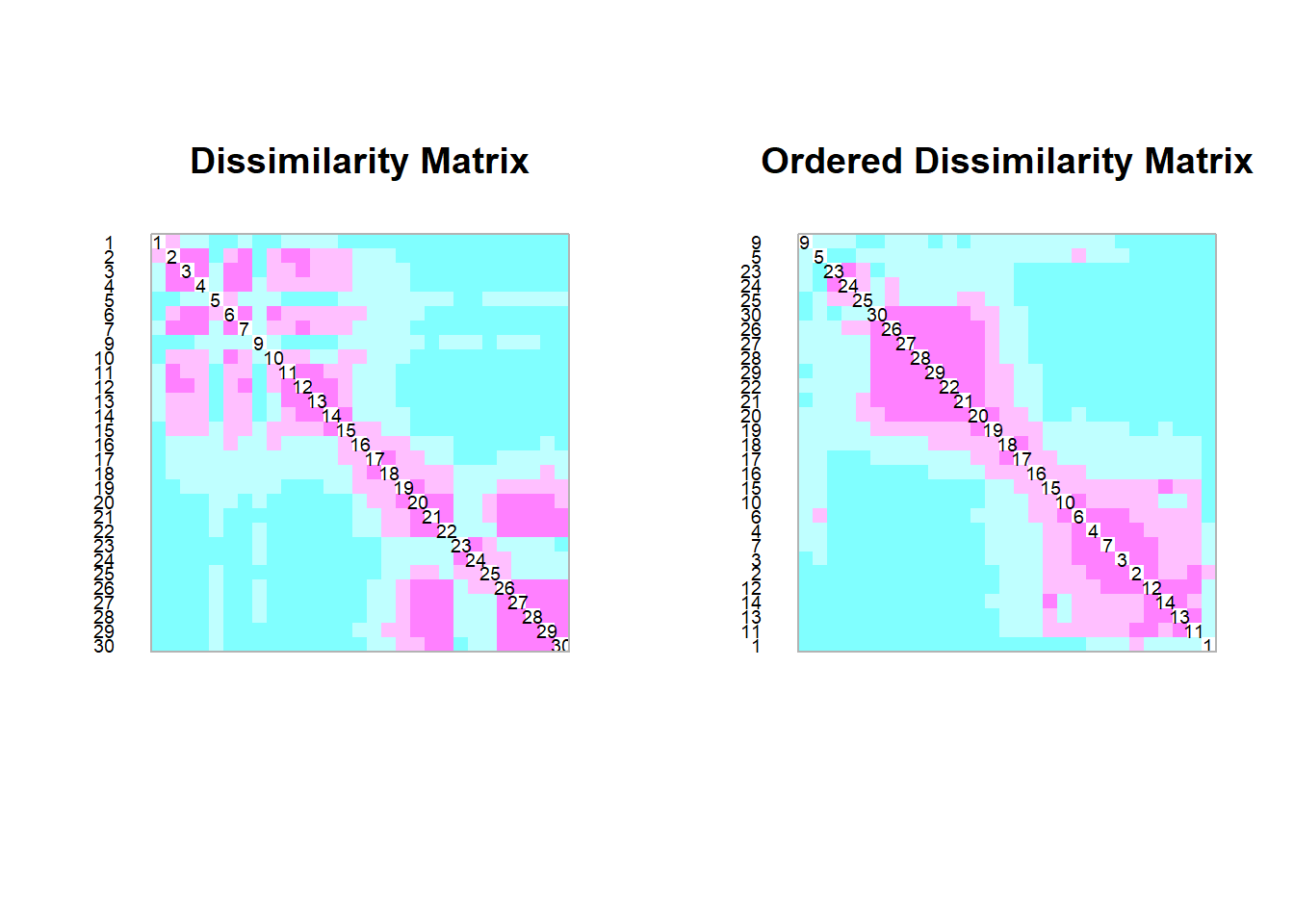
Un cop tenim la matriu de distàncies apropiada, ja podem dur a terme l’anàlisi k-means. Si ja tenim predefinit el número de grups o clústers, és tan senzil com utilitzar la funció kmeans(). Per exemple, podem fixar el nombre de grups o clústers (k) a 3 basant-nos en els resultats de l’anàlisi jeràrquic que hem fet abans.
Però sovint el que es fa és provar diferents solucions amb diferents valors de k. Per a provar-ne un quants, podem anar re-escribint la línia de codi manualment canviant el nombre del centers", o bé podem utilitzar la funció cascadeKM() que ho fa de manera automàtica i a més ens proporcionar criteris per escollir quina és la millor solució.
spe.ch.KM.cascade <- cascadeKM(spe.ch, inf.gr = 2, sup.gr = 10, iter = 1000, criterion = "calinski") # es pot escollir entre els criteris de calinski o ssi (simple structure index)
plot(spe.ch.KM.cascade, sortg = TRUE)
2.4.1 Escollir el nombre de grups
El criteri de “calinski” compara la suma de quadrats dins de cada grup amb la suma de quadrats entre grups (similar a l’ANOVA). Funciona bé sobretot si els grups creats són de mides similars. Al panell de la dreta del gràfic superior, podem veure en vermell el valor de k (número de grups) que dóna la solució òptima segons calinski, i en taronja altres solucions que podrien ser d’interès.
Segons el criteri de Calinski, ens quedaríem amb la solució per a k=2, és a dir, dos grups o clústers. De totes maneres, provarem també altres solucions que també podrien ser interessants, les marcades en taronja en el panell de la dreta (k=4,7,8,9,10)
spe.ch.kmeans2 <- kmeans(spe.ch, centers=2, nstart=1000)
spe.ch.kmeans4 <- kmeans(spe.ch, centers=4, nstart=1000)
spe.ch.kmeans7 <- kmeans(spe.ch, centers=7, nstart=1000)
spe.ch.kmeans8 <- kmeans(spe.ch, centers=8, nstart=1000)
spe.ch.kmeans9 <- kmeans(spe.ch, centers=9, nstart=1000)
spe.ch.kmeans10 <- kmeans(spe.ch, centers=10, nstart=1000)Igual que amb els mètodes jeràrquics, podem calcular les Silhouette widths per veure si hi ha algunes observacions mal classificades i també per acabar de decidir amb quants grups ens quedem:
par(mfrow=c(2,3))
sil2 <- silhouette(spe.ch.kmeans2$cluster, spe.ch)
rownames(sil2) <- row.names(spe)
plot(sil2, main="Silhouette plot - k-means ; k=2", cex.names=0.8, col=rainbow(2,s = 0.5), nmax=100)#average width=0.39
sil4 <- silhouette(spe.ch.kmeans4$cluster, spe.ch)
rownames(sil4) <- row.names(spe)
plot(sil4, main="Silhouette plot - k-means ; k=4", cex.names=0.8, col=rainbow(4,s = 0.5), nmax=100)#average width=0.37
sil7 <- silhouette(spe.ch.kmeans7$cluster, spe.ch)
rownames(sil7) <- row.names(spe)
plot(sil7, main="Silhouette plot - k-means ; k=7", cex.names=0.8, col=rainbow(7,s = 0.5), nmax=100)#average width=0.31
sil8 <- silhouette(spe.ch.kmeans8$cluster, spe.ch)
rownames(sil8) <- row.names(spe)
plot(sil8, main="Silhouette plot - k-means ; k=8", cex.names=0.8, col=rainbow(8,s = 0.5), nmax=100)#average width=0.31
sil9 <- silhouette(spe.ch.kmeans9$cluster, spe.ch)
rownames(sil9) <- row.names(spe)
plot(sil9, main="Silhouette plot - k-means ; k=9", cex.names=0.8, col=rainbow(9,s = 0.5), nmax=100)#average width=0.32
sil10 <- silhouette(spe.ch.kmeans10$cluster, spe.ch)
rownames(sil10) <- row.names(spe)
plot(sil10, main="Silhouette plot - k-means ; k=10", cex.names=0.8, col=rainbow(10, s = 0.5), nmax=100)#average width=0.32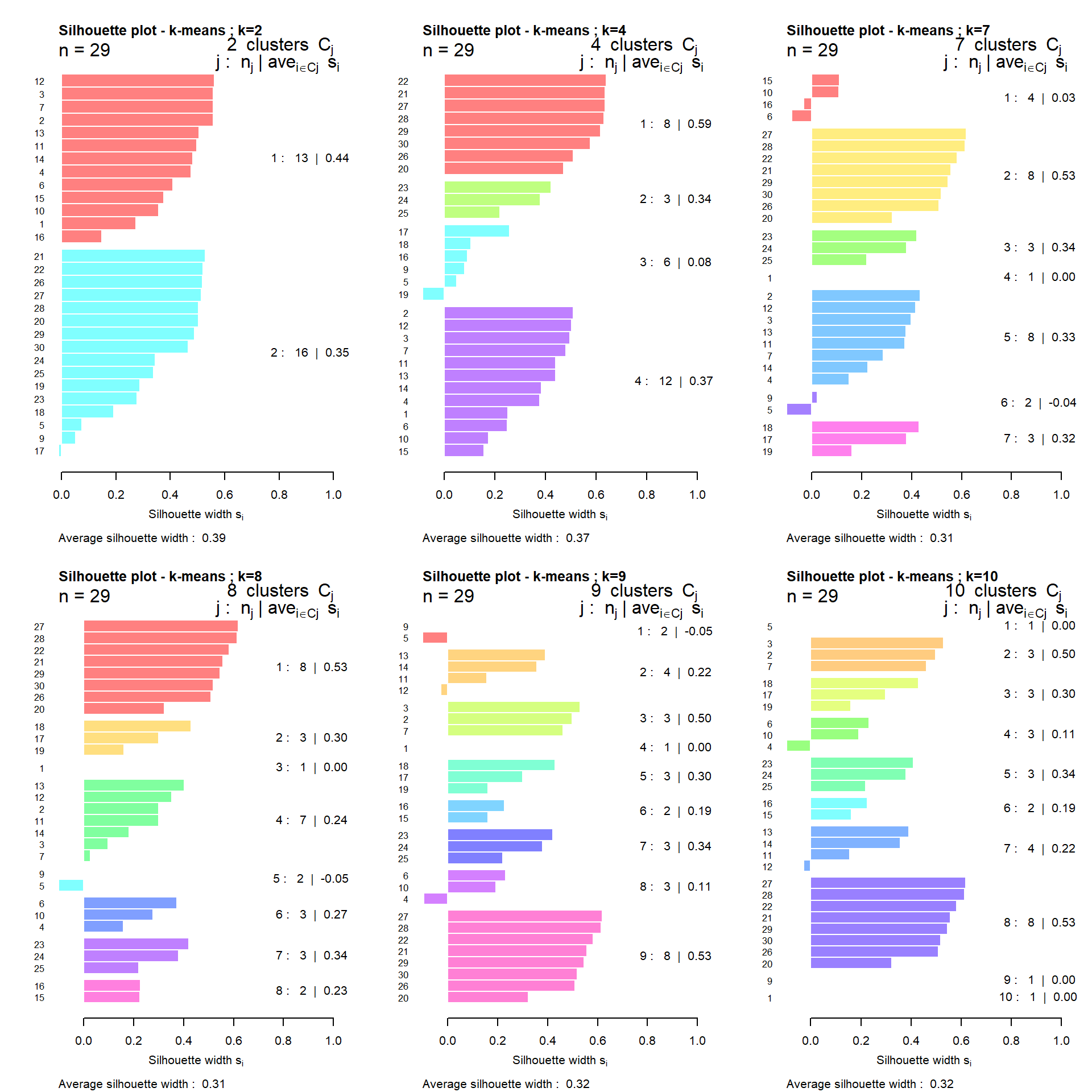
Si comparem les average silhouette widths, ens quedaríem amb les solucions per a 2 i 4 grups, que tenen una average width semblant (0.39 i 0.37) i força més gran que la resta de solucions.
2.4.2 Visualització dels resultats
Ja tenim els nostres clústers k-means finals! Ara podem visualitzar-los sobre el mapa per veure si són més o menys coeherents amb l’anàlisi jeràquica que havíem fet abans:
par(mfrow=c(1,2))
plot(spa, asp = 1.5, type = "n", main = "k = 2", xlab = "x coordinate (km)", ylab = "y coordinate (km)")
lines(spa, col = "light blue")
text(spa, row.names(spa), cex = 1)
text(68, 20, "Upstream", cex = 1.2, col = "cornflowerblue")
text(15, 35, "Downstream", cex = 1.2, col = "cornflowerblue")
colors <- c(2:3)
text(spa, row.names(spa), cex = 1, col=colors[spe.ch.kmeans2$cluster])
legend('topleft', c('Group 1', 'Group 2'), fill = 2:3)
plot(spa, asp = 1.5, type = "n", main = "k = 4", xlab = "x coordinate (km)", ylab = "y coordinate (km)")
lines(spa, col = "light blue")
text(spa, row.names(spa), cex = 1)
text(68, 20, "Upstream", cex = 1.2, col = "cornflowerblue")
text(15, 35, "Downstream", cex = 1.2, col = "cornflowerblue")
colors <- c(6,7,8,9)
text(spa, row.names(spa), cex = 1, col=colors[spe.ch.kmeans4$cluster])
legend('topleft', c('Group 1', 'Group 2', 'Group 3', 'Group 4'), fill = c(6,7,8,9))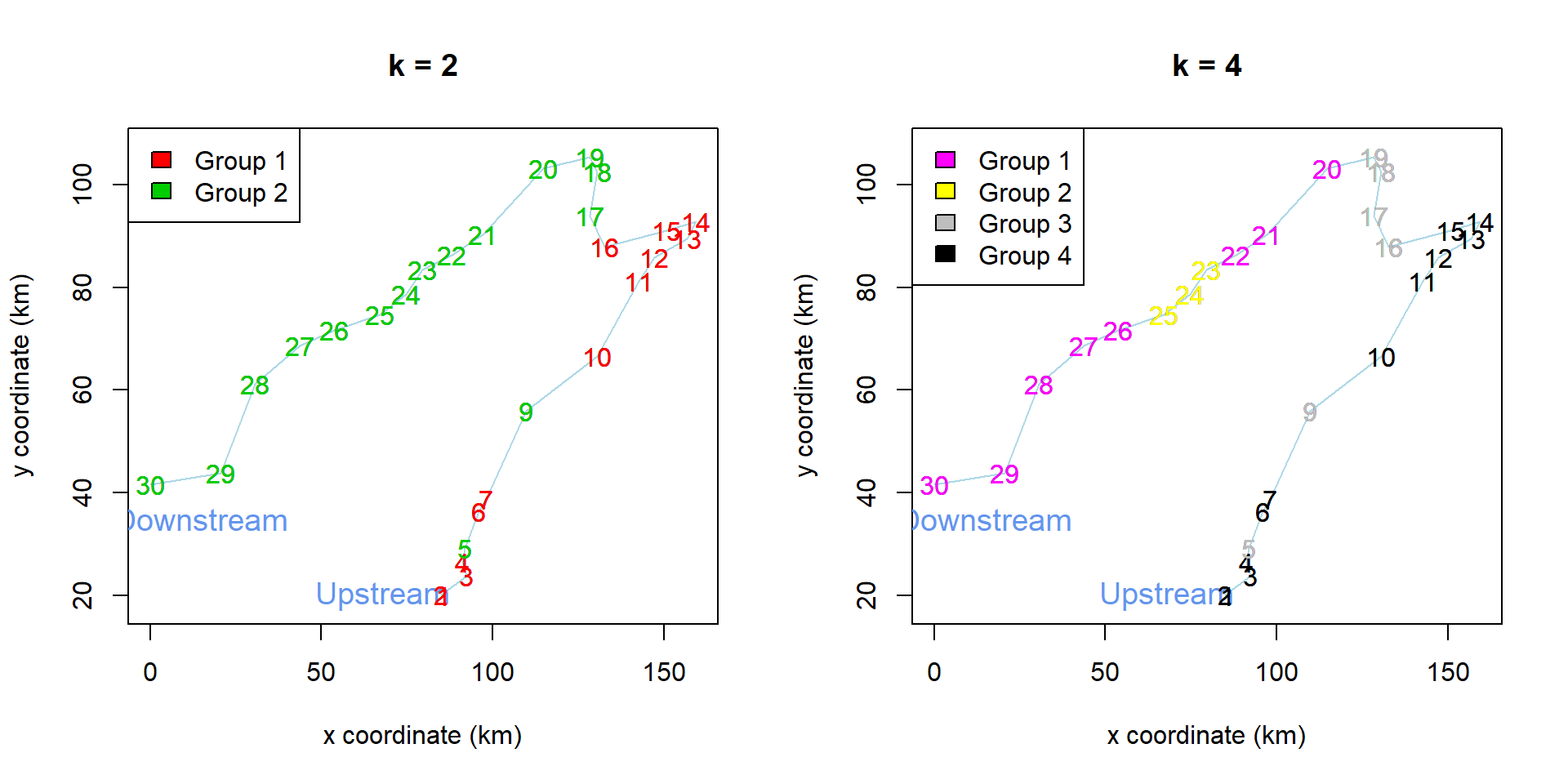
Ambdós solucions són molt coherents amb els resultats que havíem obtingut mitjançant la classificació jeràrquica. De nou, podem veure diferenciat el curs alt i baix del riu pel que fa a la comunitat de peixos, especialment en la classificació en dos clúster. Després, si ens fixem en la de 4 grups, podem veure com també identifica els punts 23, 24 i 25 com a llocs amb una comunitat molt diferenciada, tal i com havíem vist anteriorment. La solució per a 4 grups també indica que hi ha una comunitat de peixos diferent en els punts 16-19, la qual cosa podria suggerir una mena de transició o gradient entre el curs alt i baix del riu.
IMPORTANT: Com hem anat veient, no hi ha una manera única de fer una anàlisi de classificació. La gràcia està en combinar diferents mètodes per tal d’entendre les dades que tenim a les mans i obtenir conclusions robustes.
2.5 Relació entre els grups de peixos i variables ambientals
Ara ja tenim una idea de com varia la comunitat de peixos al llarg del riu Doubs, al menys de manera discreta o discontínua.
El següent pas seria veure què pot estar determinant aquests diferents grups o clústers al llarg del riu. Una bona manera de començar a explorar-ho és mirar si aquests grups basats en la comunitat de peixos coincideixen amb discontinuitats de caràcter ambiental al llarg del riu.
Podem començar per visualitzar algunes de les variables ambientals al llarg del riu:
par(mfrow = c(2, 2))
plot(spa, asp = 1, cex.axis = 0.8, main = "Discharge", pch = 21, col = "white", bg = "gray30", cex = 5 * env$dis / max(env$dis), xlab = "x", ylab = "y")
lines(spa, col = "light blue")
plot(spa, asp = 1, cex.axis = 0.8, main = "Oxygen", pch = 21, col = "white", bg = "gray30", cex = 5 * env$oxy / max(env$oxy),xlab = "x", ylab = "y")
lines(spa, col = "light blue")
plot(spa, asp = 1, cex.axis = 0.8, main = "Nitrate", pch = 21, col = "white", bg = "gray30", cex = 5 * env$nit / max(env$nit), xlab = "x", ylab = "y")
lines(spa, col = "light blue")
plot(spa, asp = 1, cex.axis = 0.8,main = "Ammonium", pch = 21, col = "white", bg = "gray30", cex = 5 * env$amm / max(env$amm), xlab = "x", ylab = "y")
lines(spa, col = "light blue")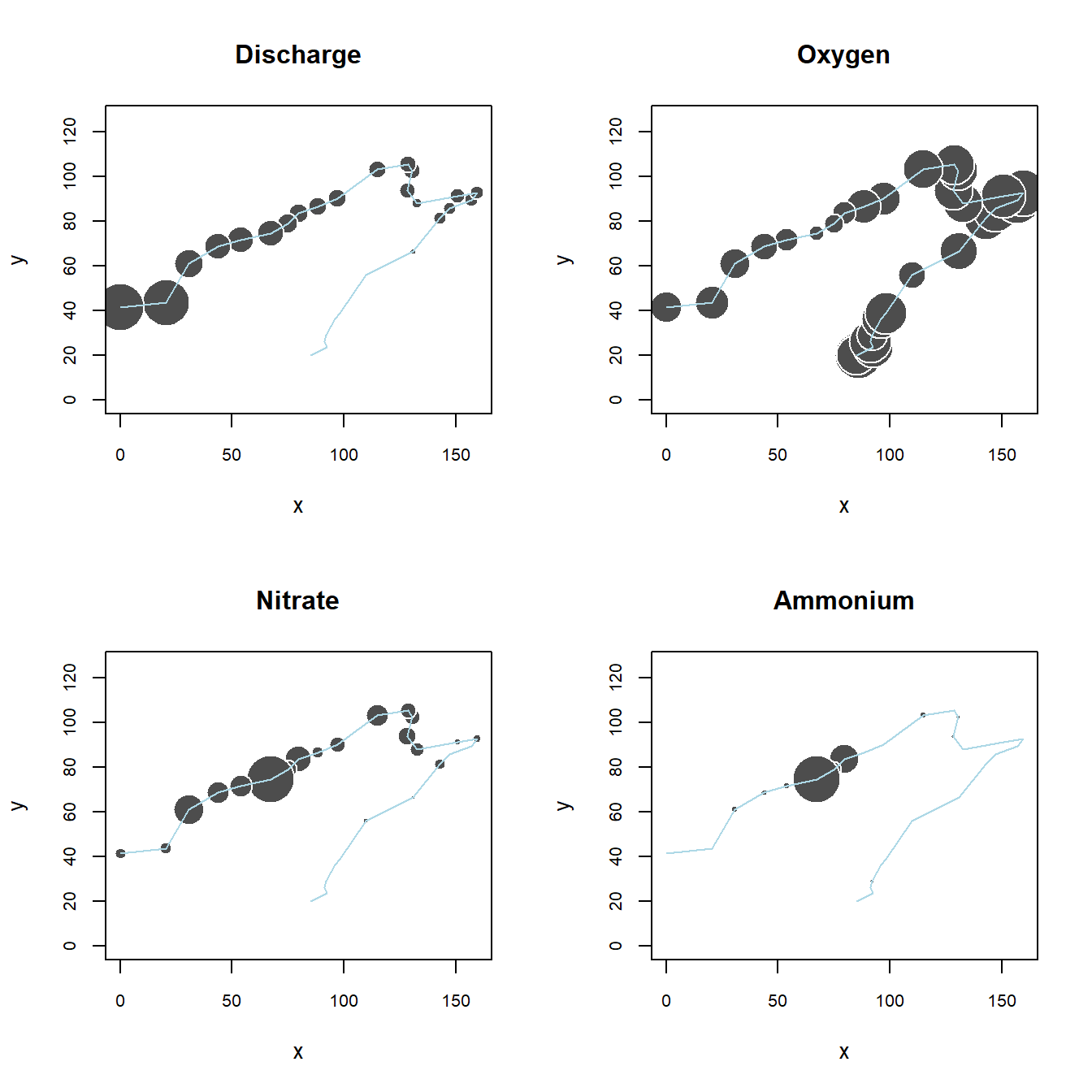
Fent una ullada ràpida als gràfics sembla que els grups o clústers que hem calculat podrien tenir una relació molt directa amb el cabal i les condicions fisicoquímiques del riu, oi?. Entre els cursos alt i baix del riu hi ha forces diferències. Tenim un cabal que creix gradualment, i per tant el curs alt té cabals molt més baixos que el curs baix. També, sembla que el curs alt té més oxigen i molts menys nutrients. I fixeu-vos que a meitat del tram baix, coincidint amb els punts 23-25, tenim molt poc oxigen i un pic de nitrat i amoni.
Ho podem explorar també quantitativament a través de boxplots separats per cada grup o clúster i testar-ho mitjançant una ANOVA. Agafem com a exemple els 3 grups derivats de l’anàlisi jeràrquica (dendrograma):
par(mfrow = c(2, 2))
boxplot(env$dis ~ cutg, main = "Discharge", las = 1, ylab = expression("Discharge (m"^3*"s"^-1*")"), col = (1:k) + 1, varwidth = TRUE, xlab='Cluster group')
boxplot(env$oxy ~ cutg, main = "Oxygen", las = 1, ylab = "Dissolved oxygen (mg/L)", col = (1:k) + 1, varwidth = TRUE, xlab='Cluster group')
boxplot(env$nit ~ cutg, main = "Nitrate", las = 1, ylab = "Nitrate (mg/L)", col = (1:k) + 1, varwidth = TRUE, xlab='Cluster group')
boxplot(env$amm ~ cutg, main = "Ammonium", las = 1, ylab = "Ammonium (mg/L)", col = (1:k) + 1, varwidth = TRUE, xlab='Cluster group')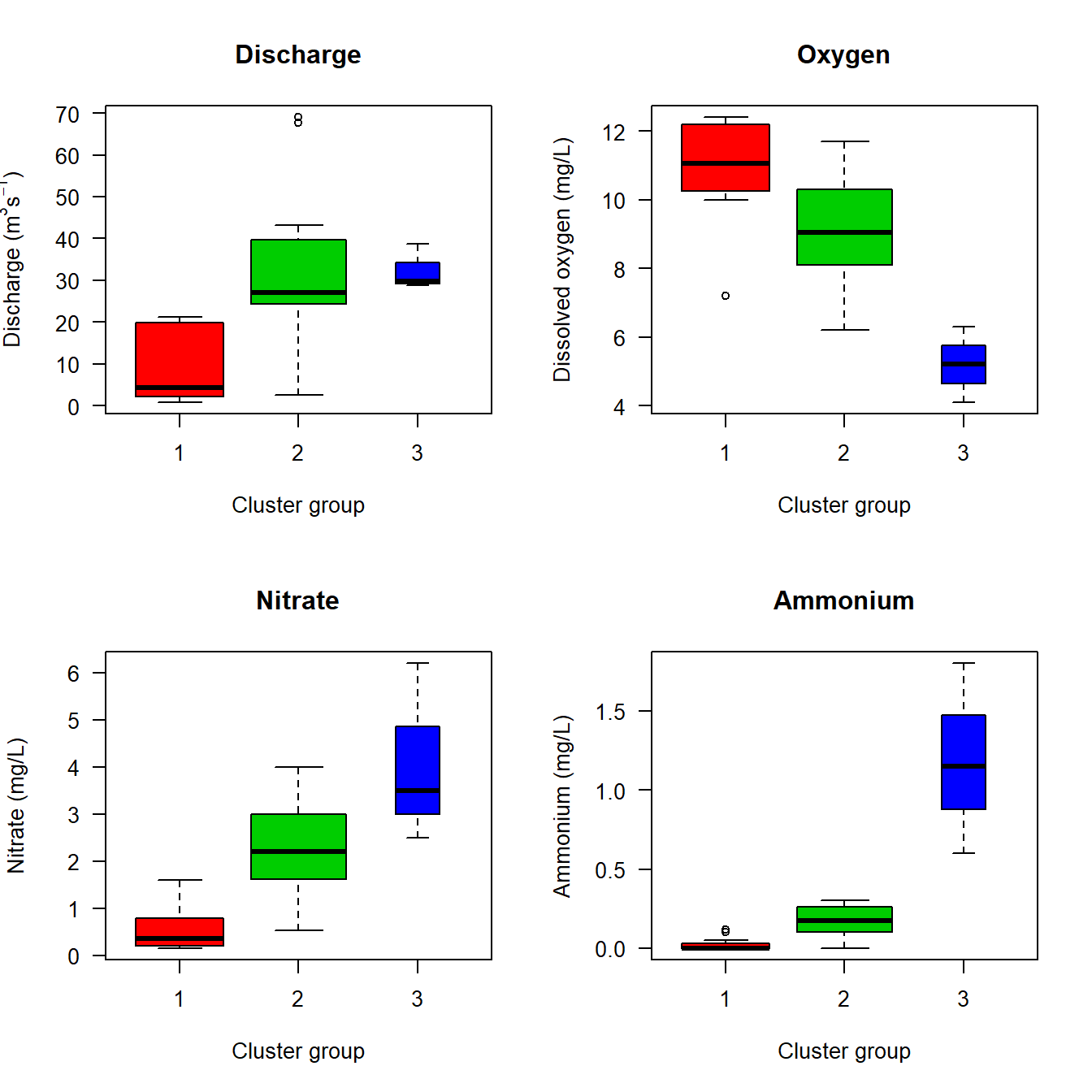
# si volem mirar-ho també per als 2 o 4 grups derivats de k-means, cal canviar la variable 'cutg' per spe.ch.kmeans2$cluster o spe.ch.kmeans4$cluster A primera vista sembla que es confirma el que vèiem en els gràfics anteriors, però abans que res cal verificar que les diferències entre grups són estadísticament significatives mitjançant una ANOVA. Avui, per anar directe al gra, no ensenyarem tots els passos de comprovació de les assumpcions de model lineal (normalitat de residus i homogeneitat de variàncies). Tots els casos compleixen les assumpcions, i les ANOVAs són significatives en tots els casos:
anova(lm(sqrt(env$dis) ~ as.factor(cutg))) # Sí, hi ha diferències estadísticament significatives (alpha=0.05)## Analysis of Variance Table
##
## Response: sqrt(env$dis)
## Df Sum Sq Mean Sq F value Pr(>F)
## as.factor(cutg) 2 57.244 28.6222 12.125 0.0001905 ***
## Residuals 26 61.375 2.3606
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 anova(lm(env$oxy ~ as.factor(cutg))) # Sí, hi ha diferències estadísticament significatives (alpha=0.05)## Analysis of Variance Table
##
## Response: env$oxy
## Df Sum Sq Mean Sq F value Pr(>F)
## as.factor(cutg) 2 80.894 40.447 18.954 8.365e-06 ***
## Residuals 26 55.483 2.134
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 anova(lm(log(env$nit) ~ as.factor(cutg))) # Sí, hi ha diferències estadísticament significatives (alpha=0.05)## Analysis of Variance Table
##
## Response: log(env$nit)
## Df Sum Sq Mean Sq F value Pr(>F)
## as.factor(cutg) 2 22.049 11.0247 24.362 1.096e-06 ***
## Residuals 26 11.766 0.4525
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 anova(lm(sqrt(env$amm) ~ as.factor(cutg))) # Sí, hi ha diferències estadísticament significatives (alpha=0.05)## Analysis of Variance Table
##
## Response: sqrt(env$amm)
## Df Sum Sq Mean Sq F value Pr(>F)
## as.factor(cutg) 2 2.3829 1.19146 46.298 2.702e-09 ***
## Residuals 26 0.6691 0.02573
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Així, podem afirmar que els grups o clústers basats en la comunitat de peixos es corresponen amb parts del riu de característiques ambientals diferents.
CONCLUSIONS
A partir de les anàlisis que hem fet durant aquesta sessió podem concloure que:
Al curs alt del riu (cabal petit, molt oxigenat, baix en nitrats i amoni) predominen comunitats del grup o clúster 1, és a dir, comunitats de peixos moderadament diverses dominades principalment per les espècies Thth, Satr, Cogo, PhPh, Babl.
Al curs baix del riu (cabal alt, menys oxigenat, concentracions més altes de nitrats i amoni) predominen comunitats del grup o clúster 2: comunitats molt diverses formades per espècies que generalment no es troben al curs alt del riu.
Al voltant de la ciutat de Besançon (punts 23-25; veure mapa interactiu a dalt) tenim unes aigües molt impactades, molt pobres en oxígen, i amb concentracions nutrients molt elevades, especialment d’amoni. En aquestes aigües hi trobem comunitats del grup o clúster 3, és a dir, amb molt poca diversitat de peixos i on bàsicament predomina l’espècie Alal.
NOTA: Els mètodes de classificació anteriors s’han presentat amb exemples de dades d’abundància d’espècies, però també es poden aplicar a qualsevol altre tipus de dades, per exemple dades ambientals. Això sí, recordeu escollir les mesures d’associació i transformacions o estandaritzacions adequades per a cada tipus de dades!!