1 Mesures de Similaritat
Autors: J.P. Casas-Ruiz & Gascón S.
Aquesta sessió servirà per a aprendre a calcular matrius de distància (o dissimilaritat), qué són la base dels anàlisis multivariants que treballarem més endavant
La majoria dels mètodes d’anàlisi multivariant, especialment els d’ordenació i classificació, es basen en la comparació entre tots els possibles parells d’observacions (Q mode) de la matriu de dades. La combinació d’questes comparacions dóna lloc a mesures d’associació, i s’organitzen en forma de matrius quadrades i simètriques anomenades matrius de distància o de dissimilaritat. Avui en calcularem algunes per anar agafant pràctica.
Com heu vist a les sessions teòriques, hi ha diferents mesures d’associació que es poden utilitzar. La mesura o mesures més adients dependran sempre del tipus de dades que tinguem. Escollir bé és important, ja que totes les anàlisis posteriors es basarán en aquesta mesura.
Per a informació detallada sobre distàncies i com escollir-les podeu fer una ullada al següent blog: https://sites.google.com/site/mb3gustame/reference/dissimilarity
o, encara millor, al llibre:
Legendre P, Legendre L. Numerical Ecology. 2nd ed. Amsterdam: Elsevier, 1998. ISBN 978-0444892508
A l’exemple d’avui, calcularem diverses matrius de dissimilaritat a partir d’unes bases de dades d’abundància de peixos i fisicoquímica del riu Doubs. Provarem diferents mesures d’associació i transformacions i les compararem entre elles per veure com varien.
1.1 Preparació de les dades per mesures d’associació
Primer de tot, carreguem els packages que serán necessaris per l’anàlisi. És recomanable carregar ade4 abans que vegan per evitar conflictes.
i assignem el directori de treball. Canvieu el de l’exemple per el vostre.
o alternativament creeu un projecte d’R, amb el nom que desitjeu.
Aprofitem també per carregar algunes funcions custom que necessitarem. Si la funció està guardada al directori de treball o a la carpeta on heu creat el projecte, es pot cridar amb la funció source. Sinó, cal especificar-ne el directori dins de la mateixa funció.
Entrem les dades a través d’un grup d’arxius d’R comprimit (extensió .Rdata). De nou, si l’arxiu comprimit és dins del directori de treball o la carpeta del projecte, és tan senzill com utilizar la funció load. Sinó, caldria especificar el directori on està guardat l’arxiu.
L’arxiu es descomprimeix automàticament i es desplega en 5 datasets: env, fishtraits, latlong, spa i spe. Per a l’exemple d’avui utilitzarem els dataset spe i env, que contenen dades d’abundància de peixos i dades fisicoquímiques de l’aigua de 30 punts de mostreig (o sites en anglès) al llarg del riu. Podeu fer una exploració ràpida de les dues matrius per familiaritzar-vos amb les dades (funcions summary(), hist(), etc)
Abans de començar, eliminarem la fila o objecte 8, que no té dades.
1.2 Distàncies per a dades d’abundància
Començarem per la base de dades spe. Com que tenim dades d’abundància, ens trobem amb un cas de dades (semi)quantitatives on tots els valors són positius o zero. Per a dades d’abundància generalment s’utilitzen mesures d’associació de tipus assimètriques per tal d’evitar possibles problemes de doble-zero.
Doble-zero. Per a algunes variables, que dues observacions tinguin un valor de zero no indica necessàriament similitud real entre aquests observacions. Per exemple, en el cas d’abundàcia d’espècies, un zero podria derivar d’una absència real d’una espècie (realment no hi ha cap individu) però també de que hi ha individus però simplement l’observador no els va veure. En ambdós casos a la matriu hi tenim un zero però en realitat reflecteix coses diferents. En aquests casos cal utilitzar mesures d’associació del tipus assimètriques (e.g. Bray-Curtis, Chord, Hellinger, etc.), que tracten els zeros de manera diferent a la resta de valors.
Anem doncs a calcular algunes matrius de distància o dissimilaritat basades en mesures d’associació assimètriques. Les calcularem mitjançant la funció vegdist. Podem especificar la mesura d’associació que volguem al cridar la funció mitjançant el paràmetre method. Entreu vegdist per més detalls sobre la funció i les diferents mesures d’associació que la funció pot calcular.
Distància de Bray-Curtis:
Ara hem creat un nou objecte spe.db que, si l’expresem en format de matriu, veureu que és una matriu quadrada que conté les distàncies Bray-Curtis entre totes les combinacions dels 30 punts de mostreig. La diagonal mostra la distància entre cada punt de mostreig i ell mateix, que és sempre 0.
A sota podeu veure una petita part de la matriu (només pels punts de mostreig de l’1 al 5):
round(as.matrix(spe.db)[1:5,1:5], digits = 1) # elimineu [1:5,1:5] de la línia de codi si voleu veure la matriu sencera## 1 2 3 4 5
## 1 0.0 0.6 0.7 0.8 0.9
## 2 0.6 0.0 0.1 0.3 0.7
## 3 0.7 0.1 0.0 0.2 0.7
## 4 0.8 0.3 0.2 0.0 0.5
## 5 0.9 0.7 0.7 0.5 0.0Recordeu, com més petita és la distància, més similars són els punts de mostreig!.
Si volem, podem visualitzar la matriu de distàncies mitjançant la funció coldiss que hem carregat abans:
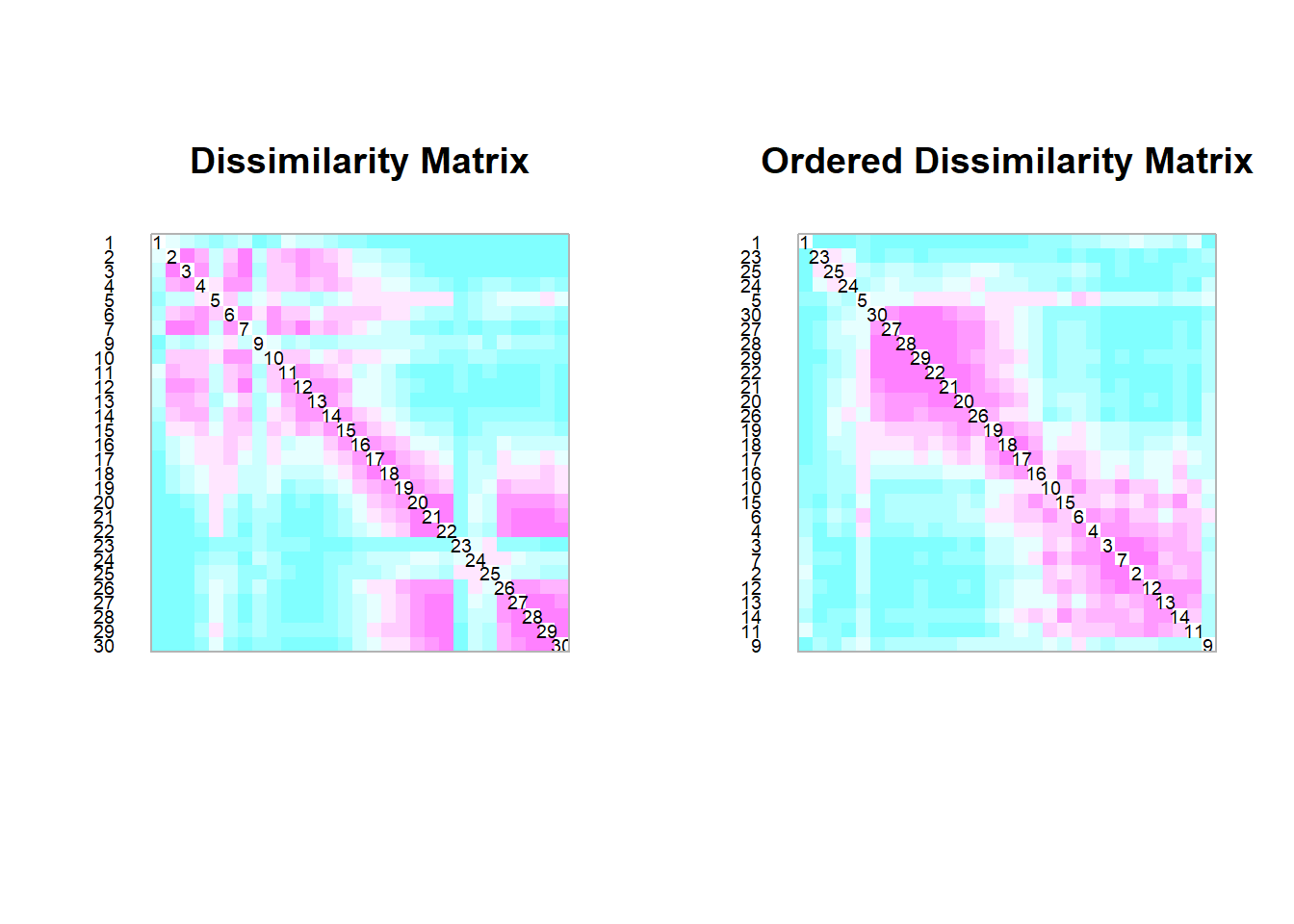
El color magenta indica valors propers a 0 –> menor distància (major similaritat)
El color blau indica valors propers a 1 –> major distància (menor similaritat)
Bray-Curtis transformada:
Ara calcularem la mateixa matriu de distància Bray-Curtis però sobre dades prèviament transformades.
Per què ens interessa transformar les dades? Doncs perquè Bray-Curtis tracta les diferències d’abundància per igual, independement de que sigui una espècie abundant o amb molt pocs individus. Per exemple, per Bray-Curtis, una diferència de 5 individus té el mateix pes quan les abundàncies de dos observacions són 3 i 8 que quan són 6203 i 6208. Però en realitat, des del punt de vista de l’ecologia o dinàmica de poblacions, una diferència de cinc individus és molt més rellevant per una població petita que quan hi ha milers d’individus. Transformar prèviament les dades ajuda a ponderar la importància de les diferències en nombre d’individus quan els rangs d’abundància entre especies són molt diferents.
Per a veure-ho, podem recalcular la matrius de distància de Bray-Curtis però transformant prèviament les dades mitjançant la transformació logarítmica. Ull, com que tenim molts valors de zero a la matriu, transformem les dades amb \(log (x+1)\):
spe.dbln <- vegdist(log1p(spe), method = 'bray')
coldiss(spe.dbln, nc=10, byrank = FALSE, diag = TRUE)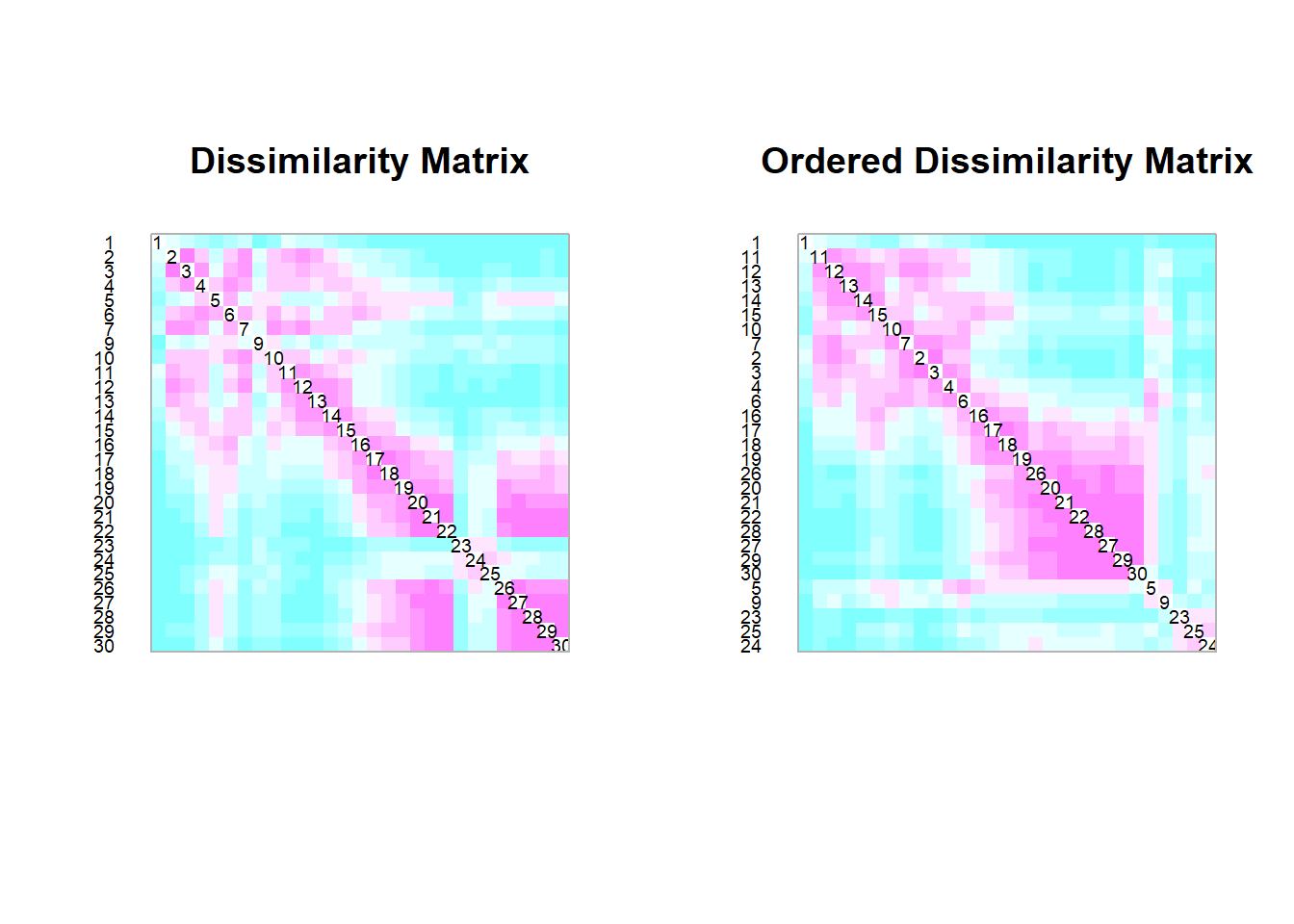
Compareu les matrius de distància de Bray-Curtis amb i sense transformació logarítmica. Veieu alguna diferència important?
En aquest cas sembla que la transformació de les dades pràcticament no té cap efecte sobre la matriu de distàncies. Amdós tenen un patrons similars (fixeu-vos que són simètrics). Això és degut a que en el nostre exemple totes les espècies (columnes de la matriu spe) tene un rang d’abundància molt semblant. Totes oscil·len entre 0 i 5. Per tant, en aquest cas concret no calia fer aquest tipus de transformació. Però en altres casos pot ser molt necessari. Cal tenir-ho sempre en compte!
A més de Bray-Curtis, hi ha altres mesures d’associació que també serien adequades per a dades d’abundància, com per exemple la distància de la corda (chord) o la distància de Hellinger, que les farem servir en sessions més avançades:
1.3 Distàncies per a dades binàries
Podem també calcular matrius de distància per a variables de tipus binari, com per exemple dades de presència-abscència d’espècies.
Per jugar amb un exemple pràctic, podem reconvertir la matriu spe (abundàncies) en dades binàries (1 i 0s) de presència-absència. Per a fer-ho, simplement convertirem a 1 (presència) tots els valors més grans que 0 i deixarem com a 0 (absència) tots els valors que ja eren 0:
## Cogo Satr Phph Babl Thth Teso Chna Pato Lele Sqce Baba Albi Gogo Eslu
## 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0
## 2 0 1 1 1 0 0 0 0 0 0 0 0 0 0
## 3 0 1 1 1 0 0 0 0 0 0 0 0 0 1
## 4 0 1 1 1 0 0 0 0 0 1 0 0 1 1
## 5 0 1 1 1 0 0 0 0 1 1 0 0 1 1
## 6 0 1 1 1 0 0 0 0 1 1 0 0 1 1
## Pefl Rham Legi Scer Cyca Titi Abbr Icme Gyce Ruru Blbj Alal Anan
## 1 0 0 0 0 0 0 0 0 0 0 0 0 0
## 2 0 0 0 0 0 0 0 0 0 0 0 0 0
## 3 0 0 0 0 0 0 0 0 0 0 0 0 0
## 4 1 0 0 0 0 1 0 0 0 0 0 0 0
## 5 1 0 0 1 0 1 0 0 0 1 0 0 0
## 6 1 0 0 0 0 1 0 0 0 1 0 0 0Per a matrius de dades binàries podem escollir entre la similaritat de Jaccard i la de Sørensen.
IMPORTANT: Tot i que existeixen mesures d’associació que expresen similaritat (e.g. Índexos de Jaccard, Sørensen o Gower), R converteix automàticament totes les mesures d’associació en distàncies. Això és important recordar-ho a l’hora d’interpretar les dades, perqué valors més petits sempre indicaran menor distància (major similaritat), independenment de la deifnició original de la mesura d’associació que s’utilitzi.
Les matrius de distàncies de Jaccard i Sørensen es poden calcular emb la funció vegdist():
spe.dj <- vegdist(spe.bin, method= 'jac')
spe.so <- vegdist(spe.bin, method = 'bray') # Sørensen és l'equivalent a fer Bray-Curtis sobre dades binàriesLes podem comparar entre elles. Són molt semblants, però Sørensen dóna una mica més de pes als casos on tenim doble 1, és a dir, on una espècie és present en els dos objectes de cada comparació. Això fa que les distància de Sørensen sigui en general una mica més petita que Jaccard, però les dues tenen un comportament molt semblant:
plot(spe.dj, spe.so, cex=1.4, las=1, xlab='Jaccard', ylab='Sorensen', fram=F, pch=21, col='transparent', bg=adjustcolor('dodgerblue3', alpha.f = 0.1))
abline(0,1, col='gray60', lty=2)
text(0.1,0.2, '1:1', col='gray60')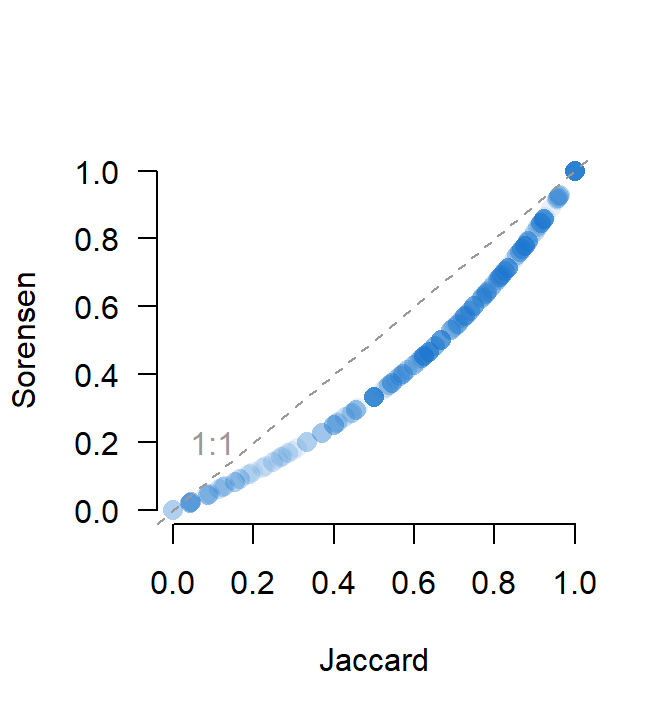
Podeu comparar Jaccard i Sørensen també a través de la funció coldiss() com hem fet per les dades d’abundància. Veureu que els patrons són pràcticament idèntics.
1.4 Distàncies per a dades ambientals
Ara passem a utilitzar l’altra base de dades que hem carregat, la matriu env. Aquesta base de dades conté dades fisicoquímiques de l’aigua dels 30 punts de mostreig al llarg del mateix riu Doubs. Tenim variables com el pH, l’oxígen dissolt, fosfats, nitrats etc. Estem parlant doncs de variables quantitatives i contínues. Per aquest tipus de dades no tenim cap problema de doble-zero, i per tant podem utilitzar mesures d’associació simètriques. La mesura simètrica més habitual per dades de tipus ambiental és la distància euclídia.
Calculem la distància euclídia entre els 30 punts de mostreig en base a la fisicoquímica de l’aigua. Per a fer-ho utilitzarem la funció dist:
env2 <- env[, -1] # excloem la primera columna dfs (distance a la capçalera del riu) perquè és una dada espacial, i nosaltres volem treballar només amb dades ambientals.
env.de <- dist(env2)
round(as.matrix(env.de)[1:5,1:5], digits = 1)## 1 2 3 4 5
## 1 0.0 45.4 49.2 95.6 104.2
## 2 45.4 0.0 21.7 84.3 94.1
## 3 49.2 21.7 0.0 63.3 72.6
## 4 95.6 84.3 63.3 0.0 14.2
## 5 104.2 94.1 72.6 14.2 0.0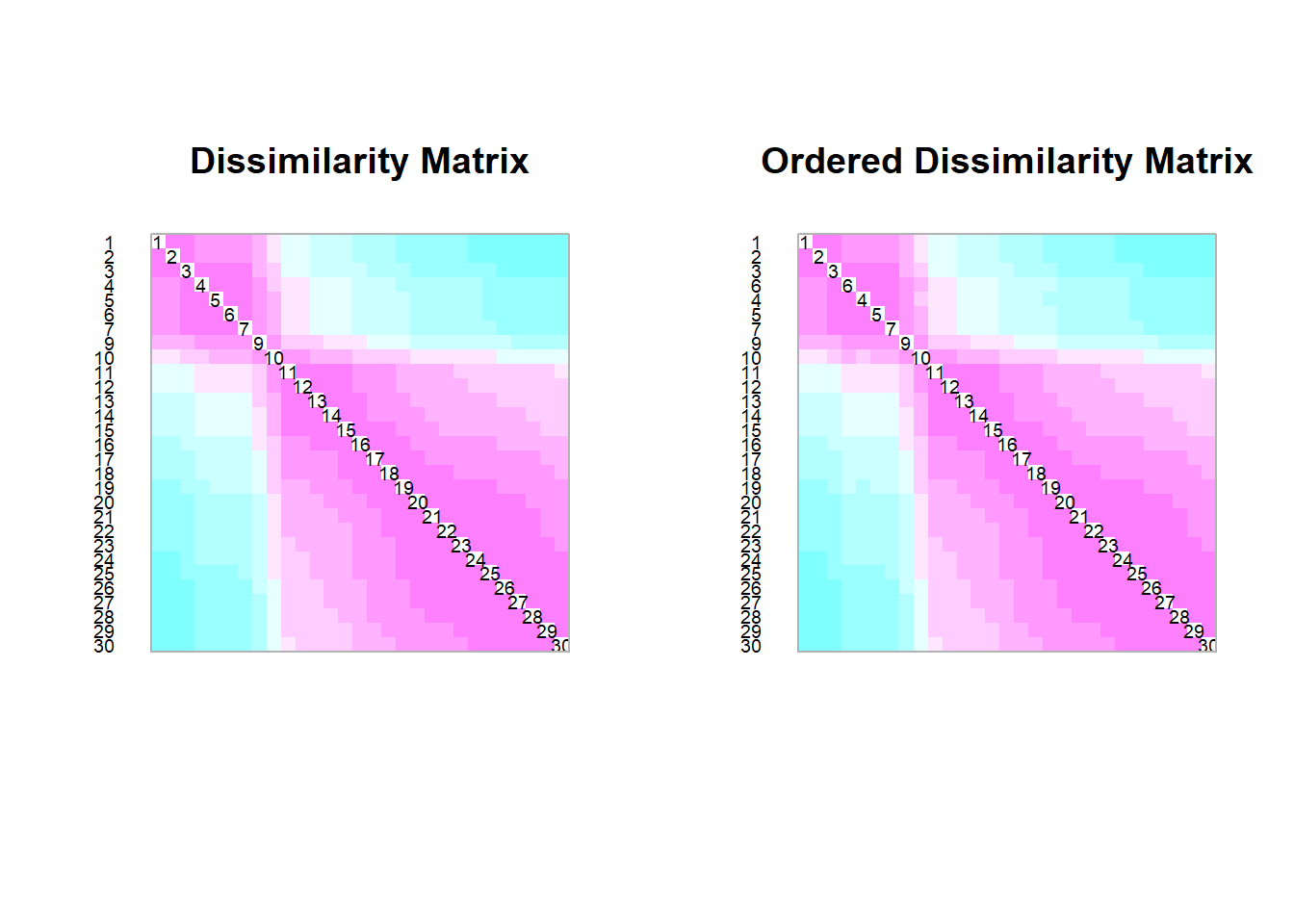
Veieu algo estrany en aquestes matrius de distància? Això és degut a que algunes variables tenen molta més influència a l’hora de calcular la matriu de distàncies simplement perquè tenen una magnitud i/o variabilitat molt més gran que la resta.
Fixeu-vos que la matriu env és una matriu que conté variables amb escales i unitats molt diferents. Algunes variables tenen valors molt baixos i varien molt poc (e.g. amm o pho), mentres que d’altres tener valors molt més alts i són més variables (e.g. ele). Podeu comprovar-ho amb la funció summary() o a través d’un boxplot de totes les dades.

Com es veu en el boxplot, la variable ele (elevació) té molta més magnitud i variabilitat que la resta, i això fa que la seva influència en el càlcul de distàncies s’infli de manera artificial. És a dir, la matriu de distància euclidia que hem calculat fa un moment pràcticament només reflecteix diferències en elevació entre els punts de mostreig.
La variable ele és el cas més evident, però també hi ha altres variables que podrien tenir el mateix problema. Podem treure la variable ele i repetir el boxplot per veure millor la diferència entre la resta de variables:
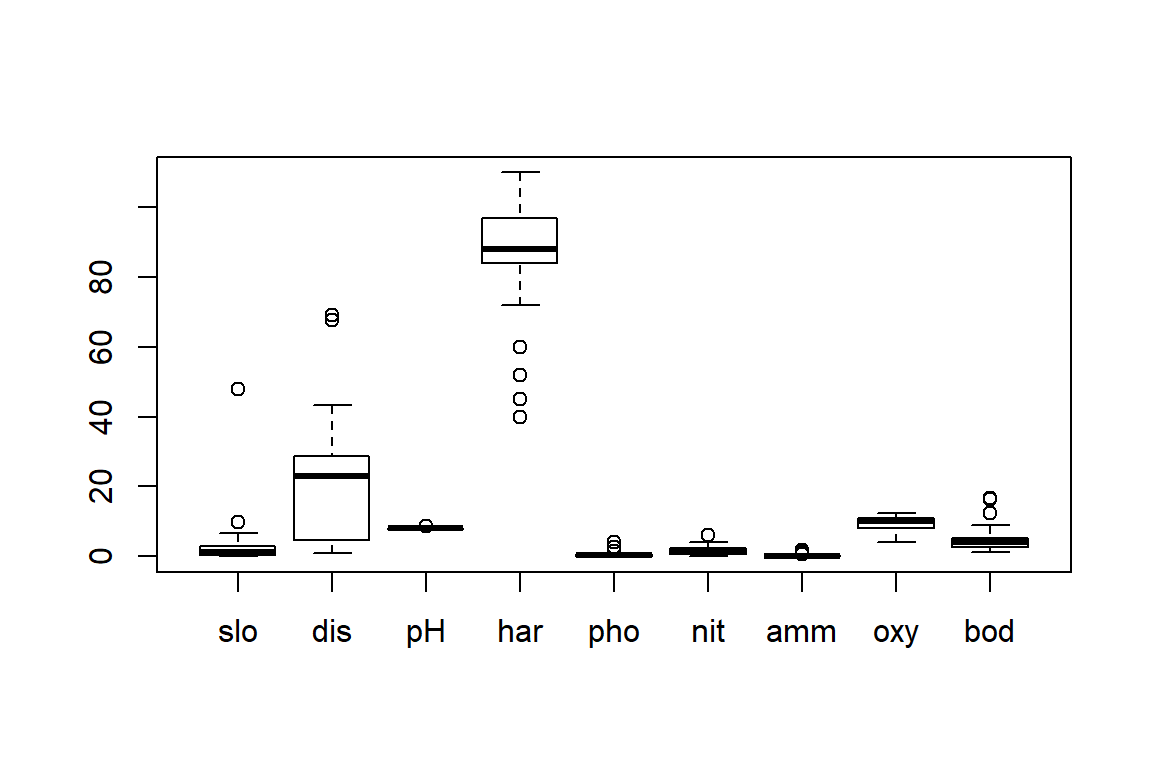
Aquest inconvenient és molt habitual en matrius de dades ambientals, ja que aquestes solen tenir dades de tipus i unitats diferents. Per a solucionar-ho, el que cal fer és una estandardització de les variables prèvia al calcul de la matriu de distàncies.
1.4.1 Estandardització de les dades
Com dèiem fa un moment, quan les dades originals presenten valors de magnitud molt diferents o són variables mesurades en diferents unitats, pot passar que s’incrementi artificialment la influència d’alguna de les variables en el càlcul de distàncies i per tant en els posteriors anàlisis de classificació i ordenació.
Per exemple, en el cas del riu Doubs, tenim les variables pH i elevació en la mateixa matriu de dades. El pH de l’aigua pot oscil·lar per definició entre 0 i 14, i en rius sol variar poc, entre 7.7 i 8.6 en el cas del riu Doubs.
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 7.700 7.900 8.000 8.048 8.100 8.600Per tant, les diferències de pH entre els punts de mostreig de la matriu env seran com a màxim de \(8.6-7.7= 0.9\) unitats.
En canvi, l’elevació no està limitada en termes de magnitud i sol ser molt més variable.
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 172.0 246.0 375.0 470.9 752.0 934.0Per tant, quan fem comparacions dos a dos d’elevació entre punts de mostreig, podríem tenir diferències de l’ordre de centenars d’unitats.
Cal tenir en compte, però, que un petit canvi en termes absoluts de pH és molt més significatiu que el mateix canvi en elevació. Per exemple, una variació de 3 unitats de pH (e.g. de 5 a 8) representa una diferència enorme en termes de fisicoquímica de l’aigua, mentres que la mateixa diferència en elevació (e.g. de 552 a 555 m) és pràcticament imperceptible. Per tant, les diferències entre punts de mostreig per a pH i elevació no són directament comparables.
Degut a això, com hem vist abans, si calculem la matriu de dissimilaritat sobre les dades originals, la variable elevació tindrá molta més influència simplement perquè la seva magnitud i variació en termes absoluts són molt més grans que les del pH.
Per a què això no passi, cal estandarditzar les dades a priori. L’estandardització és una transformació de les dades que té en compte la magnitud i variabilitat de les variables i les fa més comparables.
Hi ha diferents mètodes d’estandardització. El més simple s’anomena \(z-scores\) i consisteix en restar a cada valor \(x\) la mitjana de la seva columna (\(\bar{X}\)) i dividir-lo per la desviació estàndard (\(SD\)):
\[z = \frac{x - \bar{X}}{SD}\]
Aquesta transformació resulta en una nova variable \(z\) de mitjana = 0 i desviació estàndard = 1. Un cop estandarditzades, la variança de les diferents variables és directament comparable i ens permet evaluar-ne la influència real.
Podem jugar amb les dades de pH i elevació de la matriu env per il·lustrar com funciona l’estandardització. Les següents dues figures mostren la distribució de dades de pH (blau) i de elevació (taronja) pel riu Doubs.
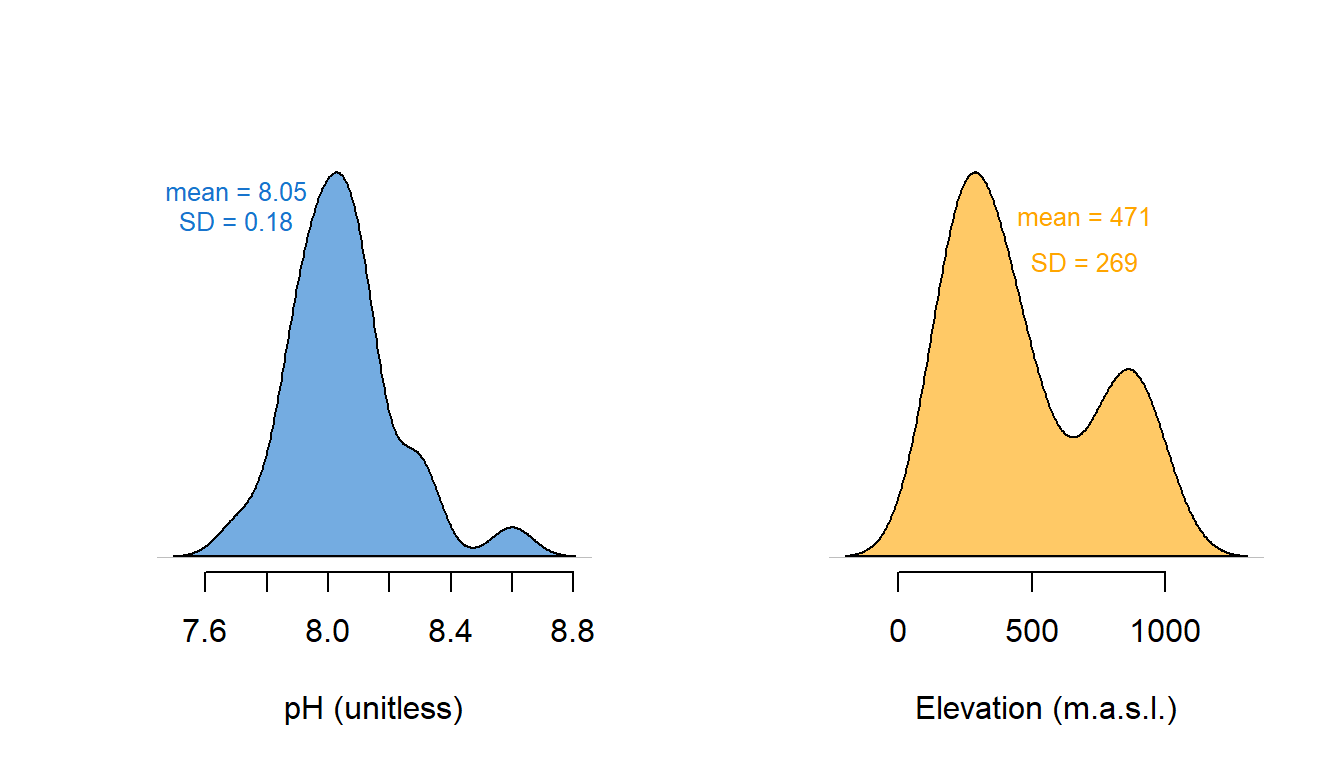
Les dues variables mostren una distribució relativament semblant. Però si les grafiquem utilitzant la mateixa escala (sobre un eix comú), és evident que la magnitud i variabilitat absoluta de l’elevació (taronja) és molt més gran que en el cas del pH (blau; pràcticament invisible):
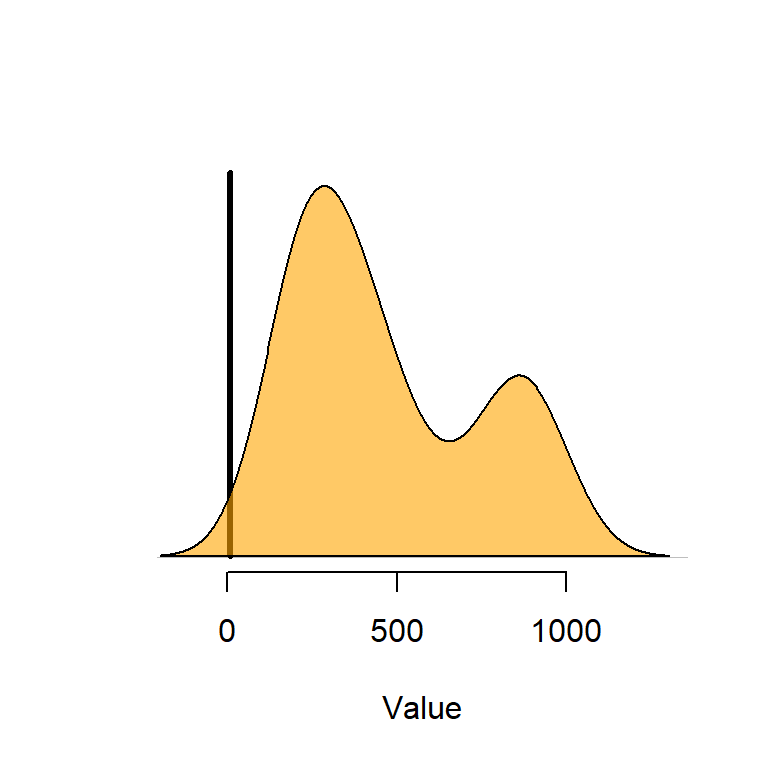
Quan estandarditzem les dades, el que fem és 1) desplaçar les dues distribucions per centrar-les sobre el valor 0 (això ho aconseguim restant la mitjana), i 2) transformar les dades de manera que la seva variabilitat es mogui entre -1 i 1 però a la vegada respectant la forma original de la distribució (això ho aconseguim dividint per la desviació estàndard):
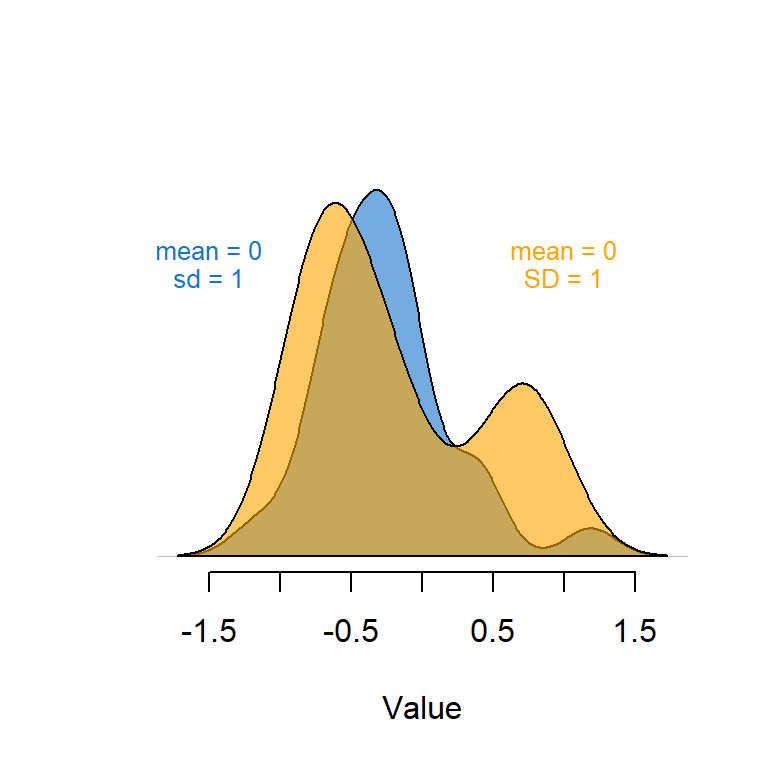
Això fa que les noves variables estandarditzades siguin directament comparables en termes de variança, i que tinguin una influència equivalent durant el càlcul de la matriu de distàncies.
La transformació \(z-score\) es pot codificar manualment, però és molt fàcil de fer a través de la funció scale o la funció decostand del package vegan:
Per veure l’efecte de l’estandardització, podem recalcular la matriu de distàncies euclídies utilitzant les noves dades estandarditzades i comparar-la amb la de les dades originals:
Sense estandaritzar
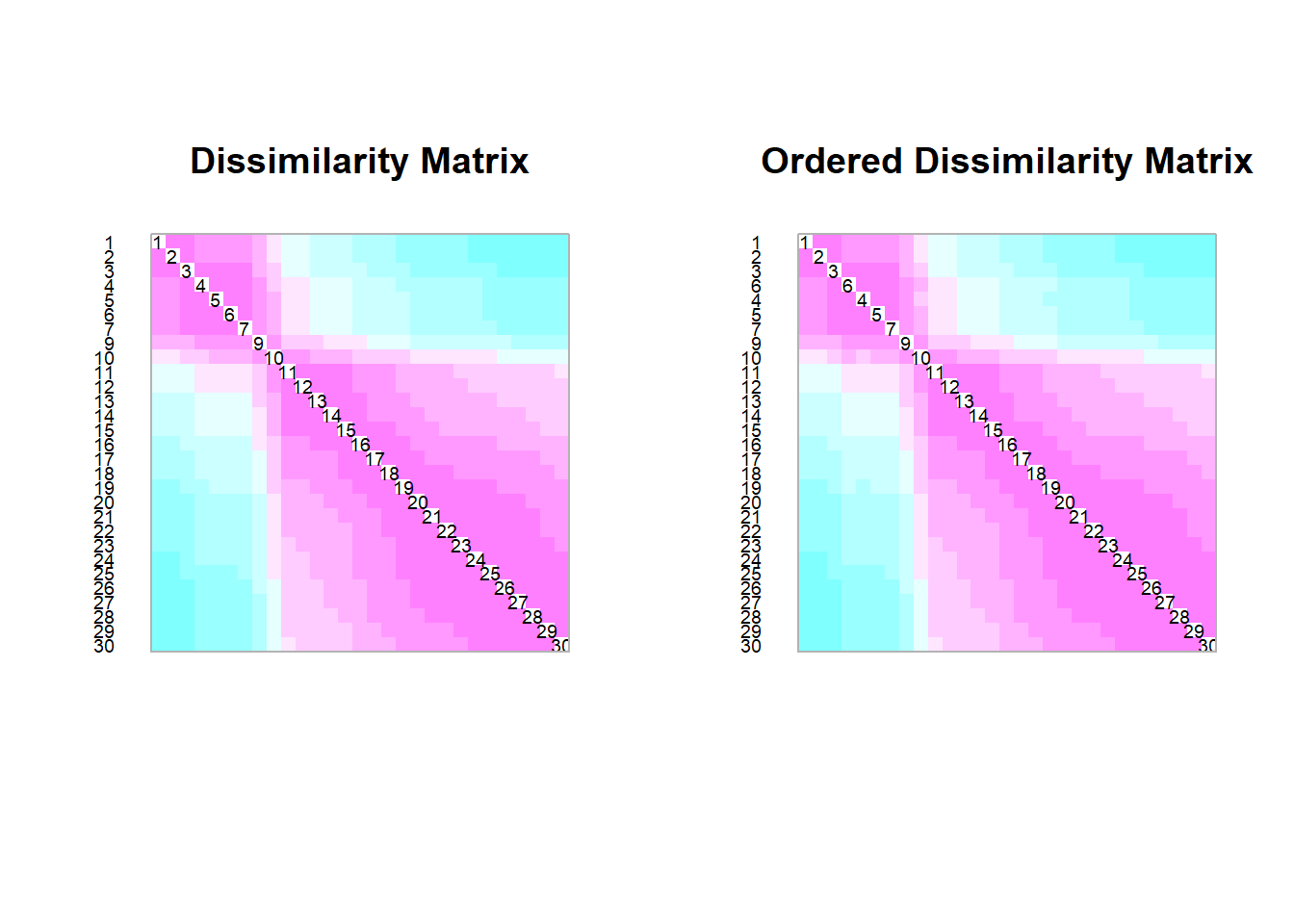
Estandaritzant
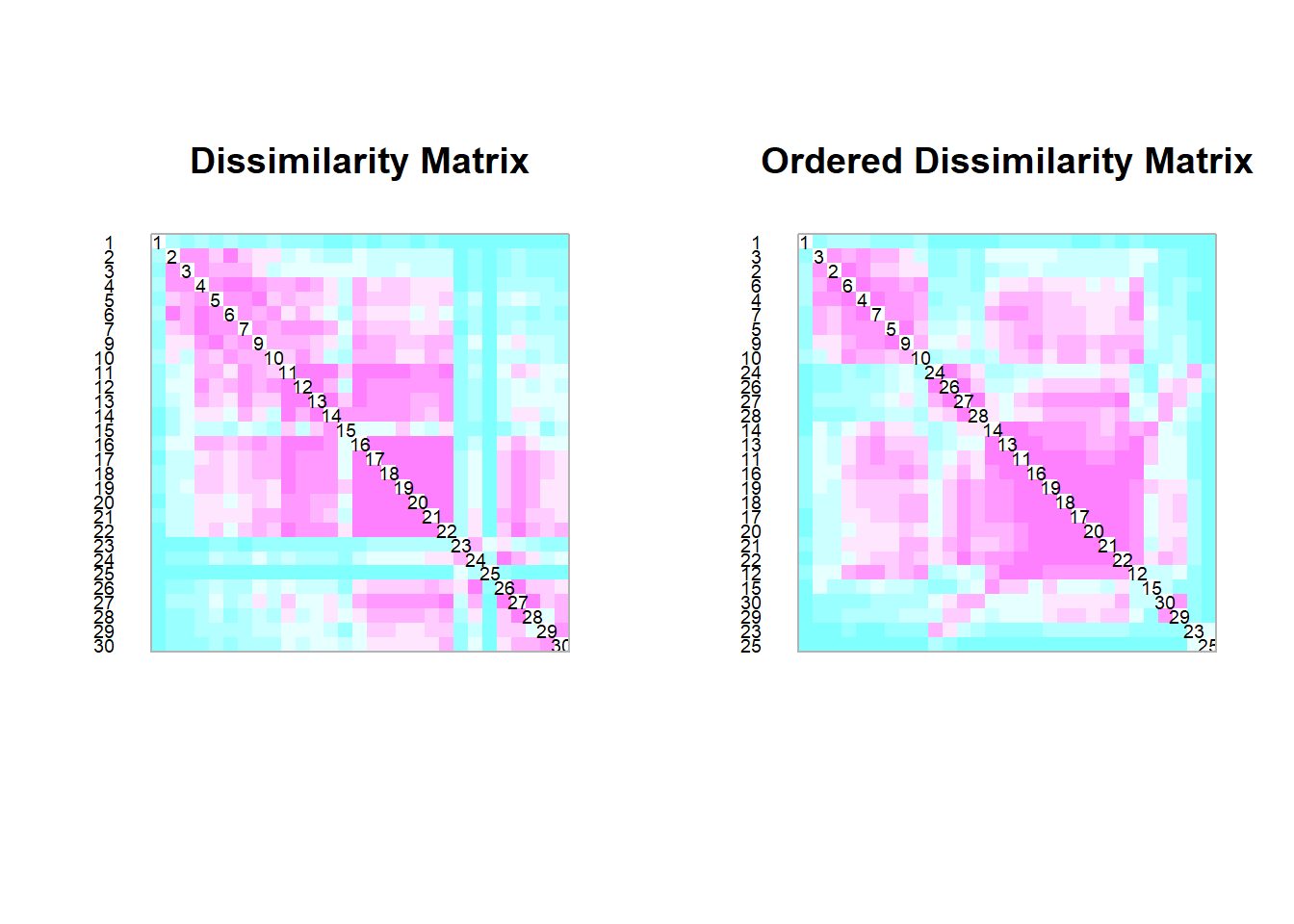
El resultat és ben diferent, oi? La matriu de distàncies sense estandarització prèvia no ens donava pràcticament cap informació més enllà de com es diferenciaven els punts de mostreig en termes d’elevació. En canvi, la matriu de distàncies basada en les dades estandarizades reflecteix una diferència més integradora entre els punts, tenint en compte totes les variables ambientals.
A més de \(z-scores\) hi ha altres tipus d’estandarització de variables. Podeu veure’n més detalls al següent blog:
https://sites.google.com/site/mb3gustame/reference/transformations