3 Ordination
Anàlisis d’ordenació
Autors: J.P. Casas-Ruiz & Gascón S.
Aquesta sessió servirà per a posar en pràctica alguns dels mètodes d’ordenació que heu vist a les sessions teòriques.
Recordeu que els mètodes d’ordenació tener per objectiu simplificar conjunts de dades multivariants transposant-les a un espai de menor nombre de dimensions. A diferència dels metodes de classificació, que busquen agrupar els diferents objectes o observacions en grups discrets, els mètodes d’ordenació es basen en ordenar els objectes al llarg de gradients.
A la sessió d’avui aplicarem tres anàlisi d’ordenació diferents (PCA, NMDS i RDA) a les dades del riu Doubs que ja hem treballat a les seccions anteriors.
3.1 Preparació de les dades per anàlisis d’Ordenació
Primer de tot, carreguem els packages que serán necessaris per l’anàlisi. Com sempre, és recomanable carregar ade4 abans que vegan per evitar conflictes:
library(ade4)
library(vegan)
library(gclus)
library(cluster)
library(RColorBrewer)
library(labdsv)
library(ape)i assignem el directori de treball o el projecte. Canvieu el de l’exemple pel vostre.
Carreguem les dades a través de l’arxiu Doubs.Rdata tal i com vam fer a les seccions anterior. Recordeu que l’arxiu ha d’estar al directori de treball que hagueu escollit o al projecte on esteu treballant. En cas contrari, cal especificar el directori a dins de la funció load():
load(file="Doubs.Rdata")
spe <- spe[-8, ] # Eliminem la fila 8 perquè no té dades
env <- env[-8, ] # Eliminem la fila 8 perquè no té dades
spa <- spa[-8, ] # Eliminem la fila 8 perquè no té dades
latlong <- latlong[-8, ] # Eliminem la fila 8 perquè no té dadesEn el primer exemple d’aquesta sessió analitzarem la matriu de dades env, que conté diverses variables ambientals de 30 punts de mostreig al llarg del riu Doubs.
## 'data.frame': 29 obs. of 11 variables:
## $ dfs: num 0.3 2.2 10.2 18.5 21.5 ...
## $ ele: int 934 932 914 854 849 846 841 752 617 483 ...
## $ slo: num 48 3 3.7 3.2 2.3 3.2 6.6 1.2 9.9 4.1 ...
## $ dis: num 0.84 1 1.8 2.53 2.64 2.86 4 4.8 10 19.9 ...
## $ pH : num 7.9 8 8.3 8 8.1 7.9 8.1 8 7.7 8.1 ...
## $ har: int 45 40 52 72 84 60 88 90 82 96 ...
## $ pho: num 0.01 0.02 0.05 0.1 0.38 0.2 0.07 0.3 0.06 0.3 ...
## $ nit: num 0.2 0.2 0.22 0.21 0.52 0.15 0.15 0.82 0.75 1.6 ...
## $ amm: num 0 0.1 0.05 0 0.2 0 0 0.12 0.01 0 ...
## $ oxy: num 12.2 10.3 10.5 11 8 10.2 11.1 7.2 10 11.5 ...
## $ bod: num 2.7 1.9 3.5 1.3 6.2 5.3 2.2 5.2 4.3 2.7 ...Com podeu veure, la matriu conté 11 variables quantitatives. Si volem fer-nos una idea de com varien les característiques ambientals al llarg del riu, podríem anar explorant totes les variables una a una i després posar-les en comú per intentar fer-nos una idea dels patrons generals al llarg del riu i les diferències entre punts de mostreig. Però això comportaria força temps, i sobretot esforç d’abstracció a l’hora de combinar els patrons de tantes variables a la vegada.
Alternativament, podem aplicar un anàlisi d’ordenació, que ens permetrà transposar tota la informació de la matriu env (actualment desplegada en 11 dimensions) a un espai de poques dimensions més fàcil de pair. Podríem escollir entre diferents mètodes, però el més habitual per a explorar dades ambientals és el PCA.
3.2 Anàlisi de components principals (PCA)
La principal aplicació del PCA en ecologia és l’ordenació de punts de mostreig en base a variables ambientals quantitatives, ja que PCA és un mètode lineal que preserva la distància euclídia entre objectes. Si es volgués aplicar a dades on la distància euclídia no és adequada (e.g. dades d’abundància, dades binàries etc), caldria fer una transformació prèvia de les dades per a transposar-les a un espai euclidià, per exemple a través de la transformació de Hellinger.
Tot i que l’anàlisi PCA es va definir originalment per a distribucions multinormals, és força robust a desviacions de la normalitat de les variables sempre i quan les distribucions d’aquestes no siguin exageradament esbiaixades. En canvi, és estrictament essencial que les dades estiguin estandarditzades per evitar que variables de major magnitud i/o rang de variabilitat tinguin una influència desproporcionada en l’anàlisi (veure secció “1.4.1.estandardització de les dades” per detalls). Aquesta estandardització es pot fer a priori, per exemple mitjançant les funcions scale() o decostand() que hem vist en seccions anteriors, o també es pot cridar directament al fer l’anàlisi PCA com veureu a sota.
L’anàlisi PCA el fem mitjançant la funció rda() del package vegan, que s’aplica directament a la matriu de dades original:
env.pca <- rda(env, scale = TRUE) # Argument scale=TRUE calls for a z-score standardization of the variables
summary(env.pca)##
## Call:
## rda(X = env, scale = TRUE)
##
## Partitioning of correlations:
## Inertia Proportion
## Total 11 1
## Unconstrained 11 1
##
## Eigenvalues, and their contribution to the correlations
##
## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6
## Eigenvalue 6.0979 2.1672 1.03761 0.70353 0.35174 0.31912
## Proportion Explained 0.5544 0.1970 0.09433 0.06396 0.03198 0.02901
## Cumulative Proportion 0.5544 0.7514 0.84571 0.90967 0.94164 0.97065
## PC7 PC8 PC9 PC10 PC11
## Eigenvalue 0.16453 0.11173 0.023134 0.01737 0.0060521
## Proportion Explained 0.01496 0.01016 0.002103 0.00158 0.0005502
## Cumulative Proportion 0.98561 0.99577 0.997870 0.99945 1.0000000
##
## Scaling 2 for species and site scores
## * Species are scaled proportional to eigenvalues
## * Sites are unscaled: weighted dispersion equal on all dimensions
## * General scaling constant of scores: 4.189264
##
##
## Species scores
##
## PC1 PC2 PC3 PC4 PC5 PC6
## dfs 1.0842 0.5150 -0.25749 -0.16168 0.21132 -0.09485
## ele -1.0437 -0.5945 0.17984 0.12282 0.12464 0.14022
## slo -0.5752 -0.5103 -0.55499 -0.80204 0.02764 0.20077
## dis 0.9577 0.6412 -0.30654 -0.19427 0.18401 0.03068
## pH -0.0586 0.4820 1.03444 -0.51378 0.14421 0.05821
## har 0.9072 0.6181 -0.02280 0.15767 -0.27865 0.50738
## pho 1.0460 -0.6093 0.18734 -0.11866 -0.15113 0.04888
## nit 1.1432 -0.1290 0.01203 -0.18471 -0.21270 -0.34907
## amm 0.9954 -0.6989 0.18597 -0.08277 -0.19234 -0.04979
## oxy -1.0089 0.4578 -0.00918 -0.23450 -0.50552 -0.05764
## bod 0.9899 -0.6836 0.11962 0.03646 0.08542 0.21993
##
##
## Site scores (weighted sums of species scores)
##
## PC1 PC2 PC3 PC4 PC5 PC6
## 1 -1.41243 -1.47560 -1.74593 -2.95533 0.23051 0.49227
## 2 -1.04173 -0.81761 0.34075 0.54364 0.92835 -1.76876
## 3 -0.94881 -0.48823 1.36059 -0.21768 1.05289 -0.69640
## 4 -0.88070 -0.29459 0.21014 0.66428 -0.23934 -0.06427
## 5 -0.42588 -0.66503 0.77631 0.78777 0.62942 1.17850
## 6 -0.77730 -0.74514 -0.06764 0.90839 0.46945 -0.32923
## 7 -0.78155 -0.09448 0.39335 0.23079 -0.45431 1.17306
## 9 -0.28732 -0.47352 0.29471 1.13215 0.69812 1.05344
## 10 -0.49324 -0.44884 -1.31854 0.78932 -0.38574 0.41597
## 11 -0.28009 0.43091 0.12225 -0.11790 -1.07206 0.45807
## 12 -0.44849 0.33200 -0.53096 0.60345 -0.96682 0.11691
## 13 -0.38850 0.68558 0.10462 0.08107 -1.10978 0.84504
## 14 -0.24996 0.74160 0.88642 -0.46709 -0.96946 0.74682
## 15 -0.31329 0.93929 1.93010 -1.27078 0.06283 0.14773
## 16 -0.14329 0.31112 -0.21270 0.24363 -0.61744 -0.52902
## 17 0.08956 0.29836 -0.18601 0.23428 -0.73164 -0.44261
## 18 0.05649 0.34914 -0.22049 0.14198 -0.76039 -0.60408
## 19 0.04513 0.40790 0.12272 -0.20091 -0.49665 -0.87755
## 20 0.16126 0.36126 -0.28796 -0.05345 -0.79294 -1.36200
## 21 0.16079 0.32644 -0.74873 0.40912 0.17568 -0.90766
## 22 0.14178 0.53551 -0.08106 -0.07021 0.58856 -0.24654
## 23 1.37614 -1.19047 0.74766 -0.35075 -0.22921 0.75808
## 24 0.98260 -0.51434 0.01123 0.40978 1.01197 0.84836
## 25 2.18633 -2.04860 0.35017 -0.29583 -1.26009 -0.39052
## 26 0.88257 -0.11921 -0.64734 0.34001 0.85793 -0.14280
## 27 0.63983 0.39438 -0.15997 -0.30089 1.09889 -0.66497
## 28 0.75833 0.80559 0.51015 -0.96863 0.42032 -0.74305
## 29 0.65324 1.09406 -1.68227 0.37796 0.43707 0.65309
## 30 0.73849 1.36252 -0.27161 -0.62819 1.42387 0.88211Al summary de l’objecte env.pca podem trobar els eigenvalues. Recordeu que els eigenvalues són mesures de la importància dels eixos o components principals resultants de l’anàlisi, i es poden expressar com a proporció explicada individual de cada eix, o com a proporció acumulada a mesura que anem combinant els eixos per ordre.
Si ens interessa, podem extreure els eigenvalues del summary a través de la següent comanda:
## PC1 PC2 PC3 PC4 PC5 PC6
## 6.097948465 2.167241207 1.037605073 0.703525467 0.351737563 0.319124654
## PC7 PC8 PC9 PC10 PC11
## 0.164529826 0.111727323 0.023133745 0.017374555 0.006052124Al final del summary també hi podem trobar els scores dels objectes i les variables, que utilitzarem més avall per a visualitzar els resultats.
NOTA: Per raons històriques, vegan sempre utilitza el nom species per referir-se a les variables, encara que aquestes no tinguin res a veure amb dades d’abundància o presència-absència d’espècies
3.2.1 Escollir el nombre d’eixos a interpretar
Un cop tenim els eigenvalues, la següent pregunta que ens hem de fer és: amb quants eixos ens quedem?
L’ideal seria buscar un compromís entre maximitzar la variabilitat explicada i minimitzar el nombre d’eixos (dimensions). La decisió pot ser completament arbitrària (per exemple, interpretar el mínim nombre d’eixos necessaris per representar el 70% de la variància de les dades), o en base a criteris estàndard com el de Kaiser–Guttman o el de broken-stick.
Kaiser-Gutman consisteix a calcular la mitjana de tots els eigenvalues i interpretar només els eixos els valors propis dels quals són més grans que aquesta mitjana. El mètode de broken-stick consisteix en calcular un model de Broken-stick i quedar-se amb tots els eixos que estan per sobre dels valors predits pel model:
par(mfrow=c(1,2))
barplot(env.pca$CA$eig, ylab='Eigenvalues', las=1, main='Kaiser-Gutman')
abline(h=mean(env.pca$CA$eig), lty=2, col='dark red')
screeplot(env.pca, bstick = TRUE, npcs = length(env.pca$CA$eig), ylab='Eigenvalues', main='Broken-Stick')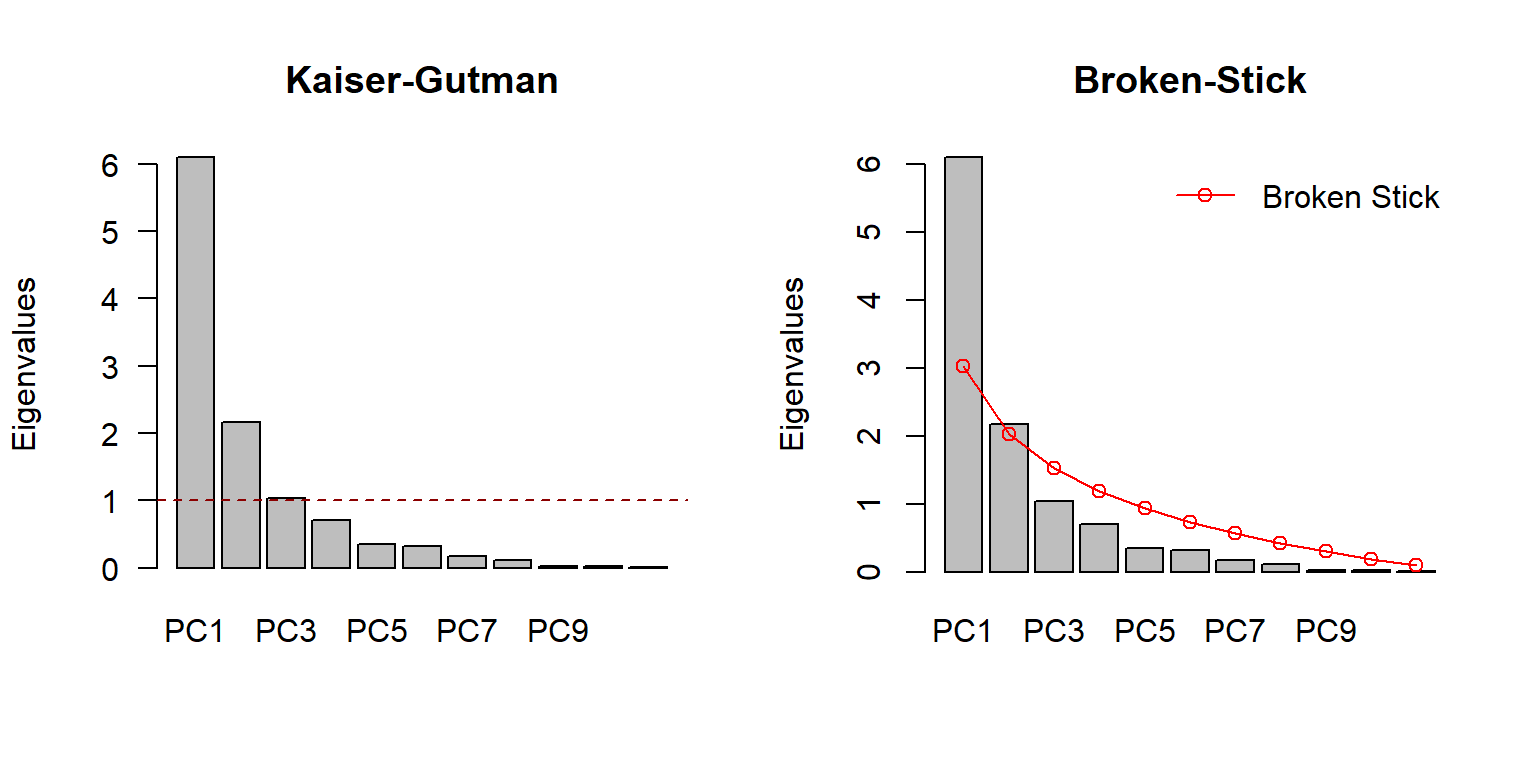
Valorant els dos criteris ens quedaríem amb els dos primers eixos (PC1 i PC2), que combinats expliquen un 75% de la variabilitat total. Fixeu-vos que hem passat de 11 dimensions a 2 conservant una gran part de la variabilitat original! Si volguéssim, també podríem explorar un tercer eix que augmentaria la variabilitat explicada fins al 85%.
3.2.2 Visualització dels resultats: Biplot
Els resultats d’un PCA es solen representar a través d’un biplot. El biplot és un gràfic de dues dimensions que mostra tant les variables com els objectes en un espai definit per els eixos que hem decidit interpretar. Les variables es grafiquen com a fletxes, i els objectes com a punts.
Podem fer un biplot fàcilment utilitzant la funció biplot(), però primer de tot cal decidir quin scaling ens interessa. Hi ha dos scalings a escollir:
Scaling 1 (distance biplot): Es prioritza que la distància entre objectes en el gràfic respecti tant com sigui possible les distàncies euclídies de la matriu original. Els angles entre vectors (variables) poden estar distorsionats.
Scaling 2 (correlation biplot): Es prioritza que els angles entre vectors respectin la correlació original entre variables. La distància entre objectes en el gràfic pot estar distorsionada.
En resum, utilitzarem scaling 1 si ens interessa més veure com es diferencien els objectes, i scaling 2 si ens interessa més veure com es relacionen les diferents variables.
par(mfrow=c(1,2))
biplot(env.pca, scaling = 1, main = "PCA - scaling 1", xlab = 'PC1 (55%)', ylab = 'PC2 (20%)')
biplot(env.pca, main = "PCA - scaling 2", xlab = 'PC1 (55%)', ylab = 'PC2 (20%)') # Default scaling 2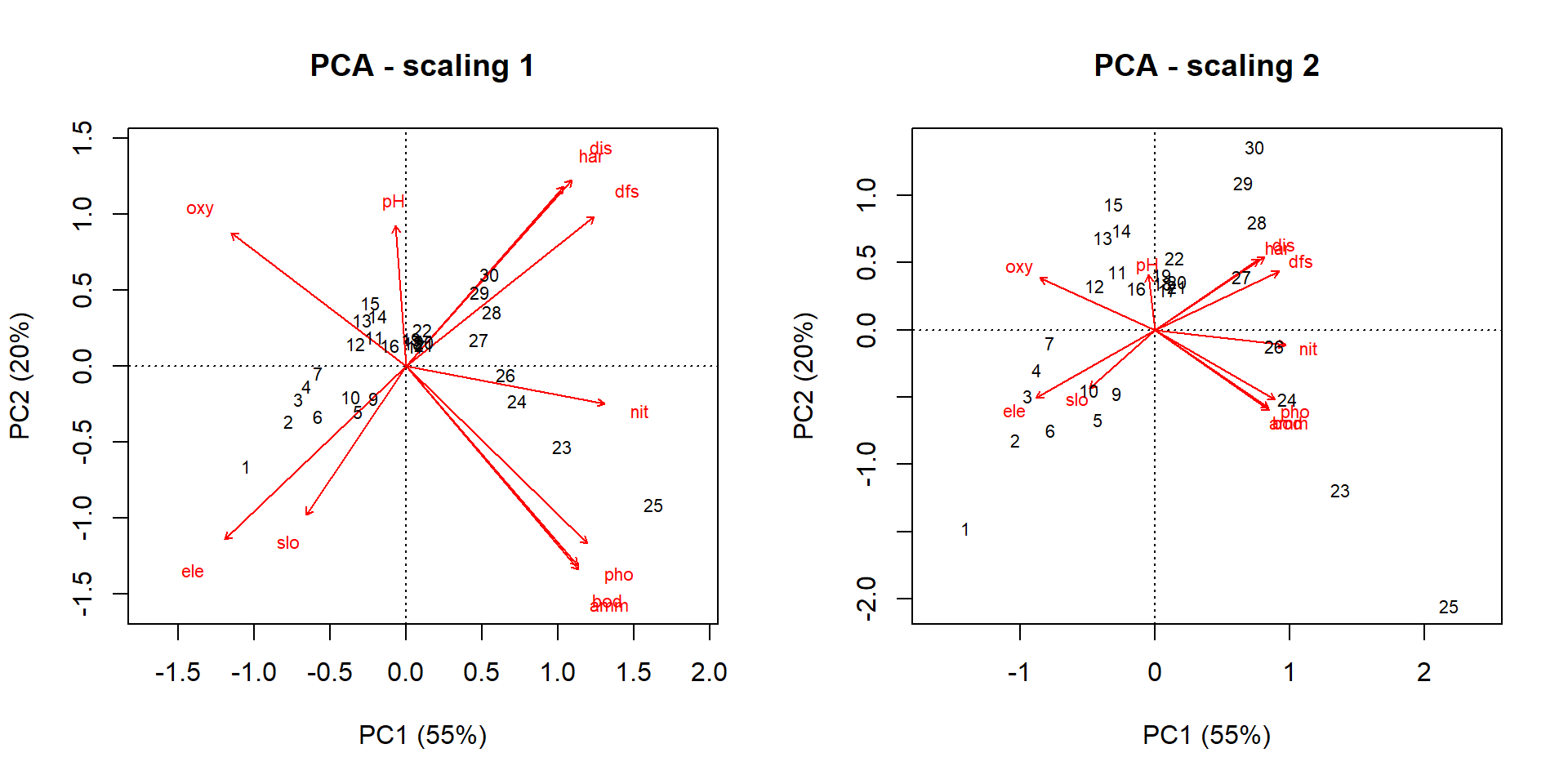
Ara és el moment d’interpretar els dos biplots. En primer lloc, estem graficant els dos primers eixos (PC1 i PC2), que com hem vist abans expliquen un 75% de la variància. Això indica que la nostra interpretació del primer parell d’eixos extreu la informació més rellevant de les dades.
El biplot amb scaling 1 mostra un gradient d’esquerra a dreta, començant per un grup format pels punts de mostreig 1-10 que mostren els valors més alts d’altitud (ele) i pendent (slo), i els valors més baixos de cabal (dis) i distància a la capçalera (dfs). El segon grup de llocs (11-16), té els valors més alts en contingut d’oxigen (oxy) i el més baix en concentració de nitrats (nit). Un tercer grup de llocs molt similars (17-22) mostra valors intermedis en gairebé totes les variables mesurades, ja que estan pràcticament centrades a les coordenades 0,0 del biplot. Finalment, els llocs 23-25 mostren valors màxims de concentració de fosfat (pho) i amoni (amm), així com de la demanda biològica d’oxigen (dbo). En general, sembla que hi ha una progressió des d’aigües oligotròfiques riques en oxigen a aigües més eutròfiques al llarg del riu, i tres punts (23-25) amb una càrrega de nutrients i matèria orgànica particularment elevades.
I ara podem fer una ullada al biplot amb scaling 2 per veure les relacions entre variables. La part inferior esquerra del biplot mostra que l’altitud (ele) i el pendent (slo) estan molt correlacionats positivament, i que aquestes dues variables estan molt correlacionades negativament amb la distància a capçalera (dfs), el cabal (dis) i la duresa de l’aigua (har). El contingut d’oxigen (oxy) està lleugeramant correlacionat positivament amb l’elelevació i el pendent, però molt negativament correlacionat amb la concentració de fosfat (pho) i amoni (amm) i la demanda biològica d’oxigen (dbo). La part dreta inferior del biplot mostra la demanda biològica d’oxigen i les concentracions de fosfat, nitrat i amoni, variables clarament vinculades a l’eutrofització. El nitrat i el pH tenen fletxes quasi ortogonals, cosa que indica una correlació propera a 0.
El biplot de scaling 2 també reflecteix la importància relativa de les variables en l’odenació a través de la llargada dels vectors. Per exemple, el pH mostra una fletxa força més curta que la resta, mostrant la seva menor importància per a l’ordenació en el pla definit per els dos primers eixos (PC1 i PC2). Les coordenades del vectors les podem consultar al summary de l’objecte env.pca (species scores) o a través de la funció scores():
## PC1 PC2 PC3
## dfs 1.08421533 0.5150025 -0.257490476
## ele -1.04368531 -0.5944910 0.179841928
## slo -0.57521299 -0.5103493 -0.554993357
## dis 0.95769253 0.6412091 -0.306540683
## pH -0.05860434 0.4819658 1.034443935
## har 0.90722836 0.6181063 -0.022797511
## pho 1.04601297 -0.6092513 0.187343796
## nit 1.14316569 -0.1290201 0.012033435
## amm 0.99540203 -0.6988712 0.185971335
## oxy -1.00893321 0.4578040 -0.009179811
## bod 0.98988541 -0.6835809 0.119622910
## attr(,"const")
## [1] 4.189264Per defecte, la funció biplot grafica els dos primers eixos, però podem especificar quins eixos volem a través de l’argument choices:
biplot(env.pca, choices = c(2,3), main = "PCA - scaling 2", xlab = 'PC2 (20%)', ylab = 'PC3 (9%)') # Default scaling 2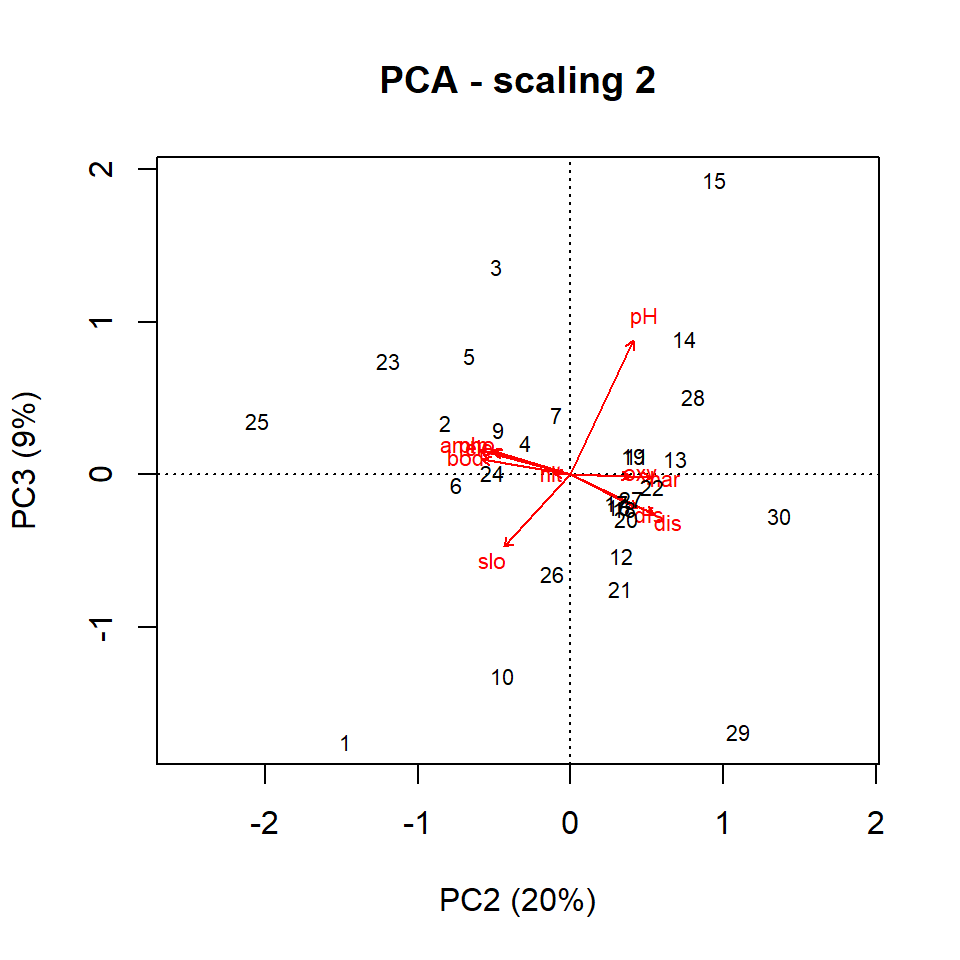
3.2.3 Combinar ordenació i classificació
Podem complementar l’anàlisi d’ordenació a través d’una anàlisi de classificació. Per exemple, ràpidament farem una anàlisi de classificació jeràrquica de la mateixa matriu env (veure secció “2.3. Anàlisis Cluster jeràrquic” per tutorial) i afegirem el resultat en el nostre biplot. Veureu com l’anàlisi de clúster ens ajuda a veure clarament si hi ha discontinuïtats al llarg del riu i a confirmar grups que ja intuíem a l’interpretar els biplots anteriors.
# Clustering the objects using the environmental data: Euclidean distance after standardizing the variables, followed by Ward clustering
env.eu <- dist(scale(env)) # estandarditzem les dades i en calculem la matriu de distàncies euclídies. Fem els dos passos a la mateixa línia de codi
env.eu.w <- hclust(env.eu, "ward.D") # apliquem l'anàlisi jeràrquic amb el mètode d'aglomeració Ward
gr <- cutree(env.eu.w, k = 4) # Tallem el dendograma per obtenir 4 grups
grl <- levels(factor(gr))
sit.sc1 <- scores(env.pca, display = "wa", scaling = 1) # Extreure els site scores amb scaling 1
biplot(env.pca, scaling = 1, main = "PCA scaling 1 + clusters", col = c('white','red'))
abline(v = 0, lty = "dotted")
abline(h = 0, lty = "dotted")
for (i in 1:length(grl)) {points(sit.sc1[gr == i, ], pch = (14 + i), cex = 1.5, col = i + 1)}
text(sit.sc1, row.names(env), cex = 0.7, pos = 3)
legend('topleft', paste("Cluster", c(1:length(grl))), pch = 14 + c(1:length(grl)), col = 1 + c(1:length(grl)), pt.cex = 2)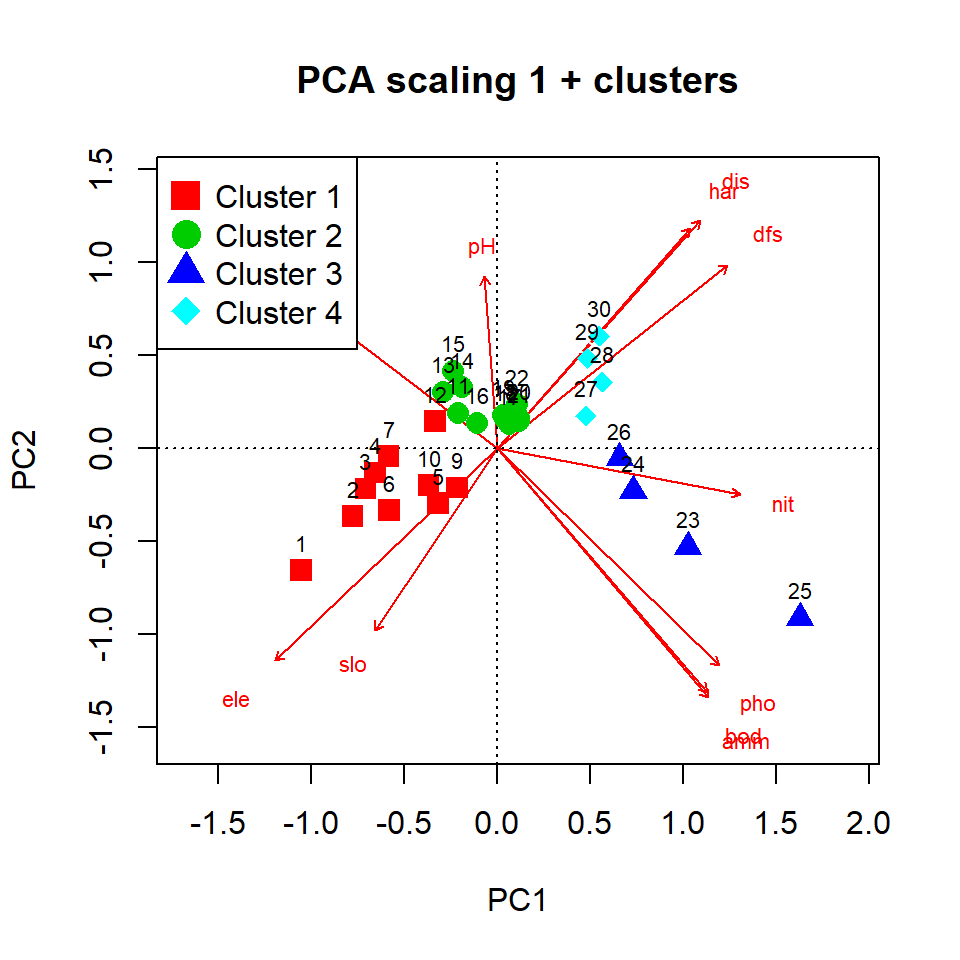
3.3 Non-Metric Multidimensional Scaling (NMDS)
En el següent exemple aplicarem el mètode NMDS a la matriu spe, que conté dades d’abundància de diferents espècies de peixos per als mateixos punts de mostreig al llarg del riu Doubs.
El mètode NMDS és més versàtil que el PCA, en el sentit que pot produir ordenacions a partir de qualsevol matriu de distàncies (euclídia, Bray-Curtis, Chord, Manhattan etc) i tipus de variables (quantitatives, ordinals, qualitatives o mixtes). És per això que és un dels mètodes més utilitzats en ecologia, tant per dades ambientals com d’abundància. El mètode està basat en rangs. Això vol dir que la prioritat de l’NMDS no és preservar la distància exacte entre objectes sinó simplement com aquests están ordenats. D’aquesta manera, tot i que perdem informació de la magnitud de les distàncies entre objectes, treballar per rangs converteix a l’NMDS en un mètode molt robust que pot treballar amb dades que tinguin qualsevol tipus de distribució, fins i tot si no segueixen cap mena de distribució identificable.
Aplicarem un NMDS a la matriu spe a través de la funció metaMDS() del package vegan, però primer ens cal calular una matriu de distàncies. La matriu de distàncies la podem calcular a part o directament a dins de la funció metaMDS() a través de l’argument distance. Per coherència amb anàlisi anteriors, escollirem Bray-Curtis com a mesura d’associació, ja que tenim dades semiquantitatives d’abundància.
spe.nmds<- metaMDS(spe, k=2, distance = "bray") # NMDS de k=2 dimensions sobre la matriu de distàncies de Bray-Curtis ## Run 0 stress 0.07477822
## Run 1 stress 0.07376308
## ... New best solution
## ... Procrustes: rmse 0.0193814 max resid 0.09469869
## Run 2 stress 0.07376314
## ... Procrustes: rmse 0.0009114911 max resid 0.004386576
## ... Similar to previous best
## Run 3 stress 0.07429355
## Run 4 stress 0.08801542
## Run 5 stress 0.1226663
## Run 6 stress 0.1218761
## Run 7 stress 0.07376382
## ... Procrustes: rmse 0.0001474421 max resid 0.0007058046
## ... Similar to previous best
## Run 8 stress 0.1136968
## Run 9 stress 0.1115879
## Run 10 stress 0.07478191
## Run 11 stress 0.07477991
## Run 12 stress 0.08841676
## Run 13 stress 0.1219308
## Run 14 stress 0.07429451
## Run 15 stress 0.1224641
## Run 16 stress 0.1225943
## Run 17 stress 0.07376584
## ... Procrustes: rmse 0.001322192 max resid 0.006354144
## ... Similar to previous best
## Run 18 stress 0.111884
## Run 19 stress 0.1141866
## Run 20 stress 0.1141846
## *** Solution reachedFixeu-vos que quan executem la funció metaMDS() apareix a la consola tot un seguit de runs amb un valor de stress associat. Això és degut a que l’NMDS funciona a través d’un procés iteratiu:
- Escollir el nombre k de dimensions (eixos) que es vol. Es pot canviar a través de l’argument k de la funció
metaMDS(). - Constuir una configuració inicial dels objectes en l’espai de k dimensions, que servirà de punt de partida.
- Anar provant diferents configuracions de posició dels objectes per tal de minimitzar el paràmetre stress (valors de 0 a 1). Stress reflecteix la discordança entre els rangs de l’ordenació i els rangs de la matriu de distàncies original.
El procés acaba quan el valor stress ja no es pot reduir més, o quan aquest assoleix un valor predeterminat que pot decidir l’usuari. Al ser un procés iteratiu, NMDS és un mètode amb força requeriment computacional.
Per a veure el valor de stress final de l’anàlisi NMDS que acabem de fer podem fer servir la següent comanda:
## [1] 0.07376308No hi ha cap criteri universal per decidir quins valors de stress són acceptables i quins no, però es sol dir que un valor per sobre de 0.2 no és massa fiable, i per sobre de 0.3 indicaria que l’ordenació és pràcticament a l’atzar. Valors al voltant de 0.1 es consideren acceptables, i valors per sota de 0.05 indicarien un molt bon resultat. Augmentar el nombre de dimensions pot reduir els valors de stress, però permetre més de 3 dimensions fa que la interpretació sigui més complicada. Com sempre, hem d’intentar buscar un compromís.
En el nostre cas (2 dimensions) tenim un stress de 0.07, que està prou bé. Provem 3 dimensions per a veure si aconseguim baixar-lo encara més:
spe.nmds.3<- metaMDS(spe, k=3, distance = "bray") # NMDS de k=3 dimensions sobre la matriu de distàncies de Bray-Curtis## [1] 0.0434686Hem baixat el valor de stress fins a 0.04, tot i que ens fa arrossegar una dimensió més. De moment ens quedarem amb el de 2 dimensions que serà més fàcil de visualitzar.
Per acabar de valorar la qualitat de l’NMDS podem fer un shepard plot, que consisteix en comparar les distàncies entre objectes a l’NMDS amb les distàncies originals:
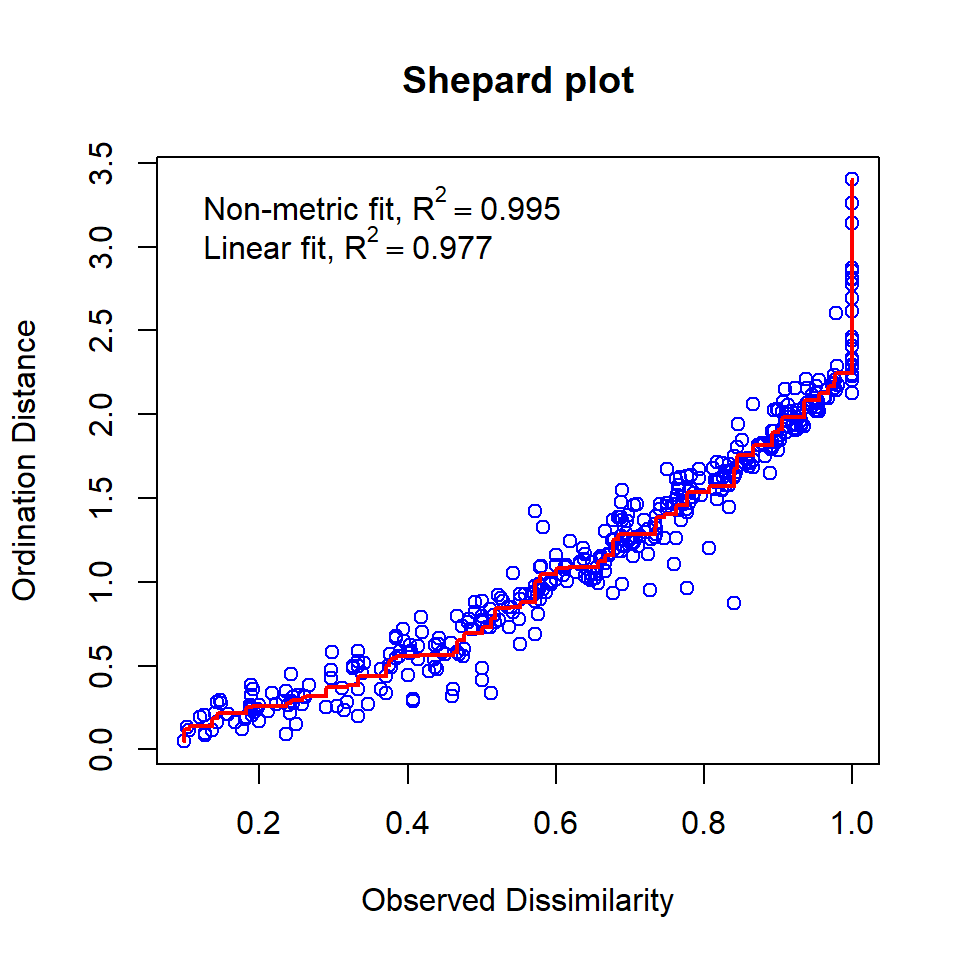
Tenim una molt bona relació entre les dues distàncies! Això confirma que hem obtingut una ordenació molt fidel a la matriu original. Si tinguéssim molta dispersió o alguns outliers ens podríem plantejar passar a 3 dimensions.
Anem a veure com ha quedat l’ordenació amb dues dimensions i a interpretar-la. Recordeu que els punts de mostreig estan ordenats de capçalera a desembocadura:
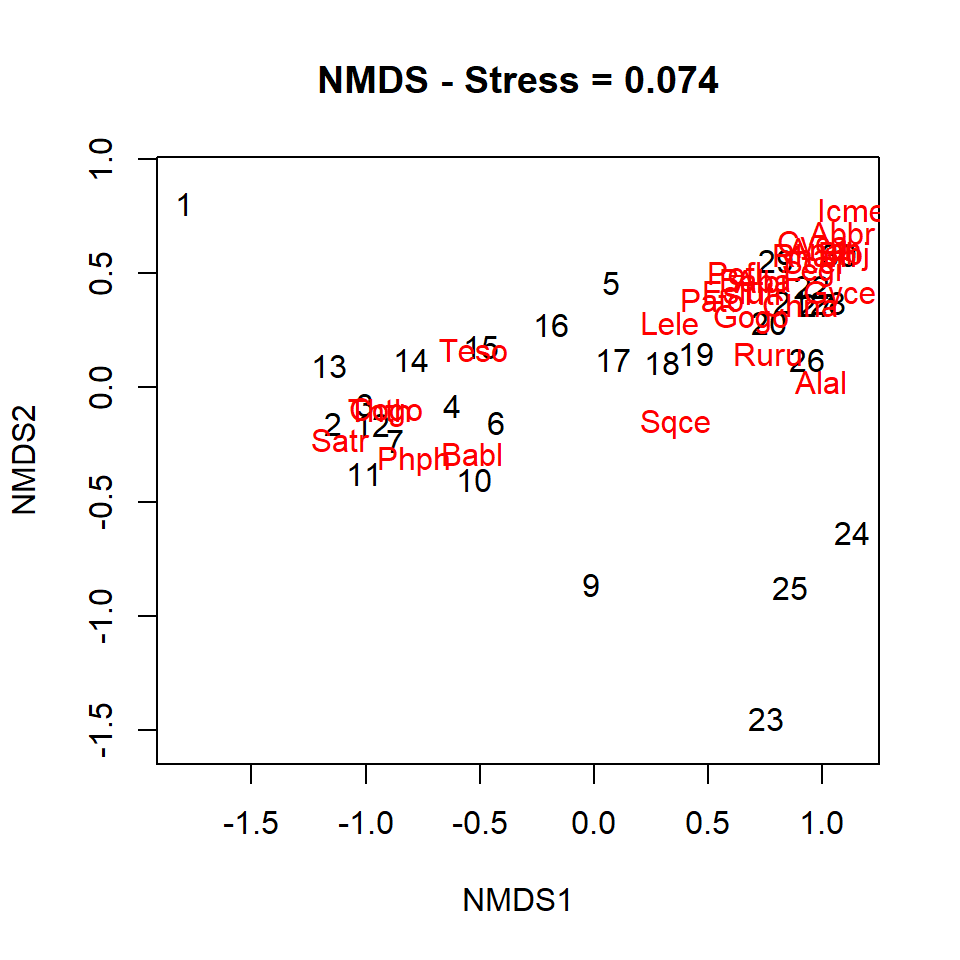
A la part central de l’NMDS hi tenim un grup de punts de mostreig (2,3,4,6,7,10,11,12,13,14,15; generalment curs alt del riu) que tenen una comunitat de peixos similar, dominada per les espècies Satr, Phph, Babl, Teso, Gogo i Thth. A la part superior-dreta hi tenim un altre grup format pels punts 20,21,22,26,27,28,29,30 (curs baix) que presenten una alta riquesa d’espècies molt diferenciada del grup anterior. Els punts 16-19 es troben entre mig dels dos grups, i mostren un canvi gradual entre els dos tipus de comunitats de peixos descrites. Després tenim els punts 9 i 23-25 a l’extrem inferior del gràfic. Aquests grups presenten comunitats molt diferenciades dominades per les espècies Alal, Sqce i Ruru. I finalment tenim el punt 1 aïllat a d’alt a l’esquerra, que també presenta una comunitat completament diferent i és difícil de dir quines espècies hi dominen.
Si us hi fixeu, la interpretació de l’NMDS ens ha portat a conclusions molt semblants a les que vam obtenir a través d’un anàlisi de classificació a la Secció “2. Cluster analysis”. I de fet podem combinar les dues anàlisis (NMDS + Cluster jeràrquic) tal i com hem fet abans amb el PCA:
sit.sc <- scores(spe.nmds) #obtenim coordenades de les mostres NMDS
plot(spe.nmds, type="t", main=paste("NMDS - Stress =",round(spe.nmds$stress,3)), cex=0.5)
#Tornem a fer ràpidament el clúster jeràrquic que vam fer a la sessió anterior
spe.db <- vegdist(spe, method = 'bray')
spe.db.UPGMA <- hclust(spe.db, method = "average")
cutg <- cutree(spe.db.UPGMA, k=3)
grp.lev <- levels(factor(cutg))
#dibuixem les mostres amb colors diferents en funció del nombre de grups
for (i in 1:length(grp.lev))
{
points(sit.sc[cutg==i,], pch=(14+i), cex=1.5, col=i+1)
}
text(sit.sc, row.names(spe), pos=4, cex=0.7)
legend('bottomleft', paste("Group",c(1:length(grp.lev))),
pch=14+c(1:length(grp.lev)), col=1+c(1:length(grp.lev)), pt.cex=2)
3.3.1 Relació Post Hoc entre l’ordenació NMDS i variables ambientals
Un cop tenim el NMDS final basat en la comunitat de peixos, podem mirar si hi ha alguna relació entre la ordenació obtinguda i la matriu de variables ambientals. Per a fer això projectarem les variables de la matriu env a l’NMDS mitjançant la funció envfit(), que utilitza permutacions per avaluar la significació estadística de cada variable en relació als eixos del NMDS (també aplicable a PCA).
spe.nmds.env<-envfit(spe.nmds,env[,-1], perm=999) # environmental fitting de la matriu env amb 999 permutacions. Hem exclòs la primera columna (distance from source), ja que és un descriptor espacial més que una variable ambiental.
spe.nmds.env##
## ***VECTORS
##
## NMDS1 NMDS2 r2 Pr(>r)
## ele -0.98905 -0.14760 0.6116 0.001 ***
## slo -0.75118 0.66010 0.3265 0.017 *
## dis 0.88555 0.46455 0.5685 0.001 ***
## pH -0.26004 0.96560 0.0181 0.764
## har 0.96387 -0.26638 0.3774 0.005 **
## pho 0.45844 -0.88873 0.5445 0.001 ***
## nit 0.87729 -0.47996 0.5818 0.001 ***
## amm 0.42843 -0.90357 0.5553 0.001 ***
## oxy -0.74163 0.67081 0.7396 0.001 ***
## bod 0.44104 -0.89749 0.6580 0.001 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Permutation: free
## Number of permutations: 999I les podem afegir a l’NMDS fàcilment:
# primer repetim el plot de NMDS amb els clústers
plot(spe.nmds, type="t", main=paste("NMDS - Stress =",round(spe.nmds$stress,3)), cex=0.5)
for (i in 1:length(grp.lev)) {points(sit.sc[cutg==i,], pch=(14+i), cex=1.5, col=i+1)}
text(sit.sc, row.names(spe), pos=4, cex=0.7)
legend('bottomleft', paste("Group",c(1:length(grp.lev))),
pch=14+c(1:length(grp.lev)), col=1+c(1:length(grp.lev)), pt.cex=2)
#ara afegim l'environmental fitting
plot(spe.nmds.env,col="grey") # dibuixa totes les variables ambientals, en gris.
plot(spe.nmds.env, p.max=0.05, col="purple") # dibuixa només les variables ambientals relacionades significativament p-valor<0.05 amb els eixos de l'NMDS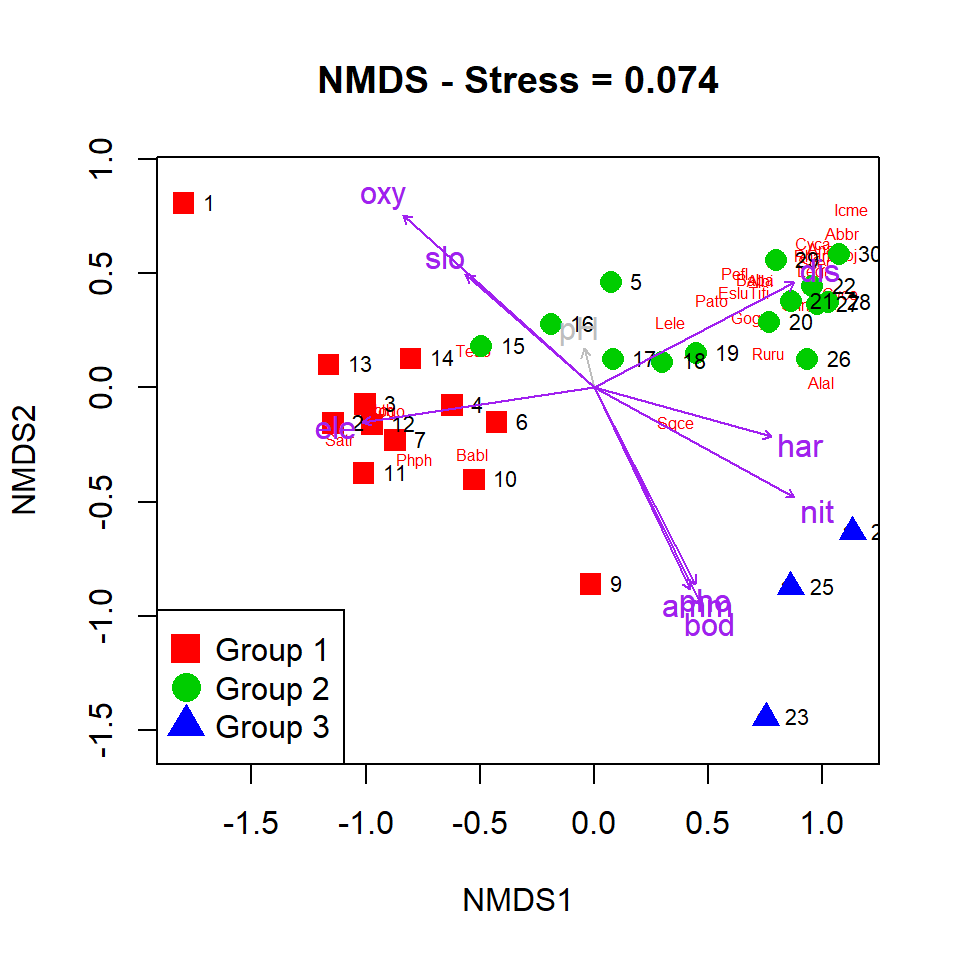
La funció envfit() és útil per tenir una idea aproximada de la relació entre la comunitat de peixos i les variables ambientals al llarg del riu Doubs. Tot i així, existeixen mètodes més adequats per analitzar específicament la influència de variables externes sobre una matriu resposta. En el següent apartat en veurem un exemple.
Els mètodes que hem vist fins ara (PCA i NMDS) es coneixen com a mètodes d’ordenació indirectes o unconstrained. Són mètodes que generen una ordenació basada en una única matriu de dades, sense cap influència directa de variables externes en l’anàlisi. Qualsevol inferència de l’influència potencial de variables externes en l’ordenació es fa de manera descriptiva a posteriori (Post Hoc; veure exemple NMDS). Altres exemples de mètodes indirectes d’ordenació serien l’Anàlisi de Coordenades Principals (PCoA) o l’anàlisi de Correspondències (CA).
Els mètodes directes (també coneguts com constrained o canonical), en canvi, generen l’ordenació d’una matriu resposta condicionada per una matriu explicativa. És a dir, hi ha una segona matriu de variables externes que forma part del procés d’ordenació. Per tant, els mètodes directes treballen sobre dues matrius; la matriu resposta i la matriu explicativa. Aquests tipus de mètodes sí que permeten testar explícitament hipòtesis relacionades amb la influència de factors externs en l’ordenació d’una matriu resposta. Un dels mètodes directes més habituals en ecologia és l’anàlisi de Redundàncies (RDA), que és una extensió del PCA.
3.4 Anàlisi de Redundàncies (RDA)
RDA és un mètode d’ordenació directe que combina regressió múltiple i PCA. Bàsicament el que fa és generar models de regressió lineal múltiple per a cada una de les variables de la matriu resposta en base a la matriu explicativa, i després fa un PCA dels valors predits per aquests models. Això força que els eixos de l’ordenació siguin dependents de la matriu explicativa. Per tant, a diferència de mètodes indirectes com el PCA i l’NMDS, en un RDA els factors externs estan explícitament integrats a l’anàlisi d’ordenació.
Igual que el PCA, l’RDA és un mètode lineal que preserva la distància euclídia. Per tant, a prori, l’RDA és adequat només per a dades compatibles amb la distància euclídia, és a dir, dades quantitatives. Tot i així, com hem comentat a l’apartat de PCA, podem igualment aplicar un RDA a variables d’altres tipus (e.g. semiquantitatives o binàries) si prèviament les transposem a un espai euclidià mitjançant la transformació de Hellinger. Per veure’n un exemple, farem un RDA de les dades d’abundància de peixos del riu Doubs condicionada per la matriu de variables ambientals.
De manera resumida, l’anàlisi RDA que farem seguirà els següents passos:
Regressionar cada variable de la matriu resposta (matriu
spe) per separat en funció de la matriu explicativa (matriuenv).Generar una nova matriu \(Ŷ\) amb els valors predits per aquests models de regressió.
Computar un PCA de la matriu de valors predits \(Ŷ\).
Però abans que res transformarem la matriu d’abundàncies de peixos mitjançant la transformació de Hellinger. També estandarditzarem la matriu de variables ambientals:
spe.hel <- decostand(spe, "hellinger")
env.std <- scale(env[,-1]) # estandardització z-score. Eliminem la primera variables (distance from source) perquè és una variable espacial més que no pas ambientalI ara sí, apliquem l’RDA. El package vegan ofereix dues maneres de cridar la funció:
spe.rda <- rda(spe.hel,env.std) # Opció 1
spe.rda <- rda(spe.hel ~ ., data=data.frame(env.std)) # Opció 2. Mateix estil que la funció lm(). Permet escollir o excloure variables explicatives fàcilment
# TIP: Fixeu-vos que, a l'opció 2,on haurien d'anar les variables explicatives hi hem posat simplement un punt "."; això vol dir que volem que consideri totes les variables que hi ha a la matriu env.std. Seria l'equivalent a posar: rda(spe.hel ~ ele + slo + dis + pH + har + pho + nit + amm + oxy + bod, data = data.frame(env.std))Per a veure el resultat utilitzem el summary de la funció. El summary és increïblement llarg, però de moment només ens fixarem en un parell o tres de coses:
##
## Call:
## rda(formula = spe.hel ~ ele + slo + dis + pH + har + pho + nit + amm + oxy + bod, data = data.frame(env.std))
##
## Partitioning of variance:
## Inertia Proportion
## Total 0.5025 1.0000
## Constrained 0.3689 0.7341
## Unconstrained 0.1336 0.2659
##
## Eigenvalues, and their contribution to the variance
##
## Importance of components:
## RDA1 RDA2 RDA3 RDA4 RDA5 RDA6
## Eigenvalue 0.2280 0.05442 0.03382 0.03007 0.007488 0.005652
## Proportion Explained 0.4538 0.10829 0.06730 0.05984 0.014901 0.011248
## Cumulative Proportion 0.4538 0.56207 0.62937 0.68921 0.704108 0.715356
## RDA7 RDA8 RDA9 RDA10 PC1 PC2
## Eigenvalue 0.004427 0.002816 0.001383 0.0007938 0.04643 0.02071
## Proportion Explained 0.008809 0.005604 0.002751 0.0015797 0.09240 0.04122
## Cumulative Proportion 0.724165 0.729770 0.732521 0.7341007 0.82650 0.86772
## PC3 PC4 PC5 PC6 PC7 PC8
## Eigenvalue 0.01746 0.01326 0.009747 0.005884 0.005118 0.004001
## Proportion Explained 0.03474 0.02638 0.019397 0.011710 0.010186 0.007962
## Cumulative Proportion 0.90246 0.92884 0.948237 0.959947 0.970133 0.978095
## PC9 PC10 PC11 PC12 PC13
## Eigenvalue 0.003032 0.002999 0.001809 0.00111 0.0007558
## Proportion Explained 0.006033 0.005969 0.003601 0.00221 0.0015040
## Cumulative Proportion 0.984128 0.990096 0.993697 0.99591 0.9974109
## PC14 PC15 PC16 PC17 PC18
## Eigenvalue 0.0005623 0.0003471 0.0002483 0.0001113 3.203e-05
## Proportion Explained 0.0011189 0.0006907 0.0004942 0.0002216 6.373e-05
## Cumulative Proportion 0.9985298 0.9992205 0.9997147 0.9999363 1.000e+00
##
## Accumulated constrained eigenvalues
## Importance of components:
## RDA1 RDA2 RDA3 RDA4 RDA5 RDA6
## Eigenvalue 0.2280 0.05442 0.03382 0.03007 0.007488 0.005652
## Proportion Explained 0.6181 0.14752 0.09168 0.08151 0.020298 0.015323
## Cumulative Proportion 0.6181 0.76566 0.85733 0.93885 0.959143 0.974466
## RDA7 RDA8 RDA9 RDA10
## Eigenvalue 0.004427 0.002816 0.001383 0.0007938
## Proportion Explained 0.012000 0.007634 0.003748 0.0021519
## Cumulative Proportion 0.986466 0.994100 0.997848 1.0000000
##
## Scaling 2 for species and site scores
## * Species are scaled proportional to eigenvalues
## * Sites are unscaled: weighted dispersion equal on all dimensions
## * General scaling constant of scores: 1.93676
##
##
## Species scores
##
## RDA1 RDA2 RDA3 RDA4 RDA5 RDA6
## Cogo 0.13168 0.102927 -0.0172396 -0.235904 0.0185404 0.0220381
## Satr 0.61829 -0.009598 0.2863130 0.078033 -0.0003366 -0.0130025
## Phph 0.49901 0.142783 -0.1999262 0.006974 -0.0636364 -0.0080153
## Babl 0.38975 0.147648 -0.2235871 0.083274 -0.0224838 -0.0273614
## Thth 0.13330 0.096058 0.0001698 -0.235509 0.0128493 0.0514745
## Teso 0.06661 0.109487 -0.0033225 -0.197073 0.0177318 0.0145384
## Chna -0.17135 0.072602 0.0081049 -0.008547 0.0209873 -0.0642848
## Pato -0.12540 0.160792 0.0106607 -0.036218 -0.0339868 -0.0911387
## Lele -0.08402 0.049439 -0.0640504 0.010157 -0.0167979 0.0178863
## Sqce -0.09595 -0.131734 -0.1809008 -0.055314 0.0899407 0.0235329
## Baba -0.17988 0.208992 0.0358209 -0.070649 0.0008484 -0.0276488
## Albi -0.15529 0.157855 0.0243902 -0.011053 -0.0326512 -0.0353536
## Gogo -0.20181 0.040025 -0.0448309 -0.008918 -0.0611504 0.0344393
## Eslu -0.10105 0.049236 -0.0458486 0.088418 -0.0871644 0.0676376
## Pefl -0.08814 0.121128 -0.0471022 0.078663 0.0028530 -0.0046025
## Rham -0.20487 0.161279 0.0451070 0.018140 -0.0157101 -0.0015698
## Legi -0.22972 0.109604 0.0186290 0.011647 0.0353135 -0.0344243
## Scer -0.16707 0.004247 0.0068001 0.036696 -0.0579099 0.0680965
## Cyca -0.17608 0.143528 0.0343894 0.011088 0.0032765 -0.0024142
## Titi -0.13246 0.128038 -0.0720992 0.108982 0.0556379 0.0136271
## Abbr -0.18790 0.117059 0.0487619 0.036122 0.0208978 0.0310905
## Icme -0.15069 0.080094 0.0487028 0.043237 0.0352901 0.0686542
## Gyce -0.31193 0.014102 0.0221617 0.022649 -0.0243167 0.0368280
## Ruru -0.31229 -0.147163 -0.1319149 0.039417 0.0484457 -0.0380610
## Blbj -0.24213 0.087377 0.0391807 0.034263 0.0542296 -0.0007183
## Alal -0.42820 -0.222450 0.0093394 -0.129525 -0.1121690 -0.0449822
## Anan -0.19190 0.140634 0.0437444 0.026015 -0.0061642 0.0151929
##
##
## Site scores (weighted sums of species scores)
##
## RDA1 RDA2 RDA3 RDA4 RDA5 RDA6
## 1 0.37843 -0.442643 1.59905 0.30377 0.460679 -0.2557
## 2 0.53341 -0.049591 0.29692 0.38397 -0.395663 -0.5804
## 3 0.49530 -0.002239 0.11569 0.47371 -0.787886 -0.1878
## 4 0.33905 0.068490 -0.22979 0.57727 -0.423662 0.3402
## 5 0.02915 -0.139175 -0.42922 0.59414 -0.101451 0.9136
## 6 0.24981 -0.039465 -0.48201 0.55786 0.130679 0.2082
## 7 0.46640 -0.103933 -0.03475 0.32310 -0.003657 -0.3319
## 9 0.04698 -0.460029 -0.94063 0.21252 1.667215 -0.3611
## 10 0.31972 -0.093398 -0.54291 0.17729 -0.156297 0.1111
## 11 0.48066 -0.059883 0.07614 -0.43930 0.310212 0.2749
## 12 0.49138 -0.007579 0.08037 -0.42930 0.303668 0.2070
## 13 0.49513 0.130727 0.32694 -0.77204 0.050937 0.3525
## 14 0.38260 0.194929 0.07186 -0.81075 -0.064202 0.7805
## 15 0.28845 0.209771 -0.13678 -0.71192 0.480942 0.5962
## 16 0.09254 0.402842 -0.15652 -0.29338 0.090123 -0.5730
## 17 -0.04895 0.439495 -0.10318 -0.38387 -0.318234 -1.1175
## 18 -0.13738 0.411769 -0.14281 -0.34481 -0.302459 -0.8030
## 19 -0.27607 0.338451 -0.28962 0.04886 -0.486963 -0.8211
## 20 -0.39384 0.241790 -0.10316 0.14588 -0.276385 -0.4900
## 21 -0.42776 0.287673 0.03589 0.21000 -0.213783 -0.0262
## 22 -0.46705 0.238920 0.12675 0.20230 0.199258 0.1154
## 23 -0.28262 -1.149532 -0.12850 -0.48736 0.285599 -0.8736
## 24 -0.41273 -0.776416 0.08742 -0.33336 0.281371 -0.7678
## 25 -0.35669 -0.783137 -0.06178 -0.17142 -1.305740 1.1008
## 26 -0.46995 0.089329 0.09814 0.21204 0.059715 0.4290
## 27 -0.47144 0.201419 0.13870 0.22357 0.159967 0.3434
## 28 -0.47462 0.215965 0.16880 0.23421 0.263014 0.4229
## 29 -0.37632 0.361863 0.23637 0.04793 0.028511 0.3884
## 30 -0.49360 0.273590 0.32259 0.24910 0.064492 0.6048
##
##
## Site constraints (linear combinations of constraining variables)
##
## RDA1 RDA2 RDA3 RDA4 RDA5 RDA6
## 1 0.412344 -0.45749 1.56900 0.34409 0.35907 -0.21850
## 2 0.313116 0.10281 0.01803 0.76346 -0.70303 -0.36054
## 3 0.410477 -0.06295 0.06759 0.45126 -0.25281 -0.02352
## 4 0.483578 0.09236 -0.28709 0.29451 -0.17519 0.19410
## 5 0.212729 -0.42709 -0.45522 0.38936 0.44906 0.09152
## 6 0.445873 -0.08763 -0.20170 0.39608 -0.22769 0.03514
## 7 0.537218 -0.10868 -0.23701 0.04236 0.26652 0.34745
## 9 0.001016 -0.26552 -0.62975 0.49922 0.62748 0.07098
## 10 0.163591 -0.07430 -0.10937 0.13791 0.22228 -0.27943
## 11 0.287166 0.23723 -0.09668 -0.27992 0.06710 0.37281
## 12 0.351712 0.14335 -0.02892 -0.39955 -0.17412 -0.22783
## 13 0.373174 0.08983 -0.02338 -0.62529 0.13096 -0.03362
## 14 0.401408 0.12479 -0.01467 -0.66011 0.13900 0.30289
## 15 0.224151 0.19486 0.18522 -0.55343 0.18245 0.35732
## 16 -0.038711 0.28730 -0.20117 -0.14596 0.07078 -0.27539
## 17 -0.076424 0.19802 -0.07889 -0.14297 -0.13796 -0.41674
## 18 -0.063309 0.28473 -0.08075 -0.17694 -0.19880 -0.16440
## 19 -0.021679 0.33057 0.01916 -0.24053 -0.25720 -0.01525
## 20 -0.215840 0.36427 0.05043 -0.07955 -0.43637 -0.60882
## 21 -0.345911 0.27730 -0.06353 0.05740 0.02938 -0.53037
## 22 -0.300109 0.10141 0.04618 -0.17494 0.34148 -0.46256
## 23 -0.192372 -1.01350 0.04958 -0.64212 -0.14128 -0.20451
## 24 -0.541984 -0.62178 -0.18969 -0.08393 0.56631 -0.36724
## 25 -0.412095 -0.89118 -0.08755 -0.13760 -1.12828 0.50555
## 26 -0.479410 0.03628 -0.17844 0.25267 0.15710 0.52130
## 27 -0.609283 0.15393 0.11604 0.25429 0.15033 -0.22435
## 28 -0.513539 0.39587 0.10506 0.17455 -0.03505 0.27849
## 29 -0.351511 0.33941 0.30795 0.16087 -0.11205 0.51975
## 30 -0.455377 0.25579 0.42954 0.12481 0.22053 0.81575
##
##
## Biplot scores for constraining variables
##
## RDA1 RDA2 RDA3 RDA4 RDA5 RDA6
## ele 0.8238 -0.19213 -0.01117 0.5162 0.06657 -0.06693
## slo 0.3418 -0.24904 0.76489 0.2273 0.20808 -0.12830
## dis -0.7791 0.22215 0.18514 -0.2497 -0.07916 0.38540
## pH 0.1026 0.16258 0.03131 -0.3151 0.14582 0.27827
## har -0.5694 0.07367 -0.27231 -0.5486 0.18949 0.37654
## pho -0.4954 -0.65444 -0.07327 -0.2186 -0.42185 0.27069
## nit -0.7764 -0.20414 -0.04926 -0.2593 -0.40020 0.06814
## amm -0.4766 -0.68864 -0.08156 -0.1806 -0.47832 0.09015
## oxy 0.7630 0.53378 0.25897 -0.2120 0.04726 -0.12872
## bod -0.5192 -0.78581 -0.13153 -0.1544 -0.17631 0.08219Partitioning of variance: la variància total es divideix en dues parts: constrained i unconstrained. La fracció constrained és la quantitat de variància total de la matriu
speexplicada per les variables de la matriuenv, en el nostre cas 0.7341 o 73%. Vindria a ser com una mena de R² de l’RDA, tot i que caldria fer-l’hi un petit ajust que veurem més avallEigenvalues, and their contribution to the variance: el nostre RDA ha produit 10 eixos canònics (eigenvalues RDA1-RDA10) i 18 eixos addicionals per als residus dels models de regressió (eigenvalues PC1-PC18). De moment nosaltres només ens fixarem en els eixos canònics. La Cumulative Proportion dels 10 eixos canònics (RDA1-RDA10) és la proporció de la variança total de la matriu
speexplicades per l’RDA. Si combinenm els 10 eixos, obtenim el valor de constrained proportion que parlàvem fa un moment.Accumulated constrained eigenvalues: És la proporció acumulativa dels eixos canònics (RDA1-RDA10) però sobre la variància explicada (constrained variance) enlloc de la variància total.
Per a calcular l’R² i l’R²-ajustat farem servir la funció RsqaureAdj():
## [1] 0.7341007## [1] 0.58637883.4.1 Test de significació permutacional
Abans de començar a visualitzar i interpretar l’RDA cal fer un test de significació. El farem mitjançant un test permutacional utilitzant la funció anova.cca(). L’argument permutations ens permet escollir el nombre de permutacions. Com més alt el número de permutacions, més robust serà el resultat. Primer testarem l’RDA de manera global:
## Permutation test for rda under reduced model
## Permutation: free
## Number of permutations: 999
##
## Model: rda(formula = spe.hel ~ ele + slo + dis + pH + har + pho + nit + amm + oxy + bod, data = data.frame(env.std))
## Df Variance F Pr(>F)
## Model 10 0.36889 4.9695 0.001 ***
## Residual 18 0.13362
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Si sortís no significatiu no valdria la pena interpretar els resultats i s’hauria de descartar l’anàlisi. Però en el nostre cas hem obtingut un RDA significatiu (p<0.001)!
Ara podem testar també la significància individual dels eixos canònics:
anova.cca(spe.rda, by = "axis", permutations = how(nperm = 999)) # 999 produeix un resultat no gaire robust, ja que varia cada vegada que l'executem. Podeu provar d'incrementar el número de permutacions a 9999 o fins i tot 99999 per assegurar que obtenim un resultat robust, però això incrementarà el cost computacional. ## Permutation test for rda under reduced model
## Forward tests for axes
## Permutation: free
## Number of permutations: 999
##
## Model: rda(formula = spe.hel ~ ele + slo + dis + pH + har + pho + nit + amm + oxy + bod, data = data.frame(env.std))
## Df Variance F Pr(>F)
## RDA1 1 0.228027 30.7183 0.001 ***
## RDA2 1 0.054418 7.3309 0.001 ***
## RDA3 1 0.033819 4.5559 0.054 .
## RDA4 1 0.030069 4.0507 0.101
## RDA5 1 0.007488 1.0087 0.999
## RDA6 1 0.005652 0.7615 1.000
## RDA7 1 0.004427 0.5963 1.000
## RDA8 1 0.002816 0.3794 1.000
## RDA9 1 0.001383 0.1863 1.000
## RDA10 1 0.000794 0.1069 1.000
## Residual 18 0.133617
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Els dos primers eixos són significatius. El tercer eix també és significatiu (testat amb 99999 permutacions), tot i que podria sortir un resultat lleugerament diferent si el nombre de permutacions és insuficient (999 en aquest cas). La resta d’eixos els podem descartar.
3.4.2 Visualització dels resultats: Triplot
Per a visualitzar els resultats d’un RDA utilitzarem un triplot, que inclou els objectes, les variables resposta i les variables explciatives en un mateix gràfic:
par(mfrow=c(1,2))
plot(spe.rda, scaling=1, main='Triplot - scaling 1')
plot(spe.rda, scaling=2, main='Triplot - scaling 2')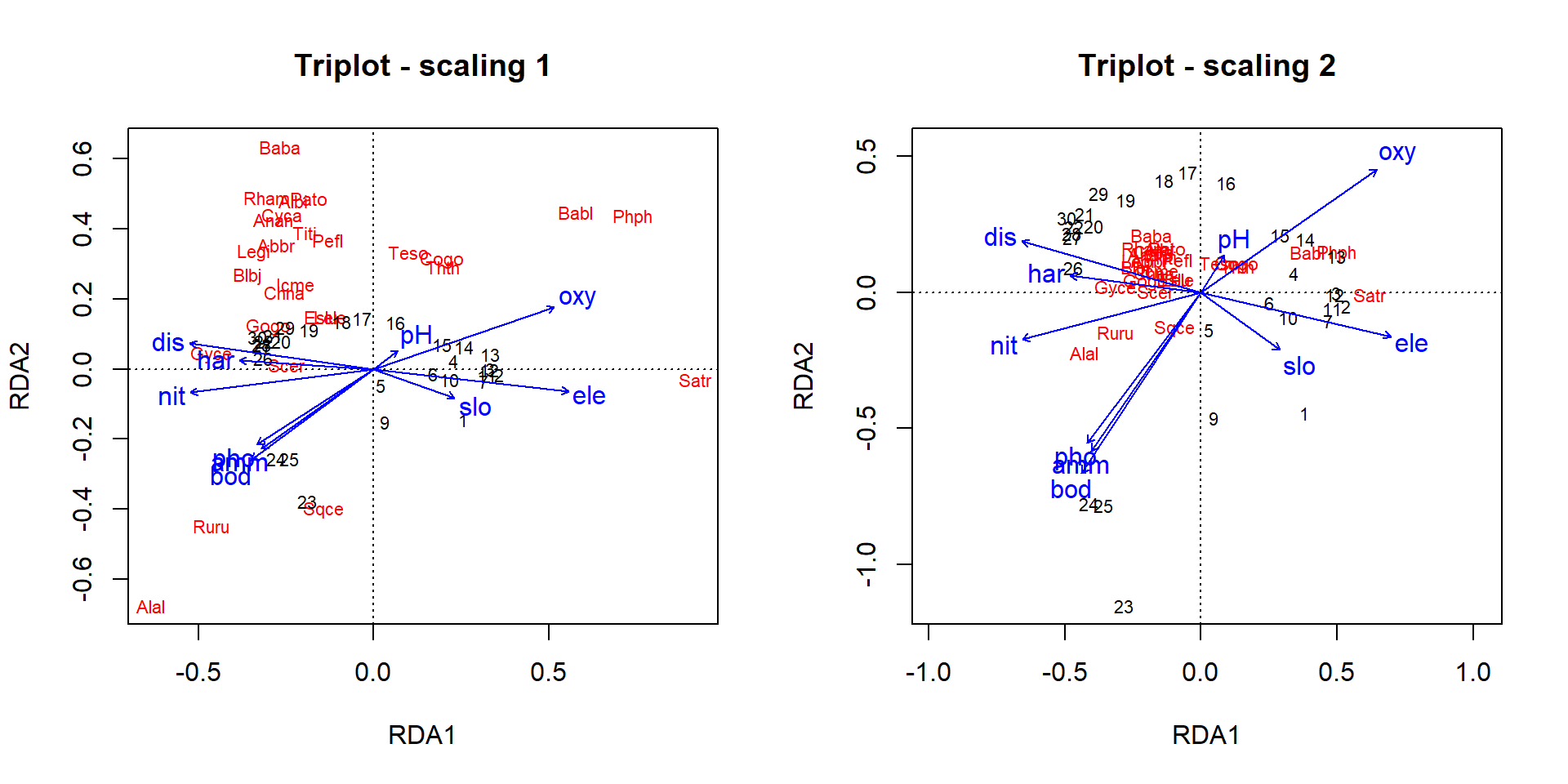
La manera d’interpretar el triplot és molt semblant a la del biplot (veure més amunt apartat PCA). Ens fixarem en el triplot de scaling 1 si ens interessa la posició dels punts de mostreig en l’espai definit per els dos eixos canònics seleccionats. Al contrari, si ens interessa més les correlacions entre variables resposta i variables explanatòries, ens fixarem en el triplot de scaling 2.
Miran els dos triplots, veiem que l’oxigen (oxy), l’altitud (ele), els nitrats (nit) i el cabal (dis) juguen un paper important en la dispersió dels llocs al llarg del primer eix canònic (RDA1). El primer eix separa clarament els cursos alt i baix del riu. El triplot de scaling 2 mostra grups d’espècies de peixos correlacionats amb diferents conjunts de variables explicatives: les espècies Satr, Babl i Phph es troben al curs alt del riu i estan correlacionades amb un alt contingut d’oxigen i una elevació i pendent elevats. Les espècies Alal, Ruru i Sqce predominen especialment els punts de mostreig 23, 24 i 25, caracteritzats per nivells elevats de fosfats (pho), amoni (amm) i demanda biològica d’oxigen (dbo). La majoria d’altres espècies predominen al curs baix del riu (punts 17-30). Fixeu-vos que estan molt agrupades i mostren projeccions als eixos RDA majoritàriament més curtes, la qual cosa indica que estan relacionades amb condicions ecològiques intermèdies.
CONCLUSIONS
A partir de les anàlisis d’ordenació que hem fet durant aquesta sessió podem concloure que:
La comunitat de peixos varia clarament al llarg del riu Doubs. Aquestes variacions de comunitat estan estadísticament associades a canvis en les variables ambientals, principalment a un increment de cabal i condicions eutròfiques aigües avall.
Al curs alt del riu predominen comunitats de peixos moderadament diverses dominades principalment per les espècies Satr, PhPh, Babl. Aquestes comunitats estan associades a aigües de poc cabal, molt oxigenades i amb poca càrrega de nutrients.
Al curs baix del riu predominen comunitats molt diverses formades per espècies que generalment no es troben al curs alt del riu, i que estan associades a cabals alts i aigües relativament més eutròfiques.
Als punts 23-25 tenim unes aigües molt impactades, molt pobres en oxígen, amb concentracions de nutrients molt elevades (especialment d’amoni) i una alta càrrega de matèria orgànica. Aquestes característiques solen estar associades a descàrregues de depuradores o col·lectors urbans. En aquestes aigües trobem comunitats de peixos amb molt poca diversitat on predominen les espècies Ruru, Sqca i especialment Alal.