Chapter 5 Conditional Process Analysis
5.1 Data Import
이번 과제에서 활용할 패키지를 불러옵니다.
분석에 사용할 데이터를 복사-붙여넣기 하여 R에서 쉽게 활용할 수 있는 RDS파일로 만들어줍니다.
# 엑셀을 열어 복사하고, data4 변수로 만들어줍니다.
# 윈도우의 경우, pipe("pbcopy") 대신 "clipboard"를 넣으시면 됩니다.
# data4 <- read.table(pipe("pbcopy"), sep = '\t', header = TRUE)
# 향후 반복해서 사용하실 수 있도록 RDS 파일로 만들어줍니다.
# saveRDS(data4,"data4.RDS")- 여러가지 변수들이 있지만, 제가 오늘 사용할 변수는 아래와 같습니다.
- presence of calling (T2)
- Transformational Leadership(T2)
- Person-Job Fit(T2)
- Job Satisfaction(T2)
- presence of calling (T2)
- 보다 편리한 분석을 위해 data4에서 필요한 변수들만 가지고
별도의 데이터 프레임을 구성합니다.
data4 <- readRDS("data4.RDS")
data4%>%select(V1, ID, T1sex,T1age, T1edu, T1religion, email, Company,
T2소명P, T2leadership, T2PJfit, T2JS, T2소명P1, T2소명P2,
T2소명P3R, T2소명P4,T2소명P5,T2소명P6,T2소명P7,T2소명P8,T2소명P9,
T2소명P10,T2소명P11,T2소명P12, T2leadership1,T2leadership2,T2leadership3,
T2leadership4,T2leadership5,T2leadership6,T2leadership7, T2PJfit1,
T2PJfit2,T2PJfiT2_A,T2PJfit4,T2PJfit5, T2JS1,T2JS2R,T2JS3,T2JS4,T2JS4,T2JS5,
T2JS6)->raw_data
str(raw_data)## 'data.frame': 151 obs. of 42 variables:
## $ V1 : int 1 2 3 4 5 6 7 8 9 10 ...
## $ ID : int 18 542 316 370 421 498 549 205 436 50 ...
## $ T1sex : int 1 1 1 2 2 1 1 1 1 1 ...
## $ T1age : int 30 25 27 24 24 26 25 25 26 25 ...
## $ T1edu : int 4 3 3 3 3 3 3 3 3 3 ...
## $ T1religion : int 3 1 1 1 1 1 4 1 4 4 ...
## $ email : chr "bj.juhng" "bk.jin" "bo.kim" "bomiu.park" ...
## $ Company : int 4 6 5 7 6 5 6 5 6 6 ...
## $ T2소명P : num 3 2.92 3.17 3.67 2.5 ...
## $ T2leadership : num 4 4.14 4 4.14 3.43 ...
## $ T2PJfit : num 5 5 6 5.4 4 5.4 5 3.8 6 5 ...
## $ T2JS : num 4 4 4.17 4.17 3.67 ...
## $ T2소명P1 : int 3 3 3 4 2 2 4 1 4 4 ...
## $ T2소명P2 : int 4 4 4 5 3 4 4 1 4 4 ...
## $ T2소명P3R : int 2 3 2 2 2 1 2 2 2 2 ...
## $ T2소명P4 : int 3 3 3 4 2 4 3 2 3 4 ...
## $ T2소명P5 : int 2 1 2 2 2 1 3 2 2 3 ...
## $ T2소명P6 : int 3 3 4 4 2 4 3 2 2 3 ...
## $ T2소명P7 : int 3 4 3 5 3 5 4 2 4 4 ...
## $ T2소명P8 : int 3 4 4 3 3 4 4 2 4 5 ...
## $ T2소명P9 : int 4 4 4 4 4 5 4 3 4 5 ...
## $ T2소명P10 : int 3 3 3 4 2 4 3 2 4 5 ...
## $ T2소명P11 : int 2 1 2 2 2 2 3 1 2 4 ...
## $ T2소명P12 : int 4 4 4 5 3 5 3 3 4 4 ...
## $ T2leadership1: int 4 4 4 4 4 2 3 2 4 3 ...
## $ T2leadership2: int 4 4 4 4 3 2 4 2 4 4 ...
## $ T2leadership3: int 4 4 4 4 3 2 4 2 4 3 ...
## $ T2leadership4: int 4 4 4 4 4 5 4 3 4 5 ...
## $ T2leadership5: int 4 4 4 4 3 4 3 2 4 4 ...
## $ T2leadership6: int 4 5 4 4 4 5 4 2 4 4 ...
## $ T2leadership7: int 4 4 4 5 3 2 4 2 4 3 ...
## $ T2PJfit1 : int 5 5 6 5 4 5 5 7 6 5 ...
## $ T2PJfit2 : int 5 5 6 6 4 6 4 6 6 4 ...
## $ T2PJfiT2_A : int 5 5 6 5 4 5 4 3 6 4 ...
## $ T2PJfit4 : int 5 5 6 6 4 5 6 2 6 6 ...
## $ T2PJfit5 : int 5 5 6 5 4 6 6 1 6 6 ...
## $ T2JS1 : int 4 4 4 4 4 4 4 1 4 5 ...
## $ T2JS2R : int 4 4 5 5 4 4 4 2 5 5 ...
## $ T2JS3 : int 4 4 4 4 4 1 4 2 4 5 ...
## $ T2JS4 : int 4 4 4 4 4 2 4 2 4 5 ...
## $ T2JS5 : int 4 4 4 4 3 5 3 2 4 4 ...
## $ T2JS6 : int 4 4 4 4 3 2 3 1 4 4 ...5.2 Descriptive analysis
5.2.1 연구대상자 특성
- 필요한 데이터들만 정리했으니, 먼저 연구 대상자의 특성을 살펴보겠습니다.
- 성별에 따른 특성을 살펴보면 아래와 같습니다.
raw_data%>%select(Company,T1sex,T1age, T1edu, T1religion)-> descriptive
mytable(T1sex~., data=descriptive)->res
myhtml(res, caption=paste0("Table1. 연구대상자의 일반적 특성"))| T1sex |
1 (N=109) |
2 (N=42) |
p |
|---|---|---|---|
| Company | 4.7 ± 1.7 | 4.6 ± 1.7 | 0.776 |
| T1age | 25.7 ± 1.4 | 23.4 ± 1.5 | 0.000 |
| T1edu | 0.223 | ||
| 3 | 102 (93.6%) | 36 (85.7%) | |
| 4 | 7 ( 6.4%) | 6 (14.3%) | |
| T1religion | 0.877 | ||
| 1 | 67 (61.5%) | 26 (61.9%) | |
| 2 | 17 (15.6%) | 7 (16.7%) | |
| 3 | 10 ( 9.2%) | 5 (11.9%) | |
| 4 | 15 (13.8%) | 4 ( 9.5%) |
- 성별은 남자가 109명, 여자가 42명으로 남자가 좀 더 많았고, 나이는 남성 편균은 25.7세, 여성 평균은 23.4세 였습니다.
- 학력 수준은 학사 출신이 총 138명, 석사가 13명이었습니다.
- 종교는 종교없음 93명, 개신교 24명, 천주교 15명, 불교가 19명입니다.
5.2.2 측정변수 기술통계
- 이제, 측정변수를 계산한 뒤, 기술통계를 살펴보겠습니다.
- 상관관계를 확인하기 위해, corstars 함수를 정의합니다.
corstars <-function(x, method=c("pearson", "spearman"), removeTriangle=c("upper", "lower"), result=c("none", "html", "latex")){
#Compute correlation matrix
require(Hmisc)
x <- as.matrix(x)
correlation_matrix<-rcorr(x, type=method[1])
R <- correlation_matrix$r # Matrix of correlation coeficients
p <- correlation_matrix$P # Matrix of p-value
## Define notions for significance levels; spacing is important.
mystars <- ifelse(p < .0001, "****", ifelse(p < .001, "*** ", ifelse(p < .01, "** ", ifelse(p < .05, "* ", " "))))
## trunctuate the correlation matrix to two decimal
R <- format(round(cbind(rep(-1.11, ncol(x)), R), 2))[,-1]
## build a new matrix that includes the correlations with their apropriate stars
Rnew <- matrix(paste(R, mystars, sep=""), ncol=ncol(x))
diag(Rnew) <- paste(diag(R), " ", sep="")
rownames(Rnew) <- colnames(x)
colnames(Rnew) <- paste(colnames(x), "", sep="")
## remove upper triangle of correlation matrix
if(removeTriangle[1]=="upper"){
Rnew <- as.matrix(Rnew)
Rnew[upper.tri(Rnew, diag = TRUE)] <- ""
Rnew <- as.data.frame(Rnew)
}
## remove lower triangle of correlation matrix
else if(removeTriangle[1]=="lower"){
Rnew <- as.matrix(Rnew)
Rnew[lower.tri(Rnew, diag = TRUE)] <- ""
Rnew <- as.data.frame(Rnew)
}
## remove last column and return the correlation matrix
Rnew <- cbind(Rnew[1:length(Rnew)-1])
if (result[1]=="none") return(Rnew)
else{
if(result[1]=="html") print(xtable(Rnew), type="html")
else print(xtable(Rnew), type="latex")
}
} - 소명(Calling), 직무몰입(Job Involvement), 인지된 조직지지(Perceived organizational support), 잡크래프팅(Job Crafting) 변수에 대한 상관 및 표준편차는 다음과 같습니다.
# 기술통계를 위한 변수 상관 구하기 : 유의성까지 포함해서 표로 보기
raw_data%>%select(T2소명P, T2leadership, T2PJfit, T2JS)%>%
reshape::rename(c(T2소명P='presence_of_calling', T2leadership='Trans_leadership',
T2PJfit='Person_Job_fit', T2JS="Job_Satisfaction"))%>%corstars(method="pearson", result="html")| presence_of_calling | Trans_leadership | Person_Job_fit | |
|---|---|---|---|
| presence_of_calling | |||
| Trans_leadership | 0.29*** | ||
| Person_Job_fit | 0.33**** | 0.43**** | |
| Job_Satisfaction | 0.41**** | 0.61**** | 0.61**** |
# 평균 및 표준편차
raw_data%>%select(T2소명P, T2leadership, T2PJfit, T2JS)%>%
reshape::rename(c(T2소명P='presence_of_calling', T2leadership='Trans_leadership',
T2PJfit='Person_Job_fit', T2JS="Job_Satisfaction"))%>%
stargazer(title='Descriptive statistics', digits = 2, type = "html",
out = "desc_4.html", summary.stat = c("n", "mean", "sd", "median", "min", "max"))| Statistic | N | Mean | St. Dev. | Median | Min | Max |
| presence_of_calling | 151 | 3.27 | 0.63 | 3.2 | 1 | 5 |
| Trans_leadership | 151 | 3.79 | 0.72 | 4 | 1 | 5 |
| Person_Job_fit | 151 | 4.85 | 0.98 | 5 | 1 | 7 |
| Job_Satisfaction | 151 | 3.59 | 0.73 | 3.7 | 2 | 5 |
기술통계 결과를 보면, 네 가지 요인이 모두 유의미한 정적 상관을 보이고 있으며,
perceived organizational support와 Job Crafting 간의 상관 관계가 가장 높게 나타났습니다.Perceived organizational support와 search for calling 간 상관은 유의미하지 않는 것으로 나타났으나, 조절변수는 이론적으로 설정하는 것이기 때문에
5.3 신뢰도 분석
# T2 presence of calling 신뢰도 분석
raw_data%>%select(T2소명P1, T2소명P2,
T2소명P3R, T2소명P4,T2소명P5,T2소명P6,T2소명P7,T2소명P8,T2소명P9,
T2소명P10,T2소명P11,T2소명P12)%>%alpha()##
## Reliability analysis
## Call: alpha(x = .)
##
## raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
## 0.88 0.88 0.91 0.38 7.5 0.015 3.3 0.63 0.4
##
## lower alpha upper 95% confidence boundaries
## 0.85 0.88 0.9
##
## Reliability if an item is dropped:
## raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
## T2소명P1 0.86 0.87 0.89 0.37 6.5 0.017 0.034 0.39
## T2소명P2 0.87 0.88 0.90 0.40 7.4 0.015 0.031 0.42
## T2소명P3R 0.89 0.89 0.91 0.43 8.3 0.013 0.017 0.42
## T2소명P4 0.87 0.87 0.90 0.38 6.9 0.016 0.031 0.40
## T2소명P5 0.87 0.87 0.90 0.39 7.0 0.016 0.032 0.40
## T2소명P6 0.86 0.87 0.89 0.37 6.5 0.017 0.032 0.39
## T2소명P7 0.86 0.87 0.89 0.37 6.6 0.016 0.029 0.38
## T2소명P8 0.87 0.88 0.90 0.40 7.3 0.015 0.030 0.40
## T2소명P9 0.87 0.87 0.90 0.39 7.0 0.015 0.031 0.41
## T2소명P10 0.86 0.86 0.89 0.37 6.4 0.017 0.030 0.38
## T2소명P11 0.86 0.87 0.89 0.37 6.4 0.017 0.031 0.39
## T2소명P12 0.86 0.86 0.88 0.36 6.2 0.017 0.028 0.38
##
## Item statistics
## n raw.r std.r r.cor r.drop mean sd
## T2소명P1 151 0.75 0.74 0.72 0.68 3.1 1.01
## T2소명P2 151 0.51 0.54 0.47 0.42 3.7 0.85
## T2소명P3R 151 0.39 0.34 0.27 0.24 2.6 1.17
## T2소명P4 151 0.65 0.66 0.62 0.57 3.1 0.98
## T2소명P5 151 0.67 0.63 0.59 0.57 2.5 1.14
## T2소명P6 151 0.76 0.75 0.72 0.69 3.2 1.02
## T2소명P7 151 0.69 0.72 0.71 0.63 3.7 0.82
## T2소명P8 151 0.53 0.56 0.50 0.44 3.5 0.88
## T2소명P9 151 0.59 0.63 0.59 0.52 4.0 0.71
## T2소명P10 151 0.78 0.78 0.77 0.71 3.3 0.99
## T2소명P11 151 0.80 0.76 0.75 0.73 2.7 1.19
## T2소명P12 151 0.79 0.82 0.82 0.74 3.8 0.80
##
## Non missing response frequency for each item
## 1 2 3 4 5 miss
## T2소명P1 0.07 0.19 0.36 0.32 0.05 0
## T2소명P2 0.02 0.05 0.27 0.51 0.15 0
## T2소명P3R 0.19 0.30 0.24 0.21 0.05 0
## T2소명P4 0.01 0.29 0.38 0.21 0.10 0
## T2소명P5 0.21 0.34 0.26 0.13 0.06 0
## T2소명P6 0.04 0.23 0.32 0.32 0.09 0
## T2소명P7 0.01 0.06 0.28 0.50 0.16 0
## T2소명P8 0.01 0.11 0.40 0.36 0.13 0
## T2소명P9 0.01 0.01 0.19 0.57 0.23 0
## T2소명P10 0.04 0.16 0.38 0.32 0.11 0
## T2소명P11 0.18 0.28 0.28 0.18 0.08 0
## T2소명P12 0.01 0.04 0.26 0.51 0.19 0# raw_alpha 0.88로 0.7 이상으로 나타남
# 모든 문항이 .8 이상으로 양호함# T2 Transformational leadership 신뢰도 분석
raw_data%>%select(T2leadership1,T2leadership2,T2leadership3,
T2leadership4,T2leadership5,T2leadership6,T2leadership7)%>%alpha()##
## Reliability analysis
## Call: alpha(x = .)
##
## raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
## 0.92 0.92 0.92 0.62 12 0.01 3.8 0.72 0.62
##
## lower alpha upper 95% confidence boundaries
## 0.9 0.92 0.94
##
## Reliability if an item is dropped:
## raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
## T2leadership1 0.91 0.91 0.91 0.62 9.9 0.012 0.0094 0.62
## T2leadership2 0.90 0.91 0.90 0.61 9.5 0.012 0.0056 0.62
## T2leadership3 0.90 0.90 0.89 0.60 9.1 0.013 0.0026 0.61
## T2leadership4 0.91 0.91 0.91 0.63 10.1 0.012 0.0084 0.62
## T2leadership5 0.91 0.91 0.91 0.62 9.9 0.012 0.0093 0.62
## T2leadership6 0.92 0.92 0.91 0.65 11.4 0.010 0.0043 0.63
## T2leadership7 0.90 0.91 0.90 0.61 9.6 0.012 0.0061 0.62
##
## Item statistics
## n raw.r std.r r.cor r.drop mean sd
## T2leadership1 151 0.82 0.82 0.78 0.75 3.6 0.88
## T2leadership2 151 0.84 0.84 0.82 0.78 3.9 0.84
## T2leadership3 151 0.87 0.88 0.87 0.82 3.8 0.85
## T2leadership4 151 0.81 0.81 0.76 0.73 3.8 0.87
## T2leadership5 151 0.82 0.82 0.78 0.75 3.7 0.88
## T2leadership6 151 0.74 0.74 0.68 0.64 4.0 0.91
## T2leadership7 151 0.85 0.84 0.82 0.78 3.7 0.92
##
## Non missing response frequency for each item
## 1 2 3 4 5 miss
## T2leadership1 0.02 0.10 0.23 0.54 0.11 0
## T2leadership2 0.01 0.05 0.17 0.54 0.24 0
## T2leadership3 0.01 0.07 0.20 0.56 0.16 0
## T2leadership4 0.01 0.08 0.19 0.54 0.17 0
## T2leadership5 0.01 0.09 0.26 0.47 0.17 0
## T2leadership6 0.01 0.06 0.15 0.46 0.32 0
## T2leadership7 0.01 0.09 0.25 0.46 0.19 0# raw_alpha 0.9로 높게 나타남
# 모든 문항이 .8 이상으로 양호함# T2 person-job fit 신뢰도 분석
raw_data%>%select(T2PJfit1,
T2PJfit2,T2PJfiT2_A,T2PJfit4,T2PJfit5)%>%alpha()##
## Reliability analysis
## Call: alpha(x = .)
##
## raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
## 0.89 0.89 0.92 0.62 8.2 0.015 4.9 0.98 0.63
##
## lower alpha upper 95% confidence boundaries
## 0.86 0.89 0.92
##
## Reliability if an item is dropped:
## raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
## T2PJfit1 0.87 0.87 0.89 0.63 6.7 0.018 0.024 0.63
## T2PJfit2 0.87 0.87 0.88 0.63 6.7 0.018 0.020 0.63
## T2PJfiT2_A 0.85 0.85 0.89 0.59 5.7 0.022 0.033 0.50
## T2PJfit4 0.88 0.88 0.87 0.65 7.4 0.016 0.016 0.68
## T2PJfit5 0.86 0.87 0.86 0.62 6.4 0.019 0.022 0.64
##
## Item statistics
## n raw.r std.r r.cor r.drop mean sd
## T2PJfit1 151 0.82 0.83 0.78 0.72 5.0 1.1
## T2PJfit2 151 0.82 0.83 0.79 0.71 4.7 1.2
## T2PJfiT2_A 151 0.88 0.88 0.85 0.81 4.5 1.1
## T2PJfit4 151 0.80 0.79 0.76 0.68 5.0 1.3
## T2PJfit5 151 0.85 0.84 0.82 0.75 5.0 1.2
##
## Non missing response frequency for each item
## 1 2 3 4 5 6 7 miss
## T2PJfit1 0.01 0.01 0.04 0.27 0.36 0.22 0.10 0
## T2PJfit2 0.01 0.02 0.14 0.25 0.35 0.18 0.06 0
## T2PJfiT2_A 0.01 0.03 0.13 0.32 0.30 0.18 0.03 0
## T2PJfit4 0.00 0.05 0.08 0.15 0.32 0.30 0.09 0
## T2PJfit5 0.01 0.02 0.09 0.20 0.32 0.29 0.07 0# raw_alpha 0.89로 높게 나타남
# 모든 문항이 .7 이상으로 양호함# T2 job satisfaction에 대해 신뢰도 분석을 다시 하고,
raw_data%>%select(T2JS1,T2JS2R,T2JS3,T2JS4,T2JS4,T2JS5,T2JS6)%>%alpha()##
## Reliability analysis
## Call: alpha(x = .)
##
## raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
## 0.88 0.88 0.89 0.56 7.6 0.016 3.6 0.73 0.6
##
## lower alpha upper 95% confidence boundaries
## 0.85 0.88 0.91
##
## Reliability if an item is dropped:
## raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
## T2JS1 0.84 0.85 0.85 0.52 5.5 0.021 0.0283 0.55
## T2JS2R 0.90 0.90 0.90 0.64 9.0 0.013 0.0065 0.65
## T2JS3 0.85 0.86 0.85 0.54 6.0 0.020 0.0237 0.59
## T2JS4 0.84 0.84 0.85 0.52 5.4 0.021 0.0215 0.56
## T2JS5 0.86 0.86 0.86 0.56 6.4 0.019 0.0249 0.59
## T2JS6 0.86 0.86 0.86 0.56 6.3 0.019 0.0221 0.57
##
## Item statistics
## n raw.r std.r r.cor r.drop mean sd
## T2JS1 151 0.87 0.87 0.84 0.80 3.7 0.95
## T2JS2R 151 0.64 0.62 0.50 0.46 3.9 1.02
## T2JS3 151 0.82 0.83 0.80 0.73 3.6 0.83
## T2JS4 151 0.87 0.87 0.86 0.80 3.7 0.87
## T2JS5 151 0.79 0.79 0.75 0.69 3.4 0.93
## T2JS6 151 0.79 0.79 0.75 0.69 3.3 0.93
##
## Non missing response frequency for each item
## 1 2 3 4 5 miss
## T2JS1 0.01 0.13 0.19 0.50 0.17 0
## T2JS2R 0.02 0.10 0.17 0.40 0.30 0
## T2JS3 0.01 0.09 0.26 0.54 0.10 0
## T2JS4 0.01 0.08 0.26 0.50 0.15 0
## T2JS5 0.02 0.15 0.31 0.42 0.10 0
## T2JS6 0.03 0.18 0.34 0.38 0.07 0# raw_alpha 0.87로 높게 나타남
# 모든 문항이 .9 이상으로 양호함5.4 Moderating effect analysis
5.4.1 조절효과 분석
- 조절된 매개효과를 분석하기에 앞서, 조절효과와 매개효과를 분석해줍니다.
reshape::rename(raw_data,c(T2소명P='presence_of_calling', T2leadership='Trans_leadership',
T2PJfit='Person_Job_fit', T2JS="Job_Satisfaction"))->raw_data
labels=list(X='presence_of_calling', Y="Job_Satisfaction", W='Person_Job_fit')
pmacroModel(1, labels = labels, radx=0.15,rady=0.05)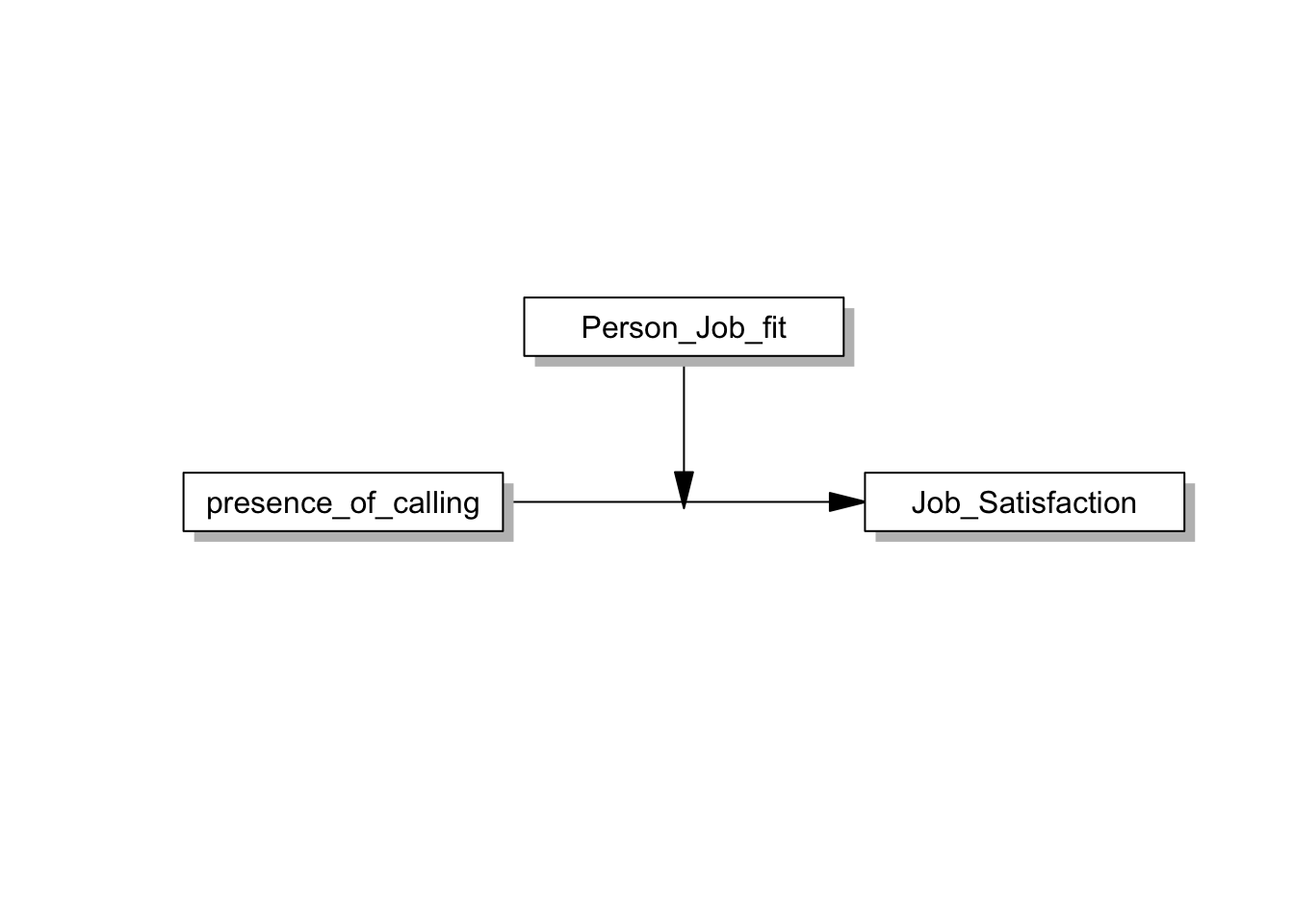
- 위와 같이 모델 설정 후, 회귀분석을 활용하여 분석합니다.
fit <- lm(Job_Satisfaction ~ presence_of_calling*Person_Job_fit, raw_data)
modelsSummaryTable(fit, labels=labels)Consequent | |||||
Job_Satisfaction(Y) | |||||
Antecedent | Coef | SE | t | p | |
presence_of_calling(X) | c1 | 0.326 | 0.330 | 0.986 | .326 |
Person_Job_fit(W) | c2 | 0.433 | 0.210 | 2.061 | .041 |
presence_of_calling:Person_Job_fit(X:W) | c3 | -0.011 | 0.062 | -0.175 | .862 |
Constant | iY | 0.602 | 1.079 | 0.558 | .578 |
Observations | 151 | ||||
R2 | 0.423 | ||||
Adjusted R2 | 0.411 | ||||
Residual SE | 0.560 ( df = 147) | ||||
F statistic | F(3,147) = 35.907, p < .001 | ||||
- 조절효과의 회귀계수는 -0.011이며, 통계적으로 유의하지 않은 것으로 나타났습니다.
5.5 매개효과 분석
- 매개효과는 다음과 같은 모델을 설정하여 분석합니다.
labels=list(X='presence_of_calling', Y="Job_Satisfaction", M='Trans_leadership')
statisticalDiagram(4,labels = labels,radx=0.15,rady=0.05)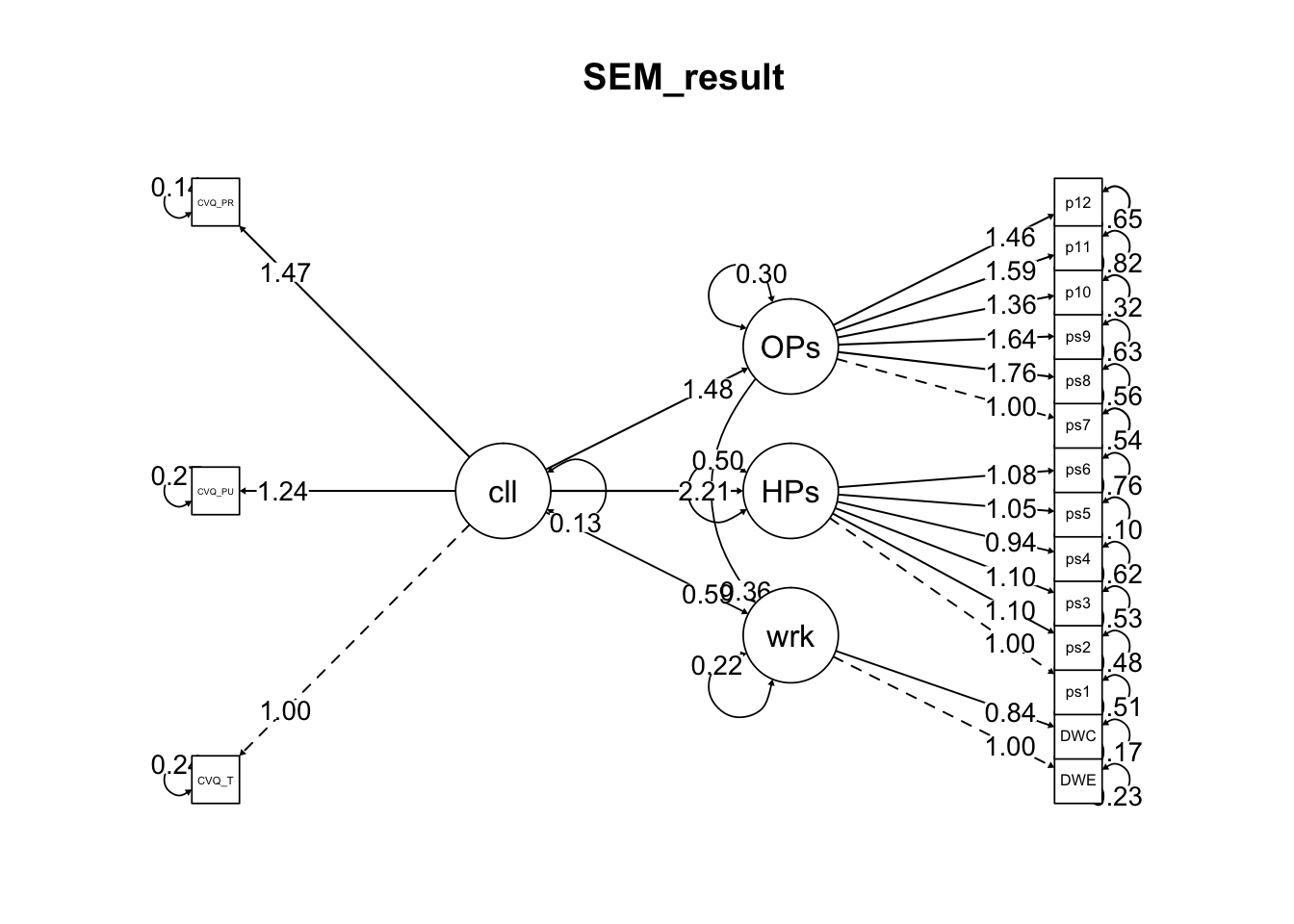 - 이 모형을 분석하면 다음과 같습니다.
- 이 모형을 분석하면 다음과 같습니다.
result <- mediationBK(labels=labels, data=raw_data)
modelsSummaryTable(result$fit, labels=labels)Consequent | |||||||||||||||||
Job_Satisfaction(Y) | Trans_leadership(M) | Job_Satisfaction(Y) | |||||||||||||||
Antecedent | Coef | SE | t | p | Coef | SE | t | p | Coef | SE | t | p | |||||
presence_of_calling(X) | c | 0.471 | 0.086 | 5.476 | <.001 | a | 0.331 | 0.089 | 3.698 | <.001 | c' | 0.293 | 0.075 | 3.921 | <.001 | ||
Trans_leadership(M) | b | 0.538 | 0.066 | 8.209 | <.001 | ||||||||||||
Constant | iY | 2.051 | 0.287 | 7.151 | <.001 | iM | 2.711 | 0.298 | 9.098 | <.001 | iY | 0.591 | 0.297 | 1.988 | .049 | ||
Observations | 151 | 151 | 151 | ||||||||||||||
R2 | 0.168 | 0.084 | 0.428 | ||||||||||||||
Adjusted R2 | 0.162 | 0.078 | 0.420 | ||||||||||||||
Residual SE | 0.668 ( df = 149) | 0.694 ( df = 149) | 0.555 ( df = 148) | ||||||||||||||
F statistic | F(1,149) = 29.986, p < .001 | F(1,149) = 13.674, p < .001 | F(2,148) = 55.364, p < .001 | ||||||||||||||
- 분석결과를 통계적 모형으로 나타내면 다음과 같습니다.
plot(result, type=1, ylim=c(0.3, 0.6))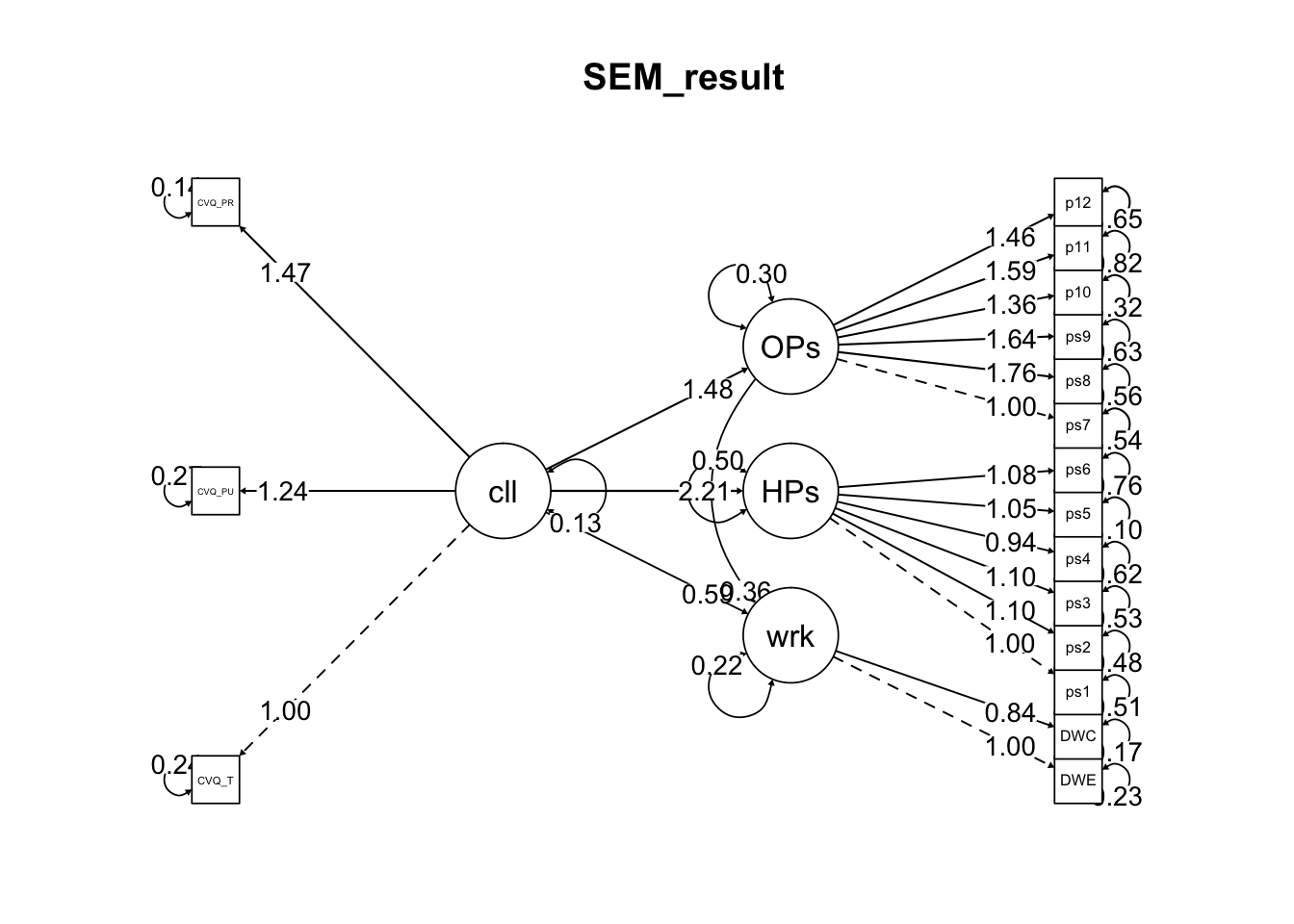
plot(result)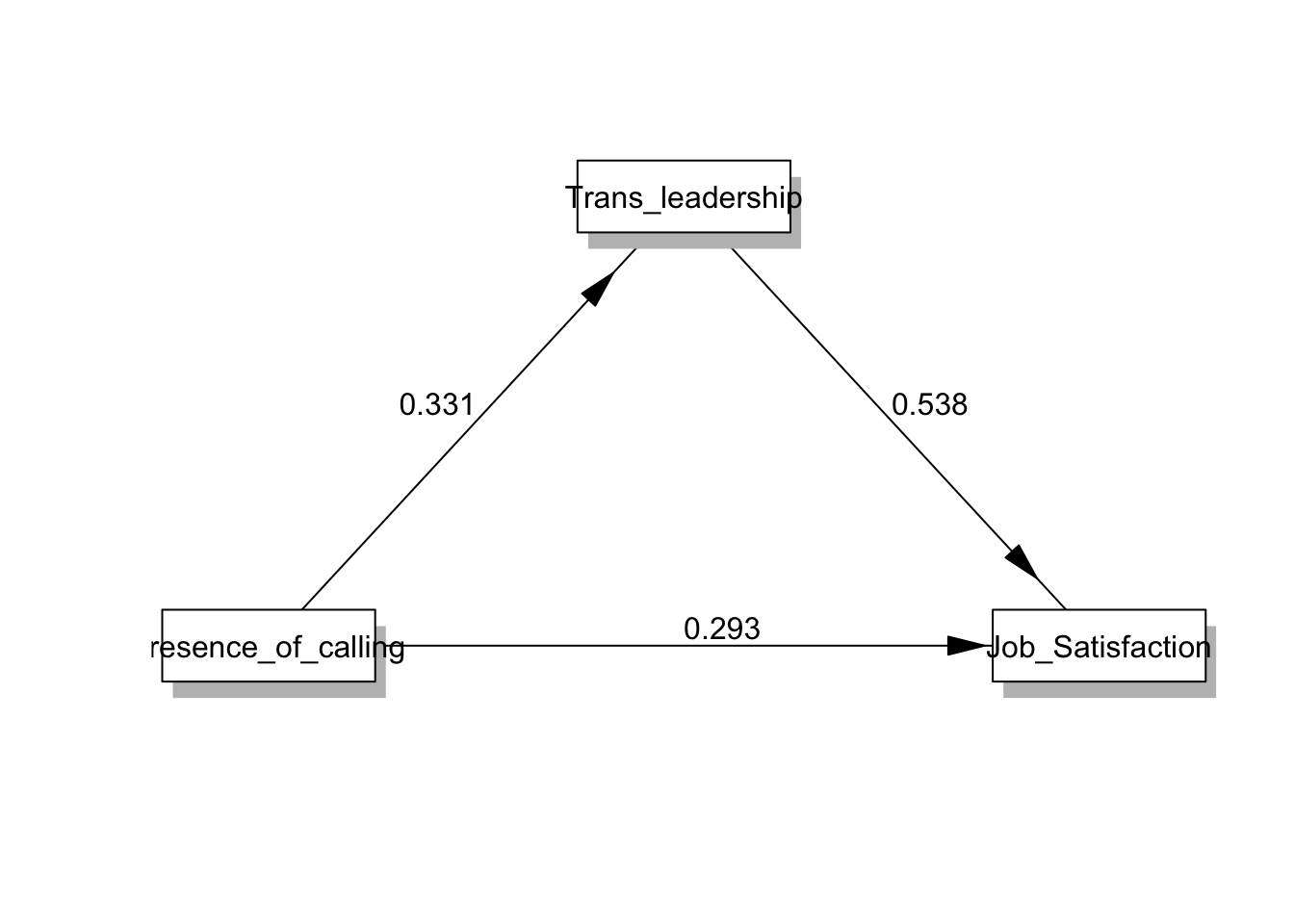
- 매개 모형의 간접효과를 부투스트래핑 방법으로 구하기 위해 laavan 패키지를 활용합니다.
model <- tripleEquation(labels=labels, data = raw_data)
set.seed(123)
semfit <- sem(model = model, data=raw_data, se="boot")
medSummaryTable(semfit)Effect | Equation | estimate | 95% Bootstrap CI |
indirect | (a)*(b) | 0.178 | (0.053 to 0.326) |
direct | c | 0.293 | (0.103 to 0.486) |
total | direct+indirect | 0.471 | (0.270 to 0.688) |
prop.mediated | indirect/total | 0.378 | (0.128 to 0.709) |
boot.ci.type = perc | |||
- 매개효과 검증 결과 간접효과를 비롯하여 산출된 신뢰구간 내에 0을 포함하고 있지 않으므로 매개효과는 유의합니다.
5.6 Moderated Mediation analysis
5.6.1 모델 설정
- 조절된 매개 모형(Process Macro Model 8)을 설정해줍니다.
labels <- list(X='presence_of_calling', Y="Job_Satisfaction", W='Person_Job_fit', M='Trans_leadership')
pmacroModel(8, labels=labels, radx=0.13,rady=0.05)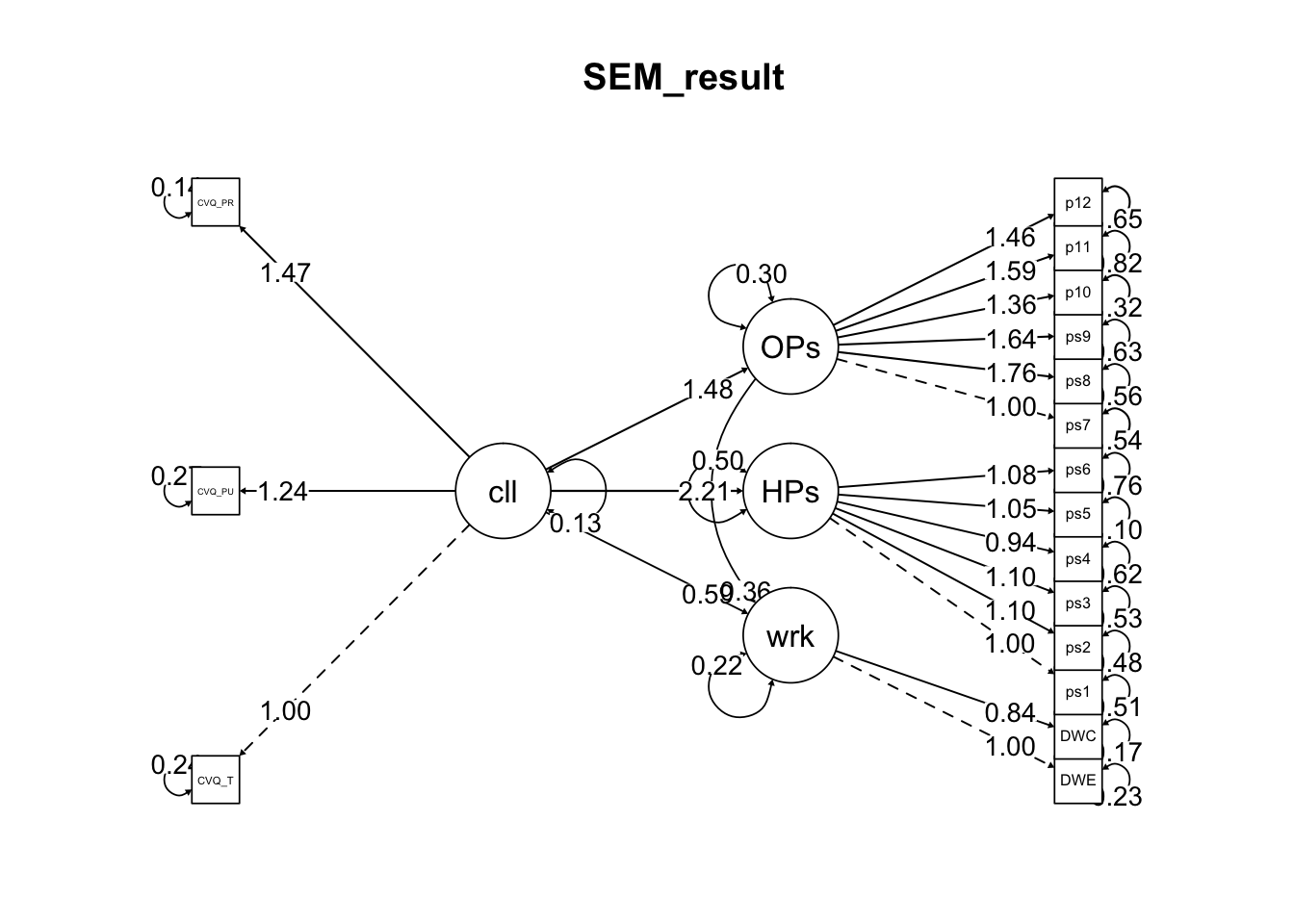
- Process Macro Model 8의 통계적 모형은 다음과 같습니다.
statisticalDiagram(8, labels=labels, radx=0.15,rady=0.05)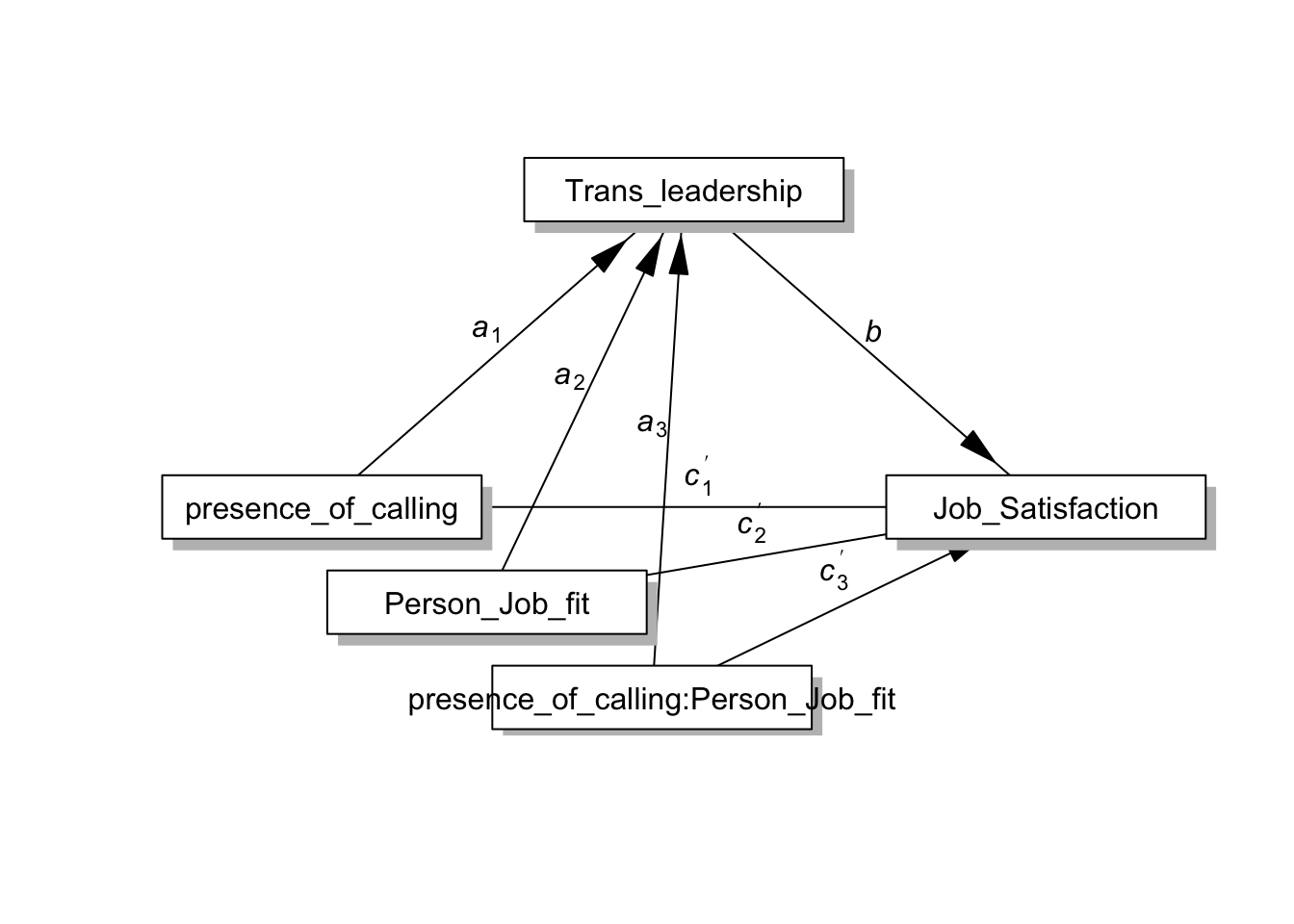 ### 회귀분석을 활용한 조절된 매개효과 분석
### 회귀분석을 활용한 조절된 매개효과 분석
- 위 모형을 회귀식으로 설정하면 다음과 같습니다.
moderator <- list(name="Person_Job_fit", site=list(c("a","c")))
equation <- tripleEquation(labels = labels, moderator=moderator, mode=1)
cat(equation)## Trans_leadership~presence_of_calling+Person_Job_fit+presence_of_calling:Person_Job_fit
## Job_Satisfaction~presence_of_calling+Person_Job_fit+presence_of_calling:Person_Job_fit+Trans_leadership- 이제 위의 회귀식을 활용해서 회귀모형의 리스트를 만듭니다.
fit=eq2fit(equation, data=raw_data)
modelsSummary(fit, labels=labels)## ====================================================================================================
## Consequent
## ---------------------------------------------------------------------------
## Trans_leadership(M) Job_Satisfaction(Y)
## ------------------------------------- -------------------------------------
## Antecedent Coef SE t p Coef SE t p
## ----------------------------------------------------------------------------------------------------
## presence_of_calling(X) a1 -0.607 0.377 -1.611 .109 c'1 0.575 0.295 1.949 .053
## Person_Job_fit(W) a2 -0.233 0.240 -0.972 .333 c'2 0.529 0.187 2.831 .005
## presence_of_calling:Person_Job_fit(X:W) a3 0.155 0.071 2.177 .031 c'3 -0.074 0.056 -1.328 .186
## Trans_leadership(M) b 0.411 0.064 6.418 <.001
## Constant iM 4.422 1.232 3.588 <.001 iY -1.214 0.997 -1.217 .225
## ----------------------------------------------------------------------------------------------------
## Observations 151 151
## R2 0.233 0.550
## Adjusted R2 0.217 0.538
## Residual SE 0.639 ( df = 147) 0.496 ( df = 146)
## F statistic F(3,147) = 14.883, p < .001 F(4,146) = 44.591, p < .001
## ====================================================================================================- 조절된 매개모형의 회귀계수는 위와 같다.
- 회귀분석 결과를 회귀계수를 이용하여 통계적 모형을 그려보면 아래와 같다.
drawModel(fit, labels = labels, whatLabel = 'est', ymargin = .000001, xmargin = .000001, rady = 0.05)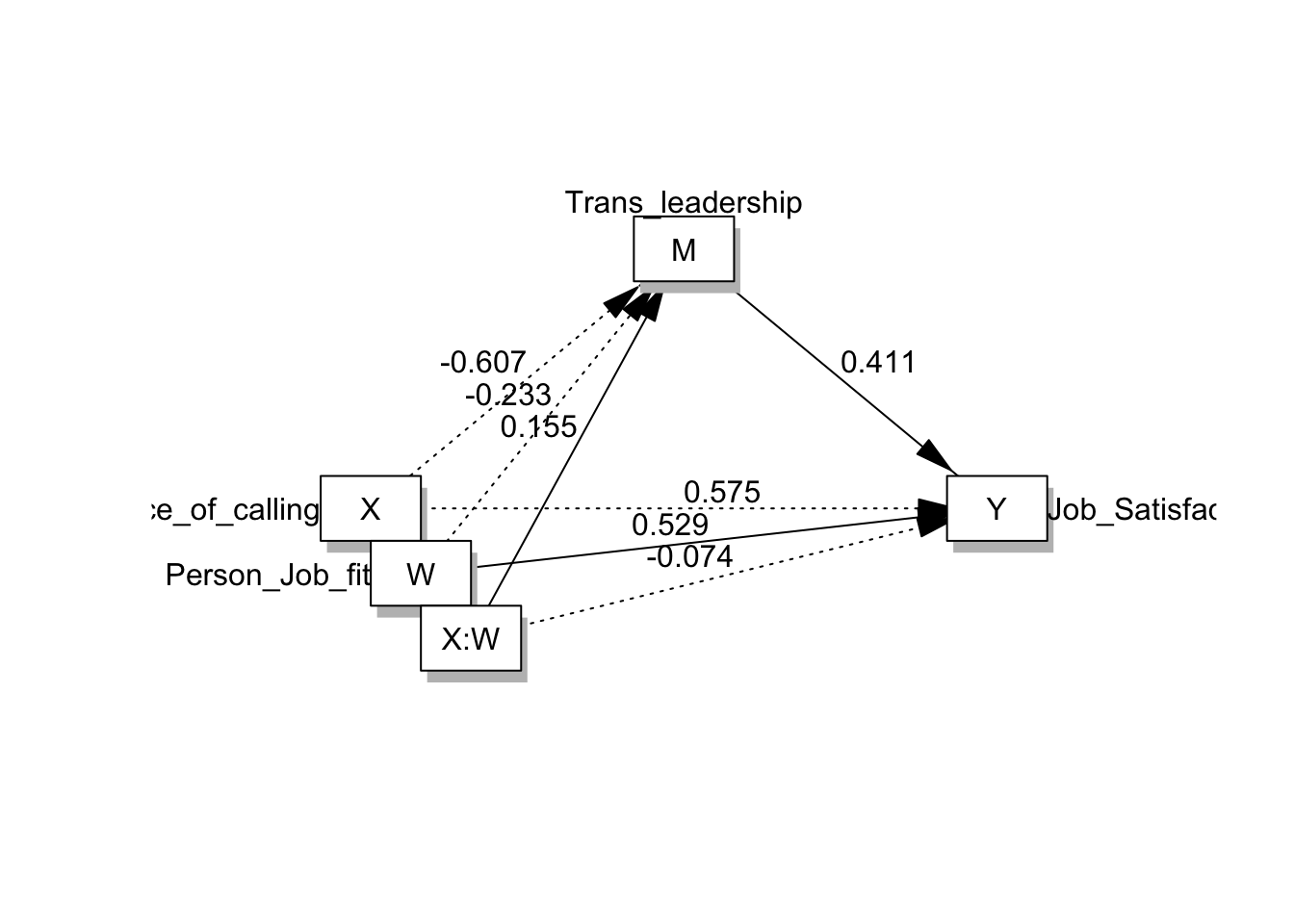
5.6.2 조건부 직접효과와 간접효과의 추정
- SEM을 활용하여 부트스트래핑을 하고, 이를 기반으로 신뢰구간을 얻기 위해 SEM syntax를 만들어줍니다.
model=tripleEquation(label=labels, moderator=moderator,rangemode=2, data=raw_data)
cat(model)## Trans_leadership~a1*presence_of_calling+a2*Person_Job_fit+a3*presence_of_calling:Person_Job_fit
## Job_Satisfaction~c1*presence_of_calling+c2*Person_Job_fit+c3*presence_of_calling:Person_Job_fit+b*Trans_leadership
## Person_Job_fit ~ Person_Job_fit.mean*1
## Person_Job_fit ~~ Person_Job_fit.var*Person_Job_fit
## CE.XonM :=a1+a3*5
## indirect :=(a1+a3*5)*(b)
## index.mod.med :=a3*b
## direct :=c1+c3*5
## total := direct + indirect
## prop.mediated := indirect / total
## CE.XonM.below :=a1+a3*3.8
## indirect.below :=(a1+a3*3.8)*(b)
## CE.XonM.above :=a1+a3*5.8
## indirect.above :=(a1+a3*5.8)*(b)
## direct.below:=c1+c3*3.8
## direct.above:=c1+c3*5.8
## total.below := direct.below + indirect.below
## total.above := direct.above + indirect.above
## prop.mediated.below := indirect.below / total.below
## prop.mediated.above := indirect.above / total.above- 이제 이를 토대로 분석을 해보겠습니다.
set.seed(1234)
semfit=sem(model=model,data= raw_data, se="boot")## Warning in lav_partable_vnames(FLAT, "ov.x", warn = TRUE): lavaan WARNING:
## model syntax contains variance/covariance/intercept formulas
## involving (an) exogenous variable(s): [Person_Job_fit]; These
## variables will now be treated as random introducing additional
## free parameters. If you wish to treat those variables as fixed,
## remove these formulas from the model syntax. Otherwise, consider
## adding the fixed.x = FALSE option.estimatesTable2(semfit)Variables | Predictors | label | B | SE | z | p | β |
Trans_leadership | presence_of_calling | a1 | -0.607 | 0.438 | -1.386 | 0.166 | -0.439 |
Trans_leadership | Person_Job_fit | a2 | -0.233 | 0.262 | -0.890 | 0.374 | -0.261 |
Trans_leadership | presence_of_calling:Person_Job_fit | a3 | 0.155 | 0.077 | 2.005 | 0.045 | 0.943 |
Job_Satisfaction | presence_of_calling | c1 | 0.575 | 0.354 | 1.626 | 0.104 | 0.508 |
Job_Satisfaction | Person_Job_fit | c2 | 0.529 | 0.200 | 2.637 | 0.008 | 0.724 |
Job_Satisfaction | presence_of_calling:Person_Job_fit | c3 | -0.074 | 0.061 | -1.223 | 0.221 | -0.554 |
Job_Satisfaction | Trans_leadership | b | 0.411 | 0.087 | 4.743 | < 0.001 | 0.502 |
- 분석결과 중, 조절 및 매개효과 부분은 다음과 같이 볼 수 있습니다.
- 조절된 매개지수가 유의함을 확인할 수 있습니다.
medSummaryTable(semfit)Effect | Equation | estimate | 95% Bootstrap CI |
CE.XonM | a1+a3*5 | 0.167 | (-0.053 to 0.356) |
indirect | (a1+a3*5)*(b) | 0.069 | (-0.019 to 0.183) |
index.mod.med | a3*b | 0.064 | (0.004 to 0.128) |
direct | c1+c3*5 | 0.203 | (0.004 to 0.387) |
total | direct+indirect | 0.271 | (0.086 to 0.458) |
prop.mediated | indirect/total | 0.253 | (-0.093 to 0.922) |
CE.XonM.below | a1+a3*3.8 | -0.019 | (-0.375 to 0.285) |
indirect.below | (a1+a3*3.8)*(b) | -0.008 | (-0.134 to 0.140) |
CE.XonM.above | a1+a3*5.8 | 0.291 | (0.078 to 0.459) |
indirect.above | (a1+a3*5.8)*(b) | 0.119 | (0.027 to 0.241) |
direct.below | c1+c3*3.8 | 0.292 | (0.004 to 0.564) |
direct.above | c1+c3*5.8 | 0.143 | (-0.024 to 0.312) |
total.below | direct.below+indirect.below | 0.284 | (-0.026 to 0.587) |
total.above | direct.above+indirect.above | 0.263 | (0.113 to 0.429) |
prop.mediated.below | indirect.below/total.below | -0.027 | (-1.746 to 0.740) |
prop.mediated.above | indirect.above/total.above | 0.455 | (0.110 to 1.174) |
boot.ci.type = perc | |||
- 조절변수 Person-Job Fit에 따른 조건부 직접효과 및 간접효과는 다음과 같습니다.
modmedSummaryTable(semfit)Indirect Effect | Direct Effect | ||||
Person_Job_fit(W) | estimate | 95% Bootstrap CI | estimate | 95% Bootstrap CI | |
3.800 | -0.008 | (-0.134 to 0.140) | 0.292 | (0.004 to 0.564) | |
5.000 | 0.069 | (-0.019 to 0.183) | 0.203 | (0.004 to 0.387) | |
5.800 | 0.119 | (0.027 to 0.241) | 0.143 | (-0.024 to 0.312) | |
boot.ci.type = perc | |||||
- 조건부 직접효과와 간접효과를 다음과 같이 시작화 할 수도 있습니다.
conditionalEffectPlot(semfit, data=raw_data)+labs(x="Person-Job fit(W)", y="Effect of presence of calling on Job Satisfaction")