Chapter 7 Final Assignment
7.1 Assignment
아래의 지시사항에 따라 논문형식으로 결과 값을 보고하고 r script 파일도 함께 제출할 것
1. ‘setwd’와 ‘read.csv’를 사용하여 calling_example2.csv 파일을 불러올 것
2. 참가자들의 나이, 성별, 주간 근무량 등의 기초통계량을 분석할 것 (table로 제시하고 간단하게 해석할 것)
3. 각 연구변인 간의 상관관계를 분석할 것 (corr.test 함수사용, table 제시 및 간단한 해석 포함)
4. 아래의 가설을 바탕으로 확인적 요인분석, 구조방정식을 분석할 것
1) calling would be positively related to workaholism
2) calling would have a positive effect on workaholism through obsessive passion
3) calling would have a positive effect on workaholism through harmonious passion
5. 확인적 요인분석 및 구조방정식 분석결과를 그림으로 제시할 것
(단, r 프로그래밍에서 제공하는 함수를 사용해도 되며, 따로 그려도 무방)
7.2 Data Import
pacman::p_load(psych, lavaan, tidyverse, processR, stargazer, semPlot, lsr, processR, moonBook, semTable, knitr)1. ‘setwd’와 ‘read.csv’를 사용하여 calling_example2.csv 파일을 불러올 것- 현재 작업 위치를, working directory로 지정하고, 과제 파일을 불러옵니다.
getwd() -> wd
wd%>% setwd
data_sem <- read.csv("calling_example2.csv")
str(data_sem)## 'data.frame': 350 obs. of 46 variables:
## $ CVQ1 : int 2 3 2 4 1 3 2 1 1 2 ...
## $ CVQ2 : int 3 2 2 4 3 3 3 2 3 3 ...
## $ CVQ3 : int 3 3 2 4 2 3 1 1 1 2 ...
## $ CVQ4 : int 2 2 2 4 1 3 2 1 1 2 ...
## $ CVQ5 : int 3 2 2 4 2 3 3 1 1 2 ...
## $ CVQ6 : int 3 2 2 4 2 2 3 1 1 2 ...
## $ CVQ7 : int 3 2 2 4 2 3 3 1 1 2 ...
## $ CVQ8 : int 4 3 2 4 3 3 3 1 1 3 ...
## $ CVQ9 : int 3 3 2 4 3 2 3 1 1 2 ...
## $ CVQ10 : int 3 2 2 4 3 2 2 1 1 2 ...
## $ CVQ11 : int 4 3 1 4 2 2 2 1 3 3 ...
## $ CVQ12 : int 4 2 2 4 3 3 3 1 1 2 ...
## $ DW1 : int 4 4 3 2 4 5 2 4 3 4 ...
## $ DW2 : int 3 2 4 2 4 4 3 2 2 4 ...
## $ DW3 : int 4 4 3 3 4 5 3 3 2 4 ...
## $ DW4 : int 4 2 2 1 5 4 4 4 2 4 ...
## $ DW5 : int 4 2 2 3 3 5 2 2 1 4 ...
## $ DW6 : int 3 2 4 4 4 5 4 4 3 4 ...
## $ DW7 : int 3 4 3 4 3 5 4 4 1 4 ...
## $ DW8 : int 3 3 3 1 4 5 4 5 3 5 ...
## $ DW9 : int 2 2 2 1 1 3 2 4 1 4 ...
## $ DW10 : int 2 1 2 1 3 1 3 2 1 3 ...
## $ WE1 : int 5 3 3 7 5 6 4 2 1 4 ...
## $ WE2 : int 5 2 3 7 5 7 4 2 2 4 ...
## $ WE3 : int 5 2 2 6 2 5 3 2 1 3 ...
## $ WE4 : int 4 4 4 7 5 7 5 3 4 6 ...
## $ WE5 : int 5 3 4 7 5 7 5 5 4 6 ...
## $ WE6 : int 7 2 4 6 3 6 5 3 4 6 ...
## $ WE7 : int 7 5 5 7 5 7 5 4 2 4 ...
## $ WE8 : int 5 2 4 7 4 7 4 4 2 4 ...
## $ WE9 : int 5 5 5 7 5 7 6 6 5 6 ...
## $ ps1 : int 5 2 5 7 5 6 5 2 4 6 ...
## $ ps2 : int 5 2 5 7 3 6 5 2 4 6 ...
## $ ps3 : int 6 2 4 6 4 7 5 3 4 5 ...
## $ ps4 : int 6 2 4 6 4 6 4 2 4 6 ...
## $ ps5 : int 5 6 3 7 5 7 5 3 3 4 ...
## $ ps6 : int 4 6 5 7 4 7 6 3 3 5 ...
## $ ps7 : int 6 4 4 7 5 6 4 5 3 6 ...
## $ ps8 : int 5 2 4 6 3 6 4 2 1 4 ...
## $ ps9 : int 4 2 4 7 3 5 2 2 1 2 ...
## $ ps10 : int 4 1 3 7 5 6 5 3 1 6 ...
## $ ps11 : int 4 1 3 7 2 3 3 2 1 2 ...
## $ ps12 : int 6 1 4 7 3 3 3 2 1 2 ...
## $ GENDER : int 2 1 2 2 2 1 1 1 2 2 ...
## $ AGE : int 41 26 35 60 26 43 38 46 44 38 ...
## $ WORKHOUR: int 43 60 40 45 45 50 43 54 49 40 ...7.3 Descriptive analysis
2. 참가자들의 나이, 성별, 주간 근무량 등의 기초통계량을 분석할 것 (table로 제시하고 간단하게 해석할 것)# 구조방정식 모형에서 표본 크기에 대한 정확한 기준은 없으나,
# 일반적으로 표본은 200개 이상이 권장되고, 측정하려는 관측변수의 20배가 권장 수준이다.
# 현재 관측변수가 총 34개이므로, 680개의 표본 수가 필요하다. 이에, 관측변수 수를 줄일 필요가 있다.
# 항목묶음을 통해 관측변수 수를 줄이자.
# Calling
data_sem %>% select(1:4) %>% apply(1,mean)->data_sem$CVQ_T
data_sem %>% select(5:8) %>% apply(1,mean)->data_sem$CVQ_PU
data_sem %>% select(9:12) %>% apply(1,mean)->data_sem$CVQ_PR
# Workaholism
data_sem %>% select(13:17) %>% apply(1,mean)->data_sem$DWE
data_sem %>% select(18:22) %>% apply(1,mean)->data_sem$DWC
# Passion척도는 상관분석을 위해서만 묶음하여 활용한다.
data_sem %>% select(32:37) %>% apply(1,mean)->data_sem$HPS
data_sem %>% select(38:43) %>% apply(1,mean)->data_sem$OPS
# 관측변인이 17개로 축소되어, 최소 340개 이상의 표본만 있으면 된다.
# 항목묶음한 변인만 다시 semdata로 저장한다.
data_sem %>% select(GENDER, AGE, WORKHOUR, CVQ_T,CVQ_PU,CVQ_PR,DWE,DWC,HPS,OPS)->semdata
# descriptive를 볼때는 아래의 세가지 함수를 자주 사용한다.
# psych의 describe, moonBook의 mytable, stargazer의 stargazer
mytable(semdata)##
## Descriptive Statistics
## -----------------------------
## N Total
## -----------------------------
## GENDER 350
## - 1 196 (56.0%)
## - 2 154 (44.0%)
## AGE 350 39.8 ± 8.9
## WORKHOUR 350 45.3 ± 5.2
## CVQ_T 350 2.1 ± 0.6
## CVQ_PU 350 2.4 ± 0.7
## CVQ_PR 350 2.1 ± 0.6
## DWE 350 2.7 ± 0.8
## DWC 350 2.9 ± 0.7
## HPS 350 4.2 ± 1.2
## OPS 350 3.1 ± 1.2
## -----------------------------semdata %>% describe## vars n mean sd median trimmed mad min max range skew
## GENDER 1 350 1.44 0.50 1.00 1.43 0.00 1 2.00 1.00 0.24
## AGE 2 350 39.83 8.89 40.00 39.51 10.38 23 61.00 38.00 0.25
## WORKHOUR 3 350 45.26 5.17 45.00 44.57 7.41 40 70.00 30.00 1.26
## CVQ_T 4 350 2.14 0.60 2.25 2.14 0.37 1 4.00 3.00 0.22
## CVQ_PU 5 350 2.38 0.68 2.25 2.37 0.74 1 4.00 3.00 0.24
## CVQ_PR 6 350 2.10 0.64 2.00 2.07 0.74 1 4.00 3.00 0.41
## DWE 7 350 2.66 0.77 2.60 2.65 0.89 1 4.60 3.60 0.07
## DWC 8 350 2.92 0.65 3.00 2.94 0.59 1 4.60 3.60 -0.34
## HPS 9 350 4.24 1.16 4.33 4.30 0.99 1 6.67 5.67 -0.42
## OPS 10 350 3.08 1.19 3.00 3.03 1.24 1 6.83 5.83 0.40
## kurtosis se
## GENDER -1.95 0.03
## AGE -0.75 0.48
## WORKHOUR 2.30 0.28
## CVQ_T 0.31 0.03
## CVQ_PU -0.22 0.04
## CVQ_PR -0.13 0.03
## DWE -0.51 0.04
## DWC 0.14 0.03
## HPS -0.03 0.06
## OPS -0.17 0.06stargazer(semdata, type = 'html')| Statistic | N | Mean | St. Dev. | Min | Pctl(25) | Pctl(75) | Max |
| GENDER | 350 | 1.440 | 0.497 | 1 | 1 | 2 | 2 |
| AGE | 350 | 39.831 | 8.894 | 23 | 33 | 46 | 61 |
| WORKHOUR | 350 | 45.257 | 5.172 | 40 | 40 | 48 | 70 |
| CVQ_T | 350 | 2.145 | 0.602 | 1.000 | 1.750 | 2.500 | 4.000 |
| CVQ_PU | 350 | 2.380 | 0.683 | 1.000 | 2.000 | 3.000 | 4.000 |
| CVQ_PR | 350 | 2.097 | 0.643 | 1.000 | 1.750 | 2.500 | 4.000 |
| DWE | 350 | 2.659 | 0.769 | 1.000 | 2.200 | 3.200 | 4.600 |
| DWC | 350 | 2.919 | 0.652 | 1.000 | 2.450 | 3.400 | 4.600 |
| HPS | 350 | 4.244 | 1.156 | 1.000 | 3.500 | 5.000 | 6.667 |
| OPS | 350 | 3.081 | 1.188 | 1.000 | 2.167 | 3.833 | 6.833 |
# 나이, 성별, 주간 근무량
# 1) 성별에 따른 나이 확인하기
mytable(GENDER~AGE+WORKHOUR, data_sem)##
## Descriptive Statistics by 'GENDER'
## _______________________________________
## 1 2 p
## (N=196) (N=154)
## ---------------------------------------
## AGE 41.2 ± 8.8 38.1 ± 8.7 0.001
## WORKHOUR 46.1 ± 5.6 44.2 ± 4.5 0.001
## ---------------------------------------# 2) 연령대 파악하고 빈도구하기
# min, max, sd, 등 기본 정보 파악 후
semdata %>% select(GENDER, AGE, WORKHOUR) %>% describe## vars n mean sd median trimmed mad min max range skew kurtosis
## GENDER 1 350 1.44 0.50 1 1.43 0.00 1 2 1 0.24 -1.95
## AGE 2 350 39.83 8.89 40 39.51 10.38 23 61 38 0.25 -0.75
## WORKHOUR 3 350 45.26 5.17 45 44.57 7.41 40 70 30 1.26 2.30
## se
## GENDER 0.03
## AGE 0.48
## WORKHOUR 0.28# 3) 구간 나눠서 몇명씩 분포해 있는지 확인
semdata %>% filter(AGE>19&AGE<30) %>% nrow## [1] 52semdata %>% filter(AGE>29&AGE<40) %>% nrow## [1] 118semdata %>% filter(AGE>39&AGE<50) %>% nrow## [1] 120semdata %>% filter(AGE>49&AGE<60) %>% nrow## [1] 56semdata %>% filter(AGE>59&AGE<70) %>% nrow## [1] 4# 4) 주당 근무시간 범위 파악하고 빈도구하기
semdata$WORKHOUR %>% range()## [1] 40 70semdata %>% filter(WORKHOUR>39&WORKHOUR<51) %>% nrow## [1] 311semdata %>% filter(WORKHOUR>49&WORKHOUR<60) %>% nrow## [1] 70semdata %>% filter(WORKHOUR>59&WORKHOUR<71) %>% nrow## [1] 9# 5) 변수간 상관 구하기
semdata[,c(4:10)] %>% corr.test## Call:corr.test(x = .)
## Correlation matrix
## CVQ_T CVQ_PU CVQ_PR DWE DWC HPS OPS
## CVQ_T 1.00 0.41 0.46 0.25 0.21 0.42 0.40
## CVQ_PU 0.41 1.00 0.57 0.24 0.24 0.42 0.38
## CVQ_PR 0.46 0.57 1.00 0.36 0.34 0.57 0.51
## DWE 0.25 0.24 0.36 1.00 0.61 0.24 0.43
## DWC 0.21 0.24 0.34 0.61 1.00 0.30 0.47
## HPS 0.42 0.42 0.57 0.24 0.30 1.00 0.56
## OPS 0.40 0.38 0.51 0.43 0.47 0.56 1.00
## Sample Size
## [1] 350
## Probability values (Entries above the diagonal are adjusted for multiple tests.)
## CVQ_T CVQ_PU CVQ_PR DWE DWC HPS OPS
## CVQ_T 0 0 0 0 0 0 0
## CVQ_PU 0 0 0 0 0 0 0
## CVQ_PR 0 0 0 0 0 0 0
## DWE 0 0 0 0 0 0 0
## DWC 0 0 0 0 0 0 0
## HPS 0 0 0 0 0 0 0
## OPS 0 0 0 0 0 0 0
##
## To see confidence intervals of the correlations, print with the short=FALSE option# correlate 함수가 유의성까지 표현해줘서 보기 더 편하다
semdata[,c(4:10)] %>% correlate(test = TRUE, corr.method = 'pearson')##
## CORRELATIONS
## ============
## - correlation type: pearson
## - correlations shown only when both variables are numeric
##
## CVQ_T CVQ_PU CVQ_PR DWE DWC HPS OPS
## CVQ_T . 0.415*** 0.463*** 0.246*** 0.210*** 0.418*** 0.399***
## CVQ_PU 0.415*** . 0.572*** 0.244*** 0.243*** 0.417*** 0.382***
## CVQ_PR 0.463*** 0.572*** . 0.358*** 0.341*** 0.571*** 0.506***
## DWE 0.246*** 0.244*** 0.358*** . 0.612*** 0.235*** 0.433***
## DWC 0.210*** 0.243*** 0.341*** 0.612*** . 0.301*** 0.472***
## HPS 0.418*** 0.417*** 0.571*** 0.235*** 0.301*** . 0.555***
## OPS 0.399*** 0.382*** 0.506*** 0.433*** 0.472*** 0.555*** .
##
## ---
## Signif. codes: . = p < .1, * = p<.05, ** = p<.01, *** = p<.001
##
##
## p-VALUES
## ========
## - total number of tests run: 21
## - correction for multiple testing: holm
##
## CVQ_T CVQ_PU CVQ_PR DWE DWC HPS OPS
## CVQ_T . 0.000 0.000 0.000 0.000 0.000 0.000
## CVQ_PU 0.000 . 0.000 0.000 0.000 0.000 0.000
## CVQ_PR 0.000 0.000 . 0.000 0.000 0.000 0.000
## DWE 0.000 0.000 0.000 . 0.000 0.000 0.000
## DWC 0.000 0.000 0.000 0.000 . 0.000 0.000
## HPS 0.000 0.000 0.000 0.000 0.000 . 0.000
## OPS 0.000 0.000 0.000 0.000 0.000 0.000 .
##
##
## SAMPLE SIZES
## ============
##
## CVQ_T CVQ_PU CVQ_PR DWE DWC HPS OPS
## CVQ_T 350 350 350 350 350 350 350
## CVQ_PU 350 350 350 350 350 350 350
## CVQ_PR 350 350 350 350 350 350 350
## DWE 350 350 350 350 350 350 350
## DWC 350 350 350 350 350 350 350
## HPS 350 350 350 350 350 350 350
## OPS 350 350 350 350 350 350 350# 열정척도는 항목묶음 하지 않고, 구조방정식모델로 진행할 수 있도록 다시 데이터를 지정한다
data_sem %>% select(GENDER, AGE, WORKHOUR, CVQ_T,CVQ_PU,CVQ_PR,DWE,DWC,ps1,ps2,ps3,ps4,ps5,ps6,ps7,ps8,ps9,ps10,ps11,ps12)->semdata7.4 CFA & SEM
7.4.1 1. CFA
- 앞서 항목묶음한 내용 기반으로 확인적 요인 분석을 실시한다
- 먼저 모델을 구성해준다
# 관측변수 17개로 Model을 구성하고 확인적 요인분석을 실시한다
CFA_model <- 'calling =~ CVQ_T+CVQ_PU+CVQ_PR
workaholism =~ DWE+DWC
HPassion =~ ps1+ps2+ps3+ps4+ps5+ps6
OPassion =~ ps7+ps8+ps9+ps10+ps11+ps12'
cat(CFA_model)## calling =~ CVQ_T+CVQ_PU+CVQ_PR
## workaholism =~ DWE+DWC
## HPassion =~ ps1+ps2+ps3+ps4+ps5+ps6
## OPassion =~ ps7+ps8+ps9+ps10+ps11+ps12# 확인적 요인분석 실시
fit <- cfa(CFA_model, semdata)
# 표준화된 결과값 편하게 보기
fit %>% parameterestimates(standardized = TRUE) %>%
filter(op=="=~") %>% mutate(stars=ifelse(pvalue < 0.001, "***",
ifelse(pvalue < 0.01, "**",ifelse(pvalue < 0.05, "*", "")))) %>%
select("Latent Factor"=lhs, Indicator=rhs, B=est,Beta=std.all, SE=se, Z=z, "p-value"=pvalue, Sig.=stars ) %>% knitr::kable(digits=3, format="pandoc", caption="Factor Loadings")| Latent Factor | Indicator | B | Beta | SE | Z | p-value | Sig. |
|---|---|---|---|---|---|---|---|
| calling | CVQ_T | 1.000 | 0.584 | 0.000 | NA | NA | NA |
| calling | CVQ_PU | 1.286 | 0.661 | 0.139 | 9.259 | 0 | *** |
| calling | CVQ_PR | 1.542 | 0.844 | 0.150 | 10.283 | 0 | *** |
| workaholism | DWE | 1.000 | 0.786 | 0.000 | NA | NA | NA |
| workaholism | DWC | 0.840 | 0.779 | 0.085 | 9.846 | 0 | *** |
| HPassion | ps1 | 1.000 | 0.830 | 0.000 | NA | NA | NA |
| HPassion | ps2 | 1.100 | 0.860 | 0.056 | 19.651 | 0 | *** |
| HPassion | ps3 | 1.099 | 0.847 | 0.057 | 19.205 | 0 | *** |
| HPassion | ps4 | 0.939 | 0.782 | 0.055 | 17.052 | 0 | *** |
| HPassion | ps5 | 1.049 | 0.727 | 0.068 | 15.375 | 0 | *** |
| HPassion | ps6 | 1.080 | 0.796 | 0.062 | 17.493 | 0 | *** |
| OPassion | ps7 | 1.000 | 0.522 | 0.000 | NA | NA | NA |
| OPassion | ps8 | 1.763 | 0.873 | 0.172 | 10.231 | 0 | *** |
| OPassion | ps9 | 1.630 | 0.839 | 0.162 | 10.070 | 0 | *** |
| OPassion | ps10 | 1.362 | 0.669 | 0.151 | 8.988 | 0 | *** |
| OPassion | ps11 | 1.585 | 0.798 | 0.161 | 9.844 | 0 | *** |
| OPassion | ps12 | 1.460 | 0.652 | 0.165 | 8.856 | 0 | *** |
결과를 보면 모든 항목이 유의하며, factor loading 값이 0.5 이하인 값도 없습니다.
이제 모형적합도를 살펴봅니다.
fit %>% fitMeasures(c('chisq','df','pvalue','cfi','nnfi','srmr','rmsea'))## chisq df pvalue cfi nnfi srmr rmsea
## 347.198 113.000 0.000 0.931 0.917 0.051 0.077- CFI>,9, TLI>.9,NNFI>.9 chisq/df<3, rmsea<.08, srmr<.05
- model fit이 좋지는 않음.. 카이스퀘어랑 srmr
resid.cor <- residuals(fit, type="cor")$cov
resid.cor[upper.tri(resid.cor, diag=TRUE)] <- NA
knitr::kable(resid.cor, digits=2, format="pandoc", caption="Residual Correlations")| CVQ_T | CVQ_PU | CVQ_PR | DWE | DWC | ps1 | ps2 | ps3 | ps4 | ps5 | ps6 | ps7 | ps8 | ps9 | ps10 | ps11 | ps12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CVQ_T | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| CVQ_PU | 0.03 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| CVQ_PR | -0.03 | 0.01 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| DWE | 0.01 | -0.02 | 0.02 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| DWC | -0.02 | -0.02 | 0.00 | 0.00 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| ps1 | 0.01 | -0.05 | 0.03 | 0.02 | 0.06 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| ps2 | 0.01 | -0.07 | -0.02 | -0.07 | -0.01 | 0.07 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| ps3 | -0.01 | -0.02 | 0.00 | 0.00 | 0.03 | -0.01 | 0.01 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| ps4 | -0.04 | 0.00 | -0.02 | -0.11 | 0.00 | -0.04 | -0.01 | 0.03 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| ps5 | 0.08 | 0.03 | 0.01 | -0.04 | 0.04 | -0.06 | -0.07 | 0.01 | 0.06 | NA | NA | NA | NA | NA | NA | NA | NA |
| ps6 | 0.09 | 0.00 | 0.05 | 0.03 | 0.05 | -0.02 | -0.03 | -0.01 | 0.00 | 0.09 | NA | NA | NA | NA | NA | NA | NA |
| ps7 | 0.03 | 0.00 | 0.09 | 0.10 | 0.16 | 0.07 | 0.05 | 0.08 | -0.01 | 0.03 | 0.04 | NA | NA | NA | NA | NA | NA |
| ps8 | 0.06 | -0.05 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | -0.02 | -0.01 | 0.04 | 0.07 | 0.01 | NA | NA | NA | NA | NA |
| ps9 | 0.09 | -0.05 | 0.03 | -0.01 | -0.03 | 0.02 | -0.03 | -0.05 | -0.06 | -0.03 | 0.02 | -0.03 | 0.02 | NA | NA | NA | NA |
| ps10 | -0.01 | 0.03 | 0.01 | 0.10 | 0.18 | 0.09 | 0.03 | 0.05 | 0.08 | 0.02 | 0.07 | 0.13 | -0.02 | -0.03 | NA | NA | NA |
| ps11 | 0.04 | -0.06 | -0.08 | -0.07 | -0.06 | -0.07 | -0.06 | -0.10 | -0.09 | -0.03 | 0.02 | -0.07 | 0.00 | 0.01 | 0.00 | NA | NA |
| ps12 | 0.04 | 0.07 | -0.04 | -0.13 | -0.05 | 0.02 | 0.03 | -0.04 | 0.05 | 0.07 | 0.05 | -0.08 | -0.03 | -0.01 | -0.06 | 0.14 | NA |
- 상관계수 잔차가 .1보다 큰 변수들은 원래 공분산 설정을 해줘야 하는데, 그냥 넘어가기로 함
modindices(fit, sort. = TRUE, minimum.value = 3) %>%
filter(op=="=~") %>% knitr::kable(digits=3, format="pandoc",
caption="Modification Indices for Factor Loadings")| lhs | op | rhs | mi | epc | sepc.lv | sepc.all | sepc.nox |
|---|---|---|---|---|---|---|---|
| workaholism | =~ | ps10 | 23.062 | 0.789 | 0.476 | 0.309 | 0.309 |
| workaholism | =~ | ps7 | 14.681 | 0.662 | 0.400 | 0.275 | 0.275 |
| calling | =~ | ps11 | 10.452 | -0.799 | -0.281 | -0.187 | -0.187 |
| workaholism | =~ | ps11 | 10.046 | -0.441 | -0.266 | -0.177 | -0.177 |
| workaholism | =~ | ps12 | 9.622 | -0.569 | -0.344 | -0.203 | -0.203 |
| HPassion | =~ | ps11 | 9.125 | -0.212 | -0.224 | -0.149 | -0.149 |
| calling | =~ | ps6 | 6.909 | 0.658 | 0.231 | 0.161 | 0.161 |
| calling | =~ | ps7 | 5.526 | 0.717 | 0.252 | 0.173 | 0.173 |
| OPassion | =~ | ps6 | 5.337 | 0.212 | 0.160 | 0.112 | 0.112 |
| workaholism | =~ | ps4 | 4.680 | -0.202 | -0.122 | -0.096 | -0.096 |
| HPassion | =~ | ps10 | 4.482 | 0.175 | 0.185 | 0.120 | 0.120 |
| workaholism | =~ | ps6 | 4.340 | 0.216 | 0.130 | 0.091 | 0.091 |
| OPassion | =~ | CVQ_T | 4.322 | 0.124 | 0.094 | 0.156 | 0.156 |
| workaholism | =~ | ps2 | 3.665 | -0.167 | -0.101 | -0.075 | -0.075 |
| calling | =~ | ps2 | 3.228 | -0.382 | -0.134 | -0.099 | -0.099 |
semTable(fit, columns = c("estse" , "p"),
paramSets = c("loadings" , "intercepts" , "residualvariances" , "latentcovariances"),
fits = c("chisq" , "rmsea","srmr","cfi","tli") , type = "html" , table.float = TRUE ,
caption = "Holzinger Swineford CFA in a longtable Float ", label = " tab : HS10 ", longtable = TRUE)| Model | ||
| Estimate(Std.Err.) | p | |
| Factor Loadings | ||
| calling | ||
| CVQ.T | 1.00+ | |
| CVQ.PU | 1.29(0.14) | .000 |
| CVQ.PR | 1.54(0.15) | .000 |
| workaholism | ||
| DWE | 1.00+ | |
| DWC | 0.84(0.09) | .000 |
| HPassion | ||
| ps1 | 1.00+ | |
| ps2 | 1.10(0.06) | .000 |
| ps3 | 1.10(0.06) | .000 |
| ps4 | 0.94(0.06) | .000 |
| ps5 | 1.05(0.07) | .000 |
| ps6 | 1.08(0.06) | .000 |
| OPassion | ||
| ps7 | 1.00+ | |
| ps8 | 1.76(0.17) | .000 |
| ps9 | 1.63(0.16) | .000 |
| ps10 | 1.36(0.15) | .000 |
| ps11 | 1.58(0.16) | .000 |
| ps12 | 1.46(0.16) | .000 |
| Residual Variances | ||
| CVQ.T | 0.24(0.02) | .000 |
| CVQ.PU | 0.26(0.02) | .000 |
| CVQ.PR | 0.12(0.02) | .000 |
| DWE | 0.23(0.04) | .000 |
| DWC | 0.17(0.03) | .000 |
| ps1 | 0.50(0.05) | .000 |
| ps2 | 0.48(0.05) | .000 |
| ps3 | 0.53(0.05) | .000 |
| ps4 | 0.63(0.05) | .000 |
| ps5 | 1.10(0.09) | .000 |
| ps6 | 0.75(0.07) | .000 |
| ps7 | 1.53(0.12) | .000 |
| ps8 | 0.56(0.06) | .000 |
| ps9 | 0.64(0.06) | .000 |
| ps10 | 1.31(0.11) | .000 |
| ps11 | 0.82(0.08) | .000 |
| ps12 | 1.65(0.13) | .000 |
| Latent Covariances | ||
| calling w/workaholism | 0.11(0.02) | .000 |
| calling w/HPassion | 0.26(0.04) | .000 |
| calling w/OPassion | 0.17(0.03) | .000 |
| workaholism w/HPassion | 0.23(0.04) | .000 |
| workaholism w/OPassion | 0.27(0.04) | .000 |
| HPassion w/OPassion | 0.48(0.07) | .000 |
| Fit Indices | ||
| χ2 | 347.20(113) | .000 |
| RMSEA | 0.08 | |
| SRMR | 0.05 | |
| CFI | 0.93 | |
| TLI | 0.92 | |
| +Fixed parameter | ||
- 확인적 요인분석 결과 그림으로 표현
fit %>%
semPaths(what = "est", edge.label.cex = 1.5, edge.label.position = .8,
edge.color = "black", edge.width = .2, rotation = 4, sizeMan = 4,
shapeMan = "rectangle", sizeLat = 8, title = TRUE, style = "mx",
minimum = .35, cut = .35, width = 600)
title("CFA Result")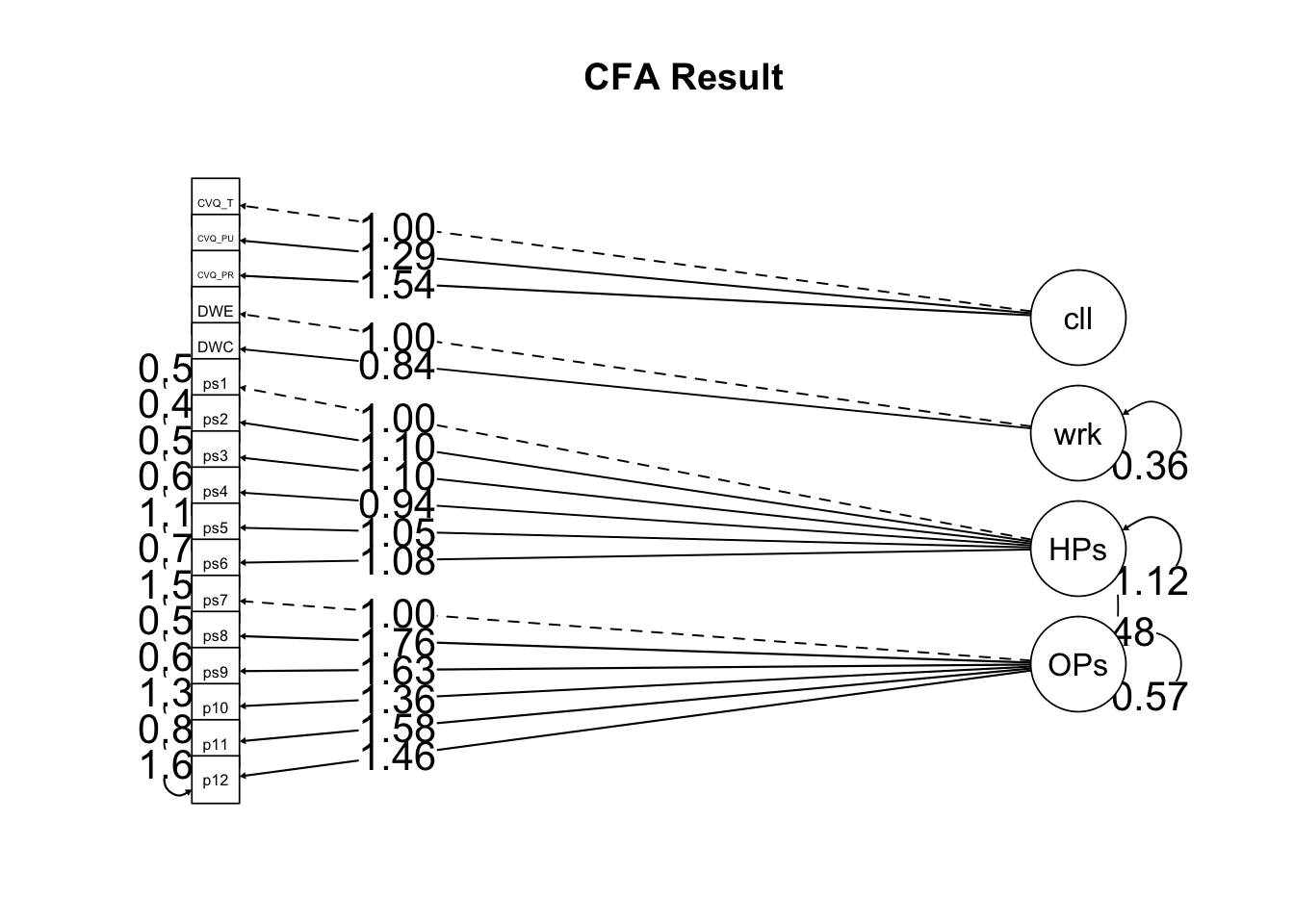
##2. SEM
4. 아래의 가설을 바탕으로 확인적 요인분석, 구조방정식을 분석할 것
1) calling would be positively related to workaholism
2) calling would have a positive effect on workaholism through obsessive passion
3) calling would have a positive effect on workaholism through harmonious passion
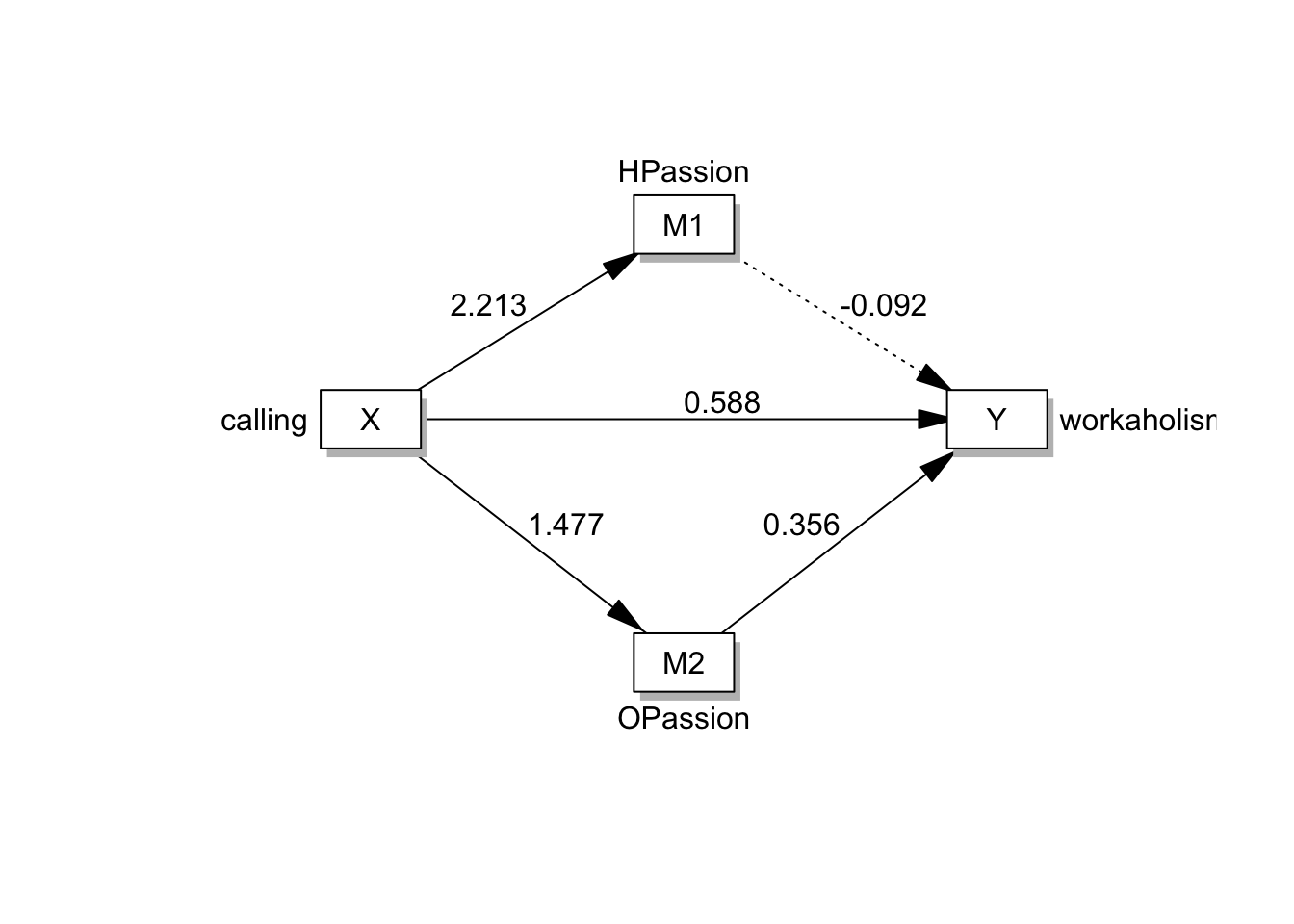
- 연구모델을 그림으로 표현하면 다음과 같다.
- 잠재변인을 네모로 표현하지만, 변인간의 관계는 한눈에 파악해볼 수 있다.
# drawModel(labels=labels,parallel=TRUE,serial=FALSE)#ProcessR을 활용하면, syntax를 조금 더 쉽게 구할 수 있음
labels=list(X='calling',Y='workaholism',M=c('HPassion','OPassion'))
multipleMediation(labels = labels) %>% cat## HPassion~a1*calling
## OPassion~a2*calling
## workaholism~b1*HPassion+b2*OPassion+c*calling
##
## # Indirect Effect(s)
##
## indirect1 := (a1)*(b1)
## direct1 :=c
## indirect2 := (a2)*(b2)
## direct2 :=c
##
## # Specific Indirect Effect Contrast(s)
##
## Contrast1 := indirect1-indirect2
##
## # Indirect/Direct/Total Effect(s)
##
## indirect := indirect1+indirect2
## direct := c
## total := indirect + direct
## prop.mediated := indirect / total# 위에서 구한 식 기반으로, 측정모델(Measurement Model)만 추가해서 연구모형을 설정한다.
SEM_model <- '#Measurement Model
calling =~ CVQ_T+CVQ_PU+CVQ_PR
workaholism =~ DWE+DWC
HPassion =~ ps1+ps2+ps3+ps4+ps5+ps6
OPassion =~ ps7+ps8+ps9+ps10+ps11+ps12
#regression
HPassion~a1*calling
OPassion~a2*calling
workaholism~b1*HPassion+b2*OPassion+c*calling
# Indirect Effect(s)
indirect1 := (a1)*(b1)
direct1 :=c
indirect2 := (a2)*(b2)
direct2 :=c
# Specific Indirect Effect Contrast(s)
Contrast1 := indirect1-indirect2
# Indirect/Direct/Total Effect(s)
indirect := indirect1+indirect2
direct := c
total := indirect + direct
prop.mediated := indirect / total'
# 언제나 동일한 결과가 나오도록 시드를 설정한 뒤, 부트스트래핑을 활용하여 분석을 실시한다.
set.seed(123)
fit_sem <- sem(model=SEM_model,data=semdata, se='bootstrap',bootstrap=1000)
#간단히 결과를 보고
fit_sem %>% summary## lavaan 0.6-8 ended normally after 53 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 39
##
## Number of observations 350
##
## Model Test User Model:
##
## Test statistic 360.188
## Degrees of freedom 114
## P-value (Chi-square) 0.000
##
## Parameter Estimates:
##
## Standard errors Bootstrap
## Number of requested bootstrap draws 1000
## Number of successful bootstrap draws 1000
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## calling =~
## CVQ_T 1.000
## CVQ_PU 1.239 0.164 7.533 0.000
## CVQ_PR 1.473 0.169 8.731 0.000
## workaholism =~
## DWE 1.000
## DWC 0.840 0.096 8.729 0.000
## HPassion =~
## ps1 1.000
## ps2 1.100 0.048 22.860 0.000
## ps3 1.102 0.069 15.996 0.000
## ps4 0.940 0.065 14.529 0.000
## ps5 1.050 0.086 12.276 0.000
## ps6 1.081 0.076 14.209 0.000
## OPassion =~
## ps7 1.000
## ps8 1.764 0.176 10.026 0.000
## ps9 1.637 0.167 9.790 0.000
## ps10 1.360 0.133 10.217 0.000
## ps11 1.591 0.180 8.827 0.000
## ps12 1.463 0.189 7.737 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## HPassion ~
## calling (a1) 2.213 0.263 8.422 0.000
## OPassion ~
## calling (a2) 1.477 0.226 6.533 0.000
## workaholism ~
## HPassion (b1) -0.092 0.061 -1.497 0.134
## OPassion (b2) 0.356 0.085 4.196 0.000
## calling (c) 0.588 0.268 2.193 0.028
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .CVQ_T 0.236 0.022 10.844 0.000
## .CVQ_PU 0.273 0.029 9.338 0.000
## .CVQ_PR 0.139 0.018 7.922 0.000
## .DWE 0.226 0.046 4.886 0.000
## .DWC 0.167 0.029 5.850 0.000
## .ps1 0.506 0.066 7.661 0.000
## .ps2 0.479 0.063 7.607 0.000
## .ps3 0.529 0.067 7.911 0.000
## .ps4 0.624 0.057 10.866 0.000
## .ps5 1.095 0.102 10.744 0.000
## .ps6 0.756 0.098 7.738 0.000
## .ps7 1.536 0.132 11.657 0.000
## .ps8 0.564 0.075 7.553 0.000
## .ps9 0.631 0.085 7.437 0.000
## .ps10 1.317 0.126 10.415 0.000
## .ps11 0.816 0.096 8.528 0.000
## .ps12 1.652 0.204 8.113 0.000
## calling 0.125 0.025 5.094 0.000
## .workaholism 0.221 0.043 5.154 0.000
## .HPassion 0.501 0.080 6.227 0.000
## .OPassion 0.297 0.061 4.882 0.000
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## indirect1 -0.203 0.142 -1.424 0.154
## direct1 0.588 0.268 2.192 0.028
## indirect2 0.527 0.125 4.200 0.000
## direct2 0.588 0.268 2.192 0.028
## Contrast1 -0.729 0.189 -3.850 0.000
## indirect 0.324 0.190 1.706 0.088
## direct 0.588 0.268 2.192 0.028
## total 0.912 0.169 5.410 0.000
## prop.mediated 0.355 0.228 1.557 0.119# 적합도 지표 확인, srmr은 기준을 넘겨서 그냥 제외했음
fitMeasures(fit_sem, c("chisq", "df", "pvalue", "rmsea", "cfi", "tli"))## chisq df pvalue rmsea cfi tli
## 360.188 114.000 0.000 0.079 0.927 0.913# 매개효과 확인
parameterEstimates(fit_sem, standardized=TRUE) %>%
filter(op=="~" | op==":=") %>%
mutate(stars=ifelse(pvalue < 0.001, "***", ifelse(pvalue < 0.01, "**", ifelse(pvalue < 0.05, "*", "")))) %>%
select(LHS=lhs, RHS=rhs, Label=label, Coefficient=est, SE=se, Z=z, "p-value"=pvalue, Sig.=stars) %>%
stargazer(type="text", title="Regression Coefficients", summary=FALSE,
digits=3, digits.extra=0, rownames=FALSE)##
## Regression Coefficients
## ======================================================================================
## LHS RHS Label Coefficient SE Z p-value Sig.
## --------------------------------------------------------------------------------------
## HPassion calling a1 2.213 0.263 8.422 0 * * *
## OPassion calling a2 1.477 0.226 6.533 0 * * *
## workaholism HPassion b1 -0.092 0.061 -1.497 0.134
## workaholism OPassion b2 0.356 0.085 4.196 0.000 * * *
## workaholism calling c 0.588 0.268 2.193 0.028 *
## indirect1 (a1)* (b1) indirect1 -0.203 0.142 -1.424 0.154
## direct1 c direct1 0.588 0.268 2.192 0.028 *
## indirect2 (a2)* (b2) indirect2 0.527 0.125 4.200 0.000 * * *
## direct2 c direct2 0.588 0.268 2.192 0.028 *
## Contrast1 indirect1-indirect2 Contrast1 -0.729 0.189 -3.850 0.000 * * *
## indirect indirect1+indirect2 indirect 0.324 0.190 1.706 0.088
## direct c direct 0.588 0.268 2.192 0.028 *
## total indirect+direct total 0.912 0.169 5.410 0.000 * * *
## prop.mediated indirect/total prop.mediated 0.355 0.228 1.557 0.119
## --------------------------------------------------------------------------------------7.5 model fit
- 연구모형의 적합도 확인하기
semTable(fit_sem, columns = c("estse" , "p"),
paramSets = c("loadings" , "intercepts" , "residualvariances" , "latentcovariances"),
fits = c("chisq" , "rmsea","cfi","tli") , type = "html" , table.float = TRUE ,
caption = "Holzinger Swineford CFA in a longtable Float ", label = " tab : HS10 ", longtable = TRUE)| Model | ||
| Estimate(Std.Err.) | p | |
| Factor Loadings | ||
| calling | ||
| CVQ.T | 1.00+ | |
| CVQ.PU | 1.24(0.16) | .000 |
| CVQ.PR | 1.47(0.17) | .000 |
| workaholism | ||
| DWE | 1.00+ | |
| DWC | 0.84(0.10) | .000 |
| HPassion | ||
| ps1 | 1.00+ | |
| ps2 | 1.10(0.05) | .000 |
| ps3 | 1.10(0.07) | .000 |
| ps4 | 0.94(0.06) | .000 |
| ps5 | 1.05(0.09) | .000 |
| ps6 | 1.08(0.08) | .000 |
| OPassion | ||
| ps7 | 1.00+ | |
| ps8 | 1.76(0.18) | .000 |
| ps9 | 1.64(0.17) | .000 |
| ps10 | 1.36(0.13) | .000 |
| ps11 | 1.59(0.18) | .000 |
| ps12 | 1.46(0.19) | .000 |
| Residual Variances | ||
| CVQ.T | 0.24(0.02) | .000 |
| CVQ.PU | 0.27(0.03) | .000 |
| CVQ.PR | 0.14(0.02) | .000 |
| DWE | 0.23(0.05) | .000 |
| DWC | 0.17(0.03) | .000 |
| ps1 | 0.51(0.07) | .000 |
| ps2 | 0.48(0.06) | .000 |
| ps3 | 0.53(0.07) | .000 |
| ps4 | 0.62(0.06) | .000 |
| ps5 | 1.10(0.10) | .000 |
| ps6 | 0.76(0.10) | .000 |
| ps7 | 1.54(0.13) | .000 |
| ps8 | 0.56(0.07) | .000 |
| ps9 | 0.63(0.08) | .000 |
| ps10 | 1.32(0.13) | .000 |
| ps11 | 0.82(0.10) | .000 |
| ps12 | 1.65(0.20) | .000 |
| Fit Indices | ||
| χ2 | 360.19(114) | .000 |
| RMSEA | 0.08 | |
| CFI | 0.93 | |
| TLI | 0.91 | |
| +Fixed parameter | ||
fit_sem %>% fitMeasures(c('chisq','df','pvalue','cfi','nnfi','srmr','rmsea'))## chisq df pvalue cfi nnfi srmr rmsea
## 360.188 114.000 0.000 0.927 0.913 0.058 0.0797.6 result
- 그림을 그려보자
semPaths(fit_sem, what = 'est',edge.label.cex = 1, edge.label.position = .8,
edge.color = "black", edge.width = .2, rotation = 2, sizeMan = 4,
shapeMan = "rectangle", sizeLat = 8, title = TRUE, style = "mx",
minimum = .1, cut = .1, width = 600, node.label.cex=.1)## Warning in qgraph::qgraph(Edgelist, labels = nLab, bidirectional = Bidir, : The
## following arguments are not documented and likely not arguments of qgraph and
## thus ignored: node.label.cextitle("SEM_result")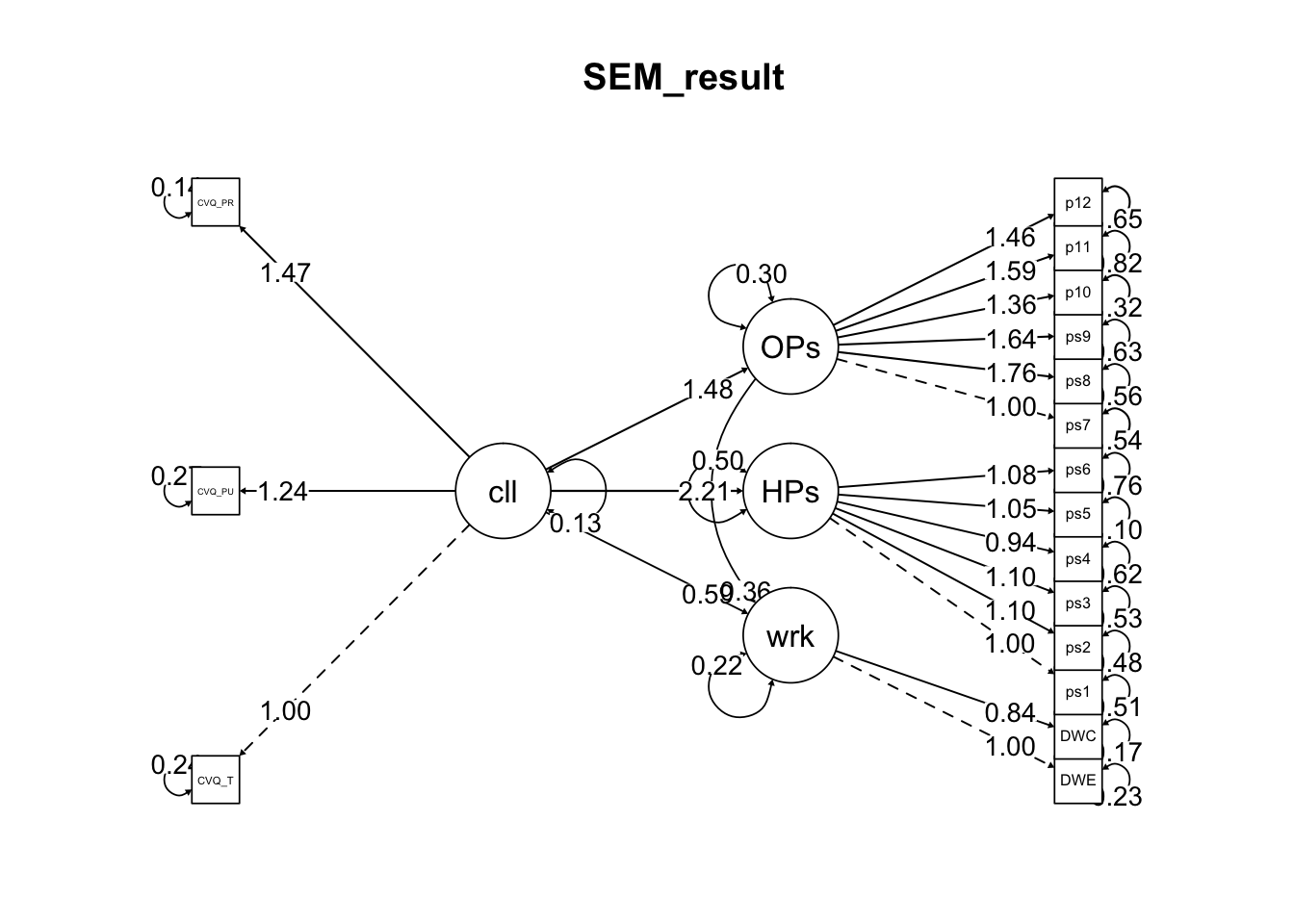
- 강박열정을 통해서 일 중독으로 가는 경로가 유의함을 알 수 있음!
# 경로계수 확인하기: HPassin에서 workaholismㄹ으로 가는 경로만 유의하지 않음
estimatesTable2(fit_sem)Variables | Predictors | label | B | SE | z | p | β |
calling | CVQ_T | 1.000 | 0.000 | 0.589 | |||
calling | CVQ_PU | 1.239 | 0.164 | 7.533 | < 0.001 | 0.643 | |
calling | CVQ_PR | 1.473 | 0.169 | 8.731 | < 0.001 | 0.813 | |
workaholism | DWE | 1.000 | 0.000 | 0.787 | |||
workaholism | DWC | 0.840 | 0.096 | 8.729 | < 0.001 | 0.780 | |
HPassion | ps1 | 1.000 | 0.000 | 0.830 | |||
HPassion | ps2 | 1.100 | 0.048 | 22.86 | < 0.001 | 0.859 | |
HPassion | ps3 | 1.102 | 0.069 | 15.996 | < 0.001 | 0.848 | |
HPassion | ps4 | 0.940 | 0.065 | 14.529 | < 0.001 | 0.783 | |
HPassion | ps5 | 1.050 | 0.086 | 12.276 | < 0.001 | 0.727 | |
HPassion | ps6 | 1.081 | 0.076 | 14.209 | < 0.001 | 0.796 | |
OPassion | ps7 | 1.000 | 0.000 | 0.521 | |||
OPassion | ps8 | 1.764 | 0.176 | 10.026 | < 0.001 | 0.871 | |
OPassion | ps9 | 1.637 | 0.167 | 9.79 | < 0.001 | 0.841 | |
OPassion | ps10 | 1.360 | 0.133 | 10.217 | < 0.001 | 0.667 | |
OPassion | ps11 | 1.591 | 0.180 | 8.827 | < 0.001 | 0.799 | |
OPassion | ps12 | 1.463 | 0.189 | 7.737 | < 0.001 | 0.652 | |
HPassion | calling | a1 | 2.213 | 0.263 | 8.422 | < 0.001 | 0.742 |
OPassion | calling | a2 | 1.477 | 0.226 | 6.533 | < 0.001 | 0.693 |
workaholism | HPassion | b1 | -0.092 | 0.061 | -1.497 | 0.134 | -0.160 |
workaholism | OPassion | b2 | 0.356 | 0.085 | 4.196 | < 0.001 | 0.444 |
workaholism | calling | c | 0.588 | 0.268 | 2.193 | 0.028 | 0.344 |
# 매개효과 확인하기!
medSummaryTable(fit_sem)Effect | Equation | estimate | 95% Bootstrap CI |
indirect1 | (a1)*(b1) | -0.203 | (-0.525 to 0.037) |
direct1 | c | 0.588 | (0.134 to 1.218) |
indirect2 | (a2)*(b2) | 0.527 | (0.301 to 0.791) |
direct2 | c | 0.588 | (0.134 to 1.218) |
Contrast1 | indirect1-indirect2 | -0.729 | (-1.144 to -0.393) |
indirect | indirect1+indirect2 | 0.324 | (-0.089 to 0.686) |
direct | c | 0.588 | (0.134 to 1.218) |
total | indirect+direct | 0.912 | (0.624 to 1.286) |
prop.mediated | indirect/total | 0.355 | (-0.099 to 0.819) |
boot.ci.type = perc | |||
semplot 말고, processR 패키지로 그리면, 아래와 같다. 네모박스는 관측변인을 뜻하지만, 관계는 좀 더 명확하게 볼 수 있다.
그림은 파워포인트로 그리는게 제일 편한 것 같다.
drawModel(fit_sem,labels=labels, whatLabel='est', parallel=TRUE)