Chapter 4 Linear Regression
4.1 Data Import
오늘 활용할 패키지를 불러옵니다.
과제를 위해 주어진 Data를 import 한뒤, 데이터가 어떻게 생겼는지 확인해봅니다.
# data 변수에 sav 데이터를 넣어줍니다.
data <- read_spss("exam03.sav")
data <- as.data.frame(data,stringAsFactor=FALSE)
# 데이터를 확인합니다.
# 관측치 n = 490개
nrow(data)
glimpse(data)- 데이터는 다음과 같습니다.
- price : 자동차 가격
- Horsepower : 자동차 마력
- MPG.city : 시내 주행연비
- NonUSA : 제조국 (0: USA, 1: non-USA)
- price : 자동차 가격
- 이번에는 위의 데이터를 기반으로, 조절효과 분석을 진행하겠습니다.
4.2 descriptive statistics
- 먼저 기술통계를 정리해보겠습니다.
- 이분형 변수의 경우, 함수에서 아직 제대로 반영이 안되기에, X와 W를 바꿔 넣어야 합니다.
# 제조국 조절효과 분석 위한 기술통게-----------------------
labels= list(W="Horsepower",Y="Price",X="NonUSA")
xlabels=c("USA condition","NonUSA condition")
# NonUSA에 따른 기술통계량 확인
meanSummaryTable(data=data, labels=labels, xlabels=xlabels, vanilla = TRUE)
| Y | W | |
Price | Horsepower | ||
USA condition | Mean | 18.573 | 147.521 |
NonUSA(X) = 0 | SD | 7.817 | 54.455 |
NonUSA condition | Mean | 20.509 | 139.889 |
NonUSA(X) = 1 | SD | 11.307 | 50.371 |
Mean | 19.510 | 143.828 | |
SD | 9.659 | 52.374 |
# SPSS label 제거
# SPSS label 제거
data %>% sapply(haven::zap_label) -> data
data %>% as.data.frame()->data위 표를 보면, USA에서 제조된 차량의 가격격의 평균이 더 높고, 자동차 마력은 작은 것을 알 수 있습니다.
이 차이가 통계적으로 유의한 것인지 t test를 통해 살펴보면, 결과는 다음과 같습니다.
# 관찰값이 30개가 넘기 때문에, 등분산성만 확인 ------------------------
var.test(data[data$NonUSA=="1",1],data[data$NonUSA=="0",1],conf.level = .95)##
## F test to compare two variances
##
## data: data[data$NonUSA == "1", 1] and data[data$NonUSA == "0", 1]
## F = 2.0922, num df = 44, denom df = 47, p-value = 0.01387
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 1.164510 3.780712
## sample estimates:
## ratio of variances
## 2.092209# p-value>.05 : 등분산성 만족, p-value<.05 : 등분산성 불만족- 위 결과를 보면, p-value가 0.05보다 작아서 등분산성을 불만족함을 알 수 있습니다.
- 이런 경우, t.test 함수에서 var.equal에 FALSE 옵션을 넣어 t test를 하면 됩니다.
t.test(Price ~ NonUSA, data=data, var.equal=FALSE)##
## Welch Two Sample t-test
##
## data: Price by NonUSA
## t = -0.95449, df = 77.667, p-value = 0.3428
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -5.974255 2.102311
## sample estimates:
## mean in group 0 mean in group 1
## 18.57292 20.50889t.test(Horsepower ~ NonUSA, data=data, var.equal=FALSE)##
## Welch Two Sample t-test
##
## data: Horsepower by NonUSA
## t = 0.7021, df = 90.985, p-value = 0.4844
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -13.96045 29.22433
## sample estimates:
## mean in group 0 mean in group 1
## 147.5208 139.8889- t-test 결과 제조국(NonUSA)에 따라 Price와 Horsepower의 차이가 없는 것으로 나타났습니다.
4.3 Moderation effect by Regression
4.3.1 제조국 조절효과
- 이번에는 아래와 같이 두가지 가설(조절효과)에 대해 검증하고자 합니다.
[분석가설]
① 자동차 마력과 자동차 가격 간의 관계에서 자동차 제조국이 조절효과를 할 것이다.
② 자동차 마력과 자동차 가격 간의 관계에서 시내 주행연비가 조절효과를 할 것이다.
- 위계적 회귀분석을 활용하면 아래와 같이 간단히 분석해볼 수 있습니다.
# 제조국의 조절효과 검증
fit_lm <- lm(Price~Horsepower*NonUSA,data=data)
labels= list(X="Horsepower",Y="Price",W="NonUSA")
summary(fit_lm)##
## Call:
## lm(formula = Price ~ Horsepower * NonUSA, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10.3091 -2.9876 -0.8328 1.6423 26.8856
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.60693 2.31843 0.693 0.49004
## Horsepower 0.11501 0.01476 7.791 1.16e-11 ***
## NonUSA -7.41287 3.37248 -2.198 0.03054 *
## Horsepower:NonUSA 0.07310 0.02214 3.303 0.00138 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.511 on 89 degrees of freedom
## Multiple R-squared: 0.6851, Adjusted R-squared: 0.6745
## F-statistic: 64.55 on 3 and 89 DF, p-value: < 2.2e-16modelsSummaryTable(fit_lm,labels = labels)Consequent | |||||
Price(Y) | |||||
Antecedent | Coef | SE | t | p | |
Horsepower(X) | c1 | 0.115 | 0.015 | 7.791 | <.001 |
NonUSA(W) | c2 | -7.413 | 3.372 | -2.198 | .031 |
Horsepower:NonUSA(X:W) | c3 | 0.073 | 0.022 | 3.303 | .001 |
Constant | iY | 1.607 | 2.318 | 0.693 | .490 |
Observations | 93 | ||||
R2 | 0.685 | ||||
Adjusted R2 | 0.674 | ||||
Residual SE | 5.511 ( df = 89) | ||||
F statistic | F(3,89) = 64.546, p < .001 | ||||
- 분석결과 Horsepower가 Price에 미치는 영향은 유의미하게 나왔고(\(B=0.12, t=7.791, p<.001\)), 제조국이 가격에 미치는 영향도 유의미하게 나왔습니다(\(B=-7.41, t=-2.20, p<.05\)).
- 또한, 제조국의 상호작용향의 영향도 유의미한 것으로 나왔습니다(\(B=0.07, t=3.30, p<.01\)).
confint(fit_lm)## 2.5 % 97.5 %
## (Intercept) -2.99974649 6.2136088
## Horsepower 0.08567557 0.1443392
## NonUSA -14.11392202 -0.7118130
## Horsepower:NonUSA 0.02912303 0.1170869confint 함수를 통해 신뢰구간도 쉽게 구해볼 수 있습니다.
이제 조절효과 그래프를 그려보면, 다음과 같습니다.
# Horsepower, 제조국에 따른 Price
modSummary2Table(fit_lm)%>%width(width=1)Horsepower | NonUSA | Price | se.fit | ymax | ymin |
92.000 | 0.000 | 12.188 | 1.142 | 13.330 | 11.045 |
140.000 | 0.000 | 17.708 | 0.803 | 18.511 | 16.905 |
189.800 | 0.000 | 23.435 | 1.011 | 24.446 | 22.424 |
92.000 | 1.000 | 11.500 | 1.140 | 12.640 | 10.361 |
140.000 | 1.000 | 20.530 | 0.822 | 21.351 | 19.708 |
189.800 | 1.000 | 29.898 | 1.163 | 31.061 | 28.735 |
# 제조국에 따른 Slope
modSummary3Table(fit_lm)## Conditional Effect = 0.115+0.073*WNonUSA(W) | slope |
1.000 | 0.188 |
0.000 | 0.115 |
0.115+0.073*W | |
# 제조국에 따른 조절효과 그래프 그리기
condPlot(fit_lm,xmode = 2, mode=2,xpos=.5)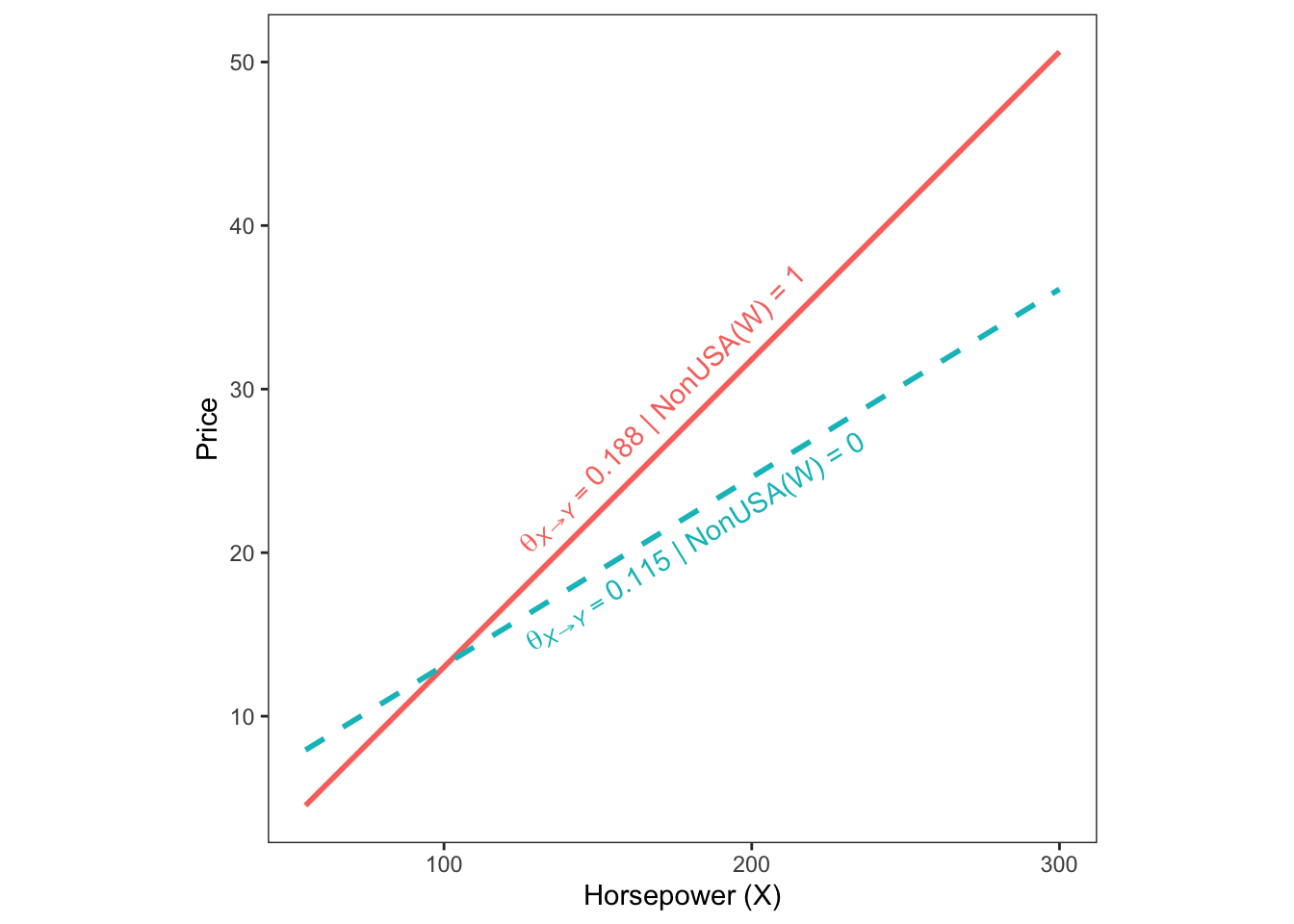
- 그래프를 보면, 제조국에 따라 기울기의 차이가 있음을 알 수 있고, 제조국이 미국이 아닌 경우, Horsepower와 Price의 정적 관계가 더 강함을 볼 수 있습니다.
4.3.2 시내주행연비 조절효과
- 이번에는 시내주행연비의 조절효과를 분석해봅니다.
# 제조국의 조절효과 검증
fit_lm <- lm(Price~Horsepower*MPG.city,data=data)
labels= list(X="Horsepower",Y="Price",W="MPG.city")
summary(fit_lm)##
## Call:
## lm(formula = Price ~ Horsepower * MPG.city, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.090 -2.775 -0.967 1.655 32.429
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.659343 6.657392 0.099 0.92133
## Horsepower 0.190782 0.056929 3.351 0.00118 **
## MPG.city 0.075057 0.293089 0.256 0.79847
## Horsepower:MPG.city -0.003399 0.003095 -1.098 0.27514
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.943 on 89 degrees of freedom
## Multiple R-squared: 0.6338, Adjusted R-squared: 0.6215
## F-statistic: 51.35 on 3 and 89 DF, p-value: < 2.2e-16modelsSummaryTable(fit_lm,labels = labels)Consequent | |||||
Price(Y) | |||||
Antecedent | Coef | SE | t | p | |
Horsepower(X) | c1 | 0.191 | 0.057 | 3.351 | .001 |
MPG.city(W) | c2 | 0.075 | 0.293 | 0.256 | .798 |
Horsepower:MPG.city(X:W) | c3 | -0.003 | 0.003 | -1.098 | .275 |
Constant | iY | 0.659 | 6.657 | 0.099 | .921 |
Observations | 93 | ||||
R2 | 0.634 | ||||
Adjusted R2 | 0.621 | ||||
Residual SE | 5.943 ( df = 89) | ||||
F statistic | F(3,89) = 51.349, p < .001 | ||||
confint(fit_lm)## 2.5 % 97.5 %
## (Intercept) -12.568753145 13.887440125
## Horsepower 0.077665472 0.303897756
## MPG.city -0.507305327 0.657419566
## Horsepower:MPG.city -0.009549485 0.002751554- 시내주행연비(MPG.city)가 Price에 미치는 영향이 유의하지 않음을 확인할 수 있습니다.
- 또한 상호작용항(Horsepower:MPG.city) 역시 유의하지 않음을 확인할 수 있습니다.
4.4 Moderation effect by ProcessR Package
4.4.1 model check
- 두 가설 모두 IV, DV, MO 각각 하나씩만 있기 때문에 Process에서 Model 1번에 해당합니다. 1번 모델 구조와 경로 계수 명칭을 확인합니다.
# 모델 확인
pmacroModel(1)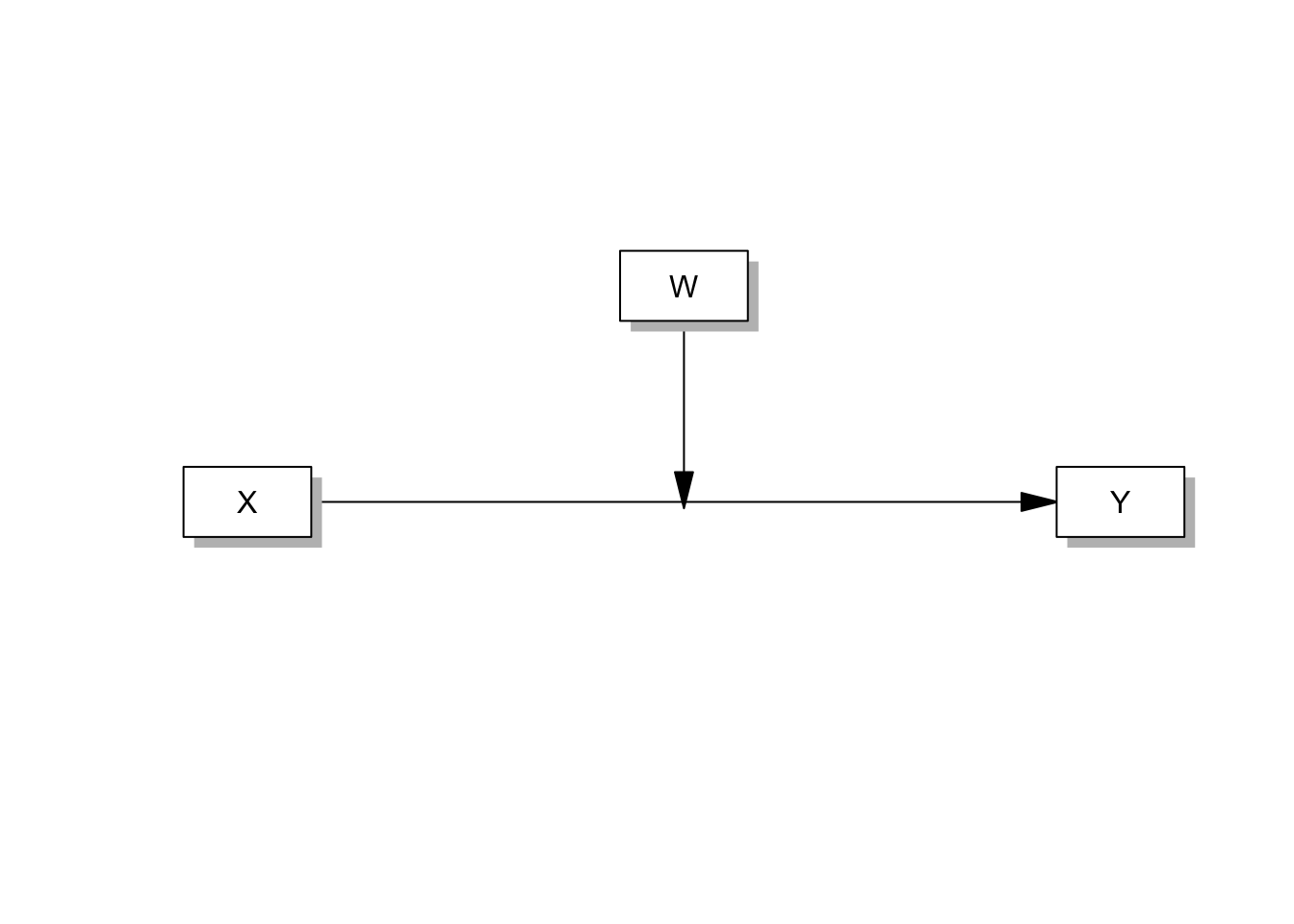
# 모델 경로 계수 명칭 확인
statisticalDiagram(1) 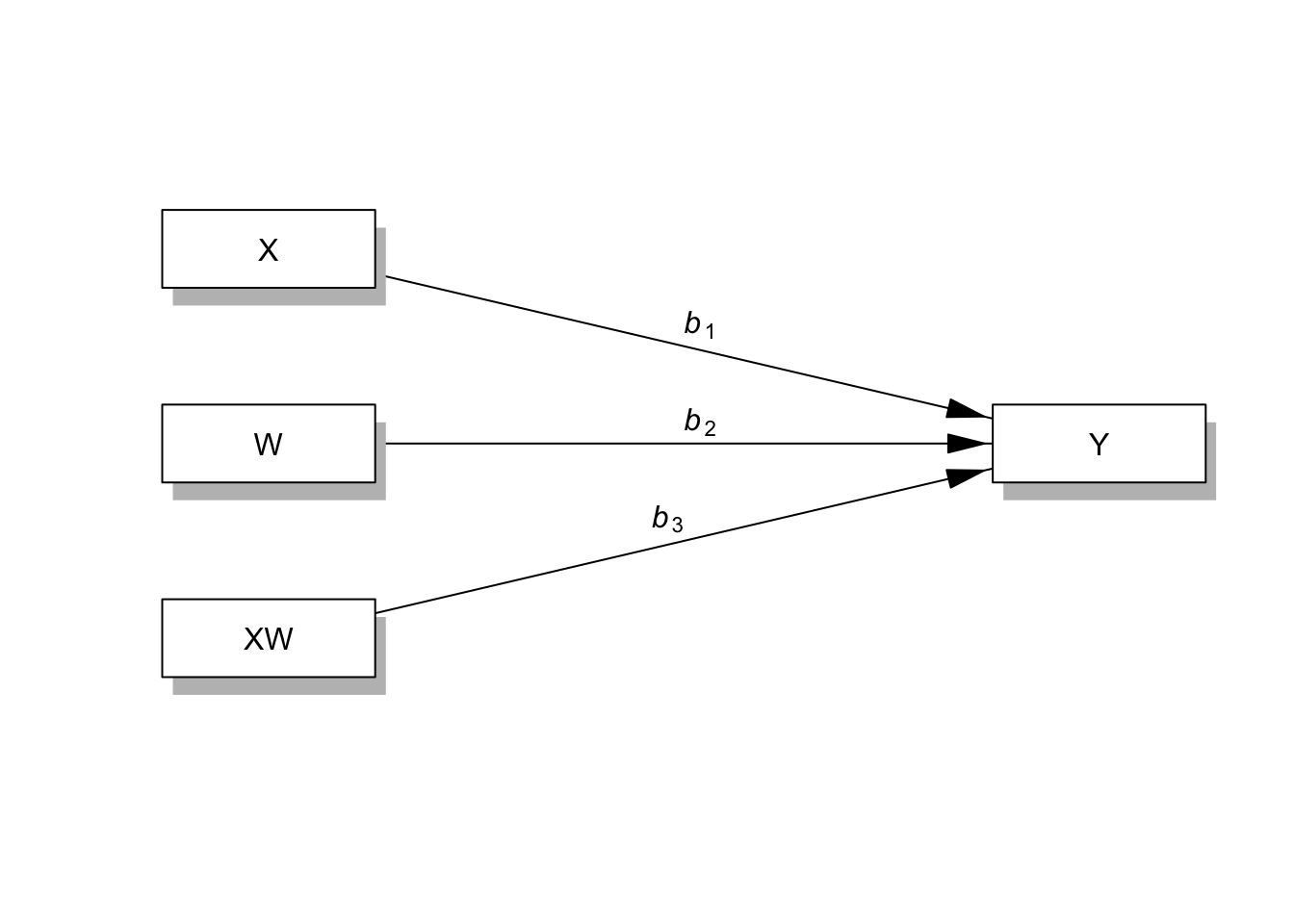
# b1 : X -> Y
# b2 : W -> Y
# b3 : XW -> Y4.4.2 model assign : 제조국
- 분석가설에 대해 모델을 설정하고 분석을 진행합니다.
[분석가설]
① 자동차 마력과 자동차 가격 간의 관계에서 자동차 제조국이 조절효과를 할 것이다.
IV : 자동차 마력(horsepower)
DV : 자동차 가격(Price)
Mo : 자동차 제조국
- 이제 모델설정을 해두었으니, 모델방정식을 만들어주면 됩니다.
- 독립변인은 Horsepower, 종속변인은 Price, 조절변인은 non-USA입니다.
- 회귀분석을 통해 조절효과를 구하면 다음과 같습니다.
- ProcessR을 활용하여 그리면 다음과 같습니다.
# 모델 설정 후 그림 그려보기
labels=list(X="Horsepower",W="NonUSA",Y="Price")
pmacroModel(1,labels=labels, radx=0.1,rady=0.07)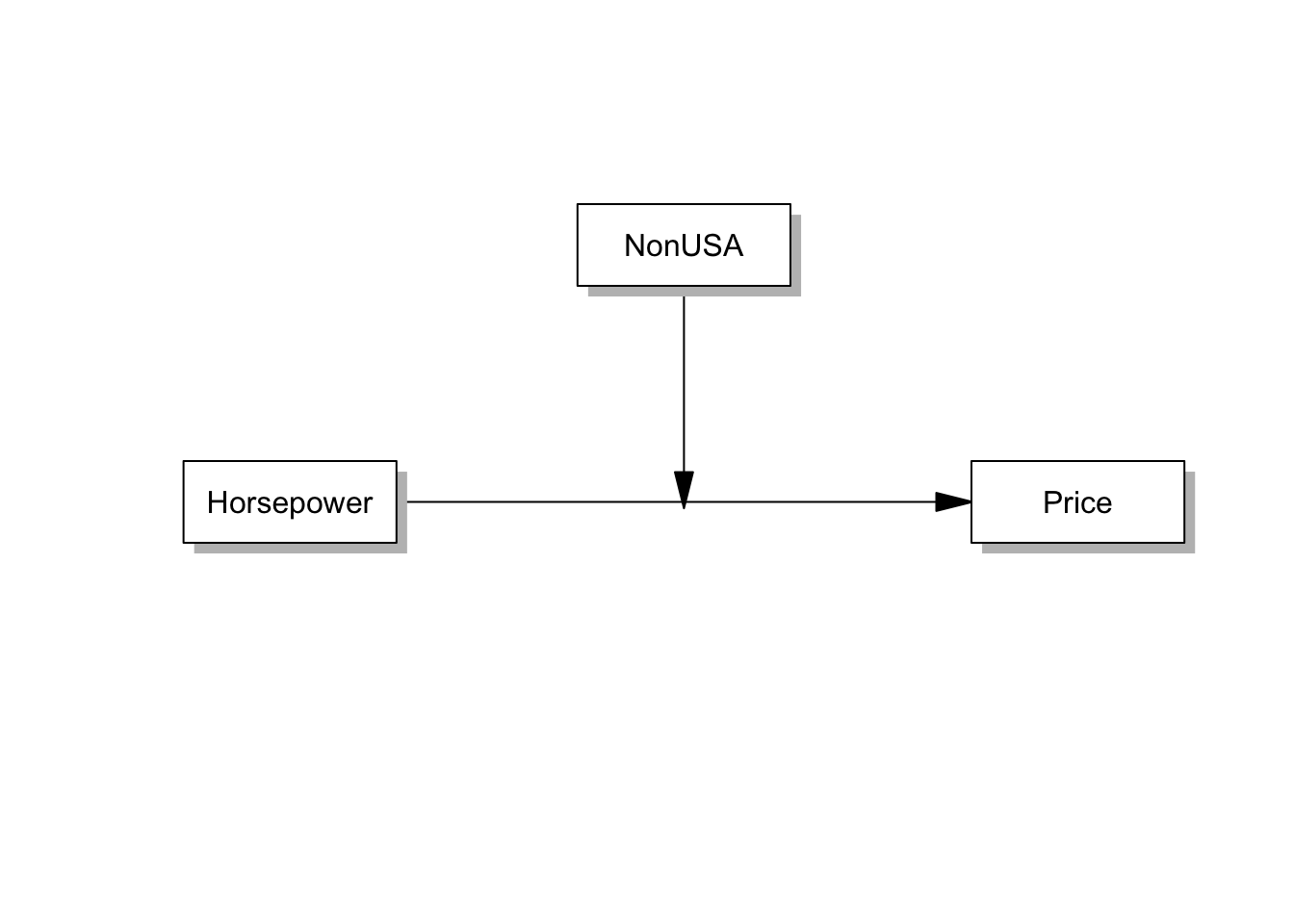
# model equation 만들기
moderator = list(name="NonUSA", site=list('c'))
model <- modmedEquation(X="Horsepower",Y="Price",labels = labels,moderator = moderator )
# model equation 확인
cat(model)##
## Price ~ c1*Horsepower+c2*NonUSA+c3*Horsepower:NonUSA
## NonUSA ~ NonUSA.mean*1
## NonUSA ~~ NonUSA.var*NonUSAModeration Equation이 제대로 설정된 것 같습니다.
이제, lavvan 패키지를 활용하여 moderation 분석을 진행하겠습니다.
library(lavaan)## This is lavaan 0.6-8
## lavaan is FREE software! Please report any bugs.#bootstrap 200회, msiing value : ml
fit <- sem(model=model,data=data,se='bootstrap',bootstrap=200,missing='ml')## Warning in lav_partable_vnames(FLAT, "ov.x", warn = TRUE): lavaan WARNING:
## model syntax contains variance/covariance/intercept formulas
## involving (an) exogenous variable(s): [NonUSA]; These variables
## will now be treated as random introducing additional free
## parameters. If you wish to treat those variables as fixed, remove
## these formulas from the model syntax. Otherwise, consider adding
## the fixed.x = FALSE option.summary(fit,fit.measures = FALSE,standardize = TRUE, rsquare = TRUE)## lavaan 0.6-8 ended normally after 29 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 7
##
## Number of observations 93
## Number of missing patterns 1
##
## Model Test User Model:
##
## Test statistic 201.166
## Degrees of freedom 2
## P-value (Chi-square) 0.000
##
## Parameter Estimates:
##
## Standard errors Bootstrap
## Number of requested bootstrap draws 200
## Number of successful bootstrap draws 200
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Price ~
## Horsepowr (c1) 0.115 0.015 7.681 0.000 0.115 0.532
## NonUSA (c2) -7.413 3.481 -2.130 0.033 -7.413 -0.329
## Hrsp:NUSA (c3) 0.073 0.030 2.468 0.014 0.073 0.506
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## NonUSA (NUSA) 0.484 0.049 9.785 0.000 0.484 0.968
## .Price 1.607 1.895 0.848 0.397 1.607 0.143
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## NonUSA (NUSA) 0.250 0.004 68.185 0.000 0.250 1.000
## .Price 29.065 7.956 3.653 0.000 29.065 0.229
##
## R-Square:
## Estimate
## Price 0.771- 분석 결과 예측변수들을 테이블로 표시할 수 있습니다.
# 모든 파라미터의 Estimates를 표시합니다.
parameterEstimates(fit,boot.ci.type = 'bca.simple',level = .95,
ci = TRUE,standardized = FALSE)## Warning in norm.inter(t, adj.alpha): extreme order statistics used as endpoints## lhs op rhs label est se z
## 1 Price ~ Horsepower c1 0.115 0.015 7.681
## 2 Price ~ NonUSA c2 -7.413 3.481 -2.130
## 3 Price ~ Horsepower:NonUSA c3 0.073 0.030 2.468
## 4 NonUSA ~1 NonUSA.mean 0.484 0.049 9.785
## 5 NonUSA ~~ NonUSA NonUSA.var 0.250 0.004 68.185
## 6 Price ~~ Price 29.065 7.956 3.653
## 7 Horsepower ~~ Horsepower 2713.583 0.000 NA
## 8 Horsepower ~~ Horsepower:NonUSA 933.807 0.000 NA
## 9 Horsepower:NonUSA ~~ Horsepower:NonUSA 6087.569 0.000 NA
## 10 Price ~1 1.607 1.895 0.848
## 11 Horsepower ~1 143.828 0.000 NA
## 12 Horsepower:NonUSA ~1 67.688 0.000 NA
## pvalue ci.lower ci.upper
## 1 0.000 0.083 0.142
## 2 0.033 -15.036 0.108
## 3 0.014 0.019 0.145
## 4 0.000 0.366 0.581
## 5 0.000 0.249 0.250
## 6 0.000 16.997 55.922
## 7 NA 2713.583 2713.583
## 8 NA 933.807 933.807
## 9 NA 6087.569 6087.569
## 10 0.397 -2.180 5.737
## 11 NA 143.828 143.828
## 12 NA 67.688 67.688# 논문작성용 테이블을 봅니다.
estimatesTable2(fit,vanilla = TRUE)Variables | Predictors | label | B | SE | z | p | β |
Price | Horsepower | c1 | 0.115 | 0.015 | 7.681 | < 0.001 | 0.532 |
Price | NonUSA | c2 | -7.413 | 3.481 | -2.130 | 0.033 | -0.329 |
Price | Horsepower:NonUSA | c3 | 0.073 | 0.030 | 2.468 | 0.014 | 0.506 |
Bootstrap을 활용한 분석 결과 Horsepower가 Price에 유의미한 정적 영향을 미치고, 제조국에 따른 조절효과가 있음을 알 수 있습니다.
t 분포가 Z 분포로 변경된 것 외에는 앞서 회귀분석을 통해 구한 지표와 동일합니다.
분석 결과를 활용해 아래와 같이 Diagram으로 나타낼 수도 있습니다.
statisticalDiagram(1,labels=labels,fit=fit,whatLabel="est", radx=0.2,rady=0.05)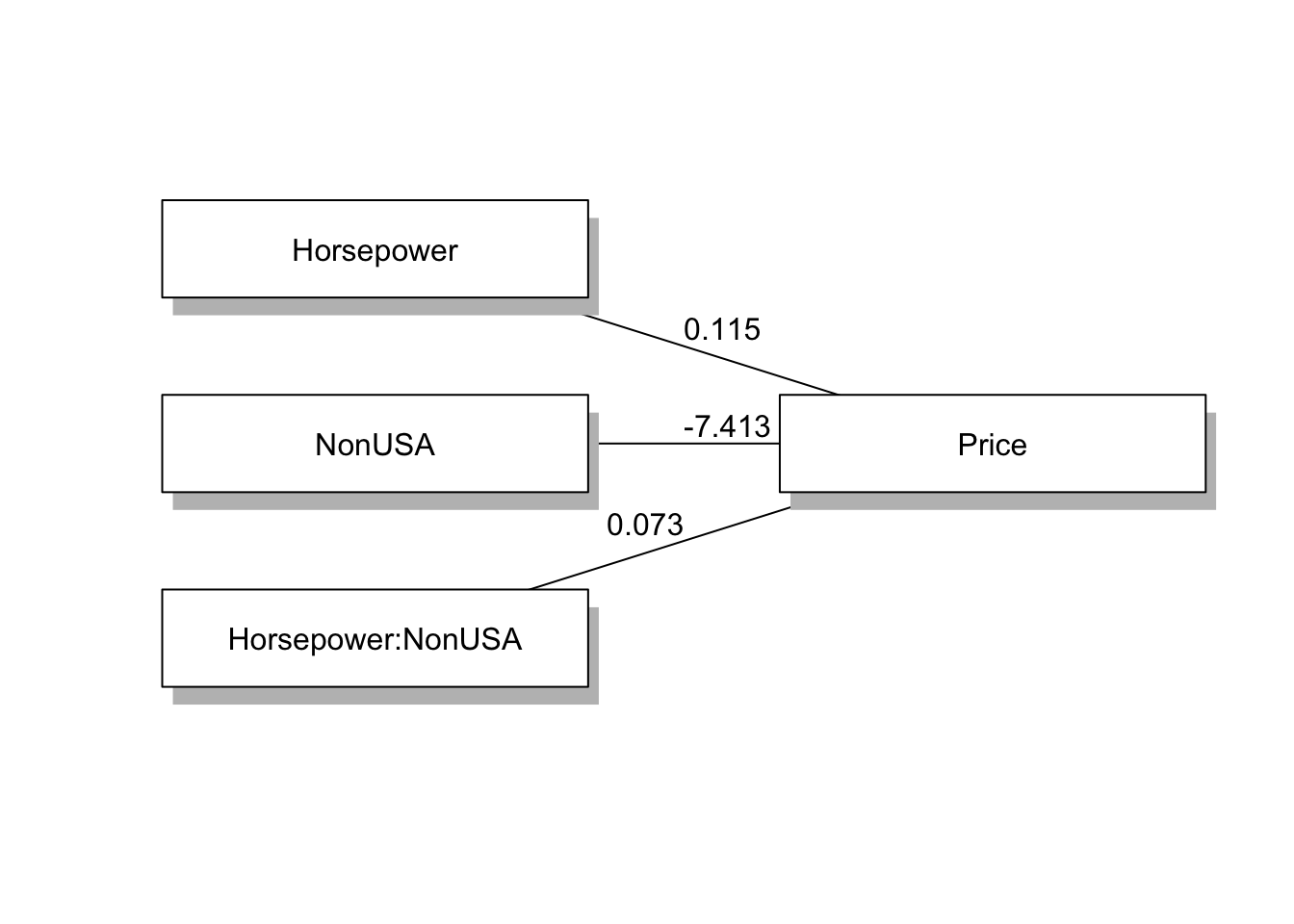
# 변수간 상관계수를 살펴볼 수도 있습니다.
corTable2(fit)rowname | Price | Horsepower | NonUSA | Horsepower.NonUSA |
Price | 1 | |||
Horsepower | 0.79*** | 1 | ||
NonUSA | 0.10 | -0.07 | 1 | |
Horsepower.NonUSA | 0.39*** | 0.23* | 0.90*** | 1 |
4.4.3 model assign : 시내주행연비
- 분석가설에 대해 모델을 설정하고 분석을 진행합니다.
[분석가설]
⓶ 자동차 마력과 자동차 가격 간의 관계에서 시내 주행연비가 조절효과를 할 것이다.
IV : 자동차 마력(horsepower)
DV : 자동차 가격(Price)
Mo : 시내 주행연비(MPG.city)
- 이제 모델설정을 해두었으니, 모델방정식을 만들어주면 됩니다.
- 독립변인은 Horsepower, 종속변인은 Price, 조절변인은 MPG.city입니다.
# 모델 설정 후 그림 그려보기
labels=list(X="Horsepower",W="MPG.city",Y="Price")
pmacroModel(1,labels=labels, radx=0.1,rady=0.07)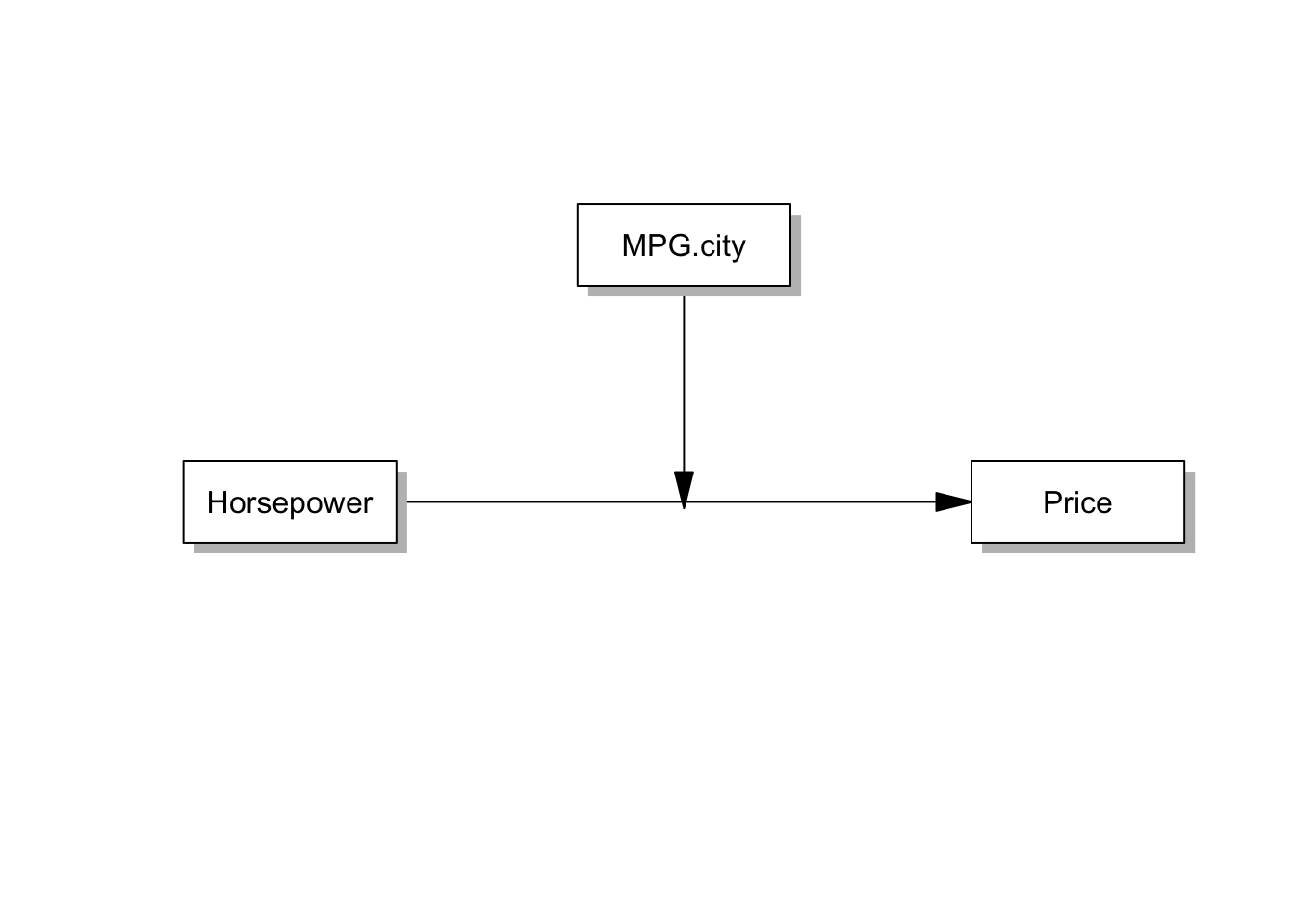
# model equation 만들기
moderator = list(name="MPG.city", site=list('c'))
model <- modmedEquation(X="Horsepower",Y="Price",labels = labels,moderator = moderator )
# model equation 확인
cat(model)##
## Price ~ c1*Horsepower+c2*MPG.city+c3*Horsepower:MPG.city
## MPG.city ~ MPG.city.mean*1
## MPG.city ~~ MPG.city.var*MPG.cityModeration Equation이 제대로 설정된 것 같습니다.
이제, lavvan 패키지를 활용하여 moderation 분석을 진행하겠습니다.
#bootstrap 200회, msiing value : ml
fit <- sem(model=model,data=data,se='bootstrap',bootstrap=200,missing='ml')## Warning in lav_partable_vnames(FLAT, "ov.x", warn = TRUE): lavaan WARNING:
## model syntax contains variance/covariance/intercept formulas
## involving (an) exogenous variable(s): [MPG.city]; These variables
## will now be treated as random introducing additional free
## parameters. If you wish to treat those variables as fixed, remove
## these formulas from the model syntax. Otherwise, consider adding
## the fixed.x = FALSE option.summary(fit,fit.measures = FALSE,standardize = TRUE, rsquare = TRUE)## lavaan 0.6-8 ended normally after 19 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 7
##
## Number of observations 93
## Number of missing patterns 1
##
## Model Test User Model:
##
## Test statistic 181.855
## Degrees of freedom 2
## P-value (Chi-square) 0.000
##
## Parameter Estimates:
##
## Standard errors Bootstrap
## Number of requested bootstrap draws 200
## Number of successful bootstrap draws 200
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Price ~
## Horsepowr (c1) 0.191 0.046 4.173 0.000 0.191 1.007
## MPG.city (c2) 0.075 0.211 0.355 0.723 0.075 0.042
## Hrsp:MPG. (c3) -0.003 0.002 -1.462 0.144 -0.003 -0.250
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## MPG.cty (MPG.) 22.366 0.598 37.390 0.000 22.366 4.001
## .Price 0.659 5.987 0.110 0.912 0.659 0.067
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## MPG.cty (MPG.) 31.243 7.598 4.112 0.000 31.243 1.000
## .Price 33.799 11.372 2.972 0.003 33.799 0.347
##
## R-Square:
## Estimate
## Price 0.653- 분석 결과 예측변수들을 테이블로 표시할 수 있습니다.
# 모든 파라미터의 Estimates를 표시합니다.
parameterEstimates(fit,boot.ci.type = 'bca.simple',level = .95,
ci = TRUE,standardized = FALSE)## lhs op rhs label est se
## 1 Price ~ Horsepower c1 0.191 0.046
## 2 Price ~ MPG.city c2 0.075 0.211
## 3 Price ~ Horsepower:MPG.city c3 -0.003 0.002
## 4 MPG.city ~1 MPG.city.mean 22.366 0.598
## 5 MPG.city ~~ MPG.city MPG.city.var 31.243 7.598
## 6 Price ~~ Price 33.799 11.372
## 7 Horsepower ~~ Horsepower 2713.583 0.000
## 8 Horsepower ~~ Horsepower:MPG.city 31928.786 0.000
## 9 Horsepower:MPG.city ~~ Horsepower:MPG.city 529054.266 0.000
## 10 Price ~1 0.659 5.987
## 11 Horsepower ~1 143.828 0.000
## 12 Horsepower:MPG.city ~1 3020.946 0.000
## z pvalue ci.lower ci.upper
## 1 4.173 0.000 0.093 0.277
## 2 0.355 0.723 -0.420 0.443
## 3 -1.462 0.144 -0.007 0.002
## 4 37.390 0.000 21.224 23.577
## 5 4.112 0.000 17.080 47.342
## 6 2.972 0.003 16.881 66.060
## 7 NA NA 2713.583 2713.583
## 8 NA NA 31928.786 31928.786
## 9 NA NA 529054.266 529054.266
## 10 0.110 0.912 -11.322 13.461
## 11 NA NA 143.828 143.828
## 12 NA NA 3020.946 3020.946# 논문작성용 테이블을 봅니다.
estimatesTable2(fit,vanilla = TRUE)Variables | Predictors | label | B | SE | z | p | β |
Price | Horsepower | c1 | 0.191 | 0.046 | 4.173 | < 0.001 | 1.007 |
Price | MPG.city | c2 | 0.075 | 0.211 | 0.355 | 0.723 | 0.042 |
Price | Horsepower:MPG.city | c3 | -0.003 | 0.002 | -1.462 | 0.144 | -0.250 |
Bootstrap을 활용한 분석 결과 Horsepower가 Price에 유의미한 정적 영향을 미치지만, MPG.city는 가격에 유의미한 영향을 미치지 않았습니다.
또한, MPG.city의 상호작용 효과역시 유의미하지 않았습니다.
분석 결과를 Diagram으로 나타내보면, Horsepower를 제외하고는 모두 유의미하지 않음을 알 수 있습니다.
statisticalDiagram(1,labels=labels,fit=fit,whatLabel="est", radx=0.2,rady=0.05)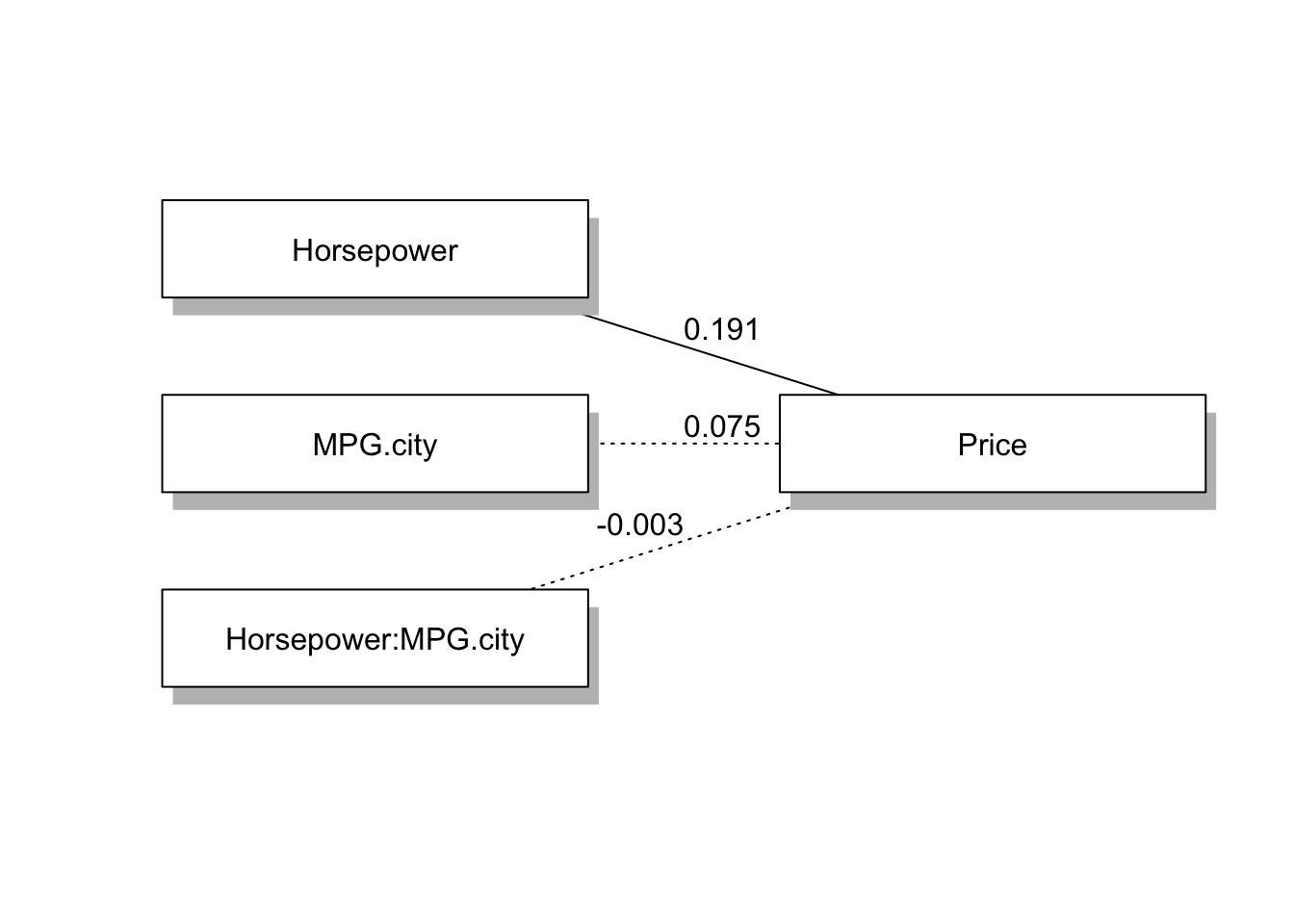
4.5 최종 결과
- 분석결과는 아래와 같습니다.
[분석결과]
① 자동차 마력과 자동차 가격 간의 관계에서 자동차 제조국이 조절효과를 할 것이다.
-> 채택됨
② 자동차 마력과 자동차 가격 간의 관계에서 시내 주행연비가 조절효과를 할 것이다.
-> 기각됨