5 Vraag5: CpG islands

Bestudeer / test wat deze functie doet en geef een korte beschrijving

dna_functie <- function( n , length ) {
  ## n = hoeveelheid te generen DNA fragmenten
  ## length = lengte per DNA fragment
  number_string <-runif( ( n * length ) ,1 ,4 ) %>% 
    round() %>% 
    str_c( collapse = "" )
  dna_random <- number_string %>% chartr( old = "1234" , new = "TAGC" )     
  start <-seq( from = 1 , to = ( n * length ) , by = length )           
  end <-start +( length-1 )       
  dna_random %>% str_sub( start = start , end = end )     
}

De functie genereert een gevraagd aantal DNA fragmenten (n) van een gevraagde lengte (length) met een random nucleotide volgorde.

2. Een CpG island is een DNA sequentie die verrijkt is voor het patroon “CG”. Deze islands zijn voornamelijk verrijkt in promoter regio’s en worden gemethyleerd wat leidt tot gen repressie.

Schrijf een functie die het percentage CpG island berekend in een DNA streng. Dit percentage wordt berekend door de (het aantal “CG” nucleotiden) te delen door (het totaal aantal nucleotiden) * 100

# functie voor berekenen gc percentage in DNA sequenties
cg_count <- function(sequentie) {
  if(str_count(sequentie, "((?i)[agct])") == str_count(sequentie)) {
    cg_percent <- str_count(sequentie, pattern = "(?i)[CG]") / str_count(sequentie) * 100 %>%
      round(digits = 1)
  }
    else 
      return("Please enter a DNA sequence containing only 'ACGT'")
}
cg_count("AaATTGGCC")

3. Gebruik de functie dna_functie van punt (A) met de volgende argumenten en bewaar in een object: n=1000 length = 200 Bereken voor iedere DNA sequentie van het object van functie dna_functie het percentage CpG islands

# Random gegenereerde tibble met 1000 gc percentages van 1000 DNA fragmenten van 200bp
sequenties <- dna_functie(1000, 200)
cg_percentages <- cg_count(sequenties)

## Warning in if (str_count(sequentie, "((?i)[agct])") == str_count(sequentie)) {:
## the condition has length > 1 and only the first element will be used

cg_percentages <- tibble(fragment = 1:1000, percentage_gc = cg_percentages)
knitr::kable(head(cg_percentages, n = 10))

fragment	percentage_gc
1	52.5
2	47.0
3	49.0
4	49.5
5	47.5
6	54.0
7	51.5
8	51.5
9	52.5
10	50.5

4. Maak een histogram van de percentages CpG islands van punt (C) met ggplot. Plot de waarden per bin als fractie van het totaal aantal berekende CG percentages

# ggplot histogram van percentages cg_percentages
cg_percentages %>% ggplot(aes(x = percentage_gc )) +
  geom_histogram(fill = 'blue') +
  labs(title = "Percentage GC",
       subtitle = "percentage G en C nucleotiden per DNA streng",
       x = "GC (%)",y = "frequency") + 
  theme_classic()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.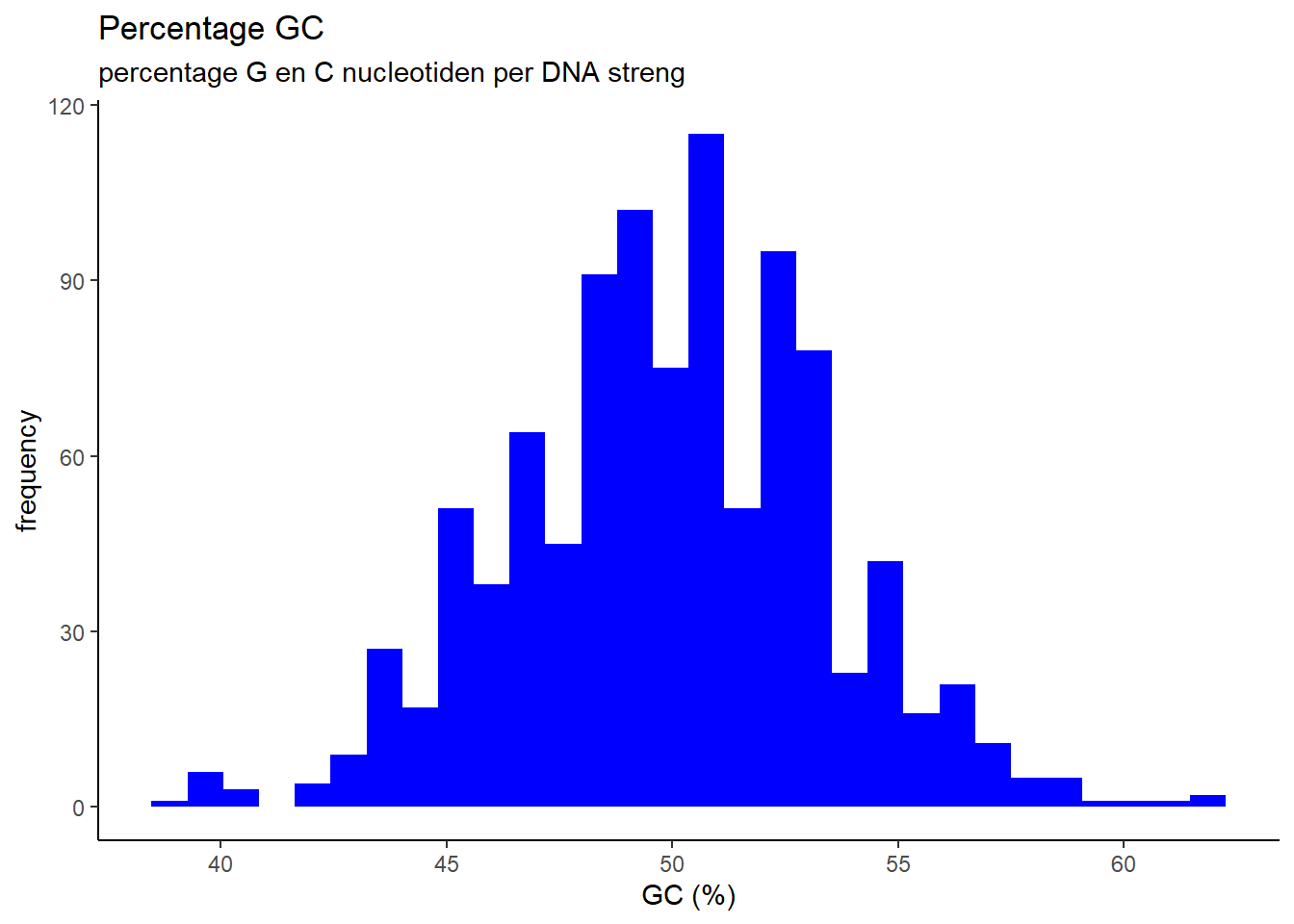

5. Bereken het gemiddelde percentage en de standaard deviatie van het aantal CpG islands

# Bereken gemiddelde en stdev van de percentages uit cg_percentages
cg_percentages %>% summarise(mean = mean(percentage_gc), 
                             stdev = sd(percentage_gc))

## # A tibble: 1 x 2
##    mean stdev
##   <dbl> <dbl>
## 1  49.9  3.51

6. Maak een grafiek van de normaal distributie gebaseerd op de argumenten van punt (E) met ggplot

# normaalverdeling ggplot van cg_percentages 
cg_percentages %>% ggplot(aes(x = percentage_gc)) +
  stat_function(fun = dnorm, n = 1000, args = list(mean = 50.0755, sd = 3.464831), size=2) + ylab("")+
  theme_classic()+
  ylab("dnorm(x)")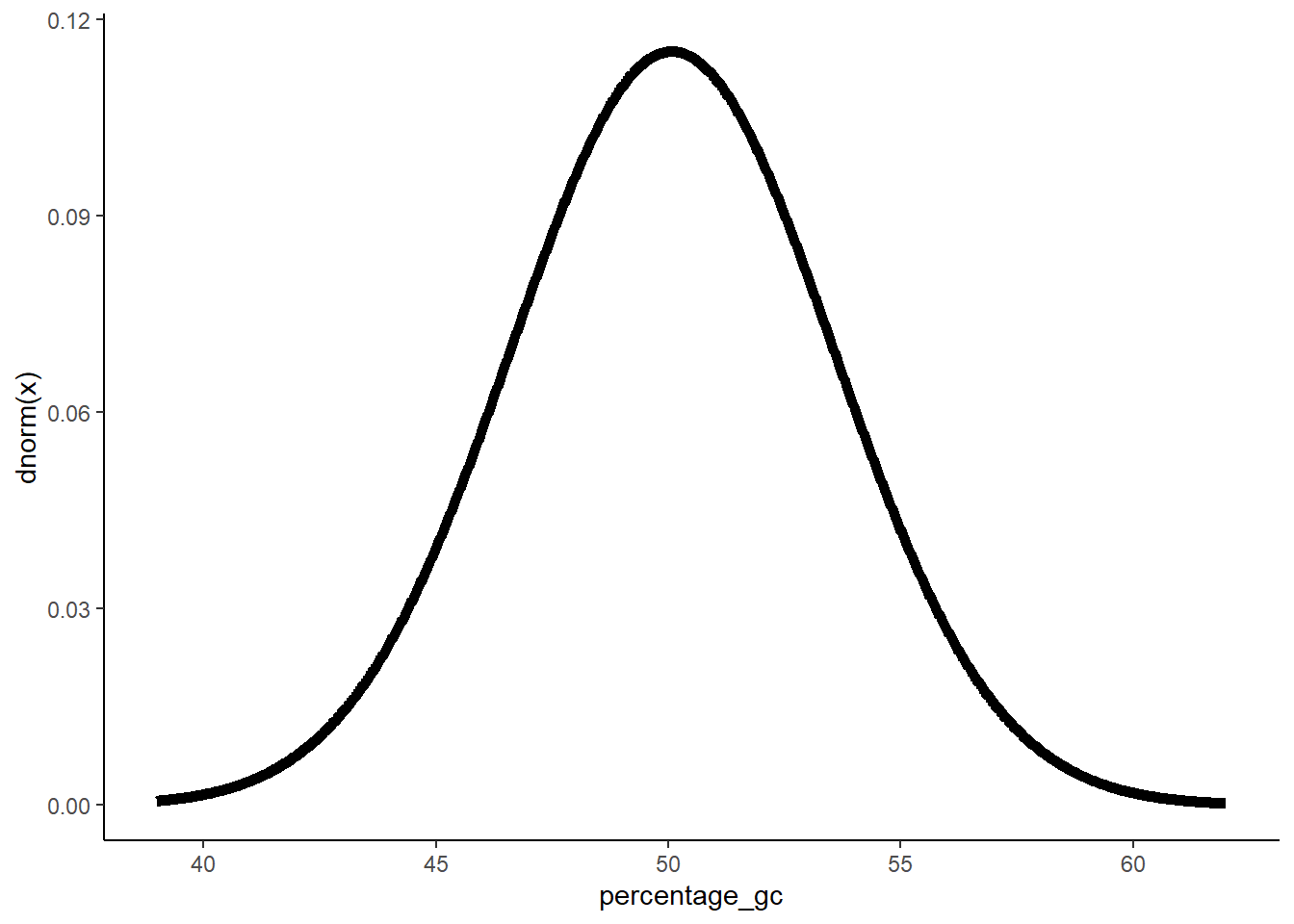

7. Hoeveel CpG island moeten er minimaal aanwezig zijn in een DNA fragment van 200 bp voor een statistische verrijking. Het significantie niveau is 5%.

Per fragment van 200bp moet minimaal 50% CG zijn waarvan 60% CpG island. Dit betekent dat 30% van de 200bp moet CpG island zijn oftewel 60bp wat gelijk staat aan 30 CpG islands +/- 5% is 28,5 - 31,5 CpG islands per 200bp.