3 Single variable regression analysis
Abstract
This chapter introduces single variable regression analysis, which is a method for estimating a parameter that describes a linear relationship.
Keywords: Regression, OLS, R-square, coefficient
3.1 Motivating regression analysis
Let us then motivate the key analysis that will run through this book in the following way. Suppose you were a candidate for the office of President of the United States, or a candidate for governor of your state, or, more realistically, a candidate for a seat on the local school district’s board of trustees. When you are talking with people about why you should be elected, you will probably repeat some platitudes about the importance of education for enabling young people to get good jobs when they are older. You might even say something like, “Studies have proven that every extra dollar spent on education generates an economic return of more than one dollar.” You’ll perhaps wonder how such studies were conducted, but it is unlikely you will be challenged. Instead, debates will rage about what specific purchases, using that extra dollar, are most effective. Should the school district, the state, or the nation invest in preschool education? Better K-6 education? Bilingual education? More science in elementary school? Data science and coding in R in high school? Free community college? Easier access to student loans?
Underlying these debates over the specificities of education spending, is a widely shared conviction that increasing a person’s educational attainment or the quality of education they receive will lead to their earnings being greater, at least on average. That is, even if crime doesn’t pay, education does! Indeed, economists have been studying the monetary “returns” to education for more than a century. They try to estimate the effect of changes in educational attainment and quality on earnings, on average, for a population of interest.
In addressing this issue, we are interested not just in the correlation between education and earnings, but more specifically in the causal connection between them. From the point of view of a policy maker deciding how to spend the taxpayers’ dollars, it is not enough to know that more educated people tend to make more money (correlation); the policy maker wants to know that increasing a given person’s education relative to what it otherwise would have been will actually cause their pay to increase. Using data analysis to infer such a causal connection is a serious challenge, and one we will explore repeatedly in this book.
The return to education question can be rephrased more generally as: Controlling for other factors, what is the effect on an outcome of a change in the value of some variable? This is the generic version of many questions studied in the social sciences. Some of the words in the generic version are worth glossing. By variable we mean a measurement of some aspect of the relevant social system. When referring to a variable as a factor, the variable has a sense of being an explanatory variable and not an outcome variable. An outcome is a measured phenomenon that we, the social scientists, are trying to explain. Just as painters usually limit their artistic expression to the confines of a canvas, so too do social scientists usually concentrate on explaining “an” outcome rather than on explaining many outcomes, in any given study. We have in mind an outcome that we measure and that we think is caused by many factors (we might also use close synonyms to the word “caused,” such as explained, or affected by). These factors that affect the outcome may or may not be measurable. If they are not measurable, then it will be hard to determine the effect on the outcome of a change in the factor.
We might think that estimating the effect of a change in one factor, when other factors do not change, is an impossible task outside of a laboratory setting. A laboratory setting is one where all the other factors except the factor of interest are carefully controlled by the researcher and thus do not vary. The laboratory is an isolated and artificial setting, by design. In the social world we live in, when one factor changes many other factors also change, and so we can never isolate the effect of a single factor on the outcome of interest. We might also reflect on the problem that factors can only change in response to some other change, and so asking the question of what will be the effect on an outcome if this particular factor changes while other factors do not, in the world that we know, may be asking for a state of the social world that is simply not possible.
These remarks suggest the difficult philosophical questions about how we understand causality, and what it means to explain something, especially in the area of human behavior. A nihilist or philosophical skeptic might remark, “Everything causes everything, little things cause big things, big things cause little things: butterfly wings beating slightly faster lead to a hurricane which leads to different survival rates of butterflies with different wing beating speeds. Why bother using the language of causality?” The common sense rebuttal might be, “When playing ping-pong, if you hit the ball hard, with a lot of spin, your opponent will likely miss the shot. You cause your opponent to miss the shot.” Both perspectives are relevant. The interested student is referred to surveys of the literature in philosophy and the social sciences that explore the meaning of causality (Gallow, 2022; Pearl, 2009). In this book we stick to the everyday, common sense, ping-pong understanding of proximate causality.
3.2 A linear model, for now
Returning to our example, we wish to estimate the average effect of changing educational attainment on earnings, for a specific population (e.g., young people in Kenya). We shall assume, for now, that the relationship between education and earnings is a linear relationship. We can then use the familiar tools of basic algebra, and describe (or encapsulate, or represent) the relationship by the following equation:
\[ Y = \beta_0 + \beta_1X\] where \(Y\) is the outcome variable, \(\beta_0\) is the intercept, \(\beta_1\) is the slope, and \(X\) is the explanatory variable. The slope is often explained as the rise over the run, or \(\Delta Y/\Delta X\). The intercept and the slope are sometimes called the parameters or the coefficients. The intercept is often called the constant term or just the constant. We could also write the equation as:
\[Earnings=\beta_0 + \beta_1Education\] where more informative variable names (usually written without spaces) stand in for the algebra conventions of \(X\) and \(Y\).
When we make assumptions, such as assuming that the relationship is linear, we sometimes refer to this as making (or building) a model. Our linear relationship is a simplification of the likely very complex social relationship. For purposes of this book, we adopt the perspective that in the social sciences we may often think of a linear model as a good approximation to an “average,” “population,” “real,” or “true” relationship. These latter terms are often used as synonyms in informal discussions of econometrics issues. For example, the “population” relationship is usually thought of as the average value of the outcome for each level of the explanatory variable, where we calculate the average for the entire population. The line tracking out that relationship may be approximated, in many cases, as a linear model.
This common sense perspective of approximating a complex social relationship elides some fundamental complexity about how we understand and explain the social world. Consider the problems of interpreting the seemingly obvious population relationship. Is the population the set of individuals in the United States in one particular year? The set of individuals over a long time period, say 1980 to 2020? The set of all possible individuals who could have lived in the United States during that time period? The set of all individuals that ever existed (some individuals died, some migrated away from the United States, some went off-line to live in the wilderness, away from data collectors)? What constitutes such a seemingly common sense notion as “the” population? Again, we are back to deep philosophical problems about our understanding of the social world.
3.3 Earnings and education in the Kenya DHS 2022 data
In order to understand how we estimate the linear relationship, it is helpful
to analyse the Kenya earnings data seen in previous chapters. You should
open and adapt a script in R. As usual in R, we do not start with a script
from scratch, but instead open an existing script, save it with a new name,
and then adapt it. Save the script with a useful descriptive name, for example
kenya earnings v1.R. Copy and paste the commands below into the
Data section of the script. You might want to delete any other content of
the Data section.
The first command we need, after the usual library() commands, is
some code to read in the data. Remember, from earlier chapters, that we
put the website address into the object “url” and then use read.csv() to
read in the data addressed by the url.
# Read Kenya DHS 2022 data from a website url <- "https://github.com/mkevane/econ42/raw/main/kenya_earnings.csv" kenya <- read.csv(url)As noted in earlier chapters, we may visualize the relationship between the two variables with a scatter plot using the package ggplot2. Consider Figure 3.1. On the x-axis we have the explanatory variable, and on the y-axis we measure the outcome variable. In this case, on the x-axis is the measure of education levels and on the y-axis is the measure of their earnings. Each dot in the scatter plot is an individual. Each dot represents two numbers \((x, y)\). The \(x\) is the education level of a person, the \(y\) is the earnings of that person. We sometimes call each dot an observation. The individual is the unit of observation, or the unit of analysis, or the entity of observation. That is, individuals are the units we are observing. The word “unit” does doubleduty in econometrics: variables are measured in units, and the entities being observed and measured are called units.
An aside on current vocabulary usage: a plot may also be called a figure or a graph; in the social sciences a plot is not usually called a chart (which is more typically used in business, and in public policy reports, rather than in academic articles). A plot is not called a table.
Here is the code to generate the scatter plot.
ggplot(data=subset(kenya,earnings_usd<=1000),
aes(x=educ_yrs,y=earnings_usd)) +
geom_point(size = 2, col = "firebrick", shape = 1) +
labs(x="Years of education", y="Earnings")+
theme_bw()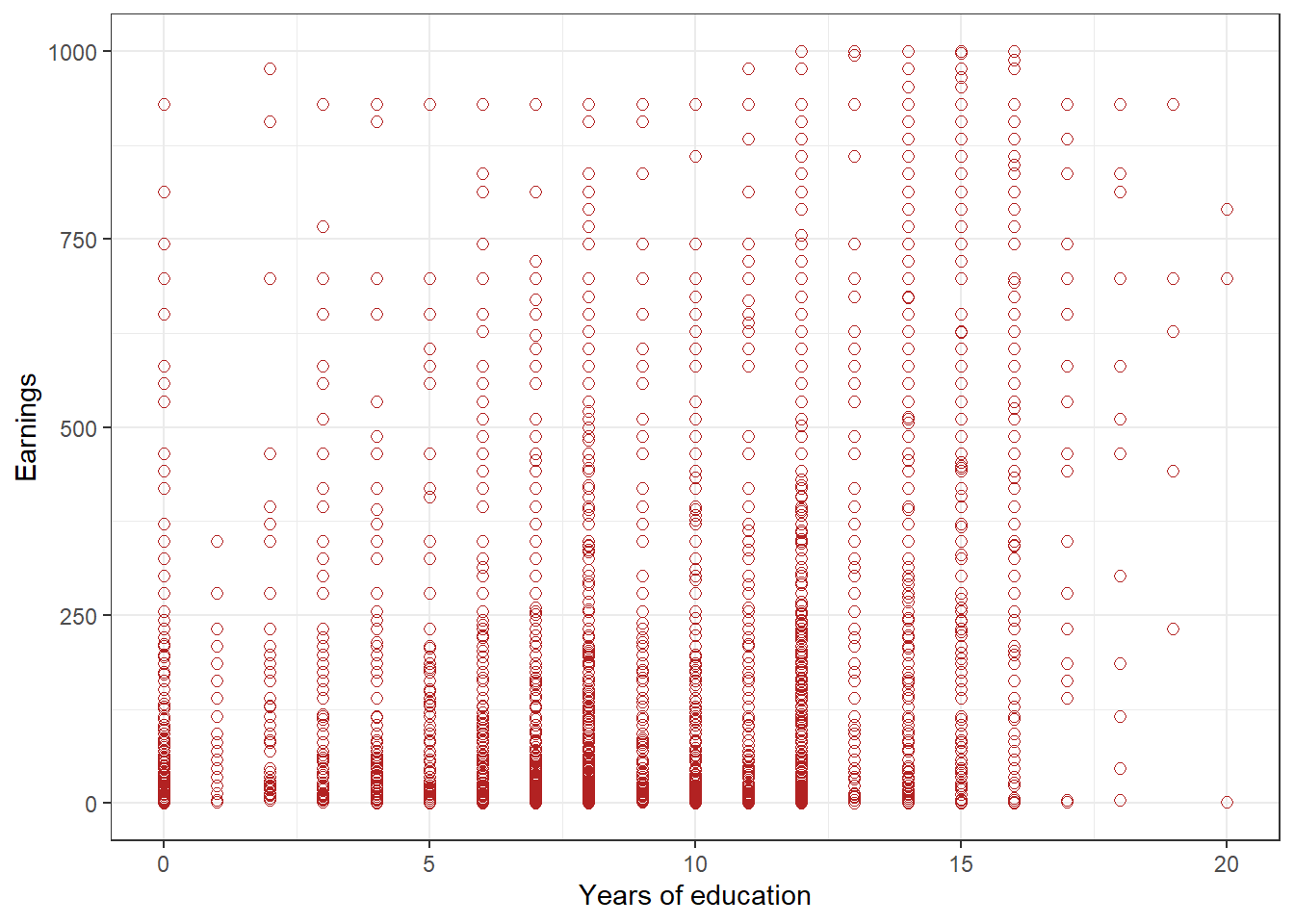
Figure 3.1: Figure 1: Scatterplot of earnings and educational attainment, in Kenya
Figure 3.1 displays the scatterplot, and the figure may help us take a guess about the relationship between the two variables. It is not completely obvious though what the relationship if for this random sample of adults in Kenya. That is because the variable years of education is an integer, taking on values 0, 1, 2 and so forth, and many of the dots (representing each observation) are on top of each other. Suppose, for a thought experiment, that there were a million dots all on top of each other at the point 0 years of education and earnings of $100. Our sample is actually about 20,000 observations, but there are only several hundred dots displayed, so some of the dots must overlap. But we do notice that as education levels increase we seem to see fewer dots at low levels of earnings. But we are just guessing, based on the scatter plot. Is the magnitude of the relationship, how much an extra year of education affects earnings, more like 25, or 20, or 10, or some other number? These magnitudes all seem plausible.
3.4 How do we estimate the relationship?
An “estimate” of \(\beta_1\) in the linear model means “a number we calculate using data on the explanatory variable and the outcome variable.” The number we calculate characterizes the magnitude of the effect on the earnings of a change in the value of the educational attainment. An “estimate” of \(\beta_0\) in the linear model also means “a number we calculate using data on the explanatory variable and the outcome variable.” In this particular case, the intercept \(\beta_0\) could be interpreted as the likely earnings if the educational attainment were equal to zero. The intercept in the linear model, usually has no simple interpretation in the social sciences, and is often ignored.
Together, an estimate of the slope and intercept describe a line, and we call this line the estimated line. As there is an infinite number of possible lines, we can think of estimating the slope and intercept as an exercise in finding a line that best fits the data available. What exactly we might mean by “best fit” shall become clear as we proceed.
Figure 3.2 draws three plausible best fit lines over the scatter plot of Figure 3.1. Is it obvious which one is best among the three? If so, is there a line that would be an even better fit? How could we agree on which one was the best fit?
ggplot(data=subset(kenya,earnings_usd<=1000),
aes(x=educ_yrs,y=earnings_usd)) +
geom_point(size = 2, col = "firebrick", shape = 1) +
labs(x="Years of education", y="Earnings")+
theme_bw()+
geom_segment(aes(x = 0, xend = 20, y = 100 , yend = 100 +20*25), linewidth=1.1)+
geom_segment(aes(x = 0, xend = 20, y = 130 , yend = 30 +10*25), linewidth=1.1)+
geom_segment(aes(x = 0, xend = 20, y = 160 , yend = 160 +25*25), linewidth=1.1)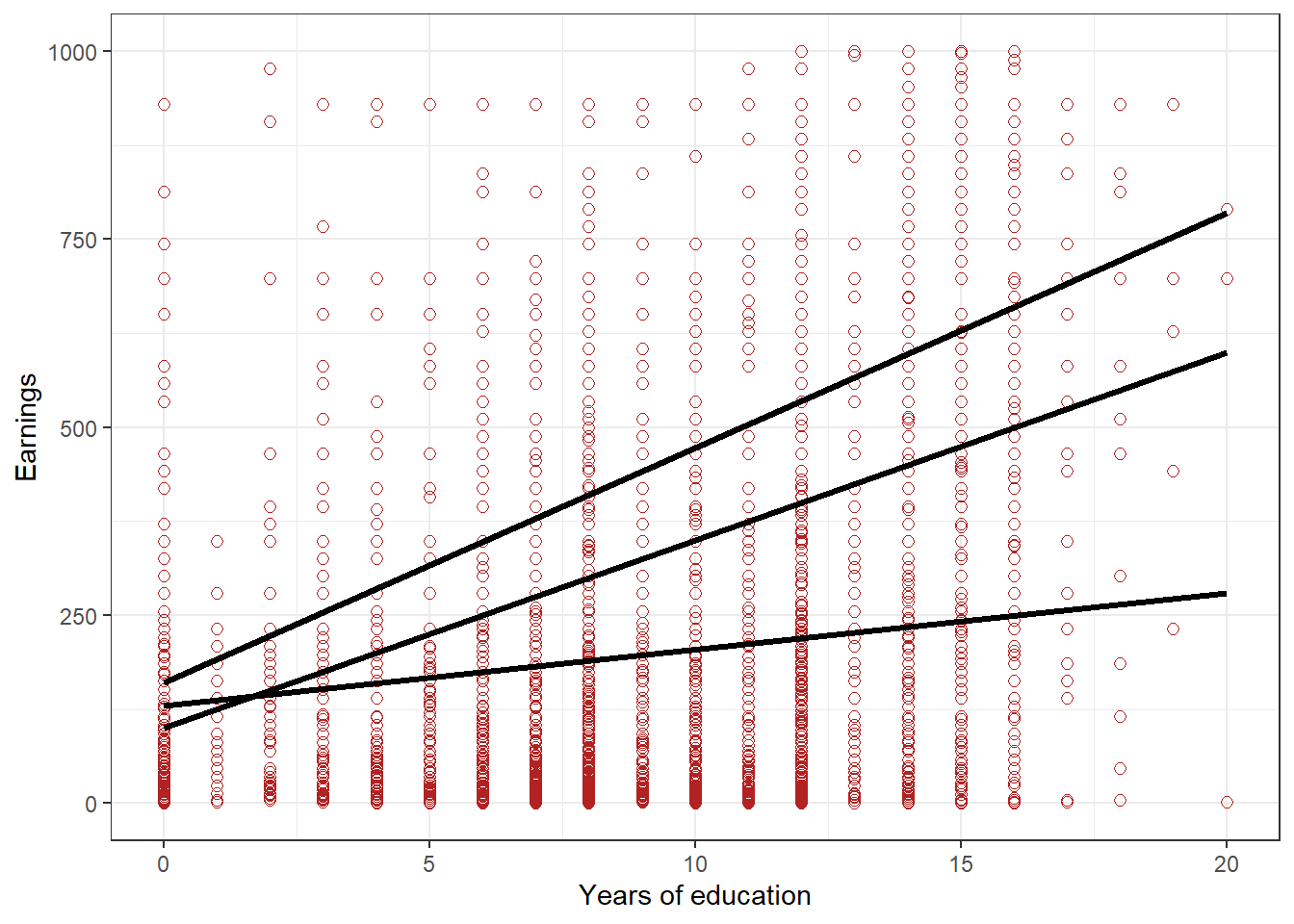
Figure 3.2: Figure 2: Scatterplot of earnings and educational attainment, in Kenya, with three possible lines
Introductory econometrics adopts, as the criterion for best fit line, a calculation procedure called minimizing the sum of squared residuals. This calculation procedure is also known as ordinary least squares, or OLS, and involves choosing estimates of the intercept (or constant term) and slope, \(\beta_0\) and \(\beta_1\), that minimize the sum, across all observations in the actual data that we have, of the squared deviations of the predicted levels of the outcome, for given values of \(X\), from the actual levels of the outcome for that level of \(X\).
In order to better illustrate this OLS method for calculating the parameters of a best fit line, we have to introduce some more notation, and make our model a bit more elaborate.
Here again is our model. We have added a new term, \(\epsilon\), that we shall think of as “other factors and measurement error term.” That is, our model supposes a linear relationship between \(X\) and \(Y\) , but the model takes into account that this is unlikely to be an exact relationship for each of our observations. Other factors, and errors in measurement, mean that for any particular observation, which has a value of \(X\) that we observe, there will be different outcomes of \(Y\) . For the same level of education, some individuals might have had high earnings and others low earnings, either because the individuals were different in other factors that affect earnings, or because earnings were measured with error (a person did not count income from their side hustle when asked about their earnings).
\[Y=\beta_0 + \beta_1X + \epsilon\] * \(X\) is called the independent variable, the control variable, the explanatory variable, the predictor variable, the regressor, the exogenous variable, or the right-hand side variable; * \(Y\) is called the dependent variable, the outcome variable, the explained variable, the predicted variable, the regressand, the endogenous variable, or the left-hand side variable; * \(\epsilon\), the Greek letter epsilon, is called the error term, or the deviation, or the random component, or the disturbance term. It is also sometimes represented as μ, the Greek letter mu, or lower-case e, or lower-case u. It represents the “other factors” that influence the outcome variable and the errors in measurement of the explanatory variable and outcome variable. * \(Y = \beta_0 + \beta_1X\), the part of the model without the error term, is sometimes referred to as the population regression line and it tells us the expected or average value of \(Y\) for the population for a given value of \(X\).
That is our model. We will estimate the parameters \(\beta_0\) and \(\beta_1\) using a dataset (also called a dataframe, or a spreadsheet, or just “data”). This dataset contains values for the educational attainment and the earnings for each individual. The Kenya dataset has about 20,000 rows, where each row is an observation. The observations come from a sample from the population of interest, or might be the entire population of interest at a given moment in time. In either case, one must remember that a different sample (or the population at a different moment in time) would generate different estimates of parameters.
If the data is a sample, it is a minimal requirement to estimate a relationship that the sample be a random sample from the population, in order for the researcher to infer anything about the population from the sample. This is obvious: if one wanted to estimate the relationship between hours of study and grades on tests for students at large public universities, having a sample consisting only of students who were on academic probation would not be very informative about the general population. We will usually assume, then, the datasets always are from random samples from the population of interest, or are arbitrary snapshots in time of the set of entities (countries, states).
Note that the data does not include measures of ϵ for each observation. We do not observe nor do we have a measurement of the error term. That is, we do not observe the part of \(Y\) that is explained by other factors, nor do we observe the extent of measurement error for each observation. For now, we shall assume that none of those other factors, nor the errors in measurement, are correlated with the level of education. That is, we shall assume that the level of education \(X\) is independent (in a statistical sense) of ϵ. Sometimes, economists use the word orthogonal to mean independent. \(X\) is orthogonal to ϵ.
Now, using the data, and our unobserved ϵ which varies from observation to observation, our model tells us that the relationship between level of education and earnings is, \[Y_i = \beta_0 + \beta_1X_i + \epsilon_i, i=1,...,N\] where \(i = 1, ...,N\) means for each observation from the first to the 20,000th, and we index by \(i\) to indicate these are the observations in the sample.
The parameters \(\beta_0\) and β_1 are unknown to us, but we can proceed by proposing values of the intercept \(b_0\) and slope \(b_1\) and using them to predict \(Y_i\) for each individual, and see how far off our prediction is. We use the notation \(\hat{Y}\) (which you may read as “Y-hat”) for the predicted value of Y. Using our proposed intercept and slope, \(\hat{Y_i} = b_0 + b_1X_i\). The residual for each observation i, then, is defined as the size of the gap between the actual \(Y\) and the predicted \(\hat{Y}\) :
\[residual_i = Y_i - \hat{Y}_i = Y_i - (b_0 + b_1X_i) = Y_i - b_0 - b_1X_i\]
The estimation method of OLS involves squaring each residual, adding them up, and calculating values b0 and b1 to minimize:
\[ SSR = \sum_{i=1}^N residual_i^2 = \sum_{i=1}^N (Y_i - b_0 - b_1X_i)^2\]
where SSR is the sum of squared residuals (also called the sum of squared deviations, or the sum of squared errors). Finding the values of \(b0\) and \(b1\) that minimize the SSR is called “running a regression.” The origins of the usage in econometrics of both terms, running and regression, are rather arcane; best to walk on by and just use the words. Another terminological convention you should master is that we refer to running a regression of \(Y\) (the outcome) on \(X\) (the regressor).
To get a better sense of how minimizing \(SSR\) works, consider Figure 3.3. In this figure, we have kept one of the proposed lines in Figure 3.2: specifically, the line with the formula \(\hat{Y_i} = 100 + 20X_i\), where \(X\) is Years of education and \(Y\) is Earnings. In this case, \(b_0 = 100\) and \(b_1 = 20\).
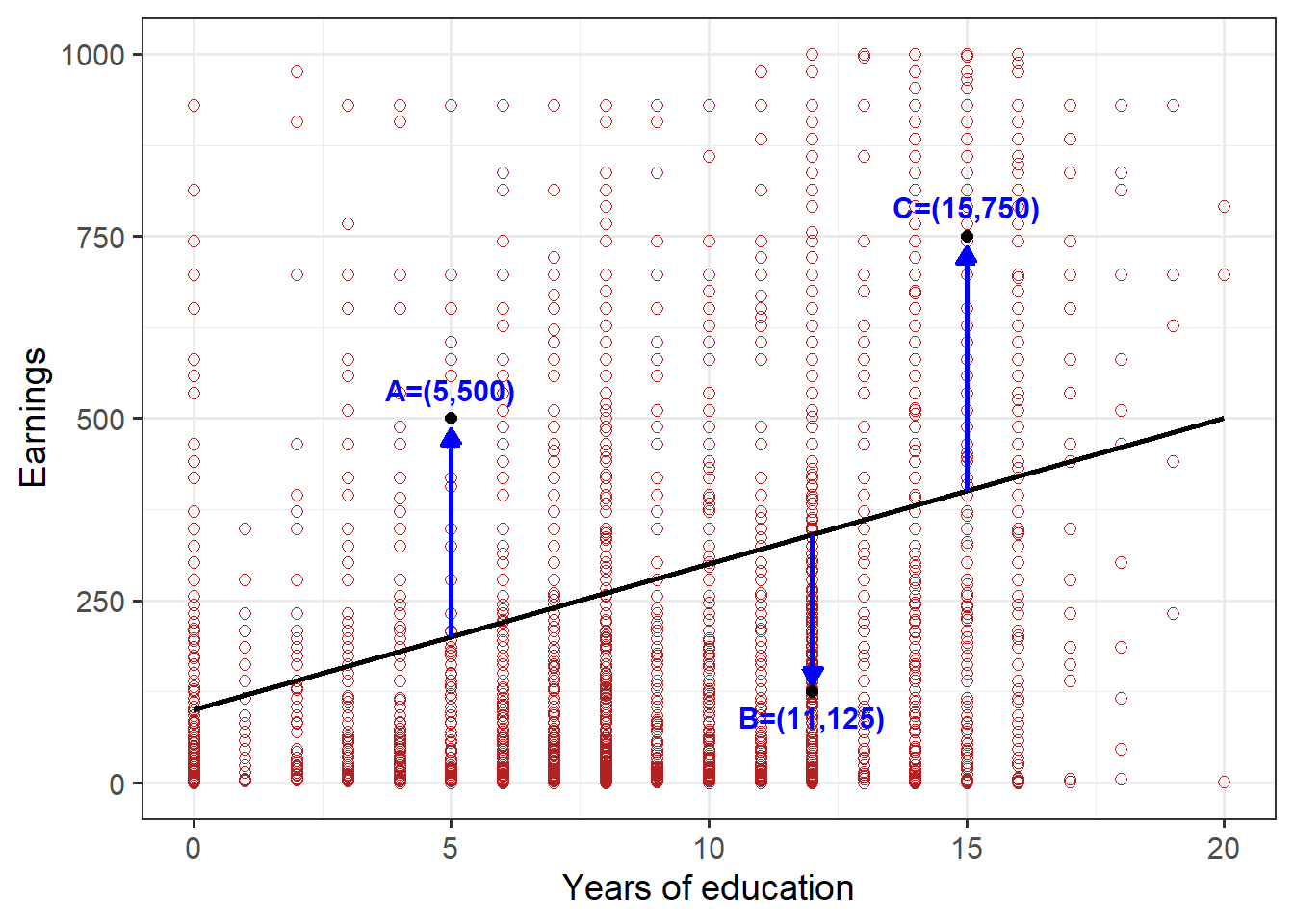
Figure 3.3: Figure 3: Scatterplot of earnings and educational attainment, in Kenya, indicating deviations from a proposed regression line
In Figure 3.3 we have identified three specific data points, represented dots labelled A, B, and C. Remember that each dot represents an individual in the Kenya earnings data set, so for example point A is an individual with 5 years of education and earnings of $500. Our proposed regression line would predict that person A, with 5 years of education, would have earnings of \(\hat{Y} = 100 + 20 \cdot 5 = \$200\). In fact, their actual earnings of (Y = $500) is much greater than predicted, so the residual for person A is ($500 − $200 = $300), which is the vertical distance of the arrow from the line to A. You can confirm that for person B, the residual is negative, because the actual earnings is less than the prediction on the line: The residual is \(125−(100+20 · 12) = −215\). The residual for C is positive. And so forth for every dot.
The residuals are vertical distances between each dot and the line. So by minimizing the sum of the square of these residuals, SSR, the OLS procedure is in a sense identifying a line that on average has the smallest (squared) vertical errors, and therefore passes through the “vertical middle” of the data. This turns out to be related to the property that the OLS prediction is conditional on a specific value of X.
Now let’s figure out the formulas for the OLS intercept and slope. Applying calculus to minimize \(SSR=\sum\nolimits_{i=1}^N(Y_i-b_0-b_1X_i)^2\) with respect to \(b_0\) and \(b_1\), we take partial derivatives, first for \(b_0\) and then for \(b_1\), and set the derivatives equal to zero. These derivatives are called the first-order conditions. If you have taken calculus, you probably recall that the first-order conditions may give you the maximum or the minimum of a function. In this case, the formula for the SSR assures that the solution minimizes SSR.
Solving the resulting first-order conditions, we can show that the values of \(b_0\) and \(b_1\) that minimize the sum of squared residuals are: \[\hat{\beta}_1 = \frac{\sum\nolimits_{i=1}^N(x_i-\overline{x})(y_i-\overline{y})}{\sum\nolimits_{i=1}^N(x_i-\overline{x})^2}\] \[\hat{\beta}_0 = \overline{y} - \hat{\beta}_1\overline{x}\] where \(\overline{x}\) is the mean of the observations of \(x\) in the dataset, \((1/N)\sum{x_i}\) and \(\overline{y}\) is the mean of the observations of \(y\) in the dataset, \((1/N)\sum{y_i}\). We will call the calculated values the estimates \(\hat{\beta}_0\) and \(\hat{\beta}_1\) and refer to the second, for example, as “beta one hat.”
The formulas may not look very meaningful, but one thing you may notice about the formula for \(\hat{\beta}_0\) is that it can be rearranged as \(\overline{y} = \hat{\beta}_0 + \hat{\beta}_1\overline{x}\). This means that \((\overline{x}, \overline{y})\) is a point on the estimated regression line, which implies that the OLS regression line passes through the sample means. In this sense the OLS regression is “well-centered” on the data.
The algebraic derivations of these formulas are presented in Box 3.1. We encourage you to work through them yourself and make sure we have not made any mistakes.
Box 3.1: Deriving the OLS estimates of slope and intercept in the single variable regression
Let us work through, step-by-step, the math of the derivation of the OLS estimators for intercept and slope. The method involves finding the values of \(b_0\) and \(b_1\) that minimize the sum of squared residuals (or sum of squared deviations):
\[SSR=\sum_{i=1}^N\epsilon_i^2 = \sum(y_i - \hat{y}_i)^2 = \sum(y_i-b_0 - b_1x_i)^2\] In this expression, the \(x_i\) and the \(y_i\) are numbers, not variables. They represent the data. Every observation \(1, . . . ,N\) is a pair of numbers \((x_i, y_i)\). What is unknown is \(b_0\) and \(b_1\). We can notice that the expression is a quadratic terms of \(b_0\) (there is an exponent of value 2 in the expression). Basic algebra tells us that the expression is a quadratic curve, and the minimum of the curve is the bottom of the curve.
We start by taking the partial derivative with respect to \(b_0\) (that is, holding \(b_1\) constant, and setting that equal to zero. This is sometimes called the first order condition. Note that in doing this we apply the chain rule, taking the derivative of the squared expression in parentheses and multiplying it by the derivative of what is “inside” the parentheses. \[\frac{\partial{SSR}}{\partial{b_0}} = \sum2(y_i - b_0 - b_1x_i)^1(-1)=0\] The 2 and the (-1) can be cancelled out. \[\sum(y_i - b_0 - b_1x_i) = 0\] Distributing the summation sign through the expression and rearranging, \[\sum b_0 = \sum{y_i-b_1}\sum{x_1}\] The summation of a constant is just N times the constant. \[Nb_0 = \sum{y_i-b_1}\sum x_i \] Divide both sides by N, \[b_0 = \frac{1}{N} \sum y_i-b_1\frac{1}{N} \sum x_i\] And we have our estimator. \[\hat{\beta}_0 = \overline{y} - b_1\overline{x}\] There are three terms on the right hand side of the equal sign. The mean of \(x\) and the mean of \(y\), which can be calculated from the data. We do not know \(b_1\).
We now take the partial derivative of SSR with respect to \(b1\), holding \(b0\) constant, and set that equal to zero,
\[\frac{\partial{SSR}}{\partial{b_1}} = \sum2(y_i - b_0 - b_1x_i)^1(-x_i)=0\] This yields, \[\sum x_i(y_i - b_0 - b_1x_i) = 0\] Distributing the summation sign throughout the expression, \[\sum x_iy_i - b_0 \sum x_i - b_1 \sum x_i^2 = 0\] Now we substitute in the above expression for \(b_0\): \[\sum x_iy_i - (\frac{1}{N}\sum y_i -b_1 \frac{1}{N} \sum x_i) \sum x_i -b_1 \sum x_i^2 = 0\] The next steps do some algebra with summation signs.
\[\sum x_iy_i - \frac{1}{N} \sum x_i \sum y_i + b_1 \frac{1}{N} (\sum x_i)^2 -b_1 \sum x_i^2 = 0\] \[\sum x_iy_i - \frac{1}{N} \sum x_i \sum y_i = -b_1 \frac{1}{N} (\sum x_i)^2 + b_1 \sum x_i^2\] \[\sum x_iy_i - \frac{1}{N} \sum x_i \sum y_i = b_1(\sum x_1^2 - \frac{1}{N}(\sum x_i)^2)\] And we have our estimator.
\[\hat{\beta}_1 = \frac{\sum x_iy_i - \frac{1}{N} \sum x_i \sum y_i}{\sum x_i^2 - \frac{1}{N} (\sum x_i)^2}\] Even more algebra can be used to show, \[\hat{\beta}_1 = \frac{\sum\nolimits_{i=1}^N(x_i - \overline{x})(y_i - \overline{y})}{\sum\nolimits_{i=1}^N(x_i - \overline{x})^2}\] which is the more common form of the estimator for the slope coefficient. This last expression for the estimator is sometimes spoken aloud as “the sum of x minus x-bar times y minus y-bar divided by the sum x minus x-bar squared.” We can plug this value of \(\hat{\beta_1}\) into equation 15, for \(b1\), and thus obtain \(\hat{\beta_0}\). We have now arrived at the formulas for the OLS intercept and slope estimators.
We sometimes call these two formula the OLS estimators for the two parameters. We take the data we have and mechanically input it into the estimator, in order to calculate the estimated coefficients. That is, in our brains, on paper, using a calculator, or using a computer, we conduct operations of addition, subtraction, multiplication, and division. We run the numbers. We run a regression.
More broadly, an estimator is a formula or rule for calculating a number from a sample of data. The number that is actually calculated is called an estimate. To repeat: we call the estimates of the coefficients (the intercept and the slope) of the best fitting line, \(\hat{\beta_0}\) and \(\hat{\beta_1}\).
These estimates then generate the fitted OLS regression line, sometimes called the sample regression line, where \(\hat{y_i}\) is the predicted value of \(y\) for a given level of \(x\): \[\hat{y_i} = \hat{\beta_0} + \hat{\beta_1}x_i\] And we can define the estimated error, or OLS residual, as: \[\hat{\epsilon_i} = y_i - \hat{y_i} = y_i - \hat{\beta_0} - \hat{\beta_1}x_i\] The estimated residual for each obervation is the difference between the actual and fitted values of \(y\), as previously noted.
3.5 Calculating OLS estimated coefficients by hand, and what happens if the measurement scale of a variable is changed?
Let us work through the calculations involved in estimating the coefficients (for intercept, or constant, and slope). We imagine a sample of five individuals where we measure their height in inches as the explanatory variable and their daily calorie consumption as the outcome variable. We might imagine that taller individuals consume more calories, on average.
| ID | Height | Calories |
|---|---|---|
| 1 | 65 | 3600 |
| 2 | 75 | 4000 |
| 3 | 65 | 3600 |
| 4 | 75 | 4200 |
| 5 | 70 | 2600 |
We can do some of the math in our heads, easily enough. The mean height is 70, while the mean calorie consumption is 3,600. But other calculations are best done carefully, in the form of a table, as below.
| ID | Height | Calories | \((x_i-\bar{x})\) | \((x_i-\bar{x})^2\) | \((y_i-\bar{y})\) | \((x_i-\bar{x})(y_i-\bar{y})\) |
|---|---|---|---|---|---|---|
| 1 | 65 | 3600 | -5 | 25 | 0 | 0 |
| 2 | 75 | 4000 | 5 | 25 | 400 | 2000 |
| 3 | 65 | 3600 | -5 | 25 | 0 | 0 |
| 4 | 75 | 4200 | 5 | 25 | 600 | 3000 |
| 5 | 70 | 2600 | 0 | 0 | 1000 | 0 |
So we see that, \[\beta_1 = \frac{\sum\nolimits_{i=1}^N(x_i-\overline{x})(y_i-\overline{y})}{\sum\nolimits_{i=1}^N(x_i-\overline{x})^2} = \frac{5,000}{100} = 50\] and then we can calculate that, \[\beta_0 = \overline{y} - b_1\overline{x} = 3,600 - 50 * 70 = 100\]
We interpret the estimated coefficients as meaning that if a person were one inch taller, their calorie consumption would be, on average, 50 calories higher. In a good example of the usual meaninglessness of the intercept term, what does it mean to say that if a person’s height were 0, the predicted calorie consumption would be 100? It is meaningful to predict the calories consumption of someone whose height was 72 inches. We would predict their calorie consumption to be 3,700. A person with height of 60 inches would be predicted to have calorie consumption of 3,100.
Notice that if the calories were measured as thousands of calories, rather than in single units, we would have the following table:
| ID | Height | Calories | \((x_i-\bar{x})\) | \((x_i-\bar{x})^2\) | \((y_i-\bar{y})\) | \((x_i-\bar{x})(y_i-\bar{y})\) |
|---|---|---|---|---|---|---|
| 1 | 65 | 3600 | -5 | 25 | 0.0 | 0 |
| 2 | 75 | 4000 | 5 | 25 | 0.4 | 2 |
| 3 | 65 | 3600 | -5 | 25 | 0.0 | 0 |
| 4 | 75 | 4200 | 5 | 25 | 0.6 | 3 |
| 5 | 70 | 2600 | 0 | 0 | 1.0 | 0 |
So we see that, \[\beta_1 = \frac{\sum\nolimits_{i=1}^N(x_i-\overline{x})(y_i-\overline{y})}{\sum\nolimits_{i=1}^N(x_i-\overline{x})^2} = \frac{5}{100} = .05\] and then we can calculate that, \[\beta_0 = \overline{y} - b_1\overline{x} = 3.6 - .05 * 70 = .1\]
The estimated intercept and slope are divided by 1,000. In general, if we change the scale of the measurement of the Y variable, the estimated coefficients are changed by the same scale. If we multiply the Y by 10, the coefficient will be multiplied by 10. If we divide the Y by 10, the coefficient will be divided by ten. (Look at Box 3.1 and see how you might prove this with algebra.)
What if the units of X changed? Suppose we measured height in centimeters rather than inches. We would have the following table (recalling that 2.54 cm = 1 inch).
| ID | Height | Calories | \((x_i-\bar{x})\) | \((x_i-\bar{x})^2\) | \((y_i-\bar{y})\) | \((x_i-\bar{x})(y_i-\bar{y})\) |
|---|---|---|---|---|---|---|
| 1 | 165 | 3.6 | -12.7 | 161 | 0.0 | 0.0 |
| 2 | 190 | 4.0 | 12.7 | 161 | 0.4 | 5.1 |
| 3 | 165 | 3.6 | -12.7 | 161 | 0.0 | 0.0 |
| 4 | 190 | 4.2 | 12.7 | 161 | 0.6 | 7.6 |
| 5 | 178 | 2.6 | 0.0 | 0 | 1.0 | 0.0 |
The mean height is now 177.8. From the table, we can see that the estimated slope coefficient is 12.7/644 = .0197. If we multiply the slope coefficient by 2.54, we get .05. So again, changing the scale of the X variable simply changes the scale of the estimated coefficients by the same scale. But now it is the reverse: if we multiply X by 2.54, the new coefficient will be the previously estimated coefficient divided by 2.54.
Let us work through another example. A researcher has a sample of babies, and has measured their weights and how many bottles of baby formula they were given per day over a period of time before they were weighed. The researcher wants to know the effects of formula bottles on weight. The variables then are weight in kg (W) and bottles of formula per day (B). The data is as follows, in the form of two ordered vectors, ordered by observation): W= (9, 13, 6, 6, 5, 3) and B= (9, 5, 14, 6, 8, 6).
We proceed to calculate estimates of \(\beta_0\) and \(\beta_1\), using the calculations below. So we see that,
| ID | B | W | \((x_i-\bar{x})\) | \((x_i-\bar{x})^2\) | \((y_i-\bar{y})\) | \((x_i-\bar{x})(y_i-\bar{y})\) |
|---|---|---|---|---|---|---|
| 1 | 9 | 9 | 1 | 1 | 2 | 2 |
| 2 | 5 | 13 | -3 | 9 | 6 | -18 |
| 3 | 14 | 6 | 6 | 36 | -1 | -6 |
| 4 | 6 | 6 | -2 | 4 | -1 | 2 |
| 5 | 8 | 5 | 0 | 0 | -2 | 0 |
| 6 | 6 | 3 | -2 | 5 | -4 | 8 |
\[\beta_1 = \frac{\sum\nolimits_{i=1}^N(x_i-\overline{x})(y_i-\overline{y})}{\sum\nolimits_{i=1}^N(x_i-\overline{x})^2} = \frac{-12}{54} = -0.22\] and then we can calculate that, \[\beta_0 = \overline{y} - b_1\overline{x} = 7 - (-0.22) * 8 = 8.78\] A sentence explaining the meaning of the slope coefficient \(\beta_1\) (that interprets the coefficient in words) might be: The estimated coefficient of -.22 means that for each increase of a bottle of formula per day, the baby’s weight goes down by .22 kg.
We might calculate the residual or error for the third observation, where W = 6 and B = 14. The predicted weight is 8.78 − .22 ∗ 14, equal to 5.67, so the residual (\(= actual−predicted\)), equals 6−5.67 = .33. If the residuals are calculated for every observation, then the goodness of fit \(R^2\) can be calculated, as in the table that follows.
| ID | B | W | residual = actual - predicted | squared deviations from mean \(w_i - \bar{w}\) (sum = TSS) | squared residuals (sum= SSR) |
|---|---|---|---|---|---|
| 1 | 9 | 9 | 2.222 | 4 | 4.94 |
| 2 | 13 | 5 | 5.333 | 36 | 28.44 |
| 3 | 6 | 14 | 0.333 | 1 | 0.11 |
| 4 | 6 | 6 | -1.444 | 1 | 2.09 |
| 5 | 5 | 8 | -2.000 | 4 | 4.00 |
| 6 | 3 | 6 | -4.444 | 16 | 19.75 |
We then have \(R^2 = 1 - SSR/TSS = 59.33/62 = 0.043\).
3.6 Running a regression in R with the Kenya DHS 2022 data
What does the best fit line look like for our sample of 20,000 individuals
in Kenya? We can estimate the coefficients with the R command lm(), which
stands for linear model.
##
## Call:
## lm(formula = earnings_usd ~ educ_yrs, data = subset(kenya, earnings_usd <=
## 1000))
##
## Coefficients:
## (Intercept) educ_yrs
## 30.2 19.9The syntax is straightforward. The tilde sign ∼ separates the outcome variable from the explanatory variable. We also tell R what dataframe to use. The output in the console tells us the estimated slope coefficient is about 19.9 and the intercept is estimated to be about 30.2.
We may also draw a scatter plot with the estimated regression line superimposed.
The following R code will do that, where we add the option
geom smooth(method = "lm", se = FALSE, col = "black") where again
lm stands for linear model. Figure 3.4 plots the estimated regression line.
kenya %>% filter(earnings_usd<=1000) %>%
ggplot(aes(x=educ_yrs, y=earnings_usd)) +
geom_point(size = 2, col = "firebrick", shape = 1) +
geom_smooth(method = "lm", se = FALSE, col = "black") +
theme_bw()+
labs(y="Earnings", x="Education attainment")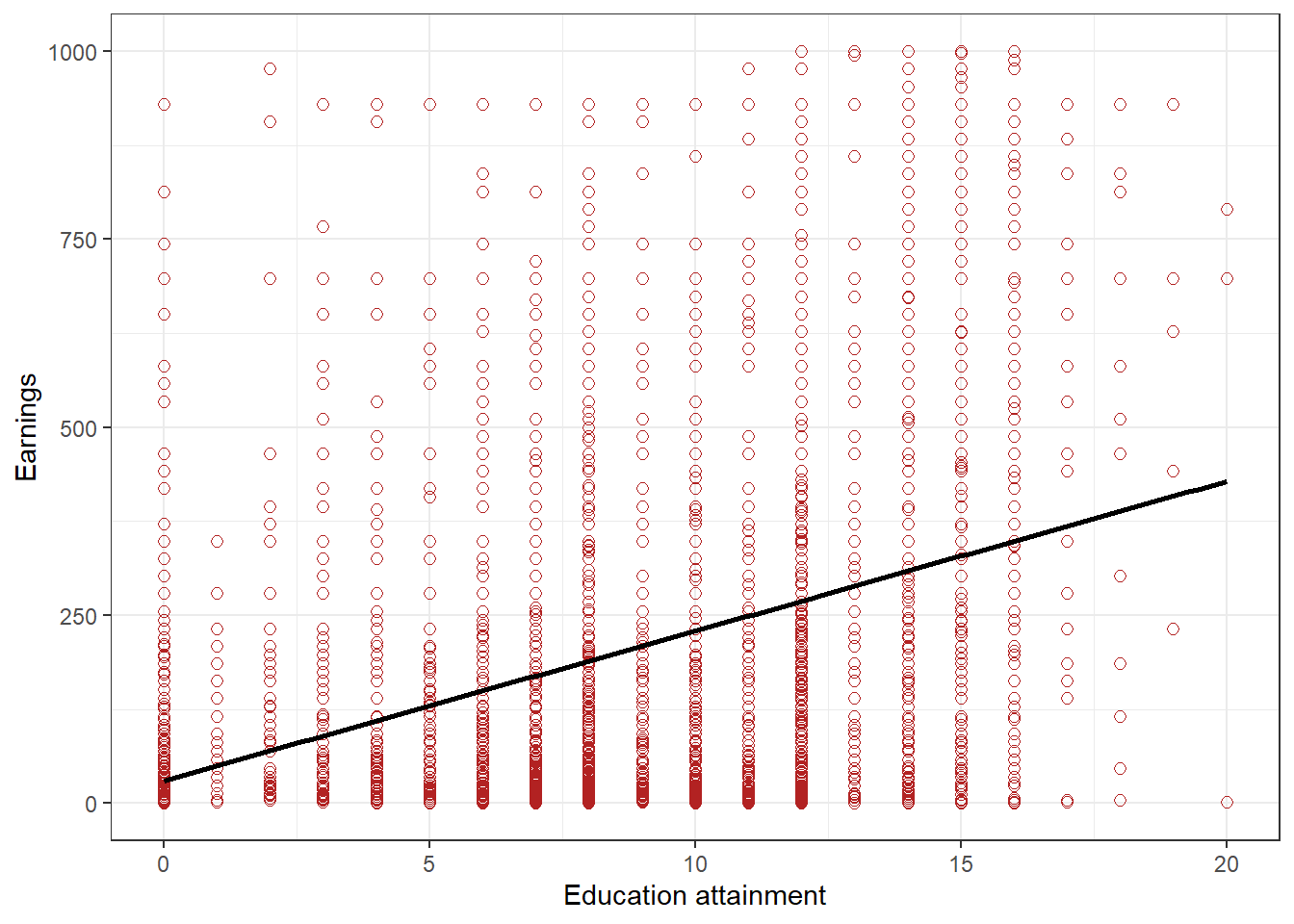
Figure 3.4: Scatterplot of earnings and educational attainment, in Kenya, with best fit line
3.7 Interpreting the coefficients
The estimated coefficients are numbers, and one of the tasks of a researcher is to communicate the meaning, or the sense, of the numbers. In regression analysis, we are usually most interested in the slope, which tells us something about how changes in the \(X\) variable are associated with changes in \(Y\) . If our estimated coefficient were 23, then we might say that a one unit increase in \(X\) is associated with a 23 unit increase in \(Y\) . Notice our careful repetition of the word “unit.” The \(X\) and \(Y\) variable may be measured in different units, rather than the same units. In the example above, the outcome is earnings in USD, while the explanatory variable is years of education. We would say, then, that an additional year of educational attainment is associated with $23 greater earnings.
The language used here—that a one-unit change in one variable is “associated with” a \(\beta_1\) unit change in the outcome—is intentionally agnostic about whether the relationship is causal. Maybe \(X\) causes \(Y\) , or maybe \(Y\) causes \(X\), or maybe both variables are caused by some third, unmeasured variable. In the social sciences, we are often interested in the potential causal impact of some \(X\) variable on some \(Y\) variable. As we proceed, we will need to be clear about the assumptions we need to make in order to assert that \(\beta_1\) captures a causal relationship. The most important assumption will be that \(X\) is independent (in a statistical sense) of the model error term \(\epsilon\) (i.e., all the other factors besides \(X\) that determine \(Y\) .
This interpretation of the coefficients only holds for the simple single variable regression, where the explanatory variable is a continuous variable. We will consider other cases where the interpretation of the coefficients will be more complex. These other cases may be thought of as other models or other specifications of the relationship.
What about interpreting the estimated coefficient \(\beta_0\)? We shan’t. The intercept or constant term rarely has any useful interpretation in the social sciences. It is the predicted average value of the outcome when the \(X\) variable takes on value zero. In the education and earnings case in Kenya, this makes some sense: what would the monthly earnings be on average for individuals without educational attainment. Many people in Kenya, especially older people, have no education. In many situations where we estimate a regression line, however, the intercept will not have any interesting meaning. For example, if we regressed earnings on age, the intercept would represent predicted earnings for someone who is 0 years old. We know of very few newborns who have paid employment!
Another way to think about interpreting the estimated regression coefficients is by using them to predict values of \(Y\) that one might expect, based on the regression results, for a given value of \(X\). Suppose we estimated a regression line that was \(Y = \hat{\beta_0} + \hat{\beta_1}X = 20 + 2X\). If \(X\) were equal to 20, we would predict that \(Y\) would be equal to 60. If \(X\) were 40, we would predict that \(Y\) would be equal to 100. If \(X\) were -10, we would predict that \(Y\) would be equal to 0. So we can use the estimated regression line to predict likely or expected values of \(Y\) for different levels of \(X\) To recap, when we are interpreting the estimated regression slope coefficient bβ1 in a regression \(Y = 20.7 − 3.2X\) we would say, or write: The regression results suggest that for a one unit change in \(X\) the outcome will decrease by 3.2.
With our regression result using the Kenya DHS 2022 data, we would use the regression results to suggest that, on average, someone with 10 years of education would have monthly earnings of \(30 + 20 ∗ 10 = 230\).
Please note the use of the word “suggest” here. Many econometricians prefer to use that word rather than a more definitive word such as “show” or “demonstrate” or, heaven forbid, “prove.” Regressions in the social sciences do not prove anything, in our usual natural sciences or philosophy sense of prove. We encourage social scientists, especially students learning social science, to be very modest in their declarative sentences.
3.8 Goodness of fit of the estimated regression line
The task of estimating the coefficients of the regression line emerged from the intuitive problem of finding the line that best fit the data in the sample at hand. It is natural to ask whether there is a measure of the “goodness of fit” of the estimated regression line. Econometricians usually examine two indicators of goodness of fit.
The first measure is called \(R^2\), pronounced “R-square” or “R-squared,” and is given by the following formula:
\[R^2 = \frac{\sum\nolimits_{i=1}{N} (\hat{y_i} - \overline{y})^2}{\sum\nolimits_{i=1}{N} (y_i - \overline{y})^2} = \frac{ESS}{TSS}\] or alternatively, \[R^2 = \frac{\sum\nolimits_{i=1}{N} (y_i - \hat{y_i})^2}{\sum\nolimits_{i=1}{N} (y_i - \overline{y})^2} = 1 - \frac{SSR}{TSS}\] where \(ESS\) is the explained sum of squares, \(SSR\) is the sum of squared residuals, and \(TSS\) is the total sum of squares (the variation in \(Y\) around its mean). \(R^2\) can be thought of as the fraction of the sample variance in \(Y\) explained by variation in \(X\), using the regression estimates. \(R^2\) varies of 0 to 1. In practice, an \(R^2\) of 0.13 can be considered to be quite a good fit in the social sciences. Many of the outcomes studied by social scientists have considerable idiosyncratic variation. It would be unlikely that a lot of the variation is explained by a single (or even several) explanatory variables.
We may calculate the \(R^2\) for the regression using basic R code. The code below will do the calculations. It is a good exercise to run these lines line by line and see how the objects appear in the environment and in the console. Try to make sure you see the link between the code and the mathematical formula. The calculated \(R^2\) will be .136. Since we are using base R, we first create a new dataset, called kenya_subset, that subsets the observations to only include those with monthly earnings less than or equal to $1,000.
kenya_subset <- kenya %>% filter(earnings_usd<=1000)
reg<-lm(earnings_usd~educ_yrs, data=kenya_subset)
b_hat <- coef(reg)
earnings_usd_pred <- b_hat["(Intercept)"] +
b_hat["educ_yrs"] * kenya_subset$educ_yrs
# And sum of squares
ESS=sum((earnings_usd_pred-mean(kenya_subset$earnings_usd))^2)
TSS=sum((kenya_subset$earnings_usd-mean(kenya_subset$earnings_usd))^2)
SSR=sum((kenya_subset$earnings_usd-earnings_usd_pred)^2)
# Calculate R-square
# R-square option 1
ESS/TSS[1] 0.136
# R-square option 2
1 - SSR/TSS[1] 0.136The second measure is called the standard error of the regression (SER), or the residual standard error, or the root mean squared error (RMSE) and it is the standard deviation of the estimated error, \[SER = \sqrt{\frac{\sum\nolimits_{i=1}{N} (y_i - \hat{y_i})^2}{n-2}} =\sqrt{\frac{SSR}{n-2}}\]
The SER or RMSE is in the same units as the \(Y\) outcome variable, and so it can be interpreted as the size of the typical regression error. You might think you could also calculate the mean residual or estimated error, but that number in fact always equals zero, because by the OLS coefficients are calculated so that the sum of deviations equals zero.
## [1] 198The SER is about 198 for this simple regression. The mean of monthly earnings, we saw earlier, is about 220, so the typical residual is about the same magnitude as the average of earnings. Note that the econometrics literature can be confusing because sometimes authors have slightly different definitions of SER and RMSE, involving whether the denominator should be the number of observations or the number of observations subtracted by the number of “degrees of freedom” (here, 2). In practice, with large sample sizes, there will be only tiny differences between the two.
3.9 Concluding thoughts
The practice of econometrics is about trading off model complexity against model parsimony, while being attentive to the credibility, confidence (in a sense informed by statistical analysis), ease of interpretation, and robustness to alternative plausible specification choices of the estimated coefficients. In subsequent chapters, the meaning of these terms shall become more clear.
We asked, in July 2024, what ChatGPT would make of the problem of estimating the relationship between education and earnings, and to generate text in the style of Cormac McCarthy. The relationship is known to economists, as we shall see later in a somewhat different specification, as the Mincer equation. Here is the generated text:
In the relentless calculus of human endeavor, the estimation of the Mincer equation emerges as a stark reckoning, tracing the jagged contours of education’s yield in the harsh terrain of economic reality. Each coefficient, each variable wrested from the data, speaks of the austere calculus of human capital. The Mincer equation, a testament to the relentless pursuit of understanding, lays bare the raw transaction between schooling and earning, casting light on the shadowed corners of opportunity and inequality. In this bleak landscape, its estimation serves not only as a tool of empirical inquiry but as a harbinger of deeper truths — of the cost of ignorance and the promise of knowledge in shaping destinies amidst the desolate expanse of economic existence. Talk about the dismal science!
Review terms and concepts: • explanatory variable or factor • outcome variable • cause, effect, affect • linear relationship • model • scatter plot • parameters, coefficients • constant, slope • regression • estimate, estimator • error term • minimize the sum of squared residuals • ordinary least squares (OLS) • predicted value • residual • specification • goodness of fit • \(R^2\) • sum of squared residuals (SSR) • total sum of squares (TSS) • explained sum of squares (ESS) • standard error of the regression (SER)