from matplotlib import pyplot as plt
from symbulate import *Exponential Distributions
Exponential distributions
W = RV(Exponential(rate = 1 / 30))
w = W.sim(10000)
w| Index | Result |
|---|---|
| 0 | 49.03697641809597 |
| 1 | 9.423805751154866 |
| 2 | 132.84656955378057 |
| 3 | 70.0802876942785 |
| 4 | 42.8600187361989 |
| 5 | 68.94044192928088 |
| 6 | 14.5918468329616 |
| 7 | 9.185332844731454 |
| 8 | 11.33988064850317 |
| ... | ... |
| 9999 | 37.85308078050787 |
plt.figure();
w.plot()
Exponential(rate = 1 / 30).plot()<symbulate.distributions.Exponential object at 0x000002292F167050>plt.show();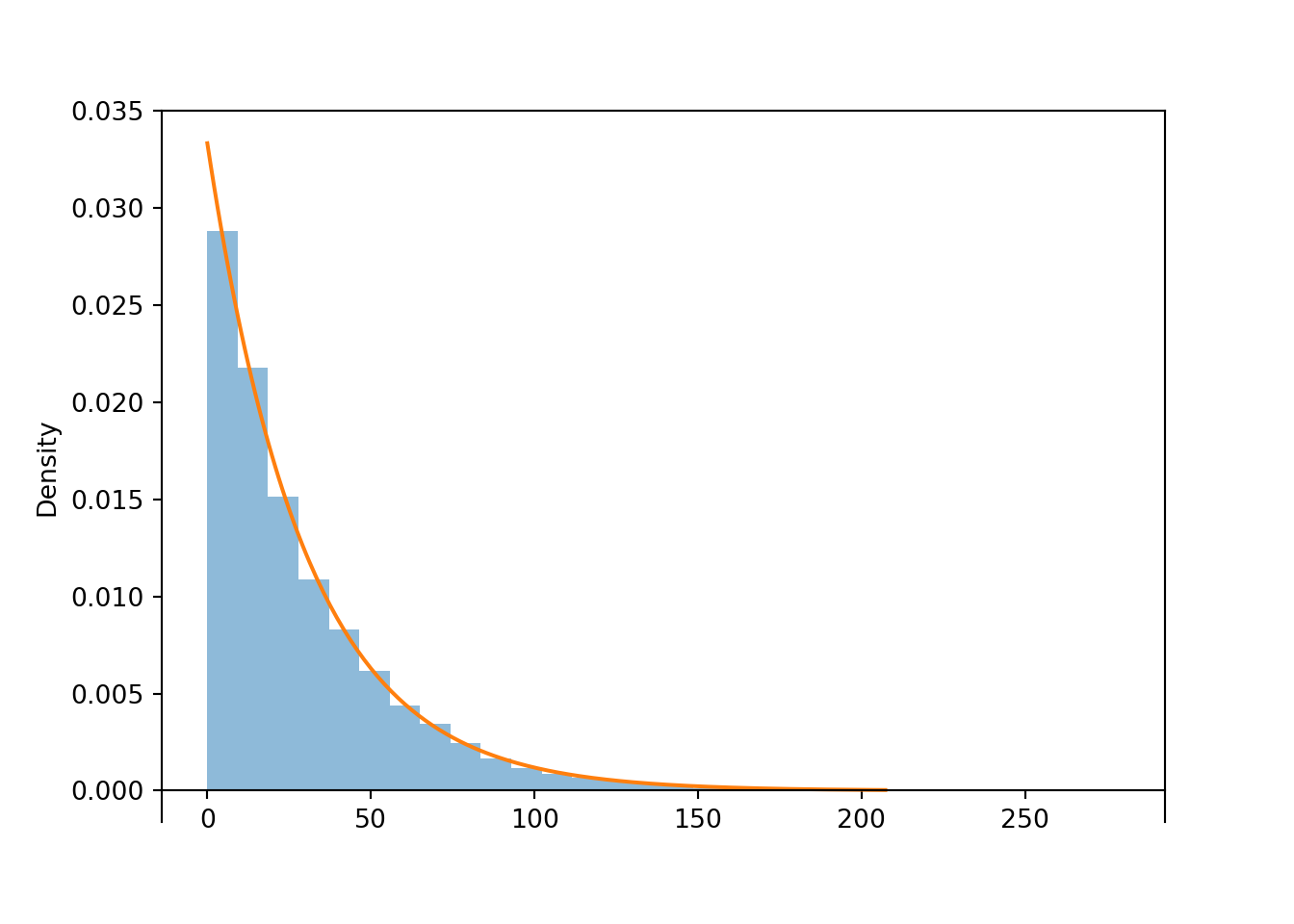
w.count_gt(45) / 10000, 1 - Exponential(rate = 1 / 30).cdf(45)(0.2228, 0.2231301601484298)Scaling
U = RV(Exponential(rate = 1))
W = U / (1 / 30)
plt.figure();
W.sim(10000).plot()
Exponential(rate = 1 / 30).plot()<symbulate.distributions.Exponential object at 0x000002292F9232D0>plt.show();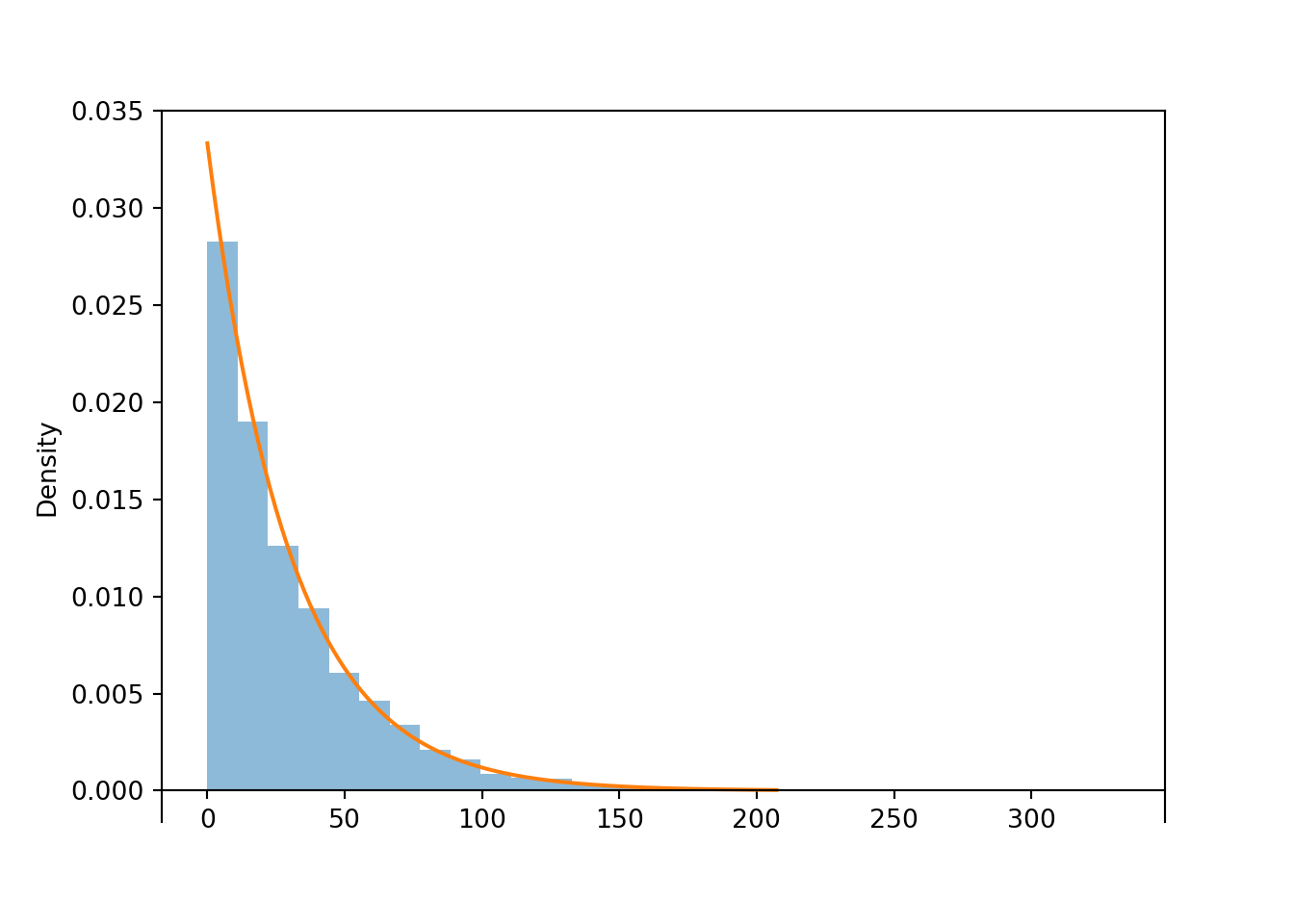
U = RV(Exponential(rate = 1))
V = U / 2
plt.figure();
V.sim(10000).plot()
Exponential(rate = 2).plot()<symbulate.distributions.Exponential object at 0x000002292F92E690>plt.show();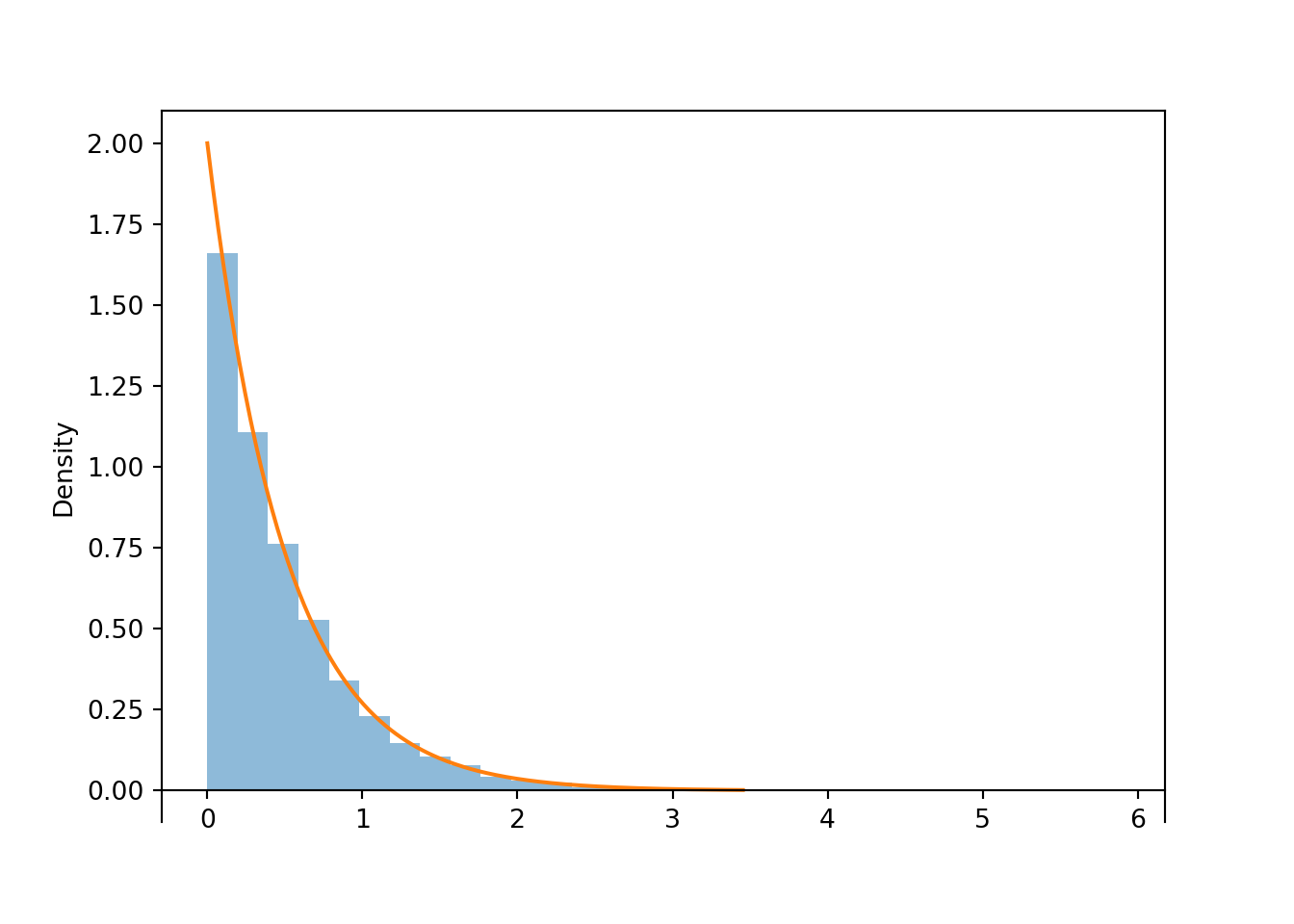
Memoryless property
plt.figure();
W.sim(10000).plot()
(W - 120 | (W > 120) ).sim(10000).plot()
plt.show();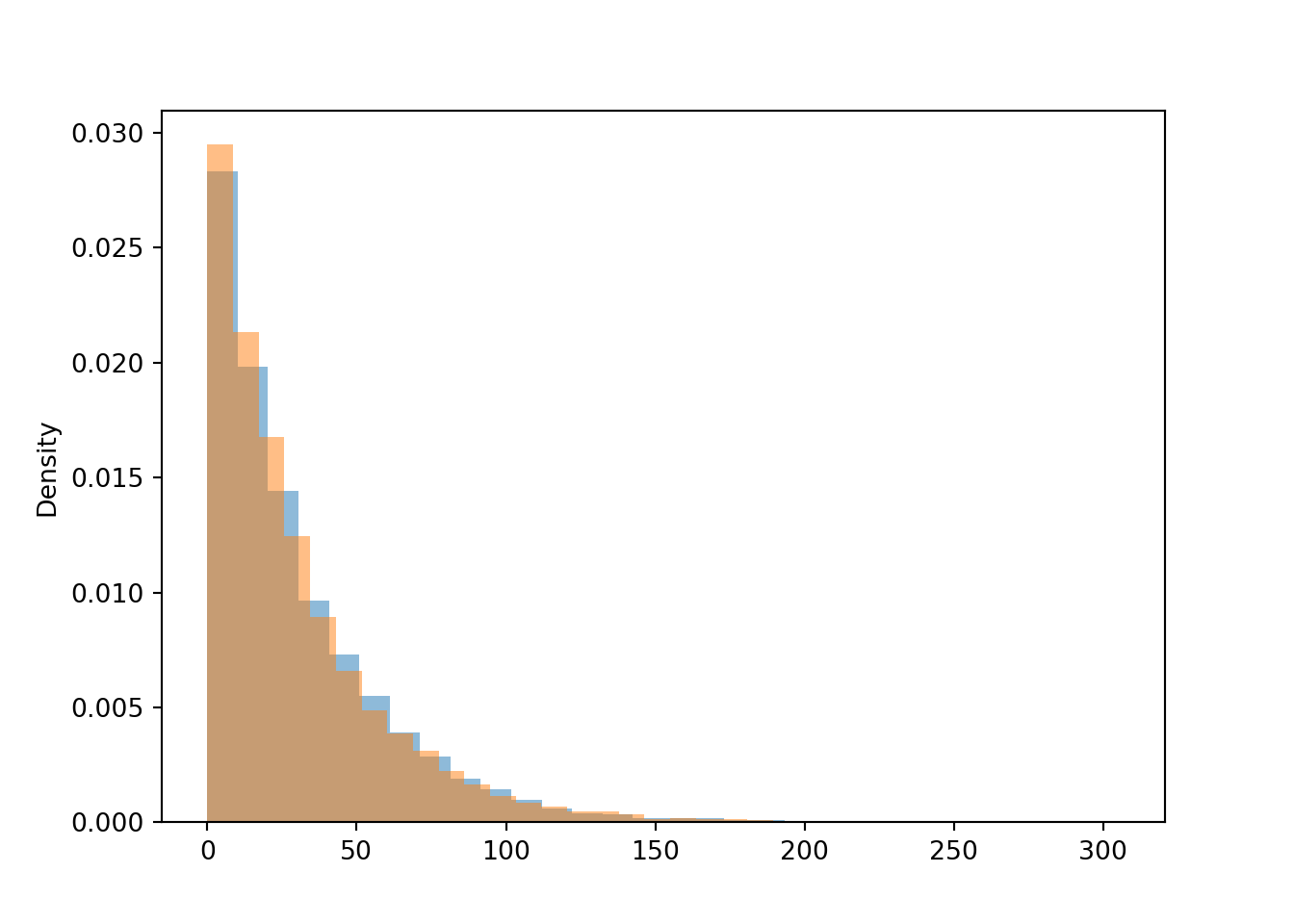
Exponential race
X, Y = RV(Exponential(rate = 1 / 10) * Exponential(rate = 1 / 20))
W = (X & Y).apply(min)xyw = (X & Y & W).sim(10000)
xyw| Index | Result |
|---|---|
| 0 | (1.6897804494190363, 54.251047424807496, 1.6897804494190363) |
| 1 | (21.073127016462692, 4.314201032443291, 4.314201032443291) |
| 2 | (5.150354478281881, 8.002545837169222, 5.150354478281881) |
| 3 | (5.443860882110773, 5.104369643190124, 5.104369643190124) |
| 4 | (7.477603528806048, 41.27253893283148, 7.477603528806048) |
| 5 | (18.56071637256133, 19.615344156346342, 18.56071637256133) |
| 6 | (5.202180555170194, 18.687985339922577, 5.202180555170194) |
| 7 | (14.114926015285025, 7.864018408834395, 7.864018408834395) |
| 8 | (5.377075413545369, 79.7288284761082, 5.377075413545369) |
| ... | ... |
| 9999 | (4.389065449318251, 7.465365345227921, 4.389065449318251) |
xyw.mean()(9.935651845714911, 20.161492769314357, 6.595751715218697)plt.figure();
W.sim(10000).plot()
Exponential(rate = 1 / 10 + 1 / 20).plot()<symbulate.distributions.Exponential object at 0x000002292FE7D450>plt.show();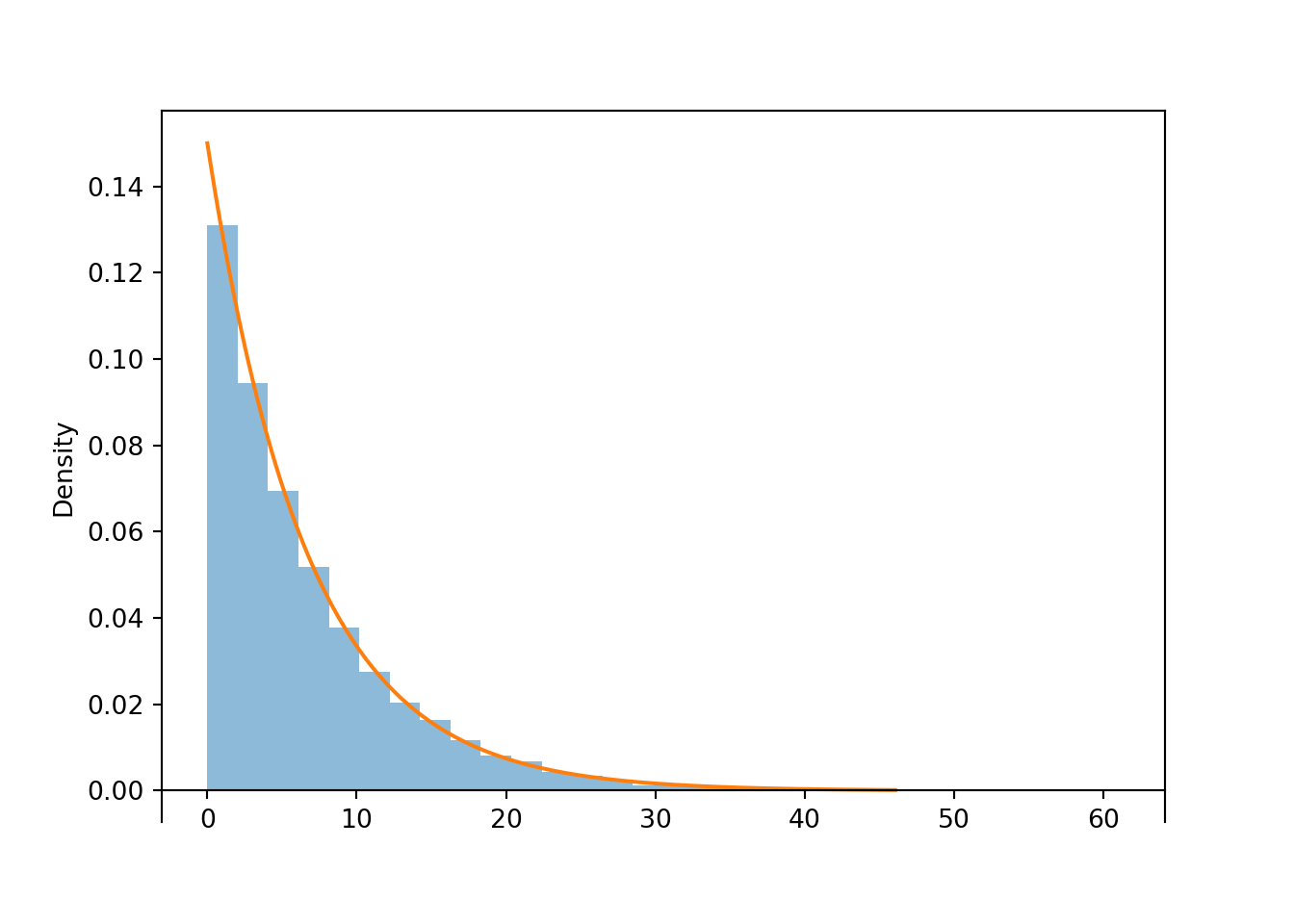
(Y > X).sim(10000).tabulate(normalize = True)| Outcome | Relative Frequency |
|---|---|
| False | 0.329 |
| True | 0.671 |
| Total | 1.0 |
plt.figure();
(W | (Y > X) ).sim(10000).plot()
(W | (Y < X) ).sim(10000).plot()
Exponential(rate = 1 / 10 + 1 / 20).plot()<symbulate.distributions.Exponential object at 0x000002292FB231D0>plt.show();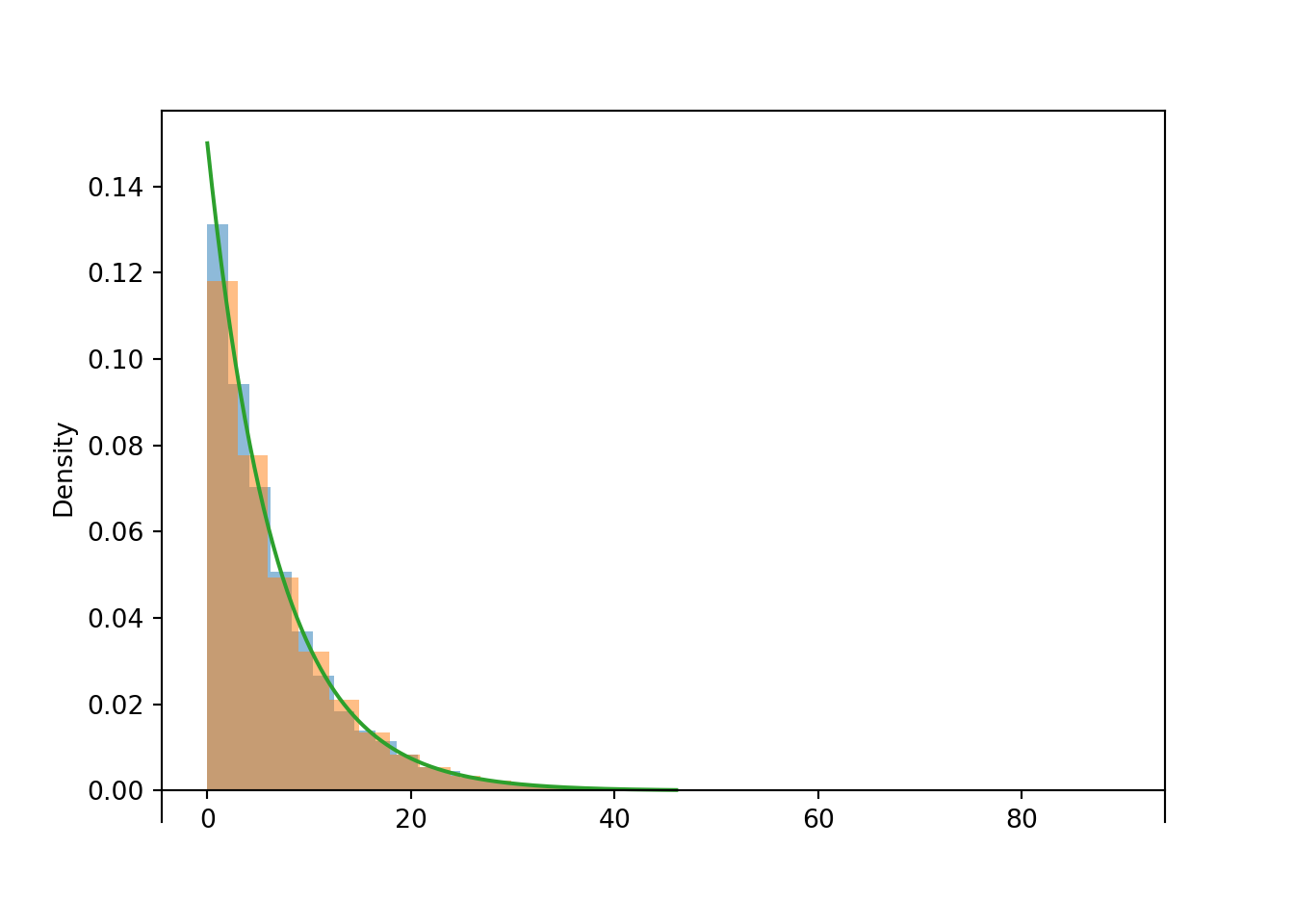
Gamma distributions
W1, W2, W3 = RV(Exponential(rate = 2) ** 3)
T = W1 + W2 + W3sim = (W1 & W2 & W3 & T).sim(10000)
sim| Index | Result |
|---|---|
| 0 | (0.06469452124560411, 1.7855682081667332, 0.5313631202689882, 2.3816258496813254) |
| 1 | (0.1584208969802546, 0.4924251031702411, 0.1163766244406055, 0.7672226245911011) |
| 2 | (1.0698065892178952, 0.07795530155530278, 0.16496695664767727, 1.3127288474208751) |
| 3 | (0.21436431905901593, 0.5583898831088366, 0.016993425807202714, 0.7897476279750554) |
| 4 | (0.0005713850629777853, 0.3881865649738012, 1.510141515540344, 1.898899465577123) |
| 5 | (0.012704265881709228, 0.4672657986103173, 0.19088675080722023, 0.6708568152992468) |
| 6 | (0.045426184155089054, 0.7530210654992747, 0.3150977064163982, 1.113544956070762) |
| 7 | (0.4596560710480708, 0.28077703838656387, 0.23965647395637424, 0.9800895833910089) |
| 8 | (0.9467156208910521, 1.0575805333836266, 0.24898627141401772, 2.2532824256886963) |
| ... | ... |
| 9999 | (0.8860052047301088, 0.060700238141574506, 0.537647553037698, 1.4843529959093813) |
sim.mean()(0.5007131157254108, 0.5000359531826972, 0.513057655279491, 1.5138067241875979)sim.var()(0.24657422498246614, 0.24389642533279743, 0.261121071967302, 0.7693369341430786)sim.sd()(0.49656240794331796, 0.4938587098885646, 0.5110000704180989, 0.8771185405309129)plt.figure();
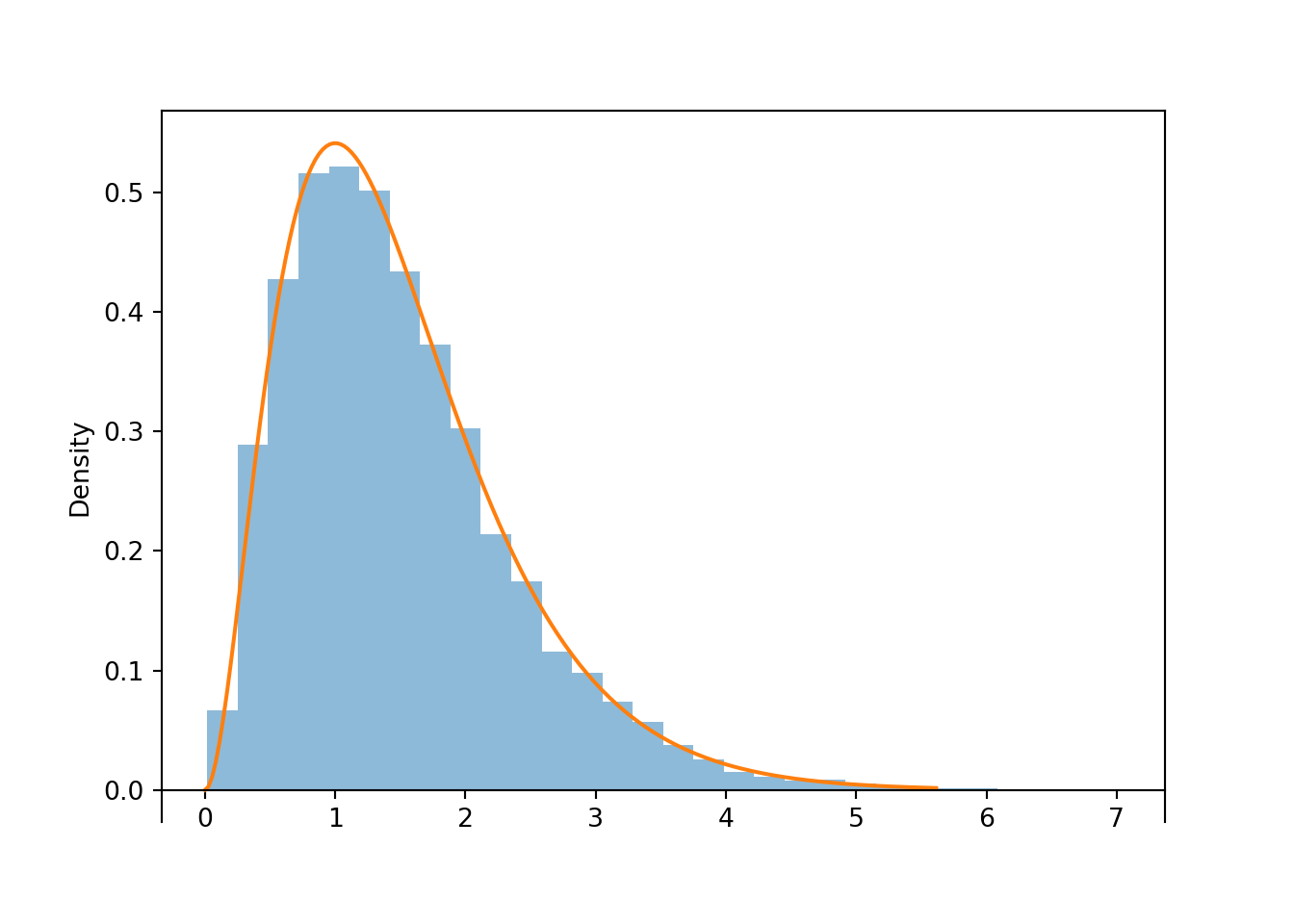
T.sim(10000).plot()
Gamma(shape = 3, rate = 2).plot()<symbulate.distributions.Gamma object at 0x000002292FAC1F50>plt.show();