2.12 Formal navigation for short crossings

We now know how to determine which way a tidal stream will be running and how to estimate how quickly it will be running. Together with the pilotage techniques covered elsewhere, this is generally sufficient knowledge to kayak in tidal waters. However, if more ambitious crossings are being contemplated, it is helpful to be able to carry out formal navigation to determine what course to steer and how long the crossing will take.

Imagine a paddler capable of 3 knots paddling speed attempts to paddle across a 1-mile wide tidal strait running at 1.5 knots to the south. If the paddler takes a bearing to a point on the far side and paddles on this bearing, they will not get to where they expect. During the 20-minute crossing, they will drift 0.5 miles southward.

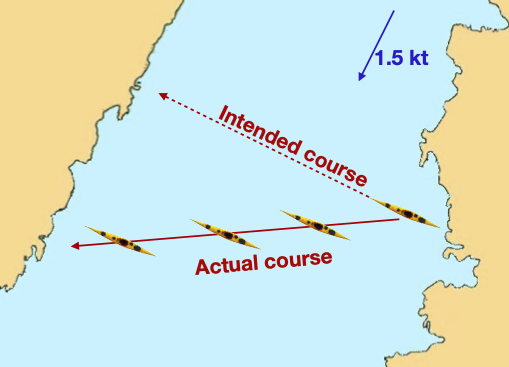
Kayak drifting down tide of the direction in which it is pointed

The solution is to angle the boat up tide enough to cancel out the southerly drift. It’s the same principle as a ferry glide on a river, just over a longer distance.

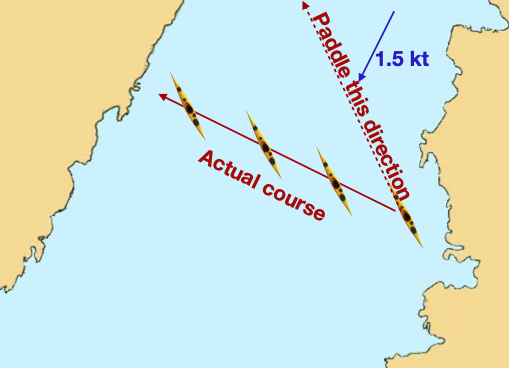
Ferry glide across a tidal strait to avoid drifting down tide

It’s clear that we will need to alter the course that we steer in tidal waters. The question is how much, and how long will a crossing take given the influence of the tide?

For the mathematically minded, this is simply a problem in vector addition to balance the effects of the tide with the paddling speed. For the rest of us, here’s a simple explanation followed by an example.

Let’s begin by considering a simpler problem. If we’re trying to paddle directly against the tide up the strait, what will happen? We’re paddling at 3 knots against a 1.5 knot tide. Most people will immediately work out that we’ll travel at 1.5 knots up tide and cover 1.5 nautical miles in an hour. But let’s take a more careful approach.

The trick we’re going to use is to avoid the complexity of the tidal flow and the paddling both happening at the same time, but instead pretending that they happen one after another. It’s as if we were playing a board game against the tide - the tide gets to make it’s move, then we get to make ours. So imagine that at 09:00, rather than paddle against the tide, we simply drift for an hour - let the tide make its move. We’d drift 1.5 knots down tide, as shown by the blue arrow in the diagram below:

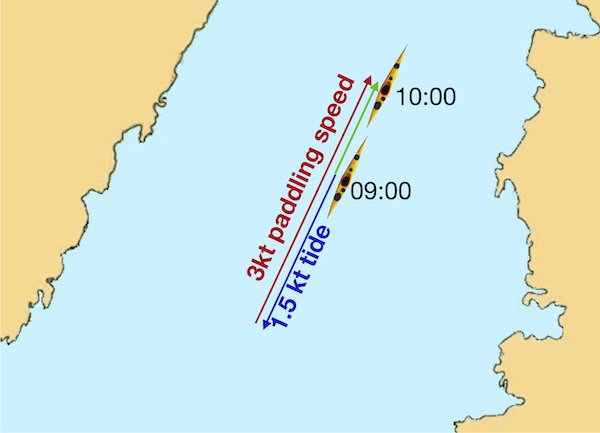
We then make our ‘move’ and paddle up tide for an hour at 3 knots, as shown by the red arrow. We’d end up at the place indicated by the second boat at 10:00. In reality, of course, the paddling and the tidal flow happen at the same time, and we follow the green arrow, but assuming one thing happens at a time allows us to draw out what occurs carefully.

Let’s try this again when we’re paddling across the strait. Once again, if we do nothing for an hour, the tide will push us 1.5 nautical miles down the strait (blue arrow):

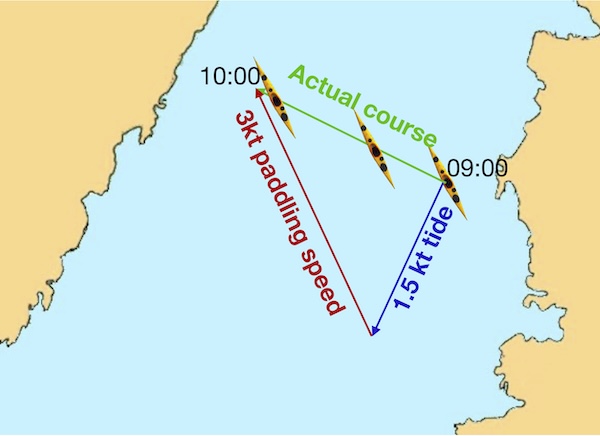
But this time we paddle at 3 knots not up the strait, but in a north-westerly direction (red arrow), ending up at the position of the second boat drawn at 10:00. And of course, in reality, we’ve carried out a ferry-glide along the green arrow.

In this example, we’ve probably ended up where we want to be by chance. But how might we use this approach to decide what direction to paddle in?

Let’s draw out the blue arrow to show what the tide does once more, and add a line to indicate what direction we actually want to travel in:

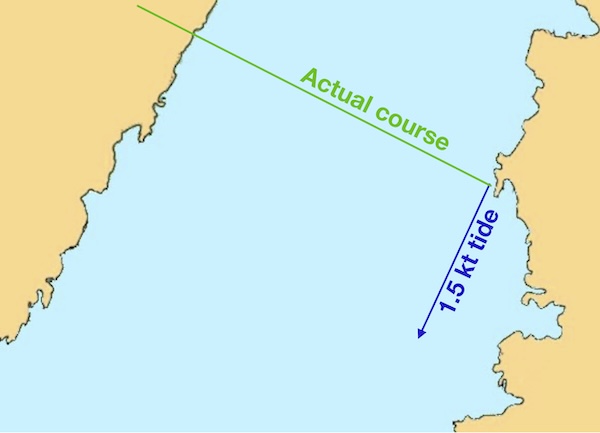
Now, imagining that the tide and our paddling occur one after the other, what are the options for our ‘move’ if we’re going to paddle at 3 knots and cover 3 nautical miles? We can choose to cover those 3 miles in any direction from our position at the end of the blue arrow:

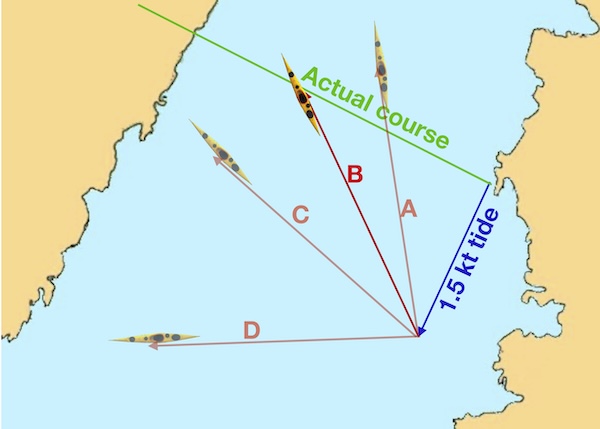
If we paddle west (D), we’ll end up way south of where we want to be. Paddling almost north (A) has us ending up too far north and up-tide. C is better, but still off our intended course. Clearly, direction B is ideal. All we’ve had to do is make sure the tip of the red arrow, which is 3 miles long to the chart scale, sits on the green line. Notice that the place we get to after an hour is still short of our destination on the far shore. That’s fine - as long as the tidal stream stays consistent, we can keep paddling in the same direction and we’ll arrive in a little over an hour.

The tips of all the red arrows that indicate our possible courses lie, of course, on a circle centered at the end of the blue arrow:

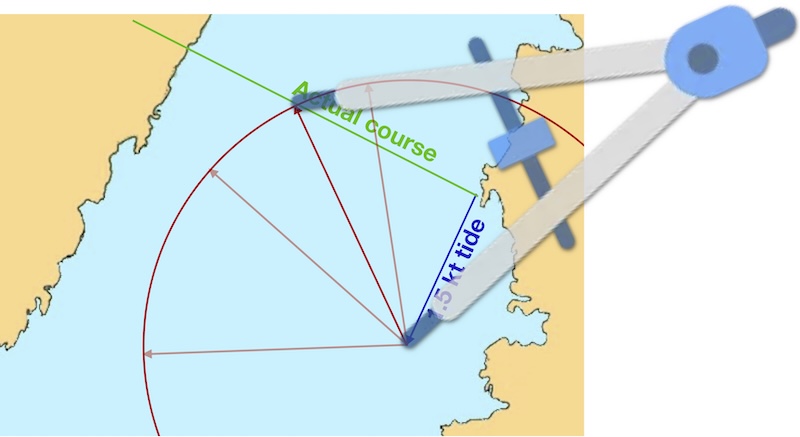
Where the circle crosses the green line is the point we want to draw our red paddling direction line to. So, we can use a pair of compasses set to 3 miles to find where this point is.

Let’s see how this works in a real example.

Estimate course to steer and time taken to cross Bardsey sound from Pen y Cil to the NE tip of Bardsey Island when a 2 knot tide is flowing NW. Your group is capable of paddling at 3 knots in still water.

Crossing Bardsey Sound - visiting the island by sea kayak makes for a fantastic day out, but requires crossing an extremely strong tidal stream. Formal planning of the crossing is advisable.

First draw a line from start point to the destination and well beyond – the green line.

Then draw a line that represents the tidal flow in one hour. In this case, we are told the flow is 2 knots, so a 2-mile long line is needed. Recall that we can use the latitude scale to measure this. We assume that the tide flows in the direction indicated by the arrow on the chart. The blue line is 2 miles long and parallel to the arrow.

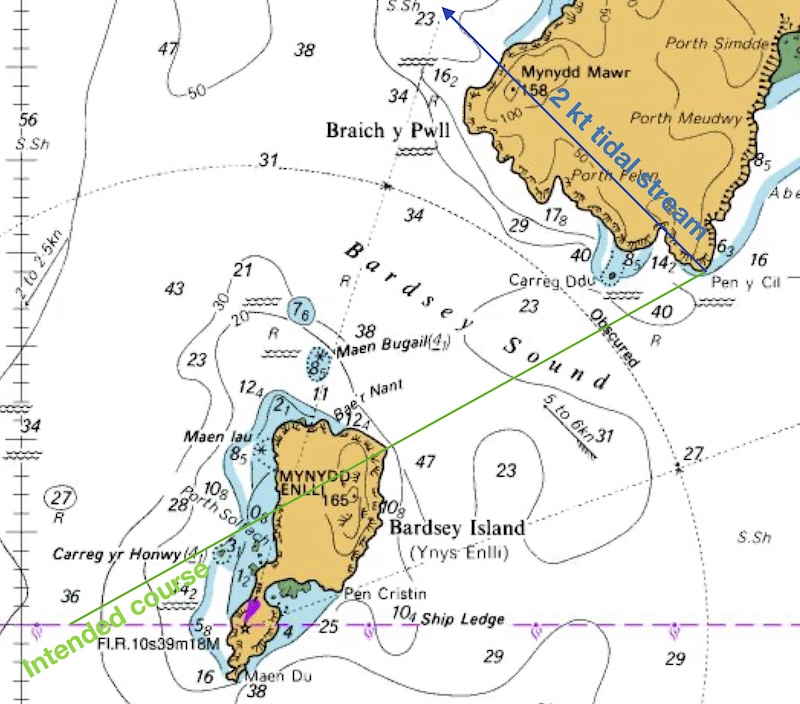
We then set our compass to the distance we intend to paddle in 1 hour - i.e. 3 nautical miles. We draw a circle (or part of a circle), centered on the end of the blue tidal stream arrow to indicate all the places that we could end up at the end of the hour:

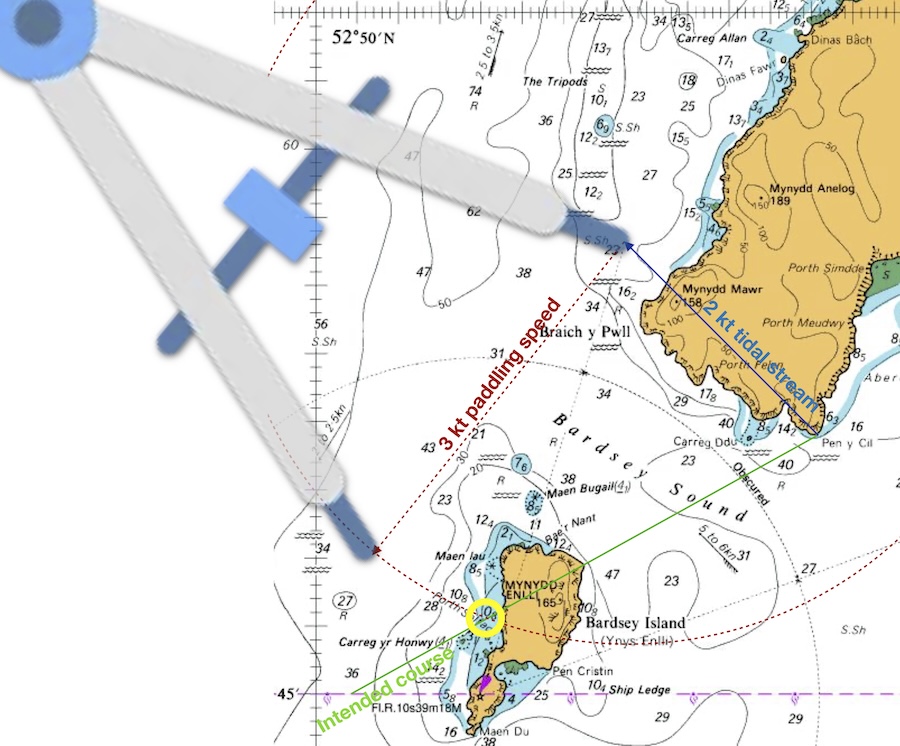
There’s a place where this circle of possibilities crosses our intended course line - indicated with a yellow circle. This is where we should draw our 3 mile paddling arrow to:

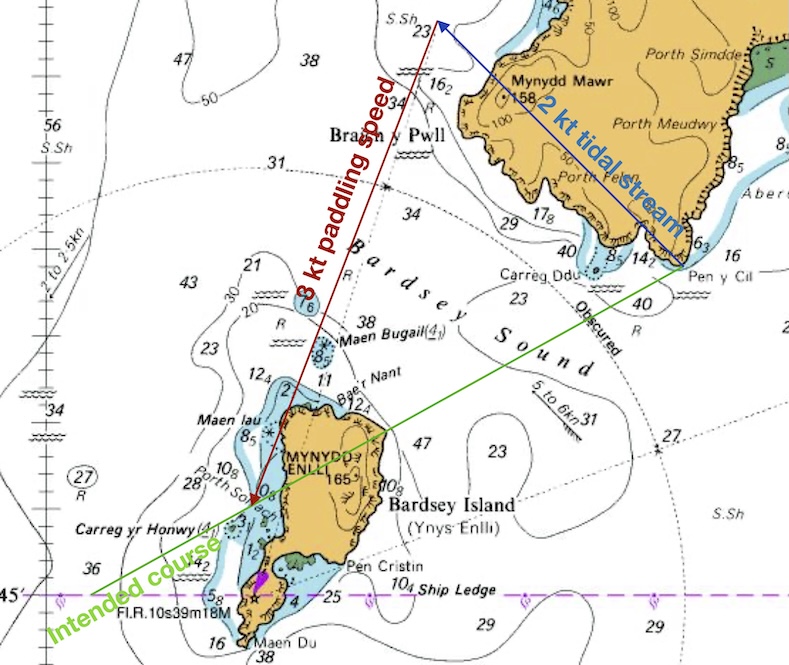
Chart of Bardsey sound marked up with vectors for a crossing

The red line on the chart now indicates the direction that you should point the boat for a successful crossing. We can measure the angle of this line from north - it’s 200˚. This is the course to steer during the crossing. If we paddle from Pen y Cil at 200˚ at 3 knots, we expect to follow the green intended course line… and hence get to Bardsey successfully.

The distance along the green line from the blue line to the red line represents the distance that you would travel if you paddled across this tide for 1 hour – in this case 2.7 miles. It is clear here that it’s going to take less than one hour to get to Bardsey. The distance to Bardsey along the green line is 2 miles. So we expect the crossing to take 60 x 2/2.7 = 45 minutes.

The error often made in this process is drawing the paddling speed (red) line directly to the destination point. Instead, it must be of the correct length to represent 1 hour’s paddling distance and this will determine where it intersects the intended course (green) line.

The method shown here assumes that the tidal stream is constant through the period of the crossing. This is a reasonable assumption for crossings less than one hour. For longer crossings, we must consider the effect of tidal streams that very in strength and direction. These techniques are beyond the scope of this course.