11 Regression I
library(rio)
anes <- import("https://github.com/marctrussler/IIS-Data/raw/main/ANESFinalProjectData.csv")When looking at the relationship between two variables in this class we have leaned a great deal on correlation. For two variables correlation will give us the strength of the relationship expressed between -1 and 1.
For example, we can use the ANES to determine the relationship between age and the feeling towards the BLM movement:
library(rio)
anes <- import("https://github.com/marctrussler/IIS-Data/raw/main/ANESFinalProjectData.csv")
#Some recoding:
summary(anes$V201507x)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> -9.00 35.00 51.00 49.04 65.00 80.00
anes$age <- anes$V201507x
anes$age[anes$age<0] <- NA
summary(anes$age)
#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 18.00 37.00 52.00 51.59 66.00 80.00 348
summary(anes$V202174)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> -9.00 0.00 50.00 47.04 85.00 999.00
anes$blm.therm <- anes$V202174
anes$blm.therm[anes$blm.therm<0 | anes$blm.therm>100] <- NA
summary(anes$blm.therm)
#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0 15.0 60.0 53.3 85.0 100.0 936
#Correlation
cor(anes$age, anes$blm.therm, use="pairwise.complete")
#> [1] -0.1307171We can see that there is a moderately negative correlation between these two things: as age goes up feeling towards BLM goes down.
There are a couple of key draw-backs to correlation that are going to push us towards linear regression as a more helpful tool.
First, the thing that is most helpful about it – that it’s unitless – is also a bit of a drawback. While “correlation” is definitely a word regular people understand, it’s pretty impossible to form a real human sentence about a correlation. Considering what we found above: that the correlation between age and feelings towards BLM is negative. That sentence is fine to say but really lacks nuance. How much does BLM change as you get older? What can I practically say about moving from being a Gen-Z to Millennial to Boomer?
The second thing is that our ability to consider a third variable is very blunt. For example if we wanted to consider the role of race, we might split the sample into white and black (leaving other races as NA) and look at the correlation in each group:
anes$white.v.black[anes$V201549x==1] <- 1
anes$white.v.black[anes$V201549x==2] <- 0
table(anes$white.v.black)
#>
#> 0 1
#> 726 5963
cor(anes$age[anes$white.v.black==1], anes$blm.therm[anes$white.v.black==1], use="pairwise.complete")
#> [1] -0.103089
cor(anes$age[anes$white.v.black==0], anes$blm.therm[anes$white.v.black==0], use="pairwise.complete")
#> [1] 0.05225065We see here that the correlation is very different in these two groups. But what if we wanted to look at this across all the racial groups? Things would get unwieldy if we had to make 6 or 7 correlations. What if the third variable is continuous, like income? What if, in addition to race, we wanted to see how education affected the relationship between age and feelings towards blm? Correlation doesn’t really allow us to do any of those things.
A third problem is that correlation is a really simplistic way to describe a relationship, such that the same correlation coefficient can describe wildly different relationships. So much so that it’s hard to actually guess correlation coefficients.
We will solve all of those problems with regression.
To understand regression let’s continue to look at the relationship between the age and the feeling thermometer for Black Lives Matter:
plot(anes$age, anes$blm.therm, xlab="Age", ylab="BLM FT")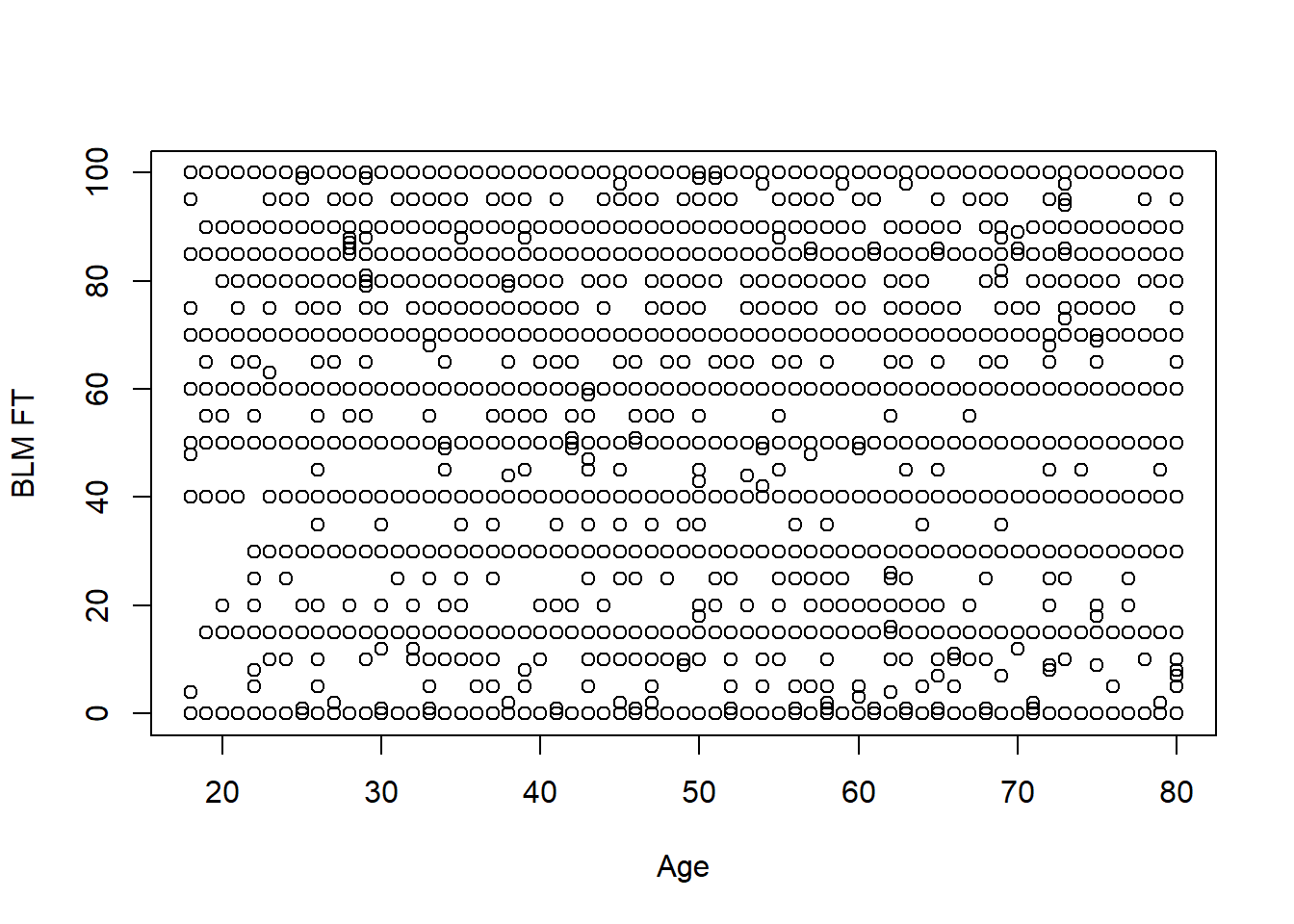
Ah! This looks terrible! It happens. The problem here is that a lot of people give similar answers on the FT so we have points stacked on top of each other. But still we can also conclude this is not a deterministic relationship: there are lots of 20 year olds that have negative views of BLM and lots of 80 year olds with positive views of BLM. The goal of linear regression is to (obviously) draw a line through these data that summarizes what is going on. How might we do that?
Well one way to do this (this is not the right way) would be to look at each value of age and find the average value of the blm feeling thermometer:
ages <- sort(unique(anes$age))
mean.blm <- rep(NA, length(ages))
for(i in 1:length(ages)){
mean.blm[i] <- mean(anes$blm.therm[anes$age==ages[i]],na.rm=T)
}
plot(anes$age, anes$blm.therm, xlab="Age", ylab="BLM FT")
points(ages, mean.blm, type="b", col="firebrick", pch=16, lwd=2)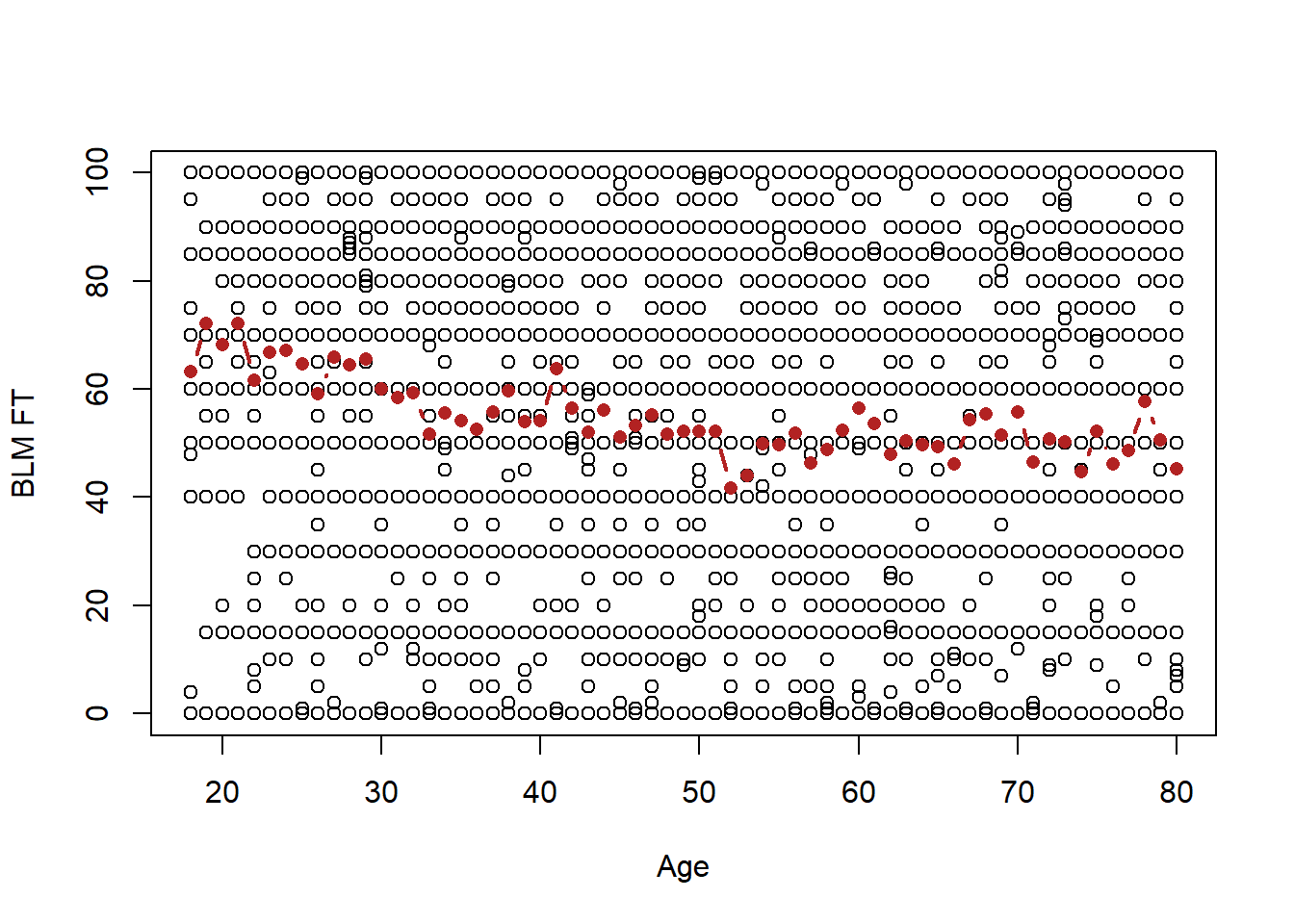
So this progression of averages generally slopes downwards, as we would anticipate given the correlation. But, this doesn’t really allow us to give a answer about the relationship between age and feelings towards BLM.
More problematically, let’s not forget the overall goal of data science, which is to form inferences about the population, not just to describe the data that we have. Here we are very religiously following the data from age to age. We would absolutely not claim that each and every up and down of this line is something that is present in the population. For example we are not going to conclude that feelings about BLM generally decline to age 40, but then from age 40 to 41 they go up a bunch, and then they go back down. In other words we are “over-fitting” the data that we have here, taking seriously every quirk in the random sample to be true.
Instead, we want to work to summarize this data in a more averaged way, we want to smooth out the random variations caused by sampling to produce a single line which gives us the overall picture of what is happening between these two variables. The way we are going to do that is through regression.
The answer to “how does regression choose a line” lies in the full name of regression which is Ordinary Least Squares or OLS.
Here is a simple dataset with some fake data I’m going to make up that will allow us to see this “least squares” process.
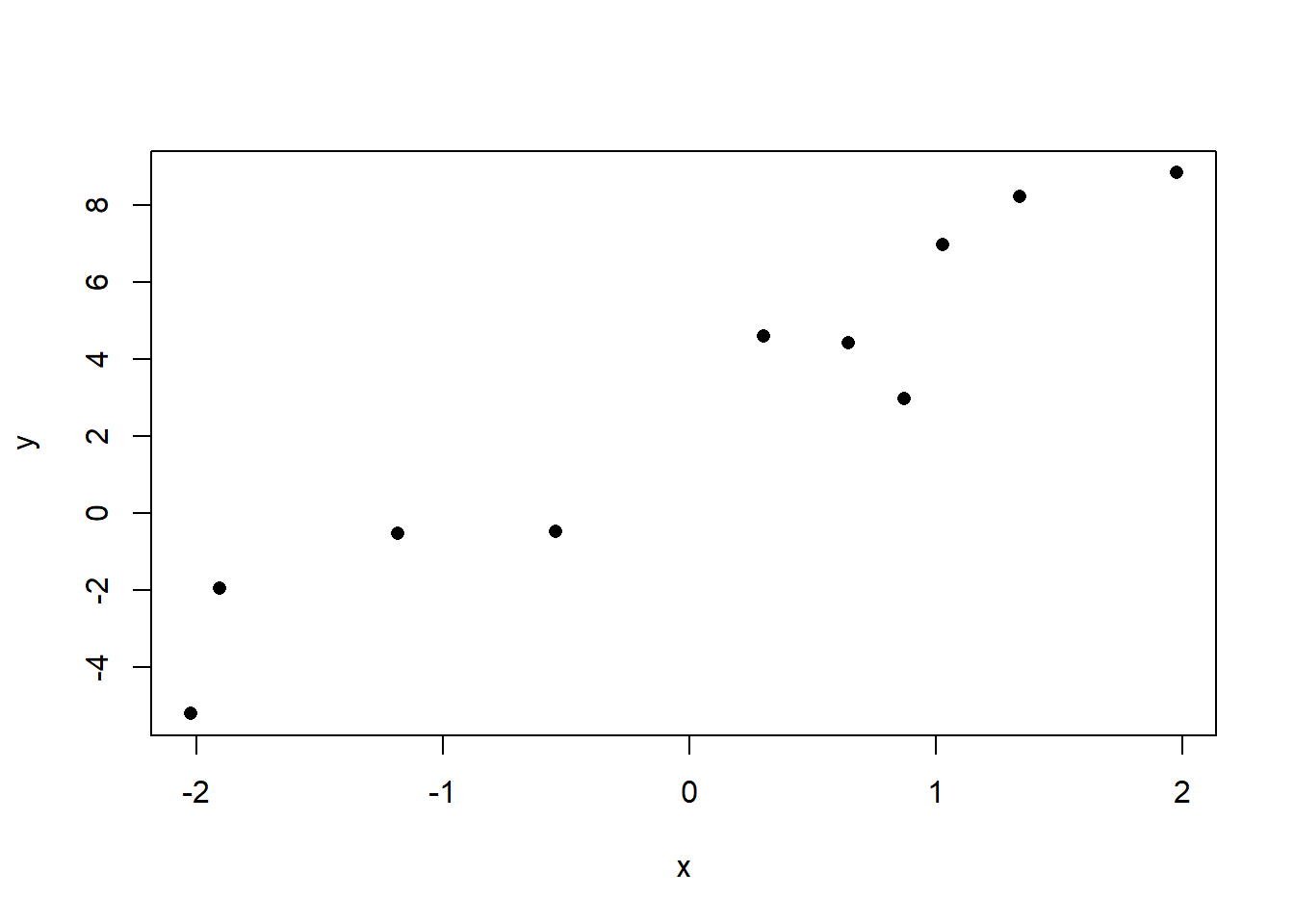
We can see that this is a positive relationship. We can get the regression summary of this relationship using the lm() command. Into that command we put the outcome/dependent variable on the left side, and the input/independent variable on the right side. The only requirement for this to work is that both of these variables have to be numbers
lm(y ~ x)
#>
#> Call:
#> lm(formula = y ~ x)
#>
#> Coefficients:
#> (Intercept) x
#> 2.616 3.225The output of the regression is the description of a line. To draw a line we need an intercept and a slope, and that’s exactly what the lm command provides.
Let’s start with the intercept. This is the value of the line when x is at 0. We can put that on the graph:
The regression line will cross the y-axis here:
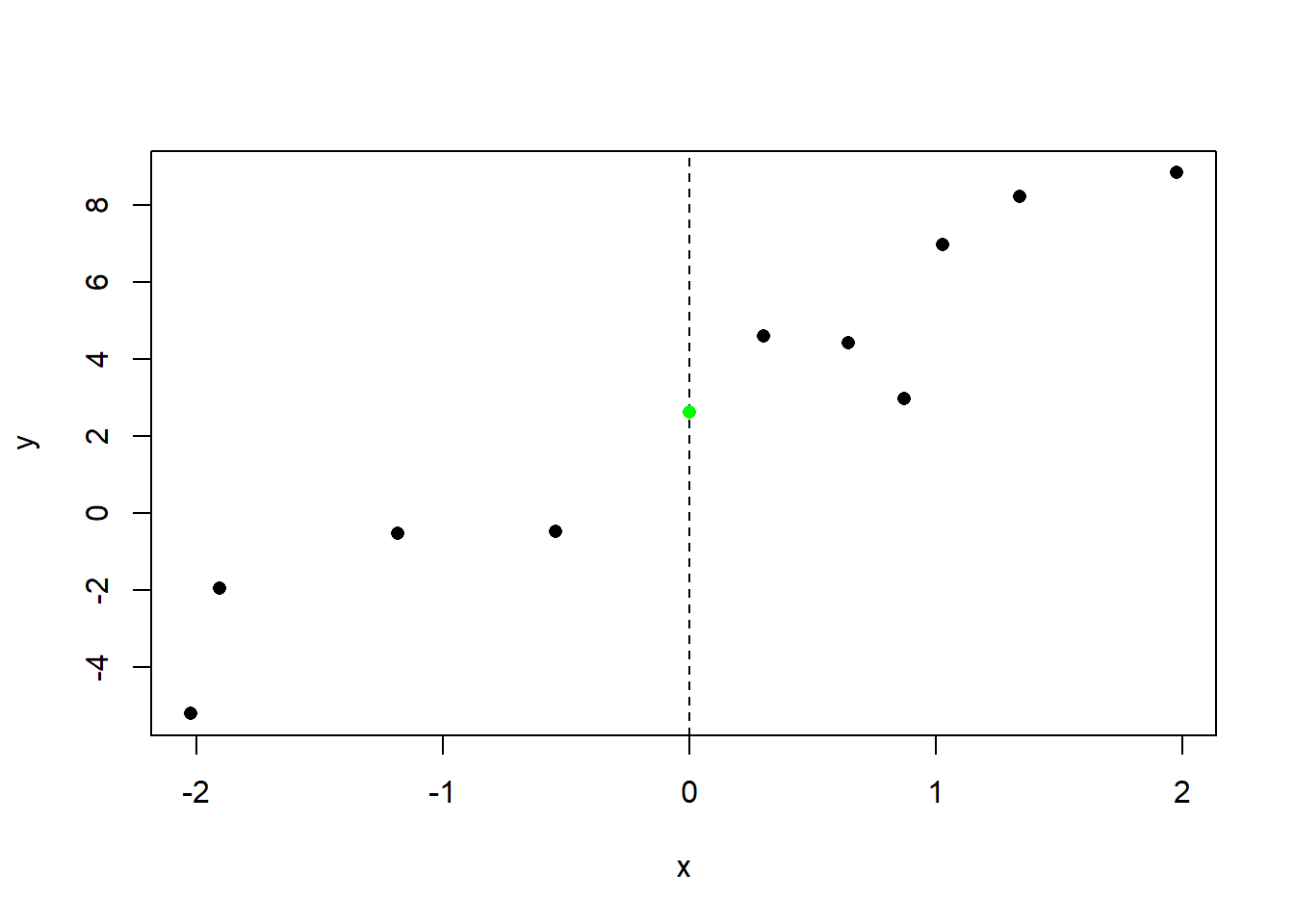
The slope of the regression line is 3.225. Slope is is simply “rise over run”: for every 1 unit increase in x, y increases by 3.225.
So, the at x=1 the line will take on a value that is 3.225 higher than when x=0:
plot(x,y, pch=16)
abline(v=0, lty=2)
points(0, 2.616, col="green", pch=16)
points(1, 2.626+3.225, col="firebrick", pch=16)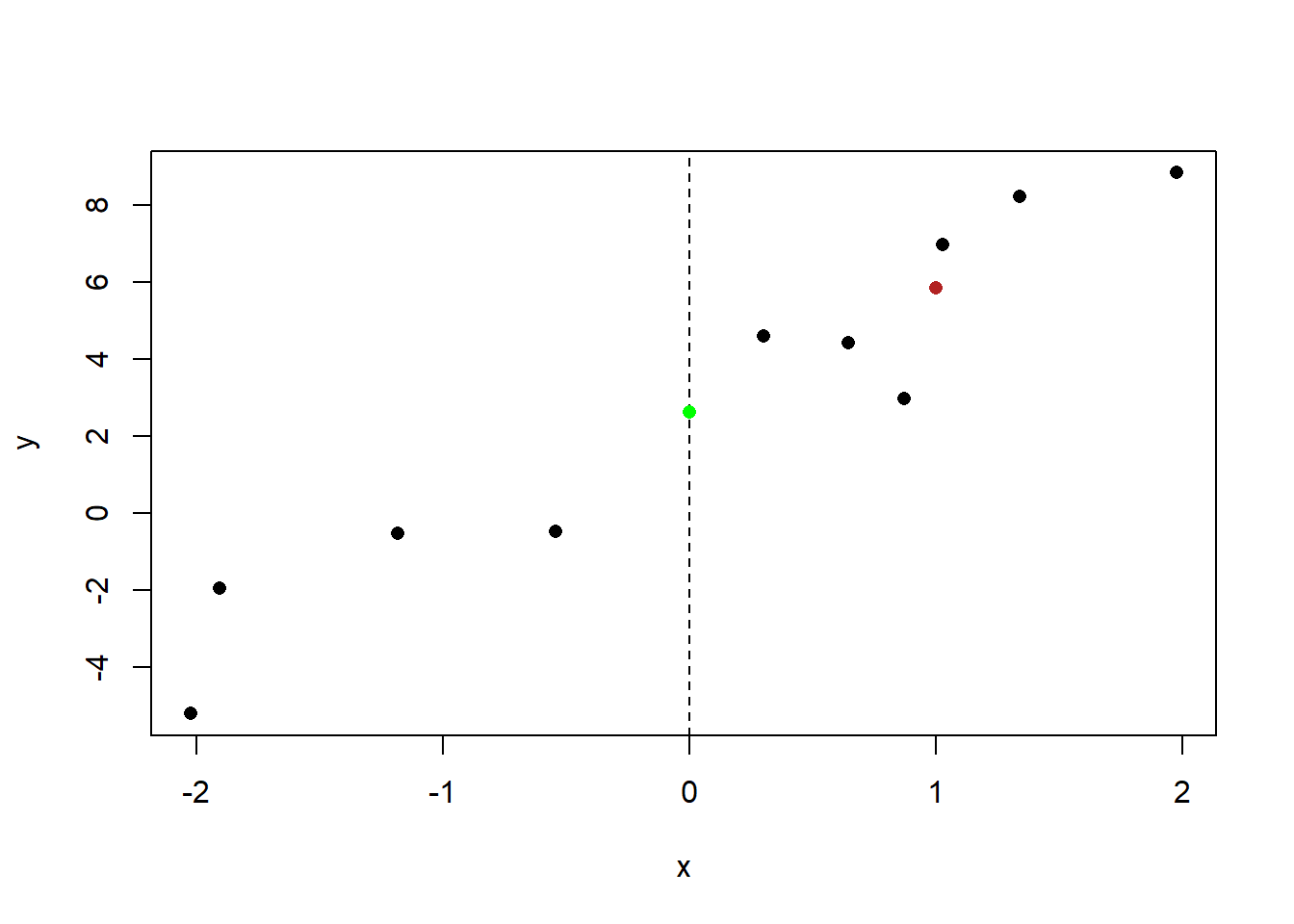
When X=2 the line will take on a value 3.225 higher than that:
plot(x,y, pch=16)
abline(v=0, lty=2)
points(0, 2.616, col="green", pch=16)
points(1, 2.626+3.225, col="firebrick", pch=16)
points(2, 2.626+3.225+3.225, col="firebrick", pch=16)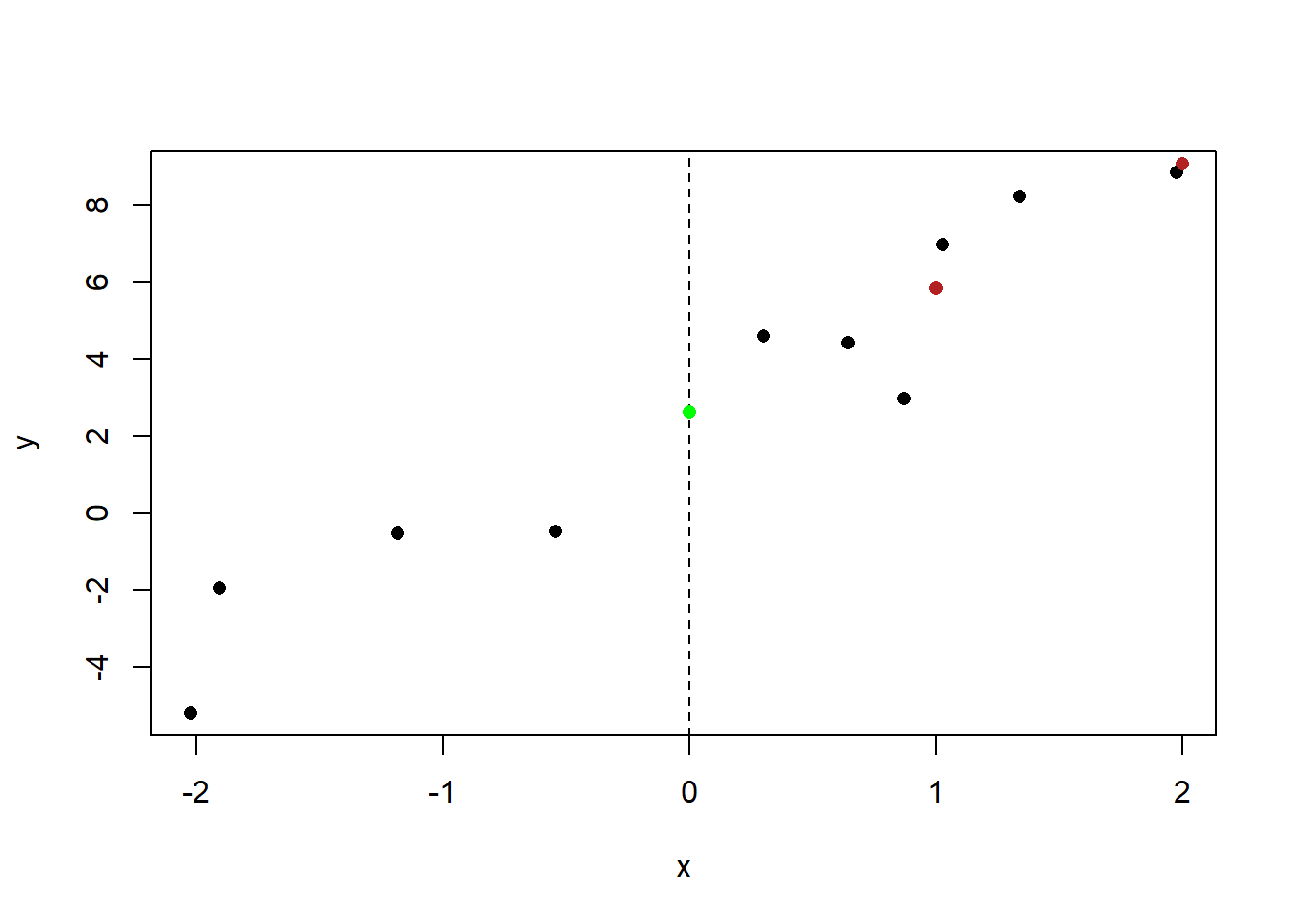
When x=-1 the value of the line will be 3.225 less than it is when x=0:
plot(x,y, pch=16)
abline(v=0, lty=2)
points(-1, 2.616-3.225, col="firebrick", pch=16)
points(0, 2.616, col="green", pch=16)
points(1, 2.626+3.225, col="firebrick", pch=16)
points(2, 2.626+3.225+3.225, col="firebrick", pch=16)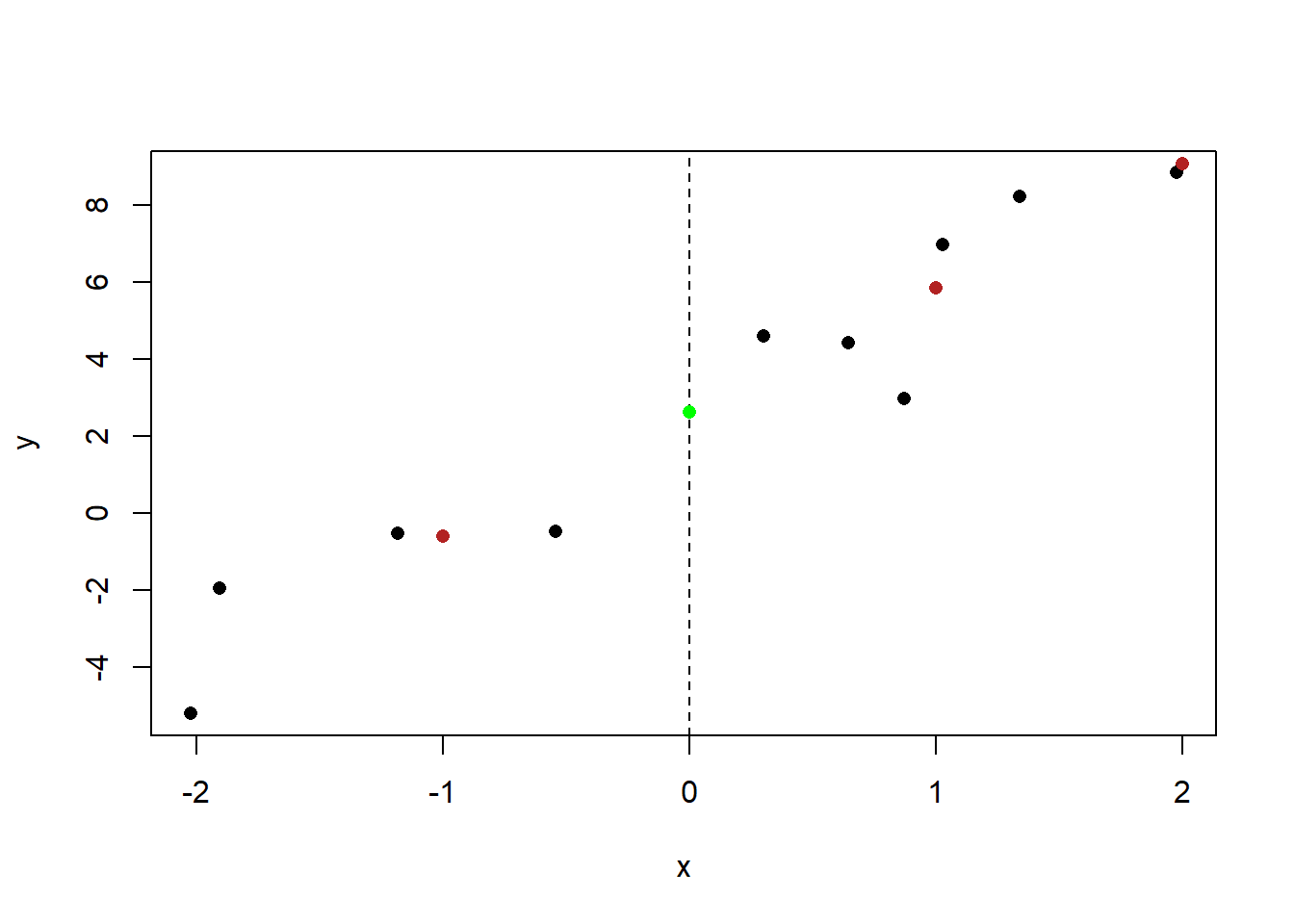
These values also scale down, so when x=-1.5, the value of the line will be \(3.225/2=1.6125\) less than it is at -1.
plot(x,y, pch=16)
abline(v=0, lty=2)
points(-1.5, 2.616-3.225-1.6125, col="firebrick", pch=16)
points(-1, 2.616-3.225, col="firebrick", pch=16)
points(0, 2.616, col="green", pch=16)
points(1, 2.626+3.225, col="firebrick", pch=16)
points(2, 2.626+3.225+3.225, col="firebrick", pch=16)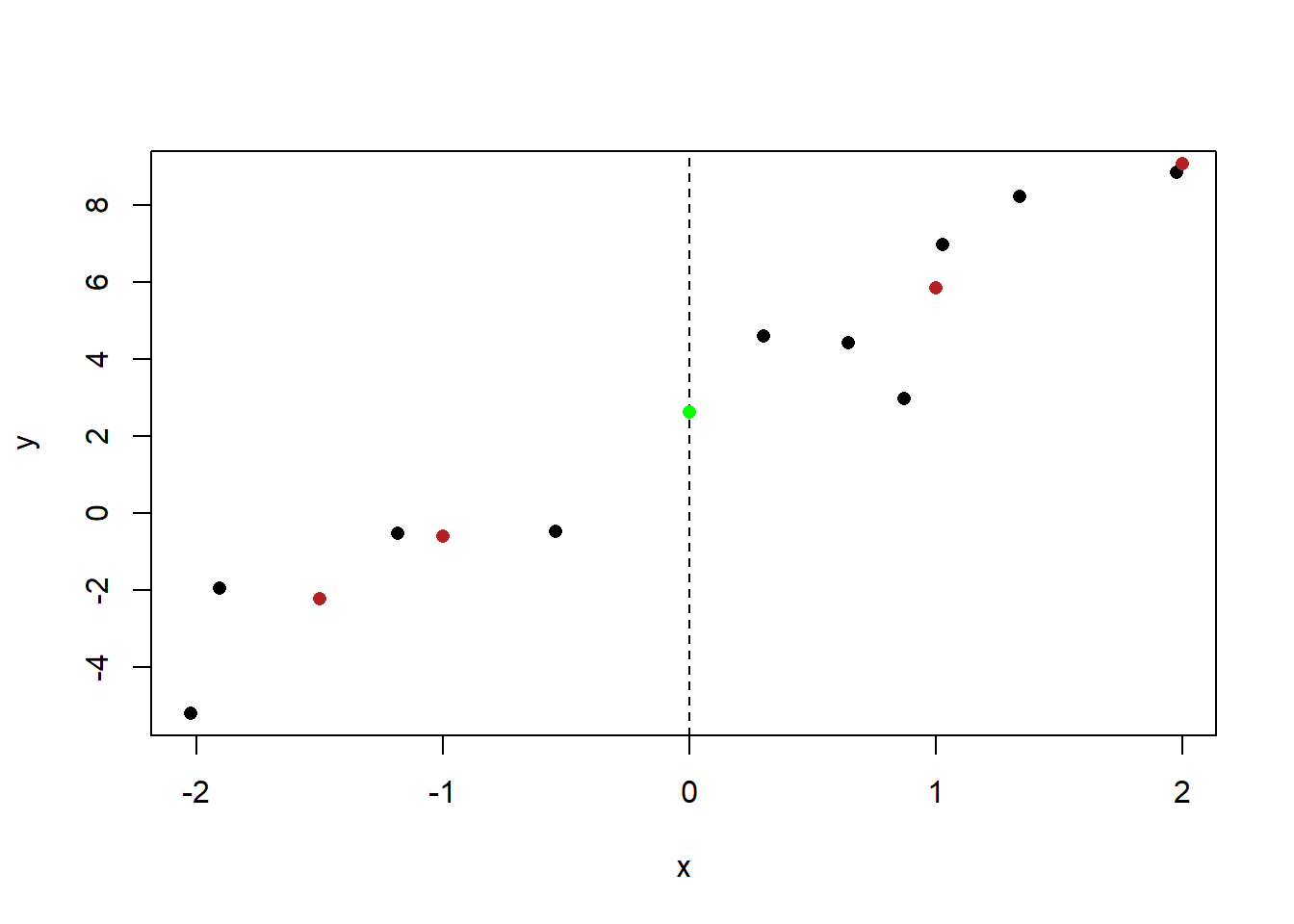
Our formula for drawing the line is therefore:
\[ y.pos.of.line = intercept + slope*value.of.x \]
This is exactly what you learned in middle/high school, that a line is defined by \(y=mx+b\), where \(b\) is the intercept and \(m\) is the slope.
In the regression world we restate things slightly to:
\[ \hat{y} = \alpha + \beta x \]
The location of our regression line \(\hat{y}\) is defined by the intercept \(\alpha\) plus the slope \(\beta\) times any value of \(x\).
So using this equation we can calculate the line any point in x:
x.pred <- seq(-2,2,.001)
line <- 2.616 +3.225*x.pred
plot(x,y, pch=16)
points(-1.5, 2.616-3.225-1.6125, col="firebrick", pch=16)
points(-1, 2.616-3.225, col="firebrick", pch=16)
points(0, 2.616, col="green", pch=16)
points(1, 2.626+3.225, col="firebrick", pch=16)
points(2, 2.626+3.225+3.225, col="firebrick", pch=16)
points(x.pred, line, col="dodgerblue", type="l")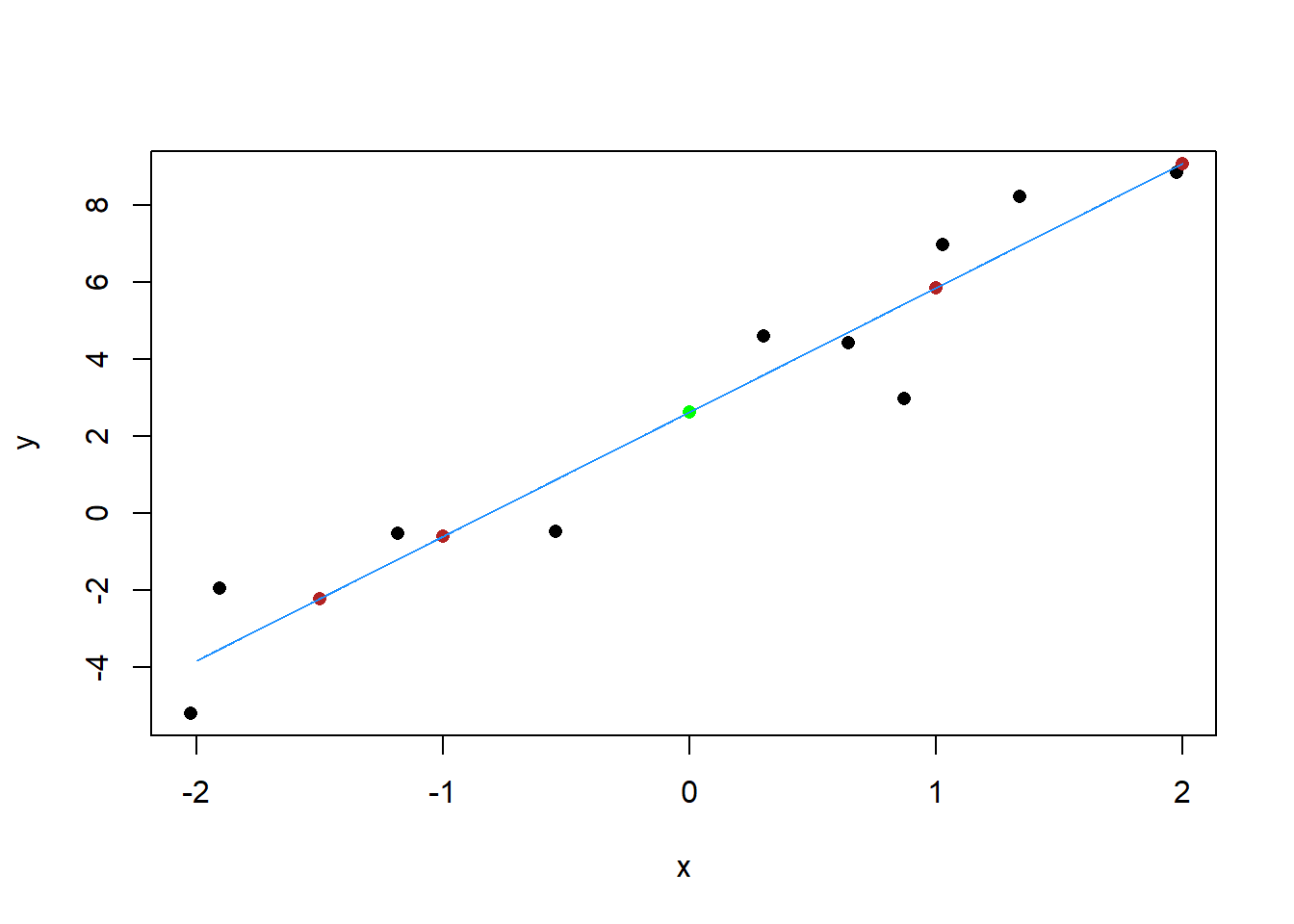
But why this line? Why is this the line that best summarizes this relationship.
As I said above, the clue is in the name “Least Squares”.
Imagine a vertical line running from each point in that graph to the line, like this:
x.resid <- 2.616 +3.225*x
x.pred <- seq(-2,2,.001)
line <- 2.616 +3.225*x.pred
plot(x,y, pch=16)
points(x.pred, line, col="dodgerblue", type="l")
segments(x,y, x, x.resid, col="firebrick", lty=2)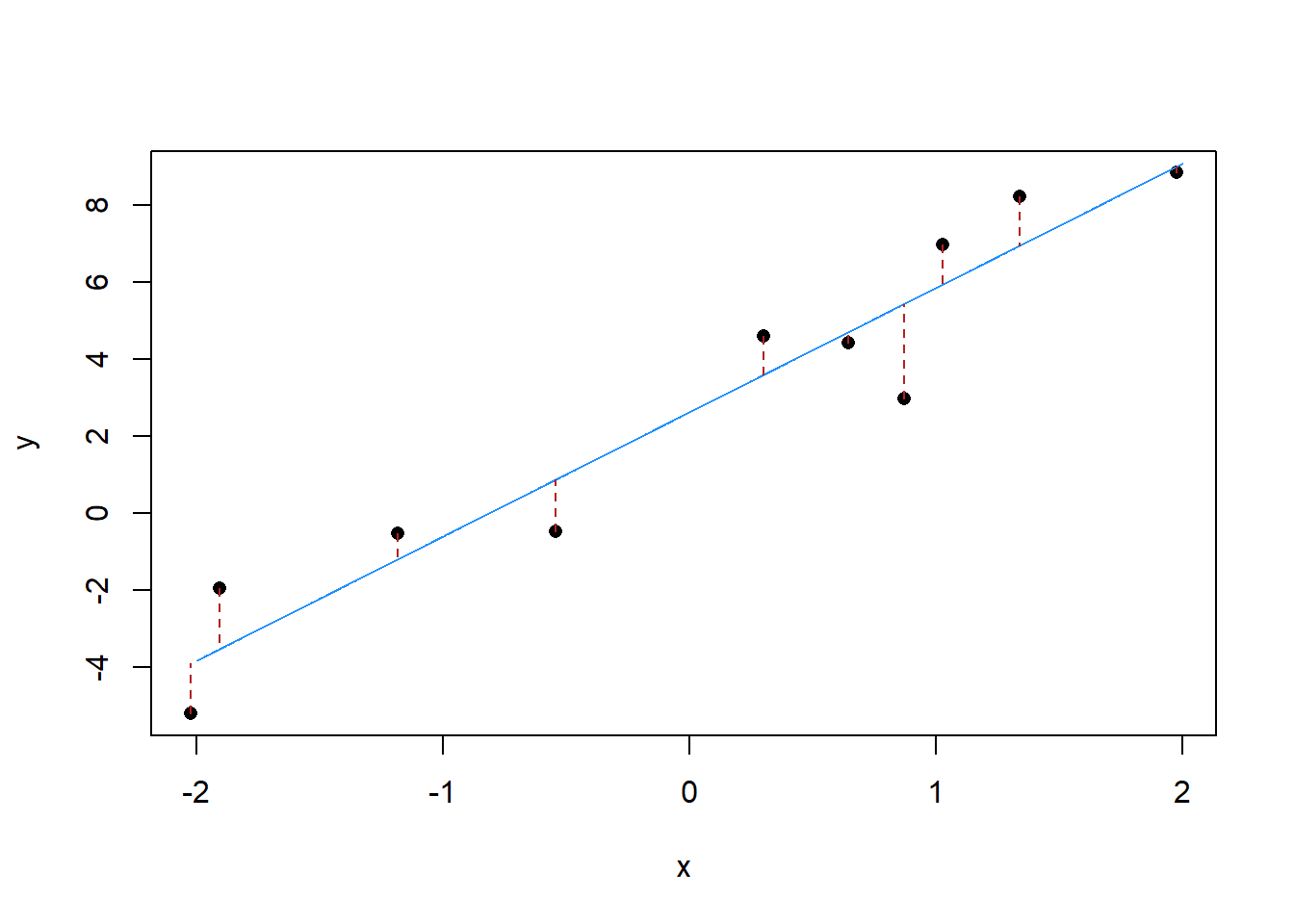
We call each of those distances a “residual”. What OLS does is choose a line that minimizes the sum of the squared residuals. The residuals have to be squared, otherwise the positive ones would just cancel out the negative ones. In other words: the blue line is the line that makes those red dotted lines as short as possible. This is why it is “least squares” regression.
Let’s go back to our real-world example to think about how this plays out:
plot(anes$age, anes$blm.therm, xlab="Age", ylab="BLM FT")
Here is what least-squares regression gives us:
lm(anes$blm.therm ~ anes$age)
#>
#> Call:
#> lm(formula = anes$blm.therm ~ anes$age)
#>
#> Coefficients:
#> (Intercept) anes$age
#> 67.55 -0.27Here \(\hat{\alpha} = 67.55\) and \(\hat{\beta}=-.27\). What those two pieces of information allow us to do is to draw a line through these data. Again, we can evaluate this equation for all values of \(x\), and for each value get a value for \(\hat{y}\), which is the line at that point.
So mechanically
age <- seq(18,80,1)
regression.line <- 67.55 - .27*age
plot(anes$age, anes$blm.therm, xlab="Age", ylab="BLM FT")
points(age, regression.line, type="l", col="firebrick", pch=16, lwd=2)
This is the line that best minimizes the sum of squared residuals for these data.
Now that we have that line, how do we interpret what we have found?
plot(anes$age, anes$blm.therm, xlab="Age", ylab="BLM FT")
#We have been drawing in the line by hand, but we can very easily have R draw it:
abline(lm(anes$blm.therm ~ anes$age), col="firebrick", lwd=2)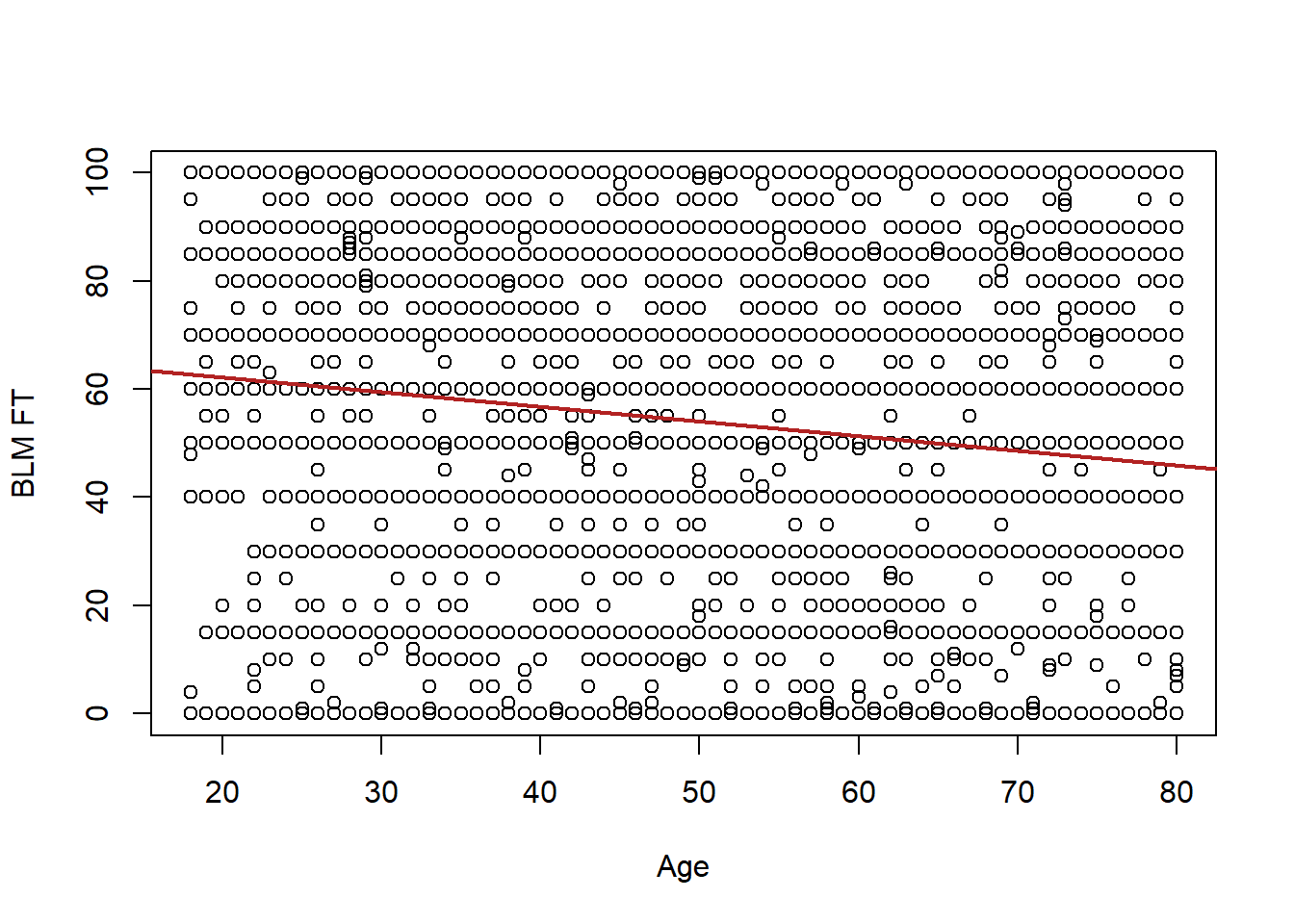
If we save the output of the regression, and use the summary command, we get all sorts of information:
m <- lm(anes$blm.therm ~ anes$age)
#Can also do
m <- lm(blm.therm ~ age, data=anes)
summary(m)
#>
#> Call:
#> lm(formula = blm.therm ~ age, data = anes)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -62.690 -33.381 4.049 32.202 54.049
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 67.54966 1.32870 50.84 <2e-16 ***
#> age -0.26998 0.02437 -11.08 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 35.12 on 7062 degrees of freedom
#> (1216 observations deleted due to missingness)
#> Multiple R-squared: 0.01709, Adjusted R-squared: 0.01695
#> F-statistic: 122.8 on 1 and 7062 DF, p-value: < 2.2e-16Let’s use what we know so far to investigate what it is we are seeing here.
At the top we get information on the distribution of the residuals. This isn’t going to be important for this class.
The two numbers for alpha and beta are present in the “Estimate” column. Again these are the two values that define the line, and are generated such that they create a line that minimizes the sum of the squared residuals.
The remaining columns give a hypothesis test. How could we determine which hypothesis is being tested? Well a t value is “how many standard errors the estimate is from the null”. So:
\[ 50.84 = \frac{67.55 -\beta_{H0}}{1.33}\\ 67.6172 = 67.55 - \beta_{H0}\\ \beta_{H0} \approx 0 \]
So we are getting hypothesis tests that these coefficients are equal to 0, or not.
This makes a lot of sense for the regression coefficient on age. We care a lot about whether a coefficient is 0, or not, because 0 is a flat line! This has a very high t-value and a very low p-score, so we would reject the null hypothesis that the slope in the population is 0.
Do we care if alpha is 0 or not? Well… in real terms what is alpha?
It is the value of \(\hat{y}\) where the line crosses the y axis.
So it is the predicted value of y when x is 0. What does an x of 0 mean here? A newborn? This is how newborns feel about BLM? Do we care about that at all?
No! Of course not. Having an \(\alpha\) is a pre-requisite to drawing a line. Like mechanically, the two ingredients to a line are its intercept and its slope. So we need to define this value, but that does not mean that it is a meaningful number.
What’s more, the hypothesis test is definitely not a meaningful hypothesis test. Do we care if the predicted level of support of BLM of newborns is 0, or not? No! Definitely not. I actually don’t even like that they give you a statistical test for this value!
Let’s move on to beta, which is the estimate for age. We have seen that it is -.27, what does that mean?
You have seen a slope before being defined as rise over run, and this is just what this number is. For every 1 unit increase in X, Y goes down by .27.
When we say 1 unit in a regression, we mean 1 unit in our number system. As in the difference between 1 and 2, and 100 and 101, and 567 and 568. This will be true for absolutely every OLS regression we ever run and you should really internalize it right now. The beta coefficient is how a 1 unit change in x relates to a \(\beta\) change in y.
The best thing about this is how it allows us to form normal human sentences about this relationship. As a person gets 1 year older their feelings about BLM drop .27 points, on average.
Note also that we can scale this up or down: If a one unit change in x is -.27, what is a 10 unit change in x? 2.7! So we might also say that as a person gets 10 years older, their feelings about BLM drop 2.7 points on average. Also good!
What this means, however, is that if we re-scale our x variable then \(\beta\) will change, even if the underlying relationship does not.
For example what if we had age in months?
anes$age.months <- anes$age*12
plot(anes$age.months, anes$blm.therm, xlab="Age (months)", ylab="BLM FT")
abline(lm(anes$blm.therm ~ anes$age.months), col="firebrick", lwd=2)
m2 <- lm(blm.therm ~ age.months, data=anes)
summary(m2)
#>
#> Call:
#> lm(formula = blm.therm ~ age.months, data = anes)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -62.690 -33.381 4.049 32.202 54.049
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 67.549664 1.328699 50.84 <2e-16 ***
#> age.months -0.022498 0.002031 -11.08 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 35.12 on 7062 degrees of freedom
#> (1216 observations deleted due to missingness)
#> Multiple R-squared: 0.01709, Adjusted R-squared: 0.01695
#> F-statistic: 122.8 on 1 and 7062 DF, p-value: < 2.2e-16Visually we can see that the relationship looks the same, we have just re-scaled the x-axis of the graph. Age explains no more or less than it did when it was measured in years.
Looking at the coefficient on age.months we see that it is smaller than it was before. Because we know that this is how a 1-unit change in x relates to a change in y, we know that this does not mean that age is “less important” in this second regression. Instead, we are now measuring the impact of a change in 1 month on BLM feelings instead of 1 year.
Indeed if we multiply that coefficient by 12:
m2$coefficients["age.months"]*12
#> age.months
#> -0.2699798We return the original coefficient.
How does this interpretation of the beta coefficient relate to other types of variables?
Let’s look at how being a liberal vs being a conservative or moderate influences your opinions of BLM:
attributes(anes$V201200)
#> NULL
anes$ideology <- anes$V201200
anes$ideology[anes$ideology %in% c(-9,-8,99)] <- NA
table(anes$ideology)
#>
#> 1 2 3 4 5 6 7
#> 369 1210 918 1818 821 1492 428
anes$liberal[anes$ideology<4] <- 1
anes$liberal[anes$ideology>=4] <- 0
table(anes$liberal, anes$ideology)
#>
#> 1 2 3 4 5 6 7
#> 0 0 0 0 1818 821 1492 428
#> 1 369 1210 918 0 0 0 0Now this scatterplot is not going to look great, because you can only take on two values for the x variable.
plot(anes$liberal, anes$blm.therm)
But all that regression requires is for your two variables to be numeric, and so nothing in the equations for alpha and beta are broken by this.
Let’s see what regression says:
m3 <- lm(blm.therm ~ liberal, data=anes)
summary(m3)
#>
#> Call:
#> lm(formula = blm.therm ~ liberal, data = anes)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -78.36 -23.00 2.00 21.64 62.00
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 37.9995 0.4676 81.26 <2e-16 ***
#> liberal 40.3579 0.7792 51.80 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 29.71 on 6306 degrees of freedom
#> (1972 observations deleted due to missingness)
#> Multiple R-squared: 0.2985, Adjusted R-squared: 0.2984
#> F-statistic: 2683 on 1 and 6306 DF, p-value: < 2.2e-16Here we have an intercept of 38.05, and a beta of 40.38.
Let’s start with the intercept, what does this intercept represent? Remember, the intercept is the average value of y when x=0, as shown mechanically by the regression equation.
This is the average value of the BLM thermometer among non-liberals. That is what it means to be 0 on this variable.
What does the slope on liberal mean? This is the effect of a 1 unit change in x on y, so moving one unit on y increases the average person’s blm thermometer by 40.38 points. Ok but what does this mean in real human terms? A one unit change in this variable indicates us moving from one group to another. We have specifically set up this variable in a way that works extremely well with regression, because changing “1-unit” brings us from one group to another. So the difference in blm feelings between liberals and non-liberals is 40.38 points.
What is the average level of feeling towards BLM among liberals?
We can answer this via the regression equation. Our predicted y is equal to
\[ \hat{y} = 38.05 + 40.38*Liberal_i \]
So we can turn liberal on and off to get that answer:
\[ \hat{y} = 38.05 + 40.38*1\\ \hat{y} = 78.43 \]
Let’s compare that to the t.test of the difference in means between these two groups on this variable, which we have already learned about:
t.test(anes$blm.therm ~ anes$liberal)
#>
#> Welch Two Sample t-test
#>
#> data: anes$blm.therm by anes$liberal
#> t = -58.117, df = 6187.8, p-value < 2.2e-16
#> alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
#> 95 percent confidence interval:
#> -41.71919 -38.99659
#> sample estimates:
#> mean in group 0 mean in group 1
#> 37.99950 78.35739The two means are 38.05 and 78.43. So OLS regression with a binary x variable exactly uncovers the means of the two groups, with beta representing the difference between those two means!
This is super helpful, and one of the reasons why I’ve made such a big deal about indicator variables throughout the semester. Indicator variables are great because they work extremely well with the math of OLS. OLS uncovers the effect of 1 unit shifts, and a 1 unit shift in an indicator indicates group membership.
As you would expect, OLS also works fine with a T F indicator variable which R treats as a 0s and 1s:
anes$liberal2[anes$ideology<4] <- T
anes$liberal2[anes$ideology>=4] <- F
m3b <- lm(blm.therm ~ liberal2, data=anes)
summary(m3b)
#>
#> Call:
#> lm(formula = blm.therm ~ liberal2, data = anes)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -78.36 -23.00 2.00 21.64 62.00
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 37.9995 0.4676 81.26 <2e-16 ***
#> liberal2TRUE 40.3579 0.7792 51.80 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 29.71 on 6306 degrees of freedom
#> (1972 observations deleted due to missingness)
#> Multiple R-squared: 0.2985, Adjusted R-squared: 0.2984
#> F-statistic: 2683 on 1 and 6306 DF, p-value: < 2.2e-16What about if we use the un-altered ideology variable as our independent variable? Remember that ideology is a 7-point scale where 1 is “very liberal” and 7 is “very conservative”.
table(anes$ideology)
#>
#> 1 2 3 4 5 6 7
#> 369 1210 918 1818 821 1492 428
plot(anes$ideology, anes$blm.therm)
m4 <- lm(blm.therm ~ ideology, data=anes)What does the intercept mean in this case? This is the average value of y when x is 0. Can x be zero? No! Definitely not, so this is a completely meaningless number.
What does beta mean in this case? For every 1 unit change in x your feelings about BLM drop 14.5 points. What does that mean in terms of this variable? Every 1 step more conservative you get you drop 14.5 points in terms of your feelings about BLM.
Now here’s a question, if we use our regression equation to determine the predicted y at 1, 2, 3…7, will that also recover the mean blm thermometer at each of those points?
ideology <- 1:7
yhat <- m4$coefficients["(Intercept)"] + m4$coefficients["ideology"]*ideology
yhat
#> [1] 96.92045 82.45866 67.99687 53.53509 39.07330 24.61152
#> [7] 10.14973
plot(anes$ideology, anes$blm.therm)
points(ideology, yhat, col="firebrick", type="b", pch=16)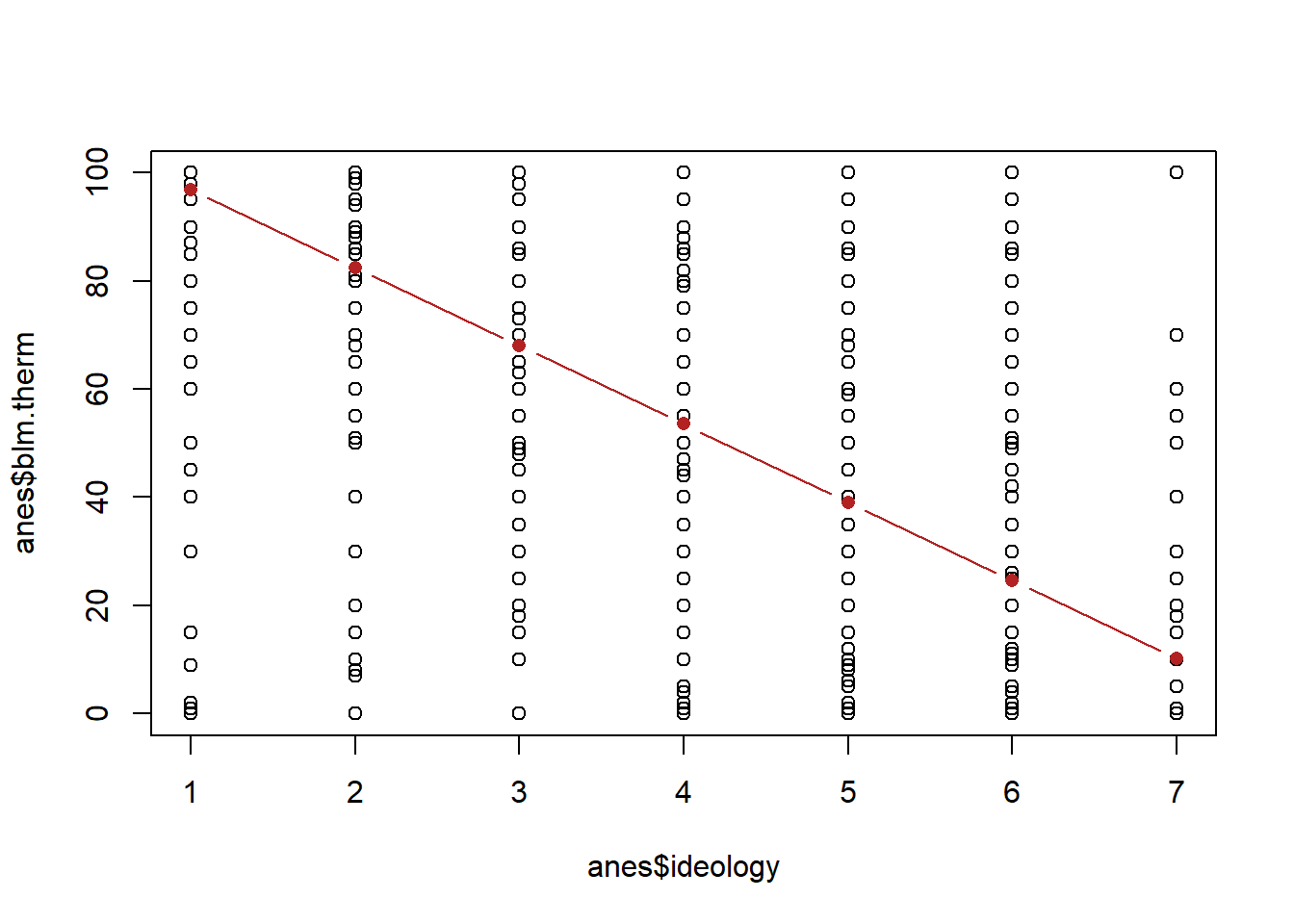
Is that the same as:
ybar <- NA
for(i in 1:7){
ybar[i] <- mean(anes$blm.therm[anes$ideology==i],na.rm=T)
}
plot(anes$ideology, anes$blm.therm)
points(ideology, yhat, col="firebrick", type="b", pch=16)
points(ideology, ybar, col="dodgerblue", type="b", pch=16)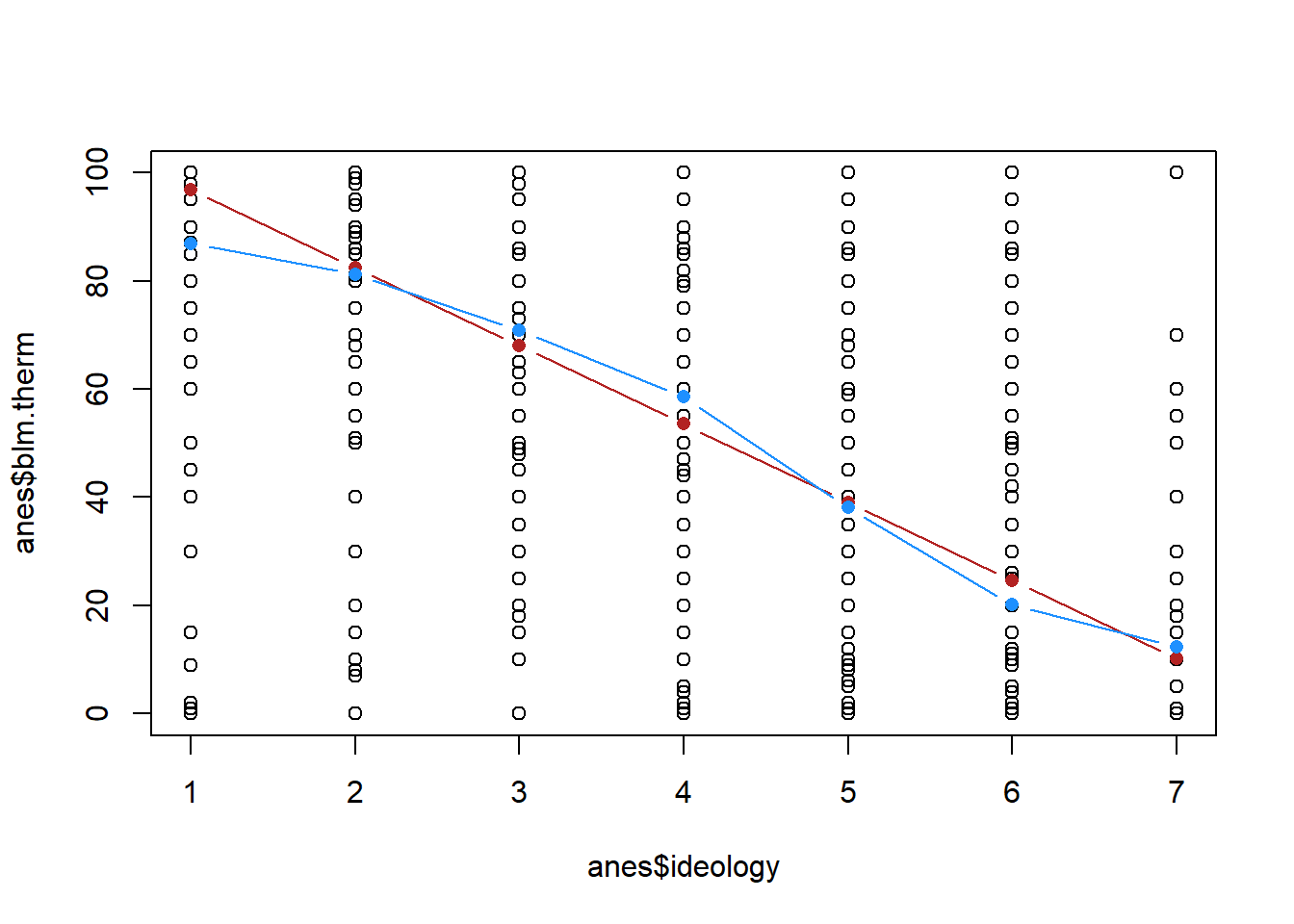
They are definitely not the same! The red line, the regression line, is constrained to being a straight line. the blue line, the connected means, is not. Which of these, in this case, better represents this data?
Regression assumes that everything you put into it is a continuous variable. That means it thinks that the variable ranges from negative to positive infinity, and that each number is evenly spaced. We are necessarily treating, with the red line, the jump from very liberal to liberal the same as the jump from somewhat liberal to moderate. Looking at the blue line, it’s somewhat clear that each of these jumps is not uniformly important. The jump from 1 to 2 and from 6 to 7 is smaller than the jumps in between. Regression returns none of that nuance, it just gives us a straight line that averages across these values.
Neither of these are right or wrong, they just present two different perspectives. But it’s important to know what’s going on under the hood in regression so you understand the assumptions you are making about your variables.
11.1 An example using what we’ve learned so far
Let’s use what we’ve learned so far to investigate the Arizona data from the 2022 election we’ve worked with before:
sm.az <- import("https://github.com/marctrussler/IIS-Data/raw/main/AZFinalWeeks.csv")I want to investigate, relative to the population we are studying (likely Arizona voters) who is in this sample. We are not going to get in to how weighting works in this class, but the basic intuition is that we define groups, and then give individual higher weights if not enough people from their groups are in the sample, relative to the population. So if we run a sample and we don’t have enough women, all women will get a higher weight to make up for it. A weighting algorithm does this simultaneously for many groups (here it is age, gender, education, race, and 2020 presidential vote). But if we see a relationship between a particular variable and the weight variable, it means that we are using weights to make up for the fact that not enough people from that group are in our sample.
Here is the relationship between age and the weight variable
plot(sm.az$age, sm.az$weight, xlab="Age", ylab="Weight")
Bit of a messy relationship that is hard to summarize without regression. Here is the regression output for this relationship:
m <- lm(weight ~ age, data=sm.az)
summary(m)
#>
#> Call:
#> lm(formula = weight ~ age, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.6194 -0.2602 -0.1573 0.2313 3.8457
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.676267 0.031362 21.563 < 2e-16 ***
#> age -0.001591 0.000545 -2.918 0.00354 **
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.5105 on 3045 degrees of freedom
#> Multiple R-squared: 0.002789, Adjusted R-squared: 0.002462
#> F-statistic: 8.517 on 1 and 3045 DF, p-value: 0.003544What is the interpretation for the coefficient on the Intercept here? The average weight when age is 0 is .67. Again, this is a fairly useless bit of information. We don’t really care what happens when age is 0. This is just a mechanically necessary number to have in order to draw a regression line.
What is the interpretation for the coefficient on age? For every additional year of age, the weight goes down by around .001. If higher weights mean that individuals from that group are less likely to be in our sample, what does this result mean? It means that younger people were harder to get into our sample (despite being online!).
What about the relationship between race and the weight variable?
Here is what race looks like:
head(sm.az$race)
#> [1] "black" "asian" "hispanic" "black" "black"
#> [6] "white"Can we put this variable into the regression as-is? (We actually can, which we will see later on, but for right now….) No. Regression takes numeric variables and this is a bunch of words. We can’t run a regression on this. We have to do some re-coding.
Let’s create a variable that splits the sample into white and non-white:
sm.az$white <- sm.az$race=="white"
table(sm.az$white)
#>
#> FALSE TRUE
#> 875 2172We’ve seen lots of times that R will helpfully treat a binary variable like 0’s and 1’s, which means that we can now put this into a regression:
m2 <- lm(weight ~ white, data=sm.az)
summary(m2)
#>
#> Call:
#> lm(formula = weight ~ white, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.6060 -0.2553 -0.1508 0.2304 3.9130
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.61384 0.01727 35.534 <2e-16 ***
#> whiteTRUE -0.03512 0.02046 -1.716 0.0862 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.511 on 3045 degrees of freedom
#> Multiple R-squared: 0.0009664, Adjusted R-squared: 0.0006384
#> F-statistic: 2.946 on 1 and 3045 DF, p-value: 0.08621What’s the interpretation of the intercept? Of the coefficient?
Finally, let’s see if there is a relationship between approval of Biden and the weight. What does the Biden approval variable look like right now?
table(sm.az$biden.approval)
#>
#> Somewhat approve Somewhat disapprove Strongly approve
#> 665 287 623
#> Strongly disapprove
#> 1449Again, these are just words, but in this case the words have an order. Let’s convert this into a numbered ordinal variable and then put that into the regression:
sm.az$biden.approval.num <- NA
sm.az$biden.approval.num[sm.az$biden.approval=="Strongly disapprove"] <- 0
sm.az$biden.approval.num[sm.az$biden.approval=="Somewhat disapprove"] <- 1
sm.az$biden.approval.num[sm.az$biden.approval=="Somewhat approve"] <- 2
sm.az$biden.approval.num[sm.az$biden.approval=="Strongly approve"] <- 3
table(sm.az$biden.approval.num)
#>
#> 0 1 2 3
#> 1449 287 665 623
m3 <- lm(weight~biden.approval.num, data=sm.az)
summary(m3)
#>
#> Call:
#> lm(formula = weight ~ biden.approval.num, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.5869 -0.2573 -0.1651 0.2282 3.9108
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.580937 0.012720 45.671 <2e-16 ***
#> biden.approval.num 0.006676 0.007563 0.883 0.377
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.5093 on 3022 degrees of freedom
#> (23 observations deleted due to missingness)
#> Multiple R-squared: 0.0002578, Adjusted R-squared: -7.302e-05
#> F-statistic: 0.7793 on 1 and 3022 DF, p-value: 0.3774What is the interpretation of the Intercept? Is it meaningful? What is the interpretation of the coefficient? Looking ahead, what does it mean that our p-value is .377?
11.2 Regression with a binary dependent variable
So far all of the regressions that we have run have had a continuous dependent variable. Is that our only option? What happens if we want to use regression on a binary dependent variable?
Let’s make a 0,1 variable of whether someone plans to vote for Mark Kelly (the Democrat) or Blake Masters (the Republican).
sm.az$vote.kelly <- NA
sm.az$vote.kelly[sm.az$senate.topline=="Democrat"] <- 1
sm.az$vote.kelly[sm.az$senate.topline=="Republican"] <- 0
table(sm.az$vote.kelly, sm.az$senate.topline)
#>
#> Democrat Other/Would not Vote Republican
#> 0 0 0 1245
#> 1 1368 0 0And use age to predict that variable:
plot(sm.az$age, sm.az$vote.kelly)
Now this is not a very appealing graph. What does the regression line on this look like?

That doesn’t even touch any of the data-points! Is that helpful at all?
Let’s think about what the regression output says:
m4 <- lm(vote.kelly~age, data=sm.az)
summary(m4)
#>
#> Call:
#> lm(formula = vote.kelly ~ age, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.5482 -0.5241 0.4627 0.4753 0.4989
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.4907882 0.0357856 13.715 <2e-16 ***
#> age 0.0005743 0.0006037 0.951 0.342
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.4996 on 2611 degrees of freedom
#> (434 observations deleted due to missingness)
#> Multiple R-squared: 0.0003465, Adjusted R-squared: -3.64e-05
#> F-statistic: 0.9049 on 1 and 2611 DF, p-value: 0.3416What is the mathematical interpretation of the intercept?
Remember, that alpha is the average value of y when x is equal to 0. What does it mean when we take the average of a binary/indicator variable? That gives us the probability of that variable being equal to 1! It’s something we have seen repeatedly in this course. So the practical interpretation of this intercept is that the probability of voting for Kelly among a newborn (I know) is approximately 49%.
If that’s what the intercept is giving us, what does the age coefficient mean? For each additional 1 unit change in x, y goes up .0005, on average. This means that every additional year someone ages their probability of voting for Kelly increases by 1 half of a percentage point.
In other words, when we have a binary dependent variable, it converts all of our explanations into probability.
Let’s do another example (with a variable that actually affects Kelly vote prob…)
Let’s look at how the Biden approval variable above relates to voting for Kelly:
m5 <- lm(vote.kelly ~ biden.approval.num, data=sm.az)
summary(m5)
#>
#> Call:
#> lm(formula = vote.kelly ~ biden.approval.num, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.1296 -0.1267 -0.1267 0.2047 0.8733
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.126699 0.007313 17.33 <2e-16 ***
#> biden.approval.num 0.334291 0.004225 79.13 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.2704 on 2595 degrees of freedom
#> (450 observations deleted due to missingness)
#> Multiple R-squared: 0.707, Adjusted R-squared: 0.7069
#> F-statistic: 6261 on 1 and 2595 DF, p-value: < 2.2e-16What is the interpretation of the intercept now? Well we set this variable to be equal to strongly disapprove of Biden at 0, so this is the probability of voting for Kelly when you strongly disapprove of Biden. What is the interpretation of the coefficient on biden.approval.num now? This is now the effect of going from strongly to somewhat disapprove, from somewhat disapprove to somewhat approve, etc. That effect .33. For every step up the approval chain the probability of voting for Kelly increases by 33%. That makes sense!
Now if we try to visualize this it’s going to look terrible:
We can somewhat improve this graph by using the jitter feature, which adds a bit of noise to our data so that we can see that each of these dots is actually a fair number of people:
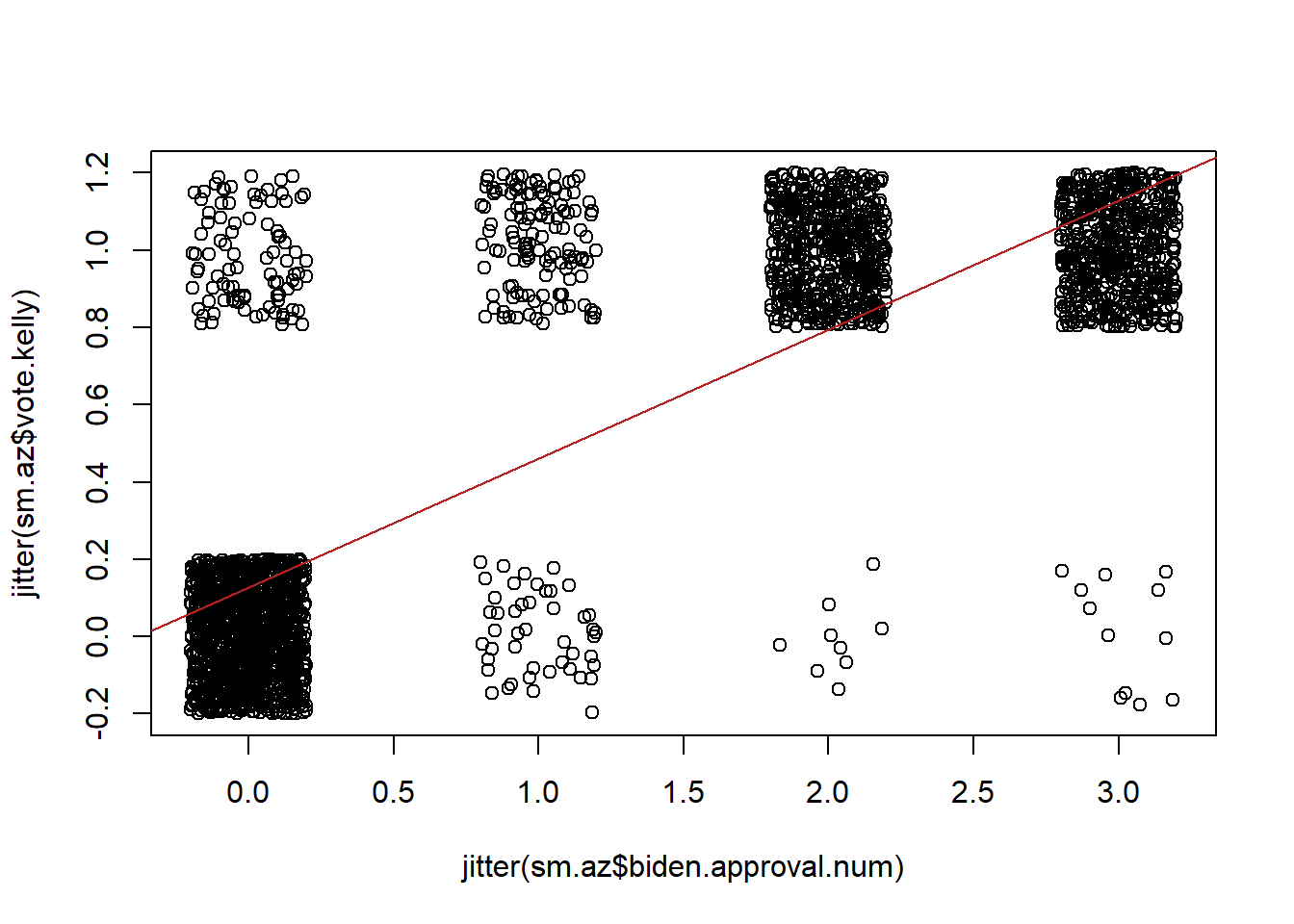
But this graph also reveals another problem here. What is the predicted probability of voting for Kelly at all the levels of Biden approval? How can we mathematically determine that?
m5$coefficients["(Intercept)"] + m5$coefficients["biden.approval.num"]*0:3
#> [1] 0.1266990 0.4609902 0.7952814 1.1295727How would we interpret this last value? If you strongly approve of Biden you have a 112% chance of voting for him! Uh oh! Broken laws of probability!
When we run an OLS regression with a binary dependent variable, it transforms what we are doing into a “Linear Probability Model” or LPM. As we’ve seen, it allows us to interpret our coefficients in terms of the probability of the dependent variable being 1. LPMs are great, and most of the time they work fantastically. I’ve use them throughout my career with no problems.
The major downside to using an LPM is that OLS regression doesn’t know or care what scale your variable are on. It treats every variable like it is a continuous variable that ranges from negative infinity to infinity. There is nothing constraining OLS, in other words, to draw a line that leads to us making a prediction that is outside the interval of \([0,1]\). This is legitimately a big problem if you are specifically using regression to make a prediction, but less of a problem if you are using regression to search for an explanation. Here I’m not super bothered that this prediction falls outside of 0,1 because I am mostly interested in saying that Biden approval has a strong, positive impact on the probability that you are going to vote for Kelly.
If you are interested in using regression for prediction and your outcome variable is binary it is often the case that using an LPM is not appropriate. An example of this would be generating a likely voter model, which definitely needs to range between 0 and 1. In those cases we use a logit or probit model, which are beyond the scope of this course, but are specifically designed to work with binary outcome variables and will not generate predictions outside of the 0,1 interval.
Ultimately any numerical variable can be put into either side of a regression. That being said, you really really have to think about what is happening each and every time. You really have to understand the scale of the variables that you are using in order to correctly interpret what is going on. Every single time.
11.3 Goodness of fit
The final bit of information we get in the regression output is at the bottom, and presents a few different measures of how good your regression fit is, overall.
The value I want to focus on is \(R^2\). Now I may mentioned I have beef with AP stats before. I’ve never actually read an AP stats textbook but for some reason a lot of people come to college with the belief that \(R^2\) is the be all end all of regression. It’s important! But much less so then you might think.
Ok but what is it? \(R^2\) is a measure of how well the \(x\) variable explains the \(y\) variable. It ranges from 0-1 and tells you what percent of the variation in \(y\) is explained by \(x\). Why is this sometimes helpful to know, but sometimes not?
As above, it really comes down to whether we want to use regression for explanation or prediction.
We aren’t explicitly covering prediction in this class, but for right now it should be clear mathematically that we are able to say: we have a regression for how age predicts BLM thermometer scores, so what would our prediction be for how a 120-year-old person would feel about BLM? We can very easily just plug that value in for age and OLS will form a prediction. In these cases, how well your explanatory variable (or variables) is explaining the outcome will be critical in determining whether this is a good or bad prediction.
For explanation we are way less concerned with goodness of fit. Here we might be interested in the question of whether age is an explanation of how people feel about BLM. We find above that it is statistically significant, but the \(R^2\) is very low. Someone might come to me and say: your \(R^2\) is low so your regression is junk! But I don’t really care about that. Of course lots of things influence how someone feels about BLM, so my regression is not going to fully explain each individual’s feelings simply based on their age. That’s not what I’m trying to do. I’m simply trying to show that this variable has a non-zero impact.
So \(R^2\) is a helpful number, but a low \(R^2\) does not mean your regression is junk. You have to know what you are using it for.