12 Regression II
12.1 Regression with more than one independent variable
First, let’s install and load the “AER” package, which has some interesting built in data. We are just using this package for the data, it’s not a necessary package for regression or anything.
#install.packages("AER")
library(AER)The AER package has some built in data on California schools
data("CASchools")
head(CASchools)
#> district school county grades
#> 1 75119 Sunol Glen Unified Alameda KK-08
#> 2 61499 Manzanita Elementary Butte KK-08
#> 3 61549 Thermalito Union Elementary Butte KK-08
#> 4 61457 Golden Feather Union Elementary Butte KK-08
#> 5 61523 Palermo Union Elementary Butte KK-08
#> 6 62042 Burrel Union Elementary Fresno KK-08
#> students teachers calworks lunch computer expenditure
#> 1 195 10.90 0.5102 2.0408 67 6384.911
#> 2 240 11.15 15.4167 47.9167 101 5099.381
#> 3 1550 82.90 55.0323 76.3226 169 5501.955
#> 4 243 14.00 36.4754 77.0492 85 7101.831
#> 5 1335 71.50 33.1086 78.4270 171 5235.988
#> 6 137 6.40 12.3188 86.9565 25 5580.147
#> income english read math
#> 1 22.690001 0.000000 691.6 690.0
#> 2 9.824000 4.583333 660.5 661.9
#> 3 8.978000 30.000002 636.3 650.9
#> 4 8.978000 0.000000 651.9 643.5
#> 5 9.080333 13.857677 641.8 639.9
#> 6 10.415000 12.408759 605.7 605.4Let’s set out a research question for these data. I want to know if the student to teacher ratio in a classroom is associated with better test scores. Specifically, as the student to teacher ratio increases, test scores should decrease.
The null hypothesis of this relationship is that student to teacher ratio has 0 association with test scores
Let’s first create two variables that capture these concepts. STR will be the student to teacher ratio:
CASchools$STR <- CASchools$students/CASchools$teachers
summary(CASchools$STR)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 14.00 18.58 19.72 19.64 20.87 25.80And the test scores will be the simple average of the reading and math test scores:
CASchools$score <- (CASchools$read + CASchools$math)/2
summary(CASchools$score)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 605.5 640.0 654.5 654.2 666.7 706.8To make my life easier I’m going to save a version of this dataset with a shorter name
dat <- CASchoolsOk, so first, what do these data look like?
plot(dat$STR, dat$score, xlab="Student:Teacher Ratio", ylab="Test Score", pch=16)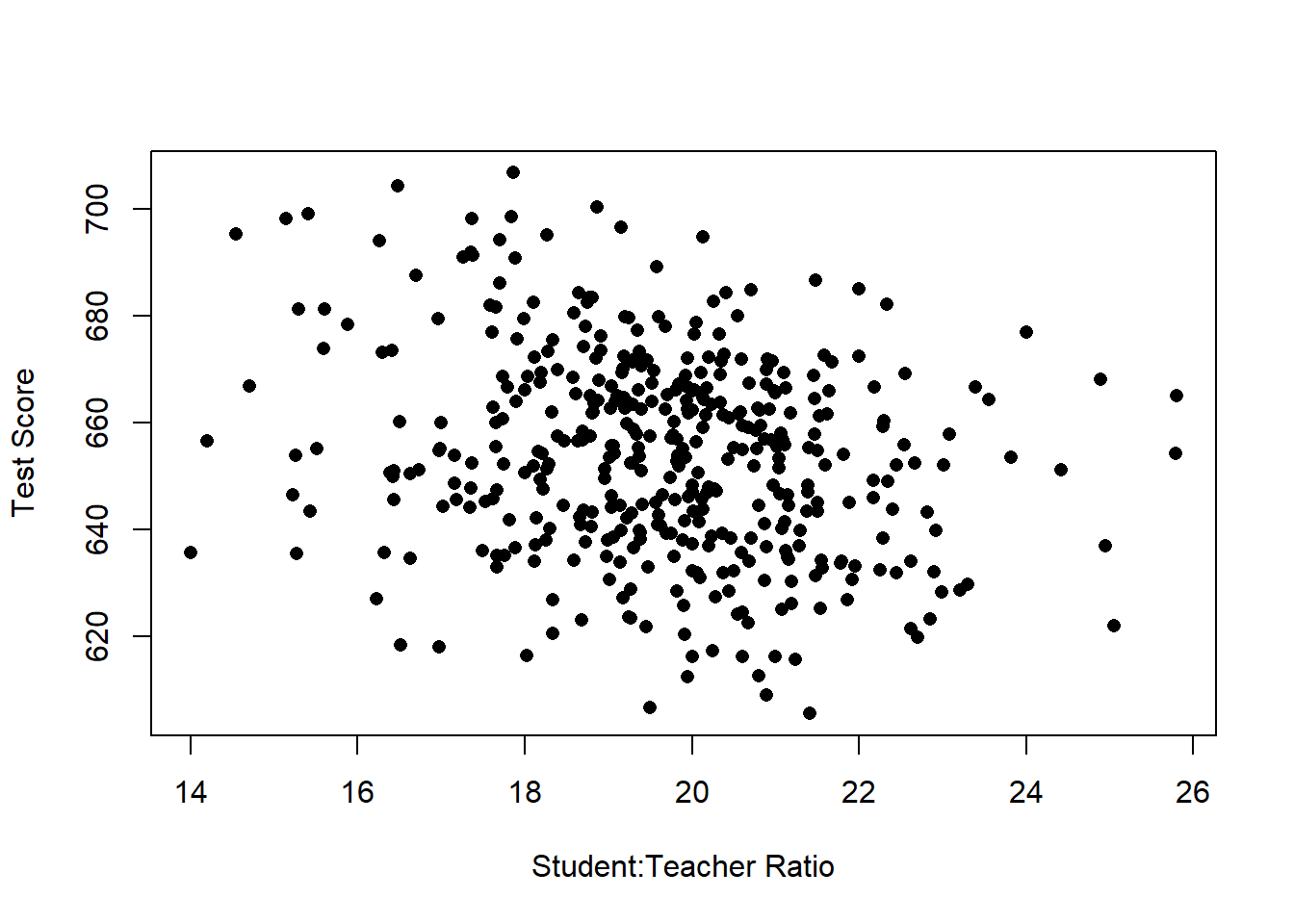
There does seem to be a generally negative relationship here, though it’s not a slam dunk, and could be due to random chance.
Let’s use our new tool of regression to describe the relationship we are seeing here.
m <- lm(score ~ STR, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = score ~ STR, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -47.727 -14.251 0.483 12.822 48.540
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 698.9329 9.4675 73.825 < 2e-16 ***
#> STR -2.2798 0.4798 -4.751 2.78e-06 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 18.58 on 418 degrees of freedom
#> Multiple R-squared: 0.05124, Adjusted R-squared: 0.04897
#> F-statistic: 22.58 on 1 and 418 DF, p-value: 2.783e-06
plot(dat$STR, dat$score, xlab="Student:Teacher Ratio", ylab="Test Score", pch=16)
abline(lm(dat$score ~ dat$STR), lwd=2, col="firebrick")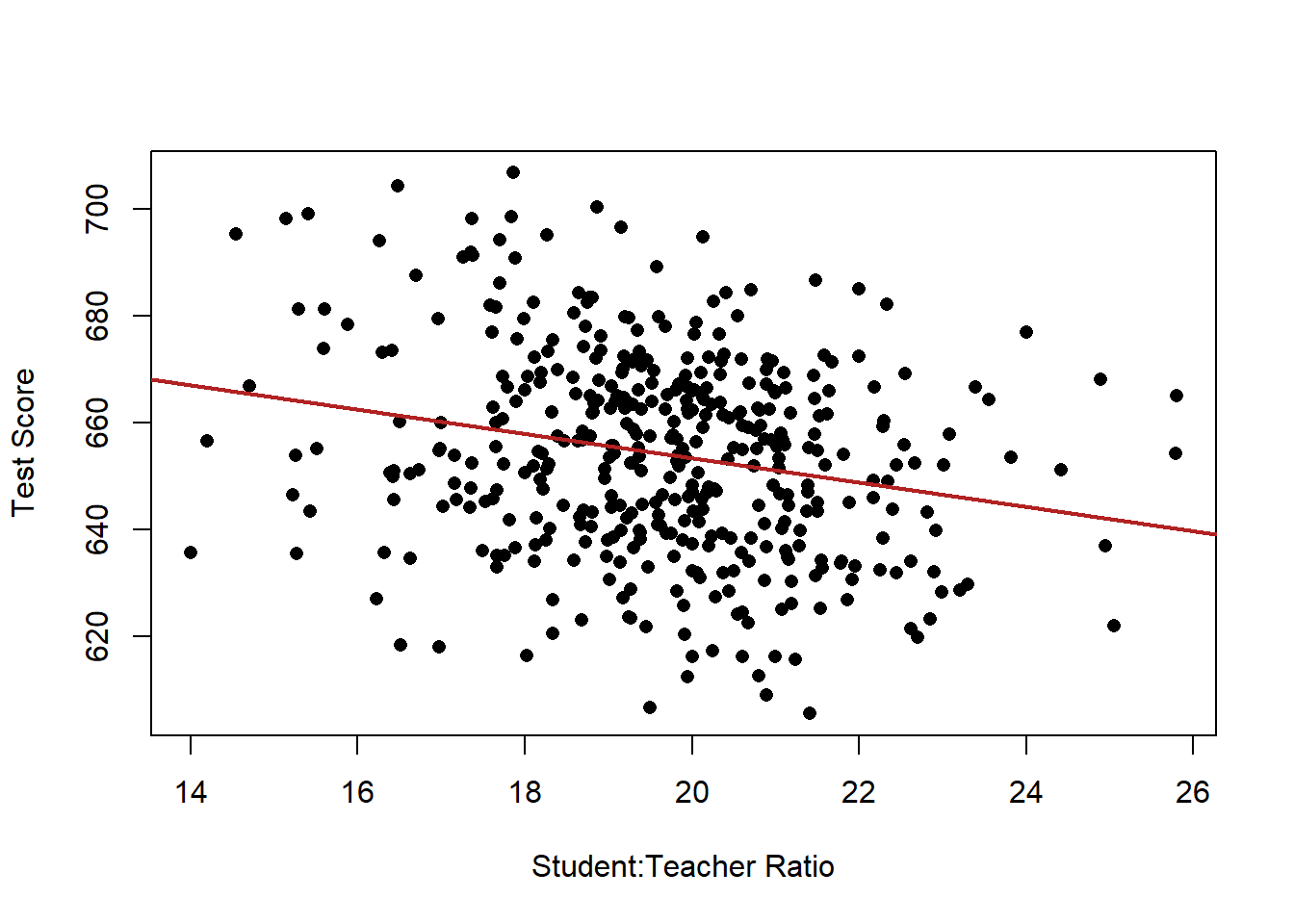
What do we see here?
The coefficient on STR is negative. When STR increases by one unit, test scores decrease by -2.3 units, approximately.
Let’s put this in English. A one unit change in STR means one additional student for every teacher. So…A classroom with one additional student for every teacher, is associated with a 2.3 point decline in test scores on average.
Looking at the hypothesis test for this, the probability of obtaining a relationship this extreme if the truth was that there was no association between STR and test scores approaches zero. We reject the null hypothesis here.
What is the intercept telling us in this case ? When STR is zero, the average test score is 698.
But this is where we have to be smarter than the regression: can STR ever be zero??
12.2 Ommited variable bias
You’ve heard time and time again: correlation does not equal causation. Honestly I’m getting a bit tired of hearing it, as people often use it to mean “Can’t trust those scientists these days!”. Over the next few weeks we’ll formalize what this means and determine situations where correlation does equal causation. For right now, what we can think about doing is ruling out other plausible reasons for why these two variables might be correlated.
Theoretically, what we are interested in are variables that cause both a high student to teacher ratio and low test scores. In other words, might it be the case that some third, unseen, variable is driving this relationship?
There are some classic absurd omitted variable bias examples: There is a negative association between the number of firemen at a fire and property damage. It would be a mistake to conclude that firemen cause property damage. The truth is that both are driven by the severity of the fire. Another example is that ice cream sales are positively associated with crime, where both are actually driven by warm weather.
Omitted variable bias occurs when we are not taking into account a variable (or variables) that cause both our independent and dependent variables.
In the case we are dealing with here, a potential explanation for why a school might have a high student to teacher ratio and lower test scores might be because it is a school with a high number of children who speak English as a second language. Schools with a high number of children who speak english as a second language may be more likely to be in areas with a poor tax base and therefore less money to hire teachers. Standardized tests have been found to not capture the innate intelligence of those who do not speak English as their primary language.
In our original data, we have a variable that captures the percent of the school who has English as second language. To start let’s create a simple dummy variable that is equal to 1 if a school is above the median for ESL children, and 0 for schools that are below the median.
dat$high.esl <-NA
dat$high.esl[dat$english>=median(dat$english)]<- 1
dat$high.esl[dat$english<median(dat$english)]<- 0Let’s visualize what this looks like
Here is our original data and regression line, where we are treating all the schools the same.
Within all these black dots, some are schools with a high number of ESL children, some are schools with a low number of ESL children.
plot(dat$STR, dat$score, xlab="Student:Teacher Ratio", ylab="Test Score", pch=16)
abline(lm(dat$score ~ dat$STR), lwd=2, col="firebrick")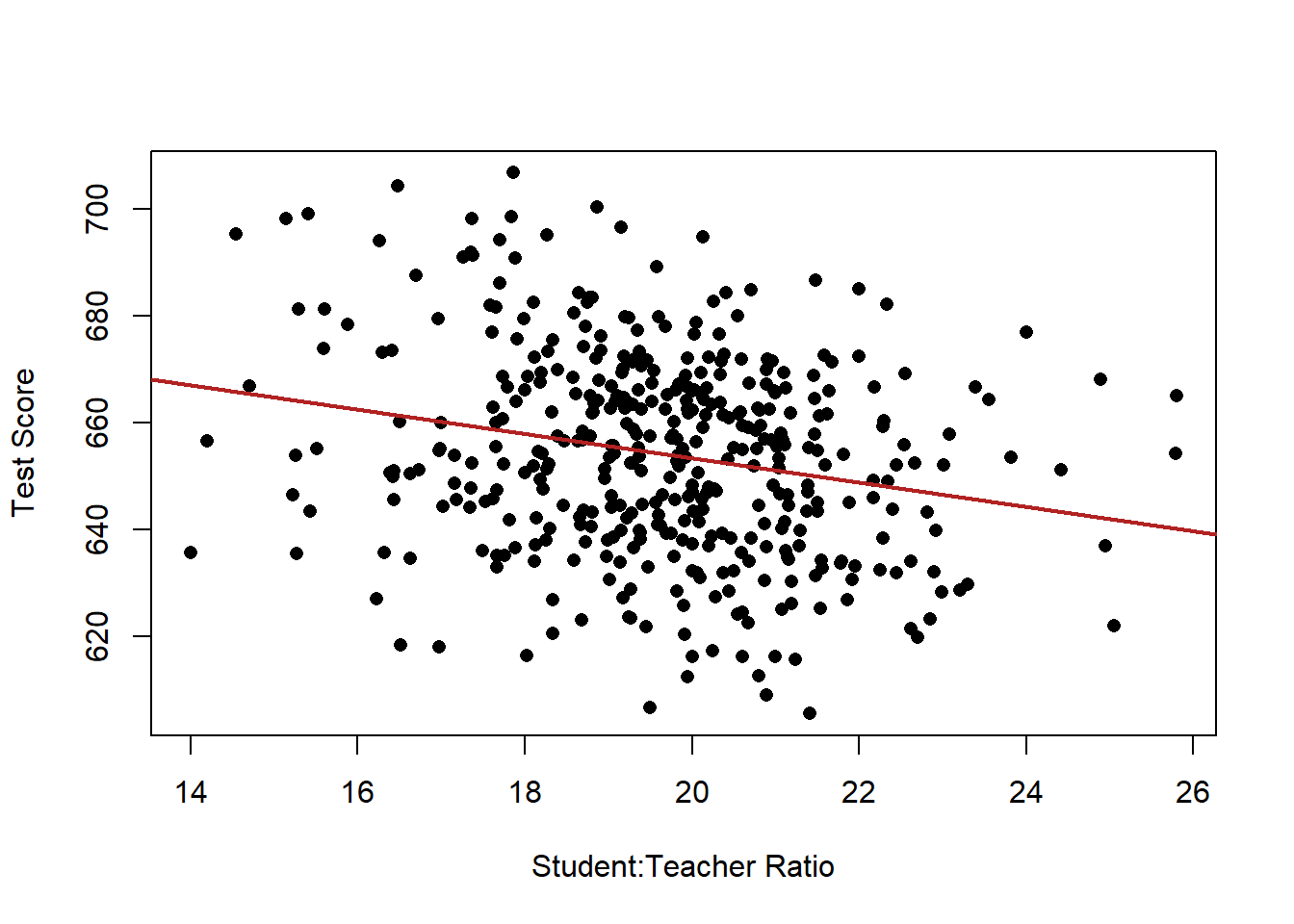
What if we reveal which points belong to which ESL group, how might we think differently about the relationship?
plot(dat$STR, dat$score, xlab="Student:Teacher Ratio", ylab="Test Score", pch=16, type="n")
points(dat$STR[dat$high.esl==0], dat$score[dat$high.esl==0], pch=16, col="darkblue")
points(dat$STR[dat$high.esl==1], dat$score[dat$high.esl==1], pch=16, col="firebrick")
legend("topright", c("Low ESL", "High ESL"), pch=c(16,16), col=c("darkblue", "firebrick"))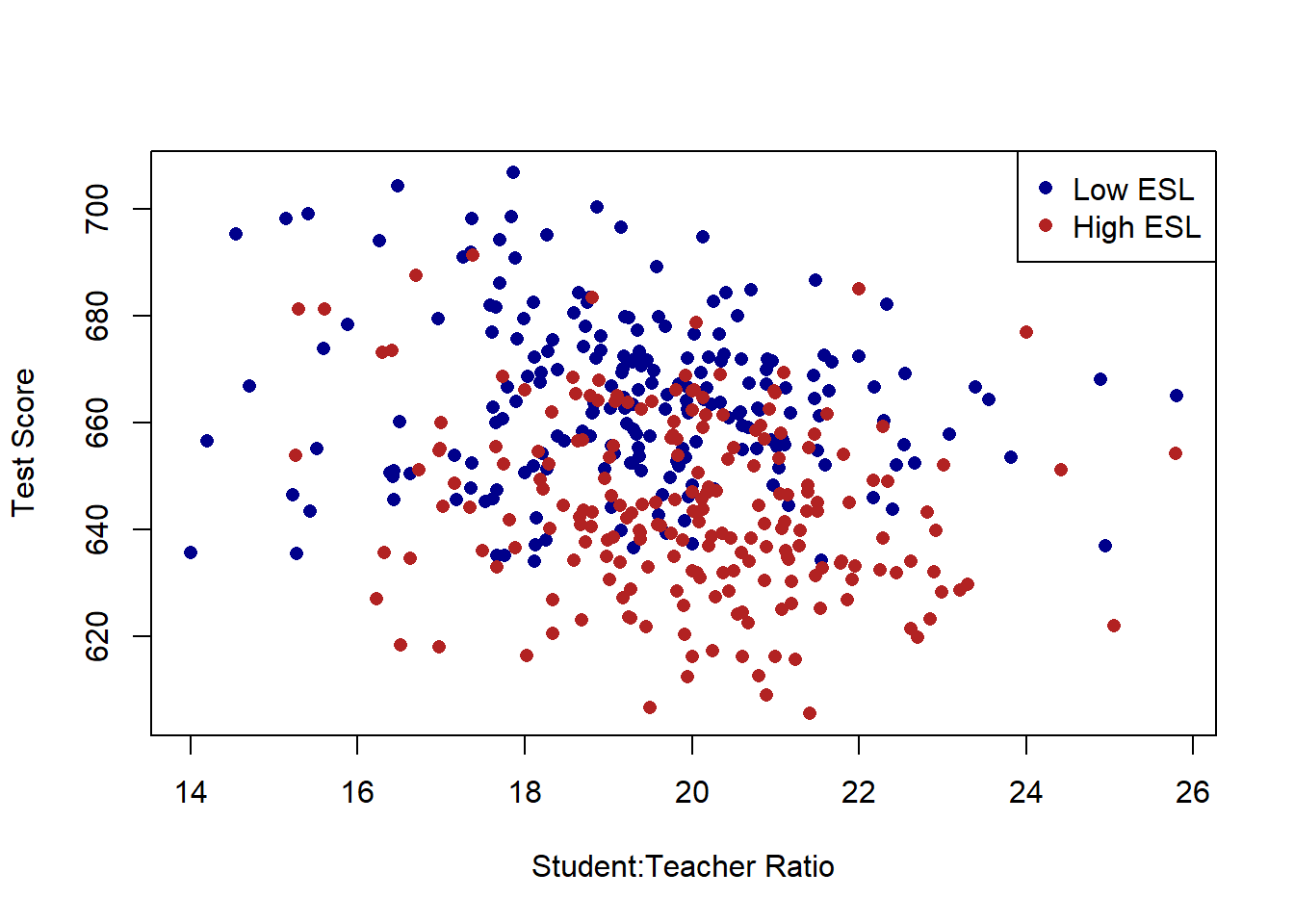
Just using the naked eye, there does seem to be a large number of schools which have both a high number of children who have English as a second language and also have lower test scores.
Here is what we want to do: Taking into account that there are two different types of schools, can we summarize what the relationship between STR and test scores are?
Mechanically, this is what regression is going to do: Choose a slope line for STR and TWO intercepts, one for each type of school, such that the sum of the squared residuals is minimized.
Visualizing this, it looks like this:
plot(dat$STR, dat$score, xlab="Student:Teacher Ratio", ylab="Test Score", pch=16, type="n")
points(dat$STR[dat$high.esl==0], dat$score[dat$high.esl==0], pch=16, col="darkblue")
points(dat$STR[dat$high.esl==1], dat$score[dat$high.esl==1], pch=16, col="firebrick")
abline(a=691.32, b=-1.3963, col="darkblue", lwd=3)
abline(a=691.32-19.49, b=-1.3963, col="firebrick", lwd=3)
legend("topright", c("Low ESL", "High ESL"), pch=c(16,16), col=c("darkblue", "firebrick"))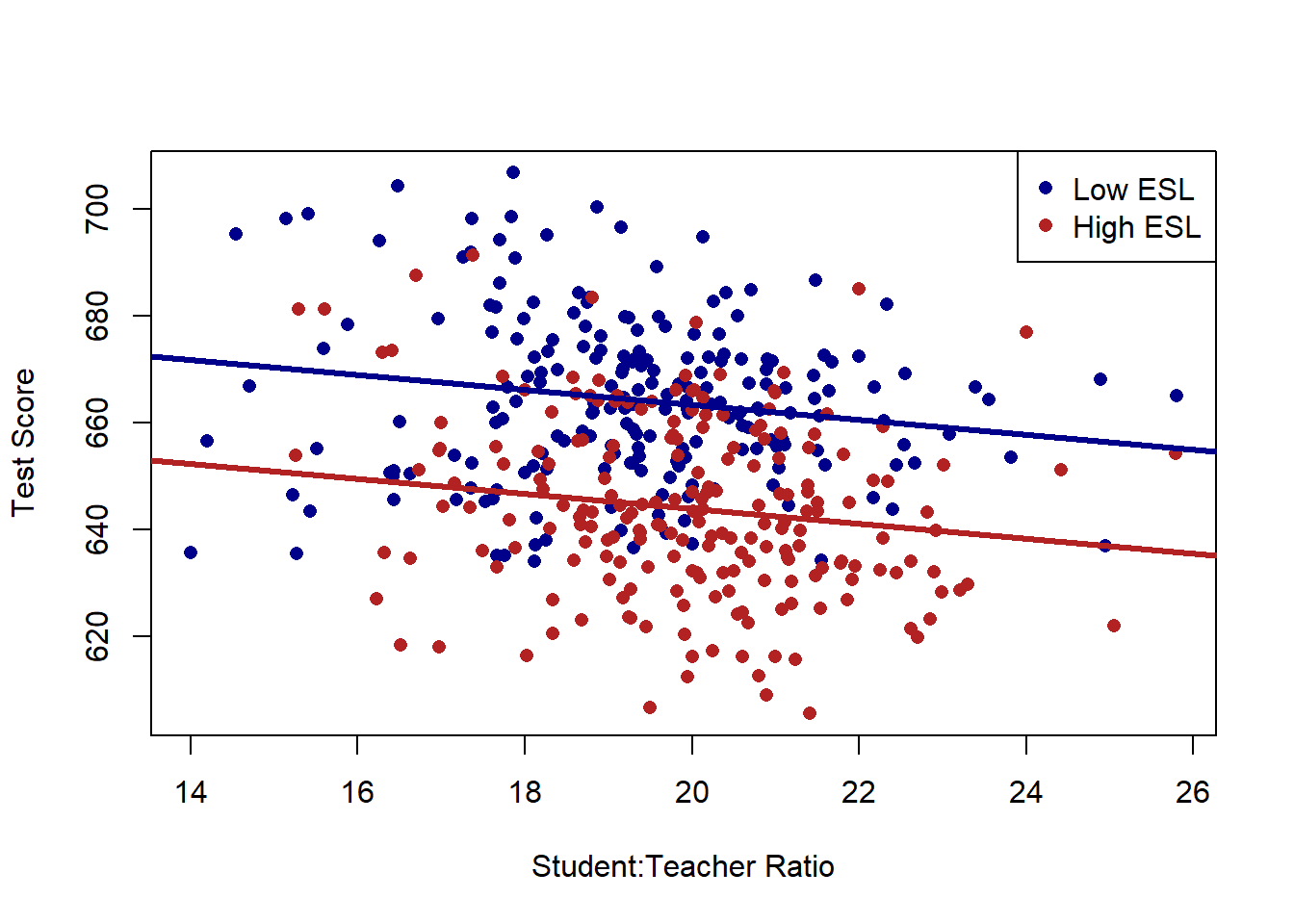
Now we are allowing each type of school to have its own intercept, and choosing a single slope that best fits the data with that limitation.
Let’s compare this new slope to what we had before.
plot(dat$STR, dat$score, xlab="Student:Teacher Ratio", ylab="Test Score", pch=16, type="n", xlim=c())
points(dat$STR[dat$high.esl==0], dat$score[dat$high.esl==0], pch=16, col="darkblue")
points(dat$STR[dat$high.esl==1], dat$score[dat$high.esl==1], pch=16, col="firebrick")
abline(a=691.32, b=-1.3963, col="darkblue", lwd=3)
abline(a=691.32-19.49, b=-1.3963, col="firebrick", lwd=3)
abline(lm(dat$score ~ dat$STR), lwd=3)
legend("topright", c("Low ESL", "High ESL"), pch=c(16,16), col=c("darkblue", "firebrick"))
abline(v=0, lty=2)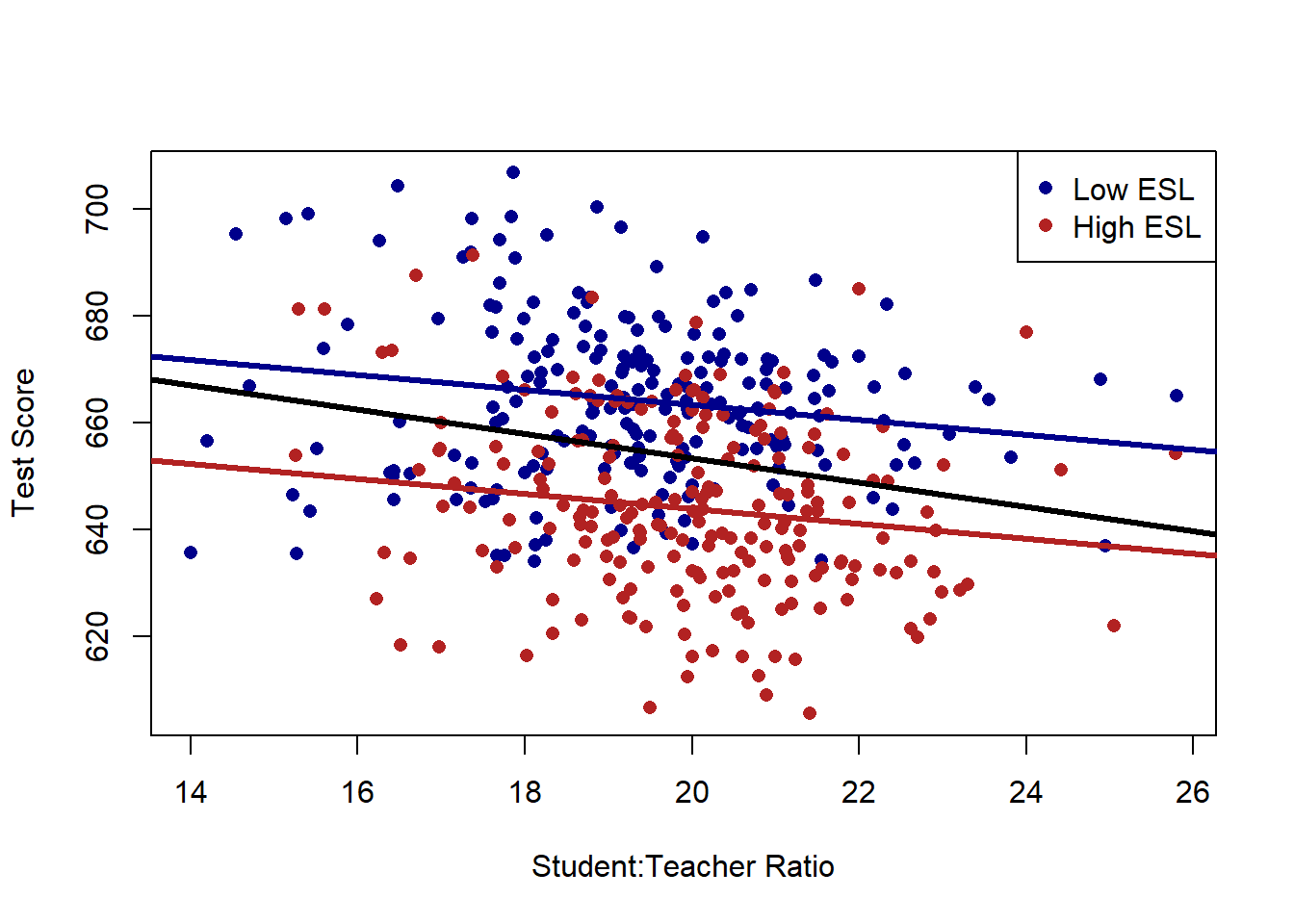
It’s much shallower. Why? The relationship between STR and test scores was driven, in part, by the fact that schools with high numbers of ESL children have both a high STR and low test scores. Once we take into account that fact (by focusing on the relationship within school types) the association between STR and test scores is much lower.
What does this look like in a regression equation?
m <- lm(score ~ STR + high.esl, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = score ~ STR + high.esl, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -37.857 -10.853 -0.626 10.198 43.834
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 691.3267 8.1315 85.019 < 2e-16 ***
#> STR -1.3963 0.4171 -3.348 0.000889 ***
#> high.esl -19.4911 1.5763 -12.365 < 2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 15.91 on 417 degrees of freedom
#> Multiple R-squared: 0.3058, Adjusted R-squared: 0.3025
#> F-statistic: 91.84 on 2 and 417 DF, p-value: < 2.2e-16Helpfully, we are going to read these coefficients in the same way as we did with univariate regression. Each variable still represents how a one unit change in each independent variable is associated with a coefficient level change in the dependent variable. The major difference is that now these numbers are the effect of this variable holding the other variable constant. Another way to think of this is: looking within levels of the other variable, what’s the effect of this variable?
So for STR, holding constant whether a school has a high number of ESL students or not, the effect of an additional student for every teacher is to reduce test scores by 1.4 points.
The other variable high.esl is an indicator, which makes interpretation easier. Just as before a “one unit change” for an indicator variable is just changing categories, here from a low to a high ESL school.
Holding constant the student teacher ratio, schools with an above average number of children who have English as their second language perform nearly 20 points worse than schools with a below average number of children who have English as their second language, holding constant the student to teacher ratio.
What about the intercept? For univariate regression we learned that the intercept is the average value of y when x is 0. Helpfully, the same thing applies here, with the caveat that now the intercept is the average value of y variable when all variables are equal to zero. In this case, the intercept is the average test scores when STR is zero (not real) and when high.esl is equal to zero.
What then, is the average test scores when STR is equal to zero in high esl schools? It would be 691-19.49! Indeed, when we look at the graph we’ve made, 19.49 is precisely the gap between the red and blue lines.
12.3 Multiple continuous variables.
What about when we have a regression with two continuous variables?
The variable “English” is the percent of the students who have English as a second language. We think that “controlling” for this variable should have a similar effect on the relationship between STR and test scores as controlling for the the high.esl variable we created above. Schools with a high percentage of ESL students are likely to have higher STR and lower test scores.
But now, thinking about our original scatterplot, we can’t easily classify these dots into “high” and “low” as we did before
plot(dat$STR, dat$score, xlab="Student:Teacher Ratio", ylab="Test Score", pch=16)
abline(lm(dat$score ~ dat$STR), lwd=2, col="firebrick")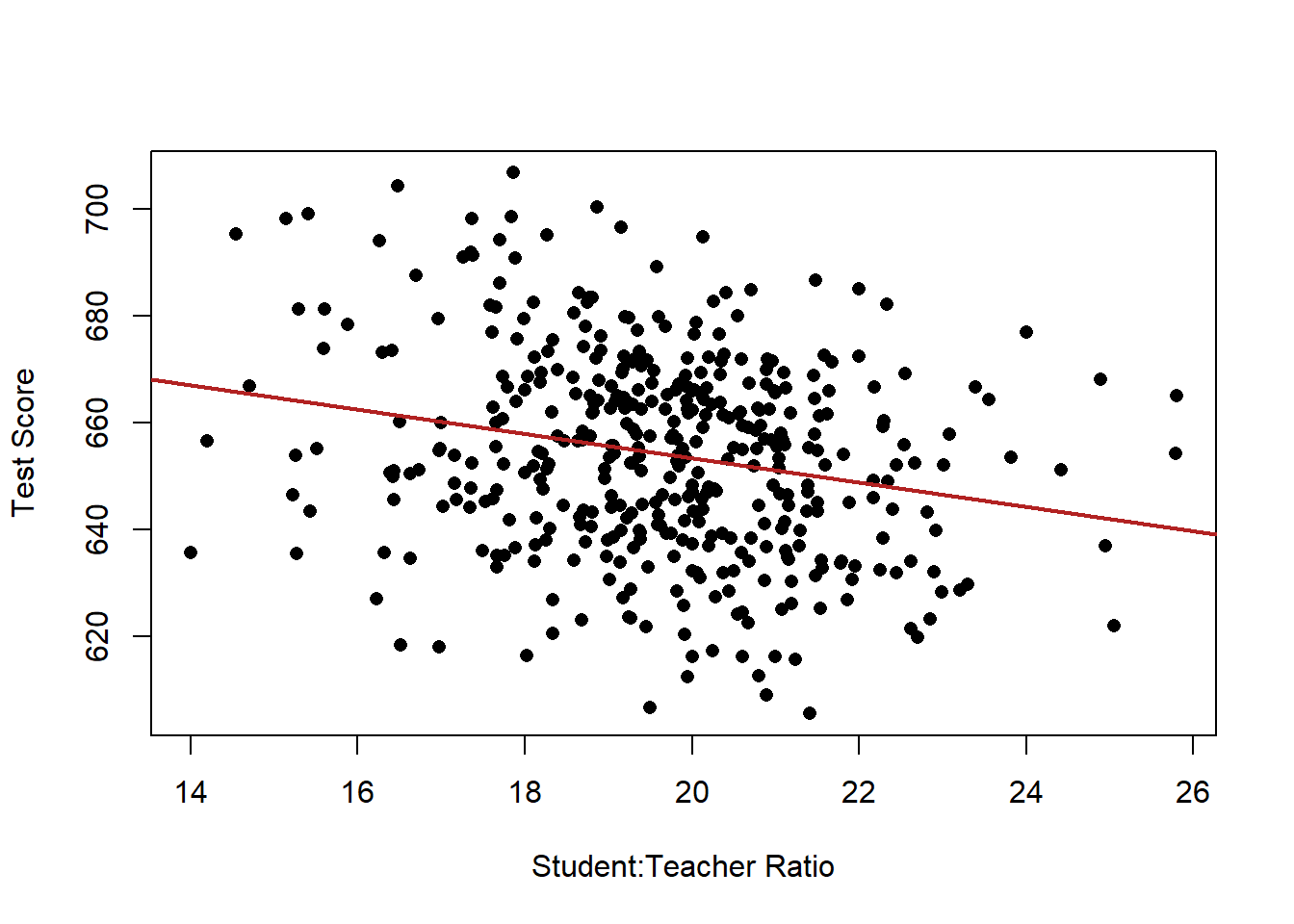
Indeed, there is a whole other dimension to these data now:
plot(dat$english, dat$score, xlab="% ESL Students", ylab="Test Score", pch=16)
abline(lm(dat$score ~ dat$english), lwd=2, col="firebrick")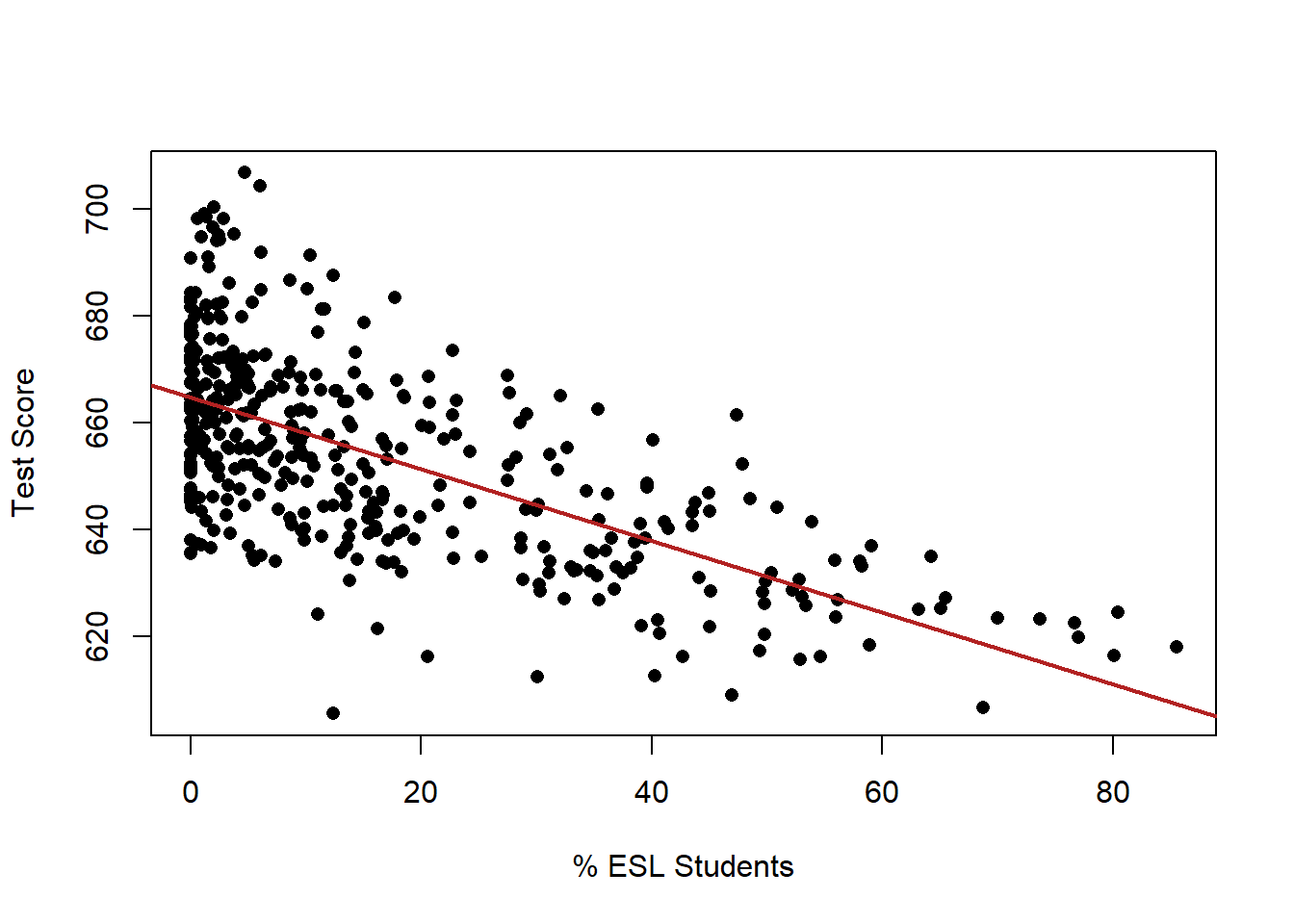
This is, unfortunately, where we leave the realm of easy-to-visualize regression.
We can think of this two variable case as a 3d plot:
#install.packages("rgl")
#library(rgl)
#plot3d(dat$STR, dat$english,dat$score, xlab="Student:Teacher Ratio", ylab="% ESL Students", zlab="Test Scores")But I pretty much never do think about this way, and if you add just one more variable there is no way to visualize!
At this point, just thinking about this through the regression output is much more helpful.
m <- lm(score ~ STR + english, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = score ~ STR + english, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -48.845 -10.240 -0.308 9.815 43.461
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 686.03224 7.41131 92.566 < 2e-16 ***
#> STR -1.10130 0.38028 -2.896 0.00398 **
#> english -0.64978 0.03934 -16.516 < 2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 14.46 on 417 degrees of freedom
#> Multiple R-squared: 0.4264, Adjusted R-squared: 0.4237
#> F-statistic: 155 on 2 and 417 DF, p-value: < 2.2e-16Again, what we are seeing here is the association between each of these variables and the dependent variable while holding constant the other.
So in plain language: Holding constant the impact of the percent of students who have English as a second language, the impact of one additional student per teacher is to reduce test scores by 1.1 points.
Further, holding constant the impact of the student to teacher ratio, the impact of an additional 1% of students having English as a second language is to reduce test scores by .65 points.
12.4 Many variables
While visualization becomes harder/impossible with additional variables, the logic of what regression coefficients mean is infinitely scalable. The coefficients will always be the impact of a one-unit change in the variable on the dependent variable, holding the other variables constant.
So if we want to assess the impact of STR while controlling for % of students getting subsidized lunch as well as the average income in the district.
m <- lm(score ~ STR + english + lunch + income, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = score ~ STR + english + lunch + income, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -30.7085 -4.9977 -0.2014 4.8411 28.7000
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 675.60821 5.30886 127.261 < 2e-16 ***
#> STR -0.56039 0.22861 -2.451 0.0146 *
#> english -0.19433 0.03138 -6.193 1.42e-09 ***
#> lunch -0.39637 0.02741 -14.461 < 2e-16 ***
#> income 0.67498 0.08333 8.100 6.19e-15 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8.448 on 415 degrees of freedom
#> Multiple R-squared: 0.8053, Adjusted R-squared: 0.8034
#> F-statistic: 429.1 on 4 and 415 DF, p-value: < 2.2e-16Note that regression does not care bout the order of variables on the “right hand” side of the equation:
m <- lm(score ~english + income + STR + lunch, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = score ~ english + income + STR + lunch, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -30.7085 -4.9977 -0.2014 4.8411 28.7000
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 675.60821 5.30886 127.261 < 2e-16 ***
#> english -0.19433 0.03138 -6.193 1.42e-09 ***
#> income 0.67498 0.08333 8.100 6.19e-15 ***
#> STR -0.56039 0.22861 -2.451 0.0146 *
#> lunch -0.39637 0.02741 -14.461 < 2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8.448 on 415 degrees of freedom
#> Multiple R-squared: 0.8053, Adjusted R-squared: 0.8034
#> F-statistic: 429.1 on 4 and 415 DF, p-value: < 2.2e-16Now each of these variables represents how a one-unit shift in that variable influences test scores, holding the other variables constant. Notably, each of these variables is “statistically significant”: we are confident that the effect is not zero in the population. Does that mean that each of these variables is equally important in determining test scores? I see that the “p-value” on STR is larger than for the other variables, does that mean it has a less important impact?
This is where we go from judging “statistical” significance to “substantive” significance.
The first pitfall is that we cannot judge how substantively significant something is based on its statistical significance. Do not do this! Statistical significance has lots of inputs (that we aren’t getting into here) which makes it completely unsuitable for judging how “important” something is. Indeed, I would encourage you to think of statistical significance as a simple “yes” or “no” and nothing more.
If we can’t use p-values to judge how substantively important something is can we use the size of coefficients? Well that’s problematic too! Remember that a regression coefficient is simply the impact of a one unit change of x on y, but “one unit” for a variable is different from “one unit” for another.
Consider the role of income in our results right now. The coefficient is .67, which indicates that for every one unit change in that variable test scores increase by .67 points. What is “one unit” for this variable?
summary(dat$income)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 5.335 10.639 13.728 15.317 17.629 55.328Now using my judgement this is almost certainly average income measured in thousands of dollars. We can rely on the documentation for data to tell us, but you also just have to look at the data and make an assesment. Use your judgement.
OK, so this is measured in thousands of dollars. What if, instead, we convert this to be in dollars?
dat$income2 <- dat$income*1000And re-run our regression:
m <- lm(score ~english + income2 + STR + lunch, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = score ~ english + income2 + STR + lunch, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -30.7085 -4.9977 -0.2014 4.8411 28.7000
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 6.756e+02 5.309e+00 127.261 < 2e-16 ***
#> english -1.943e-01 3.138e-02 -6.193 1.42e-09 ***
#> income2 6.750e-04 8.333e-05 8.100 6.19e-15 ***
#> STR -5.604e-01 2.286e-01 -2.451 0.0146 *
#> lunch -3.964e-01 2.741e-02 -14.461 < 2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8.448 on 415 degrees of freedom
#> Multiple R-squared: 0.8053, Adjusted R-squared: 0.8034
#> F-statistic: 429.1 on 4 and 415 DF, p-value: < 2.2e-16First: notice that none of the other coefficients changed their values. Second: now the coefficient for income is .00067. Is income suddenly 1000 times less important because we now we are expressing it differently? No! This is the exact same relationship, but now “one unit” means something different.
Generalizing across all the variables, because these are all different things measured on different scales we can’t rely on certain coefficients being larger than others to indicate which is more important.
One good way to understand the relative impact of variables is to determine how a one standard-deviation shift in each of the variables affects the dependent variable. This allows a like-to-like comparison based on the amount each variable….varies.
m <- lm(score ~english + income + STR + lunch, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = score ~ english + income + STR + lunch, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -30.7085 -4.9977 -0.2014 4.8411 28.7000
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 675.60821 5.30886 127.261 < 2e-16 ***
#> english -0.19433 0.03138 -6.193 1.42e-09 ***
#> income 0.67498 0.08333 8.100 6.19e-15 ***
#> STR -0.56039 0.22861 -2.451 0.0146 *
#> lunch -0.39637 0.02741 -14.461 < 2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8.448 on 415 degrees of freedom
#> Multiple R-squared: 0.8053, Adjusted R-squared: 0.8034
#> F-statistic: 429.1 on 4 and 415 DF, p-value: < 2.2e-16For STR the standard deviation is:
sd(dat$STR)
#> [1] 1.891812The coefficient in the model -.56, which indicates a one-unit shift. To find a standard deviation shift:
-.56*1.89
#> [1] -1.0584Now if we want to find the affect of all of the variables:
#We can do this a bit more programatically to determine the effect of a one sd shift for each of our variables
vars <- c("english","income","STR","lunch")
#Get sd of each
sds <- rep(NA, length(vars))
for(i in 1:length(vars)){
sds[i] <- sd( dat[,vars[i]] )
}
#The coef() command will pull the coefficients from a regression
c <- coef(m)[vars]
#Standardized impacts:
summary(m)
#>
#> Call:
#> lm(formula = score ~ english + income + STR + lunch, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -30.7085 -4.9977 -0.2014 4.8411 28.7000
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 675.60821 5.30886 127.261 < 2e-16 ***
#> english -0.19433 0.03138 -6.193 1.42e-09 ***
#> income 0.67498 0.08333 8.100 6.19e-15 ***
#> STR -0.56039 0.22861 -2.451 0.0146 *
#> lunch -0.39637 0.02741 -14.461 < 2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8.448 on 415 degrees of freedom
#> Multiple R-squared: 0.8053, Adjusted R-squared: 0.8034
#> F-statistic: 429.1 on 4 and 415 DF, p-value: < 2.2e-16
c*sds
#> english income STR lunch
#> -3.553474 4.877360 -1.060150 -10.750785We see that using this technique, given the range of these variables, the percentage of the school who gets a subsidized lunch (which is frequently used a proxy for localized poverty) is actually the most impactful variable here, where a one standard deviation shift alters test scores by over 10 points.
A nice thing about this is that it is completely sensitive to the problem above where we re-scaled a variable because the standard deviation will also be re-scaled:
#Regression with income in real dollars
m <- lm(score ~english + income2 + STR + lunch, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = score ~ english + income2 + STR + lunch, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -30.7085 -4.9977 -0.2014 4.8411 28.7000
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 6.756e+02 5.309e+00 127.261 < 2e-16 ***
#> english -1.943e-01 3.138e-02 -6.193 1.42e-09 ***
#> income2 6.750e-04 8.333e-05 8.100 6.19e-15 ***
#> STR -5.604e-01 2.286e-01 -2.451 0.0146 *
#> lunch -3.964e-01 2.741e-02 -14.461 < 2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8.448 on 415 degrees of freedom
#> Multiple R-squared: 0.8053, Adjusted R-squared: 0.8034
#> F-statistic: 429.1 on 4 and 415 DF, p-value: < 2.2e-16
#We can do this a bit more programatically to determine the effect of a one sd shift for each of our variables
vars <- c("english","income2","STR","lunch")
#Get sd of each
sds <- rep(NA, length(vars))
for(i in 1:length(vars)){
sds[i] <- sd( dat[,vars[i]] )
}
#The coef() command will pull the coefficients from a regression
c <- coef(m)[vars]
#Standardized impacts:
summary(m)
#>
#> Call:
#> lm(formula = score ~ english + income2 + STR + lunch, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -30.7085 -4.9977 -0.2014 4.8411 28.7000
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 6.756e+02 5.309e+00 127.261 < 2e-16 ***
#> english -1.943e-01 3.138e-02 -6.193 1.42e-09 ***
#> income2 6.750e-04 8.333e-05 8.100 6.19e-15 ***
#> STR -5.604e-01 2.286e-01 -2.451 0.0146 *
#> lunch -3.964e-01 2.741e-02 -14.461 < 2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8.448 on 415 degrees of freedom
#> Multiple R-squared: 0.8053, Adjusted R-squared: 0.8034
#> F-statistic: 429.1 on 4 and 415 DF, p-value: < 2.2e-16
c*sds
#> english income2 STR lunch
#> -3.553474 4.877360 -1.060150 -10.750785Income has the exact same impact as it did when measured in thousands of dollars.
12.5 What variables to add?
It’s important to note here that this is just enough information to get yourself in trouble. Specifying a regression is hard, theoretical, work. There are some big pitfalls to be aware of.
Primarily: more variables isn’t necessarily better! Indeed, adding certain types of variables can actually make your estimates worse. Regression can be tricky, and I wouldn’t go out applying this to all sorts of things without learning more about the theory.
Here’s an example: Imagine had a dataset that had whether people smoked or not, whether they got pneumonia or not and whether they died.
You think: better be careful, let’s do:
lm(die ~ smoke + pneumonia)
But people who smoke die of pneumonia. The effects of smoking within those who get pneumonia is probably close to zero, or greatly reduced.
This is what we call “post-treatment bias”. With omitted variable bias we want to control for things that cause both our independent and dependent variable. For post-treatment bias we want to avoid controlling for anything that is caused by our independent variable and in turn causes the dependent variable.
Another example is looking at the effects of gender on wages controlling for length of parental leave. Gender is a cause of longer parental leave, and longer parental leave is a cause of lower wages. Looking within levels of parental leave we will find a smaller impact of gender on wages, but this is because we are controlling away (one of) the reasons why women get paid lower wages!
12.6 Regression with categorical variables.
Let’s load in data from the American Community Survey about various features of US counties:
rm(list=ls())
library(rio)
acs <- import("https://github.com/marctrussler/IIS-Data/raw/main/ACSCountyData.csv")I want to know how population density relates to transit ridership in the US. The variable population.density is the number of people per square mile in these counties and percent.transit.commute is exactly what it sounds like. At a baseline, what is the correlation between these things?
cor(acs$population.density, acs$percent.transit.commute, use="pairwise.complete")
#> [1] 0.8230231Very high!
Having population density is great, but what if instead of this very continuous measure we simply had a classification of whether a county was rural urban or suburban, split in this way:
acs$density[acs$population.density<50] <- 1
acs$density[acs$population.density>=50 & acs$population.density<1000] <- 2
acs$density[acs$population.density>=1000] <- 3
table(acs$density)
#>
#> 1 2 3
#> 1689 1304 149How can we find the effect of this three-category population density variable on the percent of people commuting by transit?
First, let’s take a look at this relationship:
plot(acs$density, acs$percent.transit.commute)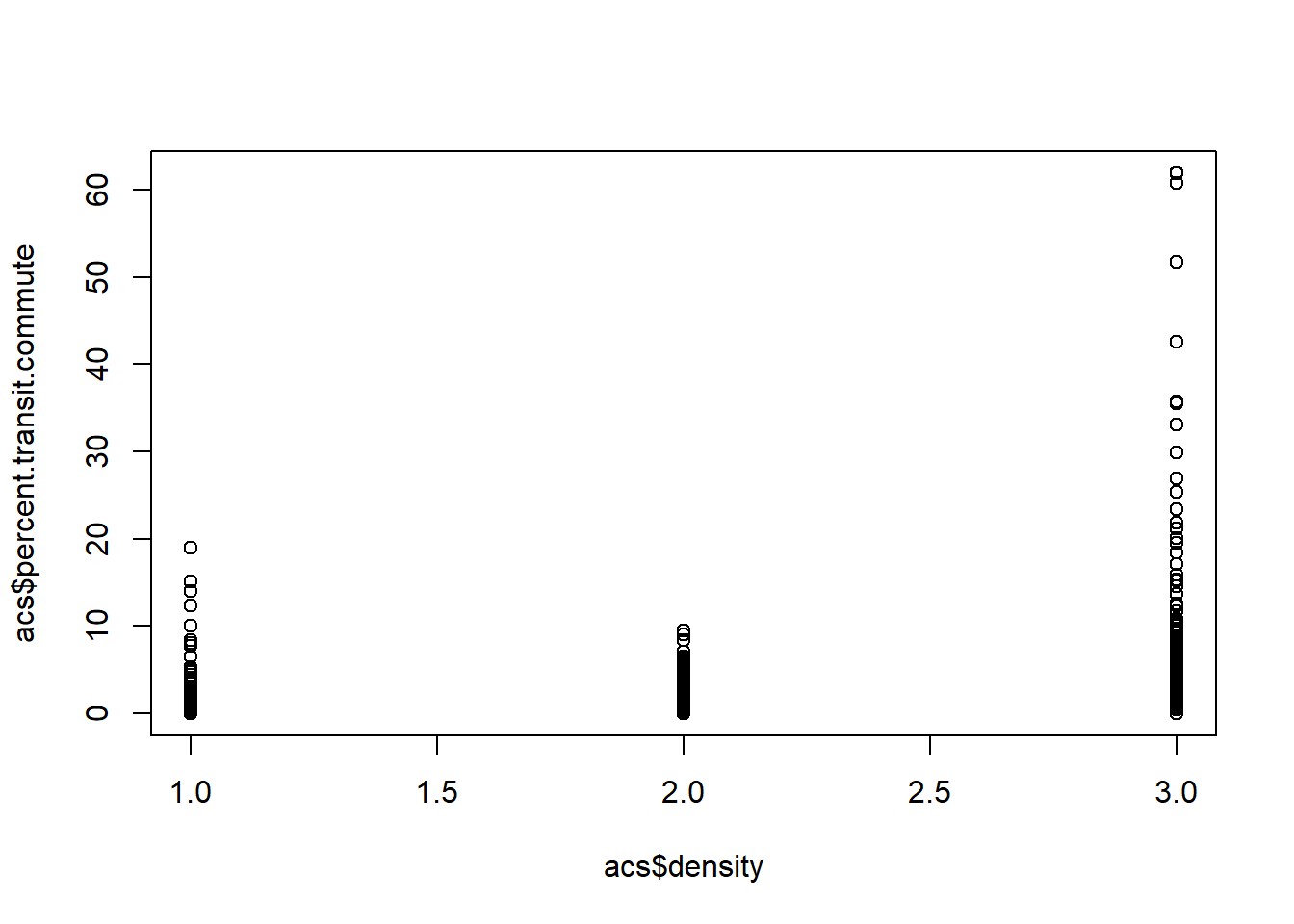
It’s pretty hard to determine what’s going on here, but it looks positive to me…
A slightly better way to visualize would be:
boxplot(acs$percent.transit.commute ~ acs$density)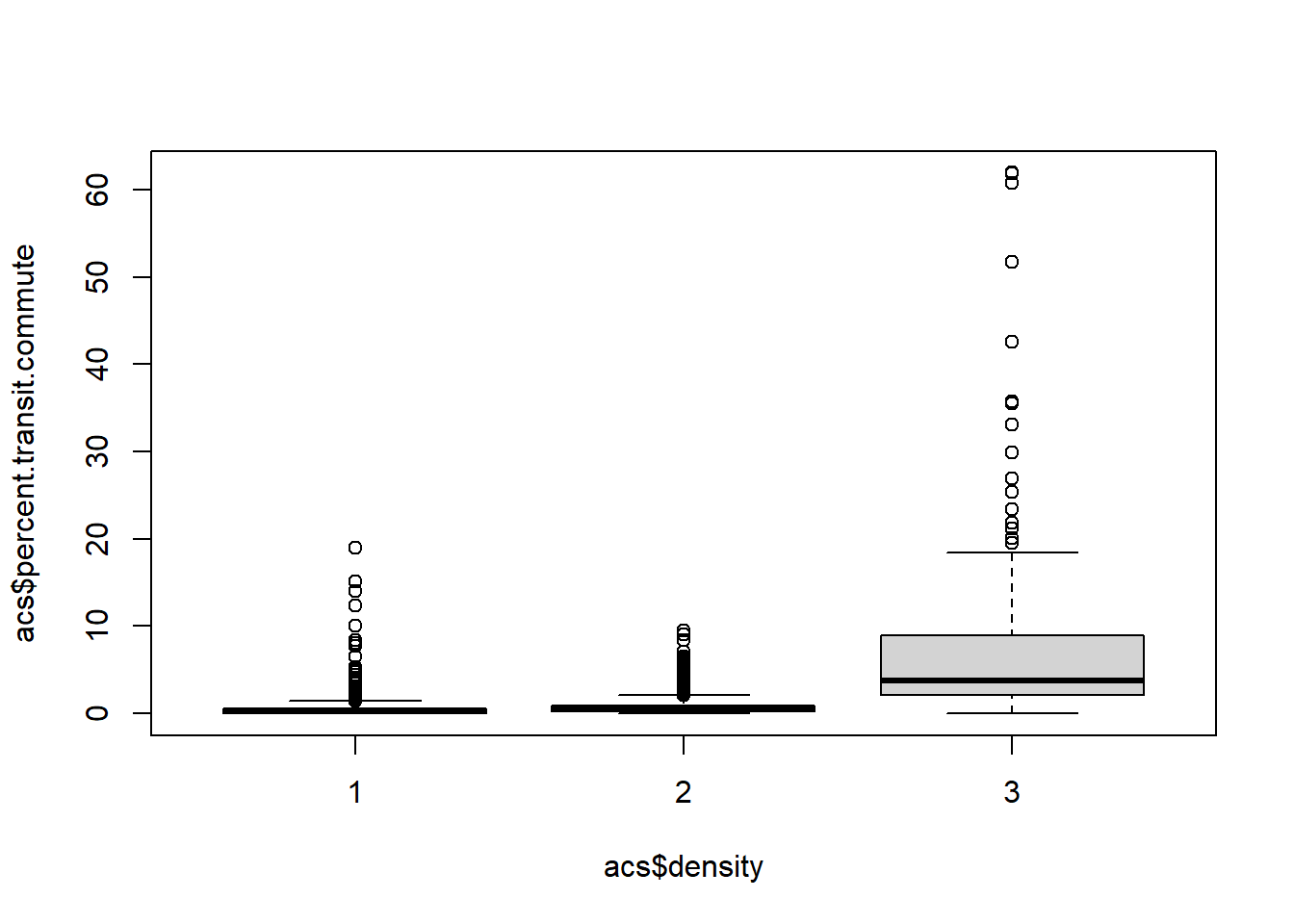
boxplot(acs$percent.transit.commute ~ acs$density, outline=F)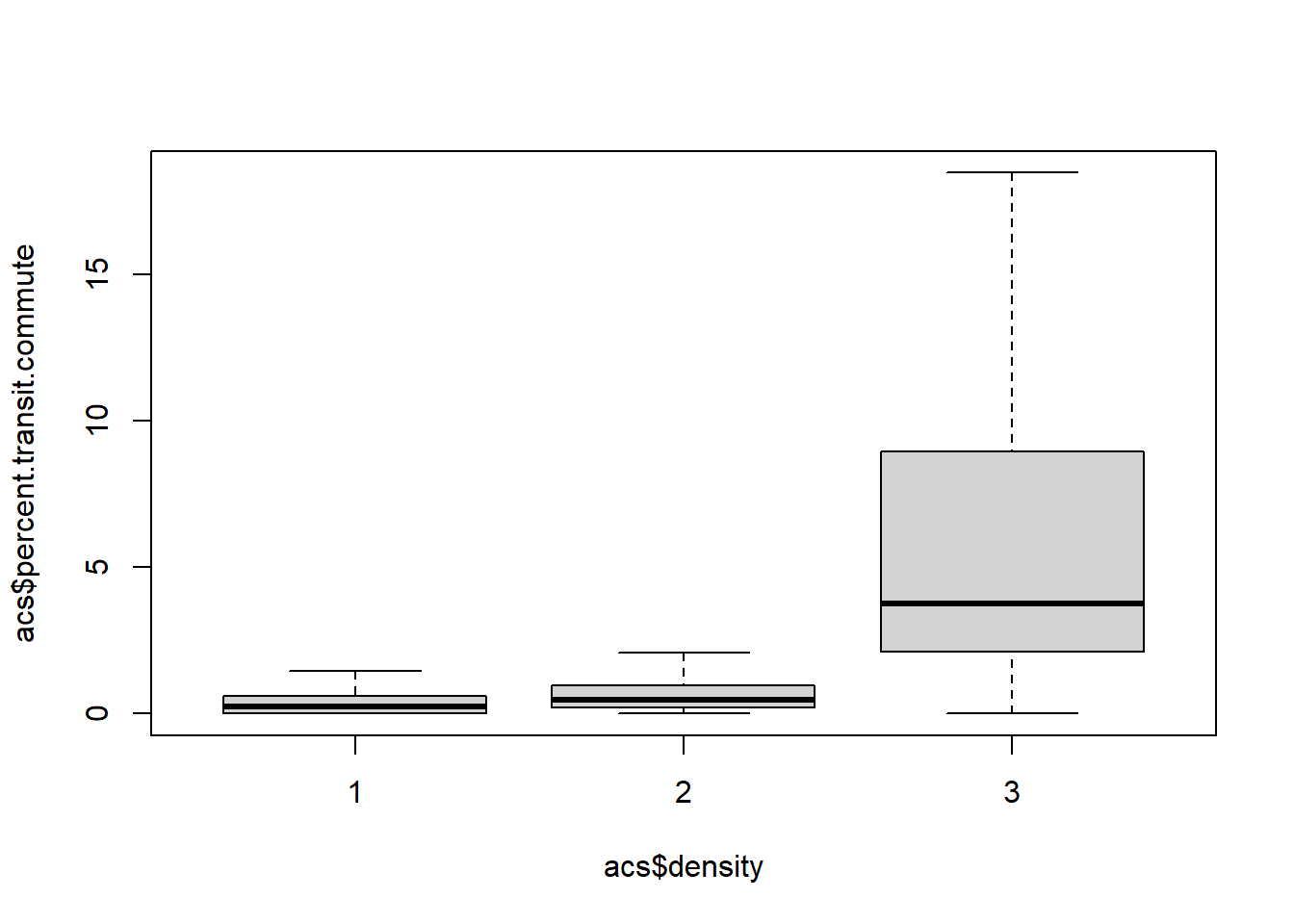
Can we summarize this with a regression?
Yes! Regression only needs numeric inputs, so this will totally work fine mechanically.
m <- lm(percent.transit.commute ~ density, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = percent.transit.commute ~ density, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.606 -1.296 -0.083 0.307 58.319
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -1.67845 0.14583 -11.51 <2e-16 ***
#> density 1.76132 0.09001 19.57 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.962 on 3139 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1087, Adjusted R-squared: 0.1084
#> F-statistic: 382.9 on 1 and 3139 DF, p-value: < 2.2e-16But we have to be careful about how we interpret this. The coefficient on density is 1.76. Every one unit increase in density leads to an additional 1.76 percentage point of the population commuting by transit. What is 1 unit for this variable? It is moving from rural to suburban, or from suburban to urban.
So what is the effect of moving from rural to urban? \(1.76+1.76=3.52\).
What does the intercept represent here? We know the intercept is the average value of percent.transit.commute when all variables are 0. What does that mean here? It’s gibberish! density can’t take on the value of 0 so this is not a helpful number.
Are we happy with this regression? Let’s look at the scatterplot:
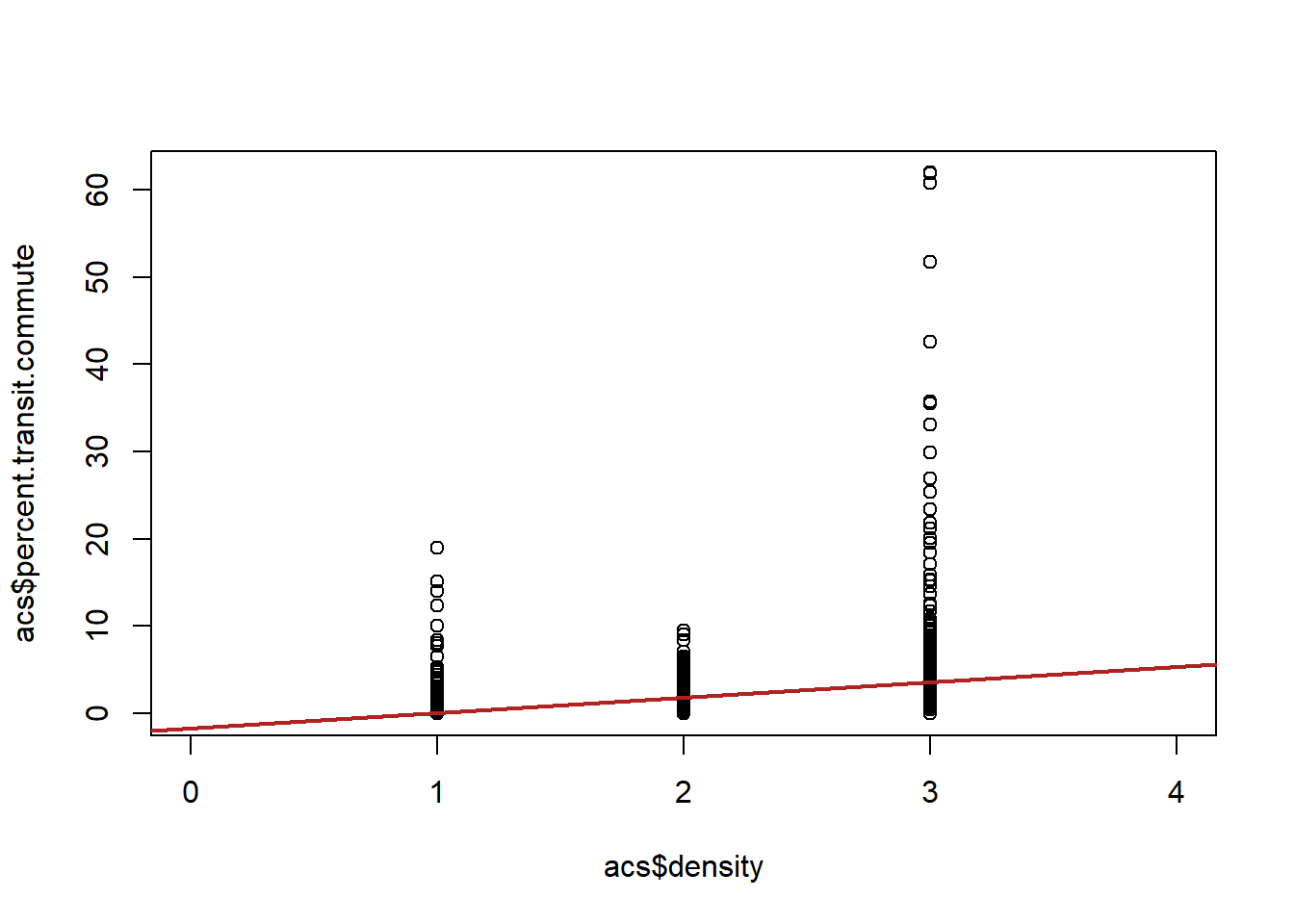
If we are willing to assume that the jumps from one level (rural to suburban, suburban to urban) are all equal then this regression is fine. We just treat the variable as-if it was a continuous variable. But in this doesn’t seem to be the case. Here the jump from suburban to urban matters a lot more and we are smoothing over it in a way that is problematic. We need a method that allows us to understand those two jumps are of different sizes.
Plus, applying this method (just convert a categorical variable to a continuous variable) breaks down when we have an un-ordered categorical variable, as we will see below.
So how can we better deal with this categorical independent variable?
The method that we use is to turn our categorical variable into a series of indicator variables and use those in a regression.
Let’s create indicators for rural, suburban, and urban:
acs$rural <- acs$density==1
acs$suburban <- acs$density==2
acs$urban <- acs$density==3
table(acs$rural, acs$density)
#>
#> 1 2 3
#> FALSE 0 1304 149
#> TRUE 1689 0 0
table(acs$suburban, acs$density)
#>
#> 1 2 3
#> FALSE 1689 0 149
#> TRUE 0 1304 0
table(acs$urban, acs$density)
#>
#> 1 2 3
#> FALSE 1689 1304 0
#> TRUE 0 0 149And now we want to include those indicator variables in our regression:
m <- lm(percent.transit.commute ~ rural + suburban + urban, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = percent.transit.commute ~ rural + suburban + urban,
#> data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -8.150 -0.484 -0.298 0.116 53.774
#>
#> Coefficients: (1 not defined because of singularities)
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 8.1501 0.2207 36.92 <2e-16 ***
#> ruralTRUE -7.6661 0.2303 -33.29 <2e-16 ***
#> suburbanTRUE -7.3445 0.2330 -31.52 <2e-16 ***
#> urbanTRUE NA NA NA NA
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.695 on 3138 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.2626, Adjusted R-squared: 0.2622
#> F-statistic: 558.9 on 2 and 3138 DF, p-value: < 2.2e-16Ok, so what happened here? We got two coefficients but we are getting an NA for urban….
To understand why, think about how we defined the intercept: it is the average value of y when all of the variables in the regression are equal to 0. What does it mean if rural, suburban, and urban are all 0? That can’t happen! A county has to be one of these things! So mechanically we cannot have all of these variables in the same regression.
To put these indicator variables in a regression we must leave out one of the categories:
m <- lm(percent.transit.commute ~ rural + suburban, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = percent.transit.commute ~ rural + suburban, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -8.150 -0.484 -0.298 0.116 53.774
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 8.1501 0.2207 36.92 <2e-16 ***
#> ruralTRUE -7.6661 0.2303 -33.29 <2e-16 ***
#> suburbanTRUE -7.3445 0.2330 -31.52 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.695 on 3138 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.2626, Adjusted R-squared: 0.2622
#> F-statistic: 558.9 on 2 and 3138 DF, p-value: < 2.2e-16Now it doesn’t actually matter which of the categories we leave out. To show that, let’s interpret what it is that we are seeing now.
Again: the intercept is the average value of y when all of the variables are equal to 0. If rural and suburban are equal to 0 what is the county? Urban! So this is just the average percent transit commute among urban counties. We can confirm with:
mean(acs$percent.transit.commute[acs$urban],na.rm=T)
#> [1] 8.150127What does the coefficient on rural mean? A coefficient always indicates how a 1 unit change in that variable affects the dependent variable. One “unit” for this variable is going from False to True, so this is the effect of going from an urban to a rural county. Rural counties have 7.6% fewer transit commuters than urban counties. Again, we can confirm with:
mean(acs$percent.transit.commute[acs$rural],na.rm=T) - mean(acs$percent.transit.commute[acs$urban],na.rm=T)
#> [1] -7.666099And by the same logic the coefficient on suburban tells us the difference in the average percent of commuting by transit between urban and suburban counties.
So using this method: dummying out the categorical variable and putting all but one indicator in the regression, returns to the differences in means in these categories.
Why is this helpful? Well first, we are going to have to do this if we want to work with a non-ordered variable like we will below. Second, this is often preferable to the “continuous” measure we used above because here we are being sensitive to the fact that the differences between the categories is not even. In other words, the jump from rural to suburban is much smaller than the jump from suburban to urban.
In the regression above we can see this by comparing the two coefficients. If the difference between urban and rural is -7.6 and the difference between urban and suburban is -7.3, then the difference between suburban and rural is clearly .3.
I said above it doesn’t matter which variable we leave out. This is true because the regression will just return the results relative to whatever our omitted category is. It does change the interpretation, however, and in this case it might make more sense to leave out suburban:
m <- lm(percent.transit.commute ~ rural + urban, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = percent.transit.commute ~ rural + urban, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -8.150 -0.484 -0.298 0.116 53.774
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.80563 0.07462 10.797 < 2e-16 ***
#> ruralTRUE -0.32160 0.09934 -3.237 0.00122 **
#> urbanTRUE 7.34450 0.23301 31.520 < 2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.695 on 3138 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.2626, Adjusted R-squared: 0.2622
#> F-statistic: 558.9 on 2 and 3138 DF, p-value: < 2.2e-16Which better reveals how similar suburban and rural counties are, and how different urban counties are from the other two categories.
Let’s consider another example.
Consider we want to run a regression where the dependent variable is median income and the independent variable is the percent of individuals commuting by public transit
m1 <- lm(median.income ~ percent.transit.commute, data=acs)
summary(m1)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -88643 -8532 -1280 6198 80684
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 50350.26 245.41 205.17
#> percent.transit.commute 1256.54 74.68 16.83
#> Pr(>|t|)
#> (Intercept) <2e-16 ***
#> percent.transit.commute <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 13130 on 3139 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.08273, Adjusted R-squared: 0.08244
#> F-statistic: 283.1 on 1 and 3139 DF, p-value: < 2.2e-16
plot(acs$percent.transit.commute, acs$median.income)
abline(lm(median.income ~ percent.transit.commute, data=acs), lwd=2, col="firebrick")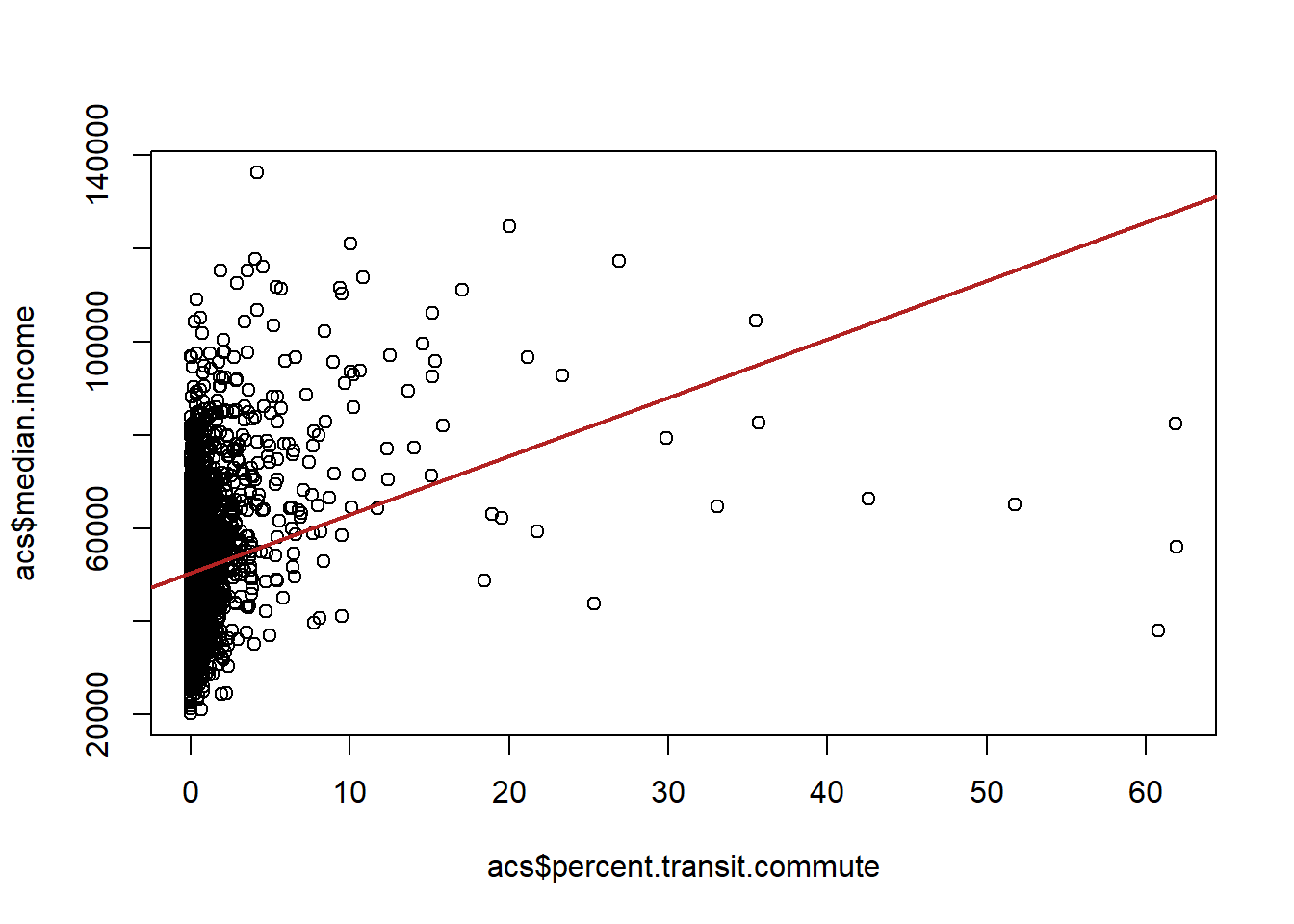
We find that there is a positive relationship, the higher percentage of a county that commutes by transit, the higher the median income of that county.
However, we might think that one reason that county may both have a higher percentage of transit commutes in it and have a higher median income is because of the region it is in. For example, places in the north-east have a well developed transit system and also are generally more well off. Alternatively, the south has poorly developed mass transit and also has several regions which have deep poverty. So it might not be that that transit commuting is related to wealth. Instead we’re just picking up the differences between regions.
So we’d like to “control” for region here. But region is not a numeric variable! It has no order. It would make no sense to do Northeast=1, South=2….
Again, we need to make indicator variables for each of these categories:
table(acs$census.region)
#>
#> midwest northeast south west
#> 1055 217 1422 448
acs$midwest[acs$census.region=="midwest"]<- 1
acs$midwest[acs$census.region!="midwest"]<- 0
acs$northeast[acs$census.region=="northeast"]<- 1
acs$northeast[acs$census.region!="northeast"]<- 0
acs$south[acs$census.region=="south"]<- 1
acs$south[acs$census.region!="south"]<- 0
acs$west[acs$census.region=="west"]<- 1
acs$west[acs$census.region!="west"]<- 0
#Check if this worked:
table(acs$census.region, acs$midwest)
#>
#> 0 1
#> midwest 0 1055
#> northeast 217 0
#> south 1422 0
#> west 448 0
table(acs$census.region, acs$northeast)
#>
#> 0 1
#> midwest 1055 0
#> northeast 0 217
#> south 1422 0
#> west 448 0
table(acs$census.region, acs$south)
#>
#> 0 1
#> midwest 1055 0
#> northeast 217 0
#> south 0 1422
#> west 448 0
table(acs$census.region, acs$west)
#>
#> 0 1
#> midwest 1055 0
#> northeast 217 0
#> south 1422 0
#> west 0 448Ok! Now we have 4 numeric indicator for which census region each county is in.
Let’s throw these into a regression, just forgetting about the transit variable for now:
m <- lm(median.income ~ midwest + northeast + south + west, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ midwest + northeast + south + west,
#> data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -31506 -8314 -2055 5236 88945
#>
#> Coefficients: (1 not defined because of singularities)
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 55590.7 614.4 90.481 < 2e-16 ***
#> midwest -2104.2 733.1 -2.870 0.00413 **
#> northeast 6403.3 1074.7 5.958 2.84e-09 ***
#> south -8268.1 704.4 -11.738 < 2e-16 ***
#> west NA NA NA NA
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12990 on 3137 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1023, Adjusted R-squared: 0.1015
#> F-statistic: 119.2 on 3 and 3137 DF, p-value: < 2.2e-16Again, we cannot include all of the categories, and have to choose one to be the “reference”.
So for example, we could omit the midwest:
m <- lm(median.income ~ northeast + south + west, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ northeast + south + west, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -31506 -8314 -2055 5236 88945
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 53486.5 399.9 133.743 < 2e-16 ***
#> northeast 8507.4 968.2 8.786 < 2e-16 ***
#> south -6163.9 527.8 -11.678 < 2e-16 ***
#> west 2104.2 733.1 2.870 0.00413 **
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12990 on 3137 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1023, Adjusted R-squared: 0.1015
#> F-statistic: 119.2 on 3 and 3137 DF, p-value: < 2.2e-16Let’s think through what these numbers mean now. The intercept is the average income when all the other variables are equal to zero. What are we talking about when northeast, south, and west, are equal to zero? The midwest! The intercept here is the average median income of counties in the midwest.
mean(acs$median.income[acs$census.region=="midwest"])
#> [1] 53486.52What do each of these coefficients represent? They represent the the change in the average median income in each of these regions, compared to the midwest, so the average median income in the northeast is:
coef(m)["(Intercept)"] + coef(m)["northeast"]
#> (Intercept)
#> 61993.96
mean(acs$median.income[acs$census.region=="northeast"])
#> [1] 61993.96Again, you get the same “answer” when you omit a different category, but the numbers will change:
m <- lm(median.income ~ midwest + south + west, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ midwest + south + west, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -31506 -8314 -2055 5236 88945
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 61994.0 881.8 70.304 < 2e-16 ***
#> midwest -8507.4 968.2 -8.786 < 2e-16 ***
#> south -14671.4 946.7 -15.497 < 2e-16 ***
#> west -6403.3 1074.7 -5.958 2.84e-09 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12990 on 3137 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1023, Adjusted R-squared: 0.1015
#> F-statistic: 119.2 on 3 and 3137 DF, p-value: < 2.2e-16Now our intercept is the average median income in the northeast, which is the same as we saw above and the coefficient for midwest is just the inverse from what we had above.
So let’s use this knowledge to control for region when estimating the effect of transit ridership on household income
m1 <- lm(median.income ~ percent.transit.commute, data=acs)
summary(m1)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -88643 -8532 -1280 6198 80684
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 50350.26 245.41 205.17
#> percent.transit.commute 1256.54 74.68 16.83
#> Pr(>|t|)
#> (Intercept) <2e-16 ***
#> percent.transit.commute <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 13130 on 3139 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.08273, Adjusted R-squared: 0.08244
#> F-statistic: 283.1 on 1 and 3139 DF, p-value: < 2.2e-16
m2 <- lm(median.income ~ percent.transit.commute + northeast + south + west, data=acs)
summary(m2)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute + northeast +
#> south + west, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -83579 -7773 -1899 5279 85257
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 52845.43 390.56 135.308
#> percent.transit.commute 1050.00 74.53 14.089
#> northeast 4995.19 971.66 5.141
#> south -6208.27 511.96 -12.126
#> west 1215.72 713.84 1.703
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> percent.transit.commute < 2e-16 ***
#> northeast 2.9e-07 ***
#> south < 2e-16 ***
#> west 0.0887 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12600 on 3136 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1558, Adjusted R-squared: 0.1547
#> F-statistic: 144.6 on 4 and 3136 DF, p-value: < 2.2e-16Indeed, controlling for region did slightly attenuate (make smaller) the effect of transit commuting. The intercept now is the average median income in the midwest for a county with 0 transit ridership (which may not exist) The coefficients on each of the region dummies is the change in the average level of median income in each of these regions relative to the midwest, controlling for transit ridership.
There is a slightly easier (but less intuitive) way to do this same thing, by treating census.region as a factor variable
acs$census.region <- as.factor(acs$census.region)When something is a factor variable and we put it in a regression, R will automatically do the work to turn it into dummies:
m <- lm(median.income ~ percent.transit.commute + census.region, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute + census.region,
#> data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -83579 -7773 -1899 5279 85257
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 52845.43 390.56 135.308
#> percent.transit.commute 1050.00 74.53 14.089
#> census.regionnortheast 4995.19 971.66 5.141
#> census.regionsouth -6208.27 511.96 -12.126
#> census.regionwest 1215.72 713.84 1.703
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> percent.transit.commute < 2e-16 ***
#> census.regionnortheast 2.9e-07 ***
#> census.regionsouth < 2e-16 ***
#> census.regionwest 0.0887 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12600 on 3136 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1558, Adjusted R-squared: 0.1547
#> F-statistic: 144.6 on 4 and 3136 DF, p-value: < 2.2e-16R will automatically choose the reference category for you in this case. We can use the relevel() command to force R to consider one of the categories to be the reference
acs$census.region <- relevel(acs$census.region, ref="northeast")
m <- lm(median.income ~ percent.transit.commute + census.region, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute + census.region,
#> data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -83579 -7773 -1899 5279 85257
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 57840.62 904.67 63.936
#> percent.transit.commute 1050.00 74.53 14.089
#> census.regionmidwest -4995.19 971.66 -5.141
#> census.regionsouth -11203.47 950.65 -11.785
#> census.regionwest -3779.47 1058.92 -3.569
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> percent.transit.commute < 2e-16 ***
#> census.regionmidwest 2.9e-07 ***
#> census.regionsouth < 2e-16 ***
#> census.regionwest 0.000363 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12600 on 3136 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1558, Adjusted R-squared: 0.1547
#> F-statistic: 144.6 on 4 and 3136 DF, p-value: < 2.2e-1612.7 Presenting regression results
Generate some regressions:
m1 <- lm(median.income ~ percent.transit.commute, data=acs)
summary(m1)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -88643 -8532 -1280 6198 80684
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 50350.26 245.41 205.17
#> percent.transit.commute 1256.54 74.68 16.83
#> Pr(>|t|)
#> (Intercept) <2e-16 ***
#> percent.transit.commute <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 13130 on 3139 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.08273, Adjusted R-squared: 0.08244
#> F-statistic: 283.1 on 1 and 3139 DF, p-value: < 2.2e-16
m2 <- lm(median.income ~ percent.transit.commute + northeast + south + west, data=acs)
summary(m2)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute + northeast +
#> south + west, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -83579 -7773 -1899 5279 85257
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 52845.43 390.56 135.308
#> percent.transit.commute 1050.00 74.53 14.089
#> northeast 4995.19 971.66 5.141
#> south -6208.27 511.96 -12.126
#> west 1215.72 713.84 1.703
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> percent.transit.commute < 2e-16 ***
#> northeast 2.9e-07 ***
#> south < 2e-16 ***
#> west 0.0887 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12600 on 3136 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1558, Adjusted R-squared: 0.1547
#> F-statistic: 144.6 on 4 and 3136 DF, p-value: < 2.2e-16If you want to run a regression and output the results in a way that looks nice, you have a couple of options. If you want to visualize, one option is to use a coefplot
#install.packages("coefplot")
library(coefplot)
#> Warning: package 'coefplot' was built under R version 4.1.3
#> Loading required package: ggplot2
coefplot(m2)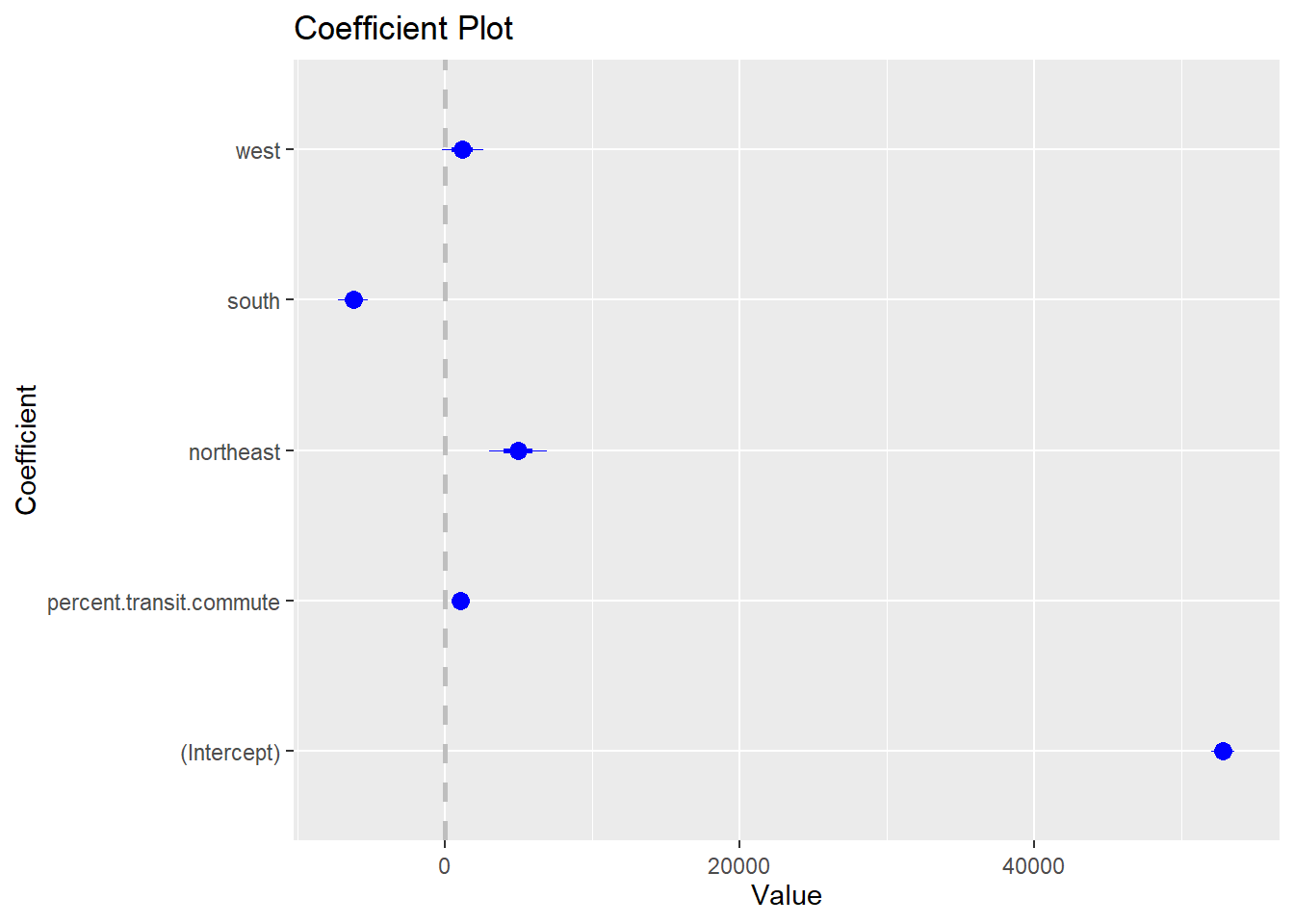
This isn’t particularly nice, and you can do this nicer in ggplot. I’ll leave you to google how to do that.
(Honestly, when I make coefficient plots I do them “by hand” extracting coefficients and confidence intervals and plotting just using the grid system):
Generating tables can be done using the “stargazer” package. One nice thing about this is that you can output multiple models with the same DV together:
library(stargazer)
#>
#> Please cite as:
#> Hlavac, Marek (2018). stargazer: Well-Formatted Regression and Summary Statistics Tables.
#> R package version 5.2.2. https://CRAN.R-project.org/package=stargazer
#The "text" type will output into R in a nice looking format:
stargazer(m1, m2, type="text")
#>
#> ===========================================================================
#> Dependent variable:
#> ---------------------------------------------------
#> median.income
#> (1) (2)
#> ---------------------------------------------------------------------------
#> percent.transit.commute 1,256.536*** 1,049.999***
#> (74.676) (74.528)
#>
#> northeast 4,995.192***
#> (971.664)
#>
#> south -6,208.274***
#> (511.962)
#>
#> west 1,215.719*
#> (713.836)
#>
#> Constant 50,350.260*** 52,845.430***
#> (245.409) (390.557)
#>
#> ---------------------------------------------------------------------------
#> Observations 3,141 3,141
#> R2 0.083 0.156
#> Adjusted R2 0.082 0.155
#> Residual Std. Error 13,126.480 (df = 3139) 12,599.180 (df = 3136)
#> F Statistic 283.129*** (df = 1; 3139) 144.642*** (df = 4; 3136)
#> ===========================================================================
#> Note: *p<0.1; **p<0.05; ***p<0.01To output into an html rmarkdown just omit the out and add results='asis' to your code chunk options
stargazer(m1, m2, type="html", style="apsr",
dep.var.labels = "Median Income",
covariate.labels = c("% Transit Commuters",
"Region: NorthEast",
"Region: South",
"Region: West"))| Median Income | ||
| (1) | (2) | |
| % Transit Commuters | 1,256.536*** | 1,049.999*** |
| (74.676) | (74.528) | |
| Region: NorthEast | 4,995.192*** | |
| (971.664) | ||
| Region: South | -6,208.274*** | |
| (511.962) | ||
| Region: West | 1,215.719* | |
| (713.836) | ||
| Constant | 50,350.260*** | 52,845.430*** |
| (245.409) | (390.557) | |
| N | 3,141 | 3,141 |
| R2 | 0.083 | 0.156 |
| Adjusted R2 | 0.082 | 0.155 |
| Residual Std. Error | 13,126.480 (df = 3139) | 12,599.180 (df = 3136) |
| F Statistic | 283.129*** (df = 1; 3139) | 144.642*** (df = 4; 3136) |
| p < .1; p < .05; p < .01 | ||
Can get wild with this.. https://www.jakeruss.com/cheatsheets/stargazer/