5.1 Charge Coupled Devices

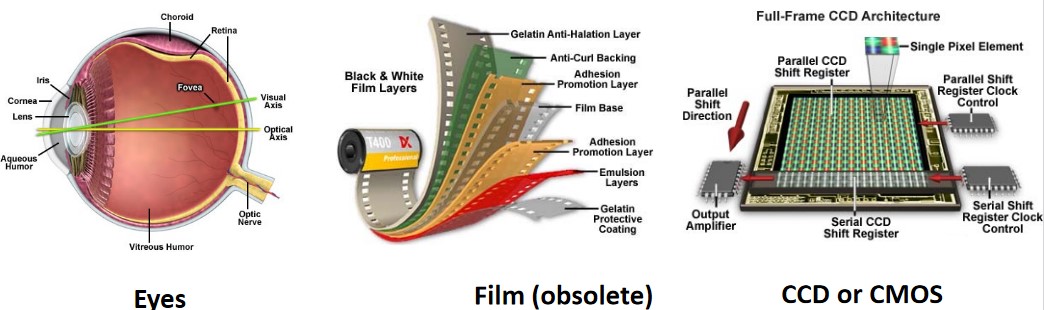
Figure 5.1: Detectors in Wide-Field Microscopy

In epi-fluorescence microscopy, a charge coupled device (i.e., CCD) or a complementary metal oxide semiconductor (i.e., CMOS) is generally used as a detector. Film is no longer used as a CCD or a CMOS has the following advantages:

1. They have high sensitivity (i.e., a single photon is all that is needed for detection).
2. They have a wide spectrum and a linear response.
3. They produce instant results
4. They can produce images in digital formats.

High performance CMOS-es or CCDs are often monochromatic or black and white.

5.1.1 How do CCDs Work?

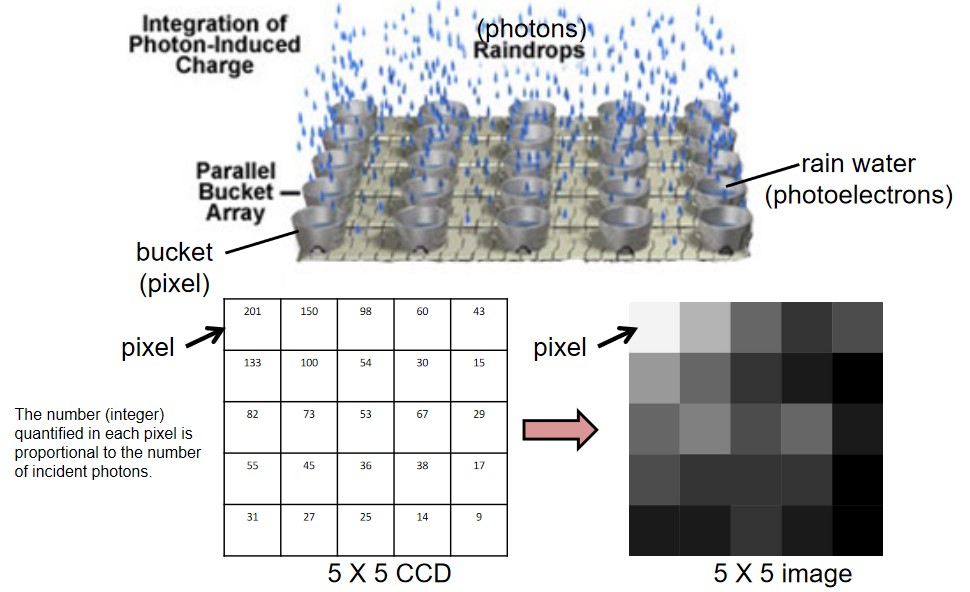
Figure 5.2: Workings of a CCD

The CCD is a semiconductor device that converts images into digital signals.

On a CCD, there are many small “wells” that have been designed to capture photons. The amount of photons entering each “well” is then quantified based on the number of incident photons detected by the well.

This - in turn - generates an image.

5.1.2 CCD Parameters

BS2010 covers three main parameters:

1. Quantum Efficiency (i.e., QE)

   Recall that:

   \[\begin{equation} QE = \frac{\text{Number of photoelectrons}}{\text{Number of photons}} \end{equation}\]

2. Full Well Capacity

   This is the number of photoelectrons that can be stored in each sensor.

3. Dynamic Range

   This is a dimensionless number that is calculated by the following equation:

   \[\begin{equation} \text{Dynamic Range} = \frac{\text{Full Well Capacity (electrons)}}{\text{Read Noise (electrons)}} \end{equation}\]

   The dynamic range represents the possible values that a pixel can take on; it also measures the ability of a device to capture high and low signal levels in one image.

   Some common dynamic CCD ranges include 8-bit, 12-bit, and 16-bit.

5.1.3 Noises in CCD Images

Figure 5.3: Noise in a Sample Image

Noise refers to unwanted specifications during image acquisition. Noise can come in one of several types:

1. Photon (i.e., shot) noise

   This is due to variation of phtoons in the CCD - it is a natural limit of noise and is independent of the CCD used.

   The number of photons generated per pixel follows a Poisson distribution. Hence, if the mean amount of photons per pixel is \(n\), then the standard deviation per photon distribution is \(\sqrt{n}\). The theoretical signal-to-noise (the noise is the standard deviation) ratio should then be: \(\displaystyle \frac{n}{\sqrt{n}} = \sqrt{n}\).

2. Dark noise

   This is usually reduced via cooling and is typically quite small.

3. Signal-to-Noise Ratio (i.e., SNR)

   This is a dimensionless number. This is caused by the amount of electrons in the electric circuit.

4. Read Noise

   This depends on the design of the CCD camera. This is also the main difference between CCD cameras.