2.4 Concepts on Light

2.4.1 Wave-Particle Duality of Light

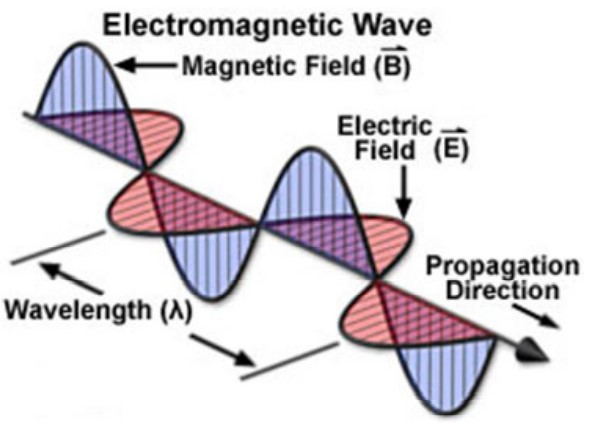
Transverse Waves Travelling Perpendicularly to One Another

Figure 2.13: Transverse Waves Travelling Perpendicularly to One Another

Light is an electromagnetic wave (a kind of transverse wave - see above graphic) that travels at \(3 \times 10^8 \text{ m/s}\) (i.e., the speed of light). Given a wavelength \(\lambda\) and a frequency \(\nu\), we say that:

\[\begin{equation} c = \lambda \cdot \nu \tag{2.1} \end{equation}\]

Given equation (2.1) and that \(\displaystyle E = h\nu\) (where \(E\) is the energy of the wave in question), we can re-arrange equation (2.1) to yield:

\[\begin{align} E &= h \cdot \frac{c}{\nu} \\ &= \boxed{\frac{hc}{\nu}} \tag{2.2} \end{align}\]

Where \(h\) is Planck’s constant (i.e., \(6.626 \times 10^{-34} \text{ J / s}\)). Equation (2.2) implies that light is a particle.

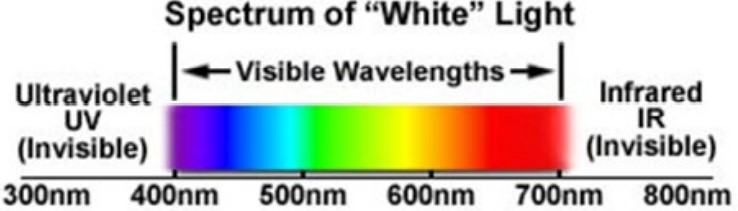
Spectrum of Visible Light

Figure 2.14: Spectrum of Visible Light

While light can be appear at any wavelength, the wave length of visible light lies between (inclusive on both ends) 400 nm to 700 nm.

2.4.2 Possible Light Sources in Microscopy

BS2010 touches upon two possible sources:

  1. Tungsten or Flourescent Light

    Spectrum of Tungsten and Flourescent Light

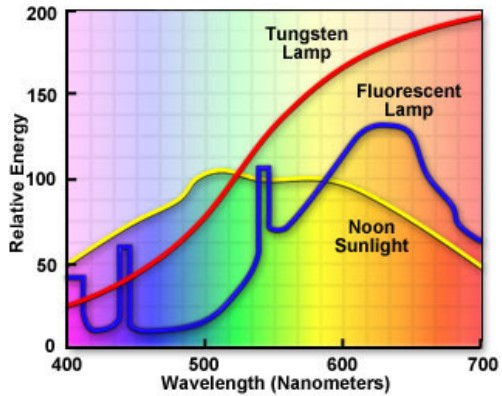
    Figure 2.15: Spectrum of Tungsten and Flourescent Light

    Note that the spectrum produced by these lights are continuous (i.e., they can take on any reading). A spectrum is a graph depicting the range of values that a light source’s readings can take on.

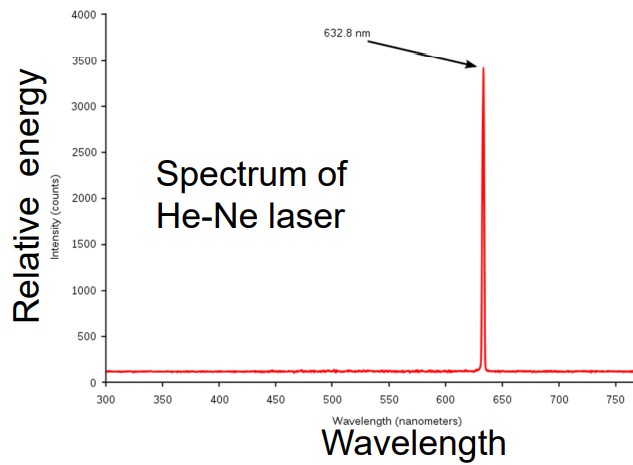
    Spectrum of a He-Ne Laser

    Figure 2.16: Spectrum of a He-Ne Laser

    The spectrum made by a laser is discrete (i.e., it can only take on certain readings). The peak is very narrow because the laser is monochromatic (i.e., it comes in a single color).

2.4.3 Refractive Indices

The refractive index is a number assigned to a material based on its ability to diffract light.

\[\begin{equation} c = \frac{n}{v} \tag{2.3} \end{equation}\]

Equation (2.3) is the equation for the refractive index, where:

  1. \(n\) is the refractive index.
  2. \(c\) is the speed of light in a vacuum
  3. \(v\) is the speed of light in a material

The law of diffraction for two mediums is:

\[\begin{equation} n_1\sin(\theta_1) = n_2\sin(\theta_2) \end{equation}\]

Material Refractive.Index
Air 1.00
Water 1.33
Glycerol 1.47
Immersion Oil 1.52
Glass 1.52

The above table also lists the refractive index of several different types of media. There is also no need to remember the above table.